北航理论力学第五章习题解答
理论力学课后答案第五章(周衍柏)上课讲义

理论力学课后答案第五章(周衍柏)第五章思考题5.1虚功原理中的“虚功”二字作何解释?用虚功原理理解平衡问题,有何优点和缺点?5.2 为什么在拉格朗日方程中,a θ不包含约束反作用力?又广义坐标与广义力的含义如何?我们根据什么关系由一个量的量纲定出另一个量的量纲?5.3广义动量a p 和广义速度a q 是不是只相差一个乘数m ?为什么a p 比a q 更富有意义?5.4既然a q T ∂∂是广义动量,那么根据动量定理,⎪⎪⎭⎫ ⎝⎛∂∂αq T dt d 是否应等于广义力a θ?为什么在拉格朗日方程()14.3.5式中多出了aq T ∂∂项?你能说出它的物理意义和所代表的物理量吗?5.5为什么在拉格朗日方程只适用于完整系?如为不完整系,能否由式()13.3.5得出式()14.3.5?5.6平衡位置附近的小振动的性质,由什么来决定?为什么22s 个常数只有2s 个是独立的?5.7什么叫简正坐标?怎样去找?它的数目和力学体系的自由度之间有何关系又每一简正坐标将作怎样的运动?5.8多自由度力学体系如果还有阻尼力,那么它们在平衡位置附近的运动和无阻尼时有何不同?能否列出它们的微分方程?5.9 dL 和L d 有何区别?a q L ∂∂和aq L ∂∂有何区别? 5.10哈密顿正则方程能适用于不完整系吗?为什么?能适用于非保守系吗?为什么?5.11哈密顿函数在什么情况下是整数?在什么情况下是总能量?试祥加讨论,有无是总能量而不为常数的情况?5.12何谓泊松括号与泊松定理?泊松定理在实际上的功用如何?5.13哈密顿原理是用什么方法运动规律的?为什么变分符号δ可置于积分号内也可移到积分号外?又全变分符号∆能否这样?5.14正则变换的目的及功用何在?又正则变换的关键何在?5.15哈密顿-雅可比理论的目的何在?试简述次理论解题时所应用的步骤.5.16正则方程()15.5.5与()10.10.5及()11.10.5之间关系如何?我们能否用一正则变换由前者得出后者?5.17在研究机械运动的力学中,刘维定理能否发挥作用?何故?5.18分析力学学完后,请把本章中的方程和原理与牛顿运动定律相比较,并加以评价.第五章思考题解答5.1 答:作.用于质点上的力在任意虚位移中做的功即为虚功,而虚位移是假想的、符合约束的、无限小的.即时位置变更,故虚功也是假想的、符合约束的、无限小的.且与过程无关的功,它与真实的功完全是两回事.从∑⋅=iii r F W δδ可知:虚功与选用的坐标系无关,这正是虚功与过程无关的反映;虚功对各虚位移中的功是线性迭加,虚功对应于虚位移的一次变分.在虚功的计算中应注意:在任意虚过程中假定隔离保持不变,这是虚位移无限小性的结果.虚功原理给出受约束质点系的平衡条件,比静力学给出的刚体平衡条件有更普遍的意义;再者,考虑到非惯性系中惯性力的虚功,利用虚功原理还可解决动力学问题,这是刚体力学的平衡条件无法比拟的;另外,利用虚功原理解理想约束下的质点系的平衡问题时,由于约束反力自动消去,可简便地球的平衡条件;最后又有广义坐标和广义力的引入得到广义虚位移原理,使之在非纯力学体系也能应用,增加了其普适性及使用过程中的灵活性.由于虚功方程中不含约束反力.故不能求出约束反力,这是虚功原理的缺点.但利用虚功原理并不是不能求出约束反力,一般如下两种方法:当刚体受到的主动力为已知时,解除某约束或某一方向的约束代之以约束反力;再者,利用拉格朗日方程未定乘数法,景观比较麻烦,但能同时求出平衡条件和约束反力.5.2 答 因拉格朗日方程是从虚功原理推出的,而徐公原理只适用于具有理想约束的力学体系虚功方程中不含约束反力,故拉格朗日方程也只适用于具有理想约束下的力学体系,αθ不含约束力;再者拉格朗日方程是从力学体系动能改变的观点讨论体系的运动,而约束反作用力不能改变体系的动能,故αθ不含约束反作用力,最后,几何约束下的力学体系其广义坐标数等于体系的自由度数,而几何约束限制力学体系的自由运动,使其自由度减小,这表明约束反作用力不对应有独立的广义坐标,故αθ不含约束反作用力.这里讨论的是完整系的拉格朗日方程,对受有几何约束的力学体系既非完整系,则必须借助拉格朗日未定乘数法对拉格朗日方程进行修正.广义坐标市确定质点或质点系完整的独立坐标,它不一定是长度,可以是角度或其他物理量,如面积、体积、电极化强度、磁化强度等.显然广义坐标不一定是长度的量纲.在完整约束下,广义坐标数等于力学体系的自由度数;广义力明威力实际上不一定有力的量纲可以是力也可以是力矩或其他物理量,如压强、场强等等,广义力还可以理解为;若让广义力对应的广义坐标作单位值的改变,且其余广义坐标不变,则广义力的数值等于外力的功由W q r F s i ni i δδθδααα==⋅∑∑==11 知,ααδθq 有功的量纲,据此关系已知其中一个量的量纲则可得到另一个量的量纲.若αq 是长度,则αθ一定是力,若αθ是力矩,则αq 一定是角度,若αq 是体积,则αθ一定是压强等.5.3 答 αp 与αq 不一定只相差一个常数m ,这要由问题的性质、坐标系的选取形式及广义坐标的选用而定。
北航理论力学 动力学5C

x
qT [x, ] qT [x,]
T 1 qT Mq
M mm21Lcoms2
m2
4 3
L cos
m2 L2
2
M是正定对称矩阵,是广义坐标的函数 14
§5-4、哈密顿方程
T 1 qT Mq 2
pj
T q j
,
( j 1,2)
p
T q
p Mq
系统的哈密顿函数H=T+V
H
T
V
1 2
对于定常约束的保守系统,哈密顿函数H就是系统的动能与
势能的和,即:
H T V
12
§5-4、哈密顿方程
例题:求自由质点在重力场中的哈密顿函数和哈密顿方程
z
1、系统的广义坐标:x, y, z
2、系统的动能 T 1 m(x2 y 2 z2 )
mg
y
2
pj
T q j
,
( j 1,2,3)
px mx py my pz mz
21
哈密顿系统的辛算法
20世纪80 年代,提出了 哈密顿系统的 辛算法。该算 法可保持长期 数值计算的稳 定性。
冯 康(1920.9~1993.8) 数学与物理学家、计 算数学家。1944年毕业于重庆中央大学物理 系。1951~1953年赴前苏联进修。
曾任中国数学会理事,计算数学分会副 理事长,中国计算机学会副主任等职。 1980 年被选为中国科学院学部委员(数学物理学部 院士)。
v1 ? v2 ? ?
10
§5-4、哈密顿方程
一、保守系统的拉格朗日方程 设:L=T-V (拉格朗日函数)
d dt
L q j
L q j
0,
( j 1,2,, k)
《理论力学》武清玺第五章_点的运动_习题全解

第五章 点的运动 习题全解[习题5-1] 一点按2123+-=t t x 的规律沿直线动动(其中t 要s 计,x 以m 计).试求:(1)最初s 3内的位移;(2)改变动动方向的时刻和所在位置;(3)最初s 3内经过的路程;(4)s t 3=时的速度和加速度;(5)点在哪段时间作加速度,哪段时间作减速运动. 解:(1)求最初s 3内的位移.m x 220120)0(3=+⨯-= m x 723123)3(3-=+⨯-=)(927)0()3(m x x x -=--=-=∆ (动点的位移为9m,位移的方向为负x 方向). (2)求改变动动方向的时刻和所在位置. 改变方向时,动点的速度为零.即: 01232=-==t dtdxv , 亦即:当s t 2=时,动点改变运动方向.此时动点所在的位置为: )(1422122)2(3m x -=+⨯-= (3)求最初s 3内经过的路程.)(23716|)14(7||214|)3~2()2~0()3~0(m S S S =+=---+--=+= (4)求s t 3=时的速度和加速度1232-==t dt dx v )/(151233)3(2s m dt dx v =-⨯== t dtdv a 6== )/(1836)3(2s m a =⨯=(5)求动点在哪段时间作加速度,哪段时间作减速运动.若v 与a 同号,则动点作加速运动; 若v 与a 异号,则动点作减速运动.即: 同号时有:0)2)(2(18)4(18)6)(123(22>+-=-=-=t t t t t t t va0)2)(2(>+-t t t20<<t .即当s t 20<<时,动点作加速动动.Oxy图题25-异号时有:0)2)(2(<+-t t t2>t即当s t 2>时,动点作减速运动.[习题5-2] 已知图示机构中,l AB OA ==,a AC DM CM ===,求出t ωϕ=时,点M 的动动方程和轨迹方程。
理论力学第5章(1)答案.doc

V M = ^M=2®R1.以。
为原点建立直角坐标系, 5点的运动学二,1. 选D 点为动点,已建立直角坐标系(即用直角坐标法求解)。
2. 建立直角坐标系下的运动方程x D = 200 cos ( 0.2 加)y D = 100sz«( 0.2 加)3. 由运动方程消除r 得轨迹方程= cos ( 0.2 加) 200丄丄=sbt (0.2加)100 轨迹方程:(如尸+心勺2“200 100易错处:1.不要写成自然法的运动方程,2.轨迹方程写成标准椭圆方程 三,该题要求分别用直角坐标法及自然法求解。
-)直角坐标法2. 运动方程: X M = R cos( l(Dt) y M =Rsin(2at)3. 求直角坐标下的速度及加速度 v Mx= x M = -2a )R sin( lot) v My =y M = 2a )Rcos( 2(Ot) V M = yl v M X + v My = 2®R(> o 丿 a Mx = v Mx = -4a )1 Rcos( 2(ot) a My = v My = -4(D 2R sin( lot)= &二+嗚=4(O 2R(> 0丿二)自然法1. 建立弧坐标,以水平轴与圆弧交点处为原点逆时针为正,2. 运动方程:s M = R (2(ot )3. 求自然轴系下的速度及加速度= = V M = 0v 2 < = = ^L = 4O )2R Ra M =打爲尸+(钮2 = 4仇(> o )自然法中,速度及加速度只需求其投影,不必求矢量。
*无论速度及全加速度,两种方法的结论应当是相同的。
*两种方法应当严格分开,不能在一种方法中又混入另一种方法。
这些作业都是点的运动问题中的第一类问题,即共同的方法都是:1. 建立指定的坐标系2. 写指定坐标系下的运动方程3. 对运动方程求导得速度、加速度。
四、宜用直角坐标法1. BC 作平动,选导杆上01点为动点, 以O 为原点建立直角坐标系,2. 运动方程:x O/ = 2Rcos (p = 0.20 cos 4t (m)3. 求速度及加速度v 0( = x = -0.80 sin 4t m/sa o = x = -3.20cos4t m/s 2(p= 30° 时:v BC = -0.4(m/s)a BC - -2.77(m/s 2)(1.选OA 杆上的A 点为动点2. 动系放置于BC 上3. 绝对运动:点的圆周运动 相对运动:点的圆周运动 牵连运动:刚体的平动)五、1. oc作定轴转动,其运动方程:vt(P - arctan—2.求角速度及角加速度= 0 =「cos (pa = d)= ~—g)sin2(p(p=45 °时:a)=(1.选AB杆上的A点为动点2.动系放置于OC上3.绝对运动:点的直线运动相对运动:点的直线运动牵连运动:刚体的定轴转动)。
北京航空航天大学理论力学课件-王琪-ch5A

O
vx = x &⎫ ⎪ vy = y &⎬ ⎪ vz = z &⎭
2015-10-28
x
加速度
x & & = a x = 0(m/s 2 )
y & & = a y = −10(m/s 2 )
曲率半径 v2 v2 20 ρ= = = m 0 an a cos 30 3
20
ax = & x& ⎫ ⎪ ay = & y &⎬ ⎪ az = & z& ⎭
2、P 点的速度和加速度
2015-10-28 8
理论力学
3、P点的运动轨迹
§5-1 点的运动学
y A P O
θቤተ መጻሕፍቲ ባይዱ
B
ϕ
x
l 2 ⎫ xp = R cosθ + L − R2 sin2 θ ⎪ L ⎬ R ⎪ y p = (L − l ) sinθ ⎭ L
消去上述方程中 参数θ可得 P 点 的轨迹方程。
z
&⎫ 解: v x = x ⎪ vy = y &⎬ ⎪ vz = z &⎭
u
v= x &2 + y &2 + z & = R2ω2 + u2 = const &2 = s
2 a= & x y z &2 + & &2 + & &2 = Rω
ωR
ax = & x& ⎫ ⎪ ay = & y &⎬ ⎪ az = & z& ⎭
T’
•曲率(curvature)
《理论力学》第5-7章习题参考解答
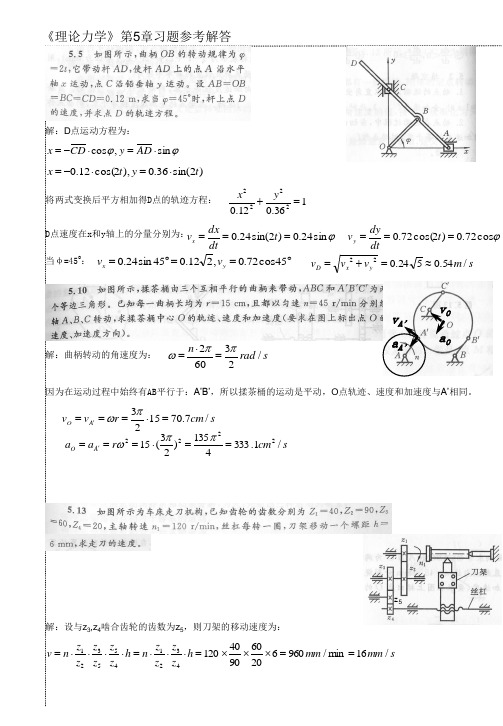
解:D点运动方程为:
x = −CD ⋅ cos ϕ , y = AD ⋅ sin ϕ
x = −0.12 ⋅ cos(2t ), y = 0.36 ⋅ sin(2t )
将两式变换后平方相加得D点的轨迹方程:
x2 y2 + =1 0.12 2 0.36 2
dx dy = 0.24 sin(2t ) = 0.24 sin ϕ v y = = 0.72 cos(2t ) = 0.72 cos ϕ dt dt o 2 2 当φ=45 : v x = 0.24 sin 45° = 0.12 2 , v y = 0.72 cos 45° vD = v x + v y = 0.24 5 ≈ 0.54m / s
ωOC
解:设杆AB上的A点为动点,摇杆OC为动系,则由速度合成定理得:
r r r v A = vr + ve
其中:
vA = v
r ac
r aA r ar rτ ae
r ve
α OC
r v投影得:
r aen
vr = v A sin ϕ = v sin 45°, ve = v A cos ϕ = v cos 45° v v cos 45° v 所以摇杆OC的角速度为: ωOC = e = = (方向如图所示) L OA 2L cos 45° r rτ r n r r 由加速度合成定理得:a A = ae + ae + ar + ac L v 2 v2 v 2v 2 2 n 其中: a A = 0, ae = OA ⋅ ωOC = ( ) = , ac = 2ωOC vr = 2 v sin 45° = cos 45° 2 L 2L 2L 2 2L rτ 2v 2 将矢量方程在 ae 方向投影得: τ 2 a 2L = v 2 α 所以OA的角加速度为: OC = e = 2v τ L OA 2 L2 0 = aτ − ac , ae = ac = e 2L cos 45°
第五章北航 材料力学 全部课件 习题答案

由此得
M ( x)
q0l x4 x3 x 2q0 3 6l 2 3l
根据上述方程,画剪力与弯矩图分别如图 b 与 c 所示,最大剪力与弯矩分别为
FS,max
q0l 3
M max
5q0l 2 48
5-13
在图示梁上,作用有集度为 m= m (x)的分布力偶。试建立力偶矩集度、剪力与
端时,梁支座内侧截面 A+ 或 B- 出现最大剪力,其绝对值为
d ) l
5-11
图。
图示各梁,承受分布载荷作用。试建立梁的剪力、弯矩方程,并画剪力、弯矩
题 5-11 图 (a)解:1.建立剪力、弯矩方程 设截面 x 处的载荷集度为 q( x ) ,由图 5-11(1)可知,
(b)
5-15
试绘制图示杆件的内力图, 并利用题 5-14 所述微分关系检查内力图的正确性。
题 5-15 图 解:题(a)的轴力图与题(b)的扭矩图,分别如图 5-15a 与 b 所示,最大轴力与最大扭矩分 别为
FN,max
ql 2
Tmax ml
11
图 5-15
5-16
图示杆件,承受平行于杆轴方向的均布载荷 q 作用。试画杆的内力图,并利
第五章 弯曲内力
5-3
试证明,在集中力 F 作用处(图 a) ,梁微段的内力满足下列关系:
FS右 FS左 F , M 右 M 左
而在矩为 Me 的集中力偶作用处(图 b) ,则恒有
FS右 FS左,
M右 M左 Me
题 5-3 图 证明:根据题图 a,由
Fy 0,FS左 F qdx FS右 0
图 5-6
理论力学(周衍柏)的习题集答案,第五章.doc

第五章习题解答5.1解如题5.1.1图杆受理想约束,在满足题意的约束条件下杆的位置可由杆与水平方向夹角所唯一确定。
杆的自由度为1,由平衡条件:即mg y =0①变换方程y=2rcos sin-= rsin2②故③代回①式即因在约束下是任意的,要使上式成立必须有:rcos2-=0④又由于cos=故cos2=代回④式得5.2解如题5.2.1图三球受理想约束,球的位置可以由确定,自由度数为1,故。
得由虚功原理故①因在约束条件下是任意的,要使上式成立,必须故②又由得:③由②③可得5.3解如题5.3.1图,在相距2a的两钉处约束反力垂直于虚位移,为理想约束。
去掉绳代之以力T,且视为主动力后采用虚功原理,一确定便可确定ABCD的位置。
因此自由度数为1。
选为广义坐。
由虚功原理:w①又取变分得代入①式得:化简得②设因在约束条件下任意,欲使上式成立,须有:由此得5.4解自由度,质点位置为。
由①由已知得故②约束方程③联立②③可求得或又由于故或5.5解如题5.5.1图按题意仅重力作用,为保守系。
因为已知,故可认为自由度为1.选广义坐标,在球面坐标系中,质点的动能:由于所以又由于故取Ox为零势,体系势能为:故力学体系的拉氏函数为:5.6解如题5.6.1图.平面运动,一个自由度.选广义坐标为,广义速度因未定体系受力类型,由一般形式的拉格朗日方程①在广义力代入①得:②在极坐标系下:③故将以上各式代入②式得5.7解如题5.7.1图又由于所以①取坐标原点为零势面②拉氏函数③代入保守系拉格朗日方程得代入保守系拉格朗日方程得5.8解:如图5.8.1图.(1)由于细管以匀角速转动,因此=可以认为质点的自由度为1.(2)取广义坐标.(3)根据极坐标系中的动能取初始水平面为零势能面,势能:拉氏函数①(4),代入拉氏方程得:(5)先求齐次方程的解.②特解为故①式的通解为③在时:④⑤联立④⑤得将代回式③可得方程的解为:5.9解如题5.9.1图.(1)按题意为保守力系,质点被约束在圆锥面内运动,故自有度数为2. (2)选广义坐标,.(3)在柱坐标系中:以面为零势能面,则:拉氏函数-①(4)因为不显含,所以为循环坐标,即常数②对另一广义坐标代入保守系拉氏方程③有得④所以此质点的运动微分方程为(为常数)所以5.10解如题5.10.1图.(1)体系自由度数为2.(2)选广义坐标(3)质点的速度劈的速度故体系动能以面为零势面,体系势能:其中为劈势能.拉氏函数①(4)代入拉格郎日方程得:②代入拉格郎日方程得③联立②,③得5.11 解如题5.11.1图(1)本系统内虽有摩擦力,但不做功,故仍是保守系中有约束的平面平行运动,自由度(2)选取广义坐标(3)根据刚体力学其中绕质心转动惯量选为零势面,体系势能:其中C为常数.拉氏函数(4)代入保守系拉氏方程得:对于物体,有5.12解如题5.12.1图.(1)棒作平面运动,一个约束,故自由度. (2)选广义坐标(3)力学体系的动能根据运动合成又故设为绕质心的回转半径,代入①得动能②(4)由③(其中)则④因为、在约束条件下任意且独立,要使上式成立,必须:⑤(5)代入一般形式的拉氏方程得:⑥又代入一般形式的拉氏方程得:⑦⑥、⑦两式为运动微分方程(6)若摆动角很小,则,代入式得:,代入⑥⑦式得:⑧又故代入⑧式得:(因为角很小,故可略去项)5.13解如题5.13.1图(1)由于曲柄长度固定,自由度.(2)选广义坐标,受一力矩,重力忽略,故可利用基本形式拉格朗日方程:①(3)系统动能②(4)由定义式③(5)代入①得:得5.14.解如题5.14.1图.(1)因体系作平面平行运动,一个约束方程:(2)体系自由度,选广义坐标.虽有摩擦,但不做功,为保守体系(3)体系动能:轮平动动能轮质心转动动能轮质心动能轮绕质心转动动能.①以地面为零势面,体系势能则保守系的拉氏函数②(1)因为不显含,得知为循环坐标.故=常数③开始时:则代入得又时,所以5.15解如题5.15.1图(1)本系统作平面平行运动,干限制在球壳内运动,自由度;选广义坐标,体系摩擦力不做功,为保守力系,故可用保守系拉氏方程证明①(2)体系动能=球壳质心动能+球壳转动动能+杆质心动能+杆绕中心转动动能②其中代入②得以地面为零势面,则势能:(其中为常数)(3)因为是循环坐标,故常熟③而代入①式得④联立③、④可得(先由③式两边求导,再与④式联立)⑤⑤试乘并积分得:又由于当5.16解如题图5.16.1.(1)由已知条件可得系统自由度.(2)取广义坐标.(3)根据刚体力学,体系动能:①又将以上各式代入①式得:设原点为零势能点,所以体系势能体系的拉氏函数②(1)因为体系只有重力势能做工,因而为保守系,故可采用③代入③式得即(5)解方程得5.17解如题5.17.1图(1)由题设知系统动能①取轴为势能零点,系统势能拉氏函数②(2)体系只有重力做功,为保守系,故可采用保守系拉氏方程.代入拉氏方程得:又代入上式得即③同理又代入上式得④令代入③④式得:欲使有非零解,则须有解得周期5.18解如题5.18.1图(1)系统自由度(2)取广义坐标广义速度(3)因为是微震动,体系动能:以为势能零点,体系势能拉氏函数(4)即①同理②同理③设代入①②③式得欲使有非零解,必须解之又故可得周期5.19解如题5.19.1图(1)体系自由度(2)取广义坐标广义速度(3)体系动能体系势能体系的拉氏函数(4)体系中只有弹力做功,体系为保守系,可用①将以上各式代入①式得:②先求齐次方程③设代入③式得要使有非零,必须即又故通解为:其中又存在特解有②③式可得式中及为积分常数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
l x2 l 2
x
2
2 2 v0 l 0 。将其代入直角坐标形式的 , y x3
运动微分方程可得: F m( g
2 2 v0 l l ) 1 。 3 x x
5-11
vB
O A
x
(a)
B O r
x
vA
A
(b)
2
解:假设绳子与圆盘的切点为 B,绳子相对圆盘无滑动,故 vB r 。如图(b)所示,绳 子始终处于拉直状态,因此绳上 A、B 两点的速度在 A、B 两点连线上的投影相等,即
ve
va
vr
va ve vr
如图(a)所示。将上式在垂直于 O1A 杆的轴上, 以及在 O1C 轴上投影得 (a)
va cos 30 0 ve cos 30 0 , va cos300 vr cos300
ve va R , va vr R , 1
根据加速度合成定理有
aC 2vr 8r 2 。根据加速度合成定理 aa ae ar aC
ae M
O
ar B
aC
A (b)
aa
x'
将上式在 x ' 轴上投影,可得: aa cos ae cos aC
,
由此求得: aa 14r 2 。
5-21 解:求汽车 B 相对汽车 A 的速度是指以汽车 A 为参考 系观察汽车 B 的速度。 动点:汽车 B; 动系:汽车 A( Ox' y' ) ; 定系:路面。 运动分析 绝对运动:圆周运动; 相对运动:圆周运动; 牵连运动:定轴转动(汽车 A 绕 O 作定轴转动) 。 求相对速度 根据速度合成定理
2r 4 x
(x2 r 2 )2
y
O
。
B r
ma F FN mg
将该式在 x, y 轴上投影可得直角坐标形式的运动 微分方程
F
FN
A
vA
mg
(c)
x
F cos m x F sin FN mg m y
其中, sin
r , cos x
FN
mg
y
v0 , 2ss 2 xx s
由此解得: x sv0 x
(a)
vo
v0 s ,将该式对时间求导得 (a)式可写成: xx
2 x x 2 s v0 v0 x
(b)
2 2 2 2 v0 x v0 l 将(a)式代入(b)式可得: ax 。 x 3 (负号表明滑块 A 的加速度向上) x x
将上式积分有
l 2 g cos a sin c 2
,上式可写成 其中 c 为积分常数(由初始条件确定) 。相对速度 vr l
vr2 g cos a sin c 2l
va ve
A (a)
ve OM
根据速度合成定理: va ve vr , 可得
r 2r cos 600
6
va ve tan 2 3r , vr
ve 4r 。 cos 600
加速度如图(b)所示,其中,
r 2 ae OM 2 2r 2 , 0 cos 60
t n aa ae ae a r aC
ve R 0.5 。 O1C 2 R
ar
a
aen
t e
如图(b)所示。将上式沿 aC 投影得
n aa sin 300 aet cos 300 ae sin 300 aC
aa
aC
其中, aa R , ae 2 R1 , aC 21vr 。
8
求得:
FO
mv2 (tan 2 1) 0.284 N 。 2 r cos
5-24
a
a
M
F mg
et
Fe
(a)
(b)
解:求重物相对吊车的速度,所以取吊车为动系,重物 M 为动点。如图(b)所示,由于动 系平移,根据质点相对运动动力学方程有
mar F mg Fe
将上式在切向量方向投影有
aat 16 10 rad/s 2 。 a 7 2 , 1 O1 A 3
5-20 解:取小环为动点,OAB 杆为动系。 运动分析 绝对运动:直线运动; 相对运动:直线运动; 牵连运动:定轴转动。 由运动分析可知点的绝对速度、相对速度 和牵连速度的方向如图(a)所示,其中,
M O
vr B
求相对加速度 如图(b)所示,由于相对运动为圆周运动,相对速度的大小为常值,因此有
7
ar arn
vr2 1.78 m/s 2 。 RB
5-23 O O
F
r
M
v
mg
r FO
M
v
mg
(a)
(b)
解:销钉 M 上作用有水平槽的约束力 F 和圆槽的约束力 FO (如图(b)所示) 。因为销钉 M 的运动是给定的,所以先求其加速度,再利用质点动力学方程求约束力。取销钉为动点, 水平槽为动系,绝对运动是圆周运动,相对运动是直线运动,牵连运动是匀速直线平移。 O
将上式两边对时间求导可得
( x 2 r 2 ) 2 xx 3 2 2 r 2 xx 2x x
可得 消去 2 x
x
2r 4 x
(x2 r 2 )2
(c)
由此可知滑块 A 的加速度方向向左,大小为 aA 取套筒 A 为研究对象,受力如图(c)所示, 根据质点矢量形式的动力学方程有
ve
va
vr
va ve vr
有 va cos ve 。 AB 杆平动,所以 va v ,由此可得 v cos ve 。 OC 杆的角速度为
ve l v cos 2 0 , OA ,所以 。当 45 时,OC 杆上 C 点速度的大小为 l cos OA
其中, aa
n
va2 v2 v 2 sin t n 。根据上式可求出 。 a a tan a a r r cos 2 r cos 3
t n m(aa aa ) F FO mg
根据矢量形式的质点运动微分方程有
将该式在 x 轴上投影:
n m(aat sin aa cos ) FO cos ,
y’
va
vr
ve
O (a) y’
x’
va ve vr
如图(a)所示,将上式沿绝对速度方向投影可得
va ve vr
因此
a rn
v r ve va
ve RB , vA , RA
O (b)
其中, va vB ,
x’
R 380 m/s 。 由此可得: vr B vA vB RA 9
vB vA cos
由图(b)可知: cos
(a)
x2 r 2 ,代入(a)式可得 A 点速度的大小为 x vA r
2
x x2 r 2
2
(b)
x r rx ,将该式两边平方可得 , 由于 vA x (b)式可写成: x
2 (x2 r 2 ) 2r 2 x2 x
vC a
av cos 2 450 av 。 l 2l
5-15 解:动点:销子 M 动系 1:圆盘 动系 2:OA 杆 定系:机座; 运动分析: 绝对运动:平面曲线运动 相对运动:直线运动 牵连运动:定轴转动 根据速度合成定理有
ve1
v r1
ve2
v r2
x
va1 ve1 vr1 ,
取套筒 A 为研究对象,受力如图所示,根据质点矢量形式的动力学方程有
ma F FN mg
将该式在 x, y 轴上投影可得直角坐标形式的运动微分方程
mg F cos m x F sin FN m y
其中, cos
x x2 l 2
, sin
at
v ,由图可知 an
av v
,
2
y
a
a n a sin
所以:
an
o x
v3 ,证毕。 av
1
5-10 解:假设初始时绳索 AB 的长度为 L , t 时刻的长度 为 s ,则有关系式
s L v0 t ,且 s l x
2 2
2
vo
F
将上面两式对时间求导得
第五章习题参考解答
5-3 解:如图所示,火箭的运动方程为: y l tan , 其中 kt 。将运动方程对时间求导并将 30 代入得
0
v y
l lk 4lk , 2 2 3 cos cos
2lk 2 sin 8 3lk 2 。 cos3 9
x2 r 2 , x
m 2 r 4 x 2
x
2r 4 x
(x 2 r 2 )2
, y 0 。代入直角坐标形式的
运动微分方程可得
F
(x2 r 2 ) 2
5
,
FN mg
m 2 r 5 x (x2 r 2 ) 2
5
。
3
5-13 解:动点:套筒 A; 动系:OC 杆; 定系:机座; 运动分析 绝对运动:直线运动; 相对运动:直线运动; 牵连运动:定轴转动。 根据速度合成定理
vr
ve va
(a)
vM vA va 2ve 2b 2 2 m/s ,
