分布密度函数作图
金融数据库——常用统计分布函数SAS实现

常用统计分布函数SAS 实现1. 正态分布密度函数作图分布函数作图产生随机数 其它作图(1)μ=2, σ=0.5, 1, 2。
三图重叠在一个坐标系内。
(2)μ=2, σ=0.5, 1, 2, 5, 10。
四图重叠在一个坐标系内。
(3)μ= 0,1,2 σ=1。
三图重叠在一个坐标系内。
(4)μ=0, σ=1用SAS 软件产生标准正态的概率分布表 其它概率计算注意)(2121)(22)(222σμπσπσμσμ-Φ===--∞---∞-⎰⎰x dt edt ex F t x t x于是,对任意的实数)(,2121x x x x <有,(1)μ=1.5,σ=2,产生正态概率分布表。
(2)μ=1.5,σ=2,求P(X>0)。
(3)μ=1.5,σ=2,求P(-1<X<2)。
(4)用SAS 计算下面概率,并与查表结果对比。
~(1,4)X N ,求( 1.6),(0 1.6),(||4)P X P X P X ≤<≤>分位数定义:设~(0,1)X N ,若Z α满足条件(),01P X Z ααα>=<<,则称Z α为标准正态分布的上α分位点。
(1)计算0.001,0.0025,0.005和0.010的下分位数。
(2) 计算0.001,0.0025,0.005和0.010的上分位数。
本人不同意分为上下分位数,分位数就是分位数,定义为:若Z α满足条件(),01P X Z ααα<=<<则称点Z α为随机变量的α分位数。
单边的, 双边的,注意和以均值为中心,1,2,3倍标准差宽度区间的概率值的区别。
其它可参考例子(1)概率的两种计算公式data ;p1=PROBNORM(1)-PROBNORM(-1); put p1=; p2= PROBNORM(2)-PROBNORM(-2); put p2=; p3= PROBNORM(3)-PROBNORM(-3); put p3=; run ;p1=0.6826894921 p2=0.9544997361 p3=0.9973002039data;p1=2*PROBNORM(1)-1; put p1=;p2=2*PROBNORM(2)-1; put p2=;p3=2*PROBNORM(3)-1; put p3=;run;p1=0.6826894921p2=0.9544997361p3=0.9973002039(2)以均值为中心的区间与概率如,以μ为中心,需要几倍标准差σ距离所构成的区间,其区间内的概率等上面(1)中的概率。
正态分布讲解(含标准表)
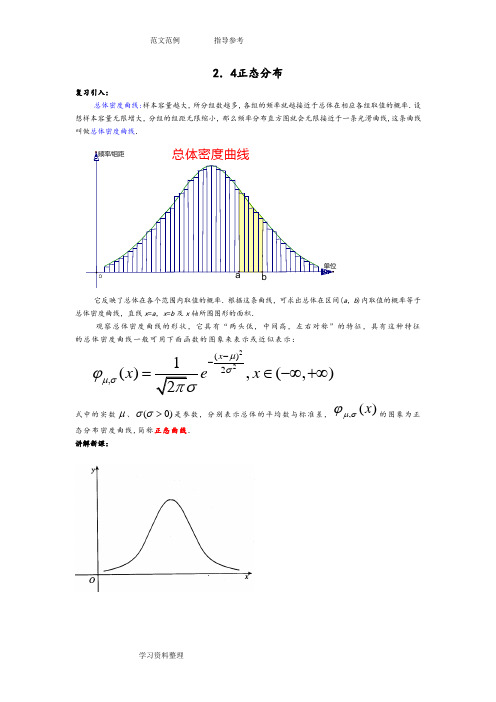
2.4正态分布复习引入:总体密度曲线:样本容量越大,所分组数越多,各组的频率就越接近于总体在相应各组取值的概率.设想样本容量无限增大,分组的组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线. 总体密度曲线b 单位O 频率/组距a它反映了总体在各个范围内取值的概率.根据这条曲线,可求出总体在区间(a ,b )内取值的概率等于总体密度曲线,直线x =a ,x =b 及x 轴所围图形的面积.观察总体密度曲线的形状,它具有“两头低,中间高,左右对称”的特征,具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示:22()2,1(),(,)2x x e x μσμσϕπσ--=∈-∞+∞ 式中的实数μ、)0(>σσ是参数,分别表示总体的平均数与标准差,,()x μσϕ的图象为正态分布密度曲线,简称正态曲线.讲解新课:一般地,如果对于任何实数a b <,随机变量X 满足,()()b aP a X B x dx μσϕ<≤=⎰, 则称 X 的分布为正态分布(normal distribution ) .正态分布完全由参数μ和σ确定,因此正态分布常记作),(2σμN .如果随机变量 X 服从正态分布,则记为X ~),(2σμN .经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似服从正态分布.例如,高尔顿板试验中,小球在下落过程中要与众多小木块发生碰撞,每次碰撞的结果使得小球随机地向左或向右下落,因此小球第1次与高尔顿板底部接触时的坐标 X 是众多随机碰撞的结果,所以它近似服从正态分布.在现实生活中,很多随机变量都服从或近似地服从正态分布.例如长度测量误差;某一地区同年龄人群的身高、体重、肺活量等;一定条件下生长的小麦的株高、穗长、单位面积产量等;正常生产条件下各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等);某地每年七月份的平均气温、平均湿度、降雨量等;一般都服从正态分布.因此,正态分布广泛存在于自然现象、生产和生活实际之中.正态分布在概率和统计中占有重要的地位.说明:1参数μ是反映随机变量取值的平均水平的特征数,可以用样本均值去佑计;σ是衡量随机变量总体波动大小的特征数,可以用样本标准差去估计.2.早在 1733 年,法国数学家棣莫弗就用n !的近似公式得到了正态分布.之后,德国数学家高斯在研究测量误差时从另一个角度导出了它,并研究了它的性质,因此,人们也称正态分布为高斯分布.2.正态分布),(2σμN )是由均值μ和标准差σ唯一决定的分布 通过固定其中一个值,讨论均值与标准差对于正态曲线的影响3.通过对三组正态曲线分析,得出正态曲线具有的基本特征是两头底、中间高、左右对称 正态曲线的作图,书中没有做要求,教师也不必补上 讲课时教师可以应用几何画板,形象、美观地画出三条正态曲线的图形,结合前面均值与标准差对图形的影响,引导学生观察总结正态曲线的性质4.正态曲线的性质:(1)曲线在x 轴的上方,与x 轴不相交(2)曲线关于直线x=μ对称(3)当x=μ时,曲线位于最高点(4)当x <μ时,曲线上升(增函数);当x >μ时,曲线下降(减函数) 并且当曲线向左、右两边无限延伸时,以x 轴为渐近线,向它无限靠近(5)μ一定时,曲线的形状由σ确定σ越大,曲线越“矮胖”,总体分布越分散;σ越小.曲线越“瘦高”.总体分布越集中:五条性质中前三条学生较易掌握,后两条较难理解,因此在讲授时应运用数形结合的原则,采用对比教学5.标准正态曲线:当μ=0、σ=l 时,正态总体称为标准正态总体,其相应的函数表示式是2221)(x e x f -=π,(-∞<x <+∞)其相应的曲线称为标准正态曲线标准正态总体N (0,1)在正态总体的研究中占有重要的地位 任何正态分布的概率问题均可转化成标准正态分布的概率问题讲解范例:例1.给出下列三个正态总体的函数表达式,请找出其均值μ和标准差σ (1)),(,21)(22+∞-∞∈=-x e x f x π(2)),(,221)(8)1(2+∞-∞∈=--x e x f x π (3)22(1)2(),(,)2x f x e x π-+=∈-∞+∞ 答案:(1)0,1;(2)1,2;(3)-1,0.5例2求标准正态总体在(-1,2)内取值的概率.解:利用等式)()(12x x p Φ-Φ=有)([]}{11)2()1()2(--Φ--Φ=-Φ-Φ=p=1)1()2(-Φ+Φ=0.9772+0.8413-1=0.8151.1.标准正态总体的概率问题: xy对于标准正态总体N (0,1),)(0x Φ是总体取值小于0x 的概率,即 )()(00x x P x <=Φ, 其中00>x ,图中阴影部分的面积表示为概率0()P x x < 只要有标准正态分布表即可查表解决.从图中不难发现:当00<x 时,)(1)(00x x -Φ-=Φ;而当00=x 时,Φ(0)=0.5 2.标准正态分布表标准正态总体)1,0(N 在正态总体的研究中有非常重要的地位,为此专门制作了“标准正态分布表”.在这个表中,对应于0x 的值)(0x Φ是指总体取值小于0x 的概率,即)()(00x x P x <=Φ,)0(0≥x .若00<x ,则)(1)(00x x -Φ-=Φ.利用标准正态分布表,可以求出标准正态总体在任意区间),(21x x 内取值的概率,即直线1x x =,2x x =与正态曲线、x 轴所围成的曲边梯形的面积1221()()()P x x x x x <<=Φ-Φ. 3.非标准正态总体在某区间内取值的概率:可以通过)()(σμ-Φ=x x F 转化成标准正态总体,然后查标准正态分布表即可 在这里重点掌握如何转化 首先要掌握正态总体的均值和标准差,然后进行相应的转化4.小概率事件的含义发生概率一般不超过5%的事件,即事件在一次试验中几乎不可能发生假设检验方法的基本思想:首先,假设总体应是或近似为正态总体,然后,依照小概率事件几乎不可能在一次试验中发生的原理对试验结果进行分析假设检验方法的操作程序,即“三步曲”一是提出统计假设,教科书中的统计假设总体是正态总体;二是确定一次试验中的a 值是否落入(μ-3σ,μ+3σ);三是作出判断讲解范例:例1. 若x ~N (0,1),求(l)P (-2.32<x <1.2);(2)P (x >2).解:(1)P (-2.32<x <1.2)=Φ(1.2)-Φ(-2.32)=Φ(1.2)-[1-Φ(2.32)]=0.8849-(1-0.9898)=0.8747.(2)P (x >2)=1-P (x <2)=1-Φ(2)=l-0.9772=0.0228.例2.利用标准正态分布表,求标准正态总体在下面区间取值的概率:(1)在N(1,4)下,求)3(F(2)在N (μ,σ2)下,求F(μ-σ,μ+σ);F(μ-1.84σ,μ+1.84σ);F(μ-2σ,μ+2σ);F(μ-3σ,μ+3σ) 解:(1))3(F =)213(-Φ=Φ(1)=0.8413 (2)F(μ+σ)=)(σμσμ-+Φ=Φ(1)=0.8413 F(μ-σ)=)(σμσμ--Φ=Φ(-1)=1-Φ(1)=1-0.8413=0.1587 F(μ-σ,μ+σ)=F(μ+σ)-F(μ-σ)=0.8413-0.1587=0.6826F(μ-1.84σ,μ+1.84σ)=F(μ+1.84σ)-F(μ-1.84σ)=0.9342F(μ-2σ,μ+2σ)=F(μ+2σ)-F(μ-2σ)=0.954F(μ-3σ,μ+3σ)=F(μ+3σ)-F(μ-3σ)=0.997对于正态总体),(2σμN 取值的概率:68.3%2σx 95.4%4σx 99.7%6σx在区间(μ-σ,μ+σ)、(μ-2σ,μ+2σ)、(μ-3σ,μ+3σ)内取值的概率分别为68.3%、95.4%、99.7% 因此我们时常只在区间(μ-3σ,μ+3σ)内研究正态总体分布情况,而忽略其中很小的一部分 例3.某正态总体函数的概率密度函数是偶函数,而且该函数的最大值为π21,求总体落入区间(-1.2,0.2)之间的概率解:正态分布的概率密度函数是),(,21)(222)(+∞-∞∈=--x e x f x σμσπ,它是偶函数,说明μ=0,)(x f 的最大值为)(μf =σπ21,所以σ=1,这个正态分布就是标准正态分布( 1.20.2)(0.2)( 1.2)(0.2)[1(1.2)](0.2)(1.2)1P x -<<=Φ-Φ-=Φ--Φ=Φ+Φ- 教学反思:1.在实际遇到的许多随机现象都服从或近似服从正态分布 在上一节课我们研究了当样本容量无限增大时,频率分布直方图就无限接近于一条总体密度曲线,总体密度曲线较科学地反映了总体分布 但总体密度曲线的相关知识较为抽象,学生不易理解,因此在总体分布研究中我们选择正态分布作为研究的突破口 正态分布在统计学中是最基本、最重要的一种分布 2.正态分布是可以用函数形式来表述的 其密度函数可写成:22()21(),(,)2x f x e x μσπσ--=∈-∞+∞, (σ>0)由此可见,正态分布是由它的平均数μ和标准差σ唯一决定的 常把它记为),(2σμN 3.从形态上看,正态分布是一条单峰、对称呈钟形的曲线,其对称轴为x=μ,并在x=μ时取最大值 从x=μ点开始,曲线向正负两个方向递减延伸,不断逼近x 轴,但永不与x 轴相交,因此说曲线在正负两个方向都是以x 轴为渐近线的4.通过三组正态分布的曲线,可知正态曲线具有两头低、中间高、左右对称的基本特征。
D分布函数与概率密度函数的近似解

1) Fn x 是单调非减跳跃函数(阶梯函数) 2) Fn x 在点 x xk 处有间断, 在每个间断点的跃度 1 为 , k 1,2,,n n
*
Fn ( x ) 0, 3) 0 Fn ( x ) 1 xlim
x
lim Fn ( x ) 1
2) 数频数 观测值落在各组的频数分别为
m1 ,2 , ,ml
频率为
ml m1 m2 , , , n n n
3) 作图 以各组为底边,以相应组的频率除以组距为高, 建立个 l 小矩形,即得总体的直方图 如图6-2 直方图中每一矩形的面积等于相应组的频率
y
f x
o
m2 m1 n a0 n a a
0,
Fn x
* x x1
* x* x x k k 1 k 1, 2, ,n 1
k , n
1,
x x* n
称 Fn x 是总体 X 的经验分布函数 其图如6-1
y
1
k n 1 n
x x
* 1
* 2
o
x
* k
x
* k 1
x
* n
x
图 6-1
由图6-1容易看出
第六章 第二节 分布函数与概率密度函数的 近似解
一、分布函数的近似解—经验分布
二、概率密度函数的近似解—直方图
一、分布函数的近似解—经验分布
设 X 1, X 2, X n 是来自总体 X 的样本, x2, xn x1,
是样本的一个观测值, 设这n个数值按由小到大的
* * x2, x* ,定义: 顺序排列后为 x1 n ,对 x R
显然满足一般分布函数的三个性质 随着 n 的增大,Fn ( x ) 越来越接近 X 的分布函数 F( x )
matlab画各种概率分布图像

Matlab画各种概率分布函数曲线help PDFPDF Density function for a specified distribution.Y = PDF(NAME,X,A) returns an array of values of the probability densityfunction for the one-parameter probability distribution specified by NAMEwith parameter values A, evaluated at the values in X.Y = PDF(NAME,X,A,B) or Y = PDF(NAME,X,A,B,C) returns values of theprobability density function for a two- or three-parameter probabilitydistribution with parameter values A, B (and C).The size of Y is the common size of the input arguments. A scalar inputfunctions as a constant matrix of the same size as the other inputs. Eachelement of Y contains the probability density evaluated at thecorresponding elements of the inputs.Acceptable strings for name are:∙'beta' (Beta distribution)∙'bino' (Binomial distribution)二项分布∙'chi2' (Chi-square distribution)卡方分布∙'exp' (Exponential distribution)指数分布∙'ev' (Extreme value distribution) 极值分布∙'f' (F distribution) 费雪分布∙'gam' (Gamma distribution) 伽马分布∙'gev' (Generalized extreme value distribution)∙'gp' (Generalized Pareto distribution) 极值分布函数∙'geo' (Geometric distribution)几何分布∙'hyge' (Hypergeometric distribution) 超几何分布∙'logn' (Lognormal distribution) 对数正态分布∙'nbin' (Negative binomial distribution) 负二项分布∙'ncf' (Noncentral F distribution) 非中心F分布∙'nct' (Noncentral t distribution)非中心t分布∙'ncx2' (Noncentral chi-square distribution) 非中心卡方分布∙'norm' (Normal distribution) 正态分布∙'poiss' (Poisson distribution) 泊松分布∙'rayl' (Rayleigh distribution) 瑞利分布∙'t' (t distribution) t分布∙'unif' (Uniform distribution) 均匀分布∙'unid' (Discrete uniform distribution) 离散均匀分布∙'wbl' (Weibull distribution)韦伯分布。
[化学反应工程原理]第十章__停留时间分布-数学期望及方差
![[化学反应工程原理]第十章__停留时间分布-数学期望及方差](https://img.taocdn.com/s3/m/7b781c5465ce0508763213e1.png)
即
F(t) 0 E(t)dt
显然,t=0时,F(t)=0;
t=∞, F(t)=1。
F(t)与E(t)的关系为:
dF (t) E(t) dt
右图为F(t)与E(t)的曲线。
三、停留时间分布的测定方法
➢采用刺激应答技术,又称示踪法,即在反应器的进 口加入某种示踪物,同时在出口测定示踪物浓度等 的变化,确定流经反应器中物料的停留时间分布。
tE(ti )ti E(ti )ti
➢若读取实验数据时时间间隔∆t相等,则上式可简化为:
tm
tE(t) E(t)
2. 方差
➢方差描述物料质点各停留时间与平均停留时间的偏离程度,
即停留时间分布的离散程度。
➢定义为:各个物料质点停留时间t与平均停留时间 t差m 的
平方的加权平均值。
方差越小,越接近平推流;
➢测定时利用示踪物的光、电、化学或放射等特性。 示踪物除具有上述特性外,还需要具有不挥发、不吸 收、易溶于主流体,在很小的浓度下也能检测出的特 性。 ➢示踪物的输入方式主要有脉冲法和阶跃法。
示踪剂的选取原则
➢示踪剂不应与主流体发生反应; ➢除了显著区别于主流体的某一可检测性质外,
示踪剂应和主流体应尽可能具有相同的物理性 质,且两者易于溶为一体; ➢示踪剂浓度很低时也能够检测到信号; ➢用于多相系统检测的示踪剂不发生相间的转移; ➢示踪剂本身应具有或易于转变为电信号或光信 号的特点。
C(t)dt
0
C(t)dt
0
dF(t) dC(t)
E(t)
dt C0dt
可直接测得
四、停留时间分布的数字特征
研究不同流型的停留时间分布,通常是比较它们的统计特征
值。常用的特征值有两个:
化学反应工程基础连续流动反应器的停留时间分布

1.阶跃示踪法
阶跃讯号响应曲线
待测定系统稳定后,将 原来反应器中流动的流休切 换为另一种含有示踪剂的流 体。一直保侍到实验结束, 并保诗切换而后流体流量不 变。
开始时,出口流体中有示踪剂流体的分率很小,随着时间的推延, 有示踪剂流体在出口流体中的分率不断增加,当t→∞时,分率趋于1。
,以C t v0
Q
对τ作图即可得停留时间分布密度函
数曲线。
▪ 脉冲示踪法要求进料瞬间完成,技术要求较高,可在生产中在线测定。
连续流动反应器的停留时间分布
停留时间分布的数字特征
由于停留时间分布密度函数E(t)对单个流体微元来讲, 就是随机变量——停留时间的概率密度函数,因此也可用 这些函数的特征值作为随机变量的比较基准来进行定量比 铰,而无需对分布曲线本身进行比较。
0
t
2
1
t
dt
2
0
2 2 2
2
无因次方差:
2
2
1
2
流动模型
理想混合流的E(t)和F(t)曲线图
t=0时,F(t)=0,E(t)= 1 ;此时E(t)取得极大值。
t=τ时,F(τ)=1-e-1 = 0.623
流动模型
非理想流动模型
1.多级理想混合模型 把实际反应器中无序的返混程度等效于N个等体积的理想混合流反
反应器内流体的返混 对化学反应的影响
和容积效率相关的因素: 1. 反应器的类型
对于同一简单反应,在相同的工艺条件下,为达到相同的转化率,平 推流反应器所需体积最小,理想混合流所需的反应器体积最大。
2. 化学反应的级数及化学反应控制的转化率 如实际反应器都选用理想混合反应器,不同反应级数的容积效率:
作图练习题
一、平面几何1. 画一个圆,半径为3cm。
2. 画一个等边三角形,边长为4cm。
3. 画一个长方形,长为5cm,宽为3cm。
4. 画一个平行四边形,相邻两边长分别为4cm和6cm。
5. 画一个梯形,上底长为3cm,下底长为5cm,高为2cm。
6. 画一个正五边形,边长为4cm。
7. 画一个圆,圆心为点O,半径为2cm,画圆上的任意两点A和B。
8. 画一个直线,经过点P(2,3)和点Q(4,5)。
9. 画一个射线,起点为点R,经过点S(1,2)。
10. 画一个角,顶点为点T,一个边为射线UT,另一个边为射线VT。
二、立体几何1. 画一个正方体,边长为3cm。
2. 画一个长方体,长为4cm,宽为2cm,高为3cm。
3. 画一个圆柱,底面半径为2cm,高为4cm。
4. 画一个圆锥,底面半径为3cm,高为5cm。
5. 画一个球,半径为2cm。
6. 画一个棱锥,底面为正三角形,边长为4cm,高为5cm。
7. 画一个棱柱,底面为矩形,长为3cm,宽为2cm,高为4cm。
8. 画一个球冠,底面半径为3cm,高为2cm。
9. 画一个球缺,底面半径为3cm,高为2cm。
10. 画一个椭球体,长轴为4cm,短轴为2cm,焦距为1cm。
三、坐标系1. 在平面直角坐标系中,画出点A(2,3)和点B(4,5)。
2. 在平面直角坐标系中,画出直线y=2x。
3. 在平面直角坐标系中,画出射线x=3。
4. 在平面直角坐标系中,画出圆x^2+y^2=9。
5. 在平面直角坐标系中,画出椭圆x^2/4+y^2/9=1。
6. 在空间直角坐标系中,画出点P(2,3,4)和点Q(4,5,6)。
7. 在空间直角坐标系中,画出直线x=2。
8. 在空间直角坐标系中,画出球面x^2+y^2+z^2=16。
9. 在空间直角坐标系中,画出椭球面x^2/4+y^2/9+z^2/16=1。
10. 在空间直角坐标系中,画出直线x+y+z=3。
四、三角函数1. 画y=sin(x)在[0, 2π]范围内的图像。
离散型随机变量均值(正态分布)
2.4正态分布复习引入:总体密度曲线:样本容量越大,所分组数越多,各组的频率就越接近于总体在相应各组取值的概率.设想样本容量无限增大,分组的组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线.它反映了总体在各个范围内取值的概率.根据这条曲线,可求出总体在区间(a ,b )内取值的概率等于总体密度曲线,直线x =a ,x=b 及x 轴所围图形的面积.观察总体密度曲线的形状,它具有“两头低,中间高,左右对称”的特征,具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示:22()2,(),(,)x x x μσμσϕ--=∈-∞+∞式中的实数μ、)0(>σσ是参数,分别表示总体的平均数与标准差,,()xμσϕ的图象为正态分布密度曲线,简称正态曲线. 讲解新课:一般地,如果对于任何实数a b <,随机变量X 满足,()()baP a X B x dx μσϕ<≤=⎰,则称 X 的分布为正态分布(normal distribution ) .正态分布完全由参数μ和σ确定,因此正态分布常记作),(2σμN .如果随机变量 X 服从正态分布,则记为X ~),(2σμN .经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似服从正态分布.例如,高尔顿板试验中,小球在下落过程中要与众多小木块发生碰撞,每次碰撞的结果使得小球随机地向左或向右下落,因此小球第1次与高尔顿板底部接触时的坐标 X 是众多随机碰撞的结果,所以它近似服从正态分布.在现实生活中,很多随机变量都服从或近似地服从正态分布.例如长度测量误差;某一地区同年龄人群的身高、体重、肺活量等;一定条件下生长的小麦的株高、穗长、单位面积产量等;正常生产条件下各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等);某地每年七月份的平均气温、平均湿度、降雨量等;一般都服从正态分布.因此,正态分布广泛存在于自然现象、生产和生活实际之中.正态分布在概率和统计中占有重要的地位.说明:1参数μ是反映随机变量取值的平均水平的特征数,可以用样本均值去佑计;σ是衡量随机变量总体波动大小的特征数,可以用样本标准差去估计.2.早在 1733 年,法国数学家棣莫弗就用n !的近似公式得到了正态分布.之后,德国数学家高斯在研究测量误差时从另一个角度导出了它,并研究了它的性质,因此,人们也称正态分布为高斯分布. 2.正态分布),(2σμN )是由均值μ和标准差σ唯一决定的分布通过固定其中一个值,讨论均值与标准差对于正态曲线的影响3.通过对三组正态曲线分析,得出正态曲线具有的基本特征是两头底、中间高、左右对称 正态曲线的作图,书中没有做要求,教师也不必补上 讲课时教师可以应用几何画板,形象、美观地画出三条正态曲线的图形,结合前面均值与标准差对图形的影响,引导学生观察总结正态曲线的性质4.正态曲线的性质:(1)曲线在x 轴的上方,与x 轴不相交(2)曲线关于直线x=μ对称(3)当x=μ时,曲线位于最高点(4)当x <μ时,曲线上升(增函数);当x >μ时,曲线下降(减函数)并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近(5)μ一定时,曲线的形状由σ确定σ越大,曲线越“矮胖”,总体分布越分散; σ越小.曲线越“瘦高”.总体分布越集中:五条性质中前三条学生较易掌握,后两条较难理解,因此在讲授时应运用数形结合的原则,采用对比教学5.标准正态曲线:当μ=0、σ=l 时,正态总体称为标准正态总体,其相应的函数表示式是2221)(x ex f -=π,(-∞<x <+∞)其相应的曲线称为标准正态曲线标准正态总体N (0,1)在正态总体的研究中占有重要的地位任何正态分布的概率问题均可转化成标准正态分布的概率问题讲解范例:例1.给出下列三个正态总体的函数表达式,请找出其均值μ和标准差σ(1)),(,21)(22+∞-∞∈=-x ex f x π(2)),(,221)(8)1(2+∞-∞∈=--x ex f x π(3)22(1)(),(,)x f x x -+=∈-∞+∞例2求标准正态总体在(-1,2)内取值的概率.1.标准正态总体的概率问题:对于标准正态总体N (0,1),)(0x Φ是总体取值小于0x 的概率, 即 )()(00x x P x <=Φ,其中00>x ,图中阴影部分的面积表示为概率0()P x x <只要有标准正态分布表即可查表解决.从图中不难发现:当00<x 时,)(1)(00x x -Φ-=Φ;而当00=x 时,Φ(0)=0.52.标准正态分布表 标准正态总体)1,0(N 在正态总体的研究中有非常重要的地位,为此专门制作了“标准正态分布表”.在这个表中,对应于0x 的值)(0x Φ是指总体取值小于0x 的概率,即 )()(00x x P x <=Φ,)0(0≥x .若00<x ,则)(1)(00x x -Φ-=Φ.利用标准正态分布表,可以求出标准正态总体在任意区间),(21x x 内取值的概率,即直线1x x =,2x x =与正态曲线、x 轴所围成的曲边梯形的面积1221()()()P x x x x x <<=Φ-Φ.3.非标准正态总体在某区间内取值的概率:可以通过)()(σμ-Φ=x x F 转化成标准正态总体,然后查标准正态分布表即可 在这里重点掌握如何转化 首先要掌握正态总体的均值和标准差,然后进行相应的转化4.小概率事件的含义发生概率一般不超过5%的事件,即事件在一次试验中几乎不可能发生假设检验方法的基本思想:首先,假设总体应是或近似为正态总体,然后,依照小概率事件几乎不可能在一次试验中发生的原理对试验结果进行分析假设检验方法的操作程序,即“三步曲”一是提出统计假设,教科书中的统计假设总体是正态总体;二是确定一次试验中的a 值是否落入(μ-3σ,μ+3σ); 三是作出判断讲解范例:例1. 若x ~N (0,1),求(l)P (-2.32<x <1.2);(2)P (x >2).例2.利用标准正态分布表,求标准正态总体在下面区间取值的概率: (1)在N(1,4)下,求)3(F(2)在N (μ,σ2)下,求F(μ-σ,μ+σ); F(μ-1.84σ,μ+1.84σ);F(μ-2σ,μ+2σ); F(μ-3σ,μ+3σ)对于正态总体),(2σμN 取值的概率:在区间(μ-σ,μ+σ)、(μ-2σ,μ+2σ)、(μ-3σ,μ+3σ)内取值的概率分别为68.3%、95.4%、99.7% 因此我们时常只在区间(μ-3σ,μ+3σ)内研究正态总体分布情况,而忽略其中很小的一部分例3.某正态总体函数的概率密度函数是偶函数,而且该函数的最大值为π21,求总体落入区间(-1.2,0.2)之间的概率巩固练习:书本第74页 1,2,3课后作业: 书本第75页 习题2. 4 A 组 1 , 2 B 组1 , 2教学反思:1.在实际遇到的许多随机现象都服从或近似服从正态分布在上一节课我们研究了当样本容量无限增大时,频率分布直方图就无限接近于一条总体密度曲线,总体密度曲线较科学地反映了总体分布但总体密度曲线的相关知识较为抽象,学生不易理解,因此在总体分布研究中我们选择正态分布作为研究的突破口正态分布在统计学中是最基本、最重要的一种分布2.正态分布是可以用函数形式来表述的其密度函数可写成:22()2(),(,)xf x xμσ--=∈-∞+∞,(σ>0)由此可见,正态分布是由它的平均数μ和标准差σ唯一决定的常把它记为),(2σμN3.从形态上看,正态分布是一条单峰、对称呈钟形的曲线,其对称轴为x=μ,并在x=μ时取最大值从x=μ点开始,曲线向正负两个方向递减延伸,不断逼近x轴,但永不与x轴相交,因此说曲线在正负两个方向都是以x轴为渐近线的4.通过三组正态分布的曲线,可知正态曲线具有两头低、中间高、左右对称的基本特征。
实验一常见分布的概率密度、分布函数生成
实验一:常见分布的概率密度、分布函数生成实验目的:会利用 Matlab 软件计算离散型随机变量的概率、连续型随机变量概率密度值,以及产生离散型随机变量的概率分布(即分布律)。
利用 Matlab 软件计算分布函数值, 或计算形如事件{X≤x}的概率。
求上α分位点以及分布函数的反函数值。
实验分析:本次实验主要需要运用matlab,掌握常见分布的分布律和概率密度的产生命令,如binopdf,normpdf等,常见分布的分布分布函数命令,如binocdf,normcdf等。
常见分布的分布分布函数反函数命令,如binoinv,norminv等实验过程:1. 事件 A 在每次试验中发生的概率是 0.3(1)在 10 次试验中 A 恰好发生 6 次的概率实验程序>> binopdf(6,10,0.3)运行结果为:ans =0.0368(2)生成事件A发生次数的概率分布实验程序>> binopdf(0:10,10,0.3)运行结果为:ans =Columns 1 through 90.0282 0.1211 0.2335 0.2668 0.2001 0.1029 0.0368 0.0090 0.0014Columns 10 through 110.0001 0.0000(3)在 10 次试验中 A 至少发生 6 次的概率实验程序>> binocdf(6,10,0.3)运行结果为:ans =0.9894(4)设事件A发生次数为X,且X的分布函数为F(x),求F(6.1);又已知F(x)=0.345,求x实验程序>> binocdf(6.1,10,0.3)运行结果为:ans =0.98942.设随机变量 X服从参数是 3 的泊松分布(1)概率 P{X=6}实验程序>> poisscdf(6,3)运行结果为:ans =0.0504(2)X的分布律前七项实验程序>> poisscdf(0:6,3)运行结果为:ans =0.0498 0.1494 0.2240 0.2240 0.1680 0.1008 0.0504 (3)设X的分布函数为F(x),求F(6.1);又已知F(x)=0.345,求x实验程序>> poisscdf(6.1,3)运行结果为ans =0.9665>> poissinv(0.345,3)运行结果为:ans =23.设随机变量 X服从区间[2, 6]上的均匀分布(1))X=4 时的概率密度值实验程序>> unifpdf(4,2,6)运行结果为:ans =0.2500(2)P{X≤5}实验程序>> unifcdf(5,2,6)运行结果为:ans =0.7500(3)若P{X≤x}=0.345,求x实验程序>> unifinv(0.345,2,6)运行结果为:ans =3.38004.设随机变量 X 服从参数是 6 的指数分布(1)X=0,1,2,3,4,5,6 时的概率密度值实验程序>> exppdf(0:6,6)运行结果为:ans =0.1667 0.1411 0.1194 0.1011 0.0856 0.0724 0.0613(2)P{X≤5}实验程序>> expcdf(5,6)运行结果为:ans =0.5654(3)若P{X≤x}=0.345,求x实验程序>> expinv(0.345,6)运行结果为:ans =2.53875.设随机变量 X 服从均值是 6,标准差是2 的正态分布(1)X=3,4,5,6,7,8,9 时的概率密度值实验程序>> normpdf(3:9,6,2)运行结果为:ans =0.0648 0.1210 0.1760 0.1995 0.1760 0.1210 0.0648(2)X=3,4,5,6,7,8,9 时的分布函数值实验程序>> normcdf(3:9,6,2)运行结果为:ans =0.0668 0.1587 0.3085 0.5000 0.6915 0.8413 0.9332 (3) 若P{X≤x}=0.345,求x 实验程序>> norminv(0.345,6,2)运行结果为:ans =5.2023(4)求标准正态分布的上0.05分为点实验程序>> norminv(0.95,0,1)运行结果为:ans =1.6449实验二:随机数的生成实验目的:通过本次实验,了解Matlab在概率与数理统计领域的应用,学会用matlab掌握常见分布的随机数产生的有关命令,掌握利用随机数进行随机模拟的方法。
Excel有关正态分布函数NORMSDIST做正态分布图
Excel做正态分布图用正态分布函数NORMSDIST正态分布函数的语法是NORMDIST(x,mean,standard_dev,cumulative)cumulative为一逻辑值,如果为0则是密度函数,如果为1则是累积分布函数。
如果画正态分布图,则为0。
例如均值10%,标准值为20%的正态分布,先在A1中敲入一个变量,假定-50,选中A列,点编辑-填充-序列,选择列,等差序列,步长值10,终止值70。
然后在B1中敲入NORMDIST(A1,10,20,0),返回值为0.000222,选中B1,当鼠标在右下角变成黑十字时,下拉至B13,选中A1B13区域,点击工具栏上的图表向导-散点图,选中第二排第二个图,点下一步,默认设置,下一步,标题自己写,网格线中的勾去掉,图例中的勾去掉,点下一步,完成。
图就初步完成了。
下面是微调把鼠标在图的坐标轴上点右键,选坐标轴格式,在刻度中填入你想要的最小值,最大值,主要刻度单位(x轴上的数值间隔),y轴交叉于(y为0时,x多少)等等。
确定后,正态分布图就大功告成了。
PS:标准正态分布的语法为NORMSDIST(z),均值:分布的均值;标准差:分布的标准差;累积:若1,则为分布函数;若0,则为概率密度函数。
当均值为0,标准差为1时,正态分布函数NORMDIST即为标准正态分布函数NORMDIST。
例3已知考试成绩服从正态分布,,,求考试成绩低于500分的概率。
解在Excel中单击任意单元格,输入公式:“=NORMDIST (500,600,100,1 )”,得到的结果为0.158655,即,表示成绩低于500分者占总人数的15.8655%。
例4假设参加某次考试的考生共有2000人,考试科目为5门,现已知考生总分的算术平均值为360,标准差为40分,试估计总分在400分以上的学生人数。
假设5门成绩总分近似服从正态分布。
解设表示学生成绩的总分,根据题意,,。
第一步,求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绘制二维正态分布
x=-20:0.5:20; y=-20:0.5:20; mu=[-1,2]; sigma=[1 1; 1 3]; % 输入均值向量和协方差 矩阵,可以根据需要修改 [X,Y]=meshgrid(x,y); % 产生网格数据并处理 p=mvnpdf([X(:),Y(:)],mu,sigma);(多维正态密 度函数值) P=reshape(p,size(X)); % 求取联合概率密度 surf(X,Y,P) title('条件概率密度函数曲线');
二项式分布 卡方分布 指数分布 F分布 几何分布 正态分布 泊松分布 T分布 均匀分布 离散均匀分布 Binomial Chisquare Exponential F Geometric Normal Poisson T Uniform Discrete Uniform bino chi2 exp f geo norm poiss t unif unid
x=0:0.1:20; y=chi2pdf(x,4); plot(x,y) x=0:0.1:20; y=chi2pdf(x,10); plot(x,y)
抽样分布: F 分布
设随机变量 X ~ 2 ( m), Y ~ 2 ( n) ,且 X 与 Y 相 互独立,则称随机变量
X /m F Y /n
离散分布: Poisson 分布
泊松分布也属于离散分布,是1837年由发个数 学家 Poisson 首次提出,其概率分布列为:
P( X k)
k
k!
e
k 0,
1, 2, , 0
记做:X ~ P ( )
泊松分布是一种常用的离散分布,它与单位时间(或单 位面积、单位产品等)上的计数过程相联系。如:单位时 间内,电话总机接到用户呼唤次数;1 平方米内,玻璃上的 气泡数等。
正态分布也称高斯分布,是概率论中最重要的一个分布。 如果一个变量是大量微小、独立的随机因素的叠加,那么 它一定满足正态分布。如测量误差、产品质量、月降雨量等
正态分布举例
例:标准正态分布和非标准正态分布密度函数图形
x=-8:0.1:8; y=normpdf(x,0,1); y1=normpdf(x,1,2); plot(x,y,x,y1,':')
……
……
Matlab相关命令介绍
其它函数
cdf 系列函数:累积分布函数 inv 系列函数:逆累积分布函数 rnd 系列函数:随机数发生函数
例: p=normcdf(-2:2,0,1)
x=norminv([0.025 0.975],0,1) n=normrnd(0,1,[1 5])
常见的概率分布
Poisson 分布举例
例: =25 时的泊松分布密度函数图
x=0:50; y=poisspdf(x,25); plot(x,y)
离散分布:均匀分布
如果随机变量 X 的分布列为:
1 P( X k) n
k 1, 2,
, n
则称这种分布为离散均匀分布。记做: ~ U X
[1, 2,, n]
分布密度函数作图
Matlab相关命令介绍
pdf 概率密度函数
y=pdf(name,x,A) 返回由 name 指定的单参数分布的概率密度,x为样本数据 y=pdf(name,x,A,B) 或 y=pdf(name,x,A,B,C) 返回由 name 指定的双参数或三参数分布的概率密度 name 用来指定分布类型,其取值可以是: 'beta'、'bino'、'chi2'、'exp'、'ev'、'f' 、 'gam'、'gev'、'gp'、'geo'、'hyge'、'logn'、 'nbin'、'ncf'、'nct'、'ncx2'、'norm'、 'poiss'、'rayl'、't'、'unif'、'unid'、'wbl'。
均匀分布举例
x=-10:0.01:10; r=1; y=unifpdf(x,0,2*pi*r); plot(x,y);
连续分布:指数分布
指数分布(连续分布)
如果随机变量 X 的密度函数为:
e x , x 0 f ( x) , x0 0
0
~ Exp( )
例: n=20 时的离散均匀分布密度函数图
n=20; x=1:n; y=unidpdf(x,n); plot(x,y,'o-')
抽样分布: 2分布
设随机变量 X1, X2, … , Xn 相互独立,且同服从正态 分布 N(0,1),则称随机变量 n2= X12+X22+ … +Xn2服从 2 自由度为 n 的 2 分布,记作 n ~ 2 ( n) ,亦称随 机变量 n2 为 2 变量。 例: n=4 和 n=10 时的 2 p (1 p ) n k k 0,1, , n k 则称这种分布为二项式分布。记做: X ~ b( n, p)
例: n=500,p=0.05 时的二项式分布密度函数图
x=0:50; y=binopdf(x,500,0.05); plot(x,y)
Matlab相关命令介绍
例: x=-8:0.1:8;
y=pdf('norm',x,0,1); y1=pdf('norm',x,1,2); plot(x,y,x,y1,':') 注: y=pdf('norm',x,0,1) 相类似地, y=pdf('beta',x,A,B) y=pdf('bino,x,N,p) y=betapdf(x,A,B) y=binopdf(x,N,p) y=normpdf(x,0,1)
X T Y /n
为服从自由度 n 的 t 分布。记做:T ~ t ( n) 例: t (4) 的分布密度函数图
x=-6:0.01:6; y=tpdf(x,4); plot(x,y)
专用函数计算概率密度函数表
专用函数的累积概率值函数表
常用临界值函数表
常见分布的均值和方差
常见分布的随机数产生
k 1
k 1, 2,
pq k 1 的一般项,于是人们称它为 其右端项是几何级数
几何分布。
例: p=0.5 时的几何分布密度函数图
x=0:30; y=geopdf(x,0.5); plot(x,y)
离散分布:二项式分布
二项式分布属于离散分布
如果随机变量 X 的分布列为:
绘制二维正态分布
x=-20:0.5:20; y=-20:0.5:20; mu=[-1,2]; sigma=[1 1; 1 3]; [X,Y]=meshgrid(x,y); p=mvnpdf([X(:),Y(:)],mu,sigma); P=reshape(p,size(X)); mesh(X,Y,P) title('条件概率密度函数曲线');
指数分布举例
例: =4 时的指数分布密度函数图
x=0:0.1:30; y=exppdf(x,4); plot(x,y)
离散分布:几何分布
几何分布是一种常见的离散分布
在贝努里实验中,每次试验成功的概率为 p,设试验进行
到第 次才出现成功,则 的分布满足:
P ( k ) pq k 1
则称 X 服从参数为 的指数分布。记做: X
在实际应用问题中,等待某特定事物发生所需要的时间往 往服从指数分布。如某些元件的寿命;随机服务系统中的服 务时间;动物的寿命等都常常假定服从指数分布。 指数分布具有无记忆性: P{ X s t | X s} P{ X t }
连续分布:均匀分布
均匀分布(连续分布)
如果随机变量 X 的密度函数为:
1 , a xb f ( x) b a 0, 其他
则称 X 服从均匀分布。记做:
X ~ U[a, b]
均匀分布在实际中经常使用,譬如一个半径为 r 的汽车轮 胎,因为轮胎上的任一点接触地面的可能性是相同的,所以 轮胎圆周接触地面的位置 X 是服从 [0,2r] 上的均匀分布。
为服从自由度 (m, n) 的 F 分布。记做: ~ F ( m, n) F 例: F(4,10) 的分布密度函数图
x=0.01:0.1:8.01; y=fpdf(x,4,10); plot(x,y)
抽样分布: t 分布
设随机变量 X ~ N (0,1), Y ~ 2 ( n) ,且 X 与 Y 相 互独立,则称随机变量
常见分布函数表
连续分布:正态分布
正态分布(连续分布)
如果随机变量 X 的密度函数为:
( X )2 2 2 e
1 f ( x) 2
x , 0
~ N ( , 2 )
则称 X 服从正态分布。记做:X 标准正态分布:N (0, 1)
