不可压缩粘性流体的运动微分方程
粘性流体动力学基础
ρ
1 p dvx fx = ρ x dt 1 p dv y fy = ρ y dt 1 p dvz fz = ρ z dt
方程中, f :作用在单位质量流体上的质量力
1
ρ
p :作用在单位质量流体上的表面力
dv :作用在单位质量流体上的惯性力 dt
这一方程就是以应力形式表示的运动微分方程。
在这一方程中,通常质量力 f x 、 f y 、 f z 是已知的,对不可压缩流体 ρ
τ 也是已知的。方程组中的未知量有:三个法向应力 pii ,六个切向应力 ij ,
三个速度分量vi 。 运动微分方程加上连续性方程共四个, 无法求解 12 个未 知量,下面寻求补充方程。 三 、 切应力分量之间的关系 切应力分量之间存在着一定的联系, 应用力矩平衡原理可以证明切应 力具有对称性。 τ xy = τ yx τ yz = τ zy
τ yz dz τ zy dz τ yz dxdydz τ zy dxdydz + dxdydz dxdydz = 0 y 2 z 2
略去高阶无穷小,可得:
τ yz = τ zy
同理可得:
τ xy = τ yx
τ xz = τ zx
可见应力分量中的切应力是两两对称的。 四 、 切应力与变形速度的关系 牛顿内摩擦定律(平面流动) dv dα τ = x =
M ,六面体为 ABCD, A 点的应力为:
pxx τ yx τ zx
τ xy
p yy
τ zy
τ xz τ yz
pzz
其方向确定为:法向应力以内法线方向为正,切向应力(正) ,过 A 点 的三个面上切向应力与坐标方向相反,其它三个面则相同。 采用泰勒级数展开并取前二项可写出其它三个面上的应力分量。
不可压缩粘性流体的流动

§7-2 不可压粘性流体运动的
基本方程简介
将微元体所受的惯性力、质量力和 表面力代入牛顿第二定理 ΣF = ma 可得不可压粘流的运动微分方程:N-S方程
∂p ∂ 2u ∂ 2u ∂ 2u ax = fx − + µ( 2 + + ) 2 2 ρ∂x ∂x ∂y ∂z
ay
∂p ∂ 2v ∂ 2v ∂ 2v = fy − + µ( 2 + + ) 2 2 ρ∂y ∂x ∂y ∂z
引入特征量:将N-S方程中的各物理量无 量纲化。
x y u v p x ′ = ,y ′ = ,u ′ = ,v ′ = , p ′ = L δ U V P 这些无量纲化的物理量与1具有相同的量级
N-S方程的无量纲化
∂u ′ VL ∂u ′ P ∂p ′ ν ∂ 2u ′ L 2 ∂ 2u ′ u′ +( ) ′ v = −( 2 ) + [ 2 +( ) ] 2 ∂x ′ ∂y ′ δ ∂y ′ Uδ ρU ∂x ′ UL ∂x ′ 1 2 ×1 1 1 1 ε 1×1 ε ×1 ε
理想流体没有切向力,只有法向力 pii 实际流体既有法向力,也有切向力,如图, 由于应力的对称性,应力中只有6个分量 是独立的。它们是: 主应力: 切应力:
p xx
p yy
p zz
p xz = p zx
p xy = p yx p zy = p yz
对不可压流体,主应力可表示为: ∂u p xx = − p + 2µ ∂x ∂v p yy = − p + 2µ ∂y ∂w p zz = − p + 2µ ∂z 一般情况下,三个法向应力不相等, 其关系是: 1 − p = ( p xx + p yy + p zz ) 3
流体力学第七章不可压缩流体动力学基础

第七章不可压缩流体动力学基础在前面的章节中,我们学习了理想流体和粘性流体的流动分析,按照水力学的观点,求得平均量。
但是,很多问题需要求得更加详细的信息,如流速、压强等流动参数在二个或三个坐标轴方向上的分布情况。
本章的内容介绍流体运动的基本规律、基本方程、定解条件和解决流体问题的基本方法。
第一节流体微团的运动分析运动方式:①移动或单纯的位移(平移)②旋转③线性变形④角变形。
位移和旋转可以完全比拟于刚体运动,至于线性变形和脚变形有时统称为变形运动则是基于液体的易流动性而特有的运动形式,在刚体是没有的。
在直角坐标系中取微小立方体进行研究。
一、平移:如果图(a )所示的基体各角点的质点速度向量完全相同时,则构成了液体基体的单纯位移,其移动速度为z y x u u u 、、。
基体在运动中可能沿直线也可能沿曲线运动,但其方位与形状都和原来一样(立方基体各边的长度保持不变)。
二、线变形:从图(b )中可以看出,由于沿y 轴的速度分量,B 点和C 点都比A 点和D 点大了dy yu y ∂∂,而yu y ∂∂就代表1=dy 时液体基体运动时,在单位时间内沿y 轴方向的伸长率。
x u x ∂∂,y u y ∂∂,zuz ∂∂ 三、角变形(角变形速度)ddd DCABCDBAdt yu dy dt dy y u d x x ∂∂=⋅∂∂=α dt x udx dt dx x u d yy∂∂=⋅∂∂=β θβθα+=-d d 2βαθd d -=∴ 角变形: ⎪⎪⎭⎫⎝⎛∂∂+∂∂=+=-=x u y u d d d y x z 212βαθαθ ⎪⎭⎫⎝⎛∂∂+∂∂=x u z u z x y 21θ⎪⎪⎭⎫⎝⎛∂∂+∂∂=y u z u z y x 21θ 四、旋转(旋转角速度)⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=-=y u x u x y z 21θω ⎪⎪⎭⎫⎝⎛∂∂-∂∂=z u y u y zx 21ω 即, ⎪⎭⎫⎝⎛∂∂-∂∂=x u z u z x y 21ωzyxu u u z y x k ji ∂∂∂∂∂∂=21ω 那么,代入欧拉加速度表达式,得:z x x x x x x z y y z z y y y y y y y x z z x x z z z z z z z y x x y y x x y du u u u u u u u dt t xu u u u u u u u dt t y u u uu u u u u dt t z αθθωωαθθωωαθθωω∂∂⎫==++++-⎪∂∂⎪∂∂∂⎪==++++-⎬∂∂⎪⎪∂∂∂==++++-⎪∂∂⎭各项含义: (1) 平移速度(2)线变形运动所引起的速度增量(3)(4)角变形运动所引起的速度增量 (5)(6)微团的旋转运动所产生的速度增量流体微团的运动可分解为平移运动,旋转运动,线变形运动和角变形运动之和。
粘性流体的不可压缩流动

Chapter 9-1 粘性不可压缩流体流动§1概述一、粘性不可压缩流动模型1、关于粘性 粘性摩擦的存在必导致绕流阻力的存在,运动的衰减及涡量的扩散。
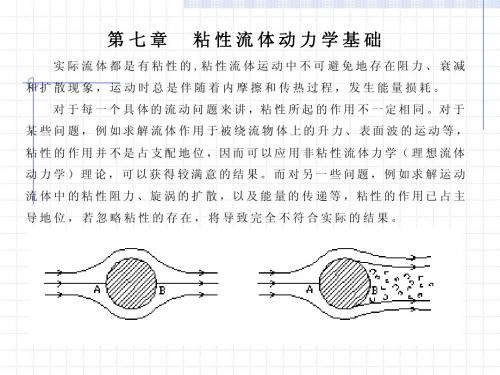
在大e R 数下,惯性力>>粘性力,采用理想流体模型,理想流体理论对不脱体绕流情况下的升力,压力分布和速度分布给出了符合实际的结果,但在阻力等与粘性效应相关的问题上却无能为力。
因而,在研究阻力等起源于粘性的现象时须抛弃理想流体假设。
在小e R 数和中e R 数情况下,粘性作用不可忽略。
2、关于不可压缩流动(流体的压缩性对流动的影响可略)液体压缩系数小,一般可认为不可压缩(极端情况如激波等除外)。
气体在低速运动(速度远小于声速)、非定常时速度变化缓慢,且重力方向上流场的尺度<10km 时,可略其压缩性。
(当研究对流层(~10km )内大气运动时,不能忽略重力场引起的压缩效应)。
3、基本方程组和边界条件均质不可压缩流体.const ρ=,且温度变化小,const μ=,故有20V dV pF V dt γρ⎫∇⋅=⎪⎬∇=-+∇⎪⎭求速度和压力场的完备方程组。
能量方程22:dUk T S S dtρμ=∇+ 用于求温度场 本构方程 2P p I S μ=-+ 用于求应力边界条件:在固壁表面上,流体的法向和切向速度分别等于固体表面的对应速度分量。
在自由表面上,0, 0nn n p p p τ=-=。
二、粘性流动分类,求解问题的几种途径层流:流体运动规则、稳定,各部分分层流动互不掺混,质点轨迹光滑。
脉线清晰 湍流:流体运动极不规则、极不稳定,伴有高频扰动,各部分激烈掺混,质点轨迹杂乱无章。
决定流动状态的参数是e R 数(Batchlor page255),e R <<2000 一定是层流,此时粘性力足以保持流动的稳定。
层流:极少有准确解(某些特殊的简单问题,非线性方程得以简化) 近似解法:大e R 数,边界层理论小e R 数,部分或全部忽略惯性力。
不可压缩粘性流体动力学基础_OK
uz y
u y z
zx
xz
1 ux 2 z
uz x
(7—3)
14
江汉大学化环学院
流体力学与流体机械
综上所述,可写出表示流体微团运动的基本形式如下:
表示平移的平移速度:u x、u、y u。z
表示线变形的线变形速度(又称线变率):
x
u x x
y
u y y
z
u z y
表示角变形的角变形速度(又称角变率):
一、流体微团(Material Elements of Fluid) 流体微团是由大量的流体质点所组成的一个微小质团,它
具有微小的体积,是研究流体运动的一个基本单元。
4
江汉大学化环学院
流体力学与流体机械
流体微团的尺度在微观上足够大,大到能包含大量的 分子,使得在统计平均后能得到其物理量的确定值,质 点的尺度在宏观上又足够小,远小于所研究问题的特征 尺度,使得其平均物理量可看成是均匀的;而且可以把 流体微团看成是几何上的一个点。
dx dy dz
x y z
21
江汉大学化环学院
流体力学与流体机械
在给定瞬时,在漩涡场中任取一个不是涡线的封闭曲线, 通过这条曲线上每一点作一根涡线,这些涡线就构成一个管 状曲面,称为涡管(Vortex Tube);涡管中充满着作旋涡运 动的流体,称为涡束,或称为元涡(Vortex Filament)。 涡通量(Vortex Flux)或旋涡强度(Intensity of Vorticity),以 J表示。元涡的涡通量为微元涡的断面积和速度涡量(简称涡 量)的乘积,即
y
ux d yd t y
D
C
C
uy
u y y
dy
第六章——不可压缩粘性流体的内部流动

Du Dt
fx
1
p x
2u x2
2u y2
2u z 2
1
3
( V ) x
利用已知条件:
(1) =常数;=常数
(2)定常流动: 0
t
(3)充分发展流动:
u x
2u x2
0
,
u u( y )
(4)质量力沿x分量: fx 0
化简后得:
dp dx
d2u dy2
17
6.3 平板间的层流
压强p与y无关,速度u与x无关,积分得:
单位宽度上的流量为:
Q
h
udy
h g sin ( y2 2hy)dy gh3 sin
0
0 2
3
25
6.4 管内湍流 1. 湍流脉动现象与值 湍流(紊流) :流动雷诺数Re> 2300的流动 湍流脉动现象:湍流流动参数随时间和空间作随机变化的现象。
26
6.4 管内湍流
图6-10 某热线仪测得的管内轴向瞬时速度
6
6.1 流动阻力
【解】油的平均流速为 V G 0.329(m / s)
A
流动沿程阻力损失为:
hf
l
d
V2 2g
9.94(m)
建立入口和出口间的伯努利方程
V12 2g
z1
p1
g
V22 2g
z2
p2
g
hw
出口端的油压
p0 p2 (V12 V22 ) g(z1 z2 ) p1 ghw 305090(Pa)
u U (1 y ) 2h
6-26
此时,平板间的速度随y呈线性分布,这种由上平板运动带
动流体产生的流动称为库艾特剪切流
纳维斯托克斯方程(NS方程)详细推导

本构方程和NS方程
粘性流体动力学基础
平移运动、旋转运动、线变形运动和角变形运动 右图为任意t时刻在平面流场中所取的一个正方形流体微团。由 于流体微团上各点的运动速度不一致,经过微小的时间间隔后, 该流体微团的形状和大小会发生变化,变成了斜四边形。
本构方程和NS方程
粘性流体动力学基础
流体微团的运动形式
流体质点运动的分析
•分析流场中任意流体微团运动是研究整个流场运动的基础。 •流体运动要比刚体运动复杂得多,流体微团基本运动形式 有平移运动、旋转运动、线变形和角变形运动等。实际运 动也可能遇到只有其中的某几种形式所组成。 •当流体微团无限小而变成质点时,其运动也是由平动、线 变形、角变形及旋转四种基本形式所组成。
理想流体的运动微分方程
理想流体运动微分方程式是研究流体运动学的重要理论基 础。可以用牛顿第二定律加以推导。 a F 受力分析:
1、质量力:
fxρdxdydz
x轴正方向
2、表面力:
切向应力=0(理想流体) 法向应力=压强
p
p dx x 2
p
p dx x 2
x轴正方向
x轴负方向
本构方程和NS方程
微元体上X和Z方向的表面力
yx xy
yz zy
zx xz
本构方程和NS方程
粘性流体动力学基础
微元体表面力的总力分量
X方向的表面力:
yx x zx dxdydz dydxdz dzdxdy x y z x yx zx dxdydz x y z
旋转角速度 把对角线的旋转角速度定义为整个流体微团在平 面上的旋转角速度。
;
;
1 u z u y x ( ) 2 y z
流体力学第八章答案

流体力学第八章答案【篇一:流体力学第8、10、11章课后习题】>一、主要内容(一)边界层的基本概念与特征1、基本概念:绕物体流动时物体壁面附近存在一个薄层,其内部存在着很大的速度梯度和漩涡,粘性影响不能忽略,我们把这一薄层称为边界层。
2、基本特征:(1)与物体的长度相比,边界层的厚度很小;(2)边界层内沿边界层厚度方向的速度变化非常急剧,即速度梯度很大;(3)边界层沿着流体流动的方向逐渐增厚;(4)由于边界层很薄,因而可以近似地认为边界层中各截面上压强等于同一截面上边界层外边界上的压强;(5)在边界层内粘性力和惯性力是同一数量级;(6)边界层内流体的流动与管内流动一样,也可以有层流和紊流2种状态。
(二)层流边界层的微分方程(普朗特边界层方程)??v?vy?2v1?p?vy?????vx?x?y??x?y2????p??0?y???v?vy???0?x?y??其边界条件为:在y?0处,vx?vy?0 在y??处,vx?v(x)(三)边界层的厚度从平板表面沿外法线到流速为主流99%的距离,称为边界层的厚度,以?表示。
边界层的厚度?顺流逐渐加厚,因为边界的影响是随着边界的长度逐渐向流区内延伸的。
图8-1 平板边界层的厚度1、位移厚度或排挤厚度?1?1?2、动量损失厚度?2?vx1?(v?v)dy?(1?)dy x??00vv?2?1?v2???vx(v?vx)dy???vxv(1?x)dy vv(四)边界层的动量积分关系式??2???p?vdy?v?vdy?????wdx xx??00?x?x?x对于平板上的层流边界层,在整个边界层内每一点的压强都是相同的,即p?常数。
这样,边界层的动量积分关系式变为?wd?2d?vdy?vvdy?? x?x??00dxdx?二、本章难点(一)平板层流边界层的近似计算根据三个关系式:(1)平板层流边界层的动量积分关系式;(2)层流边界层内的速度分布关系式;(3)切向应力关系式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
边界层内,这是由于层外的流体质点不断地穿入到边界层里 去的缘故。
总结上面所述,边界层的基本特征有:
• 与物体的长度相比,边界层的厚度很小; •边界层内沿边界层厚度的速度变化非常急剧,即速
度梯度很大;
•边界层沿着流体流动的方向逐渐增厚;
•由于边界层很薄,因而可近似地认为,边界层中各
截面上的压强等于同一截面上边界层外边界上的压强;
v v y x ~1 y x
为了便于讨论,将各项的数量级记载方程组(8-37)相应项 的下面。现在来分析方程组(8-37)各项的数量级,以达到 简化方程的目的。
v v v x x 惯性项 vx 和 vy 具有相同的数量级1,而惯性项 vx xy y x v y v 和 y y 也具有另一个相同的数量级 ,比较这两个惯
现在来研究粘性流体在大雷诺数下平滑地绕流某静止 物体(例如机翼的翼型,图8-9)的情况。在紧靠物体表 面的薄层内,流速将由物体表面上的零值迅速地增加到与 来流速度 v 同数量级的大小,这种在大雷诺数下紧靠物 体表面流速从零急剧增加到与来流速度相同数量级的薄层 称为边界层。在边界层内,流体在物体表面法线方向上的 速度梯度很大,即使粘度很小的流体,表现出的粘滞力也 较大,决不能忽略。所以,边界层内的流体有相当大的涡 通量。当边界层内的有旋流离开物体而流入下游时,在物 体后形成尾涡区域。在边界层外,速度梯度很小,即使粘 度较大的流体,粘滞力也很小,可以忽略不计。所以可以 认为,在边界层外的流动是无旋的势流。
2v x ~1 2 x
v 1 x ~ y
2出其它各量的数量级,由连续方程 因此 v ~ ,于是又得到以下数量级: y
v y ~ x 2 v y ~ 2 x v y ~1 y 2 v 1 y ~ 2 y
(8-37)
v v y x 0 x y 1 1
式中 Re l vl 。很显然,在边界层内, x与v、x与l 以及y v 与 是同一数量级,于是可取 v ~ 1, x ~ 1和y ~ x
(符号~表示数量级相同),所以得到如下一些数量级:
v x ~1 x
和惯性项
vx
v x x
p dv v x dx
具有同一个数量级。
对于在壁面上的各点, y 0, vx v y 0, 由式(8-38) 的第一式可得
2vx y 2 1 dp 1 dv v dx y 0 dx
(8-40)
方程组(8-38)是在物体壁面为平面的假设下得到的, 但是,对于曲面物体,只要壁面上任何点的曲率半径与该 处边界层厚度相比很大时(机翼翼型和叶片叶型即如此), 该方程组仍然是适用的,并具有足够的精确度。这时,应 用曲线坐标,x轴沿着物体的曲面,y轴垂直于曲面。
•在边界层内粘滞力和惯性力是同一数量级的;
•边界层内流体的流动与管内流动一样,也可以有层
流和紊流两种流动状态。
对平板而言,层流转变为紊流的临界雷诺数为
Re x 5 105 ~ 3 106
边界层从层流转变为紊流的临界雷诺数的大小决定于许多因 素,如前方来流的紊流度、物体壁面的粗糙度等。实验证明, 增加紊流度或增加粗糙度都会使临界雷诺数值降低,即提早 使层流转变为紊流。如机翼前端的边界层很薄,不大的粗糙 度凸出就会透过边界层,导致层流变为紊流。
由此可见,当粘性流体绕过物体流动时,可以将物体外面的 流场划分为两个区域:在边界层和尾涡区域内,必须考虑流 体的粘滞力,它应当被看作是粘性流体的有旋流动;在边界 层和尾涡区以外的区域内,粘滞力很小,可以看作是理想流 体的无旋流动。实际上,边界层内、外区域并没有一个明显 的分界面,一般在实际应用中规定从固体壁面沿外法线到速 度达到势流速度的99%处距离为边界层的厚度,以 表示, 见图8-9。解决大雷诺数下绕过物体流动的近似方法是以边界 层理论为基础的。 用微型测速管直接测量紧靠机翼表面附近的流速得知, 实际上边界层很薄,通常边界层的厚度仅为弦长的几百分之 一。例如在汽轮机叶片出汽边上,最大边界层厚度一般为零 点几毫米。从图8-9中可以看出,流体在前驻点O处速度为零, 所以边界层的厚度在前驻点处等于零,然后沿着流动方向逐 渐增加。为了清晰起见,在图8-9上将边界层的尺寸放大了。 另外,边界层的外边界和流线并不重合,流线伸入
p xx
dy
xz
zx
A
xy
xy
fy
xy
fz
y
yx
dx x
zx zx dz z
fx
o z
第一个下标表示应力所在平面的法线方向 第二个下标表示应力本身的方向。
y
yx
yx y
dy
xy
dy
M
xy
xy x
dx
dx
yx
广义牛顿内 摩擦定律
其意义为:切向应力等于动力粘度和角变 形速度的乘积。
在粘性流体中,由于粘性的影响,流体微 团除发生角变形以外,同时也发生线变形。
p xx p yy p zz v x 2 p 2 v x 3 v y 2 p 2 v y 3 v z 2 p 2 v z 3
性项的数量级,方程组(8-37)中第二式中各惯性项可以 2 v 与 2 v x 忽略掉。另外,比较各粘性项的数量级,可知 2x 2
2 v x 比较,x2
y x 2 v 2 v y y 2 v 可以略去;又 x2 与 y2 比较, 2y 可以略去; x 2 v 2 v 2 v 最后,比较 y2x 和 y2y 的数量级,y2y 也可以略去。 2 v 于是在方程组(8-37)的粘性项中只剩第一式中的一项 y2x 。
vx x vy y
x
y 2
p 0 y v x v y 0 x y
(8-38)
其边界条件为
在y 0处 在y 处
v x v x
vx v y 0
(8-39)
式中 vx 是边界层外边界上势流的速度分布,可由势流理论 来决定。对于沿平板流动,vx v。 从方程组(8-38)第二式得到一个很重要的结论:在边 界层内压强p与y无关,即边界层横截面上各点的压强相等,
o 图8-2 分析切向应力之间的关系用图
x
根据达朗伯原理,作用于微元平行六面体上的各力对通过中心 M并与z轴相平行的轴的力矩之和应等于零。又由于质量力和 惯性力对该轴的力矩是四阶无穷小量,可以略去不计,故有
yx xy dz dy dx dx yx dxdz yx dy dxdy xy dydz xy dx dydz 0 2 y 2 2 x 2
现将切向应力和法向应力的关系式代入 式(8-1),化简可得不可压缩粘性流体的运动微 分方程:
纳维-斯托克斯(Navier-Stokes)方程
如果是没有粘性的理想流体,则 为 零,于是纳维-斯托克斯方程变成理想流体 的欧拉运动微分方程。
dv x dv y dv z 如果没有加速度,则 、 、 dt dt dt
(8-36)
v
y
o x
l
图8-11
vx
x
推导层流边界层的微分方程用图
可以利用边界层每一处的厚度都很小的特征,来比较方程 组(8-36)中各项的数量级,权衡主次,忽略次要项,这 样便可大大简化该方程组。
即 l或 足不等式 边界层的厚度 与平板的长度 l 相比较是很小的, ,而y的数值限制在边界层内,并满 l 1
现在根据边界层的特征,利用不可压缩粘性流体 的运动微分方程来研究边界层内流体的运动规律。为 简单起见,只讨论流体沿平板作定常的平面流动,x轴与 壁面相重合,如图8-11所示。假定边界层内的流动全 是层流,忽略质量力,则不可压缩粘性流体平面定常 流动的微分方程和连续方程为
2vx 2vx v x v x 1 p vx vy x 2 y 2 x y x 2v y 2v y 1 p vx vy x 2 x y y y 2 v x v y 0 x y v y v y
0 y
为了把方程组(8-36)变换成无量纲的,引入坐标与平板 2 长度 l 、分速度与来流速度 v ,压强与 v 之比,即引 入无量纲物理量:
x x l
y y l
vx v x v
vy
vy v
p p 2 v
将它们代入方程组(8-36),整理后得
v v p 1 2 v 2 v x x x x v v x y 2 2 Re l x x y x y 1 1 2 1 1 1 2 2 2 v v p 1 v v y y y y v v x y 2 2 x x y y Re l y 1 2 1 1
根据边界层的特征,在边界层内惯性项和粘性项具有 同样的数量级,由方程组(8-37)可知,必须使 1 Re l 和 2
同数量级,所以 l ~ 1 Re l ,即 反比于 雷诺数越大,边界层相对厚度越小。
Re l
。这表明,
这样,将式(8-37)中的某些项略去,再变换成有量纲 量,便得到了层流边界层的微分方程(称为普朗特边界层方 程): v x v x 2vx 1 p
p px 。而在边界层外边界上,边界层内的流动与外部 有势流动相合。所以压强 px 可以根据势流的速度 vx 由 伯努力方程来决定,即 p 1 v 2 常数 2 dp dv v dx dx
因为 v ~ 1 ,即 vx ~ v (或v) ,这就是说,压强项 1 x
都为零,于是上述方程变成欧拉平衡微分 方程。
所以说,上述纳维-斯托克斯方程式不 可压缩流体的最普遍的运动微分方程。
