2003年全国初中数学竞赛天津赛区
03年全国初中数学竞赛
2003年全国初中数学竞赛
嘉兴市评奖结果公告
2003年全国初中数学竞赛于2003年4月6日举行。
嘉兴市由嘉兴市教育局教研室、嘉兴市教育学会中学数学分会、嘉兴市数学会联合组织,共有6270名学生参加了本次竞赛,经成绩评定,确定嘉兴市团体优胜奖15名,个人一等奖68名、二等奖124名、三等奖127名。
现将结果公布如下:
团体优胜:
海盐县武原中学平湖市东湖中学
嘉兴三中求是实验中学
邵逸夫中学秀洲现代实验学校
嘉善泗洲中学桐乡六中
嘉兴市洪波中学嘉善四中
嘉兴秀中分校嘉善一中
海宁一中海盐县元通中学
海盐县实验中学
个人获奖:
一等奖
二等奖
嘉兴市教育局教研室嘉兴市教育学会中学数学分会
嘉兴市数学会
2003年5月8日。
2003年全国初中数学竞赛天津赛区初赛

5 EC 1 2 18 1 2 18第 4 期25 2003年全国初中数学竞赛天津赛区初赛一、选择题(每小题5 分,共30 分)(2003 - 03 - 23)AD 将△ABC 分成2 个等腰三角形. 则满足上述条件1. 化简2 4 + 2 3 - 21 - 12 3 为( ) .(A) 5 - 4 3 (B) 4 3 - 1 (C) 5 (D) 12.在凸八边形的所有内角中, 钝角至少有( ) 个.(A) 3 (B) 5 (C) 7 (D) 83.如图1 ,用3 个边长为1 的正方形组成一个对称图形,则能将其完全覆盖的圆的的不同形状(相似的认为是同一形状) 的△ABC 最多有个.三、解答题(每小题20 分,共60 分)12.有18 支足球队进行单循环赛,每个参赛队同其他各队都进行一场比赛. 假设比赛的结果没有平局,如果用a i和b i分别表示第i ( i = 1 ,2 ,3 , , 18) 支球队在整个赛程中胜与负的局数,求证:最小半径为( ) . a2+ a2+ + a2= b2+ b2+ + b2.(A) 2 (B) 5213.如图2 , PA 、PB 与⊙O 切于A 、B(C) 54 (D)5 17 图116两点, PC 是任意一条割线,且交⊙O于4.已知A 、B 为平面上的 2 个定点,且AB =5. 若点A 、B 到直线l 的距离分别等于2 、3 ,则满足条件的直线l 共有( ) 条.(A) 2 (B) 3 (C) 4 (D) 无数5.已知x 、y 、z 为3 个非负实数,且满足3 x + 2 y + z = 5 , x + y - z = 2. 若s = 2 x + y - z , 则s 的最大值与最小值的和为( ) .(A) 5 (B) 23 (C) 27 (D) 354 4 46. 使得2 n ( n + 1) ( n + 2) ( n + 3) + 12 可表示为2 个正整数平方和的自然数n ( ) .(A)不存在(B) 有1 个(C) 有2 个(D) 有无数个二、填空题(每小题6 分,共30 分)7.某编辑用0~9 这10 个数字给一本书的各页标上页码. 若共写了636 个数字, 则该书有点E、C , 交AB 于点AC2AD 图2D. 求证:BC2=BD.14. 已知函数y = ( a + 2) x2- 2 ( a2- 1) x + 1 ,其中自变量x 为正整数, a 也是正整数. 求x 为何值时,函数值最小.参考答案一、1. (C) .2. (B) .因为一个凸多边形的外角至多有 3 个钝角,故其内角中最多有 3 个锐角,所以凸八边形的内角中至少有 5 个钝角.3. (D) .如图 3 得a2+ 1 = r2,页.8.设△ABC 的面积是1 , D 是边BC 上一点,且(2 - a) 2 +122= r2.BD= 1. 若在边AC 上取一点E ,使四边形ABDE 的解得a =13, r =5 17. 图3DC 2 16 16面积为4,则A E的值为.9.已知二次函数y = ax2+ bx + c ,一次函数y =k24. (B) .以点A 、B 为圆心,半径分别为2 、3 的两圆的公切线的条数,即为所求.5. (A) .k ( x - 1) - 4 . 若它们的图像对于任意的实数k 都只有一个公共点,则二次函数的解析式为. x = s - 2 ≥0 ,10.已知α、β是方程x2α4 + 3β的值为. - x - 1 = 0 的两个根. 则3 x + 2 y + z = 5 ,由x + y - z = 2 ,2 x + y - z = s得y = 5 -4s31≥0 ,11.△ABC 中,有一内角为36°,过顶点A 的直线z = 1 - 3 s ≥0.26 中等数学。
2003年全国初中数学联合竞赛试题及解答

为使方程有正整数根要求 4 y 50 4 y 2 y 4 2500 99 y 是完全平方数.
2
经试验得到 y 25 时 是完全平方数,解出 x 20 或 30,即 2025 或者 3025 满足题意. 方法二: 设这两个两位数分别为 x , y ,则 x y 100 x y
2
由于 △ABC 是直角三角形,所以抛物线与 x 轴的交点必然在 y 轴两边,所以
c 再由射影定理得到 c 2 ,所以 ac 1 . a
c 0. a
9 3 2.设 m 是整数,且方程 3x2+mx-2=0 的两根都大于 而小于 ,则 m=_________. 5 7
【答】 4. 考虑二次函数 f ( x) 3x2 mx 2 与二次函数的两个交点, 由于 3 大于 0, 图像开口向上.
所以 故:
S△ ADE AD AE 1 AE 3 1 , S△ ABC AB AC 3 AC 4
AE 3 CE 1 ,所以 AC 4 EA 3
B
C
6.如图,在平行□ABCD 中,过 A,B,C 三点的圆交 AD 于 E,且与 CD 相切.若 AB=4, BE=5,则 DE 的长为( A.3. 【答】D. 连接 CE,由于 ABCE 四点共圆,所以:∠DEC=∠CBA, 在平行四边形 ABCD 中,∠D=∠ABC, 所以有∠DEC=∠D=∠ABC, 同时,CD 平行于 AB,且 DC 与圆相切, 可知:C 为弧 AB 中点,所以∠CEB=∠CBA,且∠DCE=∠CBE, 故由∠DEC=∠D 可知△DEC 为等腰三角形,CD=CE=AB=4, 由∠DEC=∠CBE 和∠D=∠ABC=∠CEB 可知△CDE∽△BCE, 所以:
历年初中数学竞赛真题库含答案
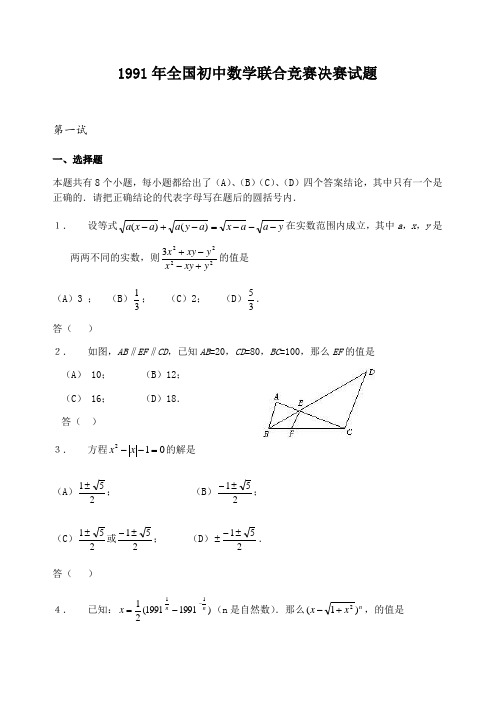
1991年全国初中数学联合竞赛决赛试题第一试一、选择题本题共有8个小题,每小题都给出了(A )、(B )(C )、(D )四个答案结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1. 设等式y a a x a y a a x a ---=-+-)()(在实数范围内成立,其中a ,x ,y 是两两不同的实数,则22223yxy x y xy x +--+的值是 (A )3 ; (B )31; (C )2; (D )35. 答( )2. 如图,AB ‖EF ‖CD ,已知AB =20,CD =80,BC =100,那么EF 的值是(A ) 10; (B )12;(C ) 16; (D )18.答( )3. 方程012=--x x 的解是(A )251±; (B )251±-; (C )251±或251±-; (D )251±-±. 答( )4.已知:)19911991(2111n n x --=(n 是自然数).那么n x x )1(2+-,的值是(A)11991-; (B)11991--;(C)1991)1(n -; (D)11991)1(--n .答( )5. 若M n 1210099321=⨯⨯⨯⨯⨯ ,其中M为自然数,n 为使得等式成立的最大的自然数,则M(A)能被2整除,但不能被3整除;(B)能被3整除,但不能被2整除;(C)能被4整除,但不能被3整除;(D)不能被3整除,也不能被2整除.答( )6. 若a ,c ,d 是整数,b 是正整数,且满足c b a =+,d c b =+,a d c =+,那么 d c b a +++的最大值是(A)1-;(B)5-;(C)0;(D)1.答( )7. 如图,正方形OPQR 内接于ΔABC .已知ΔAOR 、ΔBOP 和ΔCRQ 的面积分别是11=S ,32=S 和13=S ,那么,正方形OPQR 的边长是 (A)2;(B)3;(C)2 ;(D)3.答( )8. 在锐角ΔABC 中,1=AC ,c AB =, 60=∠A ,ΔABC 的外接圆半径R ≤1,则 (A)21< c < 2 ; (B)0< c ≤21; 答( )(C )c > 2; (D )c = 2.答( )二、填空题1.E是平行四边形ABCD 中BC 边的中点,AE 交对角线BD 于G ,如果ΔBEG 的面积是1,则平行四边形ABCD 的面积是 . 2.已知关于x 的一元二次方程02=++c bx ax 没有实数解.甲由于看错了二次项系数,误求得两根为2和4;乙由于看错了某一项系数的符号,误求得两根为-1和4,那么,=+ac b 32 .3.设m ,n ,p ,q 为非负数,且对一切x >0,qpn m x x x x )1(1)1(+=-+恒成立,则 =++q p n m 22)2( .4.四边形ABCD 中,∠ ABC 135=,∠BCD 120=,AB 6=,BC 35-=,CD = 6,则AD = .第二试x + y , x - y , x y , yx 四个数中的三个又相同的数值,求出所有具有这样性质的数对(x , y ).二、ΔABC中,AB<AC<BC,D点在BC上,E点在BA的延长线上,且BD=BE=AC,ΔBDE的外接圆与ΔABC的外接圆交于F点(如图).求证:BF=AF+CF三、将正方形ABCD分割为2n个相等的小方格(n是自然数),把相对的顶点A,C染成红色,把B,D染成蓝色,其他交点任意染成红、蓝两色中的一种颜色.证明:恰有三个顶点同色的小方格的数目必是偶数.1992年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.满足1=+-ab b a 的非负整数),(b a 的个数是(A)1; (B)2; (C)3; (D)4.2.若0x 是一元二次方程)0(02≠=++a c bx ax 的根,则判别式ac b 42-=∆与平方式20)2(b ax M +=的关系是(A)∆>M (B)∆=M (C)∆>M ; (D)不确定.3.若01132=+-x x ,则44-+x x 的个位数字是(A)1; (B)3; (C)5; (D)7.答( )4.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为(A)7; (B)6; (C)5; (D)4.答( )5.如图,正比例函数)0(>==a ax y x y 和的图像与反比例函数)0(>=k xk y 的图像分别相交于A 点和C 点.若AOB Rt ∆和COD ∆的面积分别为S 1和S 2,则S 1与S 2的关系是 (A)21S S > (B)21S S =(C)21S S < (D)不确定 答( )6.在一个由88⨯个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为1S ,把圆周经过的所有小方格的圆内部分的面积之和记为2S ,则21S S 的整数部分是 (A)0; (B)1; (C)2; (D)3.答( )7.如图,在等腰梯形ABCD 中, AB //CD , AB=2CD ,︒=∠60A ,又E 是底边AB 上一点,且FE=FB=AC , FA=AB .则AE :EB 等于(A)1:2 (B)1:3(C)2:5 (D)3:10答( )8.设9321,,,,x x x x ⋅⋅⋅均为正整数,且921x x x <⋅⋅⋅<<,220921=+⋅⋅⋅++x x x ,则当54321x x x x x ++++的值最大时,19x x -的最小值是(A)8; (B)9; (C)10; (D)11.答( )二.填空题1.若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________.2.若0≠x ,则x x x x 44211+-++的最大值是__________.3.在ABC ∆中,B A C ∠∠=∠和,90 的平分线相交于P 点,又AB PE ⊥于E 点,若3,2==AC BC ,则=⋅EB AE .4.若b a ,都是正实数,且0111=+--b a b a ,则=+33)()(ba ab . 第二试一、设等腰三角形的一腰与底边的长分别是方程062=+-a x x 的两根,当这样的三角形只有一个时,求a 的取值范围.二、如图,在ABC ∆中,D AC AB ,=是底边BC 上一点,E 是线段AD 上一点,且A CED BED ∠=∠=∠2.求证:CD BD 2=.三、某个信封上的两个邮政编码M 和N 均由0,1,2,3,5,6这六个不同数字组成,现有四个编码如下:A :320651B :105263C :612305D :316250已知编码A 、B 、C 、D 各恰有两个数字的位置与M 和N 相同.D 恰有三个数字的位置与M 和N 相同.试求:M 和N.1993年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个小题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.多项式1612+-x x 除以12-x 的余式是(A)1; (B)-1; (C)1-x ; (D)1+x ;2.对于命题Ⅰ.内角相等的圆内接五边形是正五边形.Ⅱ.内角相等的圆内接四边形是正四边形,以下四个结论中正确的是(A )Ⅰ,Ⅱ都对 (B )Ⅰ对,Ⅱ错 (C )Ⅰ错,Ⅱ对. (D )Ⅰ,Ⅱ都错.3.设x 是实数,11++-=x x y .下列四个结论:Ⅰ.y 没有最小值;Ⅱ.只有一个x 使y 取到最小值;Ⅲ.有有限多个x (不止一个)使y 取到最大值;Ⅳ.有无穷多个x 使y 取到最小值.其中正确的是(A )Ⅰ (B )Ⅱ (C )Ⅲ (D )Ⅳ4.实数54321,,,,x x x x x 满足方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=++=++=++.;;;;52154154354324321321a x x x a x x x a x x x a x x x a x x x其中54321,,,,a a a a a 是实常数,且54321a a a a a >>>>,则54321,,,,x x x x x 的大小顺序是(A)54321x x x x x >>>>; (B )53124x x x x x >>>>;(C )52413x x x x x >>>>; (D )24135x x x x x >>>>.5.不等式73)1(12+<-<-x x x 的整数解的个解(A )等于4 (B )小于4 (C )大于5 (D )等于56.在ABC ∆中,BC AO O A =∠,,是垂心是钝角,则)cos(OCB OBC ∠+∠的值是 (A)22- (B)22 (C)23 (D)21-. 答( )7.锐角三角ABC 的三边是a , b , c ,它的外心到三边的距离分别为m , n ,p ,那么m :n :p 等于 (A)c b a 1:1:1; (B)c b a :: (C)C B A cos :cos :cos (D)C B A sin :sin :sin .答( )8.13333)919294(3-+-可以化简成 (A))12(333+; (B))12(333- (C)123- (D)123+答( )二.填空题1. 当x 变化时,分式15632212++++x x x x 的最小值是___________. 2.放有小球的1993个盒子从左到右排成一行,如果最左面的盒里有7个小球,且每四个相邻的盒里共有30个小球,那么最右面的盒里有__________个小球.3.若方程k x x =--)4)(1(22有四个非零实根,且它们在数轴上对应的四个点等距排列,则k =____________.4.锐角三角形ABC 中,︒=∠30A .以BC 边为直径作圆,与AB , AC分别交于D , E ,连接DE , 把三角形ABC 分成三角形ADE 与四边形BDEC ,设它们的面积分别为S 1, S 2,则S 1:S 2=___________. 第二试一.设H 是等腰三角形ABC 垂心,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积HBC ABC S S ∆∆⋅的值变小,变大,还是不变?证明你的结论.二.ABC ∆中, BC =5, AC =12, AB =13, 在边AB ,AC 上分别取点D , E , 使线段DE 将ABC ∆分成面积相等的两部分.试求这样的线段DE 的最小长度.三.已知方程0022=++=++b cx x c bx x 及分别各有两个整数根21,x x 及21,x x '',且,021>x x 021>''x x . (1)求证:;0,0,0,02121<'<'<<x x x x (2)求证:1-b ≤c ≤1+b ; (3)求c b ,所有可能的值.1994年全国初中数学联赛试题第一试(4月3日上午8:30—9:30)考生注意:本试共两道大题,满分80分.一、选择题(本题满分48分,每小题6分)本题共有8个小题都给出了A,B、C,D,四个结论,其中只有一个是正确的,请把你认为正确结论的代表字母写在题后答案中的圆括号内,每小题选对得6分;不选、选错或选出的代表字母超过一个(不论是否写在圆括号内),一律得0分.〔答〕( )2.设a,b,c是不全相等的任意实数,若x=a2-bc,y=b2-ca,z=c2-ab,则x,y,zA.都不小于0B.都不大于0C.至少有一个小0于D.至少有一个大于0〔答〕( )3.如图1所示,半圆O的直径在梯形ABCD的底边AB上,且与其余三边BC,CD,DA相切,若BC=2,DA=3,则AB的长A.等于4B.等于5C.等于6D.不能确定〔答〕( )A.1 B.-1 C.22001D.-22001〔答〕( )5.若平行直线EF,MN与相交直线AB,CD相交成如图2所示的图形,则共得同旁内角A.4对B.8对C.12对D.16对〔答〕( )〔答〕( )7.设锐角三角形ABC的三条高AD,BE,CF相交于H。
【数学竞赛】2003年全国初中数学联赛试卷及答案

【数学竞赛】2003年全国初中数学联赛试卷第一试(4月13日上午8:30—9:30)一、选择题(本题满分42分,每小题7分)1.A .5-B .1C .5D .1[答]( )2.在凸10边形的所有内角中,锐角的个数最多是A .0B .1C .3D .5[答]( )3.若函数()0y kx k =>与函数1y x=的图象相交于A ,C 两点,AB 垂直x 轴于B ,则△ABC 的面积为 A .1 B .2 C .k D .2k[答]( )4.满足等式2003的正整数对()x y ,的个数是A .1B .2C .3D .4[答]( )5.设△ABC 的面积为1,D 是边AB 上一点,且13AD AB =.若在边AC 上取一点E ,使四边形DECB 的面积为34,则CE EA的值为 A .12 B .13 C .14 D .15[答]( )6.如图,在□ABCD 中,过A ,B ,C 三点的圆交AD 于E ,且与CD 相切.若AB =4,BE =5,则DE 的长为A .3B .4C .154D .165[答]( ) D CA B E二、填空题(本题满分28分,每小题7分)1.抛物线2y ax bx c =++与x 轴交于A ,B 两点,与y 轴交于点C .若△ABC 是直角三角形,则ac =__________.2.设m 是整数,且方程2320x mx +-=的两根都大于95-而小于37,则m =____________. 3.如图,'AA ,'BB 分别是∠EAB ,∠DBC 的平分线.若''AA BB AB ==,则∠BAC 的度数为_____________.4.已知正整数a ,b 之差为120,它们的最小公倍数是其最大公约数的105倍,那么a ,b 中较大的数是_________.2003年全国初中数学联合竞赛试卷第二试(A )(4月13日上午10:00—11:30)考生注意:本试三大题,第一题20分,第二、三题各25分,全卷满分70分.一、(本题满分20分)试求出这样的四位数,它的前两位数字与后两位数字分别组成的二位数之和的平方,恰好等于这个四位数.二、(本题满分25分)。
2003年全国初中数学竞赛天津赛区解析

第一中学
吴晋
外院附校
张晗
新华中学
郭晓煦
新华中学
包辰兰
外院附校
刘思洋
耀华中学
娄天关
新华中学
王蕾
南开中学
杜洁
新华中学
王祎
新华中学
肖潇
天津五中
高腾
耀华中学
孙鹏
双建中学(河北)
丁淼
协同中学(红桥)
单增礼
静海二中
李迪
南开中学
田玉璐
华辰中学(北辰)
崔琛
新华中学
孙丁捷
新华中学
崔晓龙
二十中学
王龙
五十五中
穆旭冉
南开中学
高玉翔
耀华中学
李玮瑜
实验中学
陈雪
育英中学(宝坻)
吴云昊
实验中学
董见地
石化一中
马剑峰
新华中学
胡珀
耀华中学
杨光
新华中学
赵学义
上骀中学(武清)
杨晓浩
实验中学
李鑫
新华中学
刘龙隆
新华中学
田力
耀华中学
周鑫南
南开中学
胡阳
南开中学
张宏
第七中学
肖月
第一中学
杨帅
外院附校
于淼
实验中学
余盛强
实验中学
陈伯雄
新华中学
王潇
一0二中(河东)
扈晓莉
南开中学
崔云溪
南开中学
张勇
耀华中学
郑小平
育华中学(塘沽)
门金龙
方舟中学(红桥)
李辰
天慈中学(河北)
刘砚辉
第七中学
李彬
油田十中
2000-2003年“五羊杯”全国初中数学竞赛试题及详解【圣才出品】
2 . (16 1.63 2.87 1250.115 0.0163963) 0.11 ( )。 A. 20 B. 26 C. 200
所以,A 的末尾的零的个数是 205 个。 故正确的答案选 B。
6 .中国首位航天员杨利伟乘神舟 5 号飞船,在约 400 公里高空绕地球 14 圈,飞行约 21 小时,成功返回,圆了中华民族千年飞天梦.假定地球是球体,半径约 6400 公里,不
计升空和降落,杨利伟飞行距离和速度分别是( )。
A. 60 万公里和 9.7 公里/秒 B. 61 万公里和 8.3 公里/秒 C. 60 万公里和 7.9 公里/秒 D. 61 万公里和 7.8 公里/秒 【来源】 2003年第 15 届“五羊杯”全国初中数学竞赛初中一年级
31 4
31 7
31 8
15 31
1 2
1 4
1 7
1 8
1 2
1 4
1 7
1 8
15 31
故正确的答案选 B。
4 .已知 3A 2B : 7A 5B 13: 31,那么 13A 12B : 17A 15B ( )。
A. 5 : 4 B. 4 : 5 C. 9 : 7
2 / 57
圣才电子书
【答案】C
【解析】因为飞船在约 400 公里高空绕地球飞行,且地球半径为 6400 公里,所以,
飞船绕行的总半径为
6400 400 6800 (公里)。 又已知杨利伟绕地球飞行 14 圈,因此,杨利伟飞行距离为 2 680014 597856
2003年信利杯全国初中数学联赛天津赛区复赛试卷及答案-
G F EDCB AOD CBA2003年“TRULY ®信利杯”全国初中数学联赛天津赛区复赛试卷1.若4x -3y -6z = 0,x +2y -7z = 0 (xyz≠0),则代数式222222103225z y x z y x ---+的值等于 ( ). (A)12-(B)192-(C)15- (D)13-2.在本埠投寄平信,每封信质量不超过20g时付邮费0.80元,超过20g 而不超过40g 时付邮费1.60元,依次类推,每增加20g 需增加邮费0.80元(信的质量在100g 以内). 如果某人所寄一封信的质量为72.5g ,那么他应付邮费 ( ).(A)2.4元 (B)2.8元(C) 3元 (D) 3.2元 3.如右图所示,∠A +∠B +∠C +∠D +∠E +∠F +∠G的值等于( ).(A) 360° (B) 450° (C) 540° (D) 720° 4.四条线段的长分别为9,5,x ,1(其中x 为正实数),用它们拼成两个直角三角形,且AB 与CD 是其中的两条线段(如右图),则x可取值的个数为( ).(A) 2个 (B) 3个 (C) 4个 (D) 6个5.某校九年级两个毕业班的学生和教师共100人一起在台阶上拍毕业照留 念,摄影师要将其排列成前多后少的梯形队阵(排数≥3),且要求各行的人数必须是连续的自然数,这样才能使后一排的人均站在前一排两人间的空当处,那么,满足上述要求的排法的方案有( ).(A) 1种 (B) 2种(C) 4种 (D) 0种6.已知31+=x ,那么2111242x x x +-+--的值等于 . 7.若实数x ,y ,z 满足41=+yx ,11=+z y ,371=+x z ,则xyz 的值为 .8.观察下列图形:① ② ③ ④根据图①、②、③的规律,图④中三角形的个数为 . 9. 如右图所示,已知电线杆AB 直立于地面上,它的影子恰好照在土坡的坡面CD 和地面BC 上,如果CD 与地面成45º,∠A = 60º,CD = 4m ,BC =()2264-m ,则电线杆AB 的长为_______m . 10.已知二次函数c bx ax y ++=2(其中a 是正整数)的图象经过点A (-1,4)与点B (2,1),并且与x 轴有两个不同的交点,则 b + c 的最大值为 .三、解答题(本大题共4题,每小题15分,满分60分)如图所示,已知AB 是⊙O 的直径,BC 是⊙O 的切线,OC 平行于弦AD ,过点D 作DE ⊥AB 于点E ,连结AC ,与DE 交于点P .问EP 与PD 是否相等?证明你的结论.某人租用一辆汽车由A 城前往B 城,沿途可能经过的城市以及通过两城市之间所需的时间(单位:小时)如图所示.若汽车行驶的平均速度为 80千米/小时,而汽车每行驶1千米需要的平均费用为1.2元.试指出此人从A 城出发到B 城的最短路线(要有推理过程),并求出所需费用最少为多少元?10111859712131761514FGO HBE DC APE DCB A OABCD已知:△ABC 中,∠ACB =90°.(1) 如图所示,当点D 在斜边AB 上(不含端点)时,求证:ABBDAD BC BD CD -=-222;(2)当点D 与点A 重合时,第(1)小题中的等式是否成立?请说明理由; (3)当点D 在BA 的延长线上时,第(1)小题中的等式是否成立?请说明理由.已知实数a ,b ,c 满足:a +b +c =2,abc =4. (1)求a ,b ,c 中的最大者的最小值; (2)求a b c ++的最小值.答案:1.答案:D .由⎩⎨⎧=-+=--,072,0634z y x z y x 解得⎩⎨⎧==.2,3z y z x 代入,得原式=1310121818451043924295222222-=---+=-⨯-⨯-⨯+⨯z z z z z z . 2. 答案:D .因为20×3<72.5<20×4,所以根据题意,可知需付邮费0.8×4=3.2(元). 3. 答案:C .如图所示,∠B +∠BMN +∠E +∠G =360°, ∠FNM +∠F +∠A +∠C =360°,而∠BMN +∠FNM =∠D +180°,所以∠A +∠B +∠C +∠D +∠E +∠F +∠G =540°. 4. 答案:D .显然AB 是四条线段中最长的,故AB =9或AB =x . (1)若AB =9,当CD =x 时,222)51(9++=x ,53=x ;当CD =5时,222)1(59++=x ,1142-=x ; 当CD =1时,222)5(19++=x ,554-=x .(2)若AB =x ,当CD =9时,222)51(9++=x ,133=x ;当CD =5时,222)91(5++=x ,55=x ; 当CD =1时,222)95(1++=x ,197=x .5. 答案:B .设最后一排有k 个人,共有n 排,那么从后往前各排的人数分别为k ,k +1,k +2,…,k +(n -1),由题意可知1002)1(=-+n n kn ,即()[]20012=-+n k n .因为k ,n 都是正整数,且n ≥3,所以n <2k +(n -1),且n 与2k +(n -1)的奇偶性不同. 将200分解质因数,可知n =5或n =8. 当n =5时,k =18;当n =8时,k =9. 共有两种不同方案.6. 答案:23-. 4341442141212222--=-+--=---++x x x x x x将31+=x代入,可得其值为23-. 7. 答案:1.因为34371137137111114--+=---+=-+=-+=+=x x x xx x z z x z x y x , 所以37)34()34(4-+-=-x x x x ,091242=+-x x ,0)32(2=-x ,故23=x .从而 353237137=-=-=x z , 5253111=-=-=z y . 于是1355223=⨯⨯=xyz .8. 答案:161.根据图中①、②、③的规律,可知图④中三角形的个数为1+4+3×4+432⨯+433⨯=1+4+12+36+108=161(个).9. 答案:26.如图,延长AD 交地面于E ,过D 作DF ⊥CE 于F . 因为∠DCF =45°,∠A =60°,CD =4(m ), 所以CF =DF =22(m ),EF =DF tan60°=62(m ). 因为3330tan == BE AB , 所以2633)22642262(33=⨯-++=⨯=BE AB (m ). 10. 答案:-4.G FE D CB ANM由于二次函数的图象过点A (-1,4),点B (2,1),所以⎩⎨⎧=++=+-,124,4c b a c b a解得⎩⎨⎧-=--=.23,1a c a b 因为二次函数图象与x 轴有两个不同的交点,所以42>-=∆ac b ,0)23(4)1(2>----a a a ,即0)1)(19(>--a a , 由于a 是正整数,故1>a ,所以a ≥2.又因为b +c =-3a +2≤-4,且当a =2,b =-3,c =-1时,满足题意,故b +c 的最大值为-4.11. 解:DP =PE . 证明如下:因为AB 是⊙O 的直径,BC 是切线,所以AB ⊥BC . 由Rt △AEP ∽Rt △ABC ,得ABAEBC EP = . ① ……(6分) 又AD ∥OC ,所以∠DAE=∠COB ,于是 Rt △AED ∽Rt △OBC . 故ABAEAB AE OB AE BC ED 221===. ② ……(12分) 由①,②得 ED =2EP . 所以 DP =PE . ……(15分) 12. 解:从A 城出发到达B 城的路线分成如下两类: (1) 从A 城出发到达B 城,经过O 城.因为从A 城到O 城所需最短时间为26小时,从O 城到B 城所需最短时间为22小时. 所以,此类路线所需 最短时间为26+22=48(小时). ……(5分)(2) 从A 城出发到达B 城,不经过O 城. 这时从A 城到达B 城,必定经过C ,D ,E 城或F ,G ,H 城,所需时间至少为49小时. ……(10分)综上,从A 城到达B 城所需的最短时间为48 小时,所走的路线为A →F →O →E →B . ……(12分)所需的费用最少为80×48×1.2=4608(元). ……(14分)答:此人从A 城到B 城最短路线是A →F →O →E →B ,所需的费用最少为4608元. ……(15分)13. 解:(1)作DE ⊥BC ,垂足为E . 由勾股定理, 得.)()()(22222222BC BE CE BE CE DE BE DE CE BD CD -=-=+-+=-所以,BC BEBC CE BC BE CE BCBD CD -=-=-222. 因为DE ∥AC ,所以ABBD BC BE AB AD BC CE ==,.故AB BDAD AB BD AB AD BCBD CD -=-=-222. ……(10分) (2)当点D 与点A 重合时,第(1)小题中的等式仍然成立.此时有AD,BD=AB.所以122222222-=-=-=-BCBCBCABACBCBDCD,1-=-=ABAB.从而第(1)小题中的等式成立.……(13分)(3)当点D在BA的延长线上时,第(1)小题中的等式不成立.作DE⊥BC,交BC的延长线于点E,则222222CD BD CE BEBC BC--=21,CE BE CEBC BC+=-=--而1-=-=-ABABABBDAD,所以ABBDADBCBDCD-≠-222.……(15分)〖说明〗第(3)小题只要回答等式不成立即可(不成立的理由表述不甚清者不扣分).14. 解:(1)不妨设a是a,b,c中的最大者,即a≥b,a≥c,由题设知a>0,且2b c a+=-,abc4=.于是b,c是一元二次方程04)2(2=+--axax的两实根,aa44)2(2⨯--=∆≥0,164423-+-aaa≥0,)4)(4(2-+aa≥0.所以a≥4.……(8分)又当a=4,b=c=-1时,满足题意. 故a,b,c中最大者的最小值为4.(2)因为abc>0,所以a,b,c为全大于0或一正二负.①若a,b,c均大于0,则由(1)知,a,b,c中的最大者不小于4,这与a+b+c=2矛盾.②若a,b,c为一正二负,设a>0,b<0,c<0,则22)2(-=--=--=++aaacbacba,由(1)知a≥4,故2a -2≥6,当a=4,b=c=-1时,满足题设条件且使得不等式等号成立.故cba++的最小值为AB DD。
2003年全国初中数学联合竞赛决赛
2003年全国初中数学联合竞赛决赛一、选择题(每小题7分,共42分) 1. 221217223-+-=_________.A 5-42 B42-1 C5 D12. 在凸10边形的所有内角中,锐角的个数最多是_________个。
A0 B1 C3 D53.若函数y =kx(k >0)与函数y =x -1的图象相交于A 、C 两点,AB 垂直x 轴于B ,则△ABC 的面积为_________.A1 B2 Ck Dk 24.满足等式x 2003xy 2003y 2003x y x y +--+=2003的正整数对的个数是 ___A1 B2 C3 D45、设△ABC 的面积为1,D 是边AB 上一点,且AD ∶AB =1∶3。
若在边AC 上取一点E ,使四边形DECB 的面积为43,则EAEC的值为__。
A 21B 31C 41 D 516.如图,在平行四边形ABCD 中,过A 、B 、C 三点的圆交AD 于E ,且与CD 相切,若AB =4,BE =5,则ED 的长为__。
A3 B4 C 415 D 516BCD AE二、填空题(每小题7分,共28分)1.抛物线y =ax +bx +c 与x 轴交于A ,B 两点,与y 轴交于点C 。
若△ABC 是直角三角形,则ac =_________.2.设m 是整数,且方程3x 2+mx -2=0的两根都大于-59而小于73,则m=_______。
3.如图,AA 1、BB 1分别是∠EAB 、∠DBC 的平分线,若AA 1=BB 1=AB ,则∠BAC 的度数为_________.4.已知正整数a 、b 之差为120,它们的最小公倍数是其最大公约数的105倍,那么a 、b 中较大的数是_________.三.(本题满分20分)在△ABC 中,D 为AB 的中点,分别延长CA 、CB 到点E 、F ,使DE =DF ;过E ,F 分别作CA 、CB 的垂线,相交于P ,设线段PA 、PB 的中点分别为M 、N 。
2003年全国初中数学竞赛获奖名单(天津赛区)
三等奖:刘明辉(实验二1)任庆春(实验二1)杜鑫(实验二1)
辅导教师:于延男
2002—2003学年度天津市中学生八年级学科竞赛(语文)
一等奖:陈灼(实验二2)姜乃静(实验二1)
二等奖:汪兆烨(实验二2)马洁芳(实验二2)
三等奖:李昂(实验二2)孙永智(实验二1)杜鑫(实验二1)
王凯(9班)郝卉(9班)郭海月(12班)
辅导教师:孙倩黄璐玲贾维陈雪春
高二年级
一等奖:黄杰西(8班)
二等奖:张晓曦(8班)曹晏(8班)薛腾(8班)
方飞(3班)母一诺(6班)
三等奖:谭静(1班)曹欣阳(2班)赵允西(5班)
辅导教师:赵美文梁延羊郑庭菊
高三年级
一等奖:李颖(8班)
二等奖:齐旻(2班)万钟(7班)
吴倩竹(实验二1)
辅导教师:赵向丽
2002年全国中学生英语能力竞赛(2003年公布成绩)
高一年级
一等奖:朱伯军(9班)付丽(11班)
二等奖:李汇川(1班)阎岩(2班)王凡(4班)
徐姝果(3班)李之(5班)孙思玉(11班)
吴小凡(11班)刘剑非(10班)解立(12班)
三等奖:王麒(8班)李雪蕾(8班)孙雅婧(5班)
辅导教师:赵津
2003年全国初中学生化学素质和实验能力竞赛(天津赛区)
二等奖:任庆春(实验二1)孙翔辰(实验二1)苏士钊(实验二2)
三等奖:刘赵昆(实验二2)谭腾(实验二2)
辅导教师:耿军华王健伟
2002—2003学年度八年级学科竞赛(英语)
一等奖:高然(实验二1)张斯宇(实验二2)傅欣(实验二2)
余雪(2班)
二等奖:赵询(2班)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
尹炜迪
耀华中学
杨玉成
雍阳中学(武清)
高兴斌
陈官屯镇中学(静海)
黄方
新华中学
李敬
第七中学
李博
芦台五中
马平川
实验中学
姜涛
礼明庄中学(蓟县)
孙健
外院附校
田艺
天慈中学(河北)
周鑫
方舟中学(红桥)
石光焓
天士力中学(河北)
王皓星
南开中学
杨倩
瀛海中学(静海)
薛建飞
育才中学(塘沽)
张一
育英中学(宝坻)
宋琳
第七中学
苏昕
第七中学
高远辰
天慈中学(河北)
吴潇萌
静海二中
王冠达
七十八中
王惊霓
新华中学
王乃鹏
南开中学
李昊辰
进取中学(河东)
陈梦凡
华辰中学(北辰)
林林
海河中学
赵洋
耀华中学
王梓
实验中学
黄颖棻
华辰中学(北辰)
孙洋
津海中学(河西)
梁嘉
长芦中学(汉沽)
王雷斌
天慈中学(河北)
王健
方舟中学(红桥)
赵爽
第七中学
刘翔宇
李毅
实验中学
郝文涛
台头中学(静海)
高哲
油田一中
王蕊
第七中学
高用鹤
大庄子中学(静海)
刘旭
王卜庄镇中学(宝坻)
王云端
海洋一中(塘沽)
刘文虎
子牙镇中学(静海)
于淼
杨柳青三中
高军
大港四中
牛梦馨
新华中学
杜晓磊
耀华中学
闫齐
尔王庄中学(宝坻)
刘洋
育才中学(塘沽)
李小红
城关二中(蓟县)
翟鹏
大丰堆镇中学(静海)
李洪蕊
高玉翔
耀华中学
李玮瑜
实验中学
陈雪
育英中学(宝坻)
吴云昊
实验中学
董见地
石化一中
马剑峰
新华中学
胡珀
耀华中学
杨光
新华中学
赵学义
上骀中学(武清)
杨晓浩
实验中学
李鑫
新华中学
刘龙隆
新华中学
田力
耀华中学
周鑫南
南开中学
胡阳
南开中学
张宏
第七中学
肖月
第一中学
杨帅
外院附校
于淼
实验中学
余盛强
实验中学
陈伯雄
新华中学
王潇
一0二中(河东)
郑浩然
南开中学
王岩
南开中学
赵天宇
渔阳中学(蓟县)
董安琪
渔阳中学(蓟县)
朱文祎
新华中学
韩超
天慈中学(河北)
刘旭东
耀华中学
于刚
大杨学校(蓟县)
纪旭
大邱庄镇中学(静海)
袁晓涛
仁和学校(红桥)
刘莹
大王古庄中学(武清)
第七中学
吴优
兴南中学(和平)
张巍昌
任风乡中(宁河)
彭承
石化一中
张妍懿
双建中学(河北)
张野平
第七中学
窦方
第一中学
曹墨源
实验中学
白桂晨
培英中学(大港)
王超
沿庄镇中学(静海)
刘一洲
实验中学
刘奇
长芦中学(汉沽)
王宇
南开中学
杨学文
方舟中学(红桥)
王枭
耀华中学
张桐江
华辰中学(北辰)
王辰
天慈中学(河北)
齐鑫桐
新华中学
扈晓莉
南开中学
崔云溪
南开中学
张勇
耀华中学
郑小平
育华中学(塘沽)
门金龙
方舟中学(红桥)
李辰
天慈中学(河北)
刘砚辉
第七中学
李彬
油田十中
商强
华辰中学(北辰)
王亮
小李中学(宁河)
梁亮
渔阳中学(蓟县)
赵瑞
瀛海中学(静海)
靳曲
双菱中学(和平)
张佳
新华中学
张明翰
新华中学
李晨亮
汉沽一中
潘磊
育华中学(塘沽)
李思祖
实验中学(塘沽)
双菱中学(和平)
黄锦涛
新华中学
李玥
第七中学
郗凌鹤
实验中学
张楠
芦台五中
石磊磊
双建中学(河北)
王萱
南开中学
李晟
方舟中学(红桥)
李珣
耀华中学
韩础
二十中学
王刚
雍阳中学(武清)
沈忱
实验中学
马洁芳
耀华中学
倪晓畅
三十二中(河东)
张欣
新华中学
蔡海轩
石化一中
鲁元珍
东丽中学
许子腾
南锋中学(南开)
张赢
天慈中学(河北)
马成
王建正
南开中学
王菁
颐和中学(红桥)
林宇婧
新华中学
蒋益
新华中学
张昊洋
仁和中学(红桥)
程强
杨村五中
董斌
大邱庄镇中学
崔彦达
石化一中
韩伟
新华中学
李建勋
育华中学(塘沽)
宋融
新华中学
曹越
耀华中学
刘旭
新华中学
于华龙
新华中学
沈梦南
石化一中
闫星旭
南开中学
李佳
天慈中学
蒋珊珊
新华中学
张薇
新华中学
任庆春
耀华中学
李晓易
新华中学
俵口中学(宁河)
秦鹏
邦均一中(蓟县)
王玉磊
东丽中学
宫泽龙
杨柳青四中
李秀举பைடு நூலகம்
俵口中学(宁河)
张平
任凤乡中学(宁河)
韩笑
渔阳中学(蓟县)
岳宗宇
育华中学(塘沽)
刘亚楠
外院附校
王磊
徐官屯中学(武清)
兰立伟
华辰中学(北辰)
王常霖
第二南开中学
张凤龙
大邱庄镇中学(静海)
陈媛
港东中学(油田)
王兴华
双环中学(河北)
刘剑
颐和中学(红桥)
范洪霞
五十四中
张志华
华辰中学(北辰)
马珺楠
静海二中
刘峥
渔阳中学(蓟县)
朱才学
王稳庄中学(西青)
侯觉
新华中学
任伟
新华中学
夏鹏
第一中学
万科研
城关二中(蓟县)
李光
育英中学(宝坻)
孟繁旺
天慈中学(河北)
柴旺里
新华中学
芦唱
南开中学
刘淳
华辰中学(北辰)
汪凤娇
白涧中学(蓟县)
袁野
方舟中学(红桥)
周萌
天士力中学
杨明
育才中学(塘沽)
刘超
新华中学
丰宝洋
杨村五中
李润
梁头学校(静海)
王金玺
实验中学
张景莹
小薄中学(宁河)
王益栋
菁华学校(津南)
杨鹏飞
小薄中学(宁河)
李金轩
港南二校(大港)
王鑫
进取中学(河东)
汤文江
第三中学
张宝路
瀛海中学(静海)
田晓磊
南华中学(津南)
邵连龙
渔阳中学(蓟县)
赵祥宇
光华中学(东丽)
李辰
第一中学
吴晋
外院附校
张晗
新华中学
郭晓煦
新华中学
包辰兰
外院附校
刘思洋
耀华中学
娄天关
新华中学
王蕾
南开中学
杜洁
新华中学
王祎
新华中学
肖潇
天津五中
高腾
耀华中学
孙鹏
双建中学(河北)
丁淼
协同中学(红桥)
单增礼
静海二中
李迪
南开中学
田玉璐
华辰中学(北辰)
崔琛
新华中学
孙丁捷
新华中学
崔晓龙
二十中学
王龙
五十五中
穆旭冉
南开中学
2003年全国初中数学竞赛天津赛区
获奖名单
一等奖(53名)
刘天强
南开中学
崔泽熙
新华中学
薛原
实验中学
李明珠
南开中学
郭嘉君
实验中学
杨宏锴
新华中学
刘煜
港南二校(油田)
张梓辰
育华中学(塘沽)
商泽超
港东学校(油田)
侯珏
新华中学
李喆
新华中学
刘洋
实验中学
张蕊
新华中学
严昊
耀华中学
张斌
南开中学
李鹏
南开中学
信跃龙
第17中学
马祖光
第七中学
陈晨
第七中学
孙翔辰
耀华中学
李康
新华中学
孙婧巍
石化一中
刘拓
第七中学
三等奖(176名)
齐乐
南开中学
戴小川
第七中学
邵帅
第一中学
岳亮
进取中学(河东)
刘昊
杨村二中
周国强
第七中学
苏立炎
实验中学
孟喆
大港四中
张博
信号厂中学(东丽)
宋佳
雍阳中学(武清)
李健
李庄中学(东丽)
王鑫磊
渔阳中学(蓟县)
沙巍
双建中学
