2010年天津市初中数学竞赛初赛试题
2010全国初中数学竞赛题及答案

三、解答题(共4题,每题20分,共80分)11.如图,△ABC 为等腰三角形,AP 是底边BC 上的高,点D 是线段PC 上的一点,BE 和CF 分别是△ABD 和△ACD 的外接圆直径,连接EF . 求证: tan EF PAD BC∠=.证明:如图,连接ED ,FD . 因为BE 和CF 都是直径,所以ED ⊥BC , FD ⊥BC ,可得…………(20分)12.如图,抛物线2y ax bx =+(a >0)与双曲线y x=相交于点A ,B . 已知点A 的坐标为(1,4),点B 在第三象限内,且△AOB 的面积为3(O 为坐标原点).(1)求实数a ,b ,k 的值;(2)过抛物线上点A 作直线AC ∥x 轴,交抛物线于另一点C ,求所有满足△EOC ∽△AOB 的点E 的坐标.(第11题)解:(1)因为点A (1,4)在双曲线k y x=上, 所以k=4. 故双曲线的函数表达式为xy 4=. 设点B (t ,4t ),0t <,AB 所在直线的函数表达式为y mx n =+,则有 44m n mt n t =+⎧⎪⎨=+⎪⎩,, 解得4m t =-,4(1)t n t +=. 于是,直线AB 与y 轴的交点坐标为4(1)0,t t +⎛⎫ ⎪⎝⎭,故 ()141132AOB t S t t∆+=⨯-=(),整理得22320t t +-=, 解得2t =-,或t =1(舍去).所以点B 的坐标为(2-,2-). ⎧⎨⎩=B '(2-,2)是CO 的延长1OA 到点1E ,使得1OE =12OA ,这时点1E (8,2-)是符合条件的点.(ii )作△BOA 关于x 轴的对称图形△2B OA ',得到点2A (1,4-);延长2OA 到点2E ,使得2OE =22OA ,这时点E 2(2,8-)是符合条件的点.所以,点E 的坐标是(8,2-),或(2,8-). …………(20分)13.求满足22282p p m m ++=-的所有素数p 和正整数m ..解:由题设得(21)(4)(2)p p m m +=-+, 所以(4)(2)p m m -+,由于p 是素数,故(4)p m -,或(2)p m +. ……(5分)(1)若(4)p m -,令4m kp -=,k 是正整数,于是2m kp +>,2223(21)(4)(2)p p p m m k p >+=-+>,故23k <,从而1k =. 所以4221m p m p -=⎧⎨+=+⎩,,解得59.p m =⎧⎨=⎩, …………(10分) (2)若(2)p m +,令2m kp +=,k 是正整数.当5p >时,有46(1)m kp kp p p k -=->-=-,223(21)(4)(2)(1)p p p m m k k p >+=-+>-,故(1)3k k -<,从而1k =,或2.由于(21)(4)(2)p p m m +=-+是奇数,所以2k ≠,从而1k =.于是4212m p m p -=+⎧⎨+=⎩,, 这不可能.当5p =时,2263m m -=,9m =;当3p =,2229m m -=,无正整数解;当2p =时,2218m m -=,无正整数解.综上所述,所求素数p =5,正整数m =9. …………(20分)14.从1,2,…,2010这2010个正整数中,最多可以取出多少个数,使得所取出的数中任意三个数之和都能被33整除?解:首先,如下61个数:11,1133+,11233+⨯,…,116033+⨯(即1991)满足题设条件. …………(5分)另一方面,设12n a a a <<< 是从1,2,…,2010中取出的满足题设条件的数,对于这n 个数中的任意4个数i j k m a a a a ,,,,因为33()i k m a a a ++, 33()j k m a a a ++,所以 33()j i a a -.因此,所取的数中任意两数之差都是33的倍数. …………(10分)设133i i a a d =+,i =1,2,3,…,n . 由12333()a a a ++,得12333(33333)a d d ++, …………(15分)故20分)。
2010年天津中考数学试卷及答案

2010年天津市初中毕业生学业考试试卷数学本试卷分为第 卷(选择题)、第 卷(非选择题)两部分。
第 卷第 页至第 页,第 卷第 页至第 页。
试卷满分 分。
考试时间 分钟。
答卷前,考生务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上,并在规定位置粘贴考试用条形码。
答题时,务必将答案涂写在“答题卡”上,答案答在试卷上无效。
考试结束后,将本试卷和“答题卡”一并交回。
祝各位考生考试顺利第 卷(选择题 共 分)注意事项:每题选出答案后,用 铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点。
一、选择题:本大题共 小题,每小题 分,共 分.在每小题给出的四个选项中,只有一项是符合题目要求的.( )sin30 的值等于( )12(2(3( )( )下列图形中,既可以看作是轴对称图形,又可以看作是中心对称图形的为( ) ( ) ( ) ( )( )上海世博会是我国第一次举办的综合类世界博览会.据统计自 年 月 日开幕至 月 日,累计参观人数约为 人,将 用科学记数法表示应为( )480310⨯( )580.310⨯( )68.0310⨯( )70.80310⨯( )在一次射击比赛中,甲、乙两名运动员 次射击的平均成绩都是 环,其中甲的成绩的方差为 ,乙的成绩的方差为 ,由此可知( )甲比乙的成绩稳定( )乙比甲的成绩稳定( )甲、乙两人的成绩一样稳定( )无法确定谁的成绩更稳定( )右图是一个由 个相同的正方体组成的立体图形,它的三视图为( ) ( )( ) ( )( )下列命题中正确的是( )对角线相等的四边形是菱形( )对角线互相垂直的四边形是菱形( )对角线相等的平行四边形是菱形( )对角线互相垂直的平行四边形是菱形第( )如图, 中,弦AB 、CD 相交于点P , 若30A ∠=︒,70APD ∠=︒,则B ∠等于( )30︒ ( )35︒ ( )40︒ ( )50︒( )比较 ,5,37的大小,正确的是( )3257<< ( )3275<< ( )3725<<( )3572<<( )如图,是一种古代计时器——“漏壶”的示意图,在壶内盛一定量的水,水从壶下的小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间.若用x 表示时间,y 表示壶底到水面的高度,下面的图象适合表示一小段时间内y 与x 的函数关系的是(不考虑水量变化对压力的影响)( ) ( )( ) ( )( )已知二次函数2y ax bx c =++ 0a ≠ 的图象如图所示,有下列结论: ①240b ac ->;②0abc >;第( )第( )③80+>;a c④930++<.a b c其中,正确结论的个数是( ) ( )( ) ( )年天津市初中毕业生学业考试试卷数 学第 卷(非选择题 共 分)注意事项:用黑色墨水的钢笔或签字笔将答案写在“答题卡”上。
天津初中数学竞赛

天津市初中数学竞赛试卷一、选择题(共6小题,每小题5分,满分30分)1.若x=a-b a+b,且a≠0,则b a等于( ) A .1-x 1+xB .1+x 1-xC .x-1 x+1D .x+1 x-1显示解析2.如图,正方体的每一个面上都有一个正整数,已知相对的两个面上两数之和都相等.如果13、9、3对面的数分别为a 、b 、c ,则a 2+b 2+c 2-ab-bc-ca 的值等于( ) A .48 B .76C .96D .152显示解析3.已知一个三角形的三条边长均为正整数.若其中仅有一条边长为5,且它又不是最短边,则满足条件的三角形个数为( ) A .4 B .6C .8D .10显示解析4.如图.在▱ABCD 中,若边AB 上的两点E 、F 满足AE=EF=FB .CEA .2b=a+c B.b=a+cC.1c=1a+1bD.1c=1a+1b★☆☆☆☆显示解析6.已知a、b都是正整数,且抛物线y=ax2+bx+l与x轴有两个不同的交点A、B.若A、B到原点的距离都小于1,则a+b的最小值等于()A.16B.10C.4D.1显示解析二、填空题(共5小题,每小题6分,满分30分)7.已知关于x的方程x2+2px+1=0的两个实数根一个小于1,另一个大于1,则实数p的取值范围是.显示解析8.有甲、乙两人,甲在汽车上碰见乙正往相反的方向走去1min后,甲下车去追赶乙.若甲的速度是乙的速度的2倍,但比汽车的速度慢4/5,则自甲下车后追上乙所用的时间为min.显示解析9.如图,已知四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,且AE=2(AB+AD).如果∠D=120°,则∠B等于.显示解析10.如果一个凸n边形恰有4个内角是钝角,那么,这个多边形的边数n最多为.显示解析11.若在4×4的方格表的16个方格中,每个方格填入一个数,使得每个方格的所有相邻方格中的数的总和均为l(注:相邻方格是指恰有一条公共边的),则方格表中16个数的总和等于.显示解析三、解答题(共3小题,满分60分)12.已知二次函数y=a(a+1)x2-(2a+1)x+1,其中a为正整数.(1)若函数y的图象与x轴相交于A、B两点,求线段AB的长;(2)若a依次取1,2,…,2005时,函数y的图象与x轴相交所截得的2005条线段分别为A1B1,A2 B2,…,A2005 B2005,试求这2005条线段长之和.显示解析13.已知p、g、2q-1p、2p-1q都是整数,且p>1,q>1.求p+q的值.显示解析14.如图.△ABC内接于⊙O,AC>BC,点D为AB的中点.求证:AD2=AC•BC+CD2.显示解析(注:可编辑下载,若有不当之处,请指正,谢谢!)。
2010年天津中考数学试卷及答案

2010年天津市初中毕业生学业考试试卷数学本试卷分为第 卷(选择题)、第 卷(非选择题)两部分。
第 卷第 页至第 页,第 卷第 页至第 页。
试卷满分 分。
考试时间 分钟。
答卷前,考生务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上,并在规定位置粘贴考试用条形码。
答题时,务必将答案涂写在“答题卡”上,答案答在试卷上无效。
考试结束后,将本试卷和“答题卡”一并交回。
祝各位考生考试顺利第 卷(选择题 共 分)注意事项:每题选出答案后,用 铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点。
一、选择题:本大题共 小题,每小题 分,共 分.在每小题给出的四个选项中,只有一项是符合题目要求的.( )sin30︒的值等于( )12(2(3( )( )下列图形中,既可以看作是轴对称图形,又可以看作是中心对称图形的为( ) ( ) ( ) ( )( )上海世博会是我国第一次举办的综合类世界博览会.据统计自 年 月 日开幕至 月 日,累计参观人数约为 人,将 用科学记数法表示应为( )480310⨯( )580.310⨯( )( )6⨯0.80310⨯78.0310( )在一次射击比赛中,甲、乙两名运动员 次射击的平均成绩都是 环,其中甲的成绩的方差为 ,乙的成绩的方差为 ,由此可知( )甲比乙的成绩稳定( )乙比甲的成绩稳定( )甲、乙两人的成绩一样稳定( )无法确定谁的成绩更稳定( )右图是一个由 个相同的正方体组成的立体图形,它的三视图为第( ) ( )( ) ( )( )下列命题中正确的是( )对角线相等的四边形是菱形( )对角线互相垂直的四边形是菱形( )对角线相等的平行四边形是菱形( )对角线互相垂直的平行四边形是菱形( )如图, 中,弦AB 、CD 相交于点P , 若30A ∠=︒,70APD ∠=︒,则B ∠等于( )30︒ ( )35︒ ( )40︒ ( )50︒( )比较 ,5,37的大小,正确的是( )3257<< ( )3275<< ( )3725<<( )3572<<( )如图,是一种古代计时器——“漏壶”的示意图,在壶内盛一定量的水,水从壶下的小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间.若用x 表示时间,y 表示壶底到水面的高度,下面的图象适合表示一小段时间内y 与x 的函数关系的是(不考虑水量变化对压力的影响)( ) ( )( ) ( )( )已知二次函数2y ax bx c =++ 0a ≠ 的图象如图所示,有下列结论: ①240b ac ->;②0abc >;第( )第( )③80+>;a c④930++<.a b c其中,正确结论的个数是( ) ( )( ) ( )年天津市初中毕业生学业考试试卷数 学第 卷(非选择题 共 分)注意事项:用黑色墨水的钢笔或签字笔将答案写在“答题卡”上。
2010年天津市中考数学试题和答案
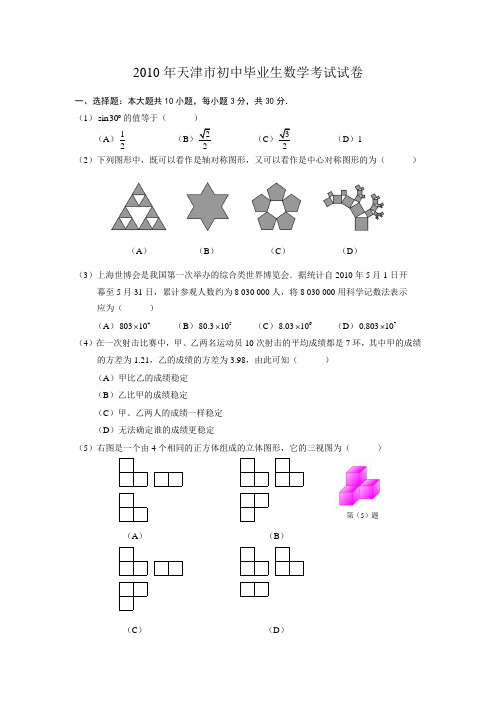
2010年天津市初中毕业生数学考试试卷一、选择题:本大题共10小题,每小题3分,共30分.(1)sin30︒的值等于()(A)12(B(C(D)1(2)下列图形中,既可以看作是轴对称图形,又可以看作是中心对称图形的为()(A)(B)(C)(D)(3)上海世博会是我国第一次举办的综合类世界博览会.据统计自2010年5月1日开幕至5月31日,累计参观人数约为8 030 000人,将8 030 000用科学记数法表示应为()(A)480310⨯(B)580.310⨯(C)68.0310⨯(D)70.80310⨯(4)在一次射击比赛中,甲、乙两名运动员10次射击的平均成绩都是7环,其中甲的成绩的方差为1.21,乙的成绩的方差为3.98,由此可知()(A)甲比乙的成绩稳定(B)乙比甲的成绩稳定(C)甲、乙两人的成绩一样稳定(D)无法确定谁的成绩更稳定(5)右图是一个由4个相同的正方体组成的立体图形,它的三视图为()(A)(B)(C)(D)第(5)题(6)下列命题中正确的是( )(A )对角线相等的四边形是菱形 (B )对角线互相垂直的四边形是菱形 (C )对角线相等的平行四边形是菱形 (D )对角线互相垂直的平行四边形是菱形(7)如图,⊙O 中,弦AB 、CD 相交于点P , 若30A ∠=︒,70APD ∠=︒,则B ∠等于( )(A )30︒ (B )35︒ (C )40︒ (D )50︒ (8)比较2)(A)2<(B)2 (C2(D2(9)如图,是一种古代计时器——“漏壶”的示意图,在壶内盛一定量的水,水从壶下的小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间.若用x 表示时间,y 表示壶底到水面的高度,下面的图象适合表示一小段时间内y 与x 的函数关系的是(不考虑水量变化对压力的影响)( )(A ) (B )(C ) (D )(10)已知二次函数2y ax bx c =++(0a ≠)的图象如图所示,有下列结论:①240b ac ->; ②0abc >; ③80a c +>; ④930a b c ++<. 其中,正确结论的个数是( )(A )1 (B )2 (C )3 (D )4第(7)题第(9)题第(10)题二、填空题:本大题共8小题,每小题3分,共24分. (11)若12a =,则221(1)(1)a a a +++的值为 . (12)已知一次函数26y x =-与3y x =-+的图象交于点P ,则点P 的坐标为 .(13)如图,已知AC FE =,BC DE =,点A 、D 、B 、F 在一条直线上,要使△ABC ≌△FDE ,还需添加一个..条件, 这个条件可以是 .(14)如图,已知正方形ABCD 的边长为3,E 为CD 边上一点,1DE =.以点A 为中心,把△ADE 顺时针旋转90︒,得△ABE ',连接EE ',则EE '的长等于 .(15)甲盒装有3个乒乓球,分别标号为1,2,3;乙盒装有2个乒乓球,分别标号为1,2.现分别从每个盒中随机地取出1个球,则取出的两球标号之和为4的概率是 .(16)已知二次函数2y ax bx c =++(0a ≠)中自变量x 和函数值y 的部分对应值如下表:则该二次函数的解析式为 . (17)如图,等边三角形ABC 中,D 、E 分别为AB 、BC 边上的点,AD BE =,AE 与CD 交于点F ,AG CD ⊥于点G ,则AG AF 的值为 . (18)有一张矩形纸片ABCD ,按下面步骤进行折叠:第一步:如图①,将矩形纸片ABCD 折叠,使点B 、D 重合,点C 落在点C '处,得折痕EF ;第二步:如图②,将五边形AEFC D '折叠,使AE 、C F '重合,得折痕DG ,再打开; 第三步:如图③,进一步折叠,使AE 、C F '均落在DG 上,点A 、C '落在点A '处,点E 、F 落在点E '处,得折痕MN 、QP .这样,就可以折出一个五边形DMNPQ .第(13)题ACD BEF第(14)题E 第(17)题DC A FBE G 第(18)题ADC ' C B EFGADC 'CBF 图①图② 图③C 'D FCAENP BE 'A 'M QG(Ⅰ)请写出图①中一组相等的线段 (写出一组即可);(Ⅱ)若这样折出的五边形DMNPQ (如图③)恰好是一个正五边形,当AB a =,AD b =,DM m =时,有下列结论:①222tan18a b ab -=︒;②tan18m ︒;③tan18b m a =+︒; ④3tan182b m m =+︒.其中,正确结论的序号是 (把你认为正确结论的序号都.填上). 三、解答题:本大题共8小题,共66分.解答应写出文字说明、演算步骤或证明过程. (19)(本小题6分)解不等式组211,84 1.x x x x ->+⎧⎨+<-⎩(20)(本小题8分)已知反比例函数1k y x-=(k 为常数,1k ≠). (Ⅰ)若点2A (1 ),在这个函数的图象上,求k 的值; (Ⅱ)若在这个函数图象的每一支上,y 随x 的增大而减小,求k 的取值范围; (Ⅲ)若13k =,试判断点34B ( ),,25C ( ),是否在这个函数的图象上,并说明理由. (21)(本小题8分)我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t ),并将调查结果绘成了如下的条形统计图.(Ⅰ)求这10个样本数据的平均数、众数和中位数;(Ⅱ)根据样本数据,估计小刚所在班50名同学家庭中月均用水量不超过7 t 的约有多少户.第(21)题户数/t(22)(本小题8分)已知AB 是⊙O 的直径,AP 是⊙O 的切线,A 是切点,BP 与⊙O 交于点C . (Ⅰ)如图①,若2AB =,30P ∠=︒,求AP 的长(结果保留根号); (Ⅱ)如图②,若D 为AP 的中点,求证直线CD 是⊙O 的切线.(23)(本小题8分)永乐桥摩天轮是天津市的标志性景观之一.某校数学兴趣小组要测量摩天轮的高度.如图,他们在C 处测得摩天轮的最高点A 的仰角为45︒,再往摩天轮的方向前进50 m 至D 处,测得最高点A 的仰角为60︒. 求该兴趣小组测得的摩天轮的高度AB1.732≈, 结果保留整数).(24)(本小题8分)注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路按下面的要求填空,完成本题的解答.也可以选用其他的解题方案,此时不必填空,只需按照解答题的一般要求进行解答.青山村种的水稻2007年平均每公顷产8 000 kg ,2009年平均每公顷产9 680 kg ,求该村水稻每公顷产量的年平均增长率.解题方案:设该村水稻每公顷产量的年平均增长率为x . (Ⅰ)用含x 的代数式表示:① 2008年种的水稻平均每公顷的产量为 ; ② 2009年种的水稻平均每公顷的产量为 ; (Ⅱ)根据题意,列出相应方程 ; (Ⅲ)解这个方程,得 ;(Ⅳ)检验: ; (Ⅴ)答:该村水稻每公顷产量的年平均增长率为 %.A图①AD图②第(22)题A45°60° 第(23)题(25)(本小题10分)在平面直角坐标系中,矩形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,3OA =,4OB =,D 为边OB 的中点.(Ⅰ)若E 为边OA 上的一个动点,当△CDE 的周长最小时,求点E 的坐标;(Ⅱ)若E 、F 为边OA 上的两个动点,且2EF =,当四边形CDEF 的周长最小时,求点E 、F 的坐标.(26)(本小题10分)在平面直角坐标系中,已知抛物线2y x bx c =-++与x 轴交于点A 、B (点A 在点B 的左侧),与y 轴的正半轴交于点C ,顶点为E .(Ⅰ)若2b =,3c =,求此时抛物线顶点E 的坐标;(Ⅱ)将(Ⅰ)中的抛物线向下平移,若平移后,在四边形ABEC 中满足 S △BCE = S △ABC ,求此时直线BC 的解析式;(Ⅲ)将(Ⅰ)中的抛物线作适当的平移,若平移后,在四边形ABEC 中满足 S △BCE = 2S △AOC ,且顶点E 恰好落在直线43y x =-+上,求此时抛物线的解析式.第(25)题2010年天津市初中毕业生学业考试 数学试题参考答案及评分标准评分说明:1.各题均按参考答案及评分标准评分。
2010年全国初中数学竞赛历年竞赛试题以及参考答案

b
c
bc
(A) 11 21
(B) 21 11
(C) 110 21
(D) 210 11
解: D
由题设得
a
b
a b
1
20 1
210
.
b c 1 c 1 1 11
b 10
2.若实数 a,b 满足 1 a ab b2 2 0 ,则 a 的取值范围是 (
).
2
(A)a 2 (B)a 4 (C)a≤ 2 或 a≥4 (D) 2 ≤a≤4
因此满足 2000 n0 3000 的正整数 k 的最小值为 9 .
4
三、解答题(共 4 题,每题 20 分,共 80 分)
11.如图,△ABC 为等腰三角形,AP 是底边 BC 上的高,点 D 是线段 PC 上的一点,BE
和 CF 分别是△ABD 和△ACD 的外接圆直径,连接 EF. 求证: tan PAD EF . BC
了货车;又过了 5 分钟,小轿车追上了客车;再过 t 分钟,货车追上了客车,则 t
=
.
解:15
设在某一时刻,货车与客车、小轿车的距离均为 S 千米,小轿车、货车、客
车的速度分别为 a,b,c (千米/分),并设货车经 x 分钟追上客车,由题意得
10a b S ,
①
15a c 2S ,
②
xb c S .
分别交 BE,BN 于点 F,C,过点 C 作 AM 的垂线 CD,垂足为 D.若 CD=CF,则 AE AD
.
解: 5 1 2
见题图,设 FC m, AF n .
(第 9 题)
因为 Rt△AFB∽Rt△ABC,所以 AB2 AF AC .
又因为 FC=DC=AB,所以 m2 n(n m),即
2010年天津市初中毕业生学业考试数学试卷答案
2010年天津市初中毕业生学业考试 数学试题参考答案及评分标准评分说明:1.各题均按参考答案及评分标准评分。
2.若考生的非选择题答案与参考答案不完全相同但言之有理,可酌情评分,但不得超过该题所分配的分数。
一、选择题:本大题共10小题,每小题3分,共30分. (1)A (2)B (3)C (4)A (5)B (6)D(7)C(8)C(9)B(10)D二、填空题:本大题共8小题,每小题3分,共24分. (11)23(12)(3,0)(13)C E ∠=∠(答案不惟一,也可以是AB FD =或AD FB =) (14)(15) 13 (16) 22y x x =+-(17(18)(Ⅰ)AD C D '=(答案不惟一,也可以是AE C F '=等);(Ⅱ)①②③三、解答题:本大题共8小题,共66分. (19)(本小题6分) 解: ∵ 211,84 1.x x x x ->+⎧⎨+<-⎩解不等式①,得2x >. 解不等式②,得3x >. ∴ 原不等式组的解集为3x >.①②(20)(本小题8分)解:(Ⅰ)∵ 点2A (1 ),在这个函数的图象上,∴ 21k =-.解得3k =. (Ⅱ)∵ 在函数1k y x-=图象的每一支上,y 随x 的增大而减小, ∴ 10k ->.解得1k >. (Ⅲ)∵ 13k =,有112k -=.∴ 反比例函数的解析式为12y x=. 将点B 的坐标代入12y x=,可知点B 的坐标满足函数关系式, ∴ 点B 在函数12y x=的图象上. 将点C 的坐标代入12y x=,由1252≠,可知点C 的坐标不满足函数关系式,∴ 点C 不在函数12y x=的图象上. (21)(本小题8分)解:(Ⅰ)观察条形图,可知这组样本数据的平均数是62 6.54717.52816.810x ⨯+⨯+⨯+⨯+⨯==.∴ 这组样本数据的平均数为6.8.∵ 在这组样本数据中,6.5出现了4次,出现的次数最多, ∴ 这组数据的众数是6.5.∵ 将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是6.5, 有6.5 6.56.52+=, ∴ 这组数据的中位数是6.5. (Ⅱ)∵ 10户中月均用水量不超过7 t 的有7户,有 7503510⨯=. ∴ 根据样本数据,可以估计出小刚所在班50名同学家庭中月均用水量不超过7 t 的约有35户.(22)(本小题8分)解:(Ⅰ)∵ AB 是⊙O 的直径,AP 是切线,∴ 90BAP ∠=︒.在Rt △PAB 中,2AB =,30P ∠=︒, ∴ 2224BP AB ==⨯=.由勾股定理,得AP == (Ⅱ)如图,连接OC 、AC ,∵ AB 是⊙O 的直径, ∴ 90BCA ∠=︒,有90ACP ∠=︒. 在Rt △APC 中,D 为AP 的中点, ∴ 12CD AP AD ==. ∴ DAC DCA ∠=∠. 又 ∵OC OA =, ∴OAC OCA ∠=∠.∵ 90OAC DAC PAB ∠+∠=∠=︒, ∴ 90OCA DCA OCD ∠+∠=∠=︒. 即 OC CD ⊥.∴ 直线CD 是⊙O 的切线.(23)(本小题8分)解:根据题意,可知45ACB ∠=︒,60ADB ∠=︒,50DC =.在Rt △ABC 中,由45BAC BCA ∠=∠=︒,得BC AB =. 在Rt △ABD 中,由tan ABADB BD∠=,得tan tan 60AB AB BD AB ADB ===∠︒.又 ∵ BC BD DC -=,∴50AB =,即(3150AB =. ∴118AB =≈. 答:该兴趣小组测得的摩天轮的高度约为118 m .AD(24)(本小题8分)解:(Ⅰ)①8000(1)x +;②28000(1)x +;(Ⅱ)28000(1)9680x +=; (Ⅲ)10.1x =,2 2.1x =-;(Ⅳ)10.1x =,2 2.1x =-都是原方程的根,但2 2.1x =-不符合题意,所以只取0.1x =; (Ⅴ)10 . (25)(本小题10分)解:(Ⅰ)如图,作点D 关于x 轴的对称点D ',连接CD '与x 轴交于点E ,连接DE .若在边OA 上任取点E '(与点E 不重合),连接CE '、DE '、DE''. 由DE CE D E CE CD D E CE DE CE '''''''+=+>=+=+, 可知△CDE 的周长最小.∵ 在矩形OACB 中,3OA =,4OB =,D 为OB∴ 3BC =,2D O DO '==,6D B '=. ∵ OE ∥BC ,∴ Rt △D OE '∽Rt △D BC ',有OE D OBC D B'='. ∴ 2316D O BC OE D B '⋅⨯==='. ∴ 点E 的坐标为(1,0).(Ⅱ)如图,作点D 关于x 轴的对称点D ',在CB 边上截取2CG =,连接D G '与x 轴交于点E ,在EA 上截取2EF =. ∵ GC ∥EF ,GC EF =,∴ 四边形GEFC 为平行四边形,有GE CF =. 又 DC 、EF 的长为定值,∴ 此时得到的点E 、F 使四边形CDEF 的周长最小. ∵ OE ∥BC ,∴ Rt △D OE '∽Rt △D BG ', 有 OE D OBG D B'='.∴ ()21163D O BG D O BC CG OE D B D B ''⋅⋅-⨯====''. ∴ 17233OF OE EF =+=+=.∴ 点E 的坐标为(13,0),点F 的坐标为(73,0).(26)(本小题10分)解:(Ⅰ)当2b =,3c =时,抛物线的解析式为223y x x =-++,即2(1)4y x =--+.∴ 抛物线顶点E 的坐标为(1,4).(Ⅱ)将(Ⅰ)中的抛物线向下平移,则顶点E 在对称轴1x =上,有2b =,∴ 抛物线的解析式为22y x x c =-++(0c >).∴ 此时,抛物线与y 轴的交点为0( )C c ,,顶点为1( 1)E c +,. ∵ 方程220x x c -++=的两个根为11x =21x = ∴ 此时,抛物线与x轴的交点为10()A,10()B . 如图,过点E 作EF ∥CB 与x 轴交于点F ,连接CF ,则S △BCE = S △BCF . ∵ S △BCE = S △ABC , ∴ S △BCF = S △ABC . ∴BF AB == 设对称轴1x =与x 轴交于点D ,则12DF AB BF =+=由EF ∥CB ,得EFD CBO ∠=∠. ∴ Rt △EDF ∽Rt △COB .有ED CODF OB=. ∴=.结合题意,解得 54c =. ∴ 点54(0 )C ,,52( 0)B ,.x设直线BC 的解析式为y mx n =+,则 5,450.2n m n ⎧=⎪⎪⎨⎪=+⎪⎩ 解得 1,25.4m n ⎧=-⎪⎪⎨⎪=⎪⎩ ∴ 直线BC 的解析式为1524y x =-+.(Ⅲ)根据题意,设抛物线的顶点为( )E h k ,,(0h >,0k >) 则抛物线的解析式为2()y x h k =--+, 此时,抛物线与y 轴的交点为2(0 )C h k -+,,与x轴的交点为0()A h,0()B h .0h >) 过点E 作EF ∥CB 与x 轴交于点F ,连接CF , 则S △BCE = S △BCF . 由S △BCE = 2S △AOC ,∴ S △BCF = 2S △AOC .得2)BF AO h ==. 设该抛物线的对称轴与x 轴交于点D . 则122DF AB BF h =+=. 于是,由Rt △EDF ∽Rt △COB ,有ED CODF OB=. ∴2=2220h k -+=.结合题意,解得h =① ∵ 点( )E h k ,在直线43y x =-+上,有43k h =-+. ② ∴1=. 有1k =,12h =. ∴抛物线的解析式为234y x x =-++.。
2010年全国初中数学竞赛天津赛区初赛考试试题.答案
2010年全国初中数学竞赛天津赛区初赛试题参考答案及评分标准一、选择题(本大题共5小题,每小题7分,满分35分) (1)计算2222010200920102009201122009--⨯+⨯的值为( ). (A )1 (B )1- (C )2 009 (D )2 010【解】选A .原式22222222010200920102009120102009(20112)20102009--===---.[例11] (2005-4)设22211148()34441004A =⨯++---,则与A 最接近的正整数是( ).(A)18 (B)20 (C)24 (D)25[解答]当n ≥3时,有()()211111422422n n n n n ⎛⎫==- ⎪--+-+⎝⎭,所以22211148()34441004A =⨯++---111111481452698102⎡⎤⎛⎫⎛⎫⎛⎫=⨯-+-+- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦111111112123499100101102⎛⎫=⨯+++---- ⎪⎝⎭1111251299100101102⎛⎫=-⨯+++ ⎪⎝⎭,因为11111111411212129910010110299999999992⎛⎫⎛⎫⨯+++<⨯+++=⨯< ⎪ ⎪⎝⎭⎝⎭, 所以与A 最接近的正整数是25,选D.[点评]数列求和问题是一类基本问题,裂项相消法则是其中一个基本方法,要特别注意裂项后哪些项没有抵消.当然,只有符合一定的特点的式子(数列)才能裂项,常见的裂项有:()1111n n k k n n k ⎛⎫=- ⎪++⎝⎭=.(3)如图,在梯形ABCD 中,AB ∥DC ,AB ⊥BC ,E 是AD 的中点,6AB BC CD ++=, BE =,则梯形ABCD 的面积等于( ).(A )13 (B )8ABCD E 第(3)题(C )132(D )4 【解】选D .如图,过点E 作//EF AB 交BC 于点F ,则12BF BC =,11()(6)22EF AB CD BC =+=-,又∵BC AB ⊥,∴EF BC ⊥∴在Rt △BFE 中,222EF BF BE +=.∴22211[(6)]()22BC BC -+=,即2680BC BC -+=,解得 2BC =或4BC =,则2EF =或1EF =, ∴ 4ABCD S EF BC =⋅=梯形. (4)某个一次函数的图象与直线132y x =+平行,与x 轴,y 轴的交点分别为A ,B ,并且过点(2-,4-),则在线段AB 上(包括点A ,B ),横、纵坐标都是整数的点有( ).(A )3个 (B )4个 (C )5个 (D )6个 【解】选B .根据题意,设一次函数的解析式为12y x b =+,由点(2-,4-)在该函数图象上,得14(2)2b -=⨯-+,解得3b =-.所以,132y x =-.可得点A (6,0),B (0,3-). 由06x ≤≤,且x 为整数,取0,2,4,6x =时,对应的y 是整数. 因此,在线段AB 上(包括点A 、B ),横、纵坐标都是整数的点有4个.(5)如图,一个半径为r 的圆形纸片在边长为a(a ≥)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( ).(A )2π3r(B2(C)2π)r (D )2πr 【解】选C .如图,当圆形纸片运动到与A ∠的两边相切的位置时,过圆形纸片的圆心1O 作两边的垂线,垂足分别为D ,E ,连1AO ,则Rt △1ADO 中,130O AD ∠=︒,1O D r =,AD =.∴12112ADO S O D AD ∆=⋅=.有1122ADO ADO E S S ∆=四形形.∵由题意,1120DO E ∠=,得12π3O DE S r =扇形,∴圆形纸片不能接触到的部分的面积为22π3)3r -2π)r =第(5)题ABC D EFCNCABDM第(8)题二、填空题(本大题共5小题,每小题7分,满分35分)(6)如图,有五张点数分别为2,3,7,8,9的扑克牌,从中任意抽取两张,则其点数之积是偶数的概率为 .【解】710. 根据题意,当不考虑抽牌顺序时,可以画出如下的树形图从上图可以看出,从五张牌中任意抽取两张,共有10种抽法,其中抽取的点数之积是偶数的有7种,所以点数之积是偶数的概率710P =.(7)如图,是一个树形图的生长过程,自上而下,一个空心圆生成一个实心圆,一个实心圆生成一个实心圆和一个空心圆,依此生长规律,第9行的实心圆的个数【解】21个.观察图形规律,可得,从第3行起,每行中的实心圆的个数都是上两行实心圆个数的和.于是,第7行实心圆的个数为3+5=8(个); 第8行实心圆的个数为5+8=13(个); 第9行实心圆的个数为8+13=21(个). (8)如图,在△ABC 中,中线CM 与高线 CD 三等分ACB ∠,则B ∠等于 (度).【解】30︒.根据题意,可得CD AB ⊥,AM MB =,ACD MCD BCM ∠=∠=∠. ∵ACD MCD ∠=∠,CD CD =,90CDA CDM ∠=∠=︒,点数之积 3 7 8 96 2 14 16 183 78921 24 27 56 78963 8 972 第(6)题1行 2行 3行 4行 5行 6行……第(7)题∴△ACD ≅△MCD ∠. ∴12AD DM AM ==. 过点M 作MN BC ⊥于点N ,∵DCM NCM ∠=∠,CM CM =,90CDM CNM ∠=∠=︒, ∴△DCM ≅△NCM ∠. ∴DM NM =.于是12NM MB =,∴在Rt △MNB 中,30B ∠=︒.(9)有n 个连续的自然数1,2,3,…,n ,若去掉其中的一个数x 后,剩下的数的平均数是16,则满足条件的n 和x 的值分别是 .(参考公式:2)1(321+=++++=n n n S n ) 【解】30n =,1x =;31n =,16x =;32n =,32x =.由已知,n 个连续的自然数的和为(1)2n n n S +=.若x n =,剩下的数的平均数是12n S n nn -=-; 若1x =,剩下的数的平均数是 1112n S nn -=+-,故16122n n+≤≤,解得 3032n ≤≤. 当30n =时,30(301)29162x ⨯+⨯=-,解得1x =; 当31n =时,31(311)30162x ⨯+⨯=-,解得16x =; 当32n =时,32(321)31162x ⨯+⨯=-,解得32x =. (10)母亲节到了,小红,小莉,小莹到花店买花送给自己的母亲.小红买了3枝玫瑰,7枝康乃馨,1枝百合花,付了14元;小莉买了4枝玫瑰,10枝康乃馨,1枝百合花,付了16元;小莹买上面三种花各2枝,则她应付 元.【解】20.方法一:设玫瑰、康乃馨、百合花的单价分别为x 元,y 元,z 元, 根据已知条件,列出方程组3714,41016.x y z x y z ++=⎧⎨++=⎩消去z ,得23x y =-. ③ 将③代入①,得82z y =+.④由③,④得 10x y z ++=.有 2()20x y z ++=. 所以,小莹应付20元. 方法二:(37)(410)2()m x y z n x y z x y z +++++=++,(34)(710)()222m n x m n y m n z x y z +++++=++.①②∴342,7102,2.m n m n m n +=⎧⎪+=⎨⎪+=⎩解得4,6.n m =-⎧⎨=⎩∴2()6(37)4(410)61441620x y z x y z x y z ++=⨯++-++=⨯-⨯=. 三、解答题(本大题共4小题,每小题满分20分,共80分) (11)(本小题满分20分)已知,抛物线2y ax bx c =++(0≠a )经过A 、B图中的曲线是它的一部分.根据图中提供的信息,(Ⅰ)确定a ,b ,c 的符号; (Ⅱ)当b 变化时,求a b c ++的取值范围.【解】(Ⅰ)如图,由抛物线开口向上,得0a >.……3由抛物线过点(0,1)-,得10c =-<. ……6分 由抛物线对称轴在y 轴的右侧,得02ba->,又 0a >,得0b <. ∴0a >,0b <,0c <. ……………………………………10分 (Ⅱ)由抛物线过点(1,0)-,得0a b c -+=.即1a b =+,由0a >,得1b >-. ……………………………………16分 ∴10b -<<,∴(1)12a b c b b b ++=++-=.∴20a b c -<++<. ……………………………………20分 (12)(本小题满分20分)设直角三角形的两条直角边长分别为,a b ,斜边长为c .若,,a b c 均为整数,且1()3c ab a b =-+,求满足条件的直角三角形的个数.【解】由勾股定理,得222c a b =+. ……………………………………3分又1()3c ab a b =-+,得2222112[()]()()()393c ab a b ab ab a b a b =-+=-+++.即2222212()()293a b ab ab a b a ab b +=-++++.整理,得6()180ab a b -++=.即(6)(6)18a b --=. ………………………8分 因为,a b 均为正整数,不妨设a b <, 可得61,618,a b -=⎧⎨-=⎩或62,69,a b -=⎧⎨-=⎩或63,6 6.a b -=⎧⎨-=⎩可解出7,24,25,a b c =⎧⎪=⎨⎪=⎩或8,15,17,a b c =⎧⎪=⎨⎪=⎩或9,12,15.a b c =⎧⎪=⎨⎪=⎩所以,满足条件的直角三角形有3个. ……………………………………20分 (13)(本小题满分20分)AC如图,在△ABC 中,45ABC ∠=,点D 在边BC 上,60ADC ∠=,且12BD CD =.将△ACD 以直线AD 为轴做轴对称变换,得到△AC D ',连接BC ',(Ⅰ)求证BC BC '⊥; (Ⅱ)求C ∠的大小.(Ⅰ)【证明】∵△AC D '是△ACD 沿AD 做轴对称变换得到的,∴△AC D '≌△ACD .有C D CD '=,ADCADC '∠=∠.………………3分∵12BD CD =,60ADC ∠=,∴12BD C D '=,18060BDC ADC ADC ''∠=-∠-∠=.……5分取C D '中点P ,连接BP ,则△BDP 为等边三角形,△BC P '为等腰三角形,…8分有113022BC D BPD BDC ''∠=∠=∠=︒.∴90C BD '∠=,即BC BC '⊥. ……10分(Ⅱ)【解】如图,过点A 分别作,,BC C D BC ''的垂线,垂足分别为,,E F G .∵ADC ADC '∠=∠,即点A 在C DC '∠的平分线上, ∴AE AF =.……13分 ∵90C BD '∠=,45ABC ∠=, ∴45GBA C BC ABC '∠=∠-∠=,即点A 在GBC ∠的平分线上,∴AG AE =.……16分 于是,AG AF =,则点A 在GC D '∠的平分线上.…………………………18分 又∵30BC D '∠=︒,有150GC D '∠=. ∴12AC D '∠=75GC D '∠=.∴C ∠75AC D '=∠=.………………………20分 (14)(本小题满分20分)(Ⅰ)如图(a ),在正方形ABCD 内,已知两个动圆1O 与2O 互相外切,且1O 与边AB 、AD 相切,2O 与边BC 、CD 相切.若正方形ABCD 的边长为1,1O 与2O 的半径分别为1r ,2r .①求1r 与2r 的关系式;②求1O 与2O 面积之和的最小值.(Ⅱ)如图(b ),若将(Ⅰ)中的正方形ABCD 改为一个ABCDC 'PA 图(a )BDC 'FGAC宽为1,长为32的矩形,其他条件不变,则1O 与2O 面积的 和是否存在最小值,若不存在,请说明理由;若存在,请求出 这个最小值.【解】(Ⅰ)如图(a ),在正方形ABCD 中,连接AC ,显然1O 与2O 在AC 上,且1AO =,1212O O r r =+,22CO =,由1122AC AO O O CO =++=,122r r +++=∴122r r += ………………………5分②根据题意,1r 12≤,2r 12≤,可得21122r r =-≤,即321r 12≤.∵1O 与2O 的面积之和2212π()S r r =+,∴2211(2)πSr r =+21122(26r r =-+-2122(32r =-+-32-2212≤,…………8分∴当1r =时,1O 与2O是等圆,其面积和的最小值为(3π-. ……………………………………10分(Ⅱ)如图(b ),作辅助线,得到Rt △12O O P , 则1212O O r r =+,1121232O P AB r r r r =--=--, 212121O P BC r r r r =--=--.∵在Rt △12O O P 中,2221212O O O P O P =+,∴2221212123()()(1)2r r r r r r +=--+--.即2121213()5()04r r r r +-++=.解得1252r r +=+1252r r +=图(a )B图(b )由于1235122r r +<+=,故1252r r +=∴1252r r +=……………………………………15分 ∵1O 与2O 的面积之和2212π()S r r =+,而2221212()2r r r r ++≥,当且仅当12r r =时,等号成立,∴当12r r =时,1O 与2O 面积和存在最小值,最小值为25(2π2-,即37(π8-. ……………………………………20分。
2010年天津市中考数学试卷及答案详解
2010年天津市中考数学试卷及答案详解一、选择题(共1小题;共5分)1. 的值等于______A. B. C. D.二、解答题(共1小题;共13分)2. 解不等式组:.三、选择题(共6小题;共30分)3. 下列图形中,既可以看作是轴对称图形,又可以看作是中心对称图形的为______A. B.C. D.4. 上海世博会是我国第一次举办的综合类世界博览会.据统计自 2010 年 5 月 1 日开幕至 5 月31日,累计参观人数约为人,将用科学记数法表示应为______A. B. C. D.5. 在一次射击比赛中,甲、乙两名运动员次射击的平均成绩都是环,其中甲的成绩的方差为,乙的成绩的方差为,由此可知______A. 甲比乙的成绩稳定B. 乙比甲的成绩稳定C. 甲、乙两人的成绩一样稳定D. 无法确定谁的成绩更稳定6. 下列命题中正确的是______A. 对角线相等的四边形是菱形B. 对角线互相垂直的四边形是菱形C. 对角线相等的平行四边形是菱形D. 对角线互相垂直的平行四边形是菱形7. 如图所示,中,弦、相交于点,若,,则等于______A. B. C. D.8. 如图所示,是一种古代计时器--“漏壶”的示意图,在壶内盛一定量的水,水从壶下的小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间.若用表示时间,表示壶底到水面的高度,下面的图象适合表示一小段时间内与的函数关系的是(不考虑水量变化对压力的影响)______A. B.C. D.四、填空题(共1小题;共5分)9. 甲盒装有个乒乓球,分别标号为,,;乙盒装有个乒乓球,分别标号为,.现分别从每个盒中随机地取出个球,则取出的两球标号之和为的概率是______.五、解答题(共4小题;共52分)10. 我国是世界上严重缺水的国家之一.为了倡导"节约用水从我做起",小刚在他所在班的名同学中,随机调查了名同学家庭中一年的月均用水量(单位:),并将调查结果绘成了如下的条形统计图.(1)求这个样本数据的平均数、众数和中位数;(2)根据样本数据,估计小刚所在班名同学家庭中月均用水量不超过的约有多少户.11. 永乐桥摩天轮是天津市的标志性景观之一.某校数学兴趣小组要测量摩天轮的高度.如图,他们在处测得摩天轮的最高点的仰角为,再往摩天轮的方向前进至处,测得最高点的仰角为.求该兴趣小组测得的摩天轮的高度(,结果保留整数).12. 注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路按下面的要求填空,完成本题的解答.也可以选用其他的解题方案,此时不必填空,只需按照解答题的一般要求进行解答.青山村种的水稻2007 年平均每公顷产,2009 年平均每公顷产,求该村水稻每公顷产量的年平均增长率.解题方案:设该村水稻每公顷产量的年平均增长率为.(i)用含的代数式表示:①2008 年种的水稻平均每公顷的产量为______;②2009年种的水稻平均每公顷的产量为______;(ii)根据题意,列出相应方程______;(iii)解这个方程,得______;(iv)检验:______;(v)答:该村水稻每公顷产量的年平均增长率为______.13. 在平面直角坐标系中,矩形的顶点在坐标原点,顶点、分别在轴、轴的正半轴上,,,为边的中点.(1)若为边上的一个动点,当的周长最小时,求点的坐标;(2)若、为边上的两个动点,且,当四边形的周长最小时,求点、的坐标.六、选择题(共3小题;共15分)14. 如图是一个由个相同的正方体组成的立体图形,它的三视图为______A. B.C. D.15. 比较,,的大小,正确的是______A. B. C. D.16. 已知二次函数的图象如图所示,有下列结论:①;②;③;④.其中,正确结论的个数是______A. B. C. D.七、填空题(共4小题;共20分)17. 如图,已知,,点,,,在一条直线上,要使,还需添加一个条件,这个条件可以是______.18. 已知二次函数中自变量和函数值的部分对应值如下表,则该二次函数的解析式为______.19. 如图,等边三角形中,,分别为,边上的点,,与交于点,于点,则的值为______.20. 有一张矩形纸片,按下面步骤进行折叠:第一步:如图①,将矩形纸片折叠,使点、重合,点落在点处,得折痕;第二步:如图②,将五边形折叠,使、重合,得折痕,再打开;第三步:如图③,进一步折叠,使、均落在上,点、落在点处,点、落在点处,得折痕、.这样,就可以折出一个五边形,(1)请写出图①中一组相等的线段______(写出一组即可);(2)若这样折出的五边形(如图③)恰好是一个正五边形,当,,时,有下列结论:①;②;③;④.其中,正确结论的序号是______(把你认为正确结论的序号都填上).八、解答题(共2小题;共26分)21. 已知反比例函数(为常数,).(1)若点在这个函数的图象上,求的值;(2)若在这个函数图象的每一支上,随的增大而减小,求的取值范围;(3)若,试判断点,是否在这个函数的图象上,并说明理由.22. 在平面直角坐标系中,已知抛物线与轴交于点、(点在点的左侧),与轴的正半轴交于点,顶点为.(1)若,,求此时抛物线顶点的坐标;(2)将(1)中的抛物线向下平移,若平移后,在四边形中满足,求此时直线的解析式;(3)将(1)中的抛物线作适当的平移,若平移后,在四边形中满足,且顶点恰好落在直线上,求此时抛物线的解析式.九、填空题(共3小题;共15分)23. 若,则的值为______.24. 已知一次函数与的图象交于点,则点的坐标为______.25. 如图,已知正方形的边长为,为边上一点,.以点为中心,把顺时针旋转,得,连接,则的长等于______.答案第一部分1. A第二部分2. 解:解不等式①得:,解不等式②得:,不等式的解集为.第三部分3. B4. C5. A6. D7. C8. B第四部分9.第五部分10. (1)观察条形图,可知这组样本数据的平均数是这组样本数据的平均数为.在这组样本数据中,出现了次,出现的次数最多,这组数据的众数是.将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是,有,这组数据的中位数是.(2)户中月均用水量不超过的有户,有.根据样本数据,可以估计出小刚所在班名同学家庭中月均用水量不超过的约有户.11. 根据题意,可知,,.在中,由,得.在中,由,得.又,,即..答:该兴趣小组测得的摩天轮的高度约为.12. (i)①;②(ii)(iii),(iv),都是原方程的根,但不符合题意,所以只取(v)13. (1)关于轴的对称点,连接与轴交于点,连接.若在边上任取点(与点不重合),连接、、.由可知的周长最小.在矩形中,,,为的中点,,,.,,有..点的坐标为.(2)关于轴的对称点,在边上截取,连接与轴交于点,在上截取.,,四边形为平行四边形,有.又、的长为定值,此时得到的点、使四边形的周长最小.,,有...点的坐标为,点的坐标为第六部分14. B 15. C16. D第七部分17. (答案不惟一,也可以是或)18.19.20. (答案不惟一,也可以是等);①②③第八部分21. (1)点在这个函数的图象上,.解得.(2)在函数图象的每一支上,随的增大而减小,.解得.(3),.反比例函数的解析式为.将点的坐标代入,可知点的坐标满足函数关系式,点在函数的图象上.将点的坐标代入,由,可知点的坐标不满足函数关系式,点不在函数的图象上.22. (1)当,时,抛物线的解析式为,即.抛物线顶点的坐标为.(2)将(1)中的抛物线向下平移,则顶点在对称轴上,有,抛物线的解析式为.此时,抛物线与轴的交点为,顶点为.方程的两个根为,此时,抛物线与轴的交点为,.如图所示,过点作与轴交于点,连接..,..设对称轴与轴交于点,则.由,得....结合题意,解得.点,.设直线的解析式为.则解得直线的解析式为.(3)根据题意,设抛物线的顶点为.则抛物线的解析式为.此时,抛物线与轴的交点为.与轴的交点为,,().过点作与轴交于点,连接(如(2)中图所示),则.由,.得.设该抛物线的对称轴与轴交于点,则.于是,由,有.,即.结合题意,解得点在直线上,有由,结合题意,解得,有,.抛物线的解析式为.第九部分23.24. ,25.。
2010年天津市初中数学竞赛初赛试题-推荐下载
2010年全国初中数学竞赛天津赛区初赛试题参考答案及评分标准一、选择题(本大题共5小题,每小题7分,满分35分)(1)计算的值为().2222010200920102009201122009--⨯+⨯(A )1 (B ) (C )2 009(D )2 0101-【解】选A .原式.22222222010200920102009120102009(20112)20102009--===---(2)如图,是一个正方体的表面展开图,正方体的每个面都标注了字母.在展开前,与标注字母的面相对的面内标注的字母为().a (A ) (B )b d (C ) (D )e f 【解】选B .(3)如图,在梯形ABCD 中,AB ∥DC ,AB ⊥BC ,E 是AD 的中点,,6AB BC CD ++=,则梯形ABCD 的面积等于().BE =(A )13(B )8(C ) (D )4132【解】选D .如图,过点E 作交BC 于点F ,//EF AB 则,,12BF BC =11()(6)22EF AB CD BC =+=-又∵,∴BC AB ⊥EF BC⊥∴在Rt △中,.BFE 222EF BF BE +=∴,即,22211[(6)]()22BC BC -+=2680BC BC -+=解得 或,则或,2BC =4BC =2EF =1EF =第(2)题A BCDEFABC DE第(3)题∴ .4ABCDS EF BC =⋅=四四(4)某个一次函数的图象与直线平行,与轴,轴的交点分别为132y x =+x y A ,B ,并且过点(,),则在线段上(包括点A ,B ),横、纵坐标都是整数的2-4-AB 点有( ).(A )3个 (B )4个 (C )5个 (D )6个【解】选B .根据题意,设一次函数的解析式为,12y x b =+由点(,)在该函数图象上,得,解得.2-4-14(2)2b -=⨯-+3b =-所以,.可得点A (6,0),B (0,).132y x =-3-由,且为整数,取时,对应的是整数.06x ≤≤x 0,2,4,6x =y 因此,在线段上(包括点A 、B ),横、纵坐标都是整数的点有4个.AB (5)如图,一个半径为的圆形纸片在边长为()的等边三角形内任ra a ≥意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( ).(A ) (B2π3r 2(C )(D )2π)r -2πr 【解】选C .如图,当圆形纸片运动到与的两边相切的位置时,过圆形纸片的圆心作两边A ∠1O 的垂线,垂足分别为D ,E ,连,则Rt △中,,,1AO 1ADO 130O AD∠=︒1O D r =.AD =∴.有.12112ADO SO D AD ∆=⋅=1122ADO ADO ES S ∆==四四四∵由题意,,得,1120DO E ∠= 12π3O DES r =四四∴圆形纸片不能接触到的部分的面积为22π3)3r -四2π)r =-第(5)题AC二、填空题(本大题共5小题,每小题7分,满分35分)(6)如图,有五张点数分别为2,3,7,8,9的扑克牌,从中任意抽取两张,则其点数之积是偶数的概率为 .【解】.710根据题意,当不考虑抽牌顺序时,可以画出如下的树形图从上图可以看出,从五张牌中任意抽取两张,共有10种抽法,其中抽取的点数之积是偶数的有7种,所以点数之积是偶数的概率.710P =(7)如图,是一个树形图的生长过程,自上而下,一个空心圆生成一个实心圆,一个实心圆生成一个实心圆和一个空心圆,依此生长规律,第9行的实心圆的个数是 .【解】21个.观察图形规律,可得,从第3行起,每行中的实心圆的个数都是上两行实心圆个数的和.于是,第7行实心圆的个数为358(个);+=第8行实心圆的个数为5813(个);+=第9行实心圆的个数为81321(个).+=(8)如图,在△ABC 中,中线CM 与高线点数之积378962141618378921242756789638972第(6)题123456……第(7)题C ABDMNCD 三等分,则等于 (度).ACB ∠B ∠【解】.30︒根据题意,可得,,.CD AB ⊥AM MB =ACD MCD BCM ∠=∠=∠∵,,,ACD MCD ∠=∠CD CD =90CDA CDM ∠=∠=︒∴△△. ∴.ACD ≅MCD ∠12AD DM AM ==过点作于点N ,M MN BC ⊥∵,,,DCM NCM ∠=∠CM CM =90CDM CNM ∠=∠=︒∴△△. ∴.DCM ≅NCM ∠DM NM =于是,∴在Rt △中,.12NM MB =MNB 30B ∠=︒(9)有个连续的自然数1,2,3,…,,若去掉其中的一个数后,剩下的数n n x 的平均数是16,则满足条件的和的值分别是 .n x (参考公式:)2)1(321+=++++=n n n S n 【解】,;,;,.30n =1x =31n =16x =32n =32x =由已知,个连续的自然数的和为.n (1)2n n n S +=若,剩下的数的平均数是 ;x n =12n S n nn -=-若,剩下的数的平均数是 ,1x =1112n S nn -=+-故,解得 .16122nn+≤≤3032n ≤≤当时,,解得;30n =30(301)29162x ⨯+⨯=-1x =当时,,解得;31n =31(311)30162x ⨯+⨯=-16x =当时,,解得.32n =32(321)31162x ⨯+⨯=-32x =(10)母亲节到了,小红,小莉,小莹到花店买花送给自己的母亲.小红买了3枝玫瑰,7枝康乃馨,1枝百合花,付了14元;小莉买了4枝玫瑰,10枝康乃馨,1枝百合花,付了16元;小莹买上面三种花各2枝,则她应付元.【解】20.方法一:设玫瑰、康乃馨、百合花的单价分别为元,元,元,x y z 根据已知条件,列出方程组3714,41016.x y z x y z ++=⎧⎨++=⎩消去,得.③z 23x y =-将③代入①,得.④82z y =+由③,④得 .有 .所以,小莹应付20元.10x y z ++=2()20x y z ++=方法二:,(37)(410)2()m x y z n x y z x y z +++++=++.(34)(710)()222m n x m n y m n z x y z +++++=++∴ 解得342,7102,2.m n m n m n +=⎧⎪+=⎨⎪+=⎩4,6.n m =-⎧⎨=⎩∴.2()6(37)4(410)61441620x y z x y z x y z ++=⨯++-++=⨯-⨯=三、解答题(本大题共4小题,每小题满分20分,共80分)(11)(本小题满分20分)已知,抛物线()经过、2y ax bx c =++0≠a A B 图中的曲线是它的一部分.根据图中提供的信息,(Ⅰ)确定,,的符号;a b c (Ⅱ)当变化时,求的取值范围.b a b c ++【解】(Ⅰ)如图,由抛物线开口向上,得.……0a >由抛物线过点,得.……6分(0,1)-10c =-<由抛物线对称轴在轴的右侧,得,又 ,得.y 02ba->0a >0b <∴,,.……………………………………10分0a >0b <0c <(Ⅱ)由抛物线过点,得.(1,0)-0a b c -+=即,由,得.……………………………………16分1a b =+0a >1b >-∴,∴.10b -<<(1)12a b c b b b ++=++-=①②∴.……………………………………20分20a b c -<++<(12)(本小题满分20分)设直角三角形的两条直角边长分别为,斜边长为.若均为整数,且,a b c ,,a b c ,求满足条件的直角三角形的个数.1()3c ab a b =-+【解】由勾股定理,得. ……………………………………3分222c a b =+又,得.1()3c ab a b =-+2222112[()]()()()393c ab a b ab ab a b a b =-+=-+++即.2222212()()293a b ab ab a b a ab b +=-++++整理,得.即. ………………………8分6()180ab a b -++=(6)(6)18a b --=因为均为正整数,不妨设,,a b a b <可得或或61,618,a b -=⎧⎨-=⎩62,69,a b -=⎧⎨-=⎩63,6 6.a b -=⎧⎨-=⎩可解出或或7,24,25,a b c =⎧⎪=⎨⎪=⎩8,15,17,a b c =⎧⎪=⎨⎪=⎩9,12,15.a b c =⎧⎪=⎨⎪=⎩所以,满足条件的直角三角形有3个.……………………………………20分(13)(本小题满分20分)如图,在△中,,点在边ABC 45ABC ∠= D 上,,且.将△以BC 60ADC ∠= 12BD CD =ACD 直线为轴做轴对称变换,得到△,连接,AD AC D 'BC '(Ⅰ)求证;BC BC '⊥(Ⅱ)求的大小.C ∠(Ⅰ)【证明】∵△是△沿做轴对称变换得到的,AC D 'ACD AD ∴△≌△.AC D 'ACD 有,.………………3分C D CD '=ADC ADC '∠=∠∵,,12BD CD =60ADC ∠= ABCDC 'ABCDC 'PBC图(b )∴,.……5分12BD C D '=18060BDC ADC ADC ''∠=-∠-∠= 取中点P ,连接,则△为等边三角形,△为等腰三角形,…8分C D 'BP BDP BC P '有.∴,即. (10)113022BC D BPD BDC ''∠=∠=∠=︒90C BD '∠= BC BC '⊥分(Ⅱ)【解】如图,过点分别作的垂线,垂足分别为.A ,,BC C D BC '',,E F G ∵,ADC ADC '∠=∠即点在的平分线上,A C DC '∠∴.……13分AE AF =∵,,90C BD '∠= 45ABC ∠= ∴,45GBA C BC ABC '∠=∠-∠= 即点在的平分线上,∴.……16分A GBC ∠AG AE =于是,,则点在的平分线上.…………………………18分AG AF =A GC D '∠又∵,有.30BC D '∠=︒150GC D '∠= ∴.∴.………………………20分12AC D '∠=75GC D '∠= C ∠75AC D '=∠= (14)(本小题满分20分)(Ⅰ)如图(),在正方形内,已知两个动圆与互相外切,且a ABCD 1O A 2O A 与边AB 、AD 相切,与边BC 、CD 相切.若正方形的边长为1,1O A 2O A ABCD 与的半径分别为,.1O A 2O A 1r 2r ①求与的关系式;1r 2r ②求与面积之和的最小值.1O A 2O A (Ⅱ)如图(b ),若将(Ⅰ)中的正方形改为一个ABCD 宽为1,长为的矩形,其他条件不变,则与面积的321O A 2O A 和是否存在最小值,若不存在,请说明理由;若存在,请求出这个最小值.BA图(a )C【解】(Ⅰ)如图(),在正方形ABCD 中,连接,显然与在上,a AC 1O 2O AC 且,,,1AO =1212O O r r =+22CO 由,1122AC AO O O CO =++=.122r r +++=∴………………………5分122r r +=-②根据题意,,,1r 12≤2r 12≤可得,即.21122r r =-≤321r 12≤∵与的面积之和,1O A 2O A 2212π()S r r =+∴2211(2)πSr r =+-21122(26rr =-+-.这里,由, (8)分212(3r =-+-3212≤∴当时,与是等圆,其面积和的最小值为.1r =1O A 2O A (3π-……………………………………10分(Ⅱ)如图(b ),作辅助线,得到Rt △,12O O P 则,1212O O r r =+,1121232O P AB r r r r =--=--.212121O P BC r r r r =--=--∵在Rt △中,,12O O P 2221212O O O P O P =+∴.2221212123()()(1)2r r r r r r +=--+--即.2121213()5()04r r r r +-++=AD图(a)A图(b )解得1252r r +=1252r r +=由于,故1235122r r +<+=1252r r +=+∴ ……………………………………15分1252r r +=∵与的面积之和,1O A 2O A 2212π()S r r =+而,当且仅当时,等号成立,2221212()2r r r r ++≥12r r =∴当时,与面积和存在最小值,12r r =1O A 2O A ,即.37(π8……………………………………20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年全国初中数学竞赛天津赛区初赛试题参考答案及评分标准一、选择题(本大题共5小题,每小题7分,满分35分) (1)计算2222010200920102009201122009--⨯+⨯的值为( ).(A )1 (B )1- (C )2 009 (D )2 010【解】选A .原式22222222010200920102009120102009(20112)20102009--===---. (2)如图,是一个正方体的表面展开图,正方体的每个面都标注了字母.在展开前,与标注字母a 的面相对的面内标注的字母为( ).(A )b (B )d (C )e (D )f 【解】选B .(3)如图,在梯形ABCD 中,AB ∥DC ,AB ⊥BC ,E 是AD 的中点,6AB BC CD ++=,BE =ABCD 的面积等于( ).(A )13 (B )8 (C )132(D )4 【解】选D .如图,过点E 作//EF AB 交BC 于点F ,则12BF BC =,11()(6)22EF AB CD BC =+=-, 又∵BC AB ⊥,∴EF BC ⊥∴在Rt △BFE 中,222EF BF BE +=.∴22211[(6)]()22BC BC -+=,即2680BC BC -+=,解得 2BC =或4BC =,则2EF =或1EF =, ∴ 4ABCD S EF BC =⋅=梯形.第(2)题ABC DE F ABCD E 第(3)题(4)某个一次函数的图象与直线132y x =+平行,与x 轴,y 轴的交点分别为A ,B ,并且过点(2-,4-),则在线段AB 上(包括点A ,B ),横、纵坐标都是整数的点有( ).(A )3个 (B )4个 (C )5个 (D )6个 【解】选B .根据题意,设一次函数的解析式为12y x b =+, 由点(2-,4-)在该函数图象上,得14(2)2b -=⨯-+,解得3b =-.所以,132y x =-.可得点A (6,0),B (0,3-). 由06x ≤≤,且x 为整数,取0,2,4,6x =时,对应的y 是整数. 因此,在线段AB 上(包括点A 、B ),横、纵坐标都是整数的点有4个.(5)如图,一个半径为r 的圆形纸片在边长为a(a ≥)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( ).(A )2π3r (B2(C)2π)r (D )2πr 【解】选C .如图,当圆形纸片运动到与A ∠的两边相切的位置时,过圆形纸片的圆心1O 作两边的垂线,垂足分别为D ,E ,连1AO ,则Rt △1ADO 中,130O AD ∠=︒,1O D r =,AD .∴12112ADO S O D AD ∆=⋅=.有1122ADO ADO E S S ∆=四形形. ∵由题意,1120DO E ∠= ,得12π3O DE S r =扇形,∴圆形纸片不能接触到的部分的面积为22π3)3r -2π)r =二、填空题(本大题共5小题,每小题7分,满分35分)(6)如图,有五张点数分别为2,3,7,8,9的扑克牌,从中任意抽取两张,则其点数之积是偶数的概率为 . 第(5)题CABDMNCABDM第(8)题【解】710. 根据题意,当不考虑抽牌顺序时,可以画出如下的树形图从上图可以看出,从五张牌中任意抽取两张,共有10种抽法,其中抽取的点数之积是偶数的有7种,所以点数之积是偶数的概率710P =. (7)如图,是一个树形图的生长过程,自上而下,一个空心圆生成一个实心圆,一个实心圆生成一个实心圆和一个空心圆,依此生长规律,第9行的实心圆的个数【解】21个.观察图形规律,可得,从第3行起,每行中的实心圆的个数都是上两行实心圆个数的和.于是,第7行实心圆的个数为3+5=8(个); 第8行实心圆的个数为5+8=13(个); 第9行实心圆的个数为8+13=21(个). (8)如图,在△ABC 中,中线CM 与高线 CD 三等分ACB ∠,则B ∠等于 (度).【解】30︒.根据题意,可得CD AB ⊥,AM M B =,ACD MCD BCM ∠=∠=∠. ∵ACD MCD ∠=∠,CD CD =,90CDA CDM ∠=∠=︒,∴△ACD ≅△MCD ∠. ∴12AD DM AM ==.点数之积 3 7 8 9 6 2 14 16 183 7 8 9 21 24 27 56 7 8 963 8 9 72 1行2行3行4行5行 6行……第(7)题过点M 作MN BC ⊥于点N ,∵DCM NCM ∠=∠,CM CM =,90CDM CNM ∠=∠=︒, ∴△DCM ≅△NCM ∠. ∴DM NM =.于是12NM MB =,∴在Rt △MNB 中,30B ∠=︒.(9)有n 个连续的自然数1,2,3,…,n ,若去掉其中的一个数x 后,剩下的数的平均数是16,则满足条件的n 和x 的值分别是 .(参考公式:2)1(321+=++++=n n n S n ) 【解】30n =,1x =;31n =,16x =;32n =,32x =. 由已知,n 个连续的自然数的和为(1)2n n n S +=. 若x n =,剩下的数的平均数是12n S n nn -=-; 若1x =,剩下的数的平均数是 1112n S nn -=+-,故16122n n+≤≤,解得 3032n ≤≤. 当30n =时,30(301)29162x ⨯+⨯=-,解得1x =; 当31n =时,31(311)30162x ⨯+⨯=-,解得16x =; 当32n =时,32(321)31162x ⨯+⨯=-,解得32x =. (10)母亲节到了,小红,小莉,小莹到花店买花送给自己的母亲.小红买了3枝玫瑰,7枝康乃馨,1枝百合花,付了14元;小莉买了4枝玫瑰,10枝康乃馨,1枝百合花,付了16元;小莹买上面三种花各2枝,则她应付 元.【解】20.方法一:设玫瑰、康乃馨、百合花的单价分别为x 元,y 元,z 元, 根据已知条件,列出方程组3714,41016.x y z x y z ++=⎧⎨++=⎩消去z ,得23x y =-. ③ 将③代入①,得82z y =+.④①②由③,④得 10x y z ++=.有 2()20x y z ++=. 所以,小莹应付20元. 方法二:(37)(410)2()m x y z n x y z x y z +++++=++,(34)(710)()222m n x m n y m n z x y z +++++=++.∴342,7102,2.m n m n m n +=⎧⎪+=⎨⎪+=⎩解得4,6.n m =-⎧⎨=⎩∴2()6(37)4(410)61441620x y z x y z x y z ++=⨯++-++=⨯-⨯=. 三、解答题(本大题共4小题,每小题满分20分,共80分) (11)(本小题满分20分) 已知,抛物线2y ax bx c =++(0≠a )经过A 、B图中的曲线是它的一部分.根据图中提供的信息, (Ⅰ)确定a ,b ,c 的符号; (Ⅱ)当b 变化时,求a b c ++的取值范围. 【解】(Ⅰ)如图,由抛物线开口向上,得0a >.……由抛物线过点(0,1)-,得10c =-<. ……6分由抛物线对称轴在y 轴的右侧,得02ba->,又 0a >,得0b <. ∴0a >,0b <,0c <. ……………………………………10分 (Ⅱ)由抛物线过点(1,0)-,得0a b c -+=.即1a b =+,由0a >,得1b >-. ……………………………………16分 ∴10b -<<,∴(1)12a b c b b b ++=++-=.∴20a b c -<++<. ……………………………………20分 (12)(本小题满分20分)设直角三角形的两条直角边长分别为,a b ,斜边长为c .若,,a b c 均为整数,且1()3c ab a b =-+,求满足条件的直角三角形的个数.【解】由勾股定理,得222c a b =+. ……………………………………3分又1()3c ab a b =-+,得2222112[()]()()()393c ab a b ab ab a b a b =-+=-+++.即2222212()()293a b ab ab a b a ab b +=-++++.整理,得6()180ab a b -++=.即(6)(6)18a b --=. ………………………8分因为,a b 均为正整数,不妨设a b <, 可得61,618,a b -=⎧⎨-=⎩或62,69,a b -=⎧⎨-=⎩或63,6 6.a b -=⎧⎨-=⎩可解出7,24,25,a b c =⎧⎪=⎨⎪=⎩或8,15,17,a b c =⎧⎪=⎨⎪=⎩或9,12,15.a b c =⎧⎪=⎨⎪=⎩所以,满足条件的直角三角形有3个. ……………………………………20分(13)(本小题满分20分) 如图,在△ABC 中,45ABC ∠= ,点D 在边 BC 上,60ADC ∠= ,且12BD CD =.将△ACD 以 直线AD 为轴做轴对称变换,得到△AC D ',连接BC ',(Ⅰ)求证BC BC '⊥; (Ⅱ)求C ∠的大小.(Ⅰ)【证明】∵△AC D '是△ACD 沿AD 做轴对称变换得到的,∴△AC D '≌△ACD .有C D CD '=,ADC ADC '∠=∠.………………3分∵12BD CD =,60ADC ∠= ,∴12BD C D '=,18060BDC ADC ADC ''∠=-∠-∠= .……5分取C D '中点P ,连接BP ,则△BDP 为等边三角形,△BC P '为等腰三角形,…8分有113022BC D BPD BDC ''∠=∠=∠=︒.∴90C BD '∠= ,即BC BC '⊥. ……10分(Ⅱ)【解】如图,过点A 分别作,,BC C D BC ''的垂线,垂足分别为,,E F G .∵ADC ADC '∠=∠,即点A 在C DC '∠的平分线上, ∴AE AF =.……13分 ∵90C BD '∠= ,45ABC ∠= , ∴45GBA C BC ABC '∠=∠-∠= ,即点A 在GBC ∠的平分线上,∴AG AE =.……16分ABC DC 'ABDC 'PBDC 'FGABC图(b )于是,AG AF =,则点A 在GC D '∠的平分线上.…………………………18分 又∵30BC D '∠=︒,有150GC D '∠= . ∴12AC D '∠=75GC D '∠= .∴C ∠75AC D '=∠= .………………………20分 (14)(本小题满分20分)(Ⅰ)如图(a ),在正方形ABCD 内,已知两个动圆1O 与2O 互相外切,且1O 与边AB 、AD 相切,2O 与边BC 、CD 相切.若正方形ABCD 的边长为1,1O 与2O 的半径分别为1r ,2r .①求1r 与2r 的关系式;②求1O 与2O 面积之和的最小值.(Ⅱ)如图(b ),若将(Ⅰ)中的正方形ABCD 改为一个宽为1,长为32的矩形,其他条件不变,则1O 与2O 面积的 和是否存在最小值,若不存在,请说明理由;若存在,请求出 这个最小值.【解】(Ⅰ)如图(a ),在正方形ABCD 中,连接AC ,显然1O 与2O 在AC 上, 且1AO,1212O O r r =+,22CO =, 由1122ACAO O O CO =++122r r ++∴122r r += ………………………5分②根据题意,1r 12≤,2r 12≤,可得21122r r =≤,即321r 12≤.∵1O 与2O 的面积之和2212π()S r r =+,B图(a )图(a )∴2211(2)πSr r =+21122(26r r =-+-212(3r =-+-32-12≤,…………8分∴当1r =时,1O 与2O是等圆,其面积和的最小值为(3π-. ……………………………………10分(Ⅱ)如图(b ),作辅助线,得到Rt △12O O P , 则1212O O r r =+,1121232O P AB r r r r =--=--, 212121O P BC r r r r =--=--.∵在Rt △12O O P 中,2221212O O O P O P =+,∴2221212123()()(1)2r r r r r r +=--+--.即2121213()5()04r r r r +-++=.解得1252r r +=1252r r += 由于1235122r r +<+=,故1252r r +=+∴1252r r +=……………………………………15分 ∵1O 与2O 的面积之和2212π()S r r =+,而2221212()2r r r r ++≥,当且仅当12r r =时,等号成立,∴当12r r =时,1O 与2O 面积和存在最小值,最小值为25(2π2-,即37(π8. ……………………………………20分图(b )。
