勾股定理证明 课件
勾股定理9种证明(有图)
勾股定理的9种证明（有图）【证法1】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上，B 、F 、C 三点在一条直线上，C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF. ∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º. ∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA. ∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形，它的面积等于()2b a +.∴()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法2】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c. 把它们拼成如图那样的一个多边形，使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P.∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ ∴ ∠EGF = ∠BED ， ∵ ∠EGF + ∠GEF = 90°， ∴ ∠BED + ∠GEF = 90°， ∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c ， ∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD. ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º.又∵ ∠BDE = 90º，∠BCP = 90º，BC = BD = a.∴ BDPC 是一个边长为a 的正方形. 同理，HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ，则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法3】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ） ，斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形，使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ，交AC 于点P. 过点B 作BM ⊥PQ ，垂足为M ；再过点 F 作FN ⊥PQ ，垂足为N.∵ ∠BCA = 90º，QP ∥BC ， ∴ ∠MPC = 90º， ∵ BM ⊥PQ ， ∴ ∠BMP = 90º，∴ BCPM 是一个矩形，即∠MBC = 90º. ∵ ∠QBM + ∠MBA = ∠QBA = 90º，∠ABC + ∠MBA = ∠MBC = 90º， ∴ ∠QBM = ∠ABC ，又∵ ∠BMP = 90º，∠BCA = 90º，BQ = BA = c ， ∴ Rt ΔBMQ ≌ Rt ΔBCA. 同理可证Rt ΔQNF ≌ Rt ΔAEF.从而将问题转化为【证法4】（梅文鼎证明）. 【证法4】（欧几里得证明）做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使H 、C 、B 三点在一条直线上，连结 BF 、CD. 过C 作CL ⊥DE ， 交AB 于点M ，交DE 于点 L.∵ AF = AC ，AB = AD ， ∠FAB = ∠GAD ， ∴ ΔFAB ≌ ΔGAD ，∵ ΔFAB 的面积等于221a，ΔGAD 的面积等于矩形ADLM 的面积的一半，∴ 矩形ADLM 的面积 =2a .同理可证，矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积∴ 222b a c += ，即 222c b a =+.【证法5】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ，AF 交GT 于F ，AF 交DT 于R. 过B 作BP ⊥AF ，垂足为P. 过D 作DE 与CB 的延长线垂直，垂足为E ，DE 交AF 于H.∵ ∠BAD = 90º，∠PAC = 90º，∴ ∠DAH = ∠BAC.又∵ ∠DHA = 90º，∠BCA = 90º，AD = AB = c ， ∴ Rt ΔDHA ≌ Rt ΔBCA. ∴ DH = BC = a ，AH = AC = b. 由作法可知， PBCA 是一个矩形， 所以 Rt ΔAPB ≌ Rt ΔBCA. 即PB = CA = b ，AP= a ，从而PH = b ―a.∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA. ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ，∠GDT = ∠HDA . 又∵ ∠DGT = 90º，∠DHF = 90º，∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º， ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ，TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形，上底TF=b ―a ，下底BP= b ，高FP=a +（b ―a ）. 用数字表示面积的编号（如图），则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-， 985S S S +=，∴ 824321S ab b S S --=+= 812S S b -- . ②把②代入①，得98812212S S S S b S S c ++--++==922S S b ++ = 22a b +.∴ 222c b a =+.【证法6】（李锐证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c. 做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使A 、E 、G 三点在一条直线上. 用数字表示面积的编号（如图）.∵ ∠TBE = ∠ABH = 90º， ∴ ∠TBH = ∠ABE. 又∵ ∠BTH = ∠BEA = 90º，BT = BE = b ， ∴ Rt ΔHBT ≌ Rt ΔABE. ∴ HT = AE = a. ∴ GH = GT ―HT = b ―a. 又∵ ∠GHF + ∠BHT = 90º，∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º， ∴ ∠GHF = ∠DBC. ∵ DB = EB ―ED = b ―a ， ∠HGF = ∠BDC = 90º， ∴ Rt ΔHGF ≌ Rt ΔBDC. 即 27S S =.过Q 作QM ⊥AG ，垂足是M. 由∠BAQ = ∠BEA = 90º，可知 ∠ABE = ∠QAM ，而AB = AQ = c ，所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE. 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ，又得QM = AE = a ，∠AQM = ∠BAE. ∵ ∠AQM + ∠FQM = 90º，∠BAE + ∠CAR = 90º，∠AQM = ∠BAE ， ∴ ∠FQM = ∠CAR.又∵ ∠QMF = ∠ARC = 90º，QM = AR = a ， ∴ Rt ΔQMF ≌ Rt ΔARC. 即64S S =. ∵ 543212S S S S S c ++++=，612S S a +=，8732S S S b ++=，又∵ 27S S =，58S S =，64S S =，∴8736122S S S S S b a ++++=+=52341S S S S S ++++ =2c ，即 222c b a =+.【证法7】（利用多列米定理证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c （如图）. 过点A 作AD ∥CB ，过点B 作BD ∥CA ，则ACBD 为矩形，矩形ACBD 内接于一个圆. 根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有BD AC BC AD DC AB •+•=•，∵ AB = DC = c ，AD = BC = a ， AC = BD = b ，∴ 222AC BC AB +=，即 222b a c +=， ∴ 222c b a =+.【证法8】（利用反证法证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D.假设222c b a ≠+，即假设 222AB BC AC ≠+，则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2，或者 BD AB BC •≠2. 即 AD ：AC ≠AC ：AB ，或者 BD ：BC ≠BC ：AB.在ΔADC 和ΔACB 中， ∵ ∠A = ∠A ，∴ 若 AD ：AC ≠AC ：AB ，则 ∠ADC ≠∠ACB. 在ΔCDB 和ΔACB 中， ∵ ∠B = ∠B ，∴ 若BD ：BC ≠BC ：AB ，则 ∠CDB ≠∠ACB. 又∵ ∠ACB = 90º，∴ ∠ADC ≠90º，∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以，222AB BC AC ≠+的假设不能成立. ∴ 222c b a =+.【证法9】（辛卜松证明）设直角三角形两直角边的长分别为a 、b ，斜边的长为c. 作边长是a+b 的正方形ABCD. 把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD 的面积为()ab b a b a 2222++=+；把正方形ABCD 划分成上方右图所示的几个部分，则正方形ABCD的面积为()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++, ∴ 222c b a =+.。
勾股定理种证明(有图)
勾股定理的9种证明（有图）【证法1】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab21.把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上，B 、F 、C 三点在一条直线上，C 、G 、D 三点在一条直线上.∵Rt ΔHAE ≌Rt ΔEBF, ∴∠AHE=∠BEF.∵∠AEH+∠AHE=90º,∴∠AEH+∠BEF=90º. ∴∠HEF=180º―90º=90º.∴四边形EFGH 是一个边长为c 的 正方形.它的面积等于c 2.∵Rt ΔGDH ≌Rt ΔHAE,∴∠HGD=∠EHA.∵∠HGD+∠GHD=90º, ∴∠EHA+∠GHD=90º. 又∵∠GHE=90º,∴∠DHA=90º+90º=180º.∴ABCD 是一个边长为a+b 的正方形，它的面积等于()2b a +.∴()22214c ab b a +⨯=+.∴222c b a =+.【证法2】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c.把它们拼成如图那样的一个多边形，使D 、E 、F 在一条直线上.过C 作AC 的延长线交DF 于点P. ∵D 、E 、F 在一条直线上,且Rt ΔGEF ≌Rt Δ∴∠EGF=∠BED ， ∵∠EGF+∠GEF=90°，∴∠BED+∠GEF=90°，∴∠BEG=180º―90º=90º. 又∵AB=BE=EG=GA=c ，∴ABEG 是一个边长为c 的正方形.∴∠ABC+∠CBE=90º.∵Rt ΔABC ≌Rt ΔEBD, ∴∠ABC=∠EBD.∴∠EBD+∠CBE=90º. 即∠CBD=90º.又∵∠BDE=90º，∠BCP=90º，BC=BD=a.∴BDPC 是一个边长为a 的正方形.同理，HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ，则abS c 2122⨯+=,∴222c b a =+. 【证法3】（项明达证明） 做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形，使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC ，交AC 于点P.过点B 作BM ⊥PQ ，垂足为M ；再过点F 作FN ⊥PQ ，垂足为N.∵∠BCA=90º，QP ∥BC ，∴∠MPC=90º，∵BM ⊥PQ ， ∴∠BMP=90º，∴BCPM 是一个矩形，即∠MBC=90º.∵∠QBM+∠MBA=∠QBA=90º，∠ABC+∠MBA=∠MBC=90º， ∴∠QBM=∠ABC ，又∵∠BMP=90º，∠BCA=90º，BQ=BA=c ， ∴Rt ΔBMQ ≌Rt ΔBCA.同理可证Rt ΔQNF ≌Rt ΔAEF. 从而将问题转化为【证法4】（梅文鼎证明）. 【证法4】（欧几里得证明）做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使H 、C 、B 三点在一条直线上，连结 BF 、CD.过C 作CL ⊥DE ， 交AB 于点M ，交DE 于点L.∵AF=AC ，AB=AD ，∠FAB=∠GAD ， ∴ΔFAB ≌ΔGAD ，∵ΔFAB 的面积等于221a，ΔGAD 的面积等于矩形ADLM 的面积的一半，∴矩形ADLM 的面积=2a .同理可证，矩形MLEB 的面积=2b .∵正方形ADEB 的面积=矩形ADLM 的面积+矩形MLEB 的面积 ∴222b a c +=，即222c b a =+. 【证法5】（杨作玫证明） 做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形.过A 作AF ⊥AC ，AF 交GT 于F ，AF 交DT 于R.过B 作BP ⊥AF ，垂足为P.过D 作DE 与CB 的延长线垂直，垂足为E ，DE 交AF 于H.∵∠BAD=90º，∠PAC=90º，∴∠DAH=∠BAC.又∵∠DHA=90º，∠BCA=90º， AD=AB=c ， ∴Rt ΔDHA ≌Rt ΔBCA.∴DH=BC=a ，AH=AC=b.由作法可知，PBCA 是一个矩形， 所以Rt ΔAPB ≌Rt ΔBCA.即PB= CA=b ，AP=a ，从而PH=b ―a.∵Rt ΔDGT ≌Rt ΔBCA, Rt ΔDHA ≌Rt ΔBCA.∴Rt ΔDGT ≌Rt ΔDHA.∴DH=DG=a ，∠GDT=∠HDA. 又∵∠DGT=90º，∠DHF=90º，∠GDH=∠GDT+∠TDH=∠HDA+∠TDH=90º， ∴DGFH 是一个边长为a 的正方形. ∴GF=FH=a.TF ⊥AF ，TF=GT ―GF=b ―a. ∴TFPB 是一个直角梯形，上底TF=b ―a ，下底BP=b ，高FP=a+（b ―a ）. 用数字表示面积的编号（如图），则以c 为边长的正方形的面积为543212S S S S S c ++++=①∵()[]()[]a b a a b b S S S -+∙-+=++21438=ab b 212-， 985S S S +=，∴824321S ab b S S --=+=812SS b --.② 把②代入①，得=922S S b ++=22a b +.∴222c b a =+.【证法6】（李锐证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c.做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使A 、E 、G 三点在一条直线上.用数字表示面积的编号（如图）.∵∠TBE=∠ABH=90º， ∴∠TBH=∠ABE. 又∵∠BTH=∠BEA=90º，BT=BE=b ， ∴Rt ΔHBT ≌Rt ΔABE. ∴HT=AE=a. ∴GH=GT ―HT=b ―a.又∵∠GHF+∠BHT=90º，∠DBC+∠BHT=∠TBH+∠BHT=90∴∠GHF=∠DBC.∵DB=EB ―ED=b ―a ，∠HGF=∠BDC=90º， ∴Rt ΔHGF ≌Rt ΔBDC.即27S S =.过Q 作QM ⊥AG ，垂足是M.由∠BAQ=∠BEA=90º，可知∠ABE =∠QAM ，而AB=AQ=c ，所以Rt ΔABE ≌Rt ΔQAM.又Rt ΔHBT ≌ Rt ΔABE.所以Rt ΔHBT ≌Rt ΔQAM.即58S S =.由Rt ΔABE ≌Rt ΔQAM ，又得QM=AE=a ，∠AQM=∠BAE. ∵∠AQM+∠FQM=90º，∠BAE+∠CAR=90º，∠AQM=∠BAE ， ∴∠FQM=∠CAR.又∵∠QMF=∠ARC=90º，QM=AR=a ，∴Rt ΔQMF ≌Rt ΔARC.即64S S =.∵543212S S S S S c ++++=，612S S a +=，8732S S S b ++=，又∵27S S =，58S S =，64S S =，∴8736122S S S S S b a ++++=+=52341S S S S S ++++ =2c ，即222c b a =+. 【证法7】（利用多列米定理证明）在Rt ΔABC 中，设直角边BC=a ，AC=b ，斜边AB=c （如图）.过点A 作AD ∥CB ，过点B 作BD ∥CA ，则ACBD 为矩形，矩形ACBD 内接于一个圆.根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有BD AC BC AD DC AB ∙+∙=∙， ∵AB=DC=c ，AD=BC=a ， AC=BD=b ， ∴222AC BC AB +=，即222b a c +=， ∴222c b a =+.【证法8】（利用反证法证明）如图，在Rt ΔABC 中，设直角边AC 、BCb ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D.假设222c b a ≠+，即假设222AB BC AC ≠+，则由AB AB AB ∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知AD AB AC ∙≠2，或者BD AB BC ∙≠2.即AD ：AC ≠AC ：AB ，或者BD ：BC ≠BC ：AB.在ΔADC 和ΔACB 中，∵∠A=∠A ，∴若AD ：AC ≠AC ：AB ，则∠ADC ≠∠ACB. 在ΔCDB 和ΔACB 中， ∵∠B=∠B ， ∴若BD ：BC ≠BC ：AB ，则 ∠CDB ≠∠ACB. 又∵∠ACB=90º，∴∠ADC ≠90º，∠CDB ≠90º.这与作法CD ⊥AB 矛盾.所以，222AB BC AC ≠+的假设不能成立.∴222c b a =+. 【证法9】（辛卜松证明）设直角三角形两直角边的长分别为a 、b ，斜边的长为c.作边长是a+b 的正方形ABCD.把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD 的面积为()ab b a b a 2222++=+；把正方形ABCD 划分成上方右图所示的几个部分，则正方形ABCD 的面积为()22214c ab b a +⨯=+=22c ab +.∴22222c ab ab b a +=++,∴222c b a =+.。
初中数学勾股定理优质课PPT课件
b b
c a
b
c b
a
a
a
a
b
赵爽弦图
勾股定理：
如果直角三角形两条直角边长分别为a、b， 斜边长为c，那么a2+b2=c2 ．
A
bc CaB
勾 股
证明方法二 面积恒等法证明
a bc
ac b
b S大正方形＝ (a+b)2
c
a S大正方形＝ S小正方形＋ 4 S直角三角形
A
4
C
B
3
① 斜边＝
分类讨论 A 4 C3 B 32 42 ② 直5 角边＝
42 32 7
4.如图，图中所有的三角形都是直角三角形，四边形都是正 方形．已知正方形A，B，C，D的面积分别是3 ，4，1，3
，求最大正方形E的面积．
B A
C D
勾股树
E
H
E
公就知DA 元知道C前道许P 和多约大中的载应3勾约总高的0B用股0公结低第0勾数元出差一年大商记I 股组前了．位，约高载定，2勾可与古在就在0理如股以勾巴公提《0公欧给，30术说股比元出周,年4元几出他，，定伦前“髀,5，前里一们．用禹理人1勾算大3德个1还来是有经三世0禹巨勾0确世关》、纪在年著股定界的中股，治，《定两上人．四古水周几理处有．、希的朝何的水史弦腊实数公汉明原证位记五数践学元时了本明”学家2期勾》．世，家，股中纪刘定的徽理东证．
2
c a2 b2 12 22 5
C 1B
② 已知b = 2, c = 4, 求a ．
A
a c2 b2 42 22 2 3
4 2
C
B
2. 在RtΔABC中, ∠B = 90º， 已知a = 2, b = 5, 求c ．
勾股定理9种证明(有图)
A 勾股定理的9种证明（有图）之老阳三干创作【证法1】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上，B 、F 、C 三点在一条直线上，C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF, ∴∠AHE = ∠BEF.∵∠AEH + ∠AHE = 90º, ∴∠AEH + ∠BEF = 90º.∴∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形.它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴∠HGD = ∠EHA.∵∠HGD + ∠GHD = 90º, ∴∠EHA + ∠GHD = 90º. 又∵∠GHE = 90º,∴∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形，它的面积等于()2b a +.∴()22214c ab b a +⨯=+. ∴222c b a =+.【证法2】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为 c. 把它们拼成如图那样的一个多边形，使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P. ∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ∴∠EGF = ∠BED ， ∵∠EGF + ∠GEF = 90°， ∴∠BED + ∠GEF = 90°， ∴∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c ，∴ ABEG 是一个边长为c 的正方形.∴∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD,∴∠ABC = ∠EBD. ∴∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵∠BDE = 90º，∠BCP = 90º，BC = BD = a.∴ BDPC 是一个边长为a 的正方形. 同理，HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ，则abS c 2122⨯+=,∴222c b a =+.【证法3】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ） ，斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形，使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC ，交AC 于点P. 过点B 作BM ⊥PQ ，垂足为M ；再过点F 作FN ⊥PQ ，垂足为N.∵∠BCA = 90º，QP ∥BC ， ∴∠MPC = 90º， ∵ BM ⊥PQ ， ∴∠BMP = 90º， ∴ BCPM 是一个矩形，即∠MBC = 90º. ∵∠QBM + ∠MBA = ∠QBA = 90º，∠ABC + ∠MBA = ∠MBC = 90º， ∴∠QBM = ∠ABC ，又∵∠BMP = 90º，∠BCA = 90º，BQ = BA = c ， ∴ Rt ΔBMQ ≌ Rt ΔBCA.同理可证Rt ΔQNF ≌ Rt ΔAEF.从而将问题转化为【证法4】（梅文鼎证明）. 【证法4】（欧几里得证明）做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使H 、C 、B 三点在一条直线上，连结 BF 、CD. 过C 作CL ⊥DE ， 交AB 于点M ，交DE 于点L.∵ AF = AC ，AB = AD ， ∠FAB = ∠GAD ， ∴ΔFAB ≌ΔGAD ， ∵ΔFAB的面积等于221a，ΔGAD 的面积等于矩形ADLM 的面积的一半，∴ 矩形ADLM 的面积 =2a .同理可证，矩形MLEB 的面积 =2b .K∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴222b a c += ，即 222c b a =+. 【证法5】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为 c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ，AF 交GT 于F ，AF 交DT 于R. 过B 作BP ⊥AF ，垂足为P. 过D 作DE 与CB 的延长线垂直，垂足为E ，DE 交AF 于H.∵∠BAD = 90º，∠PAC = 90º，∴∠DAH = ∠BAC.又∵∠DHA = 90º，∠BCA = 90º， AD = AB = c ，∴ Rt ΔDHA ≌ Rt ΔBCA.∴ DH = BC = a ，AH = AC = b.由作法可知， PBCA 是一个矩形， 所以 Rt ΔAPB ≌ Rt ΔBCA. 即PB = CA = b ，AP= a ，从而PH = b ―a. ∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA. ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ，∠GDT = ∠HDA . 又∵∠DGT = 90º，∠DHF = 90º，∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º， ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ，TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形，上底TF=b ―a ，下底BP= b ，高FP=a +（b ―a ）. 用数字暗示面积的编号（如图），则以c 为边长的正方形的面积为543212S S S S S c ++++=①∵()[]()[]a b a a b b S S S -+•-+=++21438 = ab b 212-， 985S S S +=，∴824321S ab b S S --=+= 812S S b --.②把②代入①，得= 922S S b ++ = 22a b +.∴222c b a =+.【证法6】（李锐证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c. 做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使A 、E 、G 三点在一条直线上.用数字暗示面积的编号（如图）.∵∠TBE = ∠ABH = 90º， ∴∠TBH = ∠ABE. 又∵∠BTH = ∠BEA = 90º，BT = BE = b ， ∴ Rt ΔHBT ≌ Rt ΔABE. ∴ HT = AE = a. ∴ GH = GT ―HT = b ―a. 又∵∠GHF + ∠BHT = 90º，∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º，∴∠GHF = ∠DBC.∵ DB = EB ―ED = b ―a ，∠HGF = ∠BDC = 90º，∴ Rt ΔHGF ≌ Rt ΔBDC. 即 27S S =.过Q 作QM ⊥AG ，垂足是M. 由∠BAQ = ∠BEA = 90º，可知 ∠ABE = ∠QAM ，而AB = AQ = c ，所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE. 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ，又得QM = AE = a ，∠AQM = ∠BAE.∵∠AQM + ∠FQM = 90º，∠BAE + ∠CAR = 90º，∠AQM = ∠BAE ， ∴∠FQM = ∠CAR.又∵∠QMF = ∠ARC = 90º，QM = AR = a ，∴ Rt ΔQMF ≌ Rt ΔARC. 即64S S =.∵543212S S S S S c ++++=，612S S a +=，8732S S S b ++=，又∵27S S =，58S S =，64S S =，∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c ， 即 222c b a =+.【证法7】（利用多列米定理证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c （如图）. 过点A 作AD ∥CB ，过点B 作BD ∥CA ，则ACBD 为矩形，矩形ACBD 内接于一个圆. 根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有BD AC BC AD DC AB •+•=•，∵ AB = DC = c ，AD = BC = a ， AC = BD = b ， ∴222AC BC AB +=，即 222b a c +=， ∴222c b a =+.【证法8】（利用反证法证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D.假设222c b a ≠+，即假设 222AB BC AC ≠+，则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+• 可知 AD AB AC •≠2，或者 BD AB BC •≠2. 即 AD ：AC ≠AC ：AB ，或者 BD ：BC ≠BC ：AB.在ΔADC 和ΔACB 中，∵∠A = ∠A ，∴ 若 AD ：AC ≠AC ：AB ，则∠ADC ≠∠ACB.在ΔCDB 和ΔACB 中，∵∠B = ∠B ， ∴ 若BD ：BC ≠BC ：AB ，则 ∠CDB ≠∠ACB. 又∵∠ACB = 90º，∴∠ADC ≠90º，∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以，222AB BC AC ≠+的假设不克不及成立.∴222c b a =+.【证法9】（辛卜松证明）设直角三角形两直角边的长分别为a 、b ，斜边的长为c. 作边长是a+b 的正方形ABCD. 把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD 的面积为()ab b a b a 2222++=+；把正方形ABCD 划分成上方右图所示的几个部分，则正方形ABCD的面积为()22214c ab b a +⨯=+ =22c ab +.∴22222c ab ab b a +=++,∴222c b a =+.。
勾股定理9种证明(有图)
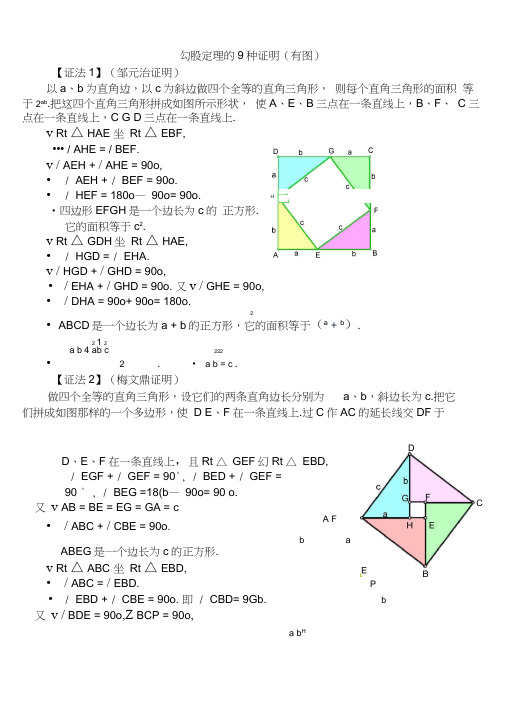
勾股定理的9种证明（有图）【证法1】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形， 则每个直角三角形的面积 等于2ab .把这四个直角三角形拼成如图所示形状， 使A 、E 、B 三点在一条直线上，B 、F 、 C 三点在一条直线上，C G D 三点在一条直线上.v Rt △ HAE 坐 Rt △ EBF, ••• / AHE = / BEF.v / AEH + / AHE = 90o, • / AEH + / BEF = 90o.• / HEF = 180o — 90o= 90o.•四边形EFGH 是一个边长为c 的 正方形.它的面积等于c 2.v Rt △ GDH 坐 Rt △ HAE, • / HGD = / EHA. v / HGD + / GHD = 90o,• / EHA + / GHD = 90o. 又v / GHE = 90o, • / DHA = 90o+ 90o= 180o.2• ABCD 是一个边长为a + b 的正方形，它的面积等于（a + b ）.21 2a b 4 ab c222•2. • a b = c .【证法2】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为 a 、b ，斜边长为c.把它 们拼成如图那样的一个多边形，使 D E 、F 在一条直线上.过C 作AC 的延长线交DF 于/ EGF + / GEF = 90°, / BED + / GEF = 90 ° , / BEG =18(b — 90o= 90 o. 又 v AB = BE = EG = GA = c• / ABC + / CBE = 90o.v Rt △ ABC 坐 Rt △ EBD, • / ABC = / EBD.• / EBD + / CBE = 90o. 即 / CBD= 9Gb. 又 v / BDE = 90o ,Z BCP = 90o ,D 、E 、F 在一条直线上，且Rt △ GEF 幻Rt △ EBD, ABEG 是一个边长为c 的正方形.a b HH匕DA FbaP bCBC = BD = a.••• BDPC 是一个边长为a 的正方形. 同理，HPFG 是一个边长为b 的正方形. 设多边形GHCB 的面积为S,则21 b S2 ab, 2 1=S 2 ab2 ,a 2 +b 2 =c 2【证法3】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为 a 、b （b>a ）c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形，使 直线上. 过点Q 作QP// BC 交AC 于点P. 过点B 作BML PQ 垂足为M ；再过点 F 作FNL PQ 垂足为N.v / BCA = 90o , QP// BC • / MPC = 90o , v BM 丄 PQ• / BMP = 90o ,• BCPM 是一个矩形，即/ MBC = 90o.v / QBM + / MBA = / QBA = 90o , / ABC + / MBA = / MBC = 90o , • / QBM = / ABC又 v / BMP = 90o ,/ BCA = 90o , BQ = BA = c , • Rt △ BMQ 坐 Rt △ BCA.同理可证Rt △ QNF 幻Rt △ AEF.从而将问题转化为【证法4】（梅文鼎证明）. 【证法4】（欧几里得证明）做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使 在一条直线上，连结BF CD.过 C 作 CL L DE 交AB 于点M 交DE 于点L.v AF = AC , AB = AD,/ FAB = / GAD• △ FAB 坐△ GADE 、A ，斜边长为C 三点在一条 H 、C B 三点 v △ FAB 的面积等于K△ GAD 的面积等于矩形ADLM 的面积的一半，二矩形ADLM 的面积二 同理可证，矩形 MLEE 的面积 v 正方形ADEB 勺面积 =矩形ADLM!勺面积+ /. c 2 a 2 b 2，即 a 2 -【证法5】(杨作玫证明) 做两个全等的直角三角形，设它们的两条直角边长分别为 a 、b (b>a ),斜边长为c. 再做一个边长为c 的正方形.把它们拼成如图所示的多边形.过A 作AF 丄AC AF 交GT 于F , AF 交DT 于 R.过B 作BP 丄AF,垂足为 E , DE 交 AF 于 H. v / BAD = 90o ,Z PAC = 90o , ••• / DAH = / BAC. 又 v / DHA = 90o ,Z BCA = 90o , AD = AB = c ,• Rt △ DHA 坐 Rt △ BCA. • DH = BC = a , AH = AC = b. 由作法可知，PBCA 是一个矩形， 所以 Rt △ APB 坐 Rt △ BCA.即 PB = CA = b , AP= a ,从v Rt △ DGT 坐 RtRt △ DHA 坐 Rt• Rt △ DGT 坐 Rt • DH = DG = a , 又 v / DGT = 90o ,2 a . =b 2 矩形MLEB 勺面积 b 2 =c 2. PH = b — a. △ BCA , △ BCA. △ DHA . / GDT = / HDA . / DHF = 90o ,P.过D 作DE 与CB 的延长线垂直，垂足为 / GDH = / GDT + / TDH = / HDA+Z TDH = 90o ,• DGFH 是一个边长为a 的正方形.• GF = FH = a . TF 丄AF , TF = GT — GF = b — a .• TFPB 是一个直角梯形，上底 TF=b-a ,下底BP= b ,高FP=a + (b —a ).用数字表示面积的编号(如图)，则以c 为边长的正方形的面积为 c 2 = Si S 2 S 3 S 4 S 51S 8 +S 3 +S 4 =- b + (b - a )】• a + (b -a /v2S5 - S 8' S 9丄21 .S 3S 4-b 2 ab・・ 2把②代入①，得c^S iS 2b 2 -S^S 8S 8S 9①b 2 -1 ab2 ,2=bS2S 9 = b 2 川 a 2【证法6】（李锐证明）设直角三角形两直角边的长分别为 a 、b （b>a ）,斜边的长为c.做三个边长分别为a 、 b 、c 的正方形，把它们拼成如图所示形状，使 A 、E 、G 三点在一条直线上.用数字表示 面积的编号（如图）.v / TBE = / ABH = 900, ••• / TBH = / ABE. 又 v / BTH = / BEA = 900,BT = BE = b , • Rt △ HBT 坐 Rt △ ABE. • HT = AE = a. • GH = GT — HT = b — a. 又 v / GHF + / BHT = 900,/ DBC + / BHT = / TBH + • / GHF = / DBC.v DB = EB — ED = b — a , / HGF = / BDC = 90o , • Rt △ HGF 坐 Rt △ BDC.即 S ^ S 2.过 Q 作 QM L AG 垂足是 M.由/ BAQ = / BEA = 90o ,可知 / ABE =/ QAM 而 AB = AQ = c ，所以 Rt △ ABE 幻 Rt △ QAM .又 Rt △ HBT 幻Rt △ ABE.所以 Rt △ HBT 幻 Rt △ QAM .即 S 8 二 S 5.由 Rt △ ABE 坐 Rt △ QAM 又得 QM = AE = a ，/ AQM = / BAE.v / AQM + / FQM = 90o ,Z BAE + / CAR = 90o ,Z AQM = / BAE • / FQM = / CAR.【证法7】（利用多列米定理证明）• Rt △ QMF 坐 Rt △ ARC.即 S 4 =S6.• • c 2 =S 1 S 2 S 3 S 4 S 5 a 2 S 6又v S 7 二 S 2 S g 二 S 5 S 4 二 S 6> > >• a 2 b 2 = S ! S 6 S 3 S 7 S 8=S iS 4 S 3 S 2 S 52=c ,即a 2 + b 2 =c 2.又 v / QMF = / ARC = 90o , QM = AR = a , b^ S 3 S 7 S 8R a A在Rt △ ABC 中，设直角边 BC= a , AC= b ,斜边AB = c (如图).过点A 作AD// CB, 过点B 作BD//CA 则ACBD 为矩形，矩形ACBD 内接于一个圆.根据多列米定理，圆内接 四边形对角线的乘积等于两对边乘积之和，有AB ・DC 二 AD ・BC AC *BD ,AB = DC = c , AD = BC = a , AC = BD = b ,AB 2 =BC 2 +AC 2，即 c 2 =a 2 +b 2 a 2 +b 2 =c 2【证法8】（利用反证法证明） 如图，在Rt △ ABC 中，设直角边 AG点C 作CDL AB 垂足是D.假设a 2 b 2=c 2，即假设AC 2 BC —AB 2，则由AB^AB *AB =AB AD BD =AB ・AD AB * BD可知 AC 2 式 AB ・AD ，或者 BC 2 式 AB ・BD .即 AD : AO AG AB 或者 BD : BO BC AB. 在厶ADC 和△ ACB 中, v / A = / A,.若 AD : AW AC AB 」 / AD 字/ ACB.在厶CDB 和△ ACB 中, v / B = / B ,.若 BD BW BC AB,贝S / CDB^Z ACB. 又v / ACB = 90o ,. / AD& 90o ,Z CD 字 90o. 这与作法CDLAB 矛盾.所以，/. a 2 b 2 = c 2.【证法9］（辛卜松证明）设直角三角形两直角边的长分别为 a 、b,斜边的长为c.作边长是a+b 的正方形ABCD. 把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD 的面积为 (a +bf =a +b +2ab ；把正方形ABCD 划分成上方右图所示的几个部分，则正方形 ABCD 勺21 2,.十.(a +b 『=4 乂一ab+c 2面积为 2= 2ab c .2 2 2.. a b 2ab 二 2ab c ,BC 的长度分别为a 、b ,斜边AB 的长为c ,过 AC 2 • BC 2 = AB 2的假设不能成立..a2+b2=c2.。
勾股定理9种证明(有图)
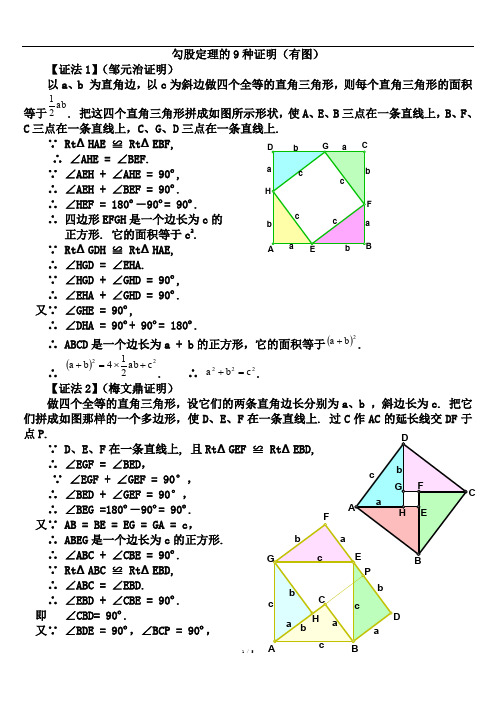
勾股定理的9种证明（有图）【证法1】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上，B 、F 、C 三点在一条直线上，C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF.∵ ∠AEH + ∠AHE = 90º,∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE,∴ ∠HGD = ∠EHA.∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形，它的面积等于()2b a +.∴ ()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法2】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c. 把它们拼成如图那样的一个多边形，使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P. ∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌∴ ∠EGF = ∠BED ， ∵ ∠EGF + ∠GEF = 90°，∴ ∠BED + ∠GEF = 90°，∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c ，∴ ABEG 是一个边长为c 的正方形.∴ ∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD. ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵ ∠BDE = 90º，∠BCP = 90º，BC = BD = a.∴ BDPC 是一个边长为a 的正方形. 同理，HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ，则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法3】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ） ，斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形，使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC ，交AC 于点P.过点B 作BM ⊥PQ ，垂足为M ；再过点F 作FN ⊥PQ ，垂足为N.∵ ∠BCA = 90º，QP ∥BC ，∴ ∠MPC = 90º，∵ BM ⊥PQ ， ∴ ∠BMP = 90º，∴ BCPM 是一个矩形，即∠MBC = 90º.∵ ∠QBM + ∠MBA = ∠QBA = 90º，∠ABC + ∠MBA = ∠MBC = 90º， ∴ ∠QBM = ∠ABC ，又∵ ∠BMP = 90º，∠BCA = 90º，BQ = BA = c ， ∴ Rt ΔBMQ ≌ Rt ΔBCA.同理可证Rt ΔQNF ≌ Rt ΔAEF. 从而将问题转化为【证法4】（梅文鼎证明）. 【证法4】（欧几里得证明）做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使H 、C 、B 三点在一条直线上，连结BF 、CD. 过C 作CL ⊥DE ， 交AB 于点M ，交DE 于点L.∵ AF = AC ，AB = AD ， ∠FAB = ∠GAD ，∴ ΔFAB ≌ ΔGAD ， ∵ ΔFAB 的面积等于221a ，ΔGAD 的面积等于矩形ADLM 的面积的一半，∴ 矩形ADLM 的面积 =2a .同理可证，矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ，即 222c b a =+. 【证法5】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ，AF 交GT 于F ，AF 交DT 于R. 过B 作BP ⊥AF ，垂足为P. 过D 作DE 与CB 的延长线垂直，垂足为E ，DE 交AF 于H.∵ ∠BAD = 90º，∠PAC = 90º，∴ ∠DAH = ∠BAC.又∵ ∠DHA = 90º，∠BCA = 90º， AD = AB = c ， ∴ Rt ΔDHA ≌ Rt ΔBCA.∴ DH = BC = a ，AH = AC = b.由作法可知， PBCA 是一个矩形， 所以 Rt ΔAPB ≌ Rt ΔBCA. 即PB = CA = b ，AP= a ，从而PH = b ―a.∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA.∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ，∠GDT = ∠HDA . 又∵ ∠DGT = 90º，∠DHF = 90º，∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º， ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ，TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形，上底TF=b ―a ，下底BP= b ，高FP=a +（b ―a ）. 用数字表示面积的编号（如图），则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+∙-+=++21438 =ab b 212-， 985S S S +=，∴ 824321S ab b S S --=+= 812S S b -- . ②把②代入①，得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +. ∴ 222c b a =+.【证法6】（李锐证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c. 做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使A 、E 、G 三点在一条直线上. 用数字表示面积的编号（如图）.∵ ∠TBE = ∠ABH = 90º， ∴ ∠TBH = ∠ABE. 又∵ ∠BTH = ∠BEA = 90º，BT = BE = b ， ∴ Rt ΔHBT ≌ Rt ΔABE. ∴ HT = AE = a. ∴ GH = GT ―HT = b ―a.又∵ ∠GHF + ∠BHT = 90º，∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC.∵ DB = EB ―ED = b ―a ，∠HGF = ∠BDC = 90º，∴ Rt ΔHGF ≌ Rt ΔBDC. 即 27S S =.过Q 作QM ⊥AG ，垂足是M. 由∠BAQ = ∠BEA = 90º，可知 ∠ABE = ∠QAM ，而AB = AQ = c ，所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE. 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ，又得QM = AE = a ，∠AQM = ∠BAE.∵ ∠AQM + ∠FQM = 90º，∠BAE + ∠CAR = 90º，∠AQM = ∠BAE ， ∴ ∠FQM = ∠CAR.又∵ ∠QMF = ∠ARC = 90º，QM = AR = a ，∴ Rt ΔQMF ≌ Rt ΔARC. 即64S S =.∵ 543212S S S S S c ++++=，612S S a +=，8732S S S b ++=，又∵ 27S S =，58S S =，64S S =，∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c ， 即 222c b a =+.【证法7】（利用多列米定理证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c （如图）. 过点A 作AD ∥CB ，过点B 作BD ∥CA ，则ACBD 为矩形，矩形ACBD 内接于一个圆. 根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有BD AC BC AD DC AB ∙+∙=∙，∵ AB = DC = c ，AD = BC = a ， AC = BD = b ，∴ 222AC BC AB +=，即 222b a c +=， ∴ 222c b a =+.【证法8】（利用反证法证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D.假设222c b a ≠+，即假设 222AB BC AC ≠+，则由AB AB AB ∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知 AD AB AC ∙≠2，或者 BD AB BC ∙≠2. 即 AD ：AC ≠AC ：AB ，或者 BD ：BC ≠BC ：AB.在ΔADC 和ΔACB 中，∵ ∠A = ∠A ，∴ 若 AD ：AC ≠AC ：AB ，则∠ADC ≠∠ACB. 在ΔCDB 和ΔACB 中， ∵ ∠B = ∠B ， ∴ 若BD ：BC ≠BC ：AB ，则 ∠CDB ≠∠ACB. 又∵ ∠ACB = 90º，∴ ∠ADC ≠90º，∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以，222AB BC AC ≠+的假设不能成立.∴ 222c b a =+. 【证法9】（辛卜松证明）设直角三角形两直角边的长分别为a 、b ，斜边的长为c. 作边长是a+b 的正方形ABCD. 把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD 的面积为()ab b a b a 2222++=+；把正方形ABCD 划分成上方右图所示的几个部分，则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.。
勾股定理ppt课件
创设情境 数学是科技发展中最重要的学科，2002年全球最顶级数学家大 会在北京召开，大会会徽是：
赵爽弦图
数学文化 赵爽，名婴，字君卿，是我国三国时期杰出的数学家， 他在注解《周髀算经》时给出的这个图.
创设情境 请你观察这个图中有哪些基本几何图形？2002年的数学家大会为 什么用这个图作为会徽呢？
继续探究
1.如图，表格中左、右各有一组图，每组图中的三个正方形的面积分 别是多少，它们之间有什么关系？（设表格中每个小正方形面积为1）
C A
B
C A
B
继续探究 2.观察图形，请完成下面表格：
两个图中正 方形C的面积 如何求呢？
项目
左图 右图 A、B、C 面积关系
A的面积 4 16
B的面积 9 9
A
8
B 6
C
应用新知
例2 如图，图中所有的三角形都是直角三角形，四边形都是正方形，已知正方形 B，D的边长分别是16，12，SE=625，S1=400，求正方形A、C的边长. 解：依题意，得SB=162=256，SD=122=144， ∵S1=SA+SB且S1=400， ∴SA=S1-SB=400-256=144， ∴正方形A的边长为 144 12， ∵SE=S1+S2且SE=625，S1=400， ∴S2=SE-S1=625-400=225， ∵S2=SC+SD，∴SC=S2-SD=225-144=81， ∴正方形C的边长 81 9 .
证明2： 如图，四个全等直角三角形拼成
如图所示的正方形，直角边为a、
b，斜边为c. S四个直角三角形面积和= 4 1 ab 2ab，
2
S四个直角三角形面积和=(a+b)2-c2
勾股定理9种证明(有图)
勾股定理的9种证明(有图)【证法1】(邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上，B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF 。
∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º。
∴ ∠HEF = 180º―90º= 90º。
∴ 四边形EFGH 是一个边长为c 的 正方形。
它的面积等于c 2。
∵ Rt ΔGDH ≌ Rt ΔHAE ，∴ ∠HGD = ∠EHA 。
∵ ∠HGD + ∠GHD = 90º， ∴ ∠EHA + ∠GHD = 90º。
又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º。
∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +。
∴()22214c ab b a +⨯=+. ∴ 222c b a =+。
【证法2】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c. 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上。
过C 作AC 的延长线交DF 于点P. ∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌∴ ∠EGF = ∠BED ， ∵ ∠EGF + ∠GEF = 90°，∴ ∠BED + ∠GEF = 90°，∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c ，∴ ABEG 是一个边长为c 的正方形.∴ ∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD ， ∴ ∠ABC = ∠EBD. ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵ ∠BDE = 90º，∠BCP = 90º,BC = BD = a. ∴ BDPC 是一个边长为a 的正方形.同理，HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ，则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法3】(项明达证明）做两个全等的直角三角形,设它们的两条直角边长分别为a 、b(b 〉a) ，斜边长为c 。
八下数学第十七章勾股定理全章课件
在Rt△ABM中，AB2＋AM2＝BM2.
在Rt△MDB′中，MD2＋DB′2=MB′2.
B′
∵MB＝MB′，∴AB2＋AM2＝MD2＋DB′2，
即92＋x2＝(9－x)2＋(9－3)2，
解得x＝2.即AM＝2.
探究新知
方法点拨
折叠问题中结合勾股定理求线段长的方法:
(1)设一条未知线段的长为x(一般设所求线段的长为x)； (2)用已知线段或含x的代数式表示出其他线段长； (3)在一个直角三角形中应用勾股定理列出一个关于x的
D
3m，宽2.2m的薄木板能否从门框内
通过？为什么？
C 2m
解：如图，连接AC。 在Rt△ABC 中，根据勾股定理，
AC AB2 BC2 12 22
AB
1m
5
5 2.236 2.2
∴木板可以从门框内通过。
巩固练习
如图，池塘边有两点A，B，点C是与BA方向成直角的AC方 向上一点，测得BC=60 m，AC=20m.求A，B两点间的距离
在Rt△AFD′中，AF2=D′F2+AD′2,
(8-x)2=x2+42， 解得x=3. ∴AF=AB-FB=8-3=5， ∴S△AFC= AF•BC=10．
互逆命题:
两个命题中, 如果第一个命题的题设是第 二个命题的结论, 而第一个命题的结论又是第 二个命题的题设,那么这两个命题叫做互逆命 题.
A的面 B的面 C的面
积
积
积
C A
图1
9
9 18
B 图2-1
C A
B 图2-2
图2
4
48
A、B、C 面积关系
SA+SB=SC
直角三角形 两直角边的平方和 三边关系 等于斜边的平方
勾股定理证明简述 公开课课件
直角三角形中两直角边a、
b的平方和，等于斜边c的
平方
a
c
a2+b2=c2
b
方法一:
△ABD≌△FBC， 矩形BL=2△ABD， 方形GB=2△FBC。 于是 矩形BL=正方形GB。 同样有 矩形CL=正方形AK。 所以 正方形GB+正方形AK=正方形BE
方法二
如图一：两个正方形边长 分别是a ,b, 它们的面积和 为a2+b2
___________________________________________________________________________ 2．达·芬奇的“蒙娜丽莎”是全人类文 化宝库 中一颗 璀璨的 明珠。 （缩写 句子） ___________________________________________________________________________ 3．我在她面前只停留了短短的几分钟。 她已经 成了我 灵魂的 一部分 。（用 关联词 连成一 句话） ___________________________________________________________________________
1、世上没有绝望的处境，只有对处境 绝望的 人。 2、挑水如同武术，武术如同做人。循序 渐进， 逐步实 现目标 ，才能 避免许 多无谓 的挫折 。 3、别想一下造出大海，必须先由小河川 开始。 4、自信是所有成功人士必备的素质之一 ，要想 成功， 首先必 须建立 起自信 心，而 你若想 在自己 内心建 立信心 ，即应 像洒扫 街道一 般，首 先将相 当于街 道上最 阴湿黑 暗之角 落的自 卑感清 除干净 ，然后 再种植 信心， 并加以 巩固。 信心建 立之后 ，新的 机会才 会随之 而来。 5、一个人在科学探索的道路上，走过弯 路，犯 过错误 ，并不 是坏事 ，更不 是什么 耻辱， 要在实 践中勇 于承认 和改正 错误。 ——爱 因斯坦 6、瓜是长大在营养肥料里的最甜，天才 是长在 恶性土 壤中的 最好。 ——培 根 7、发光并非太阳的专利，你也可以发光 。 8、人们常用“心有余而力不足”来为自 己不愿 努力而 开脱， 其实， 世上无 难事， 只怕有 心人， 积极的 思想几 乎能够 战胜世 间的一 切障碍 。 9、如果你希望成功，当以恒心为良友， 以经验 为参谋 ，以当 心为兄 弟，以 希望为 哨兵。 ——爱 迪生 10、涓滴之水终可磨损大石，不是由于 它力量 大，而 是由于 昼夜不 舍的滴 坠。只 有勤奋 不懈的 努力才 能够获 得那些 技巧， 因此， 我们可 以确切 地说： 说：不 积跬步 ，无以 致千里 。—— 贝多芬 11、一定要做最适合自己的事情，不要 迎合别 人的口 味而去 做一件 不属于 自我的 “难事 ”。一 旦“发 现自我 ”，就 要尽力 而为， 但要全 面了解 自己和 周围的 环境， 知道适 可而止 。 12、要有自信，然后全力以赴--假如具 有这种 观念， 任何事 情十之 八九都 能成功 。—— 威尔逊 13、莫找借口失败，只找理由成功。 14、一个有坚强心志的人，财产可以被 人掠夺 ，勇气 却不会 被人剥 夺的。 ——雨 果 15、积极的人在每一次忧患中都看到一 个机会 ，而消 极的人 则在每 个机会 都看到 某种忧 患。 16、不是境况造就人，而是人造就境况 。 17、在人生的竞赛场上，没有确立明确 目标的 人，是 不容易 得到成 功的。 许多人 并不乏 信心、 能力、 智力， 只是没 有确立 目标或 没有选 准目标 ，所以 没有走 上成功 的途径 。这道 理很简 单，正 如一位 百发百 中的神 射击手 ，如果 他漫无 目标地 乱射， 也不能 在比赛 中获胜 。 18、生活就像海洋，只有意志坚强的人 ，才能 到达彼 岸。— —马克 思 19、别因为落入了一把牛毛就把一锅奶 油泼掉 ，别因 为犯了 一点错 误就把 一生的 事业扔 掉。— —蒙古 20、许多人之所以在生活中一事无成， 最根本 原因在 于他们 不知道 自己到 底要做 什么。 在生活 和工作 中，明 确自己 的目标 和方向 是非常 必要的 。只有 在知道 你的目 标是什 么、你 到底想 做什么 之后， 你才能 够达到 自己的 目的， 你的梦 想才会 变成现 实。 21、怠惰是贫穷的制造厂。 22、先知三日，富贵十年。 23、自信是向成功迈出的第一步。—— 爱因斯 坦 24、一个人除非自己有信心，否则不能 带给别 人信心 ；已经 信服的 人，方 能使人 信服。 ——麦 修·阿诺 德 25、凡是挣扎过来的人都是真金不怕火 炼的； 任何幻 灭都不 能动摇 他们的 信仰： 因为他 们一开 始就知 道信仰 之路和 幸福之 路全然 不同， 而他们 是不能 选选择 的，只 有往这 条路走 ，别的 都是死 路。这 样的自 信不是 一朝一 夕所能 养成的 。你绝 不能以 此期待 那些十 五岁左 右的孩 子。在 得到这 个信念 之之前 ，先得 受尽悲 痛，流 尽眼泪 。可是 这样是 好的， 应该要 这样… …—— 罗曼·罗 兰 26、一个人在科学探索的道路上，走过 弯路， 犯过错 误，并 不是坏 事，更 不是什 么耻辱 ，要在 实践中 勇于承 认和改 正错误 。—— 爱因斯 坦88我 们的理 想应该 是高尚 的。我 们不能 登上顶 峰，但 可以爬 上半山 腰，这 总比待 在平地 上要好 得多。 如果我 们的内 心为爱 的光辉 所照亮 ，我们 面前前 又有理 想，那 么就不 会有战 胜不了 的困难 。—— 普列姆 昌德 27、旁观者的姓名永远爬不到比赛的计 分板上 。
勾股定理的证明(比较全的证明方法)课件
总统证明法
美国总统加菲尔德在1876年独 立发现了勾股定理的一种新的 证明方法，后来被称为“总统 证明法”。
总统证明法利用了代数和三角 恒等式来证明勾股定理，这种 方法与前两种几何证明方法有 所不同。
总统证明法不仅证明了勾股定 理，而且也展示了数学中代数 和三角学的紧密联系。
05
勾股定理的推广
勾股定理的逆定理
勾股定理的逆定理
如果三角形三边满足勾股定理， 则这个三角形是直角三角形。
证明方法
利用勾股定理和三角形的性质， 通过反证法证明。假设三角形不 是直角三角形，则其三边不满足 勾股定理，与已知条件矛盾。
勾股定理的推广形式
勾股定理的推广
对于任意多边形，如果其内角和为 180度，则其边长满足勾股定理。
对未来研究的展望
深入研究和探索
勾股定理的证明方法有很多种，但还有很多 值得探索和研究的地方。例如，如何将不同 的证明方法进行比较和整合，如何进一步简 化证明过程等。这些问题的研究和探索，有 助于推动数学教育的发展和进步。
与其他学科的交叉研究
勾股定理不仅在数学中有应用，在其他学科 如物理学、工程学、经济学等也有广泛的应 用。如何将勾股定理与其他学科进行交叉研 究，发挥其在解决实际问题中的作用，也是 未来研究的一个重要方向。
03
勾股定理的代数证明方法
哈里奥特证明法
哈里奥特证明法是一种基于无穷小差分的代数证明方法。它 通过将直角三角形转化为等腰直角三角形，利用无穷小差分 的性质，推导出勾股定理。
哈里奥特证明法不仅证明了勾股定理，还为微积分学的发展 奠定了基础。
欧拉证明法
华东师大版八年级数学上册1勾股定理课件
练习
5.如图，将矩形ABCD沿EF折叠，使点D与点B重合，己知AB=3,AD=9,求BE的长。
【答案】BE=5
【解析】设BE=x,则DE=BE=x,AE=AD-DE=9-x.在Rt△ABE中，AB2+AE2=BE2
∴32+(9-x)2=x2,解得x=5.
练习
6.如图，有两棵树，一棵高8米，另一棵高2米，两树相距8米，一只小鸟从
结论
勾股定理：如果直角三角形两直角边分别
为a，b，斜边为c，有
a2 + b 2 = c 2
反过来
逆定理：如果三角形的三边长a、b、c满
足 a2
+
2
b
=
直角三角形。
2
c ，那么这个三角形是
趁热打铁
判断由线段a，b，c组成的三角形是不是直角 三角形?
(1) a=15，b=17，c=8; (2) a=13，b=15，c=14
A．14 cm2
B．13 cm2
C．12 cm2
D．8 cm2
练习
4．如图，在Rt△ABC中，∠C＝90°，若a＋b＝14，c＝10，求Rt△ABC的面积．
解：∵∠C＝90°，
∴a2＋b2＝c2＝100.
∴(a＋b)2－2ab＝100.
∴142－2ab＝100.
∴ab＝48.
∴S△ABC＝ab＝24.
C
b
图甲
B
SA+SB=SC
3.猜想a、b、c 之间的关系？
a2 +b2 =c2
02
章节
PART
探究与证明
• 合作探究
• 趁热打铁
• 理论证明
合作探究
小组活动：请你利用自己准备的四个全等的直角三角形拼出
勾股定理9种证明有图
勾股定理的9种证明（有图）【证法1】（邹元治证明）以a、b为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角形的面积等于2・把这四个直角三角形拼成如图所示形状，使A、E、E三点在一条直线上, B、F、C三点在一条直线上，C、G、D三点在一条直线上.・• RtAHAE 也RtAEBF, /.ZAHE=ZBEF ・.-ZAEH + ZAHE = 90°, ••ZAEH + Z BEF= 90°.\ Z HEF = 180°—90°= 90°.・・四边形EFGH是一个边长为c的正方形.它的面积等于c2.・• RtAGDH 坐RtAHAE,•• Z HGD = Z EHA.・• Z HGD + Z GHD = 90°,・・ Z EHA + Z GHD = 90°.・• Z GHE = 90°,・・ ZDHA = 90°+ 90°= 180°.•・ABCD是一个边长为a + b的正方形，它的面积等于（。
+疔・2【证法2】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a、b ,斜边长为c.把它们拼成如图那样的一个多边形，使D、E、F在一条直线上.过C作AC的延长线交DF 于点P・•・• D、E、F在一条直线上，且RtAGEF也RtAEBD,/. Z EGF = ZBED,•/ Z EGF + ZGEF = 90° ,/. ZBED + ZGEF = 90° ,・ \ Z BEG =180°—90°= 90°・又・・・AB = BE = EG = GA = c,・・・ABEG是一个边长为c的正方形.・・・ZABC+ Z CBE = 90°.・・・ RtAABC ◎ RtAEBD,/./ABC = ZEBD ・••・ z EBD + z CBE = 90°.即Z CBD= 90°.又・・・ZBDE = 90。
《勾股定理》PPT课件
AC 2 6
1.在△ABC中，∠C=90°.
练 习
(1)若a=6，c=10，则b=
;
(2)若a=12，b=9，则c= (3)若c=25，b=15，则a=
; ;
2.等边三角形边长为10，求它的高及面积。 C 3.如图，在△ABC中，C=90°，
CD为斜边AB上的高，你可以得 b 出哪些与边有关的结论？ A m h
c2
；
a c
c a
b a
∵ c2= 4•ab/2 +(b-a)2 =2ab+b2-2ab+a2 =a2+b2 ∴a2+b2=c2
a
b
b c
b c
2 (a+b) 大正方形的面积可以表示为 ；
也可以表示为 c2 +4•ab/2
a b
a
b
c
c
a
b
c
∵ (a+b)2 = c2 + 4•ab/2 a2+2ab+b2 = c2 +2ab ∴a2+b2=c2
a
B D n
如图，在△ABC中，AB=AC，D点在CB延长线上， A 求证：AD2-AB2=BD· CD
证明：过A作AE⊥BC于E ∵AB=AC，∴BE=CE D 在Rt △ADE中， AD2=AE2+DE2 在Rt △ABE中， AB2=AE2+BE2 ∴ AD2-AB2=(AE2+DE2)-(AE2+BE2) B E C
a b
c
勾股定理的证明
证明方法3：赵爽弦图，动手拼图
勾股定理的证明
证明方法4：美国总统加菲尔德的证明方法
a b
勾股定理优秀PPT课件
b
c
a
a
这种证明方法从几何图形的面积变化入手，运用了数形结合的思 想方法.
18
-
<四>练习提升
1.议一议:观察下图,用数格子的方法判断图中三角形的三 边长是否满足a2+b2=c2.
2.一个直角三角形的斜边为20cm ,且两直角边长度比为3:4， 求两直角边的长.
19
-
<五>勾股定理的文化价值
(1) 勾股定理是联系数学中数与形的第一定理.
(2) 勾股定理反映了自然界基本规律,有文明的宇宙“人”都应 该认识它，因而勾股定理图被建议作为与“外星人”联系的信号. (3) 勾股定理导致不可通约量的发现，引发第一次数学危机. (4) 勾股定理公式是第一个不定方程，为不定方程的解题程序 树立了一个范式.
20
-
<六>小结反思
学生反思：我最大的收获； 我表现较好的方面； 我学会了哪些知识； 我还有哪些疑惑……
AB2+AC2=BC2.
11
-
第三种类型：以刘徽的“青朱出入图”为代表，证明不 需用任何数学符号和文字，更不需进行运算，隐含在图中的 勾股定理便清晰地呈现，整个证明单靠移动几块图形而得出， 被称为“无字证明”.
约公元 263 年，三国时代魏国的数学家刘徽为古籍《九 章算术》作注释时，用“出入相补法”证明了勾股定理.
方法一:三国时期吴国数学家赵爽在为《周髀算经》作注解时， 创制了一幅“勾股圆方图”，也称为“弦图”，这是我国对 勾股定理最早的证明.
2002年世界数学家大会在北京召开，这届大会会标的中央图案正是 经过艺术处理的“弦图”，标志着中国古代数学成就.
6
-
c
由面积计算,得 c2 41ab(ba)2. 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
小结：
这节课你学习了哪几种证明勾 股定理的方法？
朱实
中黄实 b (b-a)2
a
可得： c2 =a2+ b2．
赵爽弦图法
总统巧证勾股定理
D
c
a
A
b
C
cb
Ea B
美国第二十任 总统伽菲尔德
《几何原本》中的证法
关于勾股定理的证明，现在人类保存下来的最早
的文字资料是欧几里得（公元前300年左右）所著的
《几何原本》第一卷中的命题47：“直角三角形斜边
传说中的毕达哥拉斯的拼图法
赵爽弦图的证法
我国对勾股定理的证明采取的是割补法，最早的形
式见于公元三、四世纪赵爽的《勾股圆方图注》．在这
篇短文中，赵爽画了一张他所谓的“弦图”，其中每一 个直角三角形称为“朱实”，中间的一个正方形称为
c
“中黄实”，以弦为边的大正方形叫“弦实”，所以，
如果以a、b、c分别表示勾、股、弦之长，那么：
∵由于矩形ADNM和△ADC同底（AD），等高(即平行线AD和CN间的距离)，
∴S矩形ADNM＝2S△ADC．
G
又∵正方形ACHK和△ABK同底（AK）、等高（即平行线AK和
BH间的距离）， ∴S正方形ACHK＝2S△ABK． ∵AD＝AB，AC＝AK，∠CAD＝∠KAB， ∴△ADC≌△ABK．
H的证明
两千多年来，人们对勾股定理的证明颇感兴趣，因为这个定理太贴近 人们的生活实际，以至于古往今来，下至平民百姓，上至帝王总统都愿意探 讨和研究它的证明．因此不断出现关于勾股定理的新证法．
1．传说中毕达哥拉斯的证法 2．赵爽弦图的证法 3．美国第20任总统加菲尔德的证法 4．几何法
上的正方形等于两直角边上的两个正方形之和”．其
证明是用面积来进行的．
G
已知：如图，以在Rt△ABC中， ∠ACB=90°，分别以a、b、c为边向 外作正方形． 求证：a2 +b2=c2．
H C
K
b
a c
A
F B
D
E
几何法
证明：从Rt△ABC的三边向外各作一个正方形（如图），作CN⊥DE交AB于M， 那么正方形ABED被分成两个矩形．连结CD和KB．
K
b
a
A Mc
F B
由此可得S矩形ADNM＝S正方形ACHK ． 同理可证S矩形MNEB＝S正方形CBFG． ∴S矩形ADNM＋S矩形MNEB＝S正方形ACHK＋S正方形CBFG． 即S正方形ADEB＝S正方形ACHK＋S正方形CBFG ， 也就是 a2+b2=c2．
DN
E
合作探究：
运用手中的学具，你还能发现其 它的证明方法吗？