第7讲包含虚拟变量的回归分析43页
第五章_包含虚拟变量的回归模型(课堂PPT)

– 对数单位模型(Logit Model) – 概率单位模型(Probit Model)
1
《
55
包含虚拟因变量的回归模型
• 如何估计这类模型?是否可以用OLS? • 有特殊的统计推断问题吗? • 如何度量这种模型的拟合优度?
1
《
56
(一)线性概率模型(LPM)
yi 0 1xi ui
女性 : s·alaryi 17.96929 1.370714 yearsi
years
1
《
16
2定性变量+1定量变量
yi 0 1 d1i 2 d2i 3 xi ui
1, 男教师 d1i 0,女教师
1, 白种人 d2i 0, 非白种人
xi 教龄
1
《
17
思考题:以下定义方法的差别?
18.5 21.7 18.0 19.0 22.0
教育
0 1 0 0 1
1
《
7
1
《
8
y
1
1 3.28
d 0
《
d 1
x
9
• 虚拟变量系数(差别截距项系数)的经济 含义
• 赋值为0的一类常称为基准类(对比类)
1
《
10
思考题:如下定义存在什么问题?
yi 0 1 d1i 2 d2i ui
1
《
44
假说一和假说二
• 不同政策待遇的企业外国股权比例存在差 异
– 私营企业参与的合资企业比乡镇企业参与的合 资企业,其外国股权比例更高。
– 对资金有更大需求的企业比更小需求的企业, 其外国股权比例更高
1
《
45
假说三和假说四
• 由于浙江省对待不同企业的政策差异小于 江苏省,在浙江省所观察到的假说一和假 说二所描述的效应会弱于江苏省。
第七章 虚拟变量 虚拟变量回归模型ppt汇总 计量经济学

• 在回归分析中,被解释变量的影响因素 除了量(或定量)的因素还有质(或定 性)的因素,这些质的因素可能 会使回 归模型中的参数发生变化,为了估计质 的因素产生的影响,在模型中就需要引 入一种特殊的变量—虚拟变量。
2020/6/16
(二)作用
• 1、可以描述和测量定性(或属性)因素 的影响;
2、多个因素各两种属性
• 如果有m个定性因素,且每个因素各有两个不同的 属性类型,则引入m个虚拟变量。
• 例2
• 研究居民住房消费函数时,考虑到城乡差异和不同 收入层次的影响将消费函数设定为:
Yt=b0+b1Xt+a1D1t+ a2D2t+ μt
Yt=居民住房消费支出
Xt=居民可支配收入
1城镇居民
2020/6/16
虚拟变量对截距的影响
y
有适龄子女
b0&#
o
图1 虚拟变量对截距的影响
x
2020/6/16
2、乘法方式引入虚拟变量
• 基本思想:以乘法方式引入虚拟解释变量
,是在所设定的计量经济模型中,将虚拟 解释变量与其他解释变量相乘作为新 的解释变量,以达到其调整模型斜率的
目的。 • 该方式引入虚拟变量主要作用:
D=
0 无适龄子女
将家庭教育费用支出函数写成:Yt=b0+b1Xt+aDt+μt 即以加法形式引入虚拟变量。
2020/6/16
子女年龄结构不同的家庭教育 费用支出函数为:
• 无适龄子女家庭的教育费用支出函数(D=0 ):Yt=b0+b1Xt+μt
• 有适龄子女家庭的教育费用支出函数(D=1 ):Yt=(b0+a)+b1Xt+μt
第七章多元回归分析虚拟变量
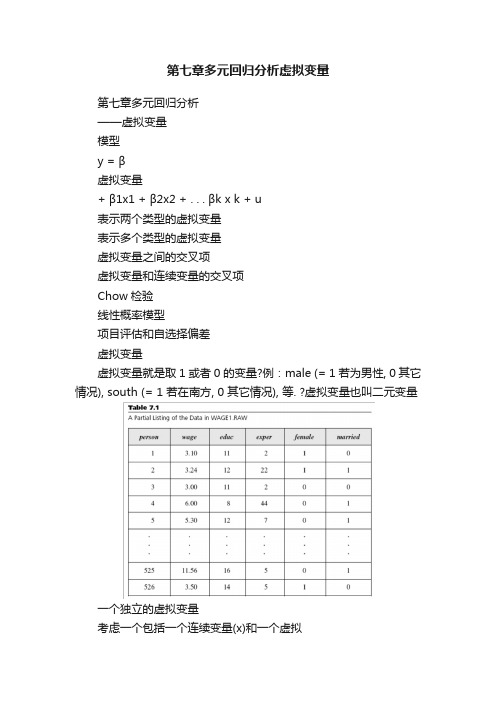
第七章多元回归分析虚拟变量第七章多元回归分析——虚拟变量模型y = β虚拟变量+ β1x1 + β2x2 + . . . βk x k + u表示两个类型的虚拟变量表示多个类型的虚拟变量虚拟变量之间的交叉项虚拟变量和连续变量的交叉项Chow检验线性概率模型项目评估和自选择偏差虚拟变量虚拟变量就是取1 或者0 的变量?例:male (= 1 若为男性, 0 其它情况), south (= 1 若在南方, 0 其它情况), 等. ?虚拟变量也叫二元变量一个独立的虚拟变量考虑一个包括一个连续变量(x)和一个虚拟变量(d)的模型y = β+ δ0d + β1x + u这可以解释成截距项的变化若d = 0, 那么y = β+ β1x + u若d = 1, 那么y = (β+ δ0) + β1x + ud = 0 的样本是参照组δ0 > 0 的例子y y = (β0 + δ0) + β1xd = 1{ δslope = β1d =0 }βy = β0 + β1xx从多个数值的类型变量到虚拟变量?我们可以用虚拟变量来控制有多种类型因素?假设样本中的个人是中学辍学或者仅仅中学毕业或者大学毕业现在要拿仅仅中学毕业和大学毕业的人和中学辍学的人比较定义hsgrad = 1 如果仅仅是中学毕业, 0 其它情况; colgrad = 1 如果大学毕业, 0 其它情况多个数值的类型变量(续)?任何类型变量都可以变成一组虚拟变量?因为参照组由常数项表示了, 那么如果一共有n 个类型,就应该由n –1 虚拟变量如果有太多的类型,通常应该对其进行分组例:前10 , 11 –25, 等虚拟变量之间的交叉项求虚拟变量的交叉项就相当于对样本进行进一步分组例:有男性(male)的虚拟变量和hsgrad(仅仅中学毕业)和colgrad (大学毕业)的虚拟变量加入male*hsgrad 和male*colgrad, 共有五个虚拟变量–> 共有六种类型参照组是女性中学辍学的人此时hsgrad 代表女性仅仅中学毕业者, colgrad 表示女性大学毕业者交叉项表示男性仅仅中学毕业者和男性大学毕业者虚拟变量之间的交叉项(续)?模型可以写成y = β0 + δ1male + δ2hsgrad +δ3colgrad + δ4male*hsgrad + δ5male*colgrad+ β1x + u, 那么:若male = 0 且hsgrad = 0 且colgrad = 0则y = β0 + β1x + u若male = 0 且hsgrad = 1 且colgrad = 0则y = β0 + δ2hsgrad + β1x + u若male = 1且hsgrad = 0且colgrad = 1则y = β0 + δ1male + δ3colgrad + δ5male*colgrad+ βx + u1其它变量与虚拟变量的交叉项?也可以考虑虚拟变量d 和连续变量x 之间的交叉项y = β+ δ1d + β1x + δ2d*x + u若d = 0, 那么y = β+ β1x + u若d = 1, 那么y = (β+ δ1) + (β1+ δ2) x + u这里的两种情况可以看成是斜率的变化δ0 > 0 且δ 1 < 0的例子yy = β+ β1xd = 0d = 1y = (β0 + δ0) + (β 1 + δ1) x。
8第八章包含虚拟变量的回归

一、虚拟变量设置原则
1、模型中只有一个两分定性变量 2、模型中一个定性变量,该变量具有多种 分类 3、小结 4、模型中有多个定性变量 返回
1、模型中只有一个两分定性变量
例如性别定性变量,只有两种分类,引入 一个虚拟变量即可,设置虚拟变量D:
=0,男性 =1,女性
不可引入两个虚拟变量,否则引起多重共线性
方差分析模型在其他社会科学中使用较多
二、方差分析模型(ANOVA):特别的, 当回归中解释变量都是虚拟变量时,此类 模型称为方差分析模型。
Y=b0+b1 D1 +b 2D2+……
返回
三、协方差模型(ANCOVA)
解释变量有定性变量也有定量变量.
Y=b0+b1 X1 +b 2X2+b3 D
两个回归截距相同而斜率不同,性别对边际消
费倾向产生了影响
3、加法方式、乘法方式混合进入模 型
例题1:性别对食品开支的影响:可能同时 改变截距和斜率。为验证这一点,可使用 以下回归: Y= b0+b1 X1+ b2 D X1 + b3 D
例题2:关于储蓄率的研究
Y=A1+A2 X
Y:个人储蓄; X个人收入,回归得到的A2 为
男性的食品开支方程 Y^=1506.244+0.06X
两条样本回归线平行加法方式引入性别虚拟变量 意味着隐含一个假定:
男女的性别差异对边际消费倾向没有影响,为b1 。 即对斜率没有影响,仅对截距产生影响 返回
2、“ 乘法”方式
虚拟变量也会对斜率发生影响
Y=b0+(b1 +b2 D) X1
含虚拟自变量的回归分析

研究成果对实践的指导意义
01
提供了一种新的回归 分析思路
本研究为回归分析提供了一种新的思 路和方法,有助于解决传统回归分析 中难以处理的问题,提高分析结果的 准确性和可靠性。
模型构建
根据行业特点和历史销 售数据,构建一个含虚 拟自变量的回归模型。 其中,虚拟自变量可以 表示季节性、促销活动
等因素。
实证分析
利用历史销售数据对模 型进行实证分析,估计 模型参数并检验虚拟自 变量的显著性。通过模 型评价和诊断确保模型
的有效性。
预测与应用
利用估计得到的回归模 型对未来销售进行预测 ,并根据预测结果制定 相应的市场策略和销售
某个虚拟自变量的系数不显著,则说明该自变量对因变量的影响不显著。
03
模型的诊断
通过残差分析、异方差性检验、多重共线性检验等方法,对模型进行诊
断。如果发现模型存在问题,则需要对模型进行改进。
模型优化与改进
变量的筛选
通过逐步回归、向前选择、向后剔除等方法,对自变量进行筛选。保留对因变量有显著影响的自变量,剔除对因变量 影响不显著的自变量。
结果展示
将实证分析的结果以表格、图形等形式进行展示,以便更 直观地了解虚拟自变量对因变量的影响程度和方向。
应用举例:某行业销售预测模型
第一季度
第二季度
第三季度
第四季度
背景介绍
以某行业的销售数据为 例,探讨含虚拟自变量 的回归分析在销售预测 中的应用。该行业销售 受到多种因素的影响, 包括季节性、促销活动 、竞争对手行为等。
参数估计方法
含虚拟自变量的回归分析

表7-6 保险公司革新情况1
17
151
0
2
26
92
0
3
21
175
0
4
30
31
0
5
22
104
0
6
0
277
0
7
12
210
0
8
19
120
0
9
4
290
0
10
16
238
0
11
28
164
1
12
15
272
1
13
11
295
1
14
38
68
1
15
31
85
1
16
21
224
1
17
20
166
1
18
13
305
1
19
在建立一个实际问题的回归方程时,经常 需要考虑这些定性变量。例如,建立粮食产量 预测方程就应考虑到正常年份与受灾年份的不 同影响;建立空调的销售模型时,除了要考虑 居民收入和商品价格这两个量的因素之外,还 必须将“季节”这个质的因素,作为一个重要 解释变量。
由于受到质的因素影响,回归模型的参数 不再是固定不变的。例如,在空调销售模型中, 收入、价格与空调销售额的关系是随着季节变 化而改变的,也就是说,在不同的季节回归模 型的参数也会有所不同。再如,我国居民的消 费行为在改革开放前后大不相同,因此消费函 数的参数也会发生变化。显然,如果忽略质的 因素,仍把模型中的参数看作是固定不变的, 得到的参数估计量就不能正确描述经济变量之 间的关系。
在回归分析中,对一些自变量是定性变量 的先作数量化处理,处理的方法是引进只取 “0”和“1”两个值的0−1型虚拟自变量。当某 一属性出现时,虚拟变量取值为“1”,否则 取值为“0”。例如,令“1”表示改革开放以 后的时期,“0”则表示改革开放以前的时期。 再如,用“l”表示某人是男性,“0”则表示
虚拟变量回归课件

例1
(1)
D
=
1 0
男 女
( 2)D=1 0
改 革 开 放 以 后 改 革 开 放 以 前
(3)D1 =0 1
天气阴 其 他(4)D2
=1 0
天气雨 其他
问题:
为何只选0、1,选2、3、4行吗?为什么?
虚拟变量回归
14
属性的状态(水平)数与虚拟变量 数量的关系
定性因素的属性既可能为两种状态,也可能为多种 状态。例如,性别(男、女两种)、季节(4种状 态),地理位置(东、中、西部),行业归属,所 有制,收入的分组等。
虚拟变量回归
11
二、虚拟变量设置规则
虚拟变量的设置规则涉及三个方面: 1.“0”和“1”选取原则 2.属性(状态、水平)因素与设置虚拟变量
数量的关系 3.虚拟变量在回归分析中的角色以及作用等
方面的问题
虚拟变量回归
12
“0”和“1”选取原则
虚拟变量取“1”或“0”的原则,应从分析问题的 目的出发予以界定。
虚拟变量回归
16
一个例子(虚拟变量陷阱)
研究居民住房消费支出 Yi 和居民可支配收入 Xi 之间的
数量关系。回归模型的设定为:Y i= 0 + 1 X i+ u i( 1 )
现在要考虑城镇居民和农村居民之间的差异,如何办?
为了对 “城镇居民”、“农村居民”进行区分,分析
各自在住房消费支出 Yi上的差异,设 D1i = 1 为城镇;
非数值性的因素。 基本思想: 直接在回归模型中加入定性因素存在诸多的困难 (那些困难?),是否可将这些定性因素进行量 化,以达到定性因素能与定量因素有着相同作用 之目的。
虚拟变量回归
10
第七章 多元回归分析-虚拟变量

• • • • • • • • • • 模型 y = β0 + β1x1 + β2x2 + . . . βkxk + u 虚拟变量 表示两个类型的虚拟变量 表示多个类型的虚拟变量 虚拟变量之间的交叉项 虚拟变量和连续变量的交叉项 Chow检验 线性概率模型 项目评估和自选择偏差
多个数值的类型变量(续)
• 任何类型变量都可以变成一组虚拟变量 • 因为参照组由常数项表示了, 那么如果一共 有n 个类型,就应该由n – 1 虚拟变量 • 如果有太多的类型,通常应该对其进行分 组 • 例:前10 , 11 – 25, 等
虚拟变量之间的交叉项
• 求虚拟变量的交叉项就相当于对样本进行进一 步分组 • 例:有男性(male)的虚拟变量和hsgrad (仅仅中学毕业) 和 colgrad (大学毕业)的 虚拟变量 • 加入 male*hsgrad 和 male*colgrad, 共有五个 虚拟变量 –> 共有六种类型 • 参照组是女性中学辍学的人 • 此时hsgrad 代表女性仅仅中学毕业者, colgrad 表示女性大学毕业者 • 交叉项表示男性仅仅中学毕业者和男性大学毕 业者
事实上是经济过程检验
• 做模型回归时我们假设所有的样本观测值 都来自同一个总体,如果总体发生改变, 那么模型参数也将发生改变,因此检验总 体也就是经济过程是否发生改变是用计量 进行经济研究的主要步骤。或者是在进行 经济计量研究时必须考虑的一个重要步 骤。其具体方法是:
• 假设我们在1到n个时期研究经济的结构关系,得到如 下的回归模型: Y=b0+b1X1+b2X2+…+bkXk+e 在第q期(1<q < n)曾出台一个经济政策,为检验该 经济政策是否影响我们所研究的经济结构可作如下检 验: 1、用1到q个观测值对模型进行回归,得到回归残差的平 方和,记为ESS1;用q+1到n个观测值对模型进行回 归,得到回归残差平方和,记为ESS2,并令 ESSUR= ESS1+ ESS2。 2、用1到n个观测值对模型进行回归,得到回归残差平方 和,记为ESSR,这可用下面的F统计量检验在k时期出 台的经济政策是否导致经济结构变化: ( ESS R − ESSUR ) / k F ( k , n − 2k ) = ESSUR /(n − 2k )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.0361121 .0407561 .0068003 .0053258 .0001122 .0068482 .0002347 .0988662
-8.04 1.30
11.64 5.06
-4.81 4.57
-2.45 4.23
0.000 0.195 0.000 0.000 0.000 0.000 0.015 0.000
一、什么是虚拟变量?
什么是虚拟变量?
变量的分类
a. 定类/类别变量(nominal/categorical variable) b. 定序/有序变量(ordinal variable) c. 定距/定量变量(interval variable)
o 问题:如何在计量分析中使用定类变量和定序变量
什么是虚拟变量?
或
o 用sx、jy、qt三个虚拟变量表示本科生毕业后的状态 sx 1 0,,升 未学 升 ; jy 学 1 0,,就 未业 就 ; q业 t 1 0,,其 升他 学情 或况 就 业
什么是虚拟变量?
o 对于定序变量和定距变量,也可以用虚拟变量表示
o 学习成绩(定序变量) g 1 1 0 ,,优 其 ; g 秀 他 2 1 0 ,,良 其 ; g 好 他 3 1 0 ,,及 其 ; g 格 他 4 1 0 ,,不 其及 他格
o 例题7_2:课本p217,例7.2
colGPA1.260.15P7 C0.44h7sGPA0.008A7CT se (0.33)(0.05)7 (0.09)4 (0.010)5 如 果 两 个 学 hs生 GP的 和 AAC相 T 同 , 拥 有 计 算 机 的 学 生 的 成 绩 平 比均 没而 有言 计 算 机 的 0.1学 5分 7生 高
lwage
Coef. Std.Err.
t P>|t| [95%Conf.Interval]
female married
educ exper expersq tenure tenursq _cons
-.2901838 .0529219 .0791547 .0269535
-.0005399 .0312962
o 年收入(定距变量,但通过划分收入区间将之转换为虚拟变量) i1 1 0 ,,1 其 万他 元 ; i2 1 0 以 ,,1 其 5 万 下 ; 他 i3 元 1 0 ,,5 其 1万 0 他 ; i4 元 1 0 ,,1 其 的 , 类说 的明 均两 值 存 在 显 著 差 异
自变量中包含一个虚拟变量
例题7_1:工资差异
wage 7 .10 2 .51 female se (0 .21 ) (0 .30 ) 男性的平均工资为 7 .10 美元 女性的平均工资为 7 .10 2 .51 4 .59 美元
自变量中包含多个虚拟变量
wage 4 .84 1.73 married se (0 .25 ) (0 .32 ) 未婚劳动者的平均工资 为 4 .84 美元 已婚劳动者的平均工资 为 4 .84 1.73 6 .57 美元
自变量中包含一个虚拟变量
自变量包含定距变量和一个虚拟变量
o 此时,虚拟变量的回归系数表示在控制其它自变量的情况下 ,两组之间的差异
-.3611279 -.0271456
.0657952 .0164907 -.0007603 .0178426 -.0010355 .2235557
-.2192396 .1329894 .0925143 .0374163
-.0003196 .0447499
-.0001134 .6120116
o 上述结果表明,性别对工资有显著影响,但婚姻状况没有 显著影响。这一模型可能存在问题,即假定婚姻状况的影 响对于男性和女性是相同的。进一步的分析应考虑婚姻状 况的影响存在性别差异。
自变量中包含一个虚拟变量
自变量包含定距变量和一个虚拟变量
o 虚拟变量可用于政策分析,虚拟变量取值为0的一组称为控制 组或对照组(control group),取值为1的一组称为实验组( experimental group)或处理组(treatment group)
o 例题7_3:课本p218,例7.3
o 对于只有两种取值的定类变量,可以用0和1表示这两种取值 。这样的变量称为虚拟变量(dummy variable)或二分变量 (binary variable)。其中,赋值为0的一组称为对照组( reference group)或基准组(benchmark group)
fem a 1 0,,女 男 le; 性 性 CC 1 0 P ,,中 非共 党 ; A 党 员 si 员 1 0 a ,,亚 非洲 亚国 洲
自变量中包含多个虚拟变量
o 自变量中包含多个虚拟变量可分为三种情况 a. 每个虚拟变量代表不同的分类 b. 若干个虚拟变量代表同一种分类,且这种分类是定类的 c. 若干个虚拟变量代表同一种分类,且这种分类是定序的
自变量中包含多个虚拟变量
每个虚拟变量代表不同的分类
例题7_4:性别和婚姻状况对工资的影响(课本p220,例7.6) o 引入性别和婚姻状况两个虚拟变量
1. 自变量中包含一个虚拟变量 2. 自变量中包含多个虚拟变量 3. 交互项
自变量中包含一个虚拟变量
自变量仅为一个虚拟变量
o 如果自变量仅为一个虚拟变量,实际上是以自变量为分类依 据,分析因变量的均值差异
对于 Y0 1Du, 当虚拟变 D量 0时, Y的均值为 E(Y: | D0)0 当虚拟变 D量 1时, Y的均值为 E(Y: | D1)0 1
o 注意:变量名的选择
什么是虚拟变量?
o 对于有多个取值的定类变量,可构造多个虚拟变量来表示
o 用east、central、west三个虚拟变量表示不同地区
1 ,东 ea s0 ,中 t
部 部 ; c 或 en 西 t1 0 ,,中 r 东 a 部 l部 部 ; w 或 e 1 s 0 西 ,,西 东 t 部 部 部
