奥数 逻辑推理问题
奥数部分简单的逻辑推理及习题答案全解

奥数部分——简单的逻辑推理1、A、B、C、D 四人,已知 B 不是最高的,但他比 A、D 高,而 A 不比 D 高,请把他们按高矮摆列。
2、甲、乙、丙、丁四人同时参加了念书比赛,赛后他们各自展望名次,甲说:“丙第一名,我第三名。
”乙说:“我第一名,丁第四名。
”丙说:“丁第二名,我第三名。
”丁没说话。
最后成绩宣布时,发现他们的展望都只对了一半。
那么,此次比赛他们的名次分别是什么?3、有一次上课坐在一个小组的三个人中有人发言,小张谴责小王和小李:“你们都在谎话。
”小李却说:“小张正在谎话。
”小王则说:“小李正在谎话。
”他们中只有 1 个人讲的是实话,试问:谁讲的是实话,谁讲的是谎话?4、甲、乙、丙、丁四位同学的校服上印有不一样的号码。
赵同学说:甲是 2 号,乙是 3 号。
钱同学说:丙是 2 号,乙是 4 号。
孙同学说:丁是 2 号,丙是 3 号。
李同学说:丁是 1 号,乙是 3 号。
已知赵、钱、孙、李每人都说对了一半,那么丙是几号?5、甲、乙、丙三人对晓明的藏书数量作了一个预计,甲说:他起码有1000本书。
乙说:他的书不到1000 本。
丙说:他最罕有 1 本书。
这三个人的预计中只有一句是对的。
晓明终究有多少本书?6、小利、小江、小敏、小磊四个同学,有一个同学在英语比赛中获奖,其他同学识他们谁是获奖者,小利说:我不是,小江说:是小磊,小敏说:是小江,小磊说:不是我。
他们中间只有一个人没有说实话,那么获奖者是谁?7、有三名学生在看1、 2、 3 号运动员进行“羽毛球冠军抢夺赛。
”赛前,关于谁会得“冠军” 称呼,三名学生都说了两句话:甲说:不是 2 号,是 3 号。
乙说:不是 2 号,是 1 号。
丙说:不是 3 号,是 2 号。
比赛结果表示,他们的话有一人全对,有一人对一半错一半,另一人全错。
请你想想,冠军是谁?8、有三位老师比年纪,他们每人说的 3 句话中有 2 句是对的,请你剖析一下他们各有多少岁?刘老师:我 22 岁,比小陈小 2 岁,比小李大 1 岁。
13题奥数逻辑推理专题

13题奥数逻辑推理专题精选13题奥数逻辑推理专题1.有甲、乙、丙、丁四人同住在一座四层的楼房里,已知:甲比乙住的楼层高,比丙住的楼层低,丁住四层。
试问:甲、乙、丙、丁各住在这座楼的几层?2.有三个小伙子,他们分别姓牛、姓马、姓龙,凑巧他们三人的属相恰好也是牛、马、龙。
属龙的说:“我们每个人的属相都跟自己的姓的不同。
”姓牛的小伙表示赞同,他说:“对!我姓牛,就不属牛。
”你能说出这三个人的姓和属相的对应关系吗?3.康大一校四年级有四个班,每个班都有正、副班长各一人。
平时如召开年级的班长会议时,各班都只派一名班长参加。
参加第一次会议的是小叶、小景、小汪和小刘;参加第二次会议的是小杨、小叶、小景、小徐。
三次会议小金因病没有参加。
问每个班是哪两位班长?4.一次羽毛球邀请赛中,来自湖北、广东、福建、北京和上海的五名运动员相遇在一起。
据了解:(1)李平仅和其它两名运动员比赛过;(2)上海运动员和其它三名运动员比赛过;(3)陈兵没有和广东运动员交过锋;(4)福建运动员和林华比赛过;(5)广东、福建和北京的三名运动员相互交过手;(6)赵欣仅与一名地运动员比赛过。
问:李平、陈兵、林华、赵欣、张强各是哪个省的运动员?5.A、B、C三个合唱队,每个合唱队都有一名指挥,他们是:小明、小芳(女)、小华(女);每个合唱队有一名伴奏,他们是琪琪、军军、斌斌。
已知:(1)A队和琪琪所在的队都是女指挥;(2)B队的女指挥不是小芳;请你判断,各队的指挥和伴奏是谁?6.在某旅馆里住着国籍不同的六个人。
他们的国籍分别是美、德、英、法、日和意大利。
他们的名字为了好记分别叫做A、B、C、D、E、F。
现在已知:(1)A和美国人是医生;(2)E和日本人是教师;(3)C和德国人是技师;(4)B和F曾经当过兵,而德国人从未参过军;(5)法国人比A年龄大,意大利比C年龄大;(6)B同美国人下周要去英国旅行,而C和法国人下周瑞士渡假。
试问:A、B、C、D、E、F各是哪国人?7.已知张新、李敏和王强三同学在北京、苏州、南京的大学里学习化学、地理、物理,张新不在北京学习;李敏不在苏州学习;在北京学习的同学不学物理;在苏州学习的同学是学化学;李敏不学地理。
小学奥数思维训练-逻辑推理问题(通用,含答案)

小学奥数思维训练-逻辑推理问题学校:___________姓名:___________班级:___________考号:___________一、填空题1.填数使下列竖式成立:(1)(2)二、排序题2.200米赛跑,张强比李军快0.2秒,王明的成绩是39.4秒,赵刚的成绩比王明慢0.9秒,但比张强快0.1秒,林林比张强慢3秒,请你给这五人排出名次来。
三、解答题3.有三个和尚,一个讲真话,一个讲假话,另外一个有时讲真话,有时讲假话。
一天,一位智者遇到这三个和尚,他先问左边的那个和尚:“你旁边的是哪一位?”和尚回答说“讲真话的。
”他又问中间的和尚:“你是哪一位?”和尚答:“我是半真半假的。
”他最后问右边的和尚:“你旁边是哪一位?”答:“讲假话的。
”根据他们的回答,智者马上分清了他们,你能分清吗?4.一次全校数学竞赛,A、B、C、D、E五位同学取得了前五名,发奖后有人问他们的名次,回答是:A说:“B是第三名,C是第五名.”B说:“D是第二名,E是第四名.”C说:“A是第一名,E是第四名.”D说:“C是第一名,B是第二名.”E说:“D是第二名,A是第三名.”最后,他们都补充说:“我们的话半真半假.”请你判断一下他们每个人的名次.5.老师有一黑两白三顶帽子,给两个学生看后,让他们闭上眼睛,从中取出两顶给他们戴上,然后让他们睁开眼睛,互相看清对方戴的帽子,并立即说出自己头上戴的帽子是什么颜色,两位同学都不能立即说出,请问你知道这两位学生戴的各是什么颜色的帽子吗?6.曾实、张晓、毛梓青在一起,一位是工程师、一位是医师、一位是教师。
现在只知道:(1)毛梓青比教师年龄大;(2)曾实和医师不同岁;(3)医师比张晓年龄小。
你能确定谁是工程师?谁是医师?谁是教师吗?7.某公安人员需查清甲、乙、丙三人谁先进办公室,三人口供如下:甲:丙第二个进去,乙第三个进去。
乙:甲第三个进去,丙第一个进去。
丙:甲第一个进去,乙第三个进去。
小学奥数 逻辑推理 知识点+例题+练习 (分类全面)
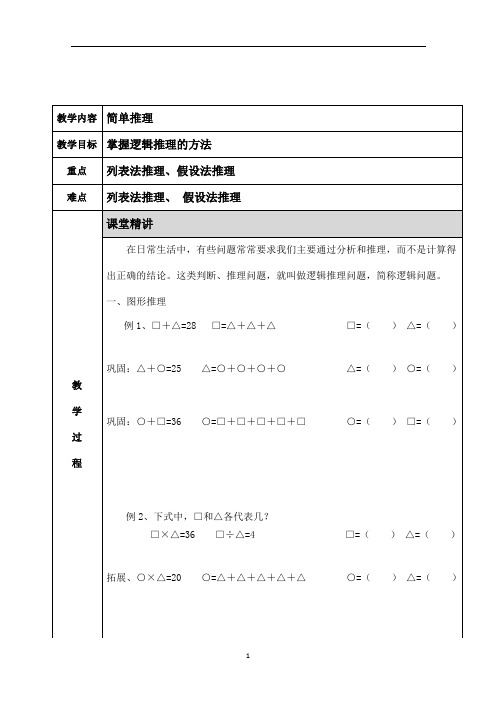
拓展、□=○+○+○+○○×□=16 □=()○=()
例3、下面三块正方体的六个面都是按相同的规律涂有红、黄、蓝、白、绿、黑六种颜色。
请判断黄色的对面是什么颜色?白色的对面是什么颜色?红色的对面是什么颜色?
(A)
黄
黑
白
(B)
红
白
绿
(C)
红
蓝
黄
拓展:一个正方体6个面上分别写着1、2、3、4、5、6。
根据下图摆放的三种情况,判断每个数字对面上的数字是几。
二、文字推理
例1、小王、小张和小李一位是工人,一位是农民,一位是教师,现在只知道:小李比教师年龄大;小王与农民不同岁;农民比小张年龄小。
问:谁是工人?谁是农民?谁是教师?
课后作业
1、☆+○=18 ☆=○+○☆=()○=()
2、○×□=16 □÷○=4 ○=()□=()
3、甲、乙、丙分别是来自中国、日本和英国的小朋友。
甲不会英文,乙不懂日语却与英国小朋友热烈交谈。
问:甲、乙、丙分别是哪国的小朋友?
4、根据一个正方体的三种不同的摆法,判断出相对的两个面上的字母各是什么?。
高中奥数推理题及答案

高中奥数推理题及答案在高中奥数竞赛中,推理题是一类常见的题型,它要求参赛者运用逻辑推理能力来解决问题。
以下是一些典型的高中奥数推理题及其答案:题目1:有5个盒子,分别标记为A、B、C、D和E。
每个盒子里都装有不同数量的球,但盒子外的标签都贴错了。
现在需要找出每个盒子里实际装有多少个球。
解答:首先,假设A盒子的标签是正确的,那么A盒子里应该有1个球。
但因为标签都贴错了,所以A盒子里不可能有1个球。
同理,其他盒子也不能有1个球。
因此,我们可以推断出每个盒子里至少有2个球。
接下来,我们考虑B盒子。
如果B盒子里有2个球,那么B盒子的标签应该是C,因为C盒子的标签是B,而C盒子里不可能有1个球。
这样,C盒子里应该有3个球。
但是,如果C盒子里有3个球,那么D盒子的标签应该是E,而E盒子的标签是D,这意味着D盒子里应该有5个球。
然而,这与我们的假设冲突,因为D盒子的标签是B,而不是E。
因此,B盒子里应该有3个球,C盒子里应该有2个球。
现在,我们可以确定D盒子里有4个球,因为E盒子的标签是D,而D盒子的标签是E。
最后,A盒子里有5个球,E盒子里有1个球。
题目2:在一个班级中,有3个学生:Alice、Bob和Charlie。
老师问他们每个人是否带了作业。
Alice说:“我没有带作业。
”Bob说:“Charlie带了作业。
”Charlie说:“Bob没有带作业。
”老师知道他们中有一个人说了真话,另外两个人说了假话。
请问谁带了作业?解答:如果Alice说了真话,那么Bob和Charlie都在说谎。
但Bob说Charlie带了作业,Charlie说Bob没有带作业,这与Alice说真话的情况矛盾。
如果Bob说了真话,那么Alice和Charlie都在说谎。
这意味着Alice 带了作业,Charlie没有带作业,这与Bob说Charlie带了作业的真话相矛盾。
因此,只能是Charlie说了真话,Bob和Alice都在说谎。
奥数逻辑思维训练500题

奥数逻辑思维训练500题1.小学生奥数逻辑推理练习题1.有五个人各说了一句话。
第一个人说:“我们中间每个人都说谎”。
第二个人说:“我们中间只有一个人说谎”。
第三个人说:“我们中间有两个人说谎”。
第四个人说:“我们中间有三个人说谎”。
第五个人说:“我们中间有四个人说谎”。
请问,他们谁说谎话,谁说真话?2.某地质学院的三名学生对一种矿石进行分析。
甲判断:不是铁,不是铜。
乙判断:不是铁,不是锡。
丙判断:不是锡,而是铁。
经化验证明,有一个人判断完全正确,有一个人只说对了一半,而另一个则完全说错了。
你知道三人中谁是对的,谁是错的,谁是只对了一半的吗?2.小学生奥数逻辑推理练习题1.五个旅游者在海滨交谈。
甲:“我从A城来,乙A城来,丙从B城来”。
乙:“我从C城来,戊从C城来,丙从B城来”。
丙:“我不从B城来,甲不从D城来,丁从E城来”。
丁:“我父亲从A城来,我母亲从D城来,我从F城来”。
戊:“甲从A城来,乙从A城来,我从F城来”。
如果他们每人都说了两句真话,一句假话,你能判断每一个人各来自哪个城市吗?2.在一次有3人参加的讲话中,小张指责小王和小李:“你们都在说谎。
”小李却说:“小张正在说谎。
”小王则说:“小李正在说谎。
”试判断他们谁讲的是真话,谁讲的是假话?前八名,老师让他们猜一下谁是第一名。
A:“或者F是第一名,或者H是第一名。
”B:“我是第一名。
”C:“G是第一名。
”D:“B不是第一名。
”E:“A说的不对。
”F:“我不是第一名,H也不是第一名”。
G:“C不是第一名。
”H:“我同意A的意见。
”老师指出,八人中有三人猜对了,那么谁是第一名?3.小学生奥数逻辑推理练习题1.A、B、C、D、E、F六年足球队进行比赛,每队都已赛过三场。
(1)A队三战得6分;(2)B队三战都负;(3)C队三战三平;(4)D、F两队进行过一场比赛,D队的三场比赛积分为1分。
比赛中凡是胜一场的。
都得了2分,平局的都得1分,负一场得0分。
小学四年级奥数逻辑推理

小学四年级数学逻辑推理例题详解例1对某班同学进行了调查,知道如下情况:①有哥哥的人没有姐姐;②没有哥哥的人有弟弟;③有弟弟的人有妹妹;试问:1有姐姐的人一定没有哥哥,对吗2有弟弟的人一定没有哥哥,对吗3没有哥哥的人一定有妹妹,对吗解答:根据条件①得到1是对的;“有弟弟且有哥哥”并不与①②③矛盾,因此得到2是不对的;根据条件②③得到3是对的;例2 有甲、乙、丙、丁四人同住在一座四层的楼房里,他们之中有工程师、工人、教师和医生.如果已知:①甲比乙住的楼层高,比丙住的楼层低,丁住第四层;②医生住在教师的楼上,在工人的楼下,工程师住最低层;试问:甲、乙、丙、丁各住在这座楼的几层各自的职业是什么解答 1由已知条件,丁住在第四层,是最高层,于是甲、乙、丙只能住在1,2,3这三层之中了.因为条件①还告诉我们,“甲比乙住的高”比“丙住的低”,所以甲肯定住在第二层,而丙住在第三层,乙住在第一层.2由条件②知道,工程师住在最低层,说明工程师是住在一层.那么,医生、教师、工人一定住在2,3,4层,条件②还告诉我们,“医生住在教师的楼上”.这说明医生不是住三层就是住四层,又由于“医生住在工人的楼下,”所以医生只能住在三层.工人住在四层,教师住在二层了.我们把1与2联系起来,就得到最后的答案:甲:教师,住二层;乙:工程师,住一层;丙:医生,住三层;丁:工人,住四层.例3徐、王、陈、赵四位师傅分别是工厂的木工、车工、电工和钳工,他们都是象棋迷;1木工只和车工下棋,而且总是输给车工2王、陈两位是邻居;3陈师傅与电工下棋互有胜负;4徐师傅比赵师师傅下得好;5木工的家离工厂最远;卢刚和医生不同岁;医生比丁飞年龄小,陈瑜比飞行员年龄大;问:谁是工程师、谁是医生、谁是飞行员解析:因为卢刚和医生不同岁,医生比丁飞年龄小,可以判断卢刚和丁飞不是医生,所以陈瑜是医生;陈瑜比丁飞小,陈瑜比飞行员年龄大,所以丁飞是工程师,卢刚是飞行员;例5:有一个正方体,每个面分别写上汉字:数学奥林匹克;三个人从不同角度观察的结果如下图所示;这个正方体的每个汉字的对面各是什么字解析:先找出出现次数最多的字奥数林“奥”的对面不是:林、匹、数、学;所以是“克”“数”的对面不是:学、奥、克、林;所以是“匹”“林”的对面是“学”例 6 有三个小朋友们在谈论谁做的好事多;冬冬说:“兰兰做的比静静多;”兰兰说:“冬冬做的比静静多;”静静说:“兰兰做的比冬冬少;”这三位小朋友中,谁做的好事最多谁做的好事最少解答:我们用“>”来表示每个小朋友之间做好事多少的关系;兰兰>静静冬冬>静静冬冬>兰兰所以,冬冬>兰兰>静静,冬冬做的好事最多,静静做的最少;例7甲、乙、丙三个孩子踢球打碎了玻璃,甲说:“是丙打碎的;”乙说:“我没有打碎破璃;”丙说:“是乙打碎的;”他们当中有一个人说了谎话,到底是谁打碎了玻璃解答:由题意推出结论,必须符合他们中只有一个人说了谎,推理时可先假设,看结论和条件是否矛盾;如果是甲打碎的,那么甲说谎话,乙说的是真话,丙说的是谎话;这样两人说的是谎话,与他们中只有一人说谎相矛盾,所以不是甲打碎的;如果是乙打碎的,那么甲说的是谎话,乙说的是谎话,丙说的是真话,与他们中只有一人说谎相矛盾,所以不是乙打碎的;如果是丙打碎的,那么甲说的是真话,乙说的是真话,而丙说的是谎话;这样有两个说的是真话,符合条件中只有一个人说的是谎话,所以玻璃是丙打碎的;例8甲、乙、丙、丁4人比赛乒乓球,每两个都要赛一场;结果甲胜了丁,并且甲、乙、丙3人胜的场数相同,问:丁胜了几场解答:4个人每两人比赛一场一共6场,甲乙丙胜场一样,甲又胜了丁,则甲至少胜一场,三人加起来3场,那么丁胜利三场,可是这样与甲胜丁一场矛盾,故甲至少胜2场,三人刚好6场,所以丁一场都不胜;分析:①假设甲乙丙同胜1场;∵甲胜丁, ∴甲输给了乙丙;又∵甲乙丙同胜1场;∴乙输给了丙丁;∴丙就胜了甲乙,即胜了两场;与假设相矛盾,∴假设不成立②假设甲乙丙丁同胜3场那么甲乙丙丁将全胜,显然不符合;该假设不成立③则,甲乙丙同胜2场∵一共进行4×3÷2=6场;三人胜的场数相同刚好6场,所以丁一场都不胜;。
小学奥数-逻辑推理

小学奥数-逻辑推理逻辑推理(一)解题思路:以重要的条件为突破口,用排除、假设、反证、筛选等方法有条理地进行推理例1公路上按一路纵队排列着五辆大客车.每辆车的后面都贴上了该车的目的地的标志.每个司机都知道这五辆车有两辆开往A市,有三辆开往B市;并且他们都只能看见在自己前面的车的标志.调度员听说这几位司机都很聪明,没有直接告诉他们的车是开往何处的,而让他们根据已知的情况进行判断.他先让第三个司机猜猜自己的车是开往哪里的.这个司机看看前两辆车的标志,想了想说“不知道”.第二辆车的司机看了看第一辆车的标志,又根据第三个司机的“不知道”,想了想,也说不知道.第一个司机也很聪明,他根据第二、三个司机的“不知道”,作出了正确的判断,说出了自己的目的地。
请同学们想一想,第一个司机的车是开往哪儿去的;他又是怎样分析出来的?例2XXX、XXX、XXX三个男同学都各有一个妹妹,六个人在一起打羽毛球,举行混合双打比赛.事先规定.兄妹二人不许搭伴。
第一盘,XXX和XXX对XXX和XXX;第二盘,XXX和XXX对XXX和XXX的妹妹。
请你判断,XXX、XXX和XXX各是谁的妹妹。
例3“迎春杯”数学竞赛后,甲、乙、丙、XXX四名同砚推测他们之中谁能获奖.甲说:“假如我能获奖,那么乙也能获奖.”乙说:“假如我能获奖,那么丙也能获奖.”丙说:“假如丁没获奖,那么我也不能获奖.”实践上,他们之中只有一小我没有获奖.并且甲、乙、丙说的话都是正确的.那么没能获奖的同砚是___。
例4数学竞赛后,XXX、XXX、XXX各获得一枚奖牌,其中一人得金牌,一人得银牌,一人得铜牌.XXX猜测:“XXX得金牌;XXX不得金牌;XXX不得铜牌.”结果XXX只猜对了一个.那么XXX得___牌,XXX得___牌,XXX得___牌。
例5有三只盒子,甲盒装了两个1克的砝码;乙盒装了两个2克的砝码;丙盒装了一个1克、一个2克的砝码.每只盒子外面所贴的标明砝码重量的标签都是错的.聪明的XXX只从一只盒子里掏出一个砝码,放到天平上称了一下,就把所有标签都矫正过来了.你晓得这是为何吗?例6四人打桥牌,某人手中有13张牌,四种花色样样有;四种花色的张数互不相同.红桃和方块共5张;红桃与黑桃共6张;有两张将牌(主牌).试问这副牌以什么花色的牌为主?1例7S、B、J、R四人分别获数学、英语、语文和逻辑学四个学科的奖学金,但他们都不知道自己获得的是哪一门获学金.他们相互猜测:S:“R得逻辑学奖”;B:“J得英语奖”;J:“S得不到数学奖”;R:“B得语文奖”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学习好资料欢迎下载
奥数模块——逻辑推理
例、已知某月中,星期二的天数比星期一的天数多,而星期三的天数比星期四的天数多,那么这个月最后一天是星期几?
练习:某年二月,星期日的天数最多,那么这个月最后一天是星期几?
练习:一个正方体,六个面分别写上A、B、C、D、E、F,你能根据这个正方体不同的摆法,求出相对的两个面的字母是什么吗?
练习:已知甲、乙、丙三人中,只有一人会开汽车。
甲说:“我会开汽车。
”乙说:“我不会开。
”丙说:“甲不会开汽车。
”如果三人中只有一人讲的是真话,那么谁会开汽车?
例:甲、乙、丙、丁四个人同时参加数学竞赛。
最后:甲说:“丙是第一名,我是第三名。
”乙说:“我是第一名,丁是第四名。
”丙说:“丁是第一名,我是第三名。
”丁没有说话。
成绩揭晓时,大家发现甲、乙、丙三个人各说对了一半。
你能说出他们的名次吗?
练习:甲、乙、丙、丁四个人进行游泳比赛,赛前名次众说不一。
有的说:“甲是第二名,丁是第三名。
”有的说:“甲是第一名,丁是第二名。
”有的说:“丙是第二名,丁是第四名。
”实际上,上面三种说法各说对了一半。
甲、乙、丙、丁各是第几名?
例:A、B、C、D与小强五个同学一起参加象棋比赛,每两人都赛一盘,比赛一段时间后统计:A赛了4盘,B赛了3盘,C赛了2盘,D赛了一盘。
问小强已经赛了几盘?
练习:上海、辽宁、北京、山东四个足球队进行循环赛,到现在为止,上海队赛了3场,辽宁队赛了2场,山东队赛了1场。
问北京队赛了几场?
例:张、王、李三个工人,在甲、乙丙三个工厂里分别当车工、钳工和电工。
①张不在甲厂,②王不在乙厂,③在甲厂的不是钳工,④在乙厂的是车工,⑤王不是电工。
这三个人分别在哪个工厂?干什么工作?
练习:某大学宿舍里A,B,C,D,E,F,G七位同学,其中两位来自哈尔滨,两位来自海南,两位来自天津,一位来自广州,还知道:
(1)D,E来自同一地方;(2)B,G,F不是北方人;(3)C没去过哈尔滨。
那么,A 来自什么地方?
例:某班44人,从A,B,C,D,E五位候选人中选举班长。
A得选票23张。
B得选票占第二位,C,D得票相同,E的选票最少,只得了4票。
那么B得选票多少张?
小升初奥数逻辑推理题真题及答案
1、A、B、C、D、E、F六人赛棋,采用单循环制。
现在知道:A、B、C、D、E五人已经分别赛过5、4、3、
2、l盘。
问:这时F已赛过________盘。
2、甲、乙、丙三人比赛象棋,每两人赛一盘.胜一盘得2分.平一盘得1分,输一盘得0分.比赛的全部三盘下完后,只出现一盘平局.并且甲得3分,乙得2分,丙得1分.那么,甲 ________乙,甲________丙,乙________丙(填胜、平、负)。
3、A、B、C、D、E、F六个选手进行乒乓球单打的单循环比赛(每人都与其它选手赛一场),每天同时在三张球台各进行一场比赛,已知第一天B对D,第二天C对E,第三天D对F,第四天B对C,问:第五天A与谁对阵?另外两张球台上是谁与谁对阵?
4、一个岛上有两种人:一种人总说真话的骑士,另一种是总是说假话的骗子。
一天,岛上的2003个人举行一次集会,并随机地坐成一圈,他们每人都声明:“我左右的两个邻居是骗子。
”第二天,会议继续进行,但是一名居民因病未到会,参加会议的2002个人再次随机地坐成一圈,每人都声明:“我左右的两个邻居都是与我不同类的人。
”问有病的居民是_________(骑士还是骗子)。
1、【解】单循环制说明每个人都要赛5盘,这样A 就跟所有人下过了,再看E,他只下过1盘,这意味着他只和A下过,再看B 下过4盘,可见他除了没跟E下过,跟其他人都下过;再看D 下过2,可见肯定是跟A,B下的,再看C,下过3盘,可见他不能跟E,D下,所以只能跟A,B,F下,所以F总共下了3盘。
2、【解】甲得3分,而且只出现一盘平局,说明甲一胜一平;乙2分,说明乙一胜一负;丙1分,说明一平一负。
这样我们发现甲平丙,甲胜乙,乙胜丙。
3、【解】天数对阵剩余对阵
第一天 B---D A、C、E、F
第二天 C---E A、B、D、F
第三天 D---F A、B、C、E
第四天 B---C A、D、E、F
第五天 A---? ?
从中我们可以发现D已经和B、F对阵了,这样第二天剩下的对阵只能是A---D、B---F;又C已经和E、B对阵了,这样第三天剩下的对阵只能是C---A、B---E;这样B就已经和C、D、E、F都对阵了,只差第五天和A对阵了,所以第五天A---B;再看C已经和A、B、E对阵了,第一天剩下的对阵只能是C---F、A---E;这样A只差和F对阵了,所以第四天A---F、D---E;所以第五天的对阵:A---B、C---D、E---F。
4、【解】:2003个人坐一起,每人都声明左右都是骗子,这样我们可以发现要么是骗子和骑士坐间隔的坐,要不就是两个骗子和一个骑士间隔着坐,因为三个以上的骗子肯定不能挨着坐,这样中间的骗子
就是说真话了。
再来讨论第一种情况,显然骑士的人数要和骗子的人数一样多,而现在总共只有2003人,所以不符合情况,这样我们只剩下第二种情况。
这样我们假设少个骗子,则其中旁边的那个骗子左右两边留下的骑士,这样说明骗子说“我左右的两个邻居都是与我不同类的人”是真话。
所以只能是少个骑士。
