反比例函数易错题集
反比例函数易错题难题

反比例函数易错题、较难题训练1、若y=(a+2)xa2 +2a-1为反比例函数关系式,则a= 。
2、已知反比例函数xy 1-=的图象上有两点),(11y x A 、),(22y x B 且21x x <,那么下列结论正确的是( )A. 21y y <B. 21y y >C. 21y y = D 1y 与2y 之间的大小关系不能确定 3、函数8y x=,若-4≤x<-2,则( ) A 、2≤y<4 B 、-4≤y<-2 C 、-2≤y<4 D 、-4<y ≤-24、点A (2,1)在反比例函数y kx=的图像上,当y<2时,x 的取值范围是 5.如图△P 1OA 1, △P 2A 1 A 2是等腰直角三角形,点1P 、2P 在函数4(0)y x x=>的图象上,斜边1OA 、12A A 都在轴上,则点2A 的坐标是____________.6.已知n 是正整数,n P (n x ,n y )是反比例函数xky =图象上的一列点,其中1x 1=,2x 2=,…,n x n =,记211y x T =,322y x T =,…,1099y x T =;若1T 1=,则921T T T ⋅⋅⋅⋅⋅⋅的值是________.7、如右图是三个反比例函数x k y 1=,xk y 2=,x k y 3=在x 轴上方的图象,由此观察得到1k 、2k 、3k 的大小关系为( )A. 321k k k >>B. 123k k k >>C. 132k k k >>D.213k k k >>8、如右图,△OPQ 是边长为2的等边三角形,若反比例函数的图象过点P ,则它的解析式是_____________.9、如图,已知双曲线)0k (xk y >=经过直角三角形OAB 斜边OB 的中点D ,与直角边AB 相交于点C .若△OBC 的面积为3,则k =____________.10、函数()()1240y x x y x x==>≥0,的图象如图所示,则结论:①两函数图象的交点的坐标为()22,;②当2x >时,21y y >;③当1x =时,3BC =;④当逐渐增大时,1y 随着的增大而增大,2y 随着的增大而减小.其中正确结论的序号是 .11、如图,直线与双曲线()交于点A .将直线向右平移个单位后,与双曲线()交于点B ,与X 轴交于点,若2=BCAO,则 .12、如图,在X 轴的正半轴上依次截取112233445OA A A A A A A A A ====,过点12345A A A A A 、、、、分别作X 轴的垂线与反比例函数()20y x x=≠的图象相交于点12345P P P P P 、、、、,得直角三角形1112233344455OPA A P A A P A A P A A P A 2、、、、,并设其面积分别为12345S S S S S 、、、、,则5S 的值为 .. 13、如图,已知一次函数1y x =+的图象与反比例函数ky x=的图象在第一象限相交于点A ,与X 轴相交于点C AB x ,⊥轴于点,AOB △的面积为1,则AC 的长为 (保留根号)..43y x =k y x =0x >43y x =92k y x =0x >C k =214、如图,过原点的直线l 与反比例函数1y x=-的图象交于M ,N 两点,根图象猜想线段MN 的长的最小值是___________.15、如图11,若正方形OABC 的顶点B 和正方形ADEF 的顶点E 都在函数 1y x=(0x >)的图象上,则点E 的坐标是( , ). 16、如图,点A 、B 是双曲线上的点,分别经过A 、B 两点向轴、轴作垂线段,若则 .17、已知, A 、B 、C 、D 、E 是反比例函数16y x=(x>0)图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是 (用含π的代数式表示)18、已知:如图,在平面直角坐标系O 中,Rt △OCD 的一边OC 在轴上,∠C=90°,点D 在第一象限,OC=3,DC=4,反比例函数的图象经过OD 的中点A .(1)求该反比例函数的解析式;(2)若该反比例函数的图象与Rt △OCD 的另一边DC 交于点B ,求过A 、B 两点的直线的解析式.19、为了预防“非典”,某学校对教室采用药熏消毒法进行消毒. 已知药物燃烧时,室内每立方米空气中的含药量y (毫克)与时间x 分钟)成正比例,药物燃烧完后,y 与x成反比3y x=1S =阴影,12S S +=例(如图所示). 现测得药物8分钟燃毕,此时室内空气中每立方米含药量为6毫克. 请根据题中所提供的信息,解答下列问题:(1)药物燃烧时,y 关于x 的函数关系式为:___________________,自变量x 的取值范围是:______________;药物燃烧后y 关于x 的函数关系式为:___________________; (2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过几分钟后,学生才能回到教室;(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效地杀灭空气中的病菌,那么此次消毒是否有效?为什么?20、如图8,直线b kx y +=与反比例函数xk y '=(<0)的图象相交于点A 、点B ,与x轴交于点C ,其中点A 的坐标为(-2,4),点B 的横坐标为-4.(1)试确定反比例函数的关系式; (2)求△AOC 的面积.。
反比例函数易错题汇编及解析
A.2 【答案】C 【解析】
B.3
C.4
D.5
【分析】
根据 SAOB 2 ,利用反比例函数系数 k 的几何意义即可求出 k 值,再根据函数在第一象限 可确定 k 的符号.
【详解】
解:由 AB x 轴于点 B , SAOB
2 ,得到 SAOB
1 2
k
2
又因图象过第一象限,
SAOB
1 2
k
2 ,解得 k
11.函数 y= 1-k 与 y=2x 的图象没有交点,则 k 的取值范围是( x
A.k<0
B.k<1
C.k>0
) D.k>1
【答案】D
【解析】
【分析】
由于两个函数没有交点,那么联立两函数解析式所得的方程无解.由此可求出 k 的取值范 围.
【详解】
令 1-k =2x,化简得:x2= 1-k ;由于两函数无交点,因此 1-k <0,即 k>1.
13.如图,若点 M 是 x 轴正半轴上任意一点,过点 M 作 PQ∥ y 轴,分别交函数
y k1 (x 0) 和 y k2 (x 0) 的图象于点 P 和 Q,连接 OP 和 OQ.则下列结论正确的是
x
x
()
A.∠POQ 不可能等于 90°
B.
PM QM
k1 k2
C.这两个函数的图象一定关于 x 轴对称
反比例函数易错题汇编及解析
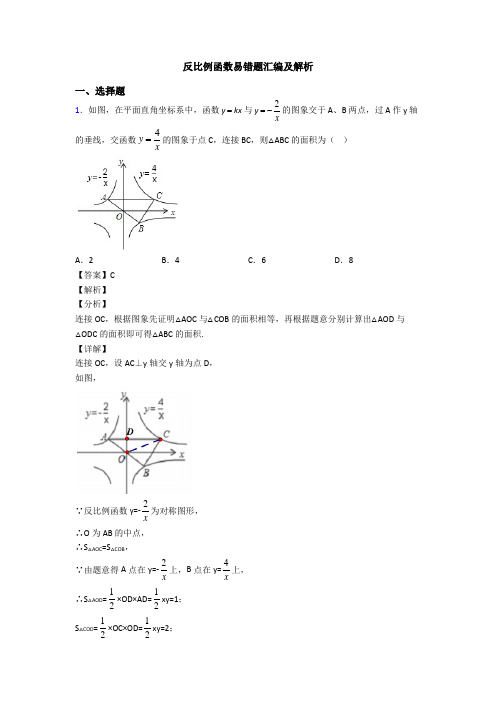
一、选择题 1.如图,在平面直角坐标系中,函数 y kx 与 y 2 的图象交于 A、B 两点,过 A 作 y 轴
x 的垂线,交函数 y 4 的图象于点 C,连接 BC,则△ABC 的面积为( )
x
A.2
B.4
反比例函数易错题汇编附答案

A.逐渐变小B.逐渐变大C.时大时小D.保持不变
【答案】D
【解析】
【分析】
如图,作辅助线;首先证明△BEO∽△OFA,,得到 ;设B为(a, ),A为(b, ),得到OE=-a,EB= ,OF=b,AF= ,进而得到 ,此为解决问题的关键性结论;运用三角函数的定义证明知tan∠OAB= 为定值,即可解决问题.
故选C.
考点:反比例函数
【点睛】
本题属于对反比例函数的基本性质以及反比例函数的在各个象限单调性的变化
7.已知点 、 都在双曲线 上,且 ,则 的取值范围是()
A. B. C. D.
【答案】D
【解析】
【分析】
根据已知得3+2m<0,从而得出m的取值范围.
【详解】
∵点 、 两点在双曲线 上,且y1>y2,
A.y1<y2<y3B.y3<y2<y1C.y3<y1<y2D.y2<y1<y3
【答案】D
【解析】
【分析】
根据k>0,在图象的每一支上,y随x的增大而减小,双曲线在第一三象限,逐一分析即可.
【详解】
∵反比例函数y= 中的k=4>0,
∴在图象的每一支上,y随x的增大而减小,双曲线在第一三象限,
∵-2<a<0,
y=k(x-1)的图象经过第一、二、四象限,
观察可知B选项符合题意,
故选B.
6.对于反比例函数 ,下列说法不正确的是( )
A.点(﹣2,﹣1)在它的图象上B.它的图象在第一、三象限
C.当x>0时,y随x的增大而增大D.当x<0时,y随x的增大而减小
九年级数学下册第二十六章反比例函数易错题集锦(带答案)

九年级数学下册第二十六章反比例函数易错题集锦单选题1、在下图中,反比例函数y=2x的图象大致是( )A.B.C.D.答案:D∵k=2,可根据k>0,反比例函数图象在第一、三象限,∴在每个象限内,y随x的增大而减小,故选D.2、下列函数中,变量y是x的反比例函数的是()A.y=x3B.y=3x+1C.y=3xD.y=3x答案:C分析:根据反比例函数的定义(一般地,形如y=kx(k是常数,k≠0)的函数叫做y是x的反比例函数)逐项判断即可得.解:A、y=x3是正比例函数,则此项不符题意;B、y=3x+1叫做y是x+1的反比例函数,则此项不符题意;C、y=3x叫做y是x的反比例函数,则此项符合题意;D、y=3x是正比例函数,则此项不符题意;故选:C.小提示:本题考查了反比例函数,熟记定义是解题关键.3、下列式子中,表示y是x的反比例函数的是()A.xy=1B.y=8x2C.y=x2D.y=xx+1答案:A分析:根据反比例函数的定义逐一进行判断.,符合反比例函数的定义,故本选项正确;A、由原式得到y=1xB、该函数式表示y与x2成反比例关系,故本选项错误;C、该函数式表示y与x成正比例关系,故本选项错误;D、该函数式不是反比例函数,故本选项错误;故选A.(k≠0)转化为y=kx-1(k≠0)的形式.小提示:本题考查了反比例函数的定义,重点是将一般式y=kx.在同一坐标系内的4、二次函数y=ax2+bx+c的图象如图,则一次函数y=ax−c与反比例函数y=b+cx图象大致为()A.B.C.D.答案:D分析:根据抛物线图象,得到a>0,c<0,b<0,即可判断出答案.>0,所解:根据抛物线图象,开口向上,即a>0;与y轴交于负半轴,故c<0;对称轴在x轴正半轴,即−b2a以b<0;∵y=ax−c中,a>0,c<0,∴排除A、B选项;∵y=b+c,b<0,c<0,∴b+c<0,故排除C选项;x故选D.小提示:本题考查了反比例函数的图象及二次函数的图象及一次函数图象,熟练掌握函数图象和性质是本题的关键.的图象上的两点,下列说法中不正确的是()5、P1(x1,y1),P2(x2,y2)是函数y=−8xA.该函数的图象经过点(−4,2)B.该函数的图象位于第二、四象限C.当0<x1<x2时,则y1<y2D.当x1<0<x2时,则y1<y2答案:D分析:根据反比例函数的图象和性质逐项判断即可.解:对于函数y=−8,x=2,当x=−4时,y=−8−4∴函数y=−8的图象经过点(−4,2),x故A正确;∵k=−8<0,的图象位于第二、四象限,∴函数y=−8x故B正确;∵−8<0,∴在第四象限内y随x的增大而增大,∴当0<x1<x2时,则y1<y2,故C正确;∵函数y=−8的图象位于第二、四象限,x函数图象的增减性分x>0和x<0两种情况讨论,故选:D.小提示:本题考查反比例函数的图象和性质.解题关键是反比例函数性质的应用.6、关于函数y=−2x,下列说法中正确的是()A.图像位于第一、三象限B.图像与坐标轴没有交点C.图像是一条直线D.y的值随x的值增大而减小答案:B分析:根据反比例函数的图像和性质即可判断.解:在y=-2x中,k=-2<0,∴图像位于第二、四象限,图像是双曲线,在每一象限内,y随着x增大而增大,故A,C,D选项不符合题意,∵x≠0,y≠0,∴函数图像与坐标轴没有交点,故B选项符合题意,故选:B.小提示:本题考查了反比例函数的图像和性质,熟练掌握反比例函数的性质与系数的关系是解题的关键.7、下列函数:①y=2x,②y=15x ,③y=x﹣1,④y=1x+1.其中,是反比例函数的有().A.0个B.1个C.2个D.3个答案:C分析:根据反比例函数的定义,逐项分析判断即可.解析式符合y=kx(k≠0)的形式为反比例函数.解:①y是x正比例函数;②y是x反比例函数;③y是x反比例函数;④y是x+1的反比例函数.综上所述,是反比例函数的有②③,共计2个小提示:本题考查了反比例函数的定义,将一般y=kx(k≠0)转化为y=kx﹣1,是解题的关键.8、已知反比例函数y=m−2x,当x>0时, y随x的增大而增大,则m的取值范围是()A.m<2B.m>2C.m≤2D.m≥2答案:A分析:先根据反比例函数y=m−2x,当x>0时y随x的增大而增大判断出m−2的符号,求出m的取值范围即可.解:∵反比例函数y=m−2x,当x>0时y随x的增大而增大,∴m−2<0,∴m<2.故选:A.小提示:本题考查的是反比例函数的性质,根据题意判断出m−2的符号是解答此题的关键.9、反比例函数的图像如图所示,则这个反比例函数的表达式可能是()A.y=−4x B.y=−3xC.y=83xD.y=−52x答案:D分析:根据点A、B的坐标结合函数图象以及反比例函数图象上点的坐标特征,即可得出-3<k<-2,再对照四个选项即可得出结论.解:观察函数图象可知:3×(-1)<k<(-2)×1,即-3<k<-2.小提示:本题考查了反比例函数的图象以及反比例函数图象上点的坐标特征,观察函数图象利用反比例函数图象上点的坐标特征找出k的取值范围是解题的关键.10、一次函数y=ax+b和反比例函数y=a−bx在同一直角坐标系中的大致图象是()A.B.C.D.答案:A分析:先由一次函数的图象确定a、b的正负,再根据a-b判断双曲线所在的象限.能统一的是正确的,矛盾的是错误的.图A、B直线y=ax+b经过第一、二、三象限,∴a>0、b>0,∵y=0时,x=-ba ,即直线y=ax+b与x轴的交点为(-ba,0)由图A、B的直线和x轴的交点知:-ba>-1,即b<a,所以b-a<0,∴a-b>0,此时双曲线在第一、三象限,故选项B不成立,选项A正确;图C、D直线y=ax+b经过第二、一、四象限,∴a<0,b>0,此时a-b<0,双曲线位于第二、四象限,故选项C、D均不成立;故选A.小提示:本题考查了一次函数、反比例函数的性质.解决本题用排除法比较方便.填空题的图形上,其中AB=11、如在平面直角坐标系中,等腰直角△ABO如图放置,直角项点A在反比例函数y=kxAO,B(-2,0),则k=___.答案:-1分析:如图,过点A作AD⊥BO,由题意知,OD=DB=AD,得A点坐标,进而求出k的值.解:如图,过点A作AD⊥BO∵△ABO是等腰直角三角形,AB=OA∴OD=DB=AD∴D点坐标为(−1,0),A点坐标为(−1,1)将A点坐标代入y=kx 中,得1=k−1解得k=−1所以答案是:−1.小提示:本题考查了等腰直角三角形的性质,反比例函数的解析式.解题的关键在于求出点A的坐标.12、在平面直角坐标系中,一次函数y=2x与反比例函数y=kx(k≠0)的图象交于A(x1,y1),B(x2,y2)两点,则y1+y2的值是____________.答案:0分析:根据正比例函数和反比例函数的图像关于原点对称,则交点也关于原点对称,即可求得y1+y2∵一次函数y=2x与反比例函数y=kx(k≠0)的图象交于A(x1,y1),B(x2,y2)两点,一次函数y=2x与反比例函数y=kx(k≠0)的图象关于原点对称,∴y1+y2=0所以答案是:0小提示:本题考查了正比例函数和反比例函数图像的性质,掌握以上性质是解题的关键.13、如图,面积为6的矩形OABC的顶点B在反比例函数y=kx(x<0)的图像上,则k=__________.答案:-6分析:根据反比例函数系数k的几何意义可得|k|=6,再根据函数所在的象限确定k的值.解:∵反比例函数y=kx(x<0)的图象经过面积为6的矩形OABC的顶点B,∴|k|=6,k=±6,∵反比例函数y=kx(x<0)的图象经过第二象限,∴k=-6.所以答案是:-6.小提示:主要考查了反比例函数y=kx(x<0)中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|.14、如图,在平面直角坐标系xOy中,点A(0,4),B(3,4),将△ABO向右平移到△CDE位置,A的对应点是C,O的对应点是E,函数y=kx(k≠0)的图像经过点C和DE的中点F,则k的值是______.答案:6分析:作FG⊥x轴,DQ⊥x轴,FH⊥y轴,设AC=EO=BD=a,表示出四边形ACEO的面积,再根据三角形中位线的性质得出FG,EG,即可表示出四边形HFGO的面积,然后根据k的几何意义得出方程,求出a,可得答案.过点F作FG⊥x轴,DQ⊥x轴,FH⊥y轴,根据题意,得AC=EO=BD,设AC=EO=BD=a,∴四边形ACEO的面积是4a.∵F是DE的中点,FG⊥x轴,DQ⊥x轴,∴FG是△EDQ的中位线,∴FG=12DQ=2,EG=12EQ=32,∴四边形HFGO的面积为2(a+32),∴k=4a=2(a+32),解得a=3,2∴k=6.所以答案是:6.小提示:本题主要考查了反比例函数中k的几何意义,正确的作出辅助线构造矩形是解题的关键.15、有一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度ρ(kg/m3)是体积V(m3)的反比例函数,它的图象如图,当V=2 m3时,气体的密度是____kg/m3.答案:4分析:由图象可知,反比例函数图象经过点(4,2),即可求解.解:由图象可知,函数图象经过点(4,2),所以ρ=8V当V=2m3时,气体的密度是4kg/m3.故答案为4.(k为常数且k≠0)的关系,那么就说y与小提示:本题考查了反比例函数的定义:若两个变量x、y满足y=kxx成反比例.解答题16、为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19min;完成2间办公室和1间教室的药物喷洒要11min.(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?(2)消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.答案:(1)校医完成一间办公室和一间教室的药物喷洒各要3min 和5min ;(2)一班学生能安全进入教室,计算说明过程见解析.分析:(1)设校医完成一间办公室和一间教室的药物喷洒各要xmin 和ymin ,再根据题干信息建立二元一次方程组,然后解方程组即可得;(2)先求出完成11间教室的药物喷洒所需时间,再根据一次函数的解析式求出点A 的坐标,然后利用待定系数法求出反比例函数的解析式,最后根据反比例函数的解析式求出x =55时,y 的值,与1进行比较即可得.(1)设校医完成一间办公室和一间教室的药物喷洒各要xmin 和ymin则{3x +2y =192x +y =11解得{x =3y =5答:校医完成一间办公室和一间教室的药物喷洒各要3min 和5min ;(2)一间教室的药物喷洒时间为5min ,则11个房间需要55min当x =5时,y =2×5=10则点A 的坐标为A(5,10)设反比例函数表达式为y =k x将点A(5,10)代入得:k 5=10,解得k =50则反比例函数表达式为y=50x<1当x=55时,y=5055故一班学生能安全进入教室.小提示:本题考查了二元一次方程组的应用、反比例函数与一次函数的综合等知识点,较难的是题(2),依据题意,正确求出反比例函数的解析式是解题关键.17、已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时).(1)求v关于t的函数表达式.(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?答案:(1)v=100;(2)平均每小时至少要卸货20吨.t分析:(1)直接利用vt=100进而得出答案;(2)直接利用要求不超过5小时卸完船上的这批货物,进而得出答案.(1)由题意可得:100=vt,;则v=100t(2)∵不超过5小时卸完船上的这批货物,∴t≤5,=20,则v≥1005答:平均每小时至少要卸货20吨.小提示:考查了反比例函数的应用,正确得出函数关系式是解题关键.的图象交于18、如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=nxA(−1,2),B(m,−1)两点.(1)求反比例函数和一次函数的解析式;(2)过点B作直线l∥y轴,过点A作直线AD⊥l于D,点C是直线l上一动点,若DC=2DA,求点C的坐标.答案:(1)y=−2,y=﹣x+1;x(2)(2,8)或(2,﹣4)分析:(1)把点A(﹣1,2)代入y=n求出n的值,即可得到反比例函数的解析式,把B(m,﹣1)代入求x得的反比例函数的解析式得到m的值,把A、B两点的坐标代入一次函数y=kx+b,求出k,b的值,即可得出一次函数的解析式;(2)根据已知条件确定AD的长及点D的坐标,由DC=2AD得到DC=6,从而求得点C的坐标.得,(1)解:把点A(﹣1,2)代入y=nx2=n,−1解得n=﹣2,∴反比例函数的解析式是y=−2,x把B(m,﹣1)代入y=−2得,x,﹣1=−2m解得m=2,∴点B的坐标是(2,﹣1),把A (﹣1,2),B (2,﹣1)代入y =kx +b 得,{−k +b =22k +b =−1, 解得{k =−1b =1, ∴一次函数的解析式为y =﹣x +1;(2)解:∵直线l ∥y 轴,AD ⊥l ,点A 的坐标是(﹣1,2),点B 的坐标是(2,﹣1),∴ 点D 的坐标是(2,2),∴ AD =2-(﹣1)=3,∵ DC =2DA ,∴ DC =6,设点C 的坐标为(2,m ),则|m -2|=6,∴ m -2=6或m -2=﹣6,解得m =8或﹣4,∴ 点C 的坐标是(2,8)或(2,﹣4)小提示:此题是一次函数与反比例函数综合题,考查的是反比例函数与一次函数的交点问题,数形结合思想的应用是解答此题的关键.。
第二十六章 反比例函数易错点集训

第二十六章反比例函数26.1.1反比例函数易错点集训易错点1:不理解反比例函数解析式的特点而出错例1、下列函数中,表示y是x的反比例函数的是( D )A.y=3xB.y=C. y=D. .y=错解辨析:即时练习:下列函数关系式中不是表示反比例函数的是()A.xy=5B. y=C. y=D. .y=易错点2:忽略反比例函数概念中k≠0的条件而出错例2、若函数y=是反比例函数,则m的值为( D )A.m=-2B.m=1C.m=2或1D. m=-2或-1错解辨析:即时练习:已知y=是反比例函数,则m=易错点3:忽略同一题中不同函数的系数不同而出错例3、已知y=y1+y2,y1与x-1成正比例,y2与x+1成反比例,当x=0时,y=-3,当x=1时,y=-1,求y的表达式。
解:∵y1与x-1成正比例,y2与x+1成反比例∴设y1=k(x-1) y2=∵y=y1+y2当x=0时,y=-3,当x=1时,y=-1∴∴k=-2∴y=-2x+2-错解辨析:即时练习:若y=y1-y2,y1-1与x成反比例,2y2与x-2成正比例,且当x=1时y=0,当x=-1时y=10,求y与x的函数解析式。
26.1.2反比例函数的图像和性质 易错点集训易错点1:忽略反比例函数的比例系数与图像所在象限的对应关系而出错例1、已知函数22-=m mxy 是反比例函数且图像的两个分支在第二四象限,则m 的值是( C )A.1B.—1C.1±D.不能确定错解辨析: 即时练习:已知一次函数y=kx+b 的图像经过第一二四象限 则反比例函数x kb y =的图像在( )A.第一二象限B.第三四象限C.第一三象限D.第二三象限易错点2:忽略反比例函数的比例系数与函数增减性的对应关系而出错例2、若反比例函数y =xk 3-的图像在每一个象限内,y 随x 的增大而增大,则有( D ) A.k 0≠ B.k 3≠ C .k<3 D.k>3错解辨析:即时练习:已知反比例函数图象与直线和的图象过同一点,则当>0时,这个反比例函数值随的增大而 (填增大或减小);易错点3:利用反比例函数的增减性比较函数值大小时,易忽略“在每个象限内” 例3、设A( 1x , 1y ) B (2x , 2y )是反比例函数xy 2-= 图像上的两点 若1x <2x <0 则1y 与 2y 之间的关系是( B )A .1y <2y <0B .2y <1y <0 C.2y >1y >0 D .1y >2y >0错解辨析: 即时练习:在函数(为常数)的图象上有三个点(-2,),(-1,),(,),函数值,,的大小为 易错点4:利用k 的几何意义求解析式,易忽略图形所在象限 如图:P 是反比例函数xk y =图象上的一点,由P 分别向x 轴和y 轴引垂线,阴影部分面积为3,函数的表达式为错解辨析: 即时练习:如图,A 为反比例函数xk y =图象上一点,AB ⊥x 轴与点B ,若3=∆AOB S ,则k 为 xk y =x y 2=1+=x y x y x xk y 22--=k 1y 2y 213y 1y 2y 3y26.2实际问题与反比例函数易错点集训易错点1:忽略函数表示的实际意义例1、已知矩形的面积为8,那么它的长y与宽x之间的关系用图象大致可表示为( C )A. B. C. D.错解辨析:即时练习:如图,市煤气公司计划在地下修建一个容积为104m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是()A. B. C. D.易错点2:题意理解不清而出错例2、李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校。
(易错题精选)初中数学反比例函数易错题汇编及答案解析

1.使关于 x 的分式方程 =2 的解为非负数,且使反比例函数 y= 限时满足条件的所有整数 k 的和为( ). A.0 B.1 C.2 D.3 【答案】B 【解析】
图象过第一、三象
试题分析:分别根据题意确定 k 的值,然后相加即可.∵关于 x 的分式方程 =2 的解为
y1 )
、
B(1,
y2
)
、
C(2,
y3 )
三个点,
1 y1 k , 1 y2 k , 2 y3 k ,
y1
k
,
y2
k
,
y3
1k 2
,
而k 0,
y1 y3 y2 . 故选: B . 【点睛】
本题考查了反比例函数图象上点的坐标特征:反比例函数 y k ( k 为常数,且 k 0 ) x
∴反比例函数 y= a b 的图象过一、三象限, x
所以此选项正确; D. 由一次函数图象过二、四象限,得 a<0,交 y 轴负半轴,则 b<0, 满足 ab>0,与已知相矛盾 所以此选项不正确; 故选 C. 【点睛】 此题考查反比例函数的图象,一次函数的图象,解题关键在于确定 a、b 的大小
9.如图,点 P 是反比例函数 y k (x0)图象上一点,过 P 向 x 轴作垂线,垂足为 M,连 x
x
A. 3,1
B. 1, 3
C. 1,3
D. 3,1
【答案】A 【解析】 【分析】
先求出 k=-3,再依次判断各点的横纵坐标乘积,等于-3 即是在该双曲线上,否则不在. 【详解】
∵点 M 1,3 在双曲线 y k 上,
x ∴ k 13 3 ,
反比例函数易错题汇编含答案

故选:B.
【点睛】
本题考查函数的图象性质与中心对称图形的性质,熟练掌握相关知识是解题的关键.
7.下列各点中,在反比例函数 图象上的是()
A.(3,1)B.(-3,1)C.(3, )D.( ,3)
【答案】A
故选A.
8.如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于点A,反比例函数y= (x>0)的图象与线段AB相交于点C,且C是线段AB的中点,若△OAB的面积为3,则k的值为()
A. B.1C.2D.3
【答案】D
【解析】
【分析】
连接OC,如图,利用三角形面积公式得到S△AOC= S△OAB= ,再根据反比例函数系数k的几何意义得到 |k|= ,然后利用反比例函数的性质确定k的值.
【详解】
∵反比例函数y= (k>0)的图象在一、三象限,
∴在每个象限内y随x的增大而减小,
∵A(-3,y1)、B(-1,y2)在第三象限双曲线上,
∴y2<y1<0,
∵C(1,y3)在第一象限双曲线上,
∴y3>0,
∴y3>y1>y2,
故选:B.
【点睛】
此题考查反比例函数的图象和性质,解题关键在于当k>0,时,在每个象限内y随x的增大而减小;当k<0时,y随x的增大而增大,注意“在每个象限内”的意义,这种类型题目用图象法比较直观得出答案.
【答案】D
【解析】
【详解】
∵点(2,-4)在反比例函数y= 的图象上,
∴k=2×(-4)=-8.
∵A中2×4=8;B中-1×(-8)=8;C中-2×(-4)=8;D中4×(-2)=-8,
反比例函数易错

图1反比例函数易错一、忽略反比例函数表达式成立的条件致错 例1若函数()221a ya x-=-是反比例函数,则a 的值为( ).A .1a = B. 1a =- C. 1a =或1a =- D. 1a =且1a =- 错解:由反比例函数的定义知,221a-=-,解得1a =或1a =-. 故选C.剖析:上面的解答只考虑到x 的指数221a -=-,却忽视了反比例函数表达式成立的条件0k ≠,即比例系数10a -≠,所以1a ≠,故只取1a =-. 正解:B.二、错误理解反比例函数关系致错例2 若y 与2x 成反比例,且当1x =-时,3y =,则y 与x 之间是( ).A .正比例函数 B. 反比例函数 C. 一次函数 D. 以上都不是 错解:B.剖析:在这个关系中,把2x 整体看成一个自变量,y 与2x 是反比例函数关系.但是如果把x 看成自变量,那么y 与x 不是反比例函数关系.正解:∵y 与2x 成反比例,∴2k yx =. 代入1x =-,3y =得3k =.∴23y x=. 显然满足23y x=的y 不是x 的一次函数和反比例函数. 故选D. 三、错误理解反比例函数的性质致错例3(2007年绵阳市)若A (a 1,b 1),B (a 2,b 2)是反比例函数xy 2-=图象上的两个点,且a 1<a 2,则b 1与b 2的大小关系是( ).A .b 1<b 2B .b 1 = b 2C .b 1>b 2D .大小不确定错解:∵0k =,∴y 随x 的增大而增大. 又∵a 1<a 2,∴12b b <. 故选A.剖析:当0k<时,在每个象限内,y 随x 的增大而增大. 注意“在每个象限内”指的是两点必须在同一象限内,才有性质“y 随x 的增大而增大”,而不在一个象限内的点,则不满足此性质.正解:由于题目没有指明A (a 1,b 1),B (a 2,b 2)是否在同一象限内,虽然有a 1<a 2,但却不能确定b 1与b 2的大小关系. 故选D.四、忽视隐含条件致错例4(2007年大连市)如图1,A B ,是双曲线ky x =且点()B a b ,在点A 的右侧,则b 的取值范围是 .剖解:观察图象知,A 点的纵坐标为2,又因为点()B a b ,在点A 的右侧,所以2b <. 故填2b <.分析:做数学题要细心,考虑问题要全面,注意隐含条件. 由于双曲线的分支不可能与坐标轴相交,所以点()B a b ,只能在第一象限内,即本题隐含着0b >这个条件正解:由于2b <,且0b >,所以b 的取值范围是02b <<.故填02b <<. 五、忽视自变量的取值范围致错例5(2007年佳木斯市)在一个可以改变容积的密闭容器内,装有一定质量m 的某种气体,当改变容积v 时,气体的密度ρ也随之改变,ρ与v 在一定范围内满足mvρ=,当7kg m =时,它的函数图象是( ).错解:由题意得7vρ=,由于此函数是反比例函数,所以其图象是双曲线. 故选A. 剖析:在利用描点法画反比例函数的图象时,一定要注意自变量的取值范围. 错解产生的原因在于没有根据实际问题去确定函数自变量的取值范围,由于本题的自变量v 表示密闭容器的容积,故0v >. 所以函数的图象只能是双曲线在第一象限的部分.正解:选D.A .)B .)C .)D .)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的解析式.
11.如图,A、B 两点在函数 y = m (x > 0) 的图象上. x
(1)求 m 的值及直线 AB 的解析式; (2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点 . 请直接写出图中阴影部分(不包括边界)所含格点的个数.
6.作出反比例函数 y = − 4 的图象,结合图象回答: x
(1)当 x=2 时,y 的值;(2)当 1<x≤4 时,y 的取值范围;(3)当 1≤y<4 时,x 的取值范围.
10.已知:如图,在平面直角坐标系 xOy 中,Rt△OCD 的一边 OC 在 x 轴上, ∠C=90°,点 D 在第一象限,OC=3,DC=4,反比例函数的图象经过 OD 的中点 A.
S2
O
x
2 题图
4.已知函数 y=y1-y2,且 y1 为 x 的反比例函数,y2 为 x 的正比例函数,且 x = − 3 和 x=1 时,y 的值都是 1.求 y 2
关于 x 的函数关系式.
5.作出反比例函数 y = 12 的图象,并根据图象解答下列问题: x
(1)当 x=4 时,求 y 的值;(2)当 y=-2 时,求 x 的值;(3)当 y>2 时,求 x 的范围.
戴氏教育龙泉校区
反比例函数易错题集
1:(2007 年浙江省初中数学竞赛)函数 y= − 1 图象的大致形状是( ) x
初三数学
9.如图,点 A、B 是函数 y=x 与 y = 1 的图象的两个交点,作 AC⊥x 轴于 C, x
作 BD⊥x 轴于 D,则四边形 ACBD 的面积为( ).
数学教研组
A
B
14.如图,双曲线 y = k (k>0)经过矩形 OABC 的边 BC 的中点 E,交 AB 于点 D。 x
若梯形 ODBC 的面积为 3,则双曲线的解析式为( ).
初三数学
数学教研组
16.如图,已知 A(-4,n),B(2,-4)是一次函数 y=kx+b 的图象和反比例函数 y = m 的图象的两个交点. x
C
D
y
2.(2009 年牡丹江市)如图,点 A 、 B 是双曲线 y = 3 上的点,分别经过 A 、 B 垂线段,若 S阴影 = 1,则 S1 + S2 =
.
3.已知 y 与 2x-3 成反比例,且 x = 1 时,y=-2,求 y 与 x 的函数关系式. 4
S1
B
作直线 AC∥y 轴交于点 C,交直线 MB 于点 D.当四边形 OADM 的面积为 6 时,请判断线段 BM 与 DM 的 大小关系,并说明理由.
2
(1)求反比例函数和一次函数的解析式; (2)求直线 AB 与 x 轴的交点 C 的坐标及△AOB 的面积;
(3)求方程 kx + b − m = 0 的解(请直接写出答案); x
(4)求不等式 kx + b − m < 0 的解集(请直接写出答案). x
15.如图,直线 y=kx+b 与反比例函数 y = k (x<0)的图象交于点 A,B,与 x 轴交 x
7.作出函数 y = 12 的图象,并根据图象回答下列问题: x
(1)当 x=-2 时,求 y 的值; (2)当 2<y<3 时,求 x 的取值范围; (3)当-3<x<2 时,求 y 的取值范围.
8.如图,A、B 是函数 y = 2 的图象上关于原点对称的任意两点, x
BC∥x 轴,AC∥y 轴, △ABC 的面积记为 S,则(s= ).
12.如图,已知点 A 在反比例函数的图象上,AB⊥x 轴于点 B,点 C(0,1), 若△ABC 的面积是 3,则反比例函数的解析式为____________.
1
戴氏教育龙泉校区
13.如图,直线 y=mx 与双曲线 y = k 交于 A,B 两点,过点 A 作 AM⊥x 轴, x
垂足为 M,连结 BM,若 S△ABM=2,则 k 的值是( ).
于点 C, 其中点 A 的坐标为(-2,4),点 B 的横坐标为-4.
(1)试确定反比例函数的关系式;
(2)求△AOC 的面积.
17.已知:如图,正比例函数 y=ax 的图象与反比例函数 y = k 的图象交于点 A(3,2). x
(1)试确定上述正比例函数和反比例函数的表达式; (2)根据图象回答,在第一象限内,当 x 取何值时,反比例函数的值大于正比例函数的值; (3)M(m,n)是反比例函数图象上的一动点,其中 0<m<3,过点 M 作直线 MB∥x 轴,交 y 轴于点 B;过点 A
