力的分解计算方法举例
力的分解和合成多个力合成为一个力的规律

力的分解和合成多个力合成为一个力的规律力的分解和合成是力学中的基本概念,它们描述了多个力的相互作用和作用效果。
根据力的分解和合成规律,我们可以将一个力分解为多个分力,也可以将多个力合成为一个合力。
本文将详细介绍力的分解和合成的规律,并通过实例加以说明。
1. 分解力的规律力的分解是将一个力分解为作用在不同方向上的两个或多个分力的过程。
根据分解规律,任何一个力都可以被分解为垂直于其作用方向的两个或多个力。
这些分力之和等于原始力,称为力的分解。
以一个斜向向上的力F作为例子,我们可以将其分解为水平方向上的分力Fx和垂直方向上的分力Fy。
根据三角函数的关系,我们可以得到以下分解公式:Fx = F * cosθFy = F * sinθ其中,θ为原始力F与水平方向的夹角。
通过分解力,我们可以得到力在各个方向上的作用效果和大小,进而进行力学分析和计算。
2. 合成力的规律合成力是将多个力合成为一个力的过程。
根据合成规律,多个力的合力可以通过向量的几何相加方法得到。
将各个力按照其作用方向用向量表示,合力的大小等于各力向量长度的矢量和,方向等于各力向量方向的矢量和。
以两个力F1和F2的合成为例子,我们可以将它们用向量F1和F2表示,然后将这两个向量进行几何相加。
合力F的大小可以通过勾股定理或正弦/余弦定理计算,合力的方向可以通过正切函数计算。
F = √(F1² + F2² + 2F1F2cosθ)θ = arctan(F2sinθ / (F1 + F2cosθ))其中,θ为F1与F2之间的夹角。
通过合成力的计算,我们可以得到多个力合力的大小和方向,进而进行力学问题的求解和分析。
3. 实例说明为了更好地理解力的分解和合成规律,下面举例说明。
假设有一个箱子沿着斜坡上升,受到斜向上的力F1作用和斜坡对箱子的支持力N的作用。
我们需要求解箱子在斜坡上升的加速度。
首先,我们将斜向上的力F1分解为垂直方向上的分力Fy和水平方向上的分力Fx。
力的合成与分解

力的合成与分解力在物理学中是一个重要的概念,它描述了物体之间相互作用的效果。
而力的合成与分解是力学中的一种基本问题,它帮助我们理解多个力作用在物体上时的结果,以及如何将一个力分解为多个力的合力,或者将一个力的合力分解为多个力。
一、力的合成力的合成是指将多个力作用于物体上时,求出它们的合力。
合力的大小和方向决定了物体受到的合力效果。
当多个力作用于物体上时,可以使用力的几何法进行合成。
力的几何法可以通过在力的作用方向上构成力的向量,并使用矢量相加的方法得到合力。
例如,假设一个物体同时受到水平向右的力F₁和竖直向上的力F₂,我们可以使用力的几何法求出它们的合力F。
首先,将力F₁和F₂分别用箭头表示在一个力的作用方向上。
然后,将F₁的箭头的起点连接到F₂的箭头的终点,得到一个新的力F的箭头。
该箭头的起点是F₁的起点,终点是F₂的终点。
最后,连接F₁的终点和F₂的起点,即得到了合力F的箭头。
根据箭头的直线方向和箭头的长度,我们可以得到合力F的大小和方向。
二、力的分解力的分解是指将一个力拆解成多个分力,使得这些分力的合成恰好等于原来的力。
力的分解可以帮助我们分析复杂情况下的力的作用效果。
当一个力作用在物体上时,有时候我们需要将这个力分解成两个或更多个分力,以便更好地理解和计算物体的运动情况或受力效果。
常见的力的分解方法有平行四边形法和正交分解法。
在平行四边形法中,我们假设一个力F可以被分解为两个分力F₁和F₂。
首先,确定一个合适的力F₄与F形成一个平行四边形。
然后,根据平行四边形法则,连接F₁的起点与F₂的起点,连接F₁的终点与F₄的起点,连接F₂的终点与F₄的终点。
这样,我们得到了两个分力F₁和F₂,它们的合力恰好等于原来的力F。
正交分解法是指将一个力拆解成一个或多个方向上的力分量。
对于任何一个力F,我们可以将它分解成多个垂直于不同方向的力分量。
例如,如果一个力F斜向上,我们可以将它拆解成一个垂直向上的力分量和一个垂直向右的力分量。
高中物理中的力的分解与合成问题

高中物理中的力的分解与合成问题力的分解与合成问题在高中物理中是一个重要的概念。
力的分解是指将一个力分解成若干个部分力,而力的合成是指将两个或多个力合成为一个力。
这两个问题的理解和掌握对于解决实际物理问题非常关键。
本文将重点讨论力的分解与合成问题的基本概念、相关公式以及一些应用。
一、力的分解问题力的分解是将一个力分解成若干个部分力的过程。
这个过程可以帮助我们分析和解决复杂的物理问题。
下面以一个简单的例子来说明力的分解的概念和应用。
假设有一个物体受到了一个斜向上的力F,我们需要将这个力分解成沿着x轴和y轴的两个分力Fx和Fy。
根据三角函数的性质,我们可以得到以下公式:Fx = F * cosθFy = F * sinθ其中,θ表示力F与x轴的夹角。
通过力的分解,我们可以将复杂的斜向力问题转化为两个独立的力问题,从而更加方便地进行计算和分析。
此外,力的分解也有助于我们理解力对物体运动的影响。
二、力的合成问题力的合成是指将两个或多个力合成为一个力的过程。
这个过程可以帮助我们了解多个力共同作用下的结果。
下面以一个简单的例子来说明力的合成的概念和应用。
假设有两个力F1和F2,我们需要将它们合成为一个合力F。
根据平行四边形法则,我们可以得到以下公式:F = √(F1^2 + F2^2 + 2F1F2cosθ)其中,θ表示力F1与力F2之间的夹角。
通过力的合成,我们可以将多个力合并为一个合力,从而便于我们分析和计算物体的运动状态。
力的合成在解决斜面运动、平衡力等问题中起到重要作用。
三、力的分解与合成问题的应用力的分解与合成问题在物理学中有广泛的应用。
下面介绍两个具体的应用例子。
1. 斜面运动问题对于一个物体在倾斜角度为θ的斜面上滑动的情况,重力可以分解为沿斜面和垂直斜面方向上的两个分力,分别记为F∥和F⊥。
通过力的分解,我们可以计算出物体在斜面上滑动的加速度,并进一步解决相关问题。
2. 平衡力问题在平衡力问题中,我们需要求解一个物体所受合力为零的情况。
力的分解(常见力按效果分解

F1=G·Sinθ 方向:沿斜面向下
F1
θ
F2 F2=G·Cosθ 方向:垂直于斜面向下
G
力分解的一般步骤:
1、根据力F的作用效果,画出两个分力的方向;和方向。
5、力分解的定解条件
(1)已知两分力的方向
Chap 2.6 decomposition of force
知识回顾:
1、力的合成: 由分力求合力 2、合成方法: 平行四边形定则
力可以合成,是否也可以分解呢?
一、力的分解法则
分力F1、F2
力的合成
合力F
力的分解
1、力的分解是力的合成的逆运算
注意:几个分力与原来那个力是等效的,它们可以互相代替, 并非同时并存!!!
V2
ΔV
3、矢量和标量
V1
矢量:有大小,又有方向,相加时遵循平行四边形定则
标量:有大小,没有方向,求和时按算术法则相加
例2 如图,物体受到与水平方向成30°角 的力F=100N作用,根据力的作用效 果对F进行分解,并求出两分力的大 小和方向。
F2
F F1=F·Cosθ= 5 0 3N
方向:水平向右
F1
F
F2 2、力的分解同样遵守平行四边行定则
把一个已知力F作为平行四边形的对角线,那么与力F 共点的平行四边形的两个邻边,就表示力F的两个分力.
3、若没有其它限制,同一个力可以分解为无数 对大小、方向不同的分力。
F6
F4
F2
F
F1
F3
F5
4、实际情况中,力的分解根据力的作用 效果进行
例1 如图,根据力的作用效果对物体所受到
30° F1 F2=F·Sinθ= 50N
力的合成与分解问题解析

力的合成与分解问题解析力的合成和分解是力学中常见的问题,它们是解决复杂力问题的重要工具。
本文将对力的合成和分解进行详细讨论,解析其原理和应用。
一、力的合成问题解析力的合成是指将多个力合成为一个等效力的过程。
当多个力作用于同一个物体时,我们可以将这些力合成为一个结果力,该结果力具有与合成前所有力相同的效果。
在合成力的过程中,首先需要确定各个力的大小、方向和作用点,然后按照力的几何相加法将这些力的矢量相加。
合成后的结果力的大小可以通过三角法、平行四边形法或三边法来求解,而合成力的方向则可以通过正切函数来计算。
举例来说,假设有两个力F1和F2,它们的大小分别为10牛顿和5牛顿,方向分别为30°和120°。
要求合成这两个力的结果力F,可以按照如下步骤进行:1. 将两个力F1和F2按照其方向画成矢量;2. 将F1按照其大小和方向延长,然后将F2的尾部与F1的头部相连;3. 从F1的尾部到F2的头部之间的线段即为合成力F的矢量表示;4. 使用三角法或平行四边形法求解F的大小和方向。
二、力的分解问题解析力的分解是指将一个力分解为多个互相垂直的力的过程。
通过将一个力分解为多个互相垂直的分力,可以更方便地研究力在不同方向上的作用效果。
在分解力的过程中,首先需要确定参考坐标系,并确定选择合适的坐标轴。
然后,利用三角函数(正弦、余弦)或平行四边形法分解力。
以一个力F为例,要求将其分解为水平方向和竖直方向上的分力F1和F2。
可以按照如下步骤进行:1. 根据坐标系的设置,将力F在参考坐标系中画出;2. 根据力F与水平方向和竖直方向的夹角,利用三角函数求解水平方向和竖直方向的分力F1和F2;3. 得到分力的大小和方向。
三、力的合成与分解的应用力的合成与分解在实际问题中有着广泛的应用。
以下是一些常见的应用场景:1. 斜面上的物体受力分析:当物体位于斜面上时,重力可以分解为沿斜面和垂直斜面方向的分力,从而方便计算物体在斜面上的运动情况。
力的分解

大小相同,方向不同。
F1 F2
F2 F F
F1
1.如下图所示,大小分别为F1、F2、F3的 三个力恰好围成封闭的直角三角形(顶角 为直角)。下列四个图中,这三个力的合 力最大的是( C )
2.杂技表演的安全网如图甲所示,网绳的结构为正方 形格子,O、a、b、c、d等为网绳的结点,安全网水平 张紧后,质量为m的运动员从高处落下,恰好落在O点 上.该处下凹至最低点时,网绳dOe、bOg均为120°张 角,如图乙所示,此时O点受到向下的冲击力大小为2F, 则这时O点周围每根网绳承受的张力大小为( A)
2 2 F F F x y
F =1N
y
Fy= 3 / 2 N
( 3 / 2) 2 (1 / 2) 2 1 N
Fx = -1/2 N
3/2 tan 3 Fx 1/ 2
Fy
x
600
课堂小结:
1、什么是力的分解? 2、如何进行力的分解? (按力所产生的实际作用效果进行分解) 3、什么是正交分解?怎样进行正交分解? (把一个已知力沿着两个互相垂直的方向进行分解)
A.F
B.
C.2F+mg
D.
例3.如图所示,绳子MO与NO所能承受的最大拉力相同,
长度MO>NO,则在不断增加重物G的重力过程中(绳 OG不会被拉断) ( A ) A、ON先被拉断
B、OM先被拉断
C、OM和ON同时被拉断 D、无法确定哪条绳子先被拉断
M
N N
O G
G1 G
G2
例12. 质量为m的木箱在拉力F的作用下,在水平地
F2
G
F2 Gcos
使物体紧压挡板 重力产生的效果 使物体紧压斜面
力的分解计算方法举例
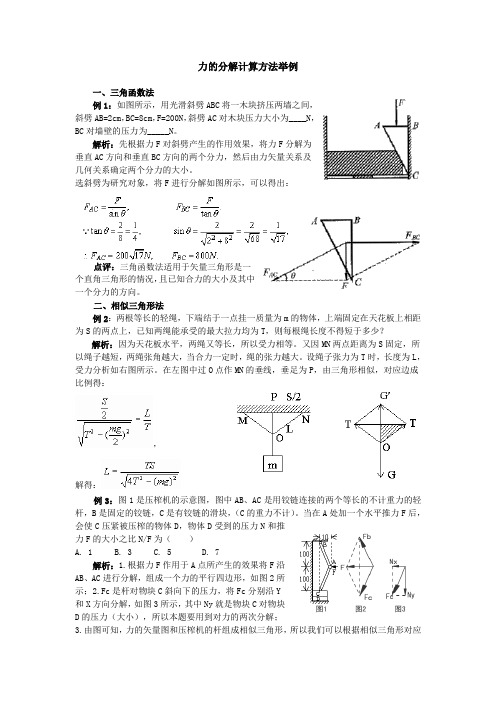
力的分解计算方法举例一、三角函数法例1:如图所示,用光滑斜劈ABC 将一木块挤压两墙之间,斜劈AB=2cm ,BC=8cm ,F=200N ,斜劈AC 对木块压力大小为____N ,BC 对墙壁的压力为_____N 。
解析:先根据力F 对斜劈产生的作用效果,将力F 分解为垂直AC 方向和垂直BC 方向的两个分力,然后由力矢量关系及几何关系确定两个分力的大小。
选斜劈为研究对象,将F 进行分解如图所示,可以得出:点评:三角函数法适用于矢量三角形是一个直角三角形的情况,且已知合力的大小及其中一个分力的方向。
二、相似三角形法例2:两根等长的轻绳,下端结于一点挂一质量为m 的物体,上端固定在天花板上相距为S 的两点上,已知两绳能承受的最大拉力均为T ,则每根绳长度不得短于多少?解析:因为天花板水平,两绳又等长,所以受力相等。
又因MN 两点距离为S 固定,所以绳子越短,两绳张角越大,当合力一定时,绳的张力越大。
设绳子张力为T 时,长度为L ,受力分析如右图所示。
在左图中过O 点作MN 的垂线,垂足为P ,由三角形相似,对应边成比例得:,解得:例3:图1是压榨机的示意图,图中AB 、AC 是用铰链连接的两个等长的不计重力的轻杆,B 是固定的铰链,C 是有铰链的滑块,(C 的重力不计)。
当在A 处加一个水平推力F 后,会使C 压紧被压榨的物体D ,物体D 受到的压力N 和推力F 的大小之比N/F 为( )A. 1B. 3C. 5D. 7解析:1.根据力F 作用于A 点所产生的效果将F 沿AB 、AC 进行分解,组成一个力的平行四边形,如图2所示;2.Fc 是杆对物块C 斜向下的压力,将Fc 分别沿Y和X 方向分解,如图3所示,其中Ny 就是物块C 对物块D 的压力(大小),所以本题要用到对力的两次分解;3.由图可知,力的矢量图和压榨机的杆组成相似三角形,所以我们可以根据相似三角形对应边的比相等,可以求出最后结果Ny来。
力的合成和分解的三角解法

力的合成和分解的三角解法力的合成和分解是物理学中重要的概念,能够帮助我们更好地理解和计算复杂的力学问题。
在本文中,我们将介绍力的合成和分解的三角解法,以及一些实际应用。
一、力的合成力的合成是指将多个力合成为一个力的过程。
当多个力作用在同一物体上时,它们的合力可以通过三角形法则进行计算。
三角形法则是指将力按照大小和方向绘制在一个平面上,然后通过三角形的几何计算得到合力的大小和方向。
具体方法如下:1. 将力按照大小和方向绘制在一个平面上,选择一个力的起点作为几何图形的起点。
2. 从第一个力的终点绘制一条与第二个力相接的线段,该线段表示两个力的合力。
3. 从几何图形的起点到合力的终点,这条线段就是合力的大小和方向。
举个例子来说,假设有两个力F1和F2作用在一个物体上,F1的大小为10 N,方向为东,F2的大小为5 N,方向为北。
我们可以使用三角形法则计算出合力的大小和方向如下:- 首先,在一个平面上绘制F1的向量,起点选择为原点。
- 然后,从F1的终点绘制一条与F2相接的线段。
- 最后,连接起点和合力的终点,这条线段表示合力,根据三角形法则计算合力的大小为√(10^2+5^2)≈11.2 N,方向为东北。
二、力的分解力的分解是指将一个力分解为多个分力的过程。
当一个力作用在物体上时,它可以被分解为与坐标轴垂直的两个力。
三角解法是一种常用的力的分解方法,可以将一个力按照角度分解为与x轴平行和与y轴平行的两个力。
具体步骤如下:1. 假设有一个力F作用在物体上,角度为θ。
我们需要将这个力分解为与x轴平行和与y轴平行的两个分力Fx和Fy。
2. 分解力的大小可以通过三角函数计算。
Fx=F*cosθ,Fy=F*sinθ。
3. 分解力的方向与x轴和y轴的方向一致。
举个例子来说,假设有一力F的大小为20 N,角度为30°。
我们可以使用三角解法将这个力分解为与x轴平行和与y轴平行的分力Fx和Fy如下:- 首先,计算Fx=F*cos30°=20*cos30°≈17.3 N,方向为x轴正向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
力的分解计算方法举例
一、三角函数法
例1:如图所示,用光滑斜劈ABC 将一木块挤压两墙之间,
斜劈AB=2cm ,BC=8cm ,F=200N ,斜劈AC 对木块压力大小为____N ,
BC 对墙壁的压力为_____N 。
解析:先根据力F 对斜劈产生的作用效果,将力F 分解为
垂直AC 方向和垂直BC 方向的两个分力,然后由力矢量关系及
几何关系确定两个分力的大小。
选斜劈为研究对象,将F 进行分解如图所示,可以得出:
点评:三角函数法适用于矢量三角形是一
个直角三角形的情况,且已知合力的大小及其中
一个分力的方向。
二、相似三角形法
例2:两根等长的轻绳,下端结于一点挂一质量为m 的物体,上端固定在天花板上相距为S 的两点上,已知两绳能承受的最大拉力均为T ,则每根绳长度不得短于多少?
解析:因为天花板水平,两绳又等长,所以受力相等。
又因MN 两点距离为S 固定,所以绳子越短,两绳张角越大,当合力一定时,绳的张力越大。
设绳子张力为T 时,长度为L ,受力分析如右图所示。
在左图中过O 点作MN 的垂线,垂足为P ,由三角形相似,对应边成比例得:
,
解得:
例3:图1是压榨机的示意图,图中AB 、AC 是用铰链连接的两个等长的不计重力的轻杆,B 是固定的铰链,C 是有铰链的滑块,(C 的重力不计)。
当在A 处加一个水平推力F 后,会使C 压紧被压榨的物体D ,物体D 受到的压力N 和推
力F 的大小之比N/F 为( )
A. 1
B. 3
C. 5
D. 7
解析:1.根据力F 作用于A 点所产生的效果将F 沿
AB 、AC 进行分解,组成一个力的平行四边形,如图2所
示;2.Fc 是杆对物块C 斜向下的压力,将Fc 分别沿Y
和X 方向分解,如图3所示,其中Ny 就是物块C 对物块
D 的压力(大小),所以本题要用到对力的两次分解;
3.由图可知,力的矢量图和压榨机的杆组成相似三角形,
所以我们可以根据相似三角形对应
边的比相等,可以求出最后结果Ny来。
先根据图示尺寸求出AC=,然后由图1和图2中的相似三角形得:F/2:Fc=10:,
由图1和图3里的相似三角形得:Fc:Ny=:100,
联立可解得:Ny/F=5,答案选C。
点评:相似三角形适用于已知几何三角形的三个边长和合力。
三、正弦定理法
例4:重为G的物体,由两根细绳悬挂。
若绳AO和BO跟竖直方向的夹角分别为α、β。
试求两绳的张力。
解析:通常用正交分解法,但运算较为复杂。
我们知道物体在重力G,绳的张力T A 和T B三个共点力作用下平衡,故G、T、T可组成一封闭的力三角形。
由正弦理可得:
,∴T=。
例5:如图,绳AB能承受的最大张力为1000N,轻杆BC能承受最大压力2000N,绳BD
能承受任何负载,求此装置能悬挂的最大重力G。
解析:用力合成法将三个力转化在同一个三角形中,虽然几何三角形各边长度未知,但力的三角形中各角角度是已知的,故该题可用正弦定理求解。
选B点为研究对象,受力分析如图所示,绳上拉力F T 和杆对B点的支持力F N的合力与重物的重力G是平衡力,B点受三力作用而平衡,绳BD拉力等于G,BC杆支持力F N,绳AB拉力F T,三力构成封闭三角形,从图中可得:
即当F T达最大值时,F N尚未达最大值,因此取F N=1000N,计算悬
挂重物G的最大值。
因此。
点评:正弦定理适用于已知力的矢量三角形的三个角和合
力。
四、正交分解法
例6:如图所示,质量为m的物体放在倾角为θ的斜面上,
在水平恒定的推力F作用下,物体沿斜面匀速向上运动,则物
体与斜面的动摩擦因数是多大?
解析:物体m受四个力作用:重力mg、推力F、支持力F N和摩擦力F f。
由于物体受力较多,我们采用正交分解法解该题。
建立如图所示直角坐标系,把重力mg和推力F分别分解到x、y轴上。
得:
,即Array ,即
所以。
点评:正交分解法法适用于已知合力和两个分力的方向。
