(参考)数学实验教程勘误表
教材勘误表

勘误表1.P.13,倒第9行,将“左”字改这“右”字。
倒第10行,将“右”字改为“左”字,将“左字改为“右”字。
2.P.14,表1-1在Form1与Label1之间加横线。
3.P.15,第五行改为“Text2.Text=”””。
4.P.24,倒第14行,将“WindowsState”改为“WindowState”。
5.P.26,倒第10行,名尾加冒号。
6.P.36,倒第9行,句中一对全角双引号改成半角双引号。
7.P.41,将“图”字改为“表”字,在“所示”后加“,”。
8.P.43,第9行,将“WindowsState”改为“WindowState”。
9.P.55,倒第20行,改为“Area=3.14*Radius*Radius”10.P.56,倒第7行,将“-298.66”改为“-298.67”。
11.P.57,第1行,将(B)”女”后的小于号改成大于号。
12.P.68,倒第3行,除去语句中间的“Tab(40);”。
13.P.69,倒第13行,将句中的“10”改成“11”。
倒12行“全角字符”前加“为”字。
14.P.73,第4行,改成“Area=3.14*Radius_out*Radius_out-3.14* Radius_in* Radius_in”15.P.75,删除倒第11行至倒第16行。
16.P.76,第18行,第19行中的“;”改为半角的“;”。
17.P.78,倒第6行,答案改为“10+20=030.00”18.P.86,第19行,在“多个”和“变量”之间加“分离的”。
第27行删除“,同时Case X*Y>0也是错误的”。
19.P91,第4行,改成“If x+y>z And x+z>y And y+z>x Then”20.P.96,倒第10行。
改为“Sub Command2_Click()”21.P.100,第3行的句尾加冒号。
22.P.106,第12行的句尾加冒号。
《高数教学课件》第二章勘误表

例如,一张用于解释函数单调性的图片,被放置在了讲解极 限的章节中,导致学生在理解时产生了困惑。
图片内容错误
总结词
部分图片的内容存在错误,与所讲解的知识 点不符。
详细描述
例如,一张用于展示函数极值的图片,其内 容实际上是一个函数的拐点,并非极值点, 这可能会误导学生对于极值概念的理解。
பைடு நூலகம்
Part
答案不完整是指提供的答案没有涵盖所有可能的解法或 步骤,可能只提供了部分解答或遗漏了一些关键信息。
详细描述
在《高数教学课件》第二章中,部分习题的答案不完整 。例如,第4题只提供了部分解题步骤,没有给出完整的 解答过程;第8题只给出了一个解,但实际上该题目有两 个解。这些不完整的答案可能会让学生感到困惑,因此 需要补充完整。
Part
05
总结与建议
总结勘误情况
公式错误
在课件中,存在一些公式表达错 误,如积分公式中的符号使用不 当。
文字错误
在课件的文字描述中,存在一些 错别字或语法错误。
概念混淆
部分内容中概念表述不清晰,容 易造成学生理解混淆。
图像问题
课件中的一些图像和图表存在比 例失调或标注不清的问题。
对教材编写的建议
04
习题答案勘误
答案错误
总结词
答案错误是指提供的答案与标准答案不一致,可能是由于计算错误、理解偏差或印刷错 误等原因造成的。
详细描述
在《高数教学课件》第二章中,部分习题的答案存在错误。例如,第2题的答案应该是1/2,但课件中提供的答案是1/2;第5题的答案应该是x=3或x=-1,但课件中提供的答
案是x=1或x=-1。这些错误可能会误导学生,因此需要更正。
生,影响教学质量。因此,对教学课件进行勘误是十分必要的。
高考数学你真的掌握了吗?勘误表(1)

第 114 页【4.14】解析部分的倒数第二行的 f ( )
f (1) 1改为h(1) 1 。 【北京吴玉会】
第 87 页, 【例 3.8】 【解析】第三行 3-6 修改为 3-2,第四行 3-7 修改为 3-3。 【湖南怀化陆俊】 第 27 页, 【例 2.9】已知 已知 f ( x) x 1
a2 a ,对应图像 Y 值为 。 【北京吴玉会】 4 2
第 165 页【例 4.11 变式 2】中所有 f(x)改为 g(x)。 【北京吴玉会】 第 113 页, 【4.12】 【解析】第一行的 "
ln x ln x 1 2a"改为“ 2a" 。 【北京吴玉会】 x x 1 3 5 1 5 改为h( ) ,倒数第三行 27 3 27
第 235 页, 【例 5.9~例 5.11 变式 2】第 2 行
g (3) 0 g (3) 0 改为 ,第 3 行 g (2) 0 g (2) 0
1 5 1 5 m 2 x ln x m 2 x ln x 3x 3 3x 3 改为 。第 5 行 m 2 x 1 2 ln x m 2 x 1 2 ln x 2x 2x 5 5 m m m h ( x ) h (1) m h( x) min h(1) 3 3 3 3 min m 改为 m .第 2 2 m p( x) min p(1) m 3 m p( x)min p(1) m 3 2 2
5 行 (, ) 改为 (, ] 。 第 45 页, 【变式 1】 | f ( x1 ) f ( x2 ) 改成 f ( x1 ) f ( x2 ) 。 【江西九江洪秀成】 第 134 页, 【变式 1】 “设定义域为 R 的”改为“已知” 。 【江西九江洪秀成】 第 181 页, 【例 4.34~例 4.38 变式 7】 (, 2) 改为 (, 2] 。 【江西九江洪秀成】 第 156 页, 【变式 3】第二行“ y h(k ) “改成” y h( x) “。 【江西九江洪秀成】 第 201 页, 【例 5.17】选项 D“ [ 2, 1] [ 2, ] “改为” [ 2, 1] [ 2, ) “。 【江 西九江洪秀成】 第 125 页, 【例 4.23】第一行少了等号。 第 170 页, 【例 4.16 变式 5】第五行“分别对应 4 个 a 的值。故选 C”改为“分别对应 4 个 a 的 值,又因为 a 0 ,所以 x 1 舍去,故选 B” 【江西九江洪秀成】
数学分析中的典型问题与方法 《勘误表》共5页word资料

数学分析中的典型问题与方法《勘误表》(1) 原书 第4页的例1.1.5有错, 2011年6月21日, 作者将此题更改写为: 例1.1.5 试证: 设 y = f(x) 是R 上的有界实函数. 且有 2f(x)2h)f(x h)f(x ++=+ (∀x R ∈). (1)(其中h 为某一正数). 则h 必是函数f 的周期. 证 根据式 (1), 有f (x + 2h ) – f (x + h ) = f (x + h ) – f (x ) (∀x R ∈). 令 F (x) = f (x + h ) – f (x ) . 上式即为 F (x + h ) = F (x ) (∀x R ∈).于是 f (x + n h ) = [ f (x + n h ) – f (x + (n - 1)h )] + [ f (x + (n – 1)h ) – f (x + (n - 2)h ) +…+ [f (x + h ) - f (x )] + f (x ) =∑=+1-n k ))(F 0kh x + f (x ) = n F (x ) + f (x ).若 F (x )≠0 , 当n +∞→时, nF (x ) 趋向无穷大, 与函数f 有界矛盾. 所以F (x )= 0. 即 f (x + h ) = f (x ). (∀x R ∈). 故h 是函数f 的周期.注意1. 对于任意给定的实数h , 若h 是函数f 的周期, 则条件 (1) 显然成立. 因此本例说明: 存在实数h 满足条件 (1), 是有界函数f 为周期函数的充分必要条件. 2. “有界”条件不可忽略, 例如f (x ) = x , 不是周期函数, 但是式 (1) 总成立.特别要道歉的是, 更正中又出现了重大遗漏将2f(x)2h)f(x h)f(x ++=+写成了 2f(x)2h)f(x f(x)++=, 虽然从证明里可以看出, 但是题目写错, 是有罪的。
线性代数与解析几何勘误表1-7章

《线性代数与解析几何》勘误表第1章:行列式p.13,例题4.1:解的第二个等号后,应加一个负号。
p.15,第三行(等号后):去掉;p.17,第7-8 行: (t=1,2,…,j-1,j+1,…,n)p.19倒数第4-5行:假设对于n-1阶范德蒙行列式V_{n-1}结论成立,p. 20,第 2 行:D_{n-1}改为V_{n-1}p.20,第6行,定理5.2中:去掉“若”字p.21,倒数第3行:…展开代入而得,p.2 4倒数第1行:(-1)的指数应为“ 1+2 - k+1+2 ----- k ” 习题1:第1题(2)答案有误:应为sin2x-cosx A2.第6题(3)答案有误:(3)n(3n-1)/2,当n=4k或者n=4k+3时为偶数,当n=4k+1 或4k+2时为奇数.第10 题(4)(5)答案有误:(4)(-1)A{(n-2)(n-1)/2}; (5)(-1)A{ n-1}a_n第11题(6)答案有误:….,当a\neq 0时,D=(-1)A{n( n-1)/2}aA{n-2}国八2-(n-1)xA2]y1 +z1z1 +x1禺+ y1p.26,第12题(2):改为:y2 +z2z2 +x2X2 + y丫3 +Z3 Z3 +X3 X3 + y―-.(n -1)(n+2)…八n A.(3): •••= [a + —1) J2“-n(4):…二送a i b n_Li =ep.27,第14题(4):(此题较难,可以去掉!)答案有误,应为:D n = [(x 、x2-4yz)n 1_(x _ I x2_4yz)n勺]/2n 1x2-4yz,当 x2= 4yz ;D n =(n1)(|)n,当 x2=4yz。
第15题答案有误:为60(11- .2)p. 27,第16题:去掉条件“若x_1+x_2+x_3+x_4=1,则”第二章:矩阵p.32,第7 行: 称其为n阶对角矩阵,…..p.35,第5-6 b_21和b_12互换位置(两处)p.36,第7行:去掉“设A , B, C分别为….矩阵,”在第10行后增加:当然, 这里假定了矩阵运算是有意义的.p.39,第 4 行: 就得到一个2*2的分块矩阵。
勘误表

勘误表“参考文献”放在书的最后一页。
详细修改请看《校正本》的前言,目录及各页。
第一章1. 第10页,最后一行:122424B m C P ==应该改为:122B m C ==2. 第19页第2题:C={20世纪90年代出版的书} 改为:C={21世纪出版的书}3. 第238页第2题的答案应该改为:(1)“21世纪以前出版的英文版数学书”;(2)在“馆中所有数学书都是21世纪出版的英文书”的条件下,等式成立;(3)“21世纪以前出版的书都是英文版的”;(4)“馆中非数学书都是英文版的,并且所有的英文版的书都不是数学书”4. 第20页,第5题最后一行:“恰好为1,2,3,4的概率”应该改为“恰好为1,2,3,4,5的概率” ,并把最后一行紧接到上一行的后面。
5. 第238页第5题的答案(3)“15”应该改为“25!”6. 第20页,第14题:“求()()P B A B P B ⋅ ”应该改为:“求()P B A B ”7. 第238页第15题(1)的答案“22222rrnn rnC C ”应该改为:“22222rrnrnC C ”8. 第239页第36题的答案“0.632”错误,应该改为()1111111234!!!!n n --+-++-9. 第22页,第38题第二行:“输出AAAA ,BBBB ,CCCC 的概率分别为”应该改为:“输入AAAA ,BBBB ,CCCC 的概率分别为”10. 第239页第39题的答案(2)()()222094006..N n C β-=应该改为:()()222094006..n n C β-=11.第239页26题的答案,应该是0.36,而非0.35第二章1、P26定义2.2.3上面一行P (X=k )改为P {X=k }2、 改为3、 P29例6(1) -12=ee λλ-⎛⎫ ⎪⎝⎭()1(1)n p kn k pkqkq+-+-=+()()p q kqkp n kqpk n -=-++=-+=111)1(改为2=ee 1-λλ-⎛⎫ ⎪⎝⎭(2) 中删去D={有两个乙类细菌};另外P(C) -12=ee λλ-⎛⎫ ⎪⎝⎭改为P(C)2=e e 1-λλ-⎛⎫ ⎪⎝⎭()()()()()()()()()()222P A P D A P C D P D P A D P D C P C P C P C P C ====2211221e2!2=ee 8e λλλλλλ----⎛⎫⎪⎝⎭=⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭改为()()()()222P A P C A P A C P C =222221e2!2=ee 18e 1λλλλλλ--⎛⎫⎪⎝⎭=⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭4、 P30定义2.2.5 ……..试验次数,称X 服从参数p 的几何分布。
2016复习全书(数三)勘误-修改

复习全书1.P21【例29】评注的第二行 原式为:ln ln 1()x xx x x e -→+∞改正为:ln ln 1()xx xe x x -→+∞2、P51第四行有错原式为:因此,()y x 的极大值为()10y -=,()y x 的极小值为()11y = 改正为:因此,()y x 的极小值为()10y -=,()y x 的极大值为()11y =3、P53 【例36】的答案写错了,应该是C4.P75【例8】的评注里面原式为:2111121xdx d x x +=--改正为:2111ln 121xdx d x x +=--5.P90【例39】解答的第二行原式为:()226csc 1t dx ππ-⎰改正为:()226csc 1t dt ππ-⎰6.P129上数第四行原式为:在4,03⎛⎫ ⎪⎝⎭点,=160∆<改正为:在4,03⎛⎫⎪⎝⎭点,=160∆>【例6】的评注原为:此函数在=0x处不可导。
改为:此函数在=1x处不可导。
8.P137【例47】的图形错误,应该没有下半部分阴影。
9.P258【例14】倒数第三行原式为:00000 00 00ab ab ab a ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦改正为:0000 00 00a bb ab ab a ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦10.P277【例10】解的第二行中的ξ应该为α11.P278【例12】解的第二行和第三行原式为:()()32322525TTTB f A A A E A A E B==-+=-+=改正为:()()332525TTTB f A A A E A A E B==-+=-+=12.P283倒数第三行原式为:110223000Bb⎡⎤-⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦改正为:25505301Bb-⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦分阶习题同步训练第10题解答原式为:()2121-1sin 1n n n n a a n λ++⎛⎫≤ ⎪+⎝⎭改正为:()-1sin11n n n n n λλλ⎛⎫≤⋅≤ ⎪++⎝⎭ 2.P159第5题解答的第二行 原式为:1523111a a a a a++=++---123βααα 改正为:1523111a a a a a ++=-++---123βααα 3.P16411题解答的最后一行 原式为:1011001001001011001003+123-23-11043043-3-63+63⎡⎤⋅⎢⎥⋅⎢⎥⎢⎥⋅⎣⎦ 改正为:1011001001001011001003+123-23-11043043-3-63+63+3⎡⎤⋅⎢⎥⋅⎢⎥⎢⎥⋅⎣⎦4.P168上面的第一行原式为:112321233344,,,,x z z z x z z z x z x z =+-⎧⎪=--⎪⎨=⎪⎪=⎩改正为:112321243344,,,,x z z z x z z z x z x z =+-⎧⎪=--⎪⎨=⎪⎪=⎩。
《自然科学中确定性问题的应用数学》勘误表-中科大版
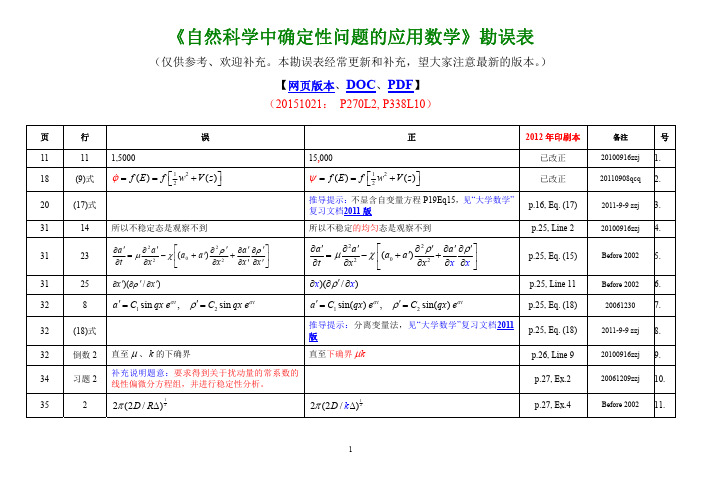
13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28.
n(t T ) E e sin E
T 是经过近日点的时间(the time of perihelion passage) n 是轨道的圆频率(注:圆频率定义为 2秒内振动的 次数,又叫角频率) 而 E(称为偏近点角, the eccentric anomaly) 真近点角(the true anomaly) 平近点角(the mean anomaly)
12.
46 51 51 51 51 51 51 52 54 56 56 57 57 57 60 60
1 11 12 12 13 14 15 3
倒数 1 倒数 2 倒数 1
1 d 2 d r 0 r dr dt
n (t T ) E e sin E T 是近日点的进动周期 n 是轨道的频率 而 E(叫做偏角心反常) 真实的反常 平均反常
《自然科学中确定性问题的应用数学》勘误表
(仅供参考、欢迎补充。本勘误表经常更新和补充,望大家注意最新的版本。 ) 【网页版本、DOC、PDF】 (20151021: P270L2, P338L10)
页 11 18 20 31 31 行 11 (9)式 (17)式 14 23 所以不稳定态是观察不到 1,5000
cos 0 t
d 2 (2) 02 (2) 2 d 02 21 h 2 cos cos 30 0 2 0 24 8
p.48, Line 16
Before 2002
31.
61
21
cos 0
p.48, Line 17
Before 2002 Before 2002 SC05004017 20061019zzj Before 2002
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(mod m)
B
*1250
175 180
J
加上一横线
!= abc+def>400
下列二行
144
4
y x2
y x2 (x 0)
209
3
Windows95/98
209
14
双击
210
6
圆括号(和)
210
8
下划线“-”
210
-5
exp(1), E
210 10,12,25
以及其它
‘
页等多处
211
75
-8
两个:GoldRatio LCD Sin(x)
…,200},{901,902,
x3 x 1
几个曲面
GoldenRatio
LCM Sin[x] …200}, …, {901,902,
x2 x 1
几个曲面(线)
89
9
x
3
94
-2
x1, x2 , , xm
xm , xm1, , x1
95
-4
bk ak
-8
fyuan 两个:GoldRatio
LCD Sin(x) …,200},{901,902,
x3 x 1
几个曲面
fywan
GoldenRatio
LCM Sin[x] …200}, …, {901,902,
x2 x 1
几个曲面(线)
9
5 -9 -2 -4
-6
5 7, 18 16 -12
-6 7
18 7、8 间
缺少一横线
加上一横线
119
11
<=
!=
120
-3
abc+gef>400
abc+def>400
130
3
下列三行
下列二行
144
4
y x2
y x2 (x 0)
209
3
209
14
210
6
210
8
210
-5
210 10,12,25
以及其它
页等多处
Windows95/98 双击
圆括号(和) 下划线“-”
exp(1), E
《数学实验教程》勘误表
(版本:2006 年 8 月第四次印刷)
页数 行数
144
4
错误内容
y x2
修正内容
y x2 (x 0)
注:行号为正数表示从该页起顺着数;行号为负数则表示由该页起倒着数。
《数学实验教程》勘误表
(版本:2005 年 9 月第三次印刷)
页数 行数
错误内容
修正内容
14
-4
18
-15
subs(x=2, S)
239
-16
delcol(A,i..j)
delcols(A,i..j)
注:行号为正数表示从该页起顺着数;行号为负数则表示由该页起倒着数。
《数学实验教程》勘误表
(版本:2004 年 4 月第二次印刷)
页数 行数
错误内容
修正内容
14
-4
18
-15
34
-11
68
-11
68 -3 分母中
!= abc+def>400
下列二行
List[List[Rule[y ]]], C[1]]]]]]
dy
dx
-1
y[_]
y[t_]
-2
x[_]
x[t_]
3
yk];
-7
得到图形 F1
11
NN 值
yk,f,y,x]; 得到一条折线 F1
去掉
4
y x2
y x2 (x 0)
3
Windows95/98
Windows95/98/XP/NT 等
97
102 103 105 109 110 112
113 115 119 120 130 132 132
135
137 137 138 146 158 144
209 209 210
(注:2004 年 4 月第二次印刷时,已改了这些勘误)
行数
错误内容
修正内容
7 -4 -15 -11 -11 -3 分母中
34
-11
68
-11
68 -3 分母中
75
-8
两个:GoldRatio LCD Sin(x)
…,200},{901,902,
x3 x 1
几个曲面
GoldenRatio
LCM Sin[x] …200}, …, {901,902,
x2 x 1
几个曲面(线)
89
9
94
-2
95
-4
97
-6
110
-6
112
16-18
关于 signum 的定义
212
17 , 如果其中含有自由变
量, 则表示成 x =x 的
形式
218
9
无法求积时
218
-11
解微分组
Windows95/98/XP/NT 等 单击
圆括号“(”和“)” 下划线“_” exp(1)
`
去掉 去掉
无法求积分时 解微分方程组
219
-9
sub(x=2, S)
|
f
(xk ) ||
f
( ak
bk 2
) |
97
-6
x* (x0 )
x* (x*)
105
16
i 从 l 到 m,j 从 l 到 n
i 从 1 到 m,j 从 1 到 n
110
-6
(modm)
(mod m)
112
7
15 175
B
*
20
180
15 175
B
*
20
180
113
18
G
J
115 7、8 间
List[List[y ]], C[1]]]]]]
y'(x)
3
, num, x] 顶头
xm , xm1, , x1
|
f
(xk ) ||
f
( ak
bk 2
) |
x* (x*)
实验 2 去掉 i 从 1 到 m,j 从 1 到 n 明文字母
(mod m)
B
*1250
175 180
J
加上一横线
7
113
18
115 7、8 间
119
11
120
-3
130
3
x x1, x2 , , xm bk ak
x* (x0 )
(modm)
B
* 1250
175 180
G 缺少一横线
<=
abc+gef>400 下列三行
3
xm , xm1, , x1
|
f
(xk ) ||
f
( ak
bk 2
) |
x* (x*)
subs(x=2, S)
239
-16
delcol(A,i..j)
delcols(A,i..j)
注:行号为正数表示从该页起顺着数;行号为负数则表示由该页起倒着数。
《数学实验教程》勘误表
(版本:2003 年 10 月第一次印刷)
页数
前言 iv 14 18 34 68 68 75 89
93 93 94
95
14
双击
单击
6
圆括号(和)
圆括号“(”和“)”
210
8
下划线“-”
11 -3 3 7 7
-11
x
, num] Clear[n, …
x1, x2 , , xm bk ak
x* (x0 )
实验二
dg[x_]:=x^2;
i 从 l 到 m,j 从 l 到 n 明文 母
(modm)
B
* 1250
175 180
G 缺少一横线
<= abc+gef>400
下列三行
‘
Windows95/98/XP/NT 等 单击
圆括号“(”和“)” 下划线“_” exp(1)
`
211
16-18
关于 signum 的定义
212
17 , 如果其中含有自由变
量, 则表示成 x =x 的
形式
218
9
无法求积时
218
-11
解微分组
去掉 去掉
无法求积分时 解微分方程组
219
-9
sub(x=2, S)
