(完整版)全等三角形题型总结材料
专题03 全等三角形的六种模型全梳理(解析版)-2024年常考压轴题攻略(8年级上册人教版)

专题03全等三角形的六种模型全梳理几何探究类问题一直属于考试压轴题范围,在三角形这一章,压轴题主要考查是证明三角形各种模型,或证明线段数量关系等,接来下我们针对其做出详细分析与梳理。
类型一、倍长中线模型目的:①构造出一组全等三角形;②构造出一组平行线。
将分散的条件集中到一个三角形中。
如图1,ABC 中,若86AB AC ==,,求BC 边上的中线小明在组内经过合作交流,得到了如下的解决方法:如图连接BE .请根据小明的方法思考:(1)如图2,由已知和作图能得到ADC EDB ≌△△A .SSS B .SAS C .AAS D .ASA(2)如图2,AD 长的取值范围是.(2)根据全等三角形的性质得到6AC BE ==,由三角形三边关系得到AB BE AE AB BE -<<+,即可求出17AD <<;(3)延长AD 到点M ,使AD DM =,连接BM ,证明ADC MDB △△≌,得到BM AC CAD M =∠=∠,,由AE EF =得到CAD AFE ∠=∠,进而推出BF BM =,即可证明AC BF =.【详解】解:(1)如图2,延长AD 到点E ,使DE AD =,连接BE .∵AD 为BC 的中线,∴BD CD =,又∵AD DE ADC BDE =∠=∠,,∴()SAS ADC EDB ≌△△,故答案为:B ;(2)解:∵ADC EDB ≌△△,∴6AC BE ==,在ABE 中,AB BE AE AB BE -<<+,∴86286AD -<<+,∴17AD <<,故答案为:C ;(3)证明:延长AD 到点M ,使AD DM =,连接BM ,∵AD 是ABC 中线,∴CD BD =,∵在ADC △和MDB △中,DC DB ADC MDB AD HD =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ADC MDB ≌△△,∴BM AC CAD M =∠=∠,,∵AE EF =,(1)如图1,求证:12BF AD =;(2)将DCE △绕C 点旋转到如图2所示的位置,连接,AE BD ,过C 点作CM ⊥①探究AE 和BD 的关系,并说明理由;②连接FC ,求证:F ,C ,M 三点共线.【答案】(1)见解析(2)①,AE BD AE BD =⊥,理由见解析②见解析【分析】(1)证明≌ACD BCE V V ,得到AD BE =,再根据点F 为BE 中点,即可得证;则:AGB CBD BHG ∠=∠+∠=∠∵CBD EAC ∠=∠,∴90BHG ACB ∠=∠=︒,∴AE BD ⊥,综上:,AE BD AE BD =⊥;②延长CF 至点P ,使PF CF =∵F 为BE 中点,∴BF FE =,∴()SAS BFP EFC ≌,∴,BP CE BPF ECF =∠=∠,∴CE BP ,∴180CBP BCE ∠+∠=︒,∵360180BCE ACD ACB DCE ∠+∠=︒-∠-∠=︒,∴CBP ACD ∠=∠,又,CE CD BP AC BC ===,∴()SAS PBC DCA ≌,∴BCP CAD ∠=∠,延长FC 交AD 于点N ,则:18090BCP ACN ACB ∠+∠=︒-∠=︒,∴90CAD ACN ∠+∠=︒,∴90ANC ∠=︒,∴CN AD ⊥,∵CM AD ⊥,∴点,M N 重合,即:F ,C ,M 三点共线.【点睛】本题考查全等三角形的判定和性质,等腰三角形判定和性质.熟练掌握手拉手全等模型,倍长中线法构造全等三角形,是解题的关键.【变式训练1】如图,ABC 中,BD DC AC ==,E 是DC 的中点,求证:2AB AE =.【答案】见解析【分析】利用中线加倍证DEF CEA △≌△(SAS ),可得DF AC BD ==,FDE C ∠=∠,由DC AC =,可得ADC CAD ∠=∠进而可证ADF ADB ∠=∠.,再证ADB ADF △≌△(SAS )即可.【详解】证明:延长AE 到F ,使EF AE =,连结DF ,∵E 是DC 中点,∴DE CE =,∴在DEF 和CEA 中,DE CE DEF CEA EF EA =⎧⎪∠=∠⎨⎪=⎩,∴DEF CEA △≌△(SAS ),∴DF AC BD ==,FDE C ∠=∠,∵DC AC =,∴ADC CAD ∠=∠,又∵ADB C CAD ∠=∠+∠,ADF FDE ADC ∠=∠+∠,∴ADF ADB ∠=∠,在ADB 和ADF △中,AD AD ADB ADF DB DF =⎧⎪∠=∠⎨⎪=⎩,∴ADB ADF △≌△(SAS ),∴2AB AF AE ==.【点睛】本题考查中线加倍构图,三角形全等判定与性质,等腰三角形性质,掌握中线加倍构图,三角形全等判定与性质,等腰三角形性质是解题关键.【变式训练2】(1)如图1,已知ABC 中,AD 是中线,求证:2AB AC AD +>;(2)如图2,在ABC 中,D ,E 是BC 的三等分点,求证:AB AC AD AE +>+;(3)如图3,在ABC 中,D ,E 在边BC 上,且BD CE =.求证:AB AC AD AE +>+.【答案】(1)见解析;(2)见解析;(3)见解析【分析】(1)利用“倍长中线”法,延长AD ,然后通过全等以及三角形的三边关系证明即可;(2)取DE 中点H ,连接AH 并延长至Q 点,使得AH =QH ,连接QE 和QC ,通过“倍长中线”思想全等证明,进而得到AB =CQ ,AD =EQ ,然后结合三角形的三边关系建立不等式证明即可得出结论;(3)同(2)处理方式一样,取DE 中点M ,连接AM 并延长至N 点,使得AM =NM ,连接NE ,CE ,结合“倍长中线”思想证明全等后,结合三角形的三边关系建立不等式证明即可得出结论.【详解】证:(1)如图所示,延长AD 至P 点,使得AD =PD ,连接CP ,∵AD 是△ABC 的中线,∴D 为BC 的中点,BD =CD ,在△ABD 与△PCD 中,BD CD ADB PDC AD PD =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△PCD (SAS ),∴AB =CP ,在△APC 中,由三边关系可得AC +PC >AP ,∴2AB AC AD +>;(2)如图所示,取DE 中点H ,连接AH 并延长至Q 点,使得AH =QH ,连接QE 和QC ,∵H 为DE 中点,D 、E 为BC 三等分点,∴DH =EH ,BD =DE =CE ,∴DH =CH ,在△ABH 和△QCH 中,BH CH BHA CHQ AH QH =⎧⎪∠=∠⎨⎪=⎩,∴△ABH ≌△QCH (SAS ),同理可得:△ADH ≌△QEH ,∴AB =CQ ,AD =EQ ,此时,延长AE ,交CQ 于K 点,∵AC +CQ =AC +CK +QK ,AC +CK >AK ,∴AC +CQ >AK +QK ,又∵AK +QK =AE +EK +QK ,EK +QK >QE ,∴AK +QK >AE +QE ,∴AC +CQ >AK +QK >AE +QE ,∵AB =CQ ,AD =EQ ,∴AB AC AD AE +>+;(3)如图所示,取DE 中点M ,连接AM 并延长至N 点,使得AM =NM ,连接NE ,CE ,∵M 为DE 中点,∴DM =EM ,∵BD =CE ,∴BM =CM ,在△ABM 和△NCM 中,BM CM BMA CMN AM NM =⎧⎪∠=∠⎨⎪=⎩∴△ABM ≌△NCM (SAS ),同理可证△ADM ≌△NEM ,∴AB =NC ,AD =NE ,此时,延长AE ,交CN 于T 点,∵AC +CN =AC +CT +NT ,AC +CT >AT ,∴AC +CN >AT +NT ,又∵AT +NT =AE +ET +NT ,ET +NT >NE ,∴AT +NT >AE +NE ,∴AC +CN >AT +NT >AE +NE ,∵AB =NC ,AD =NE ,∴AB AC AD AE +>+.【点睛】本题考查全等三角形证明问题中辅助线的添加,掌握“倍长中线”的基本思想,以及熟练运用三角形的三边关系是解题关键.【答案】(1)1.5 6.5AE <<;(2)见解析;(3)BE DF EF +=,理由见解析【分析】(1)如图①:将ACD △绕着点D 逆时针旋转180 得到EBD △可得BDE ≅ 得出5BE AC ==,然后根据三角形的三边关系求出AE 的取值范围,进而求得AD 范围;(2)如图②:FDC △绕着点D 旋转180︒得到NDB 可得BND CFD ≅ ,得出BN∴1.5 6.5AD <<;故答案为1.5 6.5AD <<;(2)证明:如图②:FDC △绕着点D 旋转180︒得到NDB∴BND CFD ≅ (SAS ),∴BN CF =,DN DF=∵DE DF⊥∴EN EF =,在BNE 中,由三角形的三边关系得:BE BN EN +>,∴BE CF EF +>;(3)BE DF EF +=,理由如下:如图③,将DCF 绕着点C 按逆时针方向旋转100︒∴△DCF ≌△BCH ,∴100CH CF DCB FCH ∠∠=︒=,=∴HBC D DF BH∠∠==,∵180ABC D ∠+∠︒=∴180HBC ABC ∠+∠︒=,∴点A 、B 、H 三点共线∵100FCH ∠=︒,50FCE ∠=︒,∴50ECH ∠=︒∴FCE ECH ∠∠=,在HCE 和FCE △中,===CF CH ECF ECH CE CE ∠∠⎧⎪⎨⎪⎩,∴HCE FCE ≌ (SAS )∴EH EF =,∵BE BH EH DF BH+==,∴BE DF EF +=.【点睛】本题属于三角形综合题,主要考查对全等三角形的性质和判定、三角形的三边关系定理、旋转的性质等知识点,通过旋转得到构造全等三角形是解答本题的关键.类型二、截长补短模型截长补短法使用范围:线段和差的证明(往往需证2次全等)(1)求证:CD BC DE=+;(2)若75B∠=︒,求E∠的度数.【答案】(1)见解析(2)105︒【分析】(1)在CD上截取CF∵CA平分BCD∠,∴BCA FCA∠=∠.在BCAV和FCA△中,⎧⎪∠⎨⎪⎩,∠=︒BAC60【答案】(1)5.8;(2)4.3【分析】(1)由已知条件和辅助线的作法,证得△ACD≌△ECD,得到由于∠A=2∠B,推出∠DEC=2∠B,等量代换得到∠B=∠EDB形,得出AC =CE =3.6,DE =BE =2.2,相加可得BC 的长;(2)在BA 边上取点E ,使BE =BC =2,连接DE ,得到△DEB ≌△DBC (SAS ),在DA 边上取点F ,使DF =DB ,连接FE ,得到△BDE ≌△FDE ,即可推出结论.【详解】解:(1)如图2,在BC 边上取点E ,使EC =AC ,连接DE .在△ACD 与△ECD 中,AC CE ACD ECD CD CD =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△ECD (SAS ),∴AD =DE ,∠A =∠DEC ,∵∠A =2∠B ,∴∠DEC =2∠B ,∴∠B =∠EDB ,∴△BDE 是等腰三角形;∴BE =DE =AD =2.2,AC =EC =3.6,∴BC 的长为5.8;(2)∵△ABC 中,AB =AC ,∠A =20°,∴∠ABC =∠C =80°,∵BD 平分∠B ,∴∠1=∠2=40°,∠BDC =60°,在BA 边上取点E ,使BE =BC =2,连接DE ,在△DEB 和△DBC 中,12BE BC BD BD =⎧⎪∠=∠⎨⎪=⎩,∴△DEB ≌△DBC (SAS ),∴∠BED =∠C =80°,∴∠4=60°,∴∠3=60°,在DA 边上取点F ,使DF =DB ,连接FE ,同理可得△BDE ≌△FDE ,∴∠5=∠1=40°,BE =EF =2,∵∠A =20°,∴∠6=20°,∴AF =EF =2,∵BD =DF =2.3,∴AD =BD +BC =4.3.【点睛】本题考查了全等三角形的性质与判定,等腰三角形的性质,熟悉这些定理是解决本题的关键.类型三、一线三等角模型应用:①通过证明全等实现边角关系的转化,便于解决对应的几何问题;②与函数综合应用中有利于点的坐标的求解。
初二数学第十二章全等三角形详细知识点及题型总结

第十二章全等三角形第一讲全等三角形性质图形全等:一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即...................................平移、翻折、旋转前后的图形全等。
“全等”用.....................≅表示,读作“全等于”..........全等三角形的定义:两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上,如∆和全等时,点A和点D,点B和点E,点C和点F是对应顶点,记作DEF ABC∆DEF∆。
ABC∆≅把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
全等三角形的性质:全等三角形的对应边相等;全等三角形的对应角相等。
........................例1.已知:如图,AB=AD,AC=AE,BC=DE,∠EAC=300,则∠DAB的大小为例2.如图,在平面上将△ABC绕B点旋转到△A’BC’的位置时,AA’∥BC,∠ABC=70°,则∠CBC’为________度.例3.如图,在△ABC中,∠A:∠B:∠C=3:5:10,又△MNC≌△ABC,则∠BCM:∠BCN等于()A.1:2 B.1:3 C.2:3 D.1:4课堂练习:∆的是( )1.根据下列条件,能画出唯一ABCA. AB=3,BC=4,CA=8B.AB=4,BC=3,∠A=300C. ∠C=600,∠B=450,AB=4D.∠C=900,AB=62.如图∠1=∠2=200,AD=AB,∠D=∠B,E在线段BC上,则∠AEC=()A.200B.700C.500D.8003.已知:如图,△ABC≌△DEF,AC∥DF,BC∥EF.则不正确的等式是()A.AC=DFB.AD=BEC.DF=EFD.BC=EF4.如图,△BCD≌△CBE,BC=6,CE=5,BE=4,则CD的长是()A.4 B.5 C.6 D.无法确定5.已知图中的两个三角形全等,则∠ 度数是()A.72°B.60°C.58°D.50°6.如图,将Rt△ABC(其中∠B=340,∠C=900)绕A点按顺时针方向旋转到△AB1 C1的位置,使得点C、A、B1在同一条直线上,那么旋转角最小等于()A.560B.680C.1240D.18007.如图,△ABE≌△ACD,∠B=50°,∠AEB=60°,则∠DAC的度数等于()A.120° B.70° C.60° D.50°8.若两个三角形的面积相等 , 则这两个三角形________全等.9.如图,△ABD≌△ACE,且∠BAD和∠CAE,∠ABD和∠ACE,∠ADB和∠AEC是对应角,则对应边_______.10.如图,△ABC≌△DBC,且∠A和∠D,∠ABC和∠DBC是对应角,其对应边:______,对应角:_________.11.如图,△ABO≌△CDO,OA=2,AB=4,BO=3,则DC= ,OC= ,OD= .12.如图,△ABC≌△DEF,A与D,B与E分别是对应顶点,∠B=320,∠A=680,AB=13cm,则∠F=______度,DE=______cm.13.已知△ABC≌△DEF,∠A=52°,∠B=67°BC=15cm则∠F=_____,FE=_____cm.14.如图,P是正△ABC内的一点,若将△PAB绕点A逆时针旋转到△P/AC,则∠PAP/的度数为________.15.将一张正方形纸片按如图的方式折叠,BC,BD为折痕,则∠CBD的大小为_________16.如图所示,,BC 的延长线交DA 于F ,交DE 于G ,,,,则的度数为17.观察图中每一个大三角形中白色三角形的排列规律,则第n 个大三角形中白色三角形有 个 .18.如图,把△ABC 绕点C 顺时针旋转350,得到△A /B /C, A /B /交AC 乎点D ,已知∠A /DC=90°,求∠A 的度数.19.如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,(1)写出图中一对全等的三角形,并写出它们的所有对应角;(2)设AED ∠的度数为x ,∠ADE 的度数为y ,那么∠1,∠2的度数分别是多少?(用含有x 或y 的代数式表示)(3)∠A 与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律.20.如图所示,已知△ABC ≌△FED ,且BC =ED ,那么AB 与EF 平行吗?为什么?ABC ADE △≌△105ACB AED ∠=∠=15CAD ∠=30B D ∠=∠=1∠课后练习:1.下列说法:①全等图形的形状相同、大小相等;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等,其中正确的说法为( )A .①②③④B .①③④C .①②④D .②③④2.下列说法错误的有( )①只有两个三角形才能完全重合;②如果两个图形全等,它们的形状和大小一定都相同;③两个正方形一定是全等图形;④边数相同的图形一定能互相重合.A.4个B.3个C.2个D.1个3.已知△ABC 与△DEF 全等,∠A=∠D=90°,∠B=37°,则∠E 的度数是( )A.37°B.53°C.37°或63°D.37°或53°4.如果D 是中BC 边上一点,并且,则是( )A.锐角三角形B.钝角三角形C.直角三角形D.等腰三角形5.对于两个图形,给出下列结论:①两个图形的周长相等;②两个图形的面积相等;③两个图形的周长和面积都相等;④两个图形的形状相同,大小也相等.其中能获得这两个图形全等的结论共有( )A.1个B.2个C.3个D.4个6.如图,△OAB 绕点O 逆时针旋转800到△OCD 的位置,已知∠AOB=450,则∠AOD ( )A.550B.450C.400D.3507.如图,△ABE ≌△ACD,AB=AC,BE=CD, ∠B=50°,∠AEC=120°,则∠DAC 的度数等于( )A.120°B.70°C.60°D.50°8.如图所示,在△ABC 中,D 、E 分别是边AC 、BC 上的点,若△ADB ≌△EDB ≌△EDC ,则∠C 的度数为( )A. 15°B. 20°C. 25°D. 30°9.如图所示,AD 是△ABC 的中线,∠ADC =45°,把△ADC 沿AD 对折,使点C 落在点C ´的位置,则图中的一个等腰直角三角形是( ) A. △ADC B. △BDC ´ C. △ADC ´ D. 不存在6.如图,已知AB=AC ,AD=AE ,∠BAD=25°,则∠CAE=ABC △ADB ADC △≌△ABC△7.如图,△ABD≌△ACE,则AB的对应边是_______,∠BAD的对应角是______.8.已知:如图,△ABE≌△ACD,∠B=∠C,则∠AEB=_______,AE=______.9.如图:△ABC≌△DCB,AB和DC是对应边,∠A和∠D是对应角,则其它对应边是______________,对应角是____________________.10.已知:如图,△ABC≌△DEF,BC∥EF,∠A=∠D,BC=EF,则另外两组对应边是____,另外两组对应角是____.11.已知:如图,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠AEB=________度.12.如图所示,△ABD≌△ACE,点B和点C是对应顶点,AB=8,BD=7,AD=6,则BE的长是___13.如图,已知△ABE≌△ACF,∠E=∠F=90°,∠CMD=70°,则∠2=______度.14.如图所示,已知△ABC≌△ADE,BC的延长线交DE于F,∠B=∠D=25°,∠ACB=∠AED=105°,∠DAC=10°,则∠DFB为15.如图,D,E分别为△ABC的AC,BC边的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=480,则∠APD等于16.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y=____17.如图,把大小为4×4的正方形方格图形分割成两个全等图形,例如图1.请在下图中,沿着虚线画出四种不同的分法,把4×4的正方形方格图形分割成两个全等图形.能力提高:1.长为L 的一根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边x 的取值范围为( ) A.64l l x ≤< B.84l l x ≤< C.64l l x << D.84l l x << 2.已知△ABC ≌△A ′B ′C ′,△ABC 的三边为3、m 、n ,△A ′B ′C ′的三边为5、p 、q ,若△ABC 的各边都是整数,则m+n+p+q 的最大值为__________3.如图,△ABC ≌△ADE ,∠DAC=60°,∠BAE=100°,BC 、DE 相交于点F ,则∠DFB 的度数是4.下图是由全等的图形组成的,其中AB =3cm ,CD =2AB ,则AF =__________.AB C D E F5.如图,△ABE 和△ADC 是△ABC 分别沿着AB 、AC 边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠a 的度数为6.如图,矩形ABCD 沿AM 折叠,使D 点落在BC 上的N 点处,如果AD=7cm,DM=5cm, ∠DAM=39°,则AN= cm, NM= cm, ∠NAB= .7.如图所示,△ABC 绕顶点A 顺时针旋转,若∠B =40°,∠C =30°.(1)顺时针旋转多少度时,旋转后的△AB'C'的顶点C'与原三角形的顶点B 和A 在同一直线上?(原△ABC 是指开始位置)(2)再继续旋转多少度时,点C 、A 、C'在同一直线上?8.如图, 在ABCD中, 将△ABE沿BE翻折, 点A落在CD边上, 成为点F, 如果△DEF和△BCF的周长分别是8cm和22cm, 求FC的长度。
全等三角形复习资料(搜集整理版)
特别鸣谢资源原创者,本人仅仅便于自己的备课整理排版了一下。
第十一章全等三角形复习一、全等三角形能够完全重合的两个三角形叫做全等三角形。
一个三角形经过平移、翻折、旋转可以得到它的全等形.2、全等三角形有哪些性质(1):全等三角形的对应边相等、对应角相等。
(2):全等三角形的周长相等、面积相等。
(3):全等三角形的对应边上的对应中线、角平分线、高线分别相等.3、全等三角形的判定边边边:三边对应相等的两个三角形全等(可简写成“SSS")边角边:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”))2、(判定)角的内部到角的两边的距离相等的点在角的平分线上。
三、学习全等三角形应注意以下几个问题:(1)要正确区分“对应边”与“对边”,“对应角”与“对角”的不同含义;(2表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;(3)“有三个角对应相等"或“有两边及其中一边的对角对应相等”的两个三角形不一定全等; (4)时刻注意图形中的隐含条件,如“公共角”、“公共边"、“对顶角”第十二章轴对称一、轴对称图形1. 把一个图形沿着一条直线折叠,如果直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形。
这条直线就是它的对称轴.这时我们也说这个图形关于这条直线(成轴)对称.2. 把一个图形沿着某一条直线折叠,如果它能与另一个图形完全重合,那么就说这两个图关于这条直线对称。
这条直线叫做对称轴.折叠后重合的点是对应点,叫做对称点4。
轴对称的性质①关于某直线对称的两个图形是全等形。
②如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
③轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
④如果两个图形的对应点连线被同条直线垂直平分,那么这两个图形关于这条直线对称。
二、线段的垂直平分线1。
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫中垂线.2.线段垂直平分线上的点与这条线段的两个端点的距离相等3.与一条线段两个端点距离相等的点,在线段的垂直平分线上三、用坐标表示轴对称小结:在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数。
(完整版)全等三角形的判定常考典型例题及练习

(完整版)全等三角形的判定常考典型例题及练习-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN全等三角形的判定一、知识点复习 ①“边角边”定理:两边和它们的夹角对应相等的两个三角形全等。
(SAS )图形分析:书写格式: 在△ABC 和△DEF 中⎪⎩⎪⎨⎧=∠=∠=EFBC E B DEAB∴△ABC ≌△DEF (SAS )②“角边角”定理:两角和它们的夹边对应相等的两个三角形全等。
(ASA)图形分析:书写格式: 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧∠=∠=∠=∠FC EF BC EB∴△ABC ≌△DEF(ASA)③“角角边”定理:两个角和其中一个角的对边对应相等的两个三角形全等。
(AAS )图形分析:书写格式:在△ABC 和△DEF 中⎪⎩⎪⎨⎧=∠=∠∠=∠EFBC F C EB∴△ABC ≌△DEF(AAS)④“边边边”定理:三边对应相等的两个三角形全等。
(SSS )图形分析:书写格式: 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧===EF BC DF AC DE AB∴△ABC ≌△DEF(AAS)⑤“斜边、直角边”定理:斜边和一条直角边对应相等的两个直角三角形全等。
(HL )图形分析:书写格式:在△ABC 和△DEF 中 ⎩⎨⎧==DF AC DE AB ∴△ABC ≌△DEF (HL )一个三角形共有三条边与三个角,你是否想到这样一问题了:除了上述四种识别法,还有其他的三角形全等识别法吗比如说“SSA ”、“AAA ”能成为判定两个三角形全等的条件吗两个三角形中对应相等的元素 两个三角形是否全等反例 SSA⨯AAA⨯二、常考典型例题分析第一部分:基础巩固1.下列条件,不能使两个三角形全等的是( )A.两边一角对应相等 B.两角一边对应相等 C.直角边和一个锐角对应相等 D.三边对应相等2.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD()A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD3.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是()A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙4.如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是()A.AB=DE B.DF∥AC C.∠E=∠ABC D.AB∥DE5.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是()A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD6.如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线OC,作法用得的三角形全等的判定方法是()A.SAS B.SSS C.ASA D.HL第二部分:考点讲解考点1:利用“SAS ”判定两个三角形全等1.如图,A 、D 、F 、B 在同一直线上,AD=BF ,AE=BC ,且AE ∥BC .求证:△AEF ≌△BCD .2.如图,AB=AC ,AD=AE ,∠BAC=∠DAE .求证:△ABD ≌△ACE .考点2:利用“SAS ”的判定方法解与全等三角形性质有关的综合问题3.已知:如图,A 、F 、C 、D 四点在一直线上,AF=CD ,AB ∥DE ,且AB=DE ,求证:FEC CBF ∠=∠考点3:利用“SAS ”判定三角形全等解决实际问题 4.有一座小山,现要在小山A 、B 的两端开一条隧道,施工队要知道A 、B 两端的距离,于是先在平地上取一个可以直接到达A 和B 的点C ,连接AC 并延长到D ,使CD=CA ,连接BC 并延长到E ,使CE=CB ,连接DE ,那么量出DE 的长,就是A 、B 的距离,你能说说其中的道理吗?考点4:利用“ASA”判定两个三角形全等5.如图,已知AB=AD,∠B=∠D,∠1=∠2,求证:△AEC≌△ADE.6.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.求证:△AEC≌△BED;考点6:利用“ASA”与全等三角形的性质解决问题:7.如图,已知EC=AC,∠BCE=∠DCA,∠A=∠E;求证:BC=DC考点7:利用“SSS”证明两个三角形全等8.如图,A、D、B、E四点顺次在同一条直线上,AC=DF,BC=EF,AD=BE,求证:△ABC≌△EDF.考点8:利用全等三角形证明线段(或角)相等9.如图,AE=DF,AC=DB,CE=BF.求证:∠A=∠D.考点9:利用“AAS”证明两个三角形全等10.如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,求证:△ABD≌△ACE.考点10:利用“AAS”与全等三角形的性质求证边相等11.(2017秋?娄星区期末)已知:如图所示,△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.(1)求证:BM=AC;(2)求△ABC的面积.考点11:利用“HL”证明两三角形全等12.如图,在△ABC中,D是BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF。
(完整版)全等三角形经典模型总结
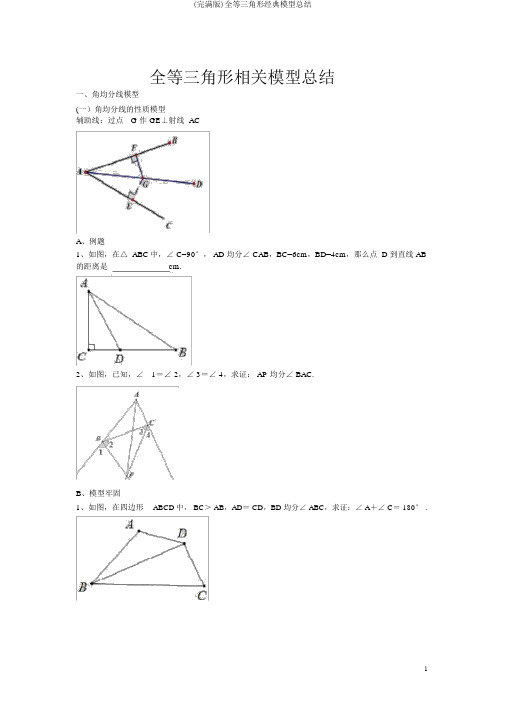
全等三角形相关模型总结一、角均分线模型(一)角均分线的性质模型辅助线:过点G 作 GE⊥射线 ACA、例题1、如图,在△ ABC中,∠ C=90°, AD 均分∠ CAB,BC=6cm,BD=4cm,那么点 D 到直线 AB 的距离是cm.2、如图,已知,∠1=∠ 2,∠ 3=∠ 4,求证: AP 均分∠ BAC.B、模型牢固1、如图,在四边形ABCD中, BC> AB,AD= CD,BD 均分∠ ABC,求证:∠ A+∠ C= 180° .(二)角均分线+垂线,等腰三角形必表现A、例题辅助线:延长ED 交射线 OB 于 F辅助线:过点 E 作 EF∥射线 OB例 1、如图,在△ABC中,∠ ABC= 3∠ C, AD 是∠ BAC的均分线, BE⊥ AD 于 F .1求证: BE( AC AB) .例 2、如图,在△ ABC中,∠ BAC的角均分线 AD 交 BC 于点 D,且 AB= AD,作 CM⊥ AD 交1AD 的延长线于M. 求证:AM( AB AC) .2(三)角分线,分两边,对称全等要记全两个图形飞辅助线都是在射线ON 上取点 B,使 OB= OA,从而使△ OAC≌△ OBC .A、例题1、如图,在△ ABC 中,∠ BAC=60°,∠ C=40°, AP 均分∠ BAC交 BC 于 P, BQ 均分∠ ABC 交AC 于 Q,求证: AB+ BP= BQ+ AQ .2、如图,在△ ABC 中, AD 是∠ BAC的外角均分线, P 是 AD 上异于点 A 的任意一点,试比较PB+ PC与 AB+ AC的大小,并说明原由 .B、模型牢固1、在△ ABC中, AB> AC, AD 是∠ BAC的均分线, P 是线段 AD 上任意一点(不与 A 重合) . 求证: AB-AC> PB- PC .2、如图,△ ABC中, AB= AC,∠ A= 100°,∠ B 的均分线交 AC 于 D,求证: AD+BD=BC .3、如图,△ ABC中, BC=AC,∠ C= 90°,∠ A 的均分线交 BC 于 D,求证: AC+ CD= AB .二、等腰直角三角形模型(一)旋转中心为直角极点,在斜边上任取一点的旋转全等:操作过程:(1)将△ ABD 逆时针旋转 90°,得△ ACM ≌ △ ABD,从而推出△ ADM 为等腰直角三角形 .(2)辅助线作法:过点 C 作 MC⊥ BC,使 CM= BD,连接 AM.(二)旋转中心为斜边中点,动点在两直角边上转动的旋转全等:操作过程:连接AD.(1)使 BF=AE(或 AF= CE),导出△ BDF ≌ △ADE.(2)使∠ EDF+∠ BAC= 180°,导出△ BDF ≌ △ ADE.A、例题1、如图,在等腰直角△ ABC中,∠BAC= 90°,点 M 、N 在斜边 BC上滑动,且∠ MAN =45°,试试究 BM、 MN 、 CN 之间的数量关系 .2、两个全等的含有 30°, 60°角的直角三角板 ADE 和 ABC,按以以下图放置, E、A、 C 三点在一条直线上,连接 BD,取 BD 的中点 M ,连接 ME、 MC.试判断△ EMC 的形状,并证明你的结论.B、模型牢固1、已知,以以下图,Rt△ABC中, AB= AC,∠ BAC=90°, O 为 BC中点,若 M 、N 分别在线段 AC、 AB 上搬动,且在搬动中保持AN= CM.(1)试判断△ OMN 的形状,并证明你的结论.(2)当 M、 N 分别在线段AC、 AB 上搬动时,四边形AMON 的面积如何变化?2、在正方形ABCD中, BE= 3,EF= 5, DF=4,求∠ BAE+∠ DCF为多少度 .(三)构造等腰直角三角形(1)利用以上(一)和(二)都可以构造等腰直角三角形(略);(2)利用平移、对称和弦图也可以构造等腰直角三角形.(四)将等腰直角三角形补全为正方形,以以下图:A、例题应用1、如图,在等腰直角△ABC 中, AC= BC,∠ ACB= 90°, P 为三角形ABC内部一点,满足 PB= PC, AP= AC,求证:∠ BCP= 15° .三、三垂直模型(弦图模型)A、例题已知:以以下图,在△ ABC中, AB= AC,∠ BAC= 90°, D 为 AC 中点, AF⊥ BD 于点 E,交 BC 于 F,连接 DF .求证:∠ ADB=∠ CDF .变式 1、已知:以以下图,在△ABC中, AB= AC,AM = CN, AF⊥ BM 于 E,交 BC 于 F,连接NF .求证:( 1)∠ AMB=∠ CNF;(2) BM= AF+ FN .变式 2、在变式 1 的基础上,其他条件不变,可是将BM 和 FN 分别延长交于点P,求证:( 1) PM= PN;( 2) PB= PF+ AF .四、手拉手模型1、△ ABE和△ ACF均为等边三角形结论:( 1)△ ABF≌△ AEC .(2)∠ BOE=∠ BAE=60° .(3) OA 均分∠ EOF .(四点共圆证)拓展:△ ABC和△ CDE均为等边三角形结论:( 1) AD= BE;(2)∠ ACB=∠ AOB;(3)△ PCQ为等边三角形;(4) PQ∥ AE;(5) AP=BQ;(6) CO均分∠ AOE;(四点共圆证)(7) OA= OB+OC;(8) OE=OC+ OD .((7),( 8)需构造等边三角形证明)例、如图①,点 M为锐角三角形 ABC内任意一点,连接 AM、BM、 CM.以 AB为一边向外作等边三角形△ ABE,将 BM绕点 B 逆时针旋转 60°获取 BN,连接 EN.(1)求证:△ AMB≌△ ENB;(2)若 AM+BM+CM的值最小,则称点 M为△ ABC的费尔马点.若点 M为△ ABC的费尔马点,试求此时∠ AMB、∠ BMC、∠ CMA的度数;(3)小翔受以上启示,获取一个作锐角三角形费尔马点的简略方法:如图②,分别以△ABC 的 AB、 AC 为一边向外作等边△ABE和等边△ ACF,连接CE、BF,设交点为M,则点M 即为△ ABC的费尔马点.试说明这种作法的依据.2、△ ABD 和△ ACE均为等腰直角三角形结论:( 1) BE= CD;(2) BE⊥ CD .3、四边形ABEF和四边形ACHD均为正方形结论:( 1) BD= CF;( 2)BD⊥ CF .变式 1、四边形 ABEF和四边形 ACHD均为正方形, AS⊥ BC 交 FD 于 T,求证:( 1) T 为 FD 中点;( 2)SV ABC SV ADF .变式 2、四边形 ABEF和四边形 ACHD均为正方形, T 为 FD 中点, TA 交 BC于 S,求证: AS⊥ BC .360 4、如图,以△ ABC的边 AB、 AC为边构造正多边形时,总有:1 2 180n五、半角模型条件: 1 , 且 + =180 ,两边相等.2思路: 1、旋转辅助线:①延长CD到 E,使 ED=BM,连 AE 或延长 CB到 F,使 FB=DN,连 AF②将△ ADN绕点 A 顺时针旋转 90°得△ ABF,注意:旋转需证F、 B、 M三点共线结论:( 1) MN = BM+ DN;(2)CV CMN=2 AB;(3) AM、 AN 分别均分∠ BMN 、∠ MND .2、翻折(对称)辅助线:①作AP⊥ MN 交 MN 于点 P②将△ ADN、△ ABM分别沿 AN、 AM翻折,但必然要证明M、P、 N 三点共线 .A、例题例1、在正方形 ABCD中,若 M、 N 分别在边 BC、 CD 上搬动,且满足 MN = BM+DN,求证:( 1)∠ MAN = 45°;(2)CV CMN=2 AB;(3) AM、 AN 分别均分∠ BMN 和∠ DNM .变式:在正方形 ABCD中,已知∠ MAN =45°,若 M 、N 分别在边 CB、DC 的延长线上搬动,AH⊥MN ,垂足为 H,(1)试试究线段 MN 、BM、 DN 之间的数量关系;(2)求证: AB= AH例 2、在四边形 ABCD 中,∠ B +∠ D = 180°, AB = AD ,若 E 、 F 分别为边 BC 、 CD 上的点,且满足 EF =BE + DF ,求证: EAF 1BAD .2变式:在四边形 ABCD 中,∠ B = 90°,∠ D = 90°, AB = AD ,若 E 、 F 分别为边 BC 、CD 上的点,且 EAF1 BAD ,求证: EF = BE +DF .2。
三角形全等的判定(6种题型)-2023年新八年级数学核心知识点与常见题型(浙教版)(解析版)
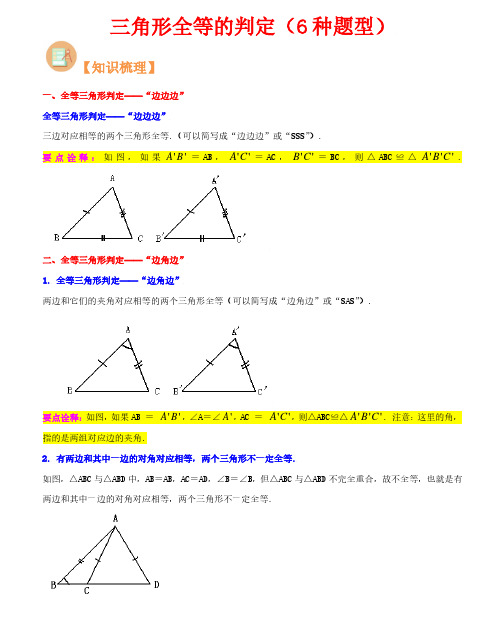
三角形全等的判定(6种题型)【知识梳理】一、全等三角形判定——“边边边”全等三角形判定——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS ”).要点诠释:如图,如果''A B =AB ,''A C =AC ,''B C =BC ,则△ABC ≌△'''A B C .二、全等三角形判定——“边角边”1. 全等三角形判定——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS ”).要点诠释:如图,如果AB = ''A B ,∠A =∠'A ,AC = ''A C ,则△ABC ≌△'''A B C . 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.三、垂直平分线:1.定义:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.2.性质定理:线段垂直平分线上的点到线段两端的距离相等四、全等三角形判定——“角边角”全等三角形判定——“角边角”两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA ”).要点诠释:如图,如果∠A =∠'A ,AB =''A B ,∠B =∠'B ,则△ABC ≌△'''A B C .五、全等三角形判定——“角角边” 1.全等三角形判定——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS ”)要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC 和△ADE 中,如果BC ,那么∠ADE =∠B ,∠AED =∠C ,又∠A =∠A ,但△ABC 和△ADE 不全等.这说明,三个角对应相等的两个三角形不一定全等.六、角平分线的性质定理:角平分线上的点到角两边的距离相等.【考点剖析】题型一、全等三角形的判定——“边边边”例1、已知:如图,△RPQ 中,RP =RQ ,M 为PQ 的中点.求证:RM 平分∠PRQ .【思路点拨】由中点的定义得PM =QM ,RM 为公共边,则可由SSS 定理证明全等.【答案与解析】证明:∵M 为PQ 的中点(已知),∴PM =QM在△RPM 和△RQM 中,()(),,RP RQ PM QM RM RM ⎧=⎪=⎨⎪=⎩已知公共边 ∴△RPM ≌△RQM (SSS ).∴ ∠PRM =∠QRM (全等三角形对应角相等).即RM 平分∠PRQ.【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中. 用全等三角形的性质和判定.【变式】已知:如图,AD =BC ,AC =BD.试证明:∠CAD =∠DBC.【答案】证明:连接DC ,在△ACD 与△BDC 中()AD BC AC BDCD DC ⎧=⎪=⎨⎪=⎩公共边 ∴△ACD≌△BDC(SSS )∴∠CAD =∠DBC (全等三角形对应角相等)【变式2】、如图,在△ABC 和△ADE 中,AB =AC ,AD =AE ,BD =CE ,求证:∠BAD =∠CAE.【答案与解析】证明:在△ABD 和△ACE 中,AB AC AD AE BD CE =⎧⎪=⎨⎪=⎩∴△ABD ≌△ACE (SSS )∴∠BAD =∠CAE (全等三角形对应角相等).【总结升华】把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的判定和性质. 要证∠BAD =∠CAE ,先找出这两个角所在的三角形分别是△BDA 和△CAE ,然后证这两个三角形全等.题型二、全等三角形的判定——“边角边”例2、已知:如图,AB =AD ,AC =AE ,∠1=∠2.求证:BC =DE .【思路点拨】由条件AB =AD ,AC =AE ,需要找夹角∠BAC 与∠DAE ,夹角可由等量代换证得相等.【答案与解析】证明: ∵∠1=∠2∴∠1+∠CAD =∠2+∠CAD ,即∠BAC =∠DAE在△ABC 和△ADE 中AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE (SAS )∴BC =DE (全等三角形对应边相等)【总结升华】证明角等的方法之一:利用等式的性质,等量加等量,还是等量.【变式】如图,将两个一大、一小的等腰直角三角尺拼接 (A 、B 、D 三点共线,AB =CB ,EB =DB ,∠ABC =∠EBD =90°),连接AE 、CD ,试确定AE 与CD 的位置与数量关系,并证明你的结论.【答案】AE =CD ,并且AE ⊥CD证明:延长AE 交CD 于F ,∵△ABC 和△DBE 是等腰直角三角形∴AB =BC ,BD =BE在△ABE 和△CBD 中90AB BC ABE CBD BE BD =⎧⎪∠=∠=︒⎨⎪=⎩∴△ABE ≌△CBD (SAS )∴AE =CD ,∠1=∠2又∵∠1+∠3=90°,∠3=∠4(对顶角相等)∴∠2+∠4=90°,即∠AFC =90°∴AE ⊥CD例3、如图,AD 是△ABC 的中线,求证:AB +AC >2AD .【思路点拨】延长AD 到点E ,使AD =DE ,连接CE .通过证全等将AB 转化到△CEA 中,同时也构造出了2AD .利用三角形两边之和大于第三边解决问题.【答案与解析】证明:如图,延长AD 到点E ,使AD =DE ,连接CE .在△ABD 和△ECD 中,AD DE ADB EDC BD CD ⎧⎪∠∠⎨⎪⎩===.∴△ABD ≌△ECD (SAS ).∴AB =CE .∵AC +CE >AE ,∴AC +AB >AE =2AD .即AC +AB >.【总结升华】证明边的大小关系主要有两个思路:(1)两点之间线段最短;(2)三角形的两边之和大于第三边.要证明AB +AC >2AD ,如果归到一个三角形中,边的大小关系就是显然的,因此需要转移线段,构造全等三角形是转化线段的重要手段.可利用旋转变换,把△ABD 绕点D 逆时针旋转180°得到△CED ,也就把AB 转化到△CEA 中,同时也构造出了2AD .若题目中有中线,倍长中线,利用旋转变换构造全等三角形是一种重要方法.例4、已知,如图:在△ABC 中,∠B =2∠C ,AD ⊥BC ,求证:AB =CD -BD .【思路点拨】在DC 上取一点E ,使BD =DE ,则△ABD ≌△AED ,所以AB =AE ,只要再证出EC =AE 即可.【答案与解析】证明:在DC 上取一点E ,使BD =DE∵ AD ⊥BC ,∴∠ADB =∠ADE在△ABD 和△AED 中,BD DE ADB=ADE AD AD ⎧⎪⎨⎪⎩=∠∠=∴△ABD ≌△AED (SAS ).∴AB =AE ,∠B =∠AED .又∵∠B =2∠C =∠AED =∠C +∠EAC .∴∠C =∠EAC .∴AE =EC .∴AB =AE =EC =CD —DE =CD —BD .【总结升华】此题采用截长或补短方法.上升到解题思想,就是利用翻折变换,构造的全等三角形,把条件集中在基本图形里面,从而使问题加以解决.如图,要证明AB =CD -BD ,把CD -BD 转化为一条线段,可利用翻折变换,把△ABD 沿AD 翻折,使线段BD 运动到DC 上,从而构造出CD -BD ,并且也把∠B 转化为∠AEB ,从而拉近了与∠C 的关系.【变式】已知,如图,在四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于E ,并且AE =12(AB +AD ), 求证:∠B +∠D =180°. AE D CB【答案】证明:在线段AE 上,截取EF =EB ,连接FC ,∵CE ⊥AB ,∴∠CEB =∠CEF =90°在△CBE 和△CFE 中,CEB CEF EC =EC EB EF =⎧⎪∠=∠⎨⎪⎩∴△CBE 和△CFE (SAS )∴∠B =∠CFE∵AE =12(AB +AD ),∴2AE = AB +AD ∴AD =2AE -AB∵AE =AF +EF ,∴AD =2(AF +EF )-AB =2AF +2EF -AB =AF +AF +EF +EB -AB =AF +AB -AB ,即AD =AF在△AFC 和△ADC 中(AF AD FAC DAC AC AC =⎧⎪∠=∠⎨⎪=⎩角平分线定义)∴△AFC ≌△ADC (SAS )∴∠AFC =∠D∵∠AFC +∠CFE =180°,∠B =∠CFE.∴∠AFC +∠B =180°,∠B +∠D =180°.题型三、全等三角形的判定——“角边角”例5、已知:如图,E ,F 在AC 上,AD ∥CB 且AD =CB ,∠D =∠B .求证:AE =CF .【答案与解析】证明:∵AD ∥CB∴∠A =∠C在△ADF 与△CBE 中A C AD CB D B ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADF ≌△CBE (ASA )∴AF =CE ,AF +EF =CE +EF故得:AE =CF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.【变式】(2022•长安区一模)已知:点B 、E 、C 、F 在一条直线上,AB ∥DE ,AC ∥DF ,BE =CF .求证:△ABC ≌△DEF .【分析】先利用平行线的性质得到∠B=∠DEF,∠ACB=∠F,再证明BC=EF,然后根据“ASA”可判断△ABC≌△DEF.【解答】证明:∵AB∥DE,∴∠B=∠DEF,∵AC∥DF,∴∠ACB=∠F,∵BE=CF,∴BE+EC=CF+EC,即BC=EF,在△ABC和△DEF中,{∠B=∠DEF BC=EF∠ACB=∠F,∴△ABC≌△DEF(ASA).5种判定方法是解决问题的关键.选用哪一种判定方法,取决于题目中的已知条件.例6、如图,G是线段AB上一点,AC和DG相交于点E.请先作出∠ABC的平分线BF,交AC于点F;然后证明:当AD∥BC,AD=BC,∠ABC=2∠ADG时,DE=BF.【思路点拨】通过已知条件证明∠DAC=∠C,∠CBF=∠ADG,则可证△DAE≌△BCF【答案与解析】证明:∵AD∥BC,∴∠DAC=∠C∵BF平分∠ABC∴∠ABC=2∠CBF∵∠ABC=2∠ADG∴∠CBF=∠ADG在△DAE 与△BCF 中⎪⎩⎪⎨⎧∠=∠=∠=∠C DAC BCAD CBF ADG ∴△DAE≌△BCF(ASA )∴DE=BF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.【变式】已知:如图,在△MPN 中,H 是高MQ 和NR 的交点,且MQ =NQ .求证:HN =PM.【答案】证明:∵MQ 和NR 是△MPN 的高,∴∠MQN =∠MRN =90°,又∵∠1+∠3=∠2+∠4=90°,∠3=∠4∴∠1=∠2在△MPQ 和△NHQ 中,12MQ NQ MQP NQH ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MPQ ≌△NHQ (ASA )∴PM =HN题型四、全等三角形的判定——“角角边”例7.(2021秋•苏州期末)如图,在四边形ABCD 中,E 是对角线AC 上一点,AD ∥BC ,∠ADC =∠ACD ,∠CED +∠B =180°.求证:△ADE ≌△CAB .【分析】由等角对等边可得AC=AD,再由平行线的性质可得∠DAE=∠ACB,由∠CED+∠B=180°,∠CED+∠AED=180°,得∠AED=∠B,从而利用AAS可判定△ADE≌△CAB.【解答】证明:∵∠ADC=∠ACD,∴AD=AC,∵AD∥BC,∴∠DAE=∠ACB,∵∠CED+∠B=180°,∠CED+∠AED=180°,∴∠AED=∠B,在△ADE与△CAB中,{∠DAE=∠ACB ∠AED=∠BAD=AC,∴△ADE≌△CAB(AAS).【点评】本题主要考查全等三角形的判定,解答的关键是由已知条件得出相应的角或边的关系.例8、已知:如图,AB⊥AE,AD⊥,∠E=∠B,DE=CB.求证:AD=AC.【思路点拨】要证AC=AD,就是证含有这两个线段的三角形△BAC≌△EAD.【答案与解析】证明:∵AB⊥AE,AD⊥AC,∴∠CAD=∠BAE=90°∴∠CAD+∠DAB=∠BAE+∠DAB ,即∠BAC=∠EAD在△BAC和△EAD中BAC EAD B E CB=DE ∠=∠⎧⎪∠=∠⎨⎪⎩∴△BAC ≌△EAD (AAS )∴AC =AD【总结升华】我们要善于把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等. 题型五:线段的垂直平分线 例9.(2023秋·浙江杭州·八年级校考开学考试)如图所示,在ABC 中,8AC =,5BC =,AB 的垂直平分线DE 交AB 于点D ,交AC 于点E ,则BCE 的周长为( )A .13B .18C .10.5D .21【答案】A 【分析】根据线段垂直平分线的性质得到AE BE =,再将BCE 的周长转化为AC BC +的长,即可求解.【详解】解:DE 是AB 的垂直平分线,∴AE BE =,∴BCE 的周长为BE EC BC AE EC BC AC BC ++=++=+,8AC =,5BC =,∴BCE 的周长为8513AC BC +=+=,故选:A .【点睛】本题主要考查的是线段垂直平分线的性质,掌握线段垂直平分线的性质是解题的关键.【变式1】(2022秋·浙江温州·八年级校考期中)如图,点D 是ABC 边AC 的中点,过点D 作AC 的垂线交BC 于点E ,已知6AC =,ABC 的周长为14,则ABE 的周长是( )A .6B .14C .8D .20【答案】C 【分析】由题意可知:ED 垂直平分AC ,故EA EC =,结合6AC =,ABC 的周长为14,即可得出答案.【详解】解:∵点D 是ABC 边AC 的中点, ED AC ⊥,∴ED 垂直平分AC ,∴EA EC =,∵6AC =,ABC 的周长为14,∴1468AB BC +=−=,∴8AB BC AB BE EC AB BE AE +=++=++=,∴ABE 的周长是8.故选:C .【点睛】此题考查了垂直平分线的性质和判定,掌握垂直平分线的性质和判定是解题的关键.【答案】C 【分析】根据垂直平分线的性质可知,到A ,B ,C 表示三个居民小区距离相等的点,是AC ,BC 两边垂直平分线的交点,由此即可求解.【详解】解:如图所示,分别作AC ,BC 两边垂直平分线MN ,PQ 交于点O ,连接OA,OB,OC,∵MN,PQ是AC,BC两边垂直平分线,==,∴OA OB OC∴点O是到三个小区的距离相等的点,即点O是AC,BC两边垂直平分线的交点,故选:C.【点睛】本题主要考查垂直平分线的性质,掌握垂直平分线的性质是解题的关键.八年级专题练习)如图,在ABC中,是ABC外的一点,且【分析】根据到线段两端距离相等的点在线段的垂直平分线上,即可证明A、D都在BC的垂直平分线上,由此即可证明结论.AB AC,【详解】证明:∵=∴点A在BC的垂直平分线上,BD CD,∵=∴点D在BC的垂直平分线上,∴A、D都在BC的垂直平分线上,∴AD垂直平分BC.【点睛】本题主要考查了线段垂直平分线的判定,熟知线段垂直平分线的判定条件是解题的关键.【变式】.(2022秋·浙江·八年级专题练习)如图,点E是△ABC的边AB的延长线上一点,∠BCE=∠A+∠ACB,求证:点E在BC的垂直平分线上.【分析】由三角形的外角性质得到∠EBC=∠A+∠ACB,结合已知推出∠BCE=∠EBC,得到BE=CE,即可得到结论.【详解】证明:∵∠BCE=∠A+∠ACB,∠EBC=∠A+∠ACB,∴∠BCE=∠EBC,∴BE=CE,∴点E在BC的垂直平分线上.【点睛】本题考查了三角形的外角性质,线段垂直平分线的判定,用到的知识点:到线段两端点的距离相等的点在线段的垂直平分线上.题型六:角平分线【答案】A【分析】根据角平分线上的点到两边的距离相等即可解答.【详解】根据题意要使集贸市场到三条公路的距离相等即集贸市场应建在三个角的角平分线的交点.故本题选A .【点睛】本题考查了角平分线的性质,熟记角平分线的性质是解答本题的关键. 的中点,ABC ,则BED 的面积为( 【答案】C【分析】作DF AC ⊥于F ,DM AB ⊥于点M ,根据角平分线的性质求出DM ,根据三角形的面积公式计算即可.【详解】解:作DF AC ⊥于F ,DM AB ⊥于点MAD 是ABC 的角平分线DF AC ⊥于F ,DM AB ⊥,112122AC DF AB DM ∴⋅+⋅=,112122AC DM AB DM ⋅+⋅=∴即:3421DM DM +=得3DM =8AB =, E 是AB 的中点,142BE AB ∴== 1143622BEDS BE DM ∴=⋅=⨯⨯= 故选:C .【点睛】本题考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记性质并利用三角形的面积列出方程是解题的关键. 例12.(2022秋·浙江·八年级专题练习)已知:如图,90B C ∠=∠=,M 是BC 的中点,DM 平分ADC ∠.(1)若连接AM ,则AM 是否平分BAD ∠?请你证明你的结论;(2)线段DM 与AM 有怎样的位置关系?请说明理由.【答案】(1)AM 平分BAD ∠,证明见解析(2)DM AM ⊥,理由见解析【分析】(1)过点M 作ME AD ⊥,垂足为E ,证明ME MC MB ==即可得证.(2)利用两直线平行,同旁内角互补,证明1390∠+∠=.【详解】(1)AM 平分BAD ∠,理由为:证明:过点M 作ME AD ⊥,垂足为E ,∵DM 平分ADC ∠,∴12∠=∠,∵ME AD ⊥,MC CD ⊥∴MC ME =(角平分线上的点到角两边的距离相等),又∵MC MB =,∴ME MB =,∵MB AB ⊥,ME AD ⊥,∴AM 平分BAD ∠(到角的两边距离相等的点在这个角的平分线上).(2)DM AM ⊥,理由如下:∵90B C ∠=∠=,∴,DC CB AB CB ⊥⊥,∴DC AB ∥(垂直于同一条直线的两条直线平行),∴180DAB CDA ∠+∠=(两直线平行,同旁内角互补)又∵111,322CDA DAB ∠=∠∠=∠(角平分线定义) ∴2123180∠+∠=,∴1390∠+∠=,∴90AMD ∠=.即DM AM ⊥.【点睛】本题考查了角平分线的性质定理和判定定理,平行线的性质,熟练掌握以上的知识是解题的关键. 【变式1】(2023秋·浙江台州·八年级统考期末)如图 90B C ∠=∠=︒,E 为BC 上一点,AE 平分BAD ∠,DE 平分CDA ∠.(1)求AED ∠的度数;(2)求证:E 是BC 的中点.【答案】(1)90︒(2)见解析.【分析】(1)利用已知条件可以得到180BAD CDA ∠+∠=︒,想要求AED ∠的度数,只需要根据三角形内角和定理和角平分线的性质即可得到结论.(2)过点E 做EF AD ⊥,根据角平分线上的点到角的两边距离相等即可得结论.【详解】(1)解:∵90B C ∠=∠=︒,∴DC AB ∥,∴180BAD CDA ∠+∠=︒,∵AE 平分BAD ∠,DE 平分CDA ∠, ∴12EAD BAD ∠=∠,12EDA CDA ∠=∠, ∴1()902EAD EDA BAD CDA ∠+∠=∠+∠=︒,∴180()90AED EAD EDA ∠=︒−∠+∠=︒;(2)证明:过点E 作EF AD ⊥于点F ,∵AE 平分BAD ∠,90B Ð=°,EF AD ⊥,∴EF EB =.∵DE 平分CDA ∠,90C ∠=︒,EF AD ⊥,∴EF EC =.∴EB EC =,即E 是BC 的中点.【点睛】本题考查了平行线的判定与性质,以及角平分线上的点到角两边距离相等的性质,熟记性质和定理并做出辅助线是解题的关键.【变式2】.(2022秋·浙江杭州·八年级校考期中)如图,在ABC 外作两个大小不同的等腰直角三角形,其中90DAB CAE ∠=∠=︒,AB AD =,AC AE =.连接DC 、BE 交于F 点.(1)求证:DAC BAE ≌△△; (2)直线DC 、BE 是否互相垂直,试说明理由;(3)求证:AF 平分DFE ∠.【答案】(1)见解析(2)DC BE ⊥,理由见解析(3)见解析【分析】(1)由题意可得AD AB =,AC AE =,由90DAB CAE ∠=∠=︒,可得到DAC BAE ∠=∠,从而可证DAC BAE ≌△△;(2)由(1)可得ACD AEB ∠=∠,再利用直角三角形的性质及等量代换即可得到结论;(3)作AM DC ⊥于M ,AN BE ⊥于N ,利用全等三角形的面积相等及角平分线的判定即可证得结论.【详解】(1)证明:∵90DAB CAE ∠=∠=︒,∴DAB BAC CAE BAC ∠+∠=∠+∠,即DAC BAE ∠=∠,又∵AD AB =,AC AE =,∴()SAS DAC BAE ≌△△;(2)解:DC BE ⊥,理由如下;∵DAC BAE ≌△△, ∴ACD AEB ∠=∠,∵90AEB AOE ∠+∠= ,AOE FOC ∠=∠,∴90FOC ACD ∠+∠=,∴90EFC ∠=,∴DC BE ⊥;(3)证明:作AM DC ⊥于M ,AN BE ⊥于N ,∵DAC BAE ≌△△, ∴DAC BAE S S ∆∆=,DC BE =, ∴1122DC AM BE AN ⋅=⋅,∴AM AN =,∴AF 平分DFE ∠.【点睛】本题主要考查全等三角形的判定和性质,及直角三角形的性质,角平分线的判定,熟练掌握判定和性质是解决本题的关键.【变式3】(2023春·浙江金华·八年级浙江省义乌市后宅中学校考阶段练习)已知:OP 平分MON ∠,点A ,B 分别在边OM ,ON 上,且180OAP OBP ∠∠+=︒.(1)如图1,当90OAP ∠=︒时,求证:OA OB =;(2)如图2,当90OAP ∠<︒时,作PC OM ⊥于点C .求证:①PA PB =;②请直接写出OA ,OB ,AC 之间的数量关系 .【答案】(1)见解析(2)①见解析;②2OA OB AC −=【分析】(1)证明()AAS OPA OPB ≌,即可得证;(2)①作PD ON ⊥于点D ,证明()AAS PAC PBD ≌,即可得证; ②证明()AAS OCP ODP ≌,得出OD =,根据AC BD =,即可得证.【详解】(1)证明:180OAP OBP ∠∠+=︒,且90OAP ∠=︒,90OAP OBP ∠∠∴==︒,OP 平分MON ∠,POA POB ∠∠∴=,OP OP =,()AAS OPA OPB ∴≌,OA OB ∴=;(2)证明:①如图2,作PD ON ⊥于点D ,PC OM ⊥于点C ,PC PD ∴=,90PCA PDB OCP ∠∠∠===︒,180OAP OBP ∠∠+=︒,180DBP OBP ∠∠+=︒,OAP DBP ∠∠∴=,在PAC 和PBD 中,CAP DBP PCA PDBPC PD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()AAS PAC PBD ∴≌, PA PB ∴=;②结论:2OA OB AC −=.理由:在OCP 和ODP 中,OCP ODP COP DOP OP OP ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS OCP ODP ∴≌,OC OD ∴=,OA AC OB BD ∴−=+,AC BD =,2OA OB AC BD AC ∴−=+=.故答案为:2OA OB AC −=.【点睛】本题考查了角平分线的性质,全等三角形的性质与判定,掌握全等三角形的性质与判定是解题的关键.【过关检测】一、单选题 1.(2022秋·浙江·八年级专题练习)如图,在ABC 中,90A ∠=︒,点D 是边AC 上一点,3DA =,若点D 到BC 的距离为3,则下列关于点D 的位置描述正确的是( )A .点D 是AC 的中点B .点D 是B ∠平分线与AC 的交点 C .点D 是BC 垂直平分线与AC 的交点D .点D 与点B 的距离为5【答案】B 【分析】作DE BC ⊥于E ,连接BD ,利用角平分线的判定定理可证明BD 是ABC ∠的角平分线,即可作答.【详解】解:如图所示:作DE BC ⊥于E ,连接BD ,∵3DA =,点D 到BC 的距离为3,∴=AD DE ,∵90A ∠=︒,∴DA BA ⊥,∵DE BC ⊥,∴BD 是ABC ∠的角平分线,即点D 是ABC ∠的角平分线与AC 的交点,故B 项正确;其余选项,利用现有条件均无法得出,故选:B .【点睛】本题主要考查了角平分线的判定定理,作出辅助线,证明BD 是ABC ∠的角平分线,是解答本题的关键. 2.(2023·浙江·九年级专题练习)如图,已知BF DE =,AB ∥DC ,要使ABF CDE ≅△△,添加的条件可以是( )A.BE DF =B .AF CE =C .AB CD = D .B D ∠=∠【答案】C 【分析】根据AB ∥DC ,可得B D ∠=∠,又BF DE =,所以添加AB CD =,根据SAS 可证ABF CDE ≅△△.【详解】解:应添加AB DC =,理由如下:AB ∥DC ,B D ∴∠=∠.在ABF △和CDE 中,AB CD B DBF DE =⎧⎪∠=∠⎨⎪=⎩,(SAS)ABF CDE ∴≅,故选:C .【点睛】本题主要考查了平行线的性质以及全等三角形的判定,熟练掌握全等三角形的判定是解题的关键.3.(2023·浙江金华·统考二模)如图,ABC 和DEF 中,AB DE ∥,A D ∠=∠,点B ,E ,C ,F 共线,添加一个条件,不能判断ABC DEF ≌△△的是( )A .AB DE =B .ACB F ∠=∠C .BE CF =D .AC DF =【答案】B 【分析】根据AB DE ∥可得B DEF ∠=∠,加上A D ∠=∠,可知ABC 和DEF 中两组对角相等,因此一组对边相等时,即可判断ABC DEF ≌△△. 【详解】解:AB DE ∥,∴B DEF ∠=∠, 又A D ∠=∠,∴ABC 和DEF 中两组对角相等,当AB DE =时,根据ASA 可证ABC DEF ≌△△,故A 选项不合题意; 当ACB F ∠=∠时,ABC 和DEF 中,三组对角相等,不能判断ABC DEF ≌△△,故B 选项符合题意; 当BE CF =时,BC EF =,根据AAS 可证ABC DEF ≌△△,故C 选项不合题意; 当AC DF =时,根据AAS 可证ABC DEF ≌△△,故D 选项不合题意; 故选B .【点睛】本题考查添加条件使三角形全等,解题的关键是熟练掌握全等三角形的各种判定方法..ABC 的三条中线的交点.ABC 三边的垂直平分线的交点.ABC 三条角平分线的交点.ABC 三条高所在直线的交点【答案】C【分析】角平分线上的点到角的两边的距离相等,由此可解.【详解】解:要使凉亭到草坪三条边的距离相等,∴凉亭应在ABC 三条角平分线的交点处.故选C .【点睛】本题考查了角平分线的性质,解题的关键是注意区分三角形中线的交点、高的交点、垂直平分线的交点以及角平分线的交点之间的区别. 5.(2020秋·浙江·八年级期末)如图,AD 是ABC 中BAC ∠的平分线,DE AB ⊥交AB 于点E ,DF AC ⊥交AC 于点F ,若7ABC S =△,2DE =,4AB =,则AC 的长为( )A .3B .4C .5D .6【答案】A 【分析】先根据角平分线的性质得到2DF DE ==,再利用三角形面积公式得到11242722AC ⨯⨯+⨯⨯=,然后解关于AC 的方程即可.【详解】解:∵AD 是BAC ∠的平分线,DE AB ⊥,DF AC ⊥,2DE =,∴2DF DE ==,∵7ABC S =△,4AB =,又∵ABD ACD ABC S S S +=△△△,∴111124272222AB DE DF AC AC ⋅+⋅=⨯⨯+⨯⨯=,∴3AC =.故选:A .【点睛】本题考查角平分线的性质:角的平分线上的点到角的两边的距离相等.理解和掌握角平分线的性质是解题的关键.本题也考查了三角形的面积及等积变换.6.(2022秋·浙江·八年级专题练习)如图,用B C ∠=∠,12∠=∠,直接判定ABD ACD ≌△△的理由是( )A .AASB .SSSC .ASAD .SAS【答案】A 【分析】根据三角形全等的判定方法判定即可.【详解】解:在ABD △和ACD 中,12B CAD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()AAS ABD ACD ≌,故A 正确. 故选:A .【点睛】本题主要考查三角形全等的判定,解题的关键是掌握证明全等三角形的几种证明方法:AAS 、ASA 、SSS 、SAS 、HL .A .2B .【答案】C 【分析】由FC AB ∥,得F ADE ∠=∠,FCE A ∠=∠,即可根据全等三角形的判定定理“AAS”证明CFE ADE ≅,则4CF AD AB BD ==−=.【详解】解:FC AB ∥,F ADE ∴∠=∠,FCE A ∠=∠,在CFE 和ADE V 中,F ADE FCE AFE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS CFE ADE ∴≅, CF AD ∴=,5AB =,1BD =,514AD AB BD ∴=−=−=,4CF ∴=,CF ∴的长度为4.故选:C .【点睛】此题重点考查平行线的性质、全等三角形的判定与性质等知识,正确地找到全等三角形的对应边和对应角并且证明CFE ADE ≅是解题的关键.A .SSS【答案】B 【分析】根据已知条件两边,及两边的夹角是对顶角解答.【详解】解:在AOB 和COD △中,OA OC AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩,()AOB COD SAS ∴≌. 故选:B .【点睛】本题考查了全等三角形的应用,准确识图判断出两组对应边的夹角是对顶角是解题的关键. 9.(2022秋·浙江嘉兴·九年级校考期中)在联欢会上,有A 、B 、C 三名选手站在一个三角形的三个顶点位置上,他们在玩“抢凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放在ABC 的( )A .三边垂直平分线的交点B .三杂中线的交点C .三条角平分线的交点D .三条高所在直线的交点【答案】A【分析】根据题意可知,当木凳所在位置到A 、B 、C 三个顶点的距离相等时,游戏公平,再由线段垂直平分线的性质即可求解.【详解】解:由题意可得:当木凳所在位置到A 、B 、C 三个顶点的距离相等时,游戏公平,∵线段垂直平分线上的点到线段两端的距离相等,∴木凳应放的最适当的位置是在ABC 的三边垂直平分线的交点,故选:A .【点睛】本题考查线段垂直平分线的性质的应用,掌握线段垂直平分线的性质是解题的关键. )可说明ABC 与△ 【答案】A 【分析】先根据垂直的定义可得90ACB ADB ∠=∠=︒,再根据角平分线的定义可得CAB DAB ∠=∠,然后根据AAS 定理即可得.【详解】解:,BC AC BD AD ⊥⊥,90ACB ADB ∴∠=∠=︒,AB 平分CAD ∠,CAB DAB ∴∠=∠,在ABC 和ABD △中,90ACB ADB CAB DABAB AB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,()AAS ABC ABD ∴≌,故选:A . 【点睛】本题主要考查了三角形全等的判定,熟练掌握三角形全等的判定方法是解题关键.二、填空题【答案】CA FD =,B E ∠=∠,A D ∠=∠,AB DE ∥等【分析】可选择CA FD =添加条件后,能用SAS 进行全等的判;也可选择B E ∠=∠添加条件后,能用ASA 进行全等的判定;也可选择A D ∠=∠添加条件后,能用AAS 进行全等的判定;也可选择AB DE ∥添加条件后,能用ASA 进行全等的判定即可;【详解】解:添加CA FD =,∵12∠=∠,BC EF =,∴()SAS ABC DEF ≌△△,故答案为:CA FD =;或者添加B E ∠=∠,∵BC EF =,12∠=∠,∴()ASA ABC DEF ≌△△,故答案为:B E ∠=∠;或者添加A D ∠=∠,∵12∠=∠,BC EF =,∴()AAS ABC DEF ≌△△,故答案为:A D ∠=∠;或者添加AB DE ∥,∵AB DE ∥,∴B E ∠=∠,∵12∠=∠,BC EF =,∴()AAS ABC DEF ≌△△,故答案为:AB DE ∥.【点睛】本题考查了全等三角形的判定,解答本题关键是掌握全等三角形的判定定理,本题答案不唯一.【答案】AB DC =【分析】添加条件AB DC =,利用SAS 证明ABC DCB △≌△即可.【详解】解:添加条件AB DC =,理由如下:在ABC 和DCB △中,AB DC ABC DCBBC CB =⎧⎪∠=∠⎨⎪=⎩, ∴()SAS ABC DCB △≌△, 故答案为:AB DC =.【点睛】本题主要考查了全等三角形的判定,熟知全等三角形的判定定理是解题的关键,全等三角形的判定定理有SSS SAS AAS ASA HL ,,,,. 13.(2023秋·浙江湖州·八年级统考期末)如图,已知AC DB =,要使得ABC DCB ≅,根据“SSS”的判定方法,需要再添加的一个条件是_______.【答案】ABDC =【分析】要使ABC DCB ≅,由于BC 是公共边,若补充一组边相等,则可用SSS 判定其全等.【详解】解:添加AB DC =.在ABC 和DCB △中AB DC BC CB AC BD =⎧⎪=⎨⎪=⎩, ∴()ABC DCB SSS ≅△△, 故答案为:AB DC =.【点睛】本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS 、HL .添加时注意:AAA 、SSA 不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择添加的条件是正确解答本题的关键.14.(2022秋·浙江丽水·八年级统考期末)如图,在ABC 中,CD 是边AB 上的高,BE 平分ABC ∠,交CD 于点E ,6BC =,若BCE 的面积为9,则DE 的长为______.【答案】3【分析】过E 作EF BC ⊥于F ,根据角平分线性质求出EF DE =,根据三角形面积公式求出即可.【详解】解:过E 作EF BC ⊥于F ,CD 是AB 边上的高,BE 平分ABC ∠,交CD 于点E ,DE EF ∴=,192BCE S BC EF =⋅=,1692EF ∴⨯⨯=,3EF DE ∴==,故答案为:3.【点睛】本题考查了角平分线性质的应用,能根据角平分线性质求出3EF DE ==是解此题的关键,注意:在角的内部,角平分线上的点到角的两边的距离相等. 八年级期末)如图,在ABC 中, 【答案】4【分析】根据线段垂直平分线的性质得到2AD BD ==,则4CD AC AD =−=.【详解】解:∵AB 的垂直平分线交AB 于点E ,交AC 于点D ,∴2AD BD ==,∵6AC =,∴4CD AC AD =−=,故答案为:4.【点睛】本题主要考查了线段垂直平分线的性质,熟知线段垂直平分线上的点到线段两端的距离相等是解题的关键. 16.(2022秋·浙江温州·八年级校联考期中)如图,在ABC 中,DE 是AC 的中垂线,分别交AC ,AB 于点D ,E .已知BCE 的周长为9,4BC =,则AB 的长为______.【答案】5【分析】先利用三角形周长得到5CE BE +=,再根据线段垂直平分线的性质得到EC EA =,然后利用等线段代换得到AB 的长.【详解】解:∵BCE 的周长为9,9CE BE BC ∴++=,又4BC =,5CE BE ∴+=,又DE 是AC 的中垂线,EC EA ∴=,5AB AE BE CE BE ∴=+=+=;故答案为:5.【点睛】本题考查了垂直平分线的性质:垂直平分线上任意一点,到线段两端点的距离相等.17.(2023秋·浙江杭州·八年级校考开学考试)如图,已知12∠=∠,要说明ABC BAD ≌,(1)若以“SAS ”为依据,则需添加一个条件是__________;(2)若以“ASA ”为依据,则需添加一个条件是__________.【答案】 BC AD = BAC ABD ∠=∠【分析】(1)根据SAS 可添加一组角相等,故可判定全等;(2)根据ASA 可添加一组角相等,故可判定全等;【详解】解:(1)已知一组角相等和一个公共边,以“SAS ”为依据,则需添加一组角,即BC AD =故答案为:BC AD =;(2)已知一组角相等,和一个公共边,以“ASA ”为依据,则需添加一组角,即BAC ABD ∠=∠. 故答案为:BAC ABD ∠=∠.【点睛】本题主要考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS SAS ASA AAS HL 、、、、.添加时注意:AAA SSA 、不能判定两个三角形全等. 18.(2019秋·浙江嘉兴·八年级校考阶段练习)如图,点B 、E 、C 、F 在一条直线上,AB ∥DE ,AB=DE ,BE=CF ,AC=6,则DF=________【答案】6.【分析】根据题中条件由SAS 可得△ABC ≌△DEF ,根据全等三角形的性质可得AC=DF=6.【详解】∵AB ∥DE ,∴∠B=∠DEF∵BE=CF ,∴BC=EF ,在△ABC 和△DEF 中,AB DE B DEFBC EF =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DEF (SAS ),∴AC=DF=6.考点:全等三角形的判定与性质.。
全等三角形知识点总结(精选18篇)

全等三角形知识点总结(精选18篇)(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如工作总结、工作计划、合同协议、条据书信、讲话致辞、规章制度、策划方案、句子大全、教学资料、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample texts for everyone, such as work summaries, work plans, contract agreements, document letters, speeches, rules and regulations, planning plans, sentence summaries, teaching materials, other sample texts, etc. If you want to learn about different sample formats and writing methods, please pay attention!全等三角形知识点总结(精选18篇)全等三角形知识点总结第1篇全等三角形的课件一、教材分析(一)本节内容在教材中的地位与作用。
(完整版)全等三角形知识总结和经典例题

全等三角形复习[ 知识要点 ]一、全等三角形1.判定和性质一般三角形直角三角形边角边( SAS)、角边角( ASA)具备一般三角形的判定方法判定斜边和一条直角边对应相等( HL )角角边( AAS)、边边边( SSS)对应边相等,对应角相等性质对应中线相等,对应高相等,对应角平分线相等注:①判定两个三角形全等必须有一组边对应相等;② 全等三角形面积相等.2.证题的思路:找夹角( SAS)已知两边找直角( HL )找第三边( SSS)若边为角的对边,则找任意角( AAS)找已知角的另一边(SAS)已知一边一角边为角的邻边找已知边的对角(AAS)找夹已知边的另一角(ASA)找两角的夹边(ASA)已知两角找任意一边(AAS)性质1、全等三角形的对应角相等、对应边相等。
2、全等三角形的对应边上的高对应相等。
3、全等三角形的对应角平分线相等。
4、全等三角形的对应中线相等。
5、全等三角形面积相等。
6、全等三角形周长相等。
( 以上可以简称 : 全等三角形的对应元素相等)7、三边对应相等的两个三角形全等。
(SSS)8、两边和它们的夹角对应相等的两个三角形全等。
(SAS)9、两角和它们的夹边对应相等的两个三角形全等。
(ASA)10、两个角和其中一个角的对边对应相等的两个三角形全等。
(AAS)11、斜边和一条直角边对应相等的两个直角三角形全等。
(HL)运用1、性质中三角形全等是条件,结论是对应角、对应边相等。
而全等的判定却刚好相反。
2、利用性质和判定,学会准确地找出两个全等三角形中的对应边与对应角是关键。
在写两个三角形全等时,一定把对应的顶点,角、边的顺序写一致,为找对应边,角提供方便。
3,当图中出现两个以上等边三角形时,应首先考虑用 SAS找全等三角形。
4、用在实际中,一般我们用全等三角形测等距离。
以及等角,用于工业和军事。
有一定帮助。
5、角平分线的性质及判定性质:角平分线上的点到这个角的两边的距离相等判定:到一个角的两边距离相等的点在这个角平分线上做题技巧一般来说考试中线段和角相等需要证明全等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形的判定题型类型一、全等三角形的判定1——“边边边”例题、已知:如图,AD =BC ,AC =BD.试证明:∠CAD =∠DBC.(答案)证明:连接DC ,在△ACD 与△BDC 中()AD BC AC BDCD DC ⎧=⎪=⎨⎪=⎩公共边 ∴△ACD ≌△BDC (SSS )∴∠CAD =∠DBC (全等三角形对应角相等)类型二、全等三角形的判定2——“边角边”例题、已知,如图,在四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于E ,并且AE =12(AB +AD ),求证:∠B +∠D =180°. (答案)证明:在线段AE 上,截取EF =EB ,连接FC ,∵CE ⊥AB ,∴∠CEB =∠CEF =90°在△CBE 和△CFE 中,CEB CEF EC =EC EB EF =⎧⎪∠=∠⎨⎪⎩∴△CBE 和△CFE (SAS )∴∠B =∠CFE∵AE =12(AB +AD ),∴2AE = AB +AD ∴AD =2AE -AB ∵AE =AF +EF ,∴AD =2(AF +EF )-AB =2AF +2EF -AB =AF +AF +EF +EB -AB =AF +AB -AB ,即AD =AF在△AFC 和△ADC 中(AF AD FAC DAC AC AC =⎧⎪∠=∠⎨⎪=⎩角平分线定义)∴△AFC ≌△ADC (SAS )∴∠AFC =∠D∵∠AFC +∠CFE =180°,∠B =∠CFE.∴∠AFC +∠B =180°,∠B +∠D =180°. 类型三、全等三角形的判定3——“角边角”例题、已知:如图,在△MPN 中,H 是高MQ 和NR 的交点,且MQ =NQ .求证:HN =PM.证明:∵MQ 和NR 是△MPN 的高, ∴∠MQN =∠MRN =90°,又∵∠1+∠3=∠2+∠4=90°,∠3=∠4 ∴∠1=∠2在△MPQ 和△NHQ 中,12MQ NQ MQP NQH ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MPQ ≌△NHQ (ASA ) ∴PM =HN类型四、全等三角形的判定4——“角角边”例题、已知Rt △ABC 中,AC =BC ,∠C =90°,D 为AB 边的中点,∠EDF =90°,∠EDF 绕D 点旋转,它的两边分别交AC 、CB 于E 、F .当∠EDF 绕D 点旋转到DE ⊥AC 于E 时(如图1),易证12DEF CEF ABC S S S +=△△△;当∠EDF 绕D 点旋转到DE 和AC 不垂直时,在图2情况下,上述结论是否成立?若成立,请给予证明;若不成立,请写出你的猜想,不需证明.解:图2成立; 证明图2:过点D 作DM AC DN BC ⊥⊥,则90DME DNF MDN ∠=∠=∠=°在△AMD 和△DNB 中,AMD=DNB=90A B AD BD ∠∠︒⎧⎪∠=∠⎨⎪=⎩∴△AMD ≌△DNB (AAS )∴DM =DN∵∠MDE +∠EDN =∠NDF +∠EDN =90°,∴∠ MDE =∠NDF在△DME 与△DNF 中,90EMD FDN DM DN MDE NDF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴△DME ≌△DNF (ASA )∴DME DNF S S =△△∴DEF CEF DMCN DECF S =S =S S .+△△四边形四边形可知ABC DMCN 1S =S 2△四边形,∴12DEF CEF ABC S S S +=△△△ 类型五、直角三角形全等的判定——“HL ”下列说法中,正确的画“√”;错误的画“×”,并举出反例画出图形.(1)一条直角边和斜边上的高对应相等的两个直角三角形全等.( )(2)有两边和其中一边上的高对应相等的两个三角形全等.( )(3)有两边和第三边上的高对应相等的两个三角形全等.( )(答案)(1)√;(2)×;在△ABC 和△DBC 中,AB =DB ,AE 和DF 是其中一边上的高,AE =DF(3)×. 在△ABC 和△ABD 中,AB =AB ,AD =AC ,AH 为第三边上的高,如下图:1、已知:如图,DE ⊥AC ,BF ⊥AC ,AD =BC ,DE =BF.求证:AB ∥DC.(答案与解析)证明:∵DE ⊥AC ,BF ⊥AC ,∴在Rt △ADE 与Rt △CBF 中.AD BC DE BF ⎧⎨⎩=,=∴Rt △ADE ≌Rt △CBF (HL ) ∴AE =CF ,DE =BF ∴AE +EF =CF +EF ,即AF =CE在Rt △CDE 与Rt △ABF 中,DE BF DEC BFA EC FA =⎧⎪∠=∠⎨⎪=⎩∴Rt △CDE ≌Rt △ABF (SAS )∴∠DCE =∠BAF ∴AB ∥DC.(点评)从已知条件只能先证出Rt △ADE ≌Rt △CBF ,从结论又需证Rt △CDE ≌Rt △ABF.我们可以从已知和结论向中间推进,证出题目.2、如图,△ABC 中,∠ACB =90°,AC =BC ,AE 是BC 边上的中线,过C 作CF ⊥AE ,垂足为F ,过B 作BD ⊥BC 交CF 的延长线于D.(1)求证:AE =CD ;(2)若AC =12cm ,求BD 的长.(答案与解析)(1)证明:∵DB ⊥BC ,CF ⊥AE ,∴∠DCB +∠D =∠DCB +∠AEC =90°.∴∠D =∠AEC .又∵∠DBC =∠ECA =90°,且BC =CA ,∴△DBC ≌△ECA (AAS ).∴AE =CD .(2)解:由(1)得AE =CD ,AC =BC ,∴△CDB ≌△AEC (HL ) ∴BD =EC =12BC =12AC ,且AC =12.∴BD =6cm .(点评)三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件三角形角平分线的性质三角形三条角平分线交于三角形内部一点,此点叫做三角形的内心且这一点到三角形三边的距离相等.三角形的一内角平分线和另外两顶点处的外角平分线交于一点.这点叫做三角形的旁心.三角形有三个旁心.所以到三角形三边所在直线距离相等的点共有4个.如图所示:△ABC 的内心为1P ,旁心为234,,P P P ,这四个点到△ABC 三边所在直线距离相等.角的平分线的性质及判定1、如图,AD 是∠BAC 的平分线,DE ⊥AB ,交AB 的延长线于点E ,DF ⊥AC于点F ,且DB =DC.求证:BE =CF.(答案)证明:∵DE ⊥AE ,DF ⊥AC ,AD 是∠BAC 的平分线, ∴DE =DF ,∠BED =∠DFC =90°在Rt △BDE 与Rt △CDF 中,DB DC DE DF=⎧⎨=⎩,∴Rt △BDE ≌Rt △CDF (HL ) ∴BE =CF2、如图,AC=DB ,△PAC 与△PBD 的面积相等.求证:OP 平分∠AOB .(答案与解析)证明:作PM ⊥OA 于M ,PN ⊥OB 于N12PAC S AC PM =△∵,12PBD S BD PN =△,且PAC S =△PBD S △ ∴ 12AC PM 12BD PN = 又∵AC =BD ∴PM =PN又∵PM ⊥OA ,PN ⊥OB ∴OP 平分∠AOB(点评)观察已知条件中提到的三角形△PAC 与△PBD ,显然与全等无关,而面积相等、底边相等,于是自然想到可得两三角形的高线相等,联系到角平分线判定定理可得.跟三角形的高结合的题目,有时候用面积会取得意想不到的效果.3、如图,DC ∥AB ,∠BAD 和∠ADC 的平分线相交于E ,过E 的直线分别交DC 、AB 于C 、B 两点. 求证:AD =AB +DC.(答案) 证明:在线段AD 上取AF =AB ,连接EF ,∵AE 是∠BAD 的角平分线,∴∠1=∠2,∵AF =AB AE =AE ,∴△ABE ≌△AFE ,∴∠B =∠AFE由CD ∥AB 又可得∠C +∠B =180°,∴∠AFE +∠C =180°,又∵∠DFE +∠AFE =180°,∴∠C =∠DFE ,∵DE 是∠ADC 的平分线,∴∠3=∠4,又∵DE =DE ,∴△CDE ≌△FDE ,∴DF =DC ,∵AD =DF +AF ,∴AD =AB +DC .类型一、全等三角形的性质和判定如图,已知:AE ⊥AB ,AD ⊥AC ,AB =AC ,∠B =∠C ,求证:BD =CE.(答案)证明:∵AE ⊥AB ,AD ⊥AC , ∴∠EAB =∠DAC =90°∴∠EAB +∠DAE =∠DAC +∠DAE ,即∠DAB =∠EAC.在△DAB 与△EAC 中,DAB EAC AB AC B C ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△DAB ≌△EAC (SAS ) ∴BD =CE.类型二、巧引辅助线构造全等三角形(1).作公共边可构造全等三角形:1、在ΔABC 中,AB =AC.求证:∠B =∠C(答案)证明:过点A 作AD ⊥BC 在Rt △ABD 与Rt △ACD 中AB AC AD AD =⎧⎨=⎩∴Rt △ABD ≌Rt △ACD (HL ) ∴∠B =∠C.(2).倍长中线法:1、已知:如图所示,CE、CB分别是△ABC与△ADC的中线,且∠ACB=∠ABC.求证:CD=2CE.(答案)证明:延长CE至F使EF=CE,连接BF.∵ EC为中线,∴ AE=BE.在△AEC与△BEF中,,,,AE BEAEC BEFCE EF=⎧⎪∠=∠⎨⎪=⎩∴△AEC≌△BEF(SAS).∴ AC=BF,∠A=∠FBE.(全等三角形对应边、角相等)又∵∠ACB=∠ABC,∠DBC=∠ACB+∠A,∠FBC=∠ABC+∠A.∴ AC=AB,∠DBC=∠FBC.∴ AB=BF.又∵ BC为△ADC的中线,∴ AB=BD.即BF=BD.在△FCB与△DCB中,,,,BF BDFBC DBCBC BC=⎧⎪∠=∠⎨⎪=⎩∴△FCB≌△DCB(SAS).∴ CF=CD.即CD=2CE.2、若三角形的两边长分别为5和7, 则第三边的中线长x的取值范围是( )A.1 <x< 6B.5 <x< 7C.2 <x< 12D.无法确定(答案)A ;提示:倍长中线构造全等三角形,7-5<2x<7+5,所以选A选项.(3).作以角平分线为对称轴的翻折变换构造全等三角形:如图,AD是ABC∆的角平分线,H,G分别在AC,AB上,且HD=BD.(1)求证:∠B与∠AHD互补;(2)若∠B+2∠DGA=180°,请探究线段AG与线段AH、HD之间满足的等量关系,并加以证明.(答案)证明:(1)在AB上取一点M, 使得AM=AH, 连接DM.∵∠CAD=∠BAD, AD=AD, ∴△AHD≌△AMD. ∴ HD=MD, ∠AHD=∠AMD.∵ HD=DB, ∴ DB= MD. ∴∠DMB=∠B.∵∠AMD+∠DMB =180︒,∴∠AHD+∠B=180︒. 即∠B与∠AHD互补.(2)由(1)∠AHD=∠AMD, HD=MD, ∠AHD+∠B=180︒.∵∠B+2∠DGA =180︒,∴∠AHD=2∠DGA.∴∠AMD=2∠DGM.∵∠AMD=∠DGM+∠GDM. ∴ 2∠DGM=∠DGM+∠GDM.∴∠DGM=∠GDM. ∴ MD=MG.∴ HD= MG.∵ AG= AM+MG, ∴ AG= AH+HD. (3).利用截长(或补短)法作构造全等三角形:1、如图,AD是△ABC的角平分线,AB>AC,求证:AB-AC>BD-DC(答案)证明:在AB上截取AE=AC,连结DE∵AD是△ABC的角平分线,∴∠BAD=∠CADM GHDCB AEA在△AED 与△ACD 中⎪⎩⎪⎨⎧=∠=∠=ADAD CAD BAD ACAE∴△AED ≌△ADC (SAS )∴DE =DC在△BED 中,BE >BD -DC即AB -AE >BD -DC ∴AB -AC >BD -DC2、如图所示,已知△ABC 中AB >AC ,AD 是∠BAC 的平分线,M 是AD 上任意一点,求证:MB -MC <AB -AC .(答案与解析)证明:∵AB >AC ,则在AB 上截取AE =AC ,连接ME .在△MBE 中,MB -ME <BE (三角形两边之差小于第三边).在△AMC 和△AME 中,()()()AC AE CAM EAM AM AM =⎧⎪∠=∠⎨⎪=⎩所作,角平分线的定义,公共边,∴ △AMC ≌△AME (SAS ).∴ MC =ME (全等三角形的对应边相等).又∵ BE =AB -AE ,∴ BE =AB -AC ,∴ MB -MC <AB -AC .(点评)因为AB >AC ,所以可在AB 上截取线段AE =AC ,这时BE =AB -AC ,如果连接EM ,在△BME 中,显然有MB -ME <BE .这表明只要证明ME =MC ,则结论成立.充分利用角平分线的对称性,截长补短是关键.(4).在角的平分线上取一点向角的两边作垂线段.1、如图所示,已知E 为正方形ABCD 的边CD 的中点,点F 在BC 上,且∠DAE =∠FAE .求证:AF =AD +CF .(答案与解析)证明: 作ME ⊥AF 于M ,连接EF .∵ 四边形ABCD 为正方形,∴ ∠C =∠D =∠EMA =90°.又∵ ∠DAE =∠FAE ,∴ AE 为∠FAD 的平分线,∴ ME =DE .在Rt △AME 与Rt △ADE 中,()()AE AE DE ME =⎧⎨=⎩公用边,已证,∴ Rt △AME ≌Rt △ADE(HL).∴ AD =AM(全等三角形对应边相等).又∵ E 为CD 中点,∴ DE =EC .∴ ME =EC .在Rt △EMF 与Rt △ECF 中,()(ME CE EF EF =⎧⎨=⎩已证,公用边),∴ Rt △EMF ≌Rt △ECF(HL).∴ MF =FC(全等三角形对应边相等).由图可知:AF =AM +MF ,∴ AF =AD +FC(等量代换).(点评)与角平分线有关的辅助线: 在角两边截取相等的线段,构造全等三角形;在角的平分线上取一点向角的两边作垂线段. 四边形ABCD为正方形,则∠D=90°.而∠DAE=∠FAE说明AE为∠FAD的平分线,按常规过角平分线上的点作出到角两边的距离,而E到AD的距离已有,只需作E到AF的距离EM即可,由角平分线性质可知ME=DE.AE=AE.Rt△AME与Rt△ADE全等有AD=AM.而题中要证AF=AD+CF.根据图知AF=AM+MF.故只需证MF=FC即可.从而把证AF=AD+CF转化为证两条线段相等的问题.2、如图所示,在△ABC中,AC=BC,∠ACB=90°,D是AC上一点,且AE垂直BD的延长线于E,12AE BD,求证:BD是∠ABC的平分线.(答案与解析)证明:延长AE和BC,交于点F,∵AC⊥BC,BE⊥AE,∠ADE=∠BDC(对顶角相等),∴∠EAD+∠ADE=∠CBD+∠BDC.即∠EAD=∠CBD.在Rt△ACF和Rt△BCD中.所以Rt△ACF≌Rt△BCD(ASA).则AF=BD(全等三角形对应边相等).∵AE=BD,∴AE=AF,即AE=EF.在Rt△BEA和Rt△BEF中,则Rt△BEA≌Rt△BEF(SAS).所以∠ABE=∠FBE(全等三角形对应角相等),即BD是∠ABC的平分线.(点评)如果由题目已知无法直接得到三角形全等,不妨试着添加辅助线构造出三角形全等的条件,使问题得以解决.平时练习中多积累一些辅助线的添加方法.类型三、全等三角形动态型问题解决动态几何问题时要善于抓住以下几点:(1)变化前的结论及说理过程对变化后的结论及说理过程起着至关重要的作用;(2)图形在变化过程中,哪些关系发生了变化,哪些关系没有发生变化;原来的线段之间、角之间的位置与数量关系是否还存在是解题的关键;(3)几种变化图形之间,证明思路存在内在联系,都可模仿与借鉴原有的结论与过程,其结论有时变化,有时不发生变化1、已知:在△ABC中,∠BAC=90°,AB=AC,点D为射线BC上一动点,连结AD,以AD为一边且在AD的右侧作正方形ADEF.(1)当点D在线段BC上时(与点B不重合),如图1,求证:CF=BD(2)当点D运动到线段BC的延长线上时,如图2,第(1)问中的结论是否仍然成立,并说明理由.(答案)证明:(1)∵正方形ADEF ∴AD =AF ,∠DAF =90°∴∠DAF -∠DAC =∠BAC -∠DAC ,即∠BAD =∠CAF在△ABD 和△ACF 中,AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△ACF (SAS ) ∴BD =CF(2)当点D 运动到线段BC 的延长线上时,仍有BD =CF此时∠DAF +∠DAC =∠BAC +∠DAC ,即∠BAD =∠CAF在△ABD 和△ACF 中,AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△ACF (SAS ) ∴BD =CF2、如图(1),△ABC 中,BC =AC ,△CDE 中,CE =CD ,现把两个三角形的C 点重合,且使∠BCA =∠ECD ,连接BE ,AD .求证:BE =AD .若将△DEC 绕点C 旋转至图(2),(3)所示的情况时,其余条件不变,BE 与AD 还相等吗?为什么?(答案)证明:∵∠BCA =∠ECD , ∴∠BCA -∠ECA =∠ECD -∠ECA ,即∠BCE =∠ACD在△ADC 与△BEC 中ACD=BCE AC BC CD CE =⎧⎪∠∠⎨⎪=⎩∴△ADC ≌△BEC(SAS) ∴BE =AD .若将△DEC 绕点C 旋转至图(2),(3)所示的情况时,其余条件不变,BE 与AD 还相等,因为还是可以通过SAS 证明△ADC ≌△BEC.。
