Matlab作业题
MATLAB习题及参考答案经典.doc

习题:1, 计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。
2, 对于B AX =,如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ,求解X 。
3, 已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ,分别计算a 的数组平方和矩阵平方,并观察其结果。
4, 角度[]604530=x ,求x 的正弦、余弦、正切和余切。
(应用sin,cos,tan.cot)5, 将矩阵⎥⎦⎤⎢⎣⎡=7524a 、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵: (1)组合成一个4⨯3的矩阵,第一列为按列顺序排列的a 矩阵元素,第二列为按列顺序排列的b 矩阵元素,第三列为按列顺序排列的c 矩阵元素,即 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡237912685574(2)按照a 、b 、c 的列顺序组合成一个行矢量,即 []2965318772546, 将(x -6)(x -3)(x -8)展开为系数多项式的形式。
(应用poly,polyvalm)7, 求解多项式x 3-7x 2+2x +40的根。
(应用roots)8, 求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。
(应用poly,polyvalm)9, 计算多项式9514124234++--x x x x 的微分和积分。
(应用polyder,polyint ,poly2sym)10, 解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡66136221143092x 。
(应用x=a\b)11, 求欠定方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡5865394742x 的最小范数解。
(应用pinv) 12, 矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=943457624a ,计算a 的行列式和逆矩阵。
(应用det,inv)13, y =sin(x ),x 从0到2π,∆x =0.02π,求y 的最大值、最小值、均值和标准差。
matlab作业题

第一章 MATLAB环境1、MATLAB通用操作界面窗口包括哪些?命令窗口、历史命令窗口、当前目录窗口、工作空间窗口各有哪些功能?答:MATLAB通用操作界面窗口包括:命令窗口、历史命令窗口、当前目录浏览器窗口、工作空间窗口、变量编辑器窗口、M文件编辑/调试器窗口、程序性能剖析窗口、MATLAB 帮助。
命令窗口是MATLAB命令操作的最主要窗口,可以把命令窗口当做高级的“草稿纸”。
在命令窗口中可以输入各种MATLAB的命令、函数和表达式,并显示除图形外的所有运算结果。
历史命令窗口用来记录并显示已经运行过的命令、函数和表达式,并允许用户对它们进行选择、复制和重运行,用户可以方便地输入和修改命令,选择多行命令以产生M文件。
当前目录窗口用来设置当前目录,可以随时显示当前目录下的M、MKL等文件的信息,扬文件类型、文件名、最后个修改时间和文件的说明信息等,并可以复制、编辑和运行M 文件及装载MAT数据文件。
工作空间窗口用来显示所有MATLAB工作空间中的变量名、数据结构、类型、大小和字节数。
2、熟悉课本中表格1.4、1.5、1.6、1.7、1.8的内容。
3、如何生成数据文件?如何把数据文件中的相关内容输入到工作空间中,用实例进行操作。
4、在工作空间中可以通过哪些命令管理变量,写出每种语法的具体操作过程。
答:(1)把工作空间中的数据存放到MAT数据文件。
语法:save filename 变量1 变量2 ……参数。
(2)从数据文件中取出变量存放到工作空间。
语法: load filename 变量1 变量2 ……。
(3)查阅MATLAB内存变量名。
语法:who(4)、查阅MATLAB内存变量变量名、大小、类型和字节数。
语法:whos(5)、删除工作空间中的变量。
语法:clear(6)查询工作空间中是否存在某个变量。
语法:i=exist(‘X’)5、MATLAB用户文件格式有几哪种?扩展名各是什么?答:MATLAB的用户文件格式通常有以下几种:(1)程序文件,扩展名为.m。
matlab试题及答案

matlab试题及答案# MATLAB试题及答案一、选择题1. MATLAB的基本数据单位是:A. 矩阵B. 向量C. 标量D. 数组答案:A2. 下列哪个命令可以用来绘制函数图形?A. `plot`B. `graph`C. `draw`D. `chart`答案:A3. MATLAB中,以下哪个是正确的矩阵转置操作?A. `transpose(A)`B. `A'`C. `A^T`D. `flip(A)`答案:B二、简答题1. 简述MATLAB中矩阵的基本操作。
答案:在MATLAB中,矩阵是最基本的数据结构,可以进行加、减、乘、除等基本运算。
矩阵的创建可以使用方括号`[]`,例如`A = [1 2;3 4]`。
矩阵的转置使用单引号`'`,例如`A'`。
矩阵的求逆使用`inv`函数,例如`inv(A)`。
2. MATLAB中如何实现循环结构?答案:MATLAB中实现循环结构主要有两种方式:`for`循环和`while`循环。
`for`循环用于已知迭代次数的情况,例如:```matlabfor i = 1:5disp(i);end````while`循环用于迭代次数未知的情况,例如:```matlabi = 1;while i <= 5disp(i);i = i + 1;end```三、计算题1. 给定矩阵A和B,请计算它们的乘积C,并求C的行列式。
A = [1 2; 3 4]B = [5 6; 7 8]答案:首先计算矩阵乘积C:```matlabC = A * B;```然后计算C的行列式:```matlabdetC = det(C);```结果为:```matlabC = [19 22; 43 50]detC = -16```2. 编写一个MATLAB函数,计算并返回一个向量的范数。
答案:```matlabfunction norm_value = vector_norm(v)norm_value = norm(v);end```四、编程题1. 编写一个MATLAB脚本,实现以下功能:- 随机生成一个3x3的矩阵。
内蒙古工业大学Matlab作业
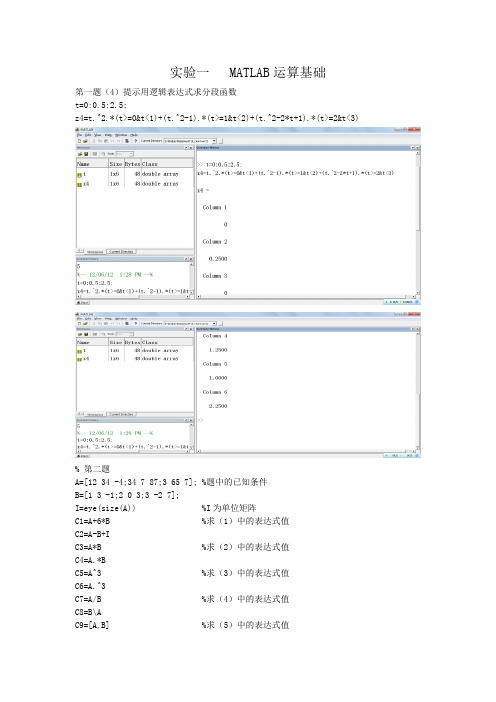
实验一 MATLAB运算基础第一题(4)提示用逻辑表达式求分段函数t=0:0.5:2.5;z4=t.^2.*(t>=0&t<1)+(t.^2-1).*(t>=1&t<2)+(t.^2-2*t+1).*(t>=2&t<3)% 第二题A=[12 34 -4;34 7 87;3 65 7]; %题中的已知条件B=[1 3 -1;2 0 3;3 -2 7];I=eye(size(A)) %I为单位矩阵C1=A+6*B %求(1)中的表达式值C2=A-B+IC3=A*B %求(2)中的表达式值C4=A.*BC5=A^3 %求(3)中的表达式值C6=A.^3C7=A/B %求(4)中的表达式值C8=B\AC9=[A,B] %求(5)中的表达式值C10=[A([1,3],:);B^2]实验二 MATLAB矩阵分析与处理5、下面是一个线性方程组%(1)求方程的解。
A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6];b=[0.95,0.67,0.52]';x=inv(A)*b%(2)将方程右边向量元素b3改为0.53,在求解,并比较b3的变化和解的相比对变化B=[0.95,0.67,0.53]';x=inv(A)*B实验三选择程序设计1求分段函数的值X<0且x≠-3,y=x^2+x-6; 0≦x<5且x≠2及x≠3,y=x^2-5x+6;其他y=x^2-x-1用if语句实现,分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y值。
%编辑程序如下:x=[-5.0,-3.0,1.0,2.0,2.5,3.0,5.0];y=[]; %建立存放所有y值的矩阵for x0=xif x0<0&x0~=-3y=[y,x0.^2+x0-6];elseif x0>=0&x0<5&x0~=2&x0~=3y=[y,x0.^2-5*x0+6];elsey=[y,x0.^2-x0-1];endendx %输出所有xy %输出所有y2、输入一个百分制成绩,要求输出成绩等级A,B,C,D,E。
MATLAB与控制系统仿真大作业

>> G1=tf(num,den);
>> G1=zpk(G1)
G1 =
5 (s+0.6) ----------------(s+3) (s+2) (s+1)
>> num=[2 1]; den=[1 2.9 1]; G2=tf(num,den); >> G2=zpk(G2)
G2 =
2 (s+0.5)
>> xlabel('x') ylabel('exp(-2.*x)')
三、simulink 建模(每题 10 分,共 20 分)
1、已知单位负反馈的开环传递函数为 G(s) =
2 s2 + 4s
,试利用
simulink
建立系在单位阶跃输入作用下的模型。
要求答案包括:(1)simulink 建模结构图;
(2)在同一个坐标中的阶跃信号和响应曲线图。
2、已知系统的开环传递函数为
G1(s)
=
2s2 + 5s + 6 s2 + 2s + 3
、G2 (s)
=
s2
s+6 + 7s +1
,H
(s)
=
5(s + 2) s +10
求:建立 Simulink 仿真模型,并求出其系统在单位阶跃响应;
要求答案包括:(1)simulink 建模结构图;
x=
-2.9709
0.5491
3.6000
0.0509
2. 已知下列矩阵
2 3 1
−1 3 5
A
=
matlab平时作业

Matlab 平时作业 第一章 习题13. 请指出如下5个变量名中,哪些是合法的? abcd-2 xyz_3 3chan a 变量 ABCDefgh 合法变量有: abcd-2 xyz_3 ABCDefgh 6. 指令clear, clf, clc 各有什么用处? clear : 从内存中清除变量和函数 clf :清除当前图形 clc :清命令窗口7. 以下两种说法对吗?(1)“MATLAB 的数值表达精度与其指令窗中的数据显示精度相同。
” (2)MATLAB 指令窗中显示的数值有效位数不超过7位。
” 答: 第二种说法不对8. 想要在MATLAB 中产生二维数组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321S ,下面哪些指令能实现目的? S=[1,2,3;4,5,6;7,8;9]S=[1 2 3;4 5 6;7 8 9]S=[1,2,3;4,5,6;7,8,9] %整个指令在中文状态下输入 答:第二种可以实现第三章 习题31.要求在闭区间]2,0[π上产生具有10个等距采样点的一维数组。
试用两种不同的指令实现。
答:指令如下:b=linspace(0,2*pi,10) b =0 0.6981 1.3963 2.0944 2.7925 3.4907 4.1888 4.8869 5.5851 6.2832>> a=0:2*pi/9:2*pi a =0 0.6981 1.3963 2.0944 2.7925 3.4907 4.1888 4.8869 5.5851 6.28322.由指令rand('state',0),A=rand(3,5)生成二维数组A ,试求该数组中所有大于0.5的元素的位置,分别求出它们的“全下标”和“单下标”。
rand('state',0),A=rand(3,5) A =0.9501 0.4860 0.4565 0.4447 0.9218 0.2311 0.8913 0.0185 0.6154 0.7382 0.6068 0.7621 0.8214 0.7919 0.1763>> L=A>0.5 L =1 0 0 0 1 0 1 0 1 1 1 1 1 1 0>> L(1)ans =15. 在时间区间 [0,10]中,绘制t e y t 2cos 15.0--=曲线。
matlab综合大作业(附详细答案)

m a t l a b综合大作业(附详细答案)-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII《MATLAB语言及应用》期末大作业报告1.数组的创建和访问(20分,每小题2分):1)利用randn函数生成均值为1,方差为4的5*5矩阵A;实验程序:A=1+sqrt(4)*randn(5)实验结果:A =0.1349 3.3818 0.6266 1.2279 1.5888-2.3312 3.3783 2.4516 3.1335 -1.67241.2507 0.9247 -0.1766 1.11862.42861.5754 1.6546 5.3664 0.8087 4.2471-1.2929 1.3493 0.7272 -0.6647 -0.38362)将矩阵A按列拉长得到矩阵B;实验程序:B=A(:)实验结果:B =0.1349-2.33121.25071.5754-1.29293.38183.37830.92471.65461.34930.62662.4516-0.17665.36640.72721.22793.13351.11860.8087-0.66471.5888-1.67242.42864.2471-0.38363)提取矩阵A的第2行、第3行、第2列和第4列元素组成2*2的矩阵C;实验程序:C=[A(2,2),A(2,4);A(3,2),A(3,4)]实验结果:C =3.3783 3.13350.9247 1.11864)寻找矩阵A中大于0的元素;]实验程序:G=A(find(A>0))实验结果:G =0.13491.25071.57543.38183.37830.92471.65461.34930.62662.45165.36640.72721.22793.13351.11860.80871.58882.42864.24715)求矩阵A的转置矩阵D;实验程序:D=A'实验结果:D =0.1349 -2.3312 1.2507 1.5754 -1.29293.3818 3.3783 0.9247 1.6546 1.34930.6266 2.4516 -0.1766 5.3664 0.72721.2279 3.1335 1.1186 0.8087 -0.66471.5888 -1.67242.4286 4.2471 -0.38366)对矩阵A进行上下对称交换后进行左右对称交换得到矩阵E;实验程序:E=flipud(fliplr(A))实验结果:E =-0.3836 -0.6647 0.7272 1.3493 -1.29294.2471 0.80875.3664 1.6546 1.57542.4286 1.1186 -0.1766 0.9247 1.2507-1.6724 3.1335 2.4516 3.3783 -2.33121.5888 1.2279 0.6266 3.3818 0.13497)删除矩阵A的第2列和第4列得到矩阵F;实验程序:F=A;F(:,[2,4])=[]实验结果:F =0.1349 0.6266 1.5888-2.3312 2.4516 -1.67241.2507 -0.17662.42861.5754 5.3664 4.2471-1.2929 0.7272 -0.38368)求矩阵A的特征值和特征向量;实验程序:[Av,Ad]=eig(A)实验结果:特征向量Av =-0.4777 0.1090 + 0.3829i 0.1090 - 0.3829i -0.7900 -0.2579 -0.5651 -0.5944 -0.5944 -0.3439 -0.1272-0.2862 0.2779 + 0.0196i 0.2779 - 0.0196i -0.0612 -0.5682 -0.6087 0.5042 - 0.2283i 0.5042 + 0.2283i 0.0343 0.6786 0.0080 -0.1028 + 0.3059i -0.1028 - 0.3059i 0.5026 0.3660 特征值Ad =6.0481 0 0 0 00 -0.2877 + 3.4850i 0 0 00 0 -0.2877 - 3.4850i 0 00 0 0 0.5915 00 0 0 0 -2.30249)求矩阵A的每一列的和值;实验程序:lieSUM=sum(A)实验结果:lieSUM =-0.6632 10.6888 8.9951 5.6240 6.208710)求矩阵A的每一列的平均值;实验程序:average=mean(A)实验结果:average =-0.1326 2.1378 1.7990 1.1248 1.24172.符号计算(10分,每小题5分):1)求方程组20,0++=++=关于,y z的解;uy vz w y z w实验程序:S = solve('u*y^2 + v*z+w=0', 'y+z+w=0','y,z');y= S. y, z=S. z实验结果:y =[ -1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))-w] [ -1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))-w] z =[ 1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))] [ 1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))]2)利用dsolve 求解偏微分方程,dx dyy x dt dt==-的解; 实验程序:[x,y]=dsolve('Dx=y','Dy=-x')实验结果:x =-C1*cos(t)+C2*sin(t)y = C1*sin(t)+C2*cos(t)3.数据和函数的可视化(20分,每小题5分):1)二维图形绘制:绘制方程2222125x y a a +=-表示的一组椭圆,其中0.5:0.5:4.5a =;实验程序:t=0:0.01*pi:2*pi; for a=0.5:0.5:4.5; x=a*cos(t); y=sqrt(25-a^2)*sin(t); plot(x,y) hold on end实验结果:2) 利用plotyy 指令在同一张图上绘制sin y x =和10x y =在[0,4]x ∈上的曲线;实验程序:x=0:0.1:4; y1=sin(x); y2=10.^x;[ax,h1,h2]=plotyy(x,y1,x,y2); set(h1,'LineStyle','.','color','r'); set(h2,'LineStyle','-','color','g'); legend([h1,h2],{'y=sinx';'y=10^x'});实验结果:3)用曲面图表示函数22z x y =+;实验程序:x=-3:0.1:3; y=-3:0.1:3; [X,Y]=meshgrid(x,y); Z=X.^2+Y.^2; surf(X,Y,Z)实验结果:4)用stem 函数绘制对函数cos 4y t π=的采样序列;实验程序:t=-8:0.1:8;y=cos(pi.*t/4); stem(y)实验结果:4. 设采样频率为Fs = 1000 Hz ,已知原始信号为)150π2sin(2)80π2sin(t t x ⨯+⨯=,由于某一原因,原始信号被白噪声污染,实际获得的信号为))((ˆt size randn x x+=,要求设计出一个FIR 滤波器恢复出原始信号。
matlab上机考试题及答案

matlab上机考试题及答案1. 题目:编写一个MATLAB函数,计算并返回一个向量中所有元素的平方和。
答案:函数定义如下:```matlabfunction sumOfSquares = calculateSumOfSquares(vector)sumOfSquares = sum(vector.^2);end```2. 题目:使用MATLAB的内置函数,找出一个矩阵中的最大元素及其位置。
答案:可以使用`max`函数来找出矩阵中的最大元素,同时使用`find`函数来获取其位置。
示例代码如下:```matlabA = [1, 2, 3; 4, 5, 6; 7, 8, 9];[maxValue, linearIndex] = max(A(:));[row, col] = ind2sub(size(A), linearIndex);```3. 题目:给定一个向量,使用MATLAB编写代码,实现向量元素的逆序排列。
答案:可以使用`flip`函数来实现向量的逆序排列。
示例代码如下:```matlabvector = [1, 2, 3, 4, 5];reversedVector = flip(vector);```4. 题目:编写一个MATLAB脚本,计算并绘制一个正弦波的图像。
答案:可以使用`sin`函数生成正弦波数据,并使用`plot`函数绘制图像。
示例代码如下:```matlabx = linspace(0, 2*pi, 100);y = sin(x);plot(x, y);xlabel('x');ylabel('sin(x)');title('Sine Wave');```5. 题目:给定一个3x3的矩阵,使用MATLAB编写代码,计算其行列式。
答案:可以使用`det`函数来计算矩阵的行列式。
示例代码如下:```matlabmatrix = [1, 2, 3; 4, 5, 6; 7, 8, 9];determinant = det(matrix);```结束语:以上是MATLAB上机考试的题目及答案,希望能够帮助大家更好地掌握MATLAB的编程技巧和函数使用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab作业题:1、作出函数y=x4-4x3+3x+5 (x [0,6])的图形,用小红点标出其在[0,6]之间的最小值点,并在最小值点附近标出该最小值点的坐标值;程序:function f=myfun(x)f=x.^4-4*x.^3+3*x+5;x=linspace(0,6,100);y=x.^4-4*x.^3+3*x+5;x1=fminbnd(@myfun,0,6)y1=myfun(x1)结果:x1 =2.9115y1 =-13.1300plot(x,y,x1,y1,'r*')text(x1,y1,'2.9115,-13.1300');2、某公司有一批以每桶2元购进的彩漆,为了获得较高的利润,希望以较高的价格卖出,但价格越高,售出量就越少,二者之间的关系由表一给出。
于是打算增加广告投入来促销。
而广告费与销售量的关系可由销售增长因子来描述。
例如,投入3万元的广告费,销售因子为1.85,意味着做广告后的销售量将是未做广告销售量的1.85倍。
根据经验,广告费与销售因子的关系如表2,现请你作出决策:投入多少广告费和售价为多少时所获得的利润最大?表1 表2彩漆的销售量摘要在经济学中,某种产品的销售量与产品自身的价格存在着负相关关系,即产品价格上升会导致产品的销售量减少,产品价格下降会导致产品的销售量增加。
与此同时,广告宣传对产品的销售量也是影响深远的。
对一个企业而言,广告费既不是越少越好,也不是多多益善。
广告活动的规模和广告费用的大小,应与企业的生产和流通规模相适应,在发展中求节约。
为研究产品销售量与售价和广告费用的关系,我们收集了某售价与预期销售量和广告费与销售增长因子的一些数据(见附录一),并建立了预期销售量1y 与售价1x 的线性模型:11^1333.54222.50x y -=销售增长因子2y 与广告费2x 的二次函数模型:22^0409.00188.1x y +=—220004.0x利润p 与售价1x 和销售增长因子2x 的模型:222211)0004.00409.00188.1)(1333.54222.50)(2(x x x x x p --+--=关键字:预期销售量 广告费 销售增长因子 线性回归一、问题重述随着经济全球化和市场经济的迅速发展,广告营销在企业营销战略中广告营销活动发挥着越来越重要的作用,是企业营销组合中的一个重要组成部分。
为了在竞争激烈的市场中获得优势,我们试图确定一种商品的售价以及广告费投入,使得可以得到最大利润:1、对数据进行初步整理,利用数据拟合手段,画出散点图以及拟合曲线,找出各个变量之间大致关系;2、 在初步分析之后,再进行拟合数据、拟合曲线等的分析,挖掘数据之间的内在联系,初步建立模型,应用MATLAB 高级软件进行优化处理,得到所需结果;3、分析模型。
二、问题分析人们购买商品,考虑得比较多的是商品的价格和品牌,一个公司如何在竞争激烈的市场中站稳脚步,靠的是顾客的青睐,而顾客的青睐度与产品的销售量是成正比的。
因此,制定合理的能让大众接受的产品价格,至关重要。
同时,打造一个良好的品牌信誉也是一个企业生存的必备条件。
由于广告促进了商品销售,也就促使生产成本和销售成本降低,也包括单位广告成本的降低,因此,广告宣传费用的投入是有其利益产生的。
但是从经济学的角度来考察,任何现实投入都存在着边际产出的问题。
也就是说,广告的费用投入同样应该适度,过度的投入不但不会使投入产出比增加,相反会引起投入产出的降低,使产品的生产和流通成本增加。
因此,广告宣传也必须掌握适度原则。
在得出销售价格和广告费用投入对销售量有重要影响的结论后,研究销售量与销售价格和广告费用之间的关系就很有意义了。
三、符号说明1y :彩漆预期销售量 2y :彩漆销售增长因子 1x :彩漆售价2x :彩漆广告费用p :彩漆销售利润四、模型的建立与求解模型建立:记彩漆预期销售量为1y ,销售增长因子为2y ,售价为1x , 广告费用为2x 为了大致分析彩漆预期销售量1y 与售价1x 和销售增长因子2y 广告费用2x 的关系,首先利用表(1)的数据分别作出1y 对1x 和2y 对2x 的散点图(见图1和图2中的圆点)(程序见附录二)23456图(1)y1对x1的散点图图(2)y2对x2的散点图从图(1)可以发现,随着1x 的增加,1y 的值有比较明显的线性递减趋势,图中的直线式用线性模型:εββ++=1101x y (1)拟合的(其中ε是随机误差)。
而在图(2)中,当2x 增大时,2y 有向上弯曲增加随后又向下弯曲减少的趋势,图中的曲线是用二次函数模型εβββ+++=2222102x x y (2)拟合的。
模型求解:直接利用matlab 统计工具箱中的命令regress 求解,使用格式为: [b,bint,rint,stats]=regress(y,x,alpha)模型(1): [b,bint,rint,stats]=regress(Y1,X1,alpha) (程序见附录三)其中输入Y1为模型(1)中y1的数据的转置,X1为对应于回归系数),(10βββ=的数据矩阵],1[1x ,alpha 为置信水平α;输出b 为β的估计值,常记作β^,bint 为b 的置信区间,r 为残差向量β^xy -,rint 为r 的置信区间,stats 为回归模型的检验统计量,有3个值,第一个是回归方程决定系数2R (R 是相关系数),第2个是F 统计量值,第3个是与F 统计量对应的概率值P.得到模型(1)的回归系数估计值及其置信区间(置信水平α=0.05)、检验统计量2R ,F ,P 的结果见表(1)结果分析:表(3)显示,2R =0.9909指因变量1y (销售量)的99.09%可由模型(1)确定,F 值远远超过F 检验的临界值,P 远小于α,因而模型(1)从整体来看是可用的。
表(3)的回归系数给出了模型(1)中0β,1β的估计值,即0^β=50.4222,2^β=-5.1333.销售量预测:将回归系数的估计值代入模型(1),即可预测公司未来的彩漆销售量y,预测值记作1^y ,得到模型(1)的预测方程:11^0^1^x y ββ+= (3)只需知道售价1x ,就可以计算预测值1^y模型(2):[b,bint,rint,stats]=regress(Y2,X2,alpha) (程序见附录四) 其中输入Y2为模型(2)中2y 的数据的转置,X2为对应于回归系数),,(210ββββ=的数据矩阵],,1[222x x ,得到模型(2)的回归系数估计值及其置信区间(置信水平α=0.05)、检验统计量2R ,F ,P 的结果见表(4)结果分析:表(4)显示,2R =0.9970指因变量1y (销售量)的99.70%可由模型 (2)确定,F 值远远超过F 检验的临界值,P 远小于α,因而模型(2)从整体来看是可用的。
表(4)的回归系数给出了模型(2)中0β,1β,2β的估计值,即0^β=1.0188,1^β=-0.0409,0004.02^-=β .销售量预测:将回归系数的估计值代入模型(2),即可预测公司未来的彩漆销售增长因子2y ,预测值记作21^y ,得到模型(2)的预测方程:21^0^2^x y ββ+=+222^x β (4)只需知道售价2x ,就可以计算预测值2^y某公司销售彩漆的利润可由以下公式算出:广告费用成本销售收入利润--=p即:22^1^1)2(x y y x p --=代入模型(1)、(2)的预测方程(3)、(4)可得:222211)0004.00409.00188.1)(1333.54222.50)(2(x x x x x p --+--= (5)利用MATLAB 工具对利润方程(5)求解(程序见附录五)得到:1x = 5.9113 =2x 35.2074 -118.9437=p可知,当售价为5.9113元,广告投入为35207元时,利润最大,最大利润为118943.7元。
模型改进:在利润模型中我们可以看到,这个模型是以产品售价和广告费为自变量的,而在实际操作中,顾客购买同类产品会更多地注意不同品牌之间价格的差异,而不是它们的价格本身,产品的销售量或者说利润,不仅与售价有关,更多的还与同时期、同种产品的价格有关,这就需要引入价格差的概念,即与同时期市场上其他商家的该产品的售价差,因此,在研究最优营销策略时,用价格差代替售价将更为合适。
五、模型总结销售利润模型中有交互项21x x ,考虑到了售价1x 和广告费用2x 的交互作用,说明该利润模型还是比较可信的。
从模型(2)的系数来看,22x 的系数2^β=-0.0004,趋近于零,对整个模型最终的结果影响不会太大,可以考虑用其他多项式组合模型来表述本问题。
六、参考文献[1] 岳朝龙,黄永兴,《SAS与现代经济统计分析》,合肥:中国科学技术大学出版社,2009年。
[2] 姜启源,谢金星,叶俊,《数学模型》,北京:高等教育出版社,2003年。
[3] 易丹辉,《数据分析与Eviews应用》,北京:中国统计出版社,2002年。
[4] 张志涌,杨祖樱,《MATLAB教程》,北京:北京航空航天大学出版社,2006年。
[5] 汪远征,徐雅静,《SAS软件与统计应用教程》,北京:机械工业出版社,2007年。
[6] 张尧庭,方开泰,《多元统计分析引论》,背北京:科学出版社,2006年。
附录一附录二x1=[2.00 2.50 3.00 3.50 4.00 4.50 5.00 5.50 6.00];y1=[41 38 34 32 29 28 25 22 20];p=polyfit(x1,y1,1);x3=linspace(2,6,100);y3=polyval(p,x3);subplot(1,2,1)plot(x1,y1,'o',x3,y3)title('图(1)')xlabel('y1对x1的散点图')x2=0:10:70;y2=[1.00 1.40 1.70 1.85 1.95 2.00 1.95 1.80];q=polyfit(x2,y2,2);x4=linspace(0,70,100);y4=polyval(q,x4);subplot(1,2,2)plot(x2,y2,'o',x4,y4)title('图(2)')xlabel('y2对x2的散点图')附录三Y1=[41 38 34 32 29 28 25 22 20]'X1=[ones(9,1) [2.00 2.50 3.00 3.50 4.00 4.50 5.00 5.50 6.00]'][b,bint,r,rint,stats]=regress(Y1,X1,0.05)附录四Y2=[1.00 1.40 1.70 1.85 1.95 2.00 1.95 1.80]';X2=[ones(8,1) [0:10:70]' [0:10:70]'.^2];[b,bint,r,rint,stats]=regress(Y2,X2,0.05)附录五function p=myfun(x)p=-(x(1)-2).*(50.4222-5.1333*x(1)).*(1.0188+0.0409*x(2)-0.0004*x(2).^2)+x(2); x0=[1,10];[x,p]=fminunc('myfun',x0)。
