2013数学建模会议分组问题
2013年参加数学建模竞赛集训面试名单及分组

2013年参加数学建模竞赛集训面试名单及分组序号姓名笔试成绩校赛成绩面试地点备注1刘栋B一等C1072邵明杰B一等C1103周晋海B一等C1154程红伟B二等C1165宋雪岩B二等C117东6许天骄B二等C117西7刘文康A特等C1078张杨杨A二等C1109张金剑A特等C11510王凯鹏A一等C11611孙浩B一等C117东12王宇轩B二等C117西13王朝蕊B一等C10714马诗洋B一等C11015潘杰B一等C11516张宇涵A一等C11617郭展扩B一等C117东18李婷B二等C117西19李璞B一等C10720童康宁B二等C11021周刘拉B一等C11522李华清B一等C11623陈人冰B一等C117东24范浩祥B二等C117西25吴玉奇B二等C10726张俊B二等C11027沈晨阳B一等C11528张聪B二等C11629赵海峰B二等C117东30王茹B二等C117西31薛沨B一等C10732汤培梁B一等C11033张容肇B二等C11534王攀B一等C11635孟昱B二等C117东36郭知君B一等C117西37王锦锦A一等C10738师恺琪B二等C11039于文辉B一等C11540程海B一等C116 41李凯鑫B一等C117东42苏春晨B一等C117西43魏国建B特等C107 44吴奇B二等C110 45王睿A二等C115 46付惠泉B一等C116 47沈唱黎B二等C117东48李雁翎B二等C117西49鱼婷A一等C107 50蒋进军B二等C110 51刘振宇B二等C115 52张盛强B二等C116 53谢仁盛B一等C117东54于泉涌B一等C117西55张美A一等C107 56秦越B二等C110 57刘保君A一等C115 58赵子越A一等C116 59赵鹏宇B二等C117东60闫佳男A二等C117西61张诗杰B一等C107 62汪建明A一等C110 63陈彬彬B一等C115 64孙浩B二等C116 65林昱溪B二等C117东66李璐A C117西67张瑞B一等C107 68黄志新B一等C110 69王孝宇B二等C115 70杨亚明A C116 71刘文东A一等C117东72刘啸泽B C117西73陈柯宇B一等C107 74张珊A特等C110 75孙召昌B二等C115 76李媛媛B二等C116 77王凯月A C117东78刘宇航A二等C117西79杨帅涛A C107 80徐炜斌B一等C110 81张婧昕A一等C115 82张忠博A一等C11683郑洋德B一等C117东84施剑华B二等C117西85吴爱萍B二等C107 86李建苗B二等C110 87刘明珠A一等C115 88宋海杰B二等C116 89伍祈应A二等C117东90辛杰B二等C117西91吴科永B二等C107 92何睿杰A一等C110 93于伟A C115 94张余 A 一等C116 95程明畅B一等C117东96刘俊伟A C117西97聂迎A一等C107 98李豪B一等C110 99蒋祥明A C115 100谢维A二等C116 101黄智宇A二等C117东102杜景南A一等C117西103司萌萌B一等C107 104宋郝开B二等C110 105史思雨A一等C115 106宋嵩焘A一等C116 107韩宇欢A二等C117东108刘晓楠A二等C117西109于莹莹B C107 110林伟宏A一等C110 111王强B二等C115 112王文胜A C116 113王薇薇A一等C117东114陈香A二等C117西115张剑如A二等C107 116汪波A一等C110 117韩子轩A二等C115 118黎南烽B二等C116 119刘鹏辉B二等C117东120王亚宁A一等C117西121王亚利A二等C107 122杜永志A二等C110 123黄代炜A二等C115 124姚威B二等C116 125邓成河B一等C117东126崔元顺B二等C117西127胡璇B C107 128刘传兴A C110 129郭庆B一等C115 130黄华建A一等C116 131李津B一等C117东132李恂B一等C117西133文雪B一等C107 134刘瑞童B一等C110 135王远远B一等C115 136周柏宇B二等C116 137张鹤A二等C117东138王晓东A二等C117西139张淑娥B二等C107 140李信信A C110 141周培坤A C115 142岳明煜B一等C116 143徐猛B二等C117东144衡通A二等C117西145李佳伟B二等C107 146陈文康A一等C110 147马丁B一等C115 148吕鑫B一等C116 149王雅馨B一等C117东150翟娜B二等C117西151王腾A C107 152张彦芳A一等C110 153王英艺B一等C115 154王兴文A二等C116 155卫晓倩B二等C117东156姜思佳B一等C117西157王耀晖B二等C107 158夏宇哲B二等C110 159苏伟鑫B二等C115 160白忠明B二等C116 161李云A二等C117东162何方A C117西163蔡宇杰B二等C107 164陈霏B一等C110 165冯志燕A一等C115 166南智文A二等C116 167 黄玉辉 B 二等C117东。
2013年全国研究生数学建模竞赛E题

2013年全国研究生数学建模竞赛E题中等收入定位与人口度量模型研究居民收入分配关系到广大民众的生活水平,分配公平程度是广泛关注的话题。
其中中等收入人口比重是反映收入分配格局的重要指标,这一人口比重越大,意味着收入分配结构越合理,称之为“橄榄型”收入分配格局。
在这种收入分配格局下,收入差距不大,社会消费旺盛,人民生活水平高,社会稳定。
一般经济发达国家都具有这种分配格局。
我国处于经济转型期,收入分配格局处于重要的调整期,“橄榄型”收入分配格局正处于形成阶段。
因此,监控收入分配格局的变化是经济社会发展的重要课题,例如需要回答,与前年比较,去年的收入分配格局改善了吗?改善了多少?可见实际上需要回答三个问题:什么是“橄榄型”收入分配格局?收入分配格局怎样的变化可以称之为改善?改善了多少?直观上,中间部分人口增加,则收入分配格局向好的方向转化。
于是基本问题回答什么是中间部分。
一个国家的收入分配可以用统计分布表示,图1是某收入分配的密度函数x是众数点,m是中位数点,μf,其中0(x)x表示收入(仅考虑正的收入),≥是平均收入。
收入分配经验分析说明,收入分配曲线一般是所谓正偏的,即峰值点向左偏,右端拖一个长尾巴,且通常有μx<<m(1)记对应的分布函数为)Fp=表示收入低于或等于x的人口比例。
由于F,则)(x(xmF,(1)式意味着收入大于或等于平均收入的人口一定不到半数,因此(=)12是少数。
记收入低于或等于x 的人口群体拥有收入占总收入的比例为)(p L ,则应有⎰=x t t tf p L 0d )(1)(μ,)(x F p = (2))(p L 称之为收入分配的洛伦兹曲线。
显然,如果)(1p L 与)(2p L 是两个不同收入分配的洛伦兹曲线,若对任何)1,0(∈p 都有)()(21p L p L ≥,则)(1p L 对应的收入分配显然更优,因为在)(1p L 中,任何低收入端人口拥有的总收入比例更大。
数学建模会议分组问题

会议分组问题摘要本文解决会议分组问题,即在会议次数以及参会人数确定的情况下求取不同地区之间最大的见面概率的会议安排方式,通过设置相应参数,逐步建立数学模型,并采用Lingo编程进行计算,并最终确定会议人员参加会议的分组方案。
下面将分别对三个问题进行阐述:问题1是已知有名代表参加会议,要分个场次,每场会议中有个小组,先对数据进行了矩阵化处理,其中引入常值元素来区分不同地区的代表,以L×N的矩阵表示每个人在某一场的出席情况,以此建立非线性整数变量规划模型。
为了达到尽可能使来自不同地区的代表能有见面交流机会的目的,本文以每组代表人数基本均衡、每个会议每个代表有且只能在一个小组内为约束条件,根据M个矩阵的加和等一系列运算的结果,得到M场会议之后与会人员的见面情况,从而进行优化,最终确立出最优的分组方案。
针对问题2,本文通过建立分组矩阵、开会矩阵,制定约束条件,构造相遇矩阵以及构造异地代表是否见面函数,逐步建立最终的数学模型。
但是用lingo 计算大量数据的非线性模型运行时间太长,无法获得运算结果(超过5个小时),因此采用分部计算的形式来求解此模型,也就是一共有次会议,须经过多次迭代,每次迭代只计算一次会议的会面情况,每次迭代时更新目标函数的系数,上一次已经会面的代表假设为同一地区,则这次计算常值系数,只计算未见面的代表会见面次数的最大值,迭代完毕之后将次结果综合考虑,并最后得到模型的最优方案。
针对问题3,将问题1中的N、M、L分别取做8、5、5,采用问题(1)所建立的模型以及问题2设计的算法,运行程序,得到的分配结果如下:表2 会议的分组方案第一组第二组第三组第四组第五组第一次2、874、513、6第二次514、63、82、7第三次3、741、82、65第四次74、82、631、5第五次41、673、82关键词:会议分组;矩阵分析;迭代运算;整数规划;约束条件一、问题的重述会议分组是一个很实际的问题,目前国内外许多重要会议都是以分组形式进行研讨,以便充分交流、沟通。
数学建模会议分组问题

会议分组问题摘要本文解决会议分组问题,即在会议次数以及参会人数确定的情况下求取不同地区之间最大的见面概率的会议安排方式,通过设置相应参数,逐步建立数学模型,并采用Lingo编程进行计算,并最终确定会议人员参加会议的分组方案。
下面将分别对三个问题进行阐述:问题1是已知有名代表参加会议,要分个场次,每场会议中有个小组,先对数据进行了矩阵化处理,其中引入常值元素来区分不同地区的代表,以L×N的矩阵表示每个人在某一场的出席情况,以此建立非线性整数变量规划模型。
为了达到尽可能使来自不同地区的代表能有见面交流机会的目的,本文以每组代表人数基本均衡、每个会议每个代表有且只能在一个小组内为约束条件,根据M个矩阵的加和等一系列运算的结果,得到M场会议之后与会人员的见面情况,从而进行优化,最终确立出最优的分组方案。
针对问题2,本文通过建立分组矩阵、开会矩阵,制定约束条件,构造相遇矩阵以及构造异地代表是否见面函数,逐步建立最终的数学模型。
但是用lingo 计算大量数据的非线性模型运行时间太长,无法获得运算结果(超过5个小时),因此采用分部计算的形式来求解此模型,也就是一共有次会议,须经过多次迭代,每次迭代只计算一次会议的会面情况,每次迭代时更新目标函数的系数,上一次已经会面的代表假设为同一地区,则这次计算常值系数,只计算未见面的代表会见面次数的最大值,迭代完毕之后将次结果综合考虑,并最后得到模型的最优方案。
针对问题3,将问题1中的N、M、L分别取做8、5、5,采用问题(1)所建立的模型以及问题2设计的算法,运行程序,得到的分配结果如下:表2 会议的分组方案关键词:会议分组;矩阵分析;迭代运算;整数规划;约束条件一、问题的重述会议分组是一个很实际的问题,目前国内外许多重要会议都是以分组形式进行研讨,以便充分交流、沟通。
本文是将相应的参数进行了设置,参会代表N 名,M个场次,每场会议L个小组,并且要求每个小组的人数基本均衡。
数学建模会议分组问题

会议分组问题摘要本文解决会议分组问题,即在会议次数以及参会人数确定的情况下求取不同地区之间最大的见面概率的会议安排方式,通过设置相应参数,逐步建立数学模型,并采用Lingo编程进行计算,并最终确定会议人员参加会议的分组方案。
下面将分别对三个问题进行阐述:问题1是已知有名代表参加会议,要分个场次,每场会议中有个小组,先对数据进行了矩阵化处理,其中引入常值元素来区分不同地区的代表,以L×N的矩阵表示每个人在某一场的出席情况,以此建立非线性整数变量规划模型。
为了达到尽可能使来自不同地区的代表能有见面交流机会的目的,本文以每组代表人数基本均衡、每个会议每个代表有且只能在一个小组内为约束条件,根据M个矩阵的加和等一系列运算的结果,得到M场会议之后与会人员的见面情况,从而进行优化,最终确立出最优的分组方案。
针对问题2,本文通过建立分组矩阵、开会矩阵,制定约束条件,构造相遇矩阵以及构造异地代表是否见面函数,逐步建立最终的数学模型。
但是用lingo 计算大量数据的非线性模型运行时间太长,无法获得运算结果(超过5个小时),因此采用分部计算的形式来求解此模型,也就是一共有次会议,须经过多次迭代,每次迭代只计算一次会议的会面情况,每次迭代时更新目标函数的系数,上一次已经会面的代表假设为同一地区,则这次计算常值系数,只计算未见面的代表会见面次数的最大值,迭代完毕之后将次结果综合考虑,并最后得到模型的最优方案。
针对问题3,将问题1中的N、M、L分别取做8、5、5,采用问题(1)所建立的模型以及问题2设计的算法,运行程序,得到的分配结果如下:表2 会议的分组方案关键词:会议分组;矩阵分析;迭代运算;整数规划;约束条件一、问题的重述会议分组是一个很实际的问题,目前国内外许多重要会议都是以分组形式进行研讨,以便充分交流、沟通。
本文是将相应的参数进行了设置,参会代表N 名,M个场次,每场会议L个小组,并且要求每个小组的人数基本均衡。
2013全国大学生数学建模竞赛B题
将008代表的矩阵C8的第二列元素与其它矩 阵的第一列元素进行两两匹配。记录元素相 同的个数,个数除以1980为C8矩阵第二列对 其它矩阵第一列的边缘匹配度,记为:
比较这18个数据,最大的即为与008匹配的 碎纸片。然后以所找到的碎纸片的第二列开 始,求出它与其它矩阵第一列的边缘匹配度, 找出最大的,以此类推把19张碎纸片拼接完 成。
三.问题2的分析
英文碎纸片的分析 通过观察可以发现英文字母的主要的 部分拥有同一上界和同一下界,例如:
将图片中每一行中黑色像素数少于13的及 字母的次要部分转变为二值化矩阵中的0, 将每一行中黑色像素大于等于13的及字母 的主要部分转化为二值化矩阵中的1,这样 得到的新的二值化矩阵 。例如图像转变为 如下图的方式:
二.问题1的分析
步骤一:使用matlab中的imread函数 可以做出图片的灰度矩阵 ,读取每 张图片文件的数据,其目的是将附件 中给的 bmp 格式的碎纸片图以灰度 值矩阵的形式存储。再将灰度值矩阵 转化为 0-1 矩阵,来得到模型的数 据基础;
由于该像素图片转换后为
的矩阵,ቤተ መጻሕፍቲ ባይዱ
论文中无法放置,所以仅简单举例说明:
以纸片000与001为例,匹配方式可能为:
将①②的边缘匹配度相加得到边缘匹配度 之和,将③④的边缘匹配度相加得边缘匹 配度之和,两者的和做出比较。若仅有一 个大于等于1.9,则计算机输出该匹配度, 人工判断是否碎纸片是否匹配;若两者均 大于等于1.9,计算机把两个匹配度之和输 出,人工选择判断碎纸片应是否匹配与如 何匹配;若两者均小于1.9,则计算输出最 大者,人工判断碎纸片是否匹配。这样可 以得到一些在同一横行的碎纸片的拼接。
总体思路
三步走:分行,行内排序,行间排序
数学建模实践-评委分组问题
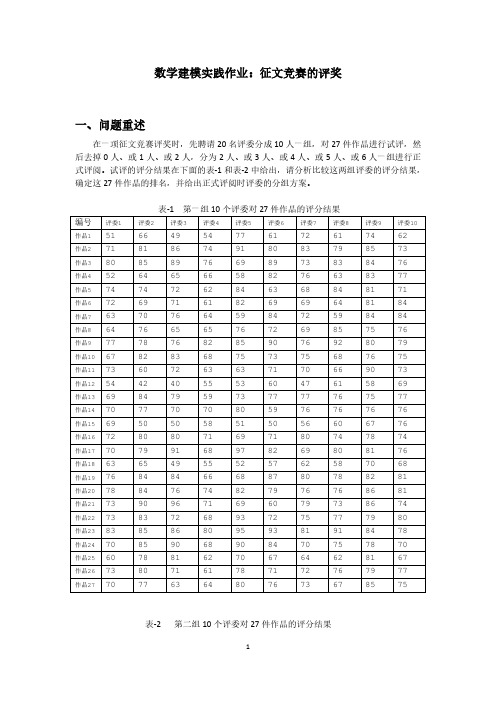
68 75 82 75 66 65 68 71 81 67 64 67 779 66 68 68 71
80 76 80 73 77 75 68 78 85 82 67 75 68 78 73 78 75 80 82 80 75 75 80 72 84 83 72
作品编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
得分均值 65.4 77.15 77.5 69.9 72.7 69.25 68.4 69.15 79.85 71.5 65.85 61.1 71.7 72.8 62.2 72.4 76.9 62.65 75.6 77.5 74.65 74.4 81.35 74.75 68.7 72.9 72.25
方差 90.46316 36.97632 45.10526 72.51579 36.22105 47.46053 88.88421 62.13421 30.66053 39.21053 70.55526 104.2 37.37895 28.06316 73.01053 24.67368 52.09474 54.13421 58.04211 28.89474 78.13421 43.72632 46.13421 51.67105 51.58947 35.35789 33.88158
53 68 63 60 76 58 47 62 69 63 50 63 70 67 59 64 75 62 64 70 62 68 67 73 60 73 69
76 74 75 77 73 66 70 69 80 66 66 73 67 76 71 73 77 64 81 84 77 69 79 68 66 74 71
数学建模综合题目参考答案

综合题目参考答案1. 赛程安排(2002年全国大学生数学建模竞赛D 题)(1)用多种方法都能给出一个达到要求的赛程。
(2)用多种方法可以证明支球队“各队每两场比赛最小相隔场次的上界”n r (如=5时上界为1)是,如:n ⎦⎤⎢⎣⎡-23n 设赛程中某场比赛是,两队, 队参加的下一场比赛是,两队(≠i j i i k k ),要使各队每两场比赛最小相隔场次为,则上述两场比赛之间必须有除,j r i ,以外的2支球队参赛,于是,注意到为整数即得。
j k r 32+≥r n r ⎥⎦⎤⎢⎣⎡-≤23n r (3)用构造性的办法可以证明这个上界是可以达到的,即对任意的编排出n 达到该上界的赛程。
如对于=8, =9可以得到:n n 1A 2A 3A 4A 5A 6A 7A 8A 每两场比赛相隔场次数相隔场次总数1A ×159131721253,3,3,3,3,3182A 1×206231126164,4,4,3,2,2193A 520×2410271522,4,4,4,3,2194A 9624×28243192,2,4,4,4,3195A 13231028×41872,2,2,4,4,4186A 171127144×8223,2,2,2,4,4177A 2126153188×124,3,2,2,2,4178A 251621972212×4,4,3,2,2,2171A 2A 3A 4A 5A 6A 7A 8A 9A 每两场比赛相隔场次数相隔场次总数1A ×366311126162114,4,4,4,4,4,4,282A 36×2277221217324,4,4,4,4,4,3273A 62×3515302025103,3,4,4,4,4,4264A 312735×318813234,4,4,4,3,3,3255A 117153×342429193,3,3,3,4,4,4246A 2622301834×49144,4,3,3,3,3237A 1612208244×33283,3,3,3,3,3,4228A 2117251329933×53,3,3,3,3,3,3,219A 13210231914285×3,4,3,4,3,4,324可以看到,=8时每两场比赛相隔场次数只有2,3,4,=9时每两场比n n 赛相隔场次数只有3,4,以上结果可以推广,即为偶数时每两场比赛相隔场n 次数只有,,,为奇数时只有,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
会议分组问题摘要通过对问题的分析,我们确定运用优化的整数规划模型、矩阵理论和置换等方面的知识和技巧。
通过矩阵将决策变量和所要求解的目标函数建立联系。
在提出模型目标函数的过程中,首先我们提出了代表相遇次数的概念,用矩阵Q 表示其任意两个代表的相遇次数,并利用矩阵的Frobenius范数控制了Q中元素的大小及其均匀程度,得到目标函数f(x),从而求解代表的相遇次数。
第一个目标函数设定后,基于f(x)在群体整体换组时不能起到控制作用的问题,决定使用共同成员概念:即任意两组(可以属于不同场次)整个会议中的交集。
利用矩阵A,对矩阵的Frobenius范数的运用使群体整体换组现象得到了有效的遏制,对与会者混合程度进行了控制。
求解模型时,使用迭代算法,利用线性规划,在目标函数可行域范围内查找最优解可以利用MATLAB软件设计出计算可行初始解->随机产生一个可行解->局部优化->全局优化从而达到全局最优解的三步求解的方法,局部->全局的步骤解出了全局最优解,简化运算步骤的同时提高了结果优化程度,降低对初值的依赖程度,很好的达到了与会者需要充分混合的目的。
基于算法的目标函数,因为在建立时具有一般性,若需建立起优化全局的目标函数,只需对参数进行改变。
这样一来模型的推广得到了算法上的支持,带来了极大的便利。
我们此次建模得到了合适的人员分配结果,达到了建模的目的。
关键词:抽屉原理相遇矩阵共同成员 Frobenius范数一、问题重述目前,国内外许多重要会议都是以分组形式进行研讨,以便充分交流、沟通。
一般地,一个由N名代表参加的会议,要分为M个场次,每场会议分为L个小组,并且要求每个小组的人数基本均衡。
问题1:请建立分组方案的数学模型,使得尽可能让任意两个来自不同地区的委员之间都有见面交流的机会。
问题2:设计求解上述分组模型的有效算法。
问题3:现有一个学术团体要举行由37位专家参加的学术研讨会,每个专家所在地区的信息见表1。
会议分5场进行,每场会议又分5个小组,每个小组人数要基本均衡。
请根据问题1所建立的模型以及问题2设计的算法,给出5场会议的每一场各个组中有哪些委员参加的安排方案。
说明:论文要附有求解问题3源程序的全部代码,并确保能够直接运行以检验结果的正确性。
二、模型假设(1)假设各场会议及各小组间是相互独立的;(2)假设所有代表严格遵守派遣方案,不会改变制定的分配方案; (3)假设来自不同地区的代表之间无其他差异; (4)假设每场会议各组人数分配为7,7,7,9,9。
注:对于假设(4),我们可以运用初等模型中的公平分配得到,具体过程如下:三、变量及符号说明和数学描述1、变量符号说明(1) ijk x :0-1决策变量,表示第i 位代表有否参加第k 场第j 组会议; (2) P :开会分组矩阵,表示整次会议每场代表的分组安排,其中k P 表示第k 场会议的分组矩阵,其行向量jk P 表示第k 场会议第j 组的分组矩阵;(3) Q :相遇矩阵; (4)()f x :目标函数一,用来控制代表相遇次数;(5) ()g x :目标函数二,用于控制不同场间组间共同成员个数; (6) ()F x :总的目标函数,综合考虑()f x 和()g x 的目标函数.2、变量符号数学描述(1)ijk 1,j 0,.x ⎧⎪=⎨⎪⎩表示第i 位代表参加第k 场第组的会议否则(2)()12=jk jkjkNjk P xx x ,k 表示第k 段会议,j 表示第j 组,k=1,2,…,M ,j=1,2,…,L,i=1,2,…,N .(3)1k 11k 21k 1k 212k 22k 2k 1k2kk x x x x x x =x x x N k N k M M NM Mk P P P P ⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭(4)111121ML L LM P P P P P P P P ⎛⎫⎪ ⎪ ⎪⎛⎫⎪ ⎪⎪ ⎪== ⎪ ⎪⎪⎪⎪⎝⎭⎪ ⎪ ⎪⎝⎭(5)()1212TT TT L L P P Q P P P PP P ⎛⎫ ⎪ ⎪== ⎪ ⎪⎝⎭四、模型建立通过使用(0-1)整数规划来建立该问题的模型。
题目要求每个小组的人数基本均衡,使得尽可能让任意两个来自不同地区的委员之间都有见面交流的机会。
从这两个要求出发,分别从相遇代表次数和共同成员数目两个角度建立了两个目标函数。
再加上题设要求以及模型假设得到的约束条件,完成本模型的建立。
具体过程以及模型如下所示。
题目要求分组名单安排计划属于分派问题,常用0-1变量表示分派的决策变量,根据本题的特点现在把分派问题视为抽屉问题。
每场会议配给L 个抽屉,每组分一个,每个抽屉分为N 个空格(第1至第N 号),每位代表的编号放入空格。
如果空格处有对应的编号则ijk x 就是1,如果没有就是0.即ijk 1,k j i ,1,2,...,,1,2,...,,1,2,...,0,x i N j L k M====⎧⎨⎩第场第组第个空格有编号否则 根据以上的分法我们可以用由ijk x 组成的矩阵来表示开会时代表分布的具体情况。
令()12=jk jkjkNjk P xx x ,这表示第k 场第j 组的与会代表的分布情况。
每场会的具体安排由矩阵排列如下:1k 11k 21k 1k 212k 22k 2k 1k2kk x x x x x x =x x x N k N k M M NM Mk P P P P ⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭1、建立目标函数基于计算过程中会遇到一个行向量与自己的转置相乘情况,运算的结果不仅对于我们的模型中无效,还会对计算情况有着较大的影响,我们先规定在计算中0,0,1,2,...,,1,2,...,.T T jk jk jk jk P P P P j L k M ====根据要求每个小组的人数基本均衡,使得尽可能让任意两个来自不同地区的委员之间都有见面交流的机会,分两部分来描述:1、会议安排应使任意两个代表在整个会议中见面的次数平均2、不同场会议在同一小组中一起开会的代表最少,最好代表之间都可以见面。
1、为了控制在不同场会议在同一小组中一起开会的代表数目并控制任意两个代表在整个会议中见面的次数,随机抽取两位代表,解出彼此在同组同时开会见面的次数见面次数采用0-1决策变量ijkx 来表示:11L Msjktjkj k xx ==∑∑表示第s 号代表与第t 号代表在M 场会议中相遇的总次数.基于运算方便的目的,列出两个代表相遇的矩阵Q 如下:()()12121122=++T TTT T TT L L L st N NL P P Q P P P P P P P P P P P q P ⨯⎛⎫⎪ ⎪==+= ⎪⎪⎝⎭其中11.L Mstsjk tjk j k q x x ===∑∑计算出全部st q 的和,求解得所有代表的相遇次数,考虑到代表彼此相遇的单个差异的不明显性,我们把()lst q 放大,再对()lst q 进行求和,设l 值等于2,使用矩阵Q 的Frobenius 范数达到放大st q 之间的差异的目的,既考虑到了全局相遇次数的同时也考虑到了单个相遇次数的差异,第一个目标函数建立如下:()()11lLLst s t f x q ===∑∑2、对于()f x ,其弱点有:当同一批人分别处于两场会议的某两组时,且在接下来的会议中会完全打乱分配,并尽可能弥补开始相遇次数增大的缺陷,保持成员见面的次数个别差异很小时,使用()f x 不能充分控制住。
因此这就需要我们再建立了一个目标函数来克服此弱点。
对于整个会议中任意抽取出的两个讨论组,称在这两个讨论组中都出现的代表称为这两个组的共同成员。
第k场第i 组与第t 场第j 组的共同成员个数为T ik jt P P . 我们用矩阵来排列这些数:()111111*********11111111111111111111121312TT TTL MLM T T T T L L L L ML MTTTTM LM M MM LM T T TT LM LM L LM MLM LM TT TT ML M P P P P P P P P P P P P P P P P A P P P P P P P P P P P P P P P P PP PP PP PP ⨯⎛⎫ ⎪⎪ ⎪ ⎪ ⎪=⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭=21222323132333123TT T T MTTTT MT T TT L L L L M P P P P P P P P P P P P P P P P P P P P P P P P ⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭A 是一个()2L M ⨯的矩阵,其中A 的对角线上的方块T k k P P 是第k 段会议段内各组的共同成员,其非对角线上的元素一定为0,而其对角线上的元素在上文中已经提到为无效量,故不计算A 对角线方块Tk k P P 中的元素,k=1,2,…,M.A 中每个元素为整个会议中任意两组(可以分别属于不同段)的共同成员个数。
如果出现上一段提出的问题,那么A 中元素的大小(除去对角线方块,1,2,...,T k k P P k M =中的元素)将会出现明显的不平均。
如果让A 中对角线方块,1,2,...,T k k P P k M =以外所有元素的尽可能平均的话,那么会议中任一组与任何该组所属的段以外的组的共同成员数量将会均匀分布。
于是,成员间自发组成的小组总在同一个讨论组中出现的现象将会得到遏制,与会成员将会尽可能平均分配。
类似上一个目标函数,为了达到描述A 中元素的平均程度的目的,可以使用矩阵A 的Frobenius 范数。
在此情况下,可以再次建立一个目标函数:()()2=T ik jt k tg x P P ≠∑)()()(21x g x f x F λλ+=其中2121,,1λλλλ=+为权系数),为总的目标函数。
2、约束条件利用已知题目条件设出相应的模型约束条件:(1) 在每一场会议中每个代表只能分入一个组里()11=111,1,2,...,.Ljk N j P k M ⨯==∑(2) 易知不同组间开会代表应该尽量相等,才可以使得相见的次数尽可能少,所以1,2,...,,1,2,,.T jk jk N p p j L k M L ⎡⎤===⎣⎦(3) 在具体计算时()f x ,相遇代表次数须在一个范围,即<M m q .(4) 类似地我们对()g x 考虑,共同成员个数也要在一个有意义的范围内,即T ik jt P P .<M-1.五、模型的求解1、详细求解方案使用MATLAB 对该模型求解。
模型变量总数为N ,对于每个变量来说,取值范围为0-1,如果N 取值较大时,求解大规模的数据时若使用穷举法,会使总的计算步骤较复杂。
