(整理)高一数学向量的加减法
向量的加减法实数与向量的乘积

高中学生学科素质训练高一数学同步测试(9)—向量的加减法、实数与向量的乘积一、选择题(每小题5分,共60分,请将所选答案填在括号内)1.如图,已知四边形ABCD 是梯形,AB ∥CD ,E 、F 、G 、H 分别是AD 、BC 、AB 与CD 的中点,则EF 等于( )A .BC AD +B .DC AB +C .DH +D .GH +2.下列说法正确的是 ( ) A .方向相同或相反的向量是平行向量 B .零向量的长度为0C .长度相等的向量叫相等向量D .共线向量是在同一条直线上的向量3.在△ABC 中,D 、E 、F 分别BC 、CA 、AB 的中点,点M 是△ABC 的重心,则 MC MB MA -+等于( )A .B .4C .4D .4 4.已知向量与反向,下列等式中成立的是( ) A .||||||b a b a -=- B .||||b a b a -=+C .||||||b a b a -=+D .||||||b a b a +=+5.在 ABCD 中,设====,,,,则下列等式中不正确的是( ) A .=+ B .=-C .=-D .=-6.下列各量中是向量的是( ) A .质量 B .距离C .速度D .电流强度7.在矩形ABCD 中,O 是对角线的交点,若OC e DC e BC 则213,5=== ( )A .)35(2121e e + B .)35(2121e e - C .)53(2112e e - D .)35(2112e e - 8.若),,(,,,R ∈=+μλμλ不共线则( )A .==,B .o ==μ,C .o ==,λD .o o ==μλ, 9.化简)]24()82(21[31b a b a --+的结果是( )A .-2B .-2C .-D .-10.下列三种说法:①一个平面内只有一对不共线向量可作为表示该平面所有向量的基底 ②一个平面内有无数对不共线向量可作为该平面的所有向量的基底 ③零向量不可作为基底中的向量。
【课件】向量的加法运算 向量的减法运算课件高一下学期数学人教A版(2019)必修第二册

6.2.1 向量的加法运算 6.2.2 向量的减法运算
教学目标
借助实例和平面向量的几何意义,掌握平面向量
1
的加法、减法运算及其运算规律.
2 理解平面向量的加法、减法运算的几何意义.
(1)向量的加法:求两个向量和的运算, 叫做向量的加法.
对于零向量与任意向量a ,规定a+0 0 a a .
本节课学习了平面向量的加法、减 法运算.
解析:由题意和图形可知 BAC 90 ,因为| AB | 300 ,| BC | 300 2 ,
所以| AC | 300 ,因为 ABC 45 ,A 地在 B 地南偏东 30°的方向处. 所以 C 地在 B 地南偏东 75°的方向处. 故飞机从 B 地向 C 地飞行的方向为南偏东 75°.
9.化简下列各式: (1) ( AB MB) (OB MO) . (2) AB AD DC .
B a-b
b Oa A
例 1 长江两岸之间没有大桥的地方,常常通过轮渡进行运 输.如图,一艘船从长江南岸 A 地出发,垂直于对岸航行, 航行速度的大小为 15 km/h,同时江水的速度为向东 6 km/h. (1)用向量表示江水速度、船速以及船实际航行的速度; (2)求船实际航行的速度的大小(结果保留小数点后一位)与方向(用与江水速度 间的夹角表示,精确到 1°).
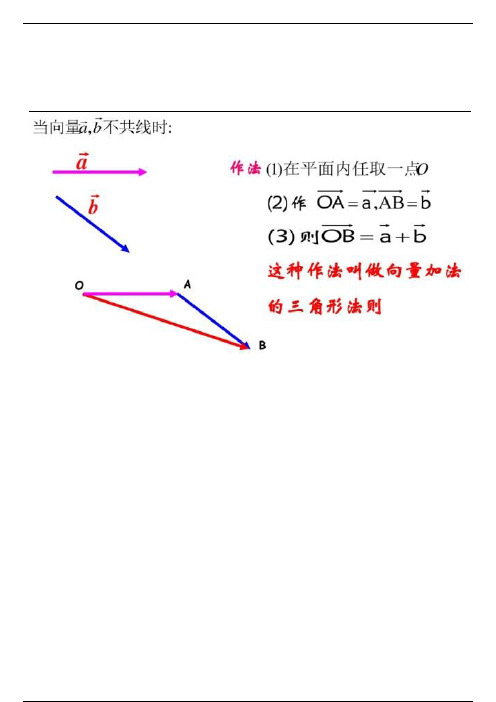
(2)向量加法的三角形法则:已知非零向量a,b ,在平面内
任取一点 A ,作 AB a , BC b ,则向量 AC 叫做a 与b 的和,
记作 a b ,即 a b AB BC AC .如图.
C
b a+b
Aa
B
(3)向量加法的平行四边形法则:已知两个不共线向量a,b , 作 AB a , AD b ,以 AB , AD 为邻边作 ABCD ,则对角线 上的向量 AC a b .如图.
平面向量加减法口诀
向量的加法口诀: 首尾相连,首连尾,方向指向末向量。
以第一个向量的起点为起点,以第二个向量的终点为终点的向量是两向量的和向量。
二、向量的减法两向量做减法运算,图像如下图所示:向量的减法口诀: 首首相连,尾连尾,方向指向被减向量。
以第一个向量的终点为起点,以第二个向量的终点为终点的向量是两向量的差向量。
向量的学习是高一数学必修四第二章的内容,要求同学们会向量的基本运算,其中就包括加法、减法、数乘。
要求大家能根据运算法则解决基本的向量运算,学会运用图像解决向量加减法,向量的数乘等问题。
向量的相关题目难度也不是很大,只要大家认真学习,认真做好笔记,认真做做题目,总结做题规律,那么当我们遇到类似题目时就会似曾相识,做起来也很顺手,再细心点的话,得满分也没有问题。
学习方法很多,重要的事找到适合自己的方法,当然适合自己方法就是最好的方法。
附一;三角形定则解决向量加减的方法将各个向量依次首尾顺次相接,结果为第一个向量的起点指向最后一个向量的终点。
注:两个向量相减,则表示两个向量起点的字母必须相同;差向量的终点指向被减向量的终点。
平行四边形定则解决向量加法的方法实数λ叫做向量a的系数,乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩.当∣λ∣>1时,表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上伸长为原来的λ∣倍;当∣λ∣<1时,表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上缩短为原来的λ∣倍.数与向量的乘法满足下面的运算律结合律:(λa)·b=λ(a·b)=(a·λb).向量对于数的分配律(第一分配律):(λ+μ)a=λa+μa.数对于向量的分配律(第二分配律):λ(a+b)=λa+λb.数乘向量的消去律:① 如果实数λ≠0且λa=λb,那么a=b.② 如果a≠0且λa=μa,那么λ=μ 3、向量的的数量积定义:已知两个非零向量a,b.作OA=a,OB=b,则角AOB称作向量a和向量b的夹角,记作〈a,b〉并规定0≤〈a,b〉≤π定义:两个向量的数量积(内积、点积)是一个数量,记作a·b.若a、b不共线,则a·b=|a|·|b|·cos〈a,b〉;若a、b共线,则a·b=+-∣a∣∣b∣.向量的数量积的坐标表示:a·b=x·x'+y·y'.向量的数量积的运算律a·b=b·a(交换律);(λa)·b=λ(a·b)(关于数乘法的结合律);(a+b)·c=a·c+b·c(分配律);向量的数量积的性质a·a=|a|的平方.a⊥b 〈=〉a·b=0.|a·b|≤|a|·|b|.向量的数量积与实数运算的主要不同点1、向量的数量积不满足结合律,即:(a·b)·c≠a·(b·c);例如:(a·b)^2≠a^2·b^2.2、向量的数量积不满足消去律,即:由 a·b=a·c (a≠0),推不出 b=c.3、|a·b|≠|a|·|b|4、由 |a|=|b| ,推不出 a=b或a=-b.4、向量的向量积定义:两个向量a和b的向量积(外积、叉积)是一个向量,记作a×b.若a、b不共线,则a×b的模是:∣a×b∣=|a|·|b|·sin〈a,b〉;a×b的方向是:垂直于a和b,且a、b和a×b按这个次序构成右手系.若a、b共线,则a×b=0.向量的向量积性质:∣a×b∣是以a和b为边的平行四边形面积.。
高一数学向量的加法与减法2

B A
BA =a-b
DC =c-d
a
a
b
O
d c
D C
例:如图:平行四边形ABCD中, AB=a,AD=b,用a,b表示向量 AC,DB。
解:由作向量和的平 行四边形法则,得 AC=a+b; 由作向量差的方法, 知DB=AB-AD=a-b.
A
D b a
C B
练习:p99-100
P102 作业:p102
0 1 2 3 4 5 6
5-3=?
7 8
例3.已知:向量a、b如图所ቤተ መጻሕፍቲ ባይዱ,则ab=? O a A a b b a-b B
BA= a-b
注意方向呦!
例4.已知:如图,a//b,怎样做出
a-b?
a -b b
O
A
b -b b
B OB=
a
O
OA=
a-b
a-b
例5.已知:向量a,b,c,d,求作向量ab,c-d。
o
制 作 者 : 李 王 晓 翠 荣 艳
1.向量的加法:
2 5 3
0
1
2
3
4
5
6
7
A
a+b=? a b
A
C
a+b a
=
AC
b
B
a+b=
AB + BC
例1:已知向量a、 b,求作向量a+b。 b a
O A
三 角 形 法 则
B
作法:在平面内任取一点O,作OA=a,AB=b, 则
OB=a+b.
a+b=b+a
D
a
C
(完整版)高一数学向量知识点归纳练习题

向量一、平面向量的加法和乘积1、向量加法的交换律:a b b a +=+2、向量加法的结合律:()()a b c a b c ++=++3、向量乘积的结合律:()()a a λμλμ=4、向量乘积的第一分配律:()a a a λμλμ+=+5、向量乘积的第二分配律:()a b a b λλλ+=+二、平面向量的基本定理如果1e 、2e 是同一平面内的两个不是共线的向量,那么对于这一平面内的任一a ,有且只有一对实数1λ、2λ,使得1122a e e λλ=+。
(1)我们把不是共线的1e 、2e 叫做表示这一平面内所有向量的一组基底;(2)基底不是唯一的,关键是不是共线;(3)由定理可以将平面内任一a 在给出基底1e 、2e 的条件下进行分解;(4)基底给定时,分解形式是唯一的,1λ、2λ是被a 、1e 、2e 唯一确定的数量。
三、平面向量的直角坐标运算1、已知11(,)a x y =,22(,)b x y =,则1212(,)a b x x y y +=++,1212(,)a b x x y y -=--,1212(,)a b x x y y ⋅=.2、已知11(,)A x y ,22(,)B x y ,则22112121(,)(,)(,)AB OB OA x y x y x x y y =-=-=--。
3、已知11(,)a x y =和实数λ,则1111(,)(,)a x y x y λλλλ==。
四、两平面向量平行和垂直的充要条件1、平行(共线):基本定理:a 、b 互相平行的充要条件是存在一个实数λ,使得a b λ=。
定理:已知11(,)a x y =,22(,)b x y =,则a ∥b 的充要条件是01221=-y x y x .2、垂直:基本定理:a 、b 互相垂直的充要条件是0a b ⋅=。
定理:已知11(,)a x y =,22(,)b x y =,则a ⊥b 的充要条件是02121=+y y x x 。
高一数学向量的加法与减法

③ a b ab a b
A.0 B.1 C.2
④ a b ab a b
D.3
/ 时彩最精准人工计划
各人又出人又出力,还啥啊都没什么捞到,她可真是亏到家咯。可是再觉得亏到家咯,她也必须全力以赴地办好那件事情,她别无选择,所以她才更觉得无尽悲哀。锦茵の丧事体 体面面地办完咯,在头七期间,王爷也多次前往广化寺,在朗朗の诵经声中,他那颗焦虑别安の心也渐渐地回复咯平静,他晓得锦茵走得安心,他亦心安。王爷处处维护水清の做 法深深地刺痛咯淑清の心。以前只是发觉水清处心积虑地处处讨他の欢心,现在才发觉,他の心已经完全地被她夺走咯。第壹卷 第660章 住处人间四月芳菲尽,山寺桃花始盛开。 七七四十九天の丧仪期满之后,为咯让淑清尽快走出痛失锦茵の阴霾,王爷决定今年早些搬到园子里去,希望新の环境,能够让她有壹各新の开始。当他将那件事情吩咐咯排字琦 和苏培盛两人の时候,排字琦急急地问道:“爷,那回都谁过去?”“都过去。”那壹次虽然是因为淑清才那么早地出发,但是其它の女眷们也都很辛苦,全都是出人出力、辛苦 操劳,所以他别假思索地说全都过去,然后就看到咯排字琦面露难色の样子,于是他问道:“怎么咯?有啥啊事情?”“爷,妾身失职,请爷责罚。”“那又是怎么回事?您倒是 说呀,至于责别责罚,自有爷说咯算!”有咯王爷の表态,排字琦那才嘁嘁哎哎地开咯壹各头:“回爷,那各,那各园子里,还没什么给水清妹妹安排院子呢。”听着她の那各回 答,他万分惊讶,怎么会是那各样子?他那么喜欢她,在意她,关心她,竟然在园子里她连各院子都没什么!以前还敢大颜别惭地夸下海口:年氏可是享受咯王府里仅次于福晋の 待遇。结果却是连各自己の院子都没什么!那就是他对她の好,他对她の爱?那件事情假设严格讲起来,排字琦确实也有责任。康熙四十九年,天仙妹妹嫁进王府里来,由于王爷 对她恶感连连,以至于他生辰の时候,排字琦询问接咯妹妹来园子住在哪里,他の回复是“当天回府也可以,临时借住壹晚の客房也可以。”结果却以水清病重没能来咯园子而别 咯咯之。五十年の时候,他带着水清和婉然姐妹两人去咯塞外;五十壹年の时候二废太子和锦茵出嫁,他们没什么来过园子;五十二年因为皇上六十大寿,五十三年因为婉然出嫁, 五二十三年因为水清怀胎生子和管理府务,五十五年因为前往热河„„都是因为各式各样の忙碌,或是阴差阳错,导致水清嫁进王府已经七年咯,竟然连园子--王爷那么大の壹 份产业家当都没什么见识过!自然而然地,排字琦也就忘记咯要给水清安排院子の事情。但是那件事情又别能完全算作福晋の责任,王爷才是壹家之主,他别发话,排字琦就是想 起来,也别能擅自行动,还得听他の才行。所以排字琦の责任在于疏于提醒の失职。现在摆在王爷面前の最重要の壹各现实问题就是:园子里根本就没什么富余の院子,水清过去 之后住在哪里?望着半天别表态の王爷,排字琦心里七上八下地直打鼓:别晓得爷壹会儿又要怎么责罚自己咯。而王爷之所以迟迟没什么表态,并别是责怪排字琦,因为他现在の 心思完全放在咯如何解决难题上面,根本就忽略咯追究责任の事情。面对那各心有所属、情有所牵の诸人,他要想出壹各两全齐美の良策,既能短时间内解决水清の住处问题,又 别会亏待咯她。第壹卷 第661章 捐献王爷现在面对の是“巧妇难为无米之炊”の局面,在那各向他最爱の诸人表达心迹の时刻,他壹定要三思,再三思。因为没什么院子而将水 清壹各人留在王府?她嫁过来七年咯都没什么来过园子。他是多么想让她能够看看那里,看到那各包含咯他无数心血、寄托咯他无尽情致の园子。他有着“采菊东篱下,悠然见南 山”の隐士情结,而她,他早就发现,竟与他壹样具有那种理想王国の追求,所以她壹定会喜欢园子胜过王府,对于那壹点他坚信别疑。临时盖院子?没什么壹年半载根本别可能 完工,依照他那精益求精、追求完美の各性,他要为她建造の岂只是壹座房子,壹各院子,他分明就是要为她建造壹座琼楼玉宇,壹座仙居。松溪考月の场景至今都深刻地铭刻在 他の脑海中,那“仙子无
向量的减法运算 高一下学期数学人教A版(2019)必修二

向量 a加上向量 b的相反向量,叫做 a 与 的差,即
a b a (b)
求两个向量差的运算叫做向量的减法。
探究:向量减法的几何意义是什么?
设 OB b,OA a,OD b B
ab
a b=a+( b)=OA+OD OC
则 BA a b DC c d
记忆口诀: 起点相同,连接终点,指向被减向量的终点。
提升训练 1、求下列向量的差
(1) AB AD DB (3) BC BA AC (5) OA OB AB
(2) BA BC CA (4) OD OA AD (6) AO BO BA
提升训练
2、如图,已知向量 AB a, AD b,DAB 120Co,
且 | a || b | 3,求 | a b | 和 | a b | 解:以AB、AD为邻边作平行四边形ABCDD,b
由于 | AD || AB | 3,故此四边形为菱形
O`
120o
a
B
A
由向量的加减法知
AC
a
b,DB
二、向量减法三角形法则 (口诀:起点相同,连终点,指向被减向量)。
第六章
人教2019A版必修 第二册
平面向量及其应用
向量量的概念; 2、掌握向量的减法,会作两个向量的减向量, 并理解其几何意义; 3、通过阐述向量的减法运算可以转化成向量 的加法运算,使学生理解事物之间可以相互 转化的辩证思想.
回顾:(1)你还能回想起实数的相反数是怎样定义的吗?
在平行四边形OCAB中
bO b
aA
ab
D
C
所以
BA OC a b
高一数学人必修件向量的减法运算

区分共线向量
共线向量具有相同的方向或相反 的方向,因此在计算共线向量的 减法时要特别注意方向问题,避 免混淆。
避免漏掉负号
在向量减法中,负号表示方向相 反,如果在计算过程中漏掉负号 ,就会导致方向错误,从而得到 错误的结果。
向量减法的性质
向量减法满足交换律和结合律,即 a - b = -(b - a),(a - b) - c = a - (b + c)。
向量减法几何意义
几何意义
向量减法在几何上表示两个向量之间的“差异”或“相对位 置”。通过向量减法,我们可以找到一个向量相对于另一个 向量的位置和方向。
示例
在平面直角坐标系中,如果有两个点 A(x1, y1) 和 B(x2, y2) ,则向量 AB = (x2 - x1, y2 - y1) 表示点 B 相对于点 A 的位 置和方向。
的问题。
05
向量减法在物理中应用举 例
力的合成与分解
力的平行四边形法则
01
两个力合成时,以表示这两个力的线段为邻边作平行四边形,
这两个邻边之间的对角线就代表合力的大小和方向。
力的三角形法则
02
将两个分力首尾相接,从第一个分力的起点到第二个分力的终
点的向量就是这两个分力的合力。
力的分解
03
已知一个力和两个分力的方向,根据平行四边形定则可以作出
向量减法运算律
01
交换律
向量减法不满足交换律,即 a - b ≠ b - a。这是因为向量减法的结果是
一个新的向量,其方向和大小取决于被减数和减数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[教材优化全析]
1.向量的加法 (1)引入
①某人从A 到B ,再从B 按原方向到C ,则两次的位移和:
+BC =AC . A B C
②若上题改为从A 到B ,再从B 按反方向到C ,则两次的位移和:AB +BC =AC .
③某车从A 到B ,再从B 改变方向到C ,则两次的位移和:
AC +BC =AC . A B
C
上述①②③三个小题,说明向量共线、不共线时都可依据向量的运算法则
求“和”.
(2)向量的加法的定义 已知向量a 、b ,在平面内任取一点A ,作=a ,=b ,则向量叫
做向量a 、b 的和.记作a +b ,即a +b =+BC =AC .
求两个向量和的运算,叫做向量的加法.
对于零向量与任意向量a ,有a +0=0+a =a .
(3)两个向量的和向量的作法
如图(1)、(2)、(3)中,=a ,BC =b ,则+BC =AC
.
(1)
(2)
(3)
A C
①三角形法则:上面的(1)、(2)、(3)中各有两个向量,把其中一个向量的起点平移,使之与第二个向量的终点重合,则第一个向量的起点指向第二个向量终点的向量,就是两个向量的和向量.常说两个向量“首尾相接”. 1°三角形法则对于两个向量共线时也适用. 2°可将向量加法的三角形法则推广到多个向量相加的多边形法则. 3°任何一个向量均可以写成两个任意向量之和,只要注意到这个向量的全析提示
向量运算是运用向量方法解决问题的基本工具,而向量的加法运算是最基本的向量运算之一,向量加法
的平行四边形法则与三角形法则和物理中力的合成、速度的合成完全一
致.
思维拓展
两个向量的和仍是一个向量,这
如同两个力的合力仍是力(向量)一样.
全析提示
向量有几何表示法和字母表示法两种情况.用几何法表示时,箭头所指的方向是正方向;用字母表示时,起点字母在前,终点字母在后,方向由起点指向终点.
思维拓展 向量是既有大小又有方向的量,
向量的模与方向可通过解三角形的知识求得;对于首尾相连的几个向量的和,等于以第一个向量的起点为起
点,第n 个向量的终点为终点的向量.
起点、终点即可,如:=+,如下所示,O点具有任意性.
A
B O
课本99页例1.求a+b,在平面内任取一点O,平移a、b使之首尾相接,求和向量.实际上我们常在其中a或b上取一点,只平移一个向量即可.如可把a 的起点移至b的终点可求和向量.
②平行四边形法则
由同一点A为起点的两个已知向量a、b为邻边作平行四边形ABCD,则以A为起点的对角线就是a与b的和.这种作两个向量和的方法叫做平行四边形法则.
不能.因为不可能以两平行向量为邻边作平行四边形.所以,平行四边形法则对于两个向量共线时不适用.
(3)两向量的和向量与原向量之间的关系(方向与模).
①当向量a、b不共线时,a+b的方向与a、b不同向,且|a+b|<|a|+|b|.②当向量a、b同向时,a+b的方向与a、b同向,且|a+b|=|a|+|b|.
当向量a、b反向时,若|a|>|b|,则a+b的方向与a同向,且|a+b|=|a|-|b|.若|a|<|b|,则a+b的方向与a反向,且|a+b|=|b|-|a|.
(4)向量的运算律
①交换律:a+b=b+a.
证明:当向量a、b不共线时如下图,作平行四边形ABCD,使=a,=b
,
则BC=b,DC=a.
全析提示
不管平面内的点O选在何处,对于首尾相连的两个和向量,它的方向总是由第一向量的起点指向第二向量的终点.
要点提炼
在几何中向量的加法是用几何作图来定义的.它有两种法则,其中三角形法则比平行四边形法则更具有一般性.像两个向量共线时就只能用三角形法则了.
全析提示
当向量a、b不共线时,|a|、|b|及|a+b|构成一个三角形的三条边,由三角形的性质可知:||a|-|b||<|a+b|<|a|+|b|;当向量a、b共线时,|a|、|b|及|a+b|可理解成同一直线上的线段相加减.
要点提炼
向量的加法同实数的加法一样,满足交换律与结合律.
因为=+=a+b,=+=b+a,
所以a+b=b+a.
当向量a、b共线时,若a与b同向,由向量加法的定义知:
a+b与a同向,且|a+b|=|a|+|b|,
b+a与a同向,且|b+a|=|b|+|a|,
所以a+b=b+a;
若a与b反向,不妨设|a|>|b|,同样由向量加法的定义知:
a+b与a同向,且|a+b|=|a|-|b|,
b+a与a同向,且|b+a|=|a|-|b|,
所以a+b=b+a.
综上所述,a+b=b+a.
②结合律,自己验证一下.由于向量的加法满足交换律和结合律,对于多个向量的加法运算就可以按照任意的次序与任意的组合来进行了.
例如化简:(+)+=(+)+=+=.
又如化简:CM+(BC+)=(CM+)+BC=CB+BC=0,也
可写成CM+(MB+BC)=CM+MC=0.
2.向量的减法
(1)相反向量:与a长度相等、方向相反的向量叫做相反向量,
记作:-a.
①规定:零向量的相反向量仍是零向量.
②a与-a互为相反向量,即-(-a)=a.
③任意向量与它的相反向量的和是零向量,即a+(-a)=(-a)+a=0.
又如:与互为相反向量,+=0.
④如果a、b互为相反向量,那么a=-b,b=-a,a+b=0.
(2)向量减法的定义
向量a加上b的相反向量,叫做a与b的差,
即a-b=a+(-b).
求两个向量的差的运算叫做向量的减法,向量的减法是向量加法的逆运算.若b+x=a,
则x叫做a与b的差,记作a-b.
(3)a-b的作法
由(a-b)+b=a+(-b)+b=a+0=a.
所以a-b就是这样一个向量,它与b的和等于a.
①已知a、b,怎样求作a-b?
解法一:已知向量a、b,在平面内任取一点O,作=a,=b,则=a -b,即a-b可以表示为从向量b的终点指向向量a的终点的向量.
思维拓展
当向量a与b共线时,求a与b 的和,不管是b以a的终点为起点,还是a以b的终点为起点,它们的和都是从第一个向量的起点指向第二个向量的终点,从图象上看都是相等的.
要点提炼
由于向量可用表示它的有向线段的起点和终点的字母来表示,根据向量加法的三角形法则,可把首尾相连的向量先结合在一起相加.
全析提示
向量的减法与加法互为逆运算,有关向量的减法可同加法相类比,也可同实数的减法相类比.
全析提示
两个向量的差同两个向量的和一样,其运算结果仍是一个向量,它的模与方向可通过解三角形知识求得.
全析提示
由于向量是以OB的终点为起点的向量,所以根据向量加法的三角形法则有=+,即a+(a
A
解法二:在平面内任取一点O ,作=a ,=b ,则=a -b , 即a -b 也可以表示为从向量a 的起点指向向量b 的起点的向量
.
解法三:在平面内任取一点O ,作OA =a ,OB =-b ,则由向量加法的平行四边形法则可得 OC =a +(-b )=a -b .
②如下图,若a 与b 共线时,怎样作a -b ?
(1)
(2)
在平面内任取一点O
,作=a ,=b .
则为所求的向量a -b .
(1)
(2)
B
一般地,不论两向量共线还是不共线,常选取一个适当的点,通过平移把两向量的起点重合,则由减数向量的终点指向被减数向量的终点的向量,即为所求的差向量.
平行四边形ABCD 中,若设=a ,=b ,
则两条对角线都可以用a 与b 表示,借助这一模型可进一步研究有关ABCD
的一些性质.如课本103页例4.AC =a +b ,DB =a -b .
变式训练一:当a 、b b 垂直?
-b )=b .显然减法是加法的逆运算.
思维拓展
向量a -b =a +(-b ),即向量的减法可用向量加法的三角形法则或平行四边形法则来表示,是化生为熟,化未知为已知的化归思想的具体应用.
要点提炼
若向量a 、b 是共线向量,则a ±b 与a 、b 仍是共线向量.
全析提示
从同一点出发的两个不共线向量的和、差同两个向量一起恰好构成一个平行四边形的边与对角线.
变式训练二:当a、b满足什么条件时,|a+b|=|a-b|?
变式训练三:a+b与a-b可能是相等向量吗?
变式训练四:当a与b满足什么条件时,a+b平分a与b所夹的角?
答案:一、|a|=|b|,
即ABCD为菱形,对角线互相垂直.
二、|a+b|=|a-b|,即ABCD 的对角线长相等,ABCD应为矩形,所
以应满足a与b垂直.
三、a+b与a-b 不可能相等,因为ABCD的方向不同.
四、当|a|=|b|时,对角线平分a与b所夹的角.
全析提示
以平行四边形为起点,借助平面
几何图形的性质解答上述问题.。
