Z变换及其收敛域
合集下载
Z变换的定义与收敛域
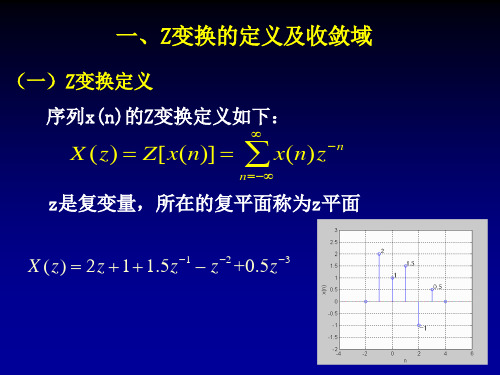
X(z) x(n)zn
n
x(n)zn
n
令： lim n an n
则： <1：收敛 >1：发散 =1：可能收敛也可能发散
3、 几类序列收敛域情况讨论
1．有限长序列的收敛域
x(n ), n 1nn 2
2．右边序列的收敛域
x ( n ) a n u n n 1 n
（三） 典型序列的z变换
1、 单位样值函数的z变换
(n)10
n0 n0
X(z) (n)zn(0)z01 n
(n)
1 1 0
n 1
ROC:整个 z 平面
Z[T (nm )]zm
2、单位阶跃序列的z变换 u(n)
1 u(n)0
n0 n0
X(z)的ROC：Rx1<|z|< Rx2
前提
双边序列的收敛域是内径为 Rx1,外径为 Rx2 的环形部分
例8-4
x(n)
(
1 3
)
n
1 2
n
n0 n0
1
Rx1
, 3
Rx2 2
ROC:
1 z 2 3
j Im( z )
1/3 2
0
Re( z )
4、 单边 z变换的收敛域
X(z)anzn
z
,| z|| a|
n0
za
x n a n u n 1 X z z
za
左边
z a 序列
当a eb ， 则
ZT
e bn u( n)
z z eb
， z eb，
双边z变换定义及收敛域
Rx+
n2 ≤ 0
7
(4)双边序列
n为任意值时皆有值
其z变 换：X (z) = x(n)z−n + ∑x(n)z−n ∑
n=0 −1 ∞
n=−∞
前式Roc: 0 ≤ z < Rx+ 后式Roc: Rx− < z ≤ ∞
∴当Rx− ≥ Rx+时，Roc : ∅ 当Rx− < Rx+时，Roc : Rx− < z < Rx+
0
Rx −
Re[z]
n1 ≥ 0
包括z =5∞处
因果序列 • n1≥0的右边序列 的右边序列 • Roc: Rx− ≤| z |≤ ∞ • 因果序列的z变换必在∞处收敛 因果序列的z变换必在∞ 收敛域一定是某个圆的外部
Rx −
j Im[z]
Re[z] n1 ≥ 0
0
包括z =∞处
6
(3)左边序列
n=−∞
∞
P( z ) 令X ( z ) = Q( z)
j Im z] [
Re[z]
则X(z)的零点：使X(z)=0的点， 即P( z ) = 0和当Q ( z )阶次高于P ( z )时 Q ( z ) → ∞ X(z)的极点：使X(z) → ∞的点， 即Q ( z ) = 0和当P ( z )阶次高于Q ( z )时P ( z ) → ∞
2
(1)有限长序列 1)有限长序列
x(n), n ≤ n ≤ n2 1 x(n) = 其 n 他 0,
其Z变换 X (z) = ∑x(n)z−n ：
n=n1 n2
j Im[z]
Roc至 为 0 < z < ∞ 少 ：
有限z平面 有限 平面
n2 ≤ 0
7
(4)双边序列
n为任意值时皆有值
其z变 换：X (z) = x(n)z−n + ∑x(n)z−n ∑
n=0 −1 ∞
n=−∞
前式Roc: 0 ≤ z < Rx+ 后式Roc: Rx− < z ≤ ∞
∴当Rx− ≥ Rx+时，Roc : ∅ 当Rx− < Rx+时，Roc : Rx− < z < Rx+
0
Rx −
Re[z]
n1 ≥ 0
包括z =5∞处
因果序列 • n1≥0的右边序列 的右边序列 • Roc: Rx− ≤| z |≤ ∞ • 因果序列的z变换必在∞处收敛 因果序列的z变换必在∞ 收敛域一定是某个圆的外部
Rx −
j Im[z]
Re[z] n1 ≥ 0
0
包括z =∞处
6
(3)左边序列
n=−∞
∞
P( z ) 令X ( z ) = Q( z)
j Im z] [
Re[z]
则X(z)的零点：使X(z)=0的点， 即P( z ) = 0和当Q ( z )阶次高于P ( z )时 Q ( z ) → ∞ X(z)的极点：使X(z) → ∞的点， 即Q ( z ) = 0和当P ( z )阶次高于Q ( z )时P ( z ) → ∞
2
(1)有限长序列 1)有限长序列
x(n), n ≤ n ≤ n2 1 x(n) = 其 n 他 0,
其Z变换 X (z) = ∑x(n)z−n ：
n=n1 n2
j Im[z]
Roc至 为 0 < z < ∞ 少 ：
有限z平面 有限 平面
z变换
半径和以|z2|为半径的两个圆之间的环状区域。
(5) 不同序列的双边Z变换可能相同，即序列与其双边Z变换不是 一一对应的。序列的双边Z变换连同收敛域一起与序列才是一 一对应的。
第 4 章 Z变换
ZT的ROC及其零极点
(1) ROC不包含任何极点； (2) 右边序列ZT的ROC 是以模最大的有限极点的模为半径的圆 外区域（不包括圆周）。
z
1
z
1
α<|z|<∞
f (k ) F ( z )
f (0) lim F ( z )
第 4 章 Z变换
4.3 Z 逆 变 换
4.3.1 双边Z逆变换的定义
1 k 1 f (k ) F ( z ) z dz C 2j
第 4 章 Z变换
4.3.2 双边Z逆变换的计算
(k m) z
k
z
m
第 4 章 Z变换 (3) f (k ) u (k ).
F ( z)
(4) f (k ) u(k 1).
k
u (k ) z
k
z z 1
k
|z|>1
F ( z)
k
[u(k 1)]z a u (k ) z
第 4 章 Z变换 3. 序列乘ak(Z域尺度变换)
若f (k ) F ( z), a z , 则
z a f (k ) F a
k
aa z a
a0
式中，a为常数（实数、虚数、复数），
第 4 章 Z变换 4. 序列域卷积 若
f1 (k ) F1 ( z ) f 2 (k ) F2 ( z )
xn=a2un的z变换及收敛域
xn=a2un的z变换及收敛域首先，我们来讨论xn=a^2un的z变换。
Z变换是一种离散时间信号的频域表示方法，它将离散时间序列xn映射到复平面上的函数X(z)。
对于给定的离散时间序列xn，其z变换X(z)定义如下：X(z) = Z{xn} = Σ(xn z^(-n))。
其中，n取遍所有整数，z为复变量。
现在我们来计算xn=a^2un的z变换。
根据定义，我们有：X(z) = Z{a^2un} = Σ((a^2un) z^(-n))。
由于un是单位阶跃函数，它的定义如下：un = 1, n >= 0。
un = 0, n < 0。
因此，我们可以将上述求和分为两个部分来计算：X(z) = Σ((a^2 1) z^(-n)), n >= 0。
= Σ(0 z^(-n)), n < 0。
对于第一个部分，我们可以将a^2提取出来，得到： X(z) = a^2 Σ(z^(-n)), n >= 0。
这是一个等比级数求和，其求和公式为：Σ(z^(-n)) = 1 / (1 z^(-1))。
将其代入上式，我们得到：X(z) = a^2 (1 / (1 z^(-1))), n >= 0。
对于第二个部分，我们有：X(z) = Σ(0 z^(-n)), n < 0。
= 0。
综上所述，xn=a^2un的z变换为：X(z) = a^2 (1 / (1 z^(-1))), n >= 0。
= 0, n < 0。
接下来我们来讨论收敛域。
收敛域是指在复平面上，z变换X(z)收敛的区域。
对于上述的X(z) = a^2 (1 / (1 z^(-1)))，它在什么区域内收敛呢？我们知道，收敛域取决于级数的绝对值是否收敛。
对于上述的X(z)，当|z| > 1时，级数1 / (1 z^(-1))绝对值不收敛，因此X(z)在|z| > 1的区域内不收敛。
当|z| < 1时，级数1 / (1 z^(-1))绝对值收敛，因此X(z)在|z| < 1的区域内收敛。
《Z变换的收敛域》课件
1
收敛域的大小与稳定性有密切
关系
信号的频域特性
2
如果系统的输入信号Z变换的收敛域包含 了稳定域，则系统是稳定的
不同的收敛域代表着信号在频域上的不
同特性，因此收敛域在信号分析中具有
重要的地位
3
滤波器设计
不同的收敛域决定了数字滤波器的性质， 因此我们可以根据需要指定收敛域来设 计所需的数字滤波器
收敛域的边界有哪些？如何确定边界？
常见的收敛域有哪些？
1 收敛于整个平面
对于某些信号，Z变换在整个平面都收敛，这在实际应用中较为少见
2 收敛于单位圆内部
当信号的绝对值随着时间的增加而指数衰减，Z变换收敛于单位圆内部
3 收敛于单位圆外部的环状区域
如果信号的绝对值并不随着时间的增加而衰减，而是不断循环波动，Z变换就会在圆环上 收敛
动态系统中收敛域的重要性是什么？
控制系统稳定性分析
Z变换和收敛域在控制系统的分 析和设计中具有广泛应用。我们 可以利用收敛域来预测系统的稳 定性，并设计控制器来改善系统 的性能
语音信号处理
语音信号的处理和分析需要考虑 其时间和频率特性。Z变换和收 敛域是分析语音信号频率特性的 有力工具之一
Z变换与收敛域在实际应用中的局限性 与挑战
边界线的特点不同
收敛域和发散域之间的边界线有很大不同。收敛域 的边界线通常是连续的，而发散域的边界线则断断 续续
收敛定理是什么？有哪些类型？
1
极限定理
如果序列的极限存在，则它的Z变换必收
稳定定理
2
敛于某个区域内
一个因果稳定的离散系统的Z变换必定在
单位圆内收敛
3
因果性定理
如果离散系统是因果的，那么它的Z变换
z变换的定义和收敛域PPT课件
——电子信息工程
第二章 离散系统的变换域分析
——电子信息工程
u( t ) 0
f
t
——电子信息工程
主要内容： • z变换及其收敛域 • 部分分式展开法求z反变换 • z变换的主要性质 • 离散系统的系统函数和频率响应 • 系统函数与差分方程的关系 • 线性时不变系统的基本结构
——电子信息工程
2.1 z变换与z逆变换
n0
n
若有 | a || b |
X(z) z z za zb
| a || z || b |
——电子信息工程
3.典型序列z变换
(1) x(n) (n) 1, 任意z
(2)
x(n)
u(n)
1
1 z 1
,
|z|1
(3)
x(n)
u(n
1)
1
1 z 1
,
|z|1
(4)
x(n)
a n u(n)
x(n) 0
——电子信息工程
例： 求序列 x(n) bnu(n 1) 的 z 变换及收敛域
1
解： X (z) x(n)zn bnzn bnzn 1 bnzn
n
n
n1
n0
当 | z |时1，级数 b
收b 敛n z n
n0
X (z)
1
n0
bnzn
1
1 1 b1z
z zb
| z || b |
注意： 左边序列和右边序列具有相同的z变换形式， 但收敛域不同。
——电子信息工程
（4）.双边序列
双边序列是指n为任意值时x(n)皆有值的序列。
1
X (z) x(n)zn x(n)zn x(n)zn
第二章 离散系统的变换域分析
——电子信息工程
u( t ) 0
f
t
——电子信息工程
主要内容： • z变换及其收敛域 • 部分分式展开法求z反变换 • z变换的主要性质 • 离散系统的系统函数和频率响应 • 系统函数与差分方程的关系 • 线性时不变系统的基本结构
——电子信息工程
2.1 z变换与z逆变换
n0
n
若有 | a || b |
X(z) z z za zb
| a || z || b |
——电子信息工程
3.典型序列z变换
(1) x(n) (n) 1, 任意z
(2)
x(n)
u(n)
1
1 z 1
,
|z|1
(3)
x(n)
u(n
1)
1
1 z 1
,
|z|1
(4)
x(n)
a n u(n)
x(n) 0
——电子信息工程
例： 求序列 x(n) bnu(n 1) 的 z 变换及收敛域
1
解： X (z) x(n)zn bnzn bnzn 1 bnzn
n
n
n1
n0
当 | z |时1，级数 b
收b 敛n z n
n0
X (z)
1
n0
bnzn
1
1 1 b1z
z zb
| z || b |
注意： 左边序列和右边序列具有相同的z变换形式， 但收敛域不同。
——电子信息工程
（4）.双边序列
双边序列是指n为任意值时x(n)皆有值的序列。
1
X (z) x(n)zn x(n)zn x(n)zn
z变换的收敛域
X (z) X1(z) X2(z) zz a Nhomakorabea
z
z
b
2z(z a (z a)(z
b) 2 b)
a z b
2z(z a b)
X(z)
2
(z a)(z b)
a z b
jIm(z)
a
b
Re(z)
思考题
• 1. 不同的序列可以得到相同的z变换式吗？ • 2. 判别正项级数的收敛性的方法有哪些？ • 3. 序列的形式与双边z变换收敛域的关系？
知识回顾 Knowledge Review
3、左边序列：只在 n n2区间内，有非零的有限值
的序列 x(n) n2
X (z) x(n)zn n n2
n
mn
nm
X (z) x(m)zm x(n)zn
m n2
nn2
lim n x(n)zn 1 lim n x(n) z 1
零的有限值的序列 x(n)
X (z) x(n)zn
n
n
1
X (z) x(n)z n x(n)z n
n
n0
圆内收敛
圆外收敛
Rx2 Rx1
j Im[ z]
Rx2 Rx1
Rx2 Rx1
有环状收敛域 没有收敛域
Re[ z]
例2：求序列x[n]=anu[n]-bnu[-n-1]的z变 换,并确定收敛域（b>a, b>0, a>0）。
lim an1
a n n
1,级数收敛。 1,级数发散。 1,不能肯定。
2) 根值判定法
z
z
b
2z(z a (z a)(z
b) 2 b)
a z b
2z(z a b)
X(z)
2
(z a)(z b)
a z b
jIm(z)
a
b
Re(z)
思考题
• 1. 不同的序列可以得到相同的z变换式吗？ • 2. 判别正项级数的收敛性的方法有哪些？ • 3. 序列的形式与双边z变换收敛域的关系？
知识回顾 Knowledge Review
3、左边序列：只在 n n2区间内，有非零的有限值
的序列 x(n) n2
X (z) x(n)zn n n2
n
mn
nm
X (z) x(m)zm x(n)zn
m n2
nn2
lim n x(n)zn 1 lim n x(n) z 1
零的有限值的序列 x(n)
X (z) x(n)zn
n
n
1
X (z) x(n)z n x(n)z n
n
n0
圆内收敛
圆外收敛
Rx2 Rx1
j Im[ z]
Rx2 Rx1
Rx2 Rx1
有环状收敛域 没有收敛域
Re[ z]
例2：求序列x[n]=anu[n]-bnu[-n-1]的z变 换,并确定收敛域（b>a, b>0, a>0）。
lim an1
a n n
1,级数收敛。 1,级数发散。 1,不能肯定。
2) 根值判定法
z变换的定义与收敛域.
1) |z|3
2 3 H ( z) 1 1 2z 1 3z 1 非稳定，因果
h[k ] (2
2) 2<|z|<3 非稳定， 非因果
k 1
3
k 1
)u[k ]
h[k ] 2k 1 u[k ] 3k 1 u[k 1]
3) |z|<2 稳定，非因果
h[k ] 2
单位圆 Im(z) Re(z)
单位圆
Im(z) Re(z)
稳定因果系统
非稳定非因果系统
单位圆
Im(z) Re(z)
稳定非因果系统
系统函数
对LTI系统:
y[k]=x [k]*h[k]
由z变换的性质：Y(z)=H(z)X(z) H(z)称为离散LTI系统的系统函数 当的H(z) ROC包含单位圆时
H ( e j ) H ( z ) z e j
k 1
u[k 1] 3
k 1
u[k 1]
留数法求Z反变换
1 k 1 x[k ] X ( z ) z dz c 2j
l
C为X(z) 的ROC中的一闭合曲线
Re s{ X ( z ) z k 1 } z p
l
1 例：X ( z ) (1 az1 ) 2
X ( z ) z k
k 0
N 1
1 zN 1 1 z
z 0
2)右边序列
X ( z)
k N1
k
x[k ]z
k
z R
例：x[k ] ak u[k ]
X ( z) a z
k 0 k
1 1 1 az
z a
3)左边序列
2 3 H ( z) 1 1 2z 1 3z 1 非稳定，因果
h[k ] (2
2) 2<|z|<3 非稳定， 非因果
k 1
3
k 1
)u[k ]
h[k ] 2k 1 u[k ] 3k 1 u[k 1]
3) |z|<2 稳定，非因果
h[k ] 2
单位圆 Im(z) Re(z)
单位圆
Im(z) Re(z)
稳定因果系统
非稳定非因果系统
单位圆
Im(z) Re(z)
稳定非因果系统
系统函数
对LTI系统:
y[k]=x [k]*h[k]
由z变换的性质：Y(z)=H(z)X(z) H(z)称为离散LTI系统的系统函数 当的H(z) ROC包含单位圆时
H ( e j ) H ( z ) z e j
k 1
u[k 1] 3
k 1
u[k 1]
留数法求Z反变换
1 k 1 x[k ] X ( z ) z dz c 2j
l
C为X(z) 的ROC中的一闭合曲线
Re s{ X ( z ) z k 1 } z p
l
1 例：X ( z ) (1 az1 ) 2
X ( z ) z k
k 0
N 1
1 zN 1 1 z
z 0
2)右边序列
X ( z)
k N1
k
x[k ]z
k
z R
例：x[k ] ak u[k ]
X ( z) a z
k 0 k
1 1 1 az
z a
3)左边序列
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
k
证明：Z x(n m)u(n) x(x(n m)u(n) x(n m)zn
n0
令 k nm 则 nkm
Z x(n m)u(n) x(k)zk zm zm x(k)zk
n0
x(n)( z )n X ( z )
n0
a
a 15
（四）Z域尺度变换（序列指数加权）
同理：
Z anx(n) X (az) Rx1 az Rx1 Z (1)n x(n) X (z) Rx1 z Rx1
在Z域反褶，则时域中函数在正负之间交 替跳跃
dz
n0
dz
x(n) (n)z(n1)
n0
z1 nx(n) zn
n0
Z nx(n) (z) dX (z)
dz
13
（三）Z域微分（序列线性加权）
例：已知 u(n) z
z 1
求n·u(n)的Z变换
解： n u(n) (z) d [ z ] dz z 1
k
同理： Z x(n m) zm X (z) 4
（二）位移性质
单边Z变换的位移性质
1、若x(n)是双边序列，其单边Z变换为：
Z x(n) u(n) X (z)
左移
Z x(n m) u(n) z
k 0
X (z) x(k)z
m
m1
x(n)的Z变换为
X (z) X1(z) 1 zN z2N
X1(z)
zN zN 1
z 1
9
（二）位移性质
例：已知单边Z变换 an z , z a za
其中an是双边序列
求 an-1u(n), an-1u(n-1) 的单边Z变换。
解：设 x(n) an 则 x(n 1) an1
Z ax(n) by(n) aX(z) bY(z), R1 z R2
其中a,b为任意常数， R1 max Rx1, Ry1 R2 min Rx2 , Ry2 2
（二）位移性质
双边Z变换： x(n)是双边序列
若 Z x(n) X (z) 则 Z x(n m) zm X (z)
1、由单边Z变换公式
an1u(n) z1 X (z) x(1)z
z1 z 1 za a
10
（二）位移性质
2、anu(n)是单边序列，所以an-1u(n-1)的Z变换为
an1u(n 1) z1X (z)
z1 z za
即 an1u(n 1) 1 za
x(n) x(n N) n 0
令x1(n)表示x(n）的第一个周期，因为x1(n)是有 限长序列，所以其Z变换为
N 1
X1(z) x1(n)zn z 0
n0
8
（二）位移性质
周期序列x(n)用x1(n)表示，为
x(n) x1(n) x1(n N ) x1(n 2N )
第四章 Z变换
4.1 Z变换及其收敛域 4.2 Z反变换 4.3 Z变换的性质 4.4 Z变换与拉普拉斯变换的关系
1
4.3 Z变换的性质
这些性质表示离散序列在时域和Z域间的关系
（一）线性性质
若 Z x(n) X (z), Rx1 z Rx2 则 Z y(n) Y (z), Ry1 z Ry2
11
（三）Z域微分（序列线性加权）
x(n)是有始序列
若 Z x(n) X (z)
则 Z nx(n) (z) dX (z)
dz
证明： X (z) x(n)zn
n0
对上式两边求导，得
12
（三）Z域微分（序列线性加权）
dX (z) x(n) d (zn )
16
（五）初值定理
若x(n)是单边序列，且 Z x(n) X (z)
则 x(0) lim X (z)
z
17
（六）终值定理
若x(n)是单边序列，且 Z x(n) X (z)
则 lim x(n) lim(z 1) X (z)
n
z1
终值定理使用的条件
1、只有在n时x(n)收敛的情况，才能用它 来确定x(n)的值。
2、X(z)的收敛半径应小于或等于1
18
（七）时域卷积定理
若 Z x(n) X (z), Rx1 z Rx2 Z y(n) Y (z), Ry1 z Ry2
m
1
k
2、若x(n)是单边序列，其单边Z变换为：
Z x(n m) u(n) z X (z) m
Z x(n m) u(n) z
k 0
X (z) x(k)z
m
m1
k
7
（二）位移性质
例 4.3-2 求周期序列 x(n)的Z变换 解：若周期序列x(n) 的周期为N，即
k m
k m
zm
x(k ) z k
m1
x(k
)
zk
k 0
k 0
zm
X
(z)
m1
x(k ) z k
k 0
6
（二）位移性质
右移
k m
Z x(n m) u(n) z X (z) x(k)z
(z
z 1)2
n
u(n)
(z
z 1)2
14
（四）Z域尺度变换（序列指数加权）
若 Z x(n) X (z), Rx1 z Rx2
则 Z anx(n) X ( z ) a
Rx1
z a
Rx1
证明：Z an x(n) an x(n)zn
证明：根据双边Z变换的定义
Z x(n m) x(n m)zn
n
3
（二）位移性质
Z x(n m) x(n m)zn
n
令 k=n+m,则上式变为
Z x(n m) x(k)z(km)
k
x(k)zk zm zm X (z)