戴维南定理练习题
戴维南定理的解析与练习
戴维宁定理一、知识点：1、二端(一端口) 网络的概念：二端网络：具有向外引出一对端子的电路或网络。
无源二端网络：二端网络中没有独立电源。
有源二端网络：二端网络中含有独立电源。
2、戴维宁（戴维南）定理任何一个线性有源二端网络都可以用一个电压为U OC的理想电压源和一个电阻R0串联的等效电路来代替。
如图所示：等效电路的电压U OC是有源二端网络的开路电压，即将负载R L断开后 a 、b两端之间的电压。
等效电路的电阻R0是有源二端网络中所有独立电源均置零（理想电压源用短路代替，理想电流源用开路代替）后, 所得到的无源二端网络a 、b两端之间的等效电阻。
二、 例题：应用戴维南定理解题：戴维南定理的解题步骤：1.把电路划分为待求支路和有源二端网络两部分，如图1中的虚线。
2.断开待求支路，形成有源二端网络（要画图），求有源二端网络的开路电压UOC 。
3.将有源二端网络内的电源置零，保留其内阻（要画图），求网络的入端等效电阻Rab 。
4.画出有源二端网络的等效电压源，其电压源电压US=UOC （此时要注意电源的极性），内阻R0=Rab 。
5.将待求支路接到等效电压源上，利用欧姆定律求电流。
例1：电路如图，已知U 1=40V ，U 2=20V ，R 1=R 2=4Ω，R 3=13 Ω，试用戴维宁定理求电流I 3。
解：(1) 断开待求支路求开路电压U OCU OC = U 2 + I R 2 = 20 +2.5 ⨯ 4 =30V或： U OC = U 1 – I R 1 = 40 –2.5 ⨯ 4 = 30VU OC 也可用叠加原理等其它方法求。
(2) 求等效电阻R 0将所有独立电源置零（理想电压源用短路代替，理想电流源用开路代替）(3) 画出等效电路求电流I 3例2：试求电流 I 1A 5.24420402121=+-=+-=R R U U I Ω=+⨯=221210R R R R R A 21323030OC 3=+=+=R R UI解：(1) 断开待求支路求开路电压U OCU OC = 10 – 3 ⨯ 1 = 7V(2) 求等效电阻R0R0 =3 Ω(3) 画出等效电路求电流I3解得：I1 = 1. 4 A 【例3】用戴维南定理计算图中的支路电流I3。
戴维南定理的解析与练习
一、知识点：1、二端(一端口) 网络的概念：二端网络：具有向外引出一对端子的电路或网络。
无源二端网络：二端网络中没有独立电源。
有源二端网络：二端网络中含有独立电源。
2、戴维宁（戴维南）定理任何一个线性有源二端网络都可以用一个电压为U OC的理想电压源和一个电阻R0串联的等效电路来代替。
如图所示：等效电路的电压U OC是有源二端网络的开路电压，即将负载R L断开后 a 、b两端之间的电压。
等效电路的电阻R0是有源二端网络中所有独立电源均置零（理想电压源用短路代替，理想电流源用开路代替）后, 所得到的无源二端网络 a 、b两端之间的等效电阻。
二、 例题：应用戴维南定理解题：戴维南定理的解题步骤：1.把电路划分为待求支路和有源二端网络两部分，如图1中的虚线。
2.断开待求支路，形成有源二端网络（要画图），求有源二端网络的开路电压UOC 。
3.将有源二端网络内的电源置零，保留其内阻（要画图），求网络的入端等效电阻Rab 。
4.画出有源二端网络的等效电压源，其电压源电压US=UOC （此时要注意电源的极性），内阻R0=Rab 。
5.将待求支路接到等效电压源上，利用欧姆定律求电流。
例1：电路如图，已知U 1=40V ，U 2=20V ，R 1=R 2=4，R 3=13 ，试用戴维宁定理求电流I 3。
解：(1) 断开待求支路求开路电压U OCU OC = U 2 + I R 2 = 20 + 4 = 30V或： U OC = U 1 – I R 1 = 40 – 4 = 30VU OC 也可用叠加原理等其它方法求。
(2) 求等效电阻R 0将所有独立电源置零（理想电压源用短路代替，理想电流源用开路代替）(3) 画出等效电路求电流I 3例2：试求电流 I 1解：(1) 断开待求支路求开路电压U OCA 5.24420402121=+-=+-=R R U U I Ω=+⨯=221210R R R R R A 21323030OC 3=+=+=R R U IU OC = 10 – 3 1 = 7V(2) 求等效电阻R 0R 0 =3(3) 画出等效电路求电流I 3解得：I 1 = 1. 4 A【例3】 用戴维南定理计算图中的支路电流I 3。
戴维南定理和最大功率传递定理典型习题
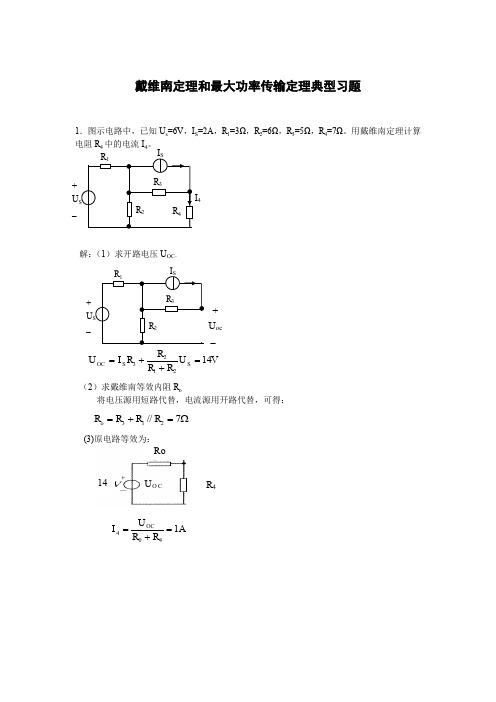
戴维南定理和最大功率传输定理典型习题1．图示电路中，已知U s =6V ，I S =2A ，R 1=3Ω，R 2=6Ω，R 3=5Ω，R 4=7Ω。
用戴维南定理计算电阻R 4中的电流I 4。
解：（1）求开路电压U OC 。
VU R R R R I U S S OC 142123=++=（2）求戴维南等效内阻R o将电压源用短路代替，电流源用开路代替，可得：Ω=+=7//213R R R R o(3)1014AR R I OC 1404=+=+ U _ I 4+ U _2．已知U S =15V ，R =1.4Ω，R 1=6Ω，R 2=1Ω，R 3=3Ω，R 4=2Ω。
用戴维南定理求图所示电路中的电流I 。
解：（1）求开路电压U OC 。
+_U OCI 1I 2VR I R I U AI I R R R R I AR R R R U I OC 131212)//(221111423324231S1=+===++==++=（2）求戴维南等效内阻R o将电压源用短路代替，可得：Ω=+=2.1//)//(4231R R R R R o（3101413AR R U I OC 54.12.1130=+=+=3．有源线性二端网络N 的开路电压U 0为9V ，若联接如图2 (a)所示，则得电流为1A 。
若解：有源线性二端网络可等效为一实际电压源且电压源VU OC 9=（a ）图可等效为：U Ω3I由此时电流为1A 可得： Ω=∴=+=118900R R I（b ）图可等效为：U A对左边网孔列写KVL 方程，可得：A I U I I R OC 3201(35o =∴=-+++））（(a)(b)4．一线性有源二端网络，它的开路电压U AB =24V 。
当有源二端网络AB 间外接一个8Ω电阻时，通过此电阻的电流是2.4A 。
如改接成如图所示电路，计算通过电阻R 支路的电流。
已知R =2.5Ω，I S =6A 。
解：有源线性二端网络可等效为一实际电压源且电压源V U OC 24=当有源二端网络AB 间外接一个8Ω电阻时电路等效为：U Ω8A4.由此时电流是2.4A 可得：Ω==+24.282400R RU A6根据叠加定理可得：AI 865.2225.2224=⨯+++=5．图示电路，求当可变电阻R为何值时，R可以获得最大的功率，并求此最大功率值。
戴维宁定理七种例题
戴维宁定理例题例1 运用戴维宁定理求下图所示电路中的电压U0图1剖析：断开待求电压地址的支路（即3Ω电阻地址支路），将剩下一端口网络化为戴维宁等效电路，需恳求开路电压U oc和等效电阻R eq。
（1）求开路电压U oc，电路如下图所示由电路联接联络得到，U oc=6I+3I，求解得到，I=9/9=1A，所以U oc=9V（2）求等效电阻R eq。
上图电路中含受控源，需求用第二（外加电源法（加电压求电流或加电流求电压））或第三种（开路电压，短路电流法）办法求解，此刻独立源应置零。
法一：加压求流，电路如下图所示，依据电路联接联络，得到U=6I+3I=9I（KVL），I=I0´6/(6+3)=(2/3)I0（并联分流），所以U=9´(2/3)I0=6I0，R eq=U/I0=6Ω法二：开路电压、短路电流。
开路电压前面已求出，U oc=9V，下面需恳求短路电流I sc。
在求解短路电流的进程中，独立源要保存。
电路如下图所示。
依据电路联接联络，得到6I1+3I=9（KVL），6I+3I=0（KVL），故I=0，得到I sc=I1=9/6=1.5A（KCL），所以R eq=U oc/I sc=6Ω终究，等效电路如下图所示依据电路联接，得到留心：核算含受控源电路的等效电阻是用外加电源法仍是开路、短路法，要详细疑问详细剖析，以核算简练为好。
戴维南定理典型例子戴维南定理指出，等效二端网络的电动势E等于二端网络开路时的电压，它的串联内阻抗等于网络内部各独立源和电容电压、电感电流都为零时，从这二端看向网络的阻抗Zi。
设二端网络N中含有独立电源和线性时不变二端元件（电阻器、电感器、电容器），这些元件之间可以有耦合，即可以有受控源及互感耦合；网络N的两端ɑ、b接有负载阻抗Z（s），但负载与网络N内部诸元件之间没有耦合，U（s）=I（s）/Z（s）。
当网络N中所有独立电源都不工作（例如将独立电压源用短路代替，独立电流源用开路代替），所有电容电压和电感电流的初始值都为零的时候，可把这二端网络记作N0。
戴维南定理的解析与练习
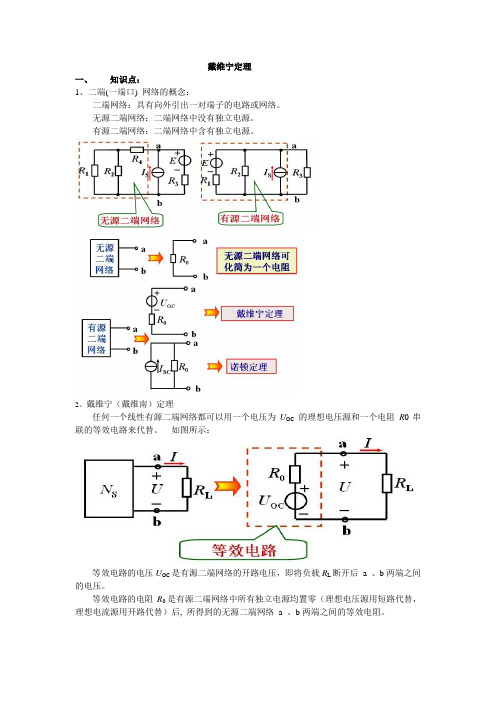
戴维宁定理一、知识点：1、二端(一端口) 网络的概念：二端网络：具有向外引出一对端子的电路或网络。
无源二端网络：二端网络中没有独立电源。
有源二端网络：二端网络中含有独立电源。
2、戴维宁（戴维南）定理任何一个线性有源二端网络都可以用一个电压为U OC的理想电压源和一个电阻R0串联的等效电路来代替。
如图所示：等效电路的电压U OC是有源二端网络的开路电压，即将负载R L断开后a 、b两端之间的电压。
等效电路的电阻R0是有源二端网络中所有独立电源均置零（理想电压源用短路代替，理想电流源用开路代替）后, 所得到的无源二端网络 a 、b两端之间的等效电阻。
二、 例题：应用戴维南定理解题：戴维南定理的解题步骤：1.把电路划分为待求支路和有源二端网络两部分，如图1中的虚线。
2.断开待求支路，形成有源二端网络（要画图），求有源二端网络的开路电压UOC 。
3.将有源二端网络内的电源置零，保留其内阻（要画图），求网络的入端等效电阻Rab 。
4.画出有源二端网络的等效电压源，其电压源电压US=UOC （此时要注意电源的极性），内阻R0=Rab 。
5.将待求支路接到等效电压源上，利用欧姆定律求电流。
例1：电路如图，已知U 1=40V ，U 2=20V ，R 1=R 2=4Ω，R 3=13 Ω，试用戴维宁定理求电流I 3。
解：(1) 断开待求支路求开路电压U OCU OC = U 2 + I R 2 = 20 +2.5 ⨯ 4 =30V或： U OC = U 1 – I R 1 = 40 –2.5 ⨯ 4 = 30VU OC 也可用叠加原理等其它方法求。
(2) 求等效电阻R 0将所有独立电源置零（理想电压源用短路代替，理想电流源用开路代替）(3) 画出等效电路求电流I 3例2：试求电流 I 1A 5.24420402121=+-=+-=R R U U I Ω=+⨯=221210R R R R R A 21323030OC 3=+=+=R R U I解：(1) 断开待求支路求开路电压U OCU OC = 10 – 3 ⨯ 1 = 7V(2) 求等效电阻R 0R 0 =3 Ω(3) 画出等效电路求电流I 3解得：I 1 = 1. 4 A【例3】 用戴维南定理计算图中的支路电流I 3。
戴维南定理解析与练习
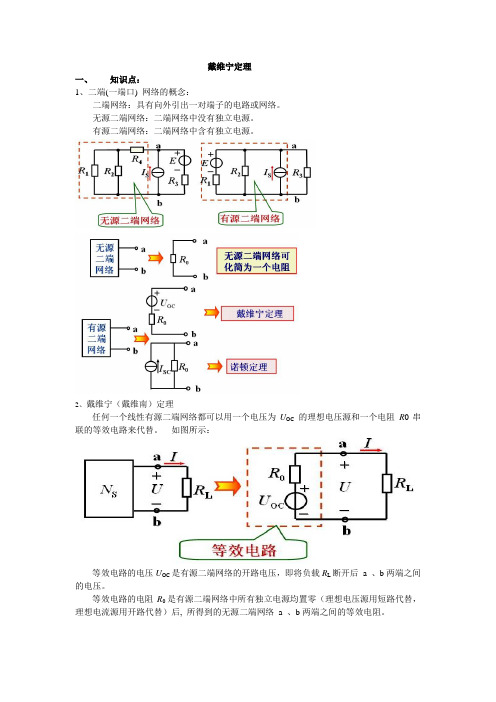
戴维宁定理一、知识点：1、二端(一端口) 网络的概念：二端网络：具有向外引出一对端子的电路或网络。
无源二端网络：二端网络中没有独立电源。
有源二端网络：二端网络中含有独立电源。
2、戴维宁（戴维南）定理任何一个线性有源二端网络都可以用一个电压为U OC的理想电压源和一个电阻R0串联的等效电路来代替。
如图所示：等效电路的电压U OC是有源二端网络的开路电压，即将负载R L断开后a 、b两端之间的电压。
等效电路的电阻R0是有源二端网络中所有独立电源均置零（理想电压源用短路代替，理想电流源用开路代替）后, 所得到的无源二端网络 a 、b两端之间的等效电阻。
二、 例题：应用戴维南定理解题：戴维南定理的解题步骤：1.把电路划分为待求支路和有源二端网络两部分，如图1中的虚线。
2.断开待求支路，形成有源二端网络（要画图），求有源二端网络的开路电压UOC 。
3.将有源二端网络内的电源置零，保留其内阻（要画图），求网络的入端等效电阻Rab 。
4.画出有源二端网络的等效电压源，其电压源电压US=UOC （此时要注意电源的极性），内阻R0=Rab 。
5.将待求支路接到等效电压源上，利用欧姆定律求电流。
例1：电路如图，已知U 1=40V ，U 2=20V ，R 1=R 2=4Ω，R 3=13 Ω，试用戴维宁定理求电流I 3。
解：(1) 断开待求支路求开路电压U OCU OC = U 2 + I R 2 = 20 +2.5 ⨯ 4 =30V或： U OC = U 1 – I R 1 = 40 –2.5 ⨯ 4 = 30VU OC 也可用叠加原理等其它方法求。
(2) 求等效电阻R 0将所有独立电源置零（理想电压源用短路代替，理想电流源用开路代替）(3) 画出等效电路求电流I 3例2：试求电流 I 1A 5.24420402121=+-=+-=R R U U I Ω=+⨯=221210R R R R R A 21323030OC 3=+=+=R R U I解：(1) 断开待求支路求开路电压U OCU OC = 10 – 3 ⨯ 1 = 7V(2) 求等效电阻R 0R 0 =3 Ω(3) 画出等效电路求电流I 3解得：I 1 = 1. 4 A【例3】 用戴维南定理计算图中的支路电流I 3。
戴维南定理补充练习
②求戴维南等效电阻Re q ：见右上图。端口加电源激励u，产生电流i’。
u 2000i'500i 1500i' u
Req i ' 1500
③画出戴维南等效电路，见右图所示。
例题3、求图示一端口的诺顿等效电路。
解：①求短路电流isc ： 用节点法：如上右图选参考节点，独立节点1的节点电压为：un
.A B.
－
U S1 +
R1
I S1
.
R2
I S2
. +
US2
－
US=UAB=(R1IS1－US1)－(R2IS2+US2)=－3V R0=R1+R2=2
图示电路中，已知：US=30V，IS=4A，R1=1， R2=3，R3=R4=6。求A，B两端的戴维宁等效电压源。
IS单独作用时：UAB'=(R3//R2)IS=8V US单独作用时:
I=
E0 R0+R
=
– 20 = – 2A 10+10
A E0 R0 I R
(c) B
例3、在图三所示电路中，已知：IS =2A，E1=8V，R1=2Ω， R2 =10Ω，试用戴 维南定理求流过R2的电流。
A
A
A
A
E
E
IS
R1
R2 IS
UAB R1
R1 UAB IS IS1
RAB R1
E0 I R2
E3 R3
E1
E2
R1
R2 I
(图二）
E3 R3 A
E1 R1 I1
E2 R2 UAB
戴维南定理的解析与练习
源端络无二网无源二端网络可 化简为一个电阻匸＞1戴维宁匸＞ I诺顿定理戴维宁定理一、知识点：1、二端（一端口）网络的概念：二端网络：具有向外引出一对端子的电路或网络。
无源二端网络：二端网络中没有独立电源。
有源二端网络：二端网络中含有独立电源。
2、戴维宁（戴维南）定理等效电路的电压 U OC 是有源二端网络的开路电压，即将负载 R L 断开后a 、b 两端之间 的电压。
等效电路的电阻 R o 是有源二端网络中所有独立电源均置零（理想电压源用短路代替， 理想电流源用开路代替）后 ，所得到的无源二端网络 a 、b 两端之间的等效电阻。
任何一个线性有源二端网络都可以用一个电压为 U oc 的理想电压源和一个电阻 R0串 联的等效电路来代替。
如图所示：二、 例题：应用戴维南定理解题：戴维南定理的解题步骤：1•把电路划分为待求支路和有源二端网络两部分，如图 1中的虚线。
2•断开待求支路，形成有源二端网络（要画图） ，求有源二端网络的开路电压UOC 。
3•将有源二端网络内的电源置零，保留其内阻（要画图），求网络的入端等效电阻 Rab 。
4•画出有源二端网络的等效电压源，其电压源电压 US=UOC （此时要注意电源的极性），内阻 R0=Rab 。
5•将待求支路接到等效电压源上，利用欧姆定律求电流。
例1:电路如图，已知 U 仁40V , U2=20V ，R 仁R2=4」R3=13门，试用戴维宁定理求电流13。
|A例2:试求电流I 1解：（1）断开待求支路求开路电压UOC5 -u 2R 1 R 240-20 4 4-2.5AUOC = U2 + I R2 = 20 +2.5 4 =30V或：UOC = U1 T R1 = 40 T 2.54 UOC 也可用叠加原理等其它方法求。
=30V⑵求等效电阻R0将所有独立电源置零（理想电压源 用短路代替，理想电流源用开路代替）RDR 1 R 2⑶画出等效电路求电流I 3U OC 30 2 13=2 Ar i .；編"眾r 牛匚I _------------- 1 ------ ---------lAOC)3A2厶a()i 2 i7Vboo或于是+ ()1OV因此E+耳 20+5=4tl② 等效电源的内阻 甩可由图1-58(c)求得塊=氏尽_20^5UOC = 10 —31 = 7V⑵求等效电阻R0R0 =3 门⑶画出等效电路求电流I3解：① 等效电源的电动势 E 可由图1-58(b)求得"尽+尽E =(/, = £. -^/ = 140-20> 2 = 1007= = + ^1 = 90+5x2 = 1007解：(1)断开待求支路求开路电压UOC【例3】 用戴维南定理计算图中的支路电流 I 3*R ta a训肾 £O^vC )E解得：11 = 1.4 A所以1.75-0 35xlC _i -0.35mA_4+F _10A【例4】 电路如图所示，R=2.5K Q,试用戴维南定理求电阻R 中的电流I将a 、b 间开路，求等效电源的电动势E ,即开路电压 U.bo 。
戴维南定理例题.
叠加原理： 对于线性电路，任何一条支路的电流，都可以看 成是由电路中各个电源（电压源或电流源）分别 作用时，在此支路中所产生的电流的代数和。 + E– R1 + E = – R2 R1
IS I1
I2
I1'
I2'
+ R2 R1
IS
I1'' (c)
I2''
R2
(a) 原电路
(b) E 单独作用
叠加原理
无源 二端 网络
a R
b + _E
a
ቤተ መጻሕፍቲ ባይዱ
无源二端网络可 化简为一个电阻
b
a
电压源 （戴维南定理） b a 有源二端网络可 化简为一个电源 电流源 （诺顿定理） b
总目录 章目录 返回 上一页 下一页
有源 二端 网络
a b
R0
IS
R0
戴维南定理 任何一个有源二端线性网络都可以用一个电动势 为E的理想电压源和内阻 R0 串联的电源来等效代替。 a I a I + 有源 + R0 RL U 二端 U RL + – E _ 网络 – b 等效电源 b 等效电源的电动势E 就是有源二端网络的开路电 压U0，即将负载断开后 a 、b两端之间的电压。 等效电源的内阻R0等于有源二端网络中所有电源 均除去（理想电压源短路，理想电流源开路）后所 得到的无源二端网络 a 、b两端之间的等效电阻。
IS单独作用
总目录 章目录 返回 上一页 下一页
应用戴维南定理求解的步骤：
1、将电路分成待求支路和有源二端网络两部分；
2、把待求支路断开，画出有源二端网络求有源二端网络的 开路电压Uoc；画出无源二端网络（即有源二端网络中的所 有独立电源不工作，非独立电源保留）求等效电阻Req； 3、画出有源二端网络的等效电路，E= Uoc R0= Req。然后 在等效电路两端接入待求支路，求出待求支路的电流。 必须注意：代替有源二端网络的电源的极性应与开路电压 Uoc一致，若Uoc为负值，则电动势的方向与图中相反。
戴维南定理的解析与练习.doc
戴维宁定理一、知识点：1、二端(一端口) 网络的概念：二端网络：具有向外引出一对端子的电路或网络。
无源二端网络：二端网络中没有独立电源。
有源二端网络：二端网络中含有独立电源。
2、戴维宁（戴维南）定理任何一个线性有源二端网络都可以用一个电压为U OC的理想电压源和一个电阻R0串联的等效电路来代替。
如图所示：等效电路的电压U OC是有源二端网络的开路电压，即将负载R L断开后a 、b两端之间的电压。
等效电路的电阻R0是有源二端网络中所有独立电源均置零（理想电压源用短路代替，理想电流源用开路代替）后, 所得到的无源二端网络 a 、b两端之间的等效电阻。
二、 例题：应用戴维南定理解题： 戴维南定理的解题步骤：1.把电路划分为待求支路和有源二端网络两部分，如图1中的虚线。
2.断开待求支路，形成有源二端网络（要画图），求有源二端网络的开路电压UOC 。
3.将有源二端网络内的电源置零，保留其内阻（要画图），求网络的入端等效电阻Rab 。
4.画出有源二端网络的等效电压源，其电压源电压US=UOC （此时要注意电源的极性），内阻R0=Rab 。
5.将待求支路接到等效电压源上，利用欧姆定律求电流。
例1：电路如图，已知U 1=40V ，U 2=20V ，R 1=R 2=4Ω，R 3=13 Ω，试用戴维宁定理求电流I 3。
解：(1) 断开待求支路求开路电压U OCU OC = U 2 + I R 2 = 20 +2.5 ⨯ 4 = 30V或： U OC = U 1 – I R 1 = 40 –2.5 ⨯ 4 = 30V U OC 也可用叠加原理等其它方法求。
(2) 求等效电阻R 0将所有独立电源置零（理想电压源用短路代替，理想电流源用开路代替）(3) 画出等效电路求电流I 3A 5.24420402121=+-=+-=R R U U I Ω=+⨯=221210R R R R R A21323030OC 3=+=+=R R U I例2：试求电流 I 1解：(1) 断开待求支路求开路电压U OC U OC = 10 – 3 ⨯ 1 = 7V (2) 求等效电阻R 0 R 0 =3 Ω(3) 画出等效电路求电流I 3解得：I 1 = 1. 4 A【例3】 用戴维南定理计算图中的支路电流I 3。
戴维南定理
戴维南定理测试题
例题1.电路如图所示，(1)用戴维南定理求I；(2)求3A电流源的功率。
例题2.电路和各元件参数如图所示，试求
(1)当RL=3时，电流I为1A，求此时的US的值；
(2)当RL为何值时可获得最大功率，此时获得的最大功率Pmax为多少；
(3)当电压源US调至何值时，RL两端的电压始终为零且与RL的值无关。
例题3.如图所示电路中，当开关打在2位置时，电流表读数为2A，当开关打在1位置时，电流表读数为1A，试求：
(1)ab虚线左侧部分电路的等效电源参数；
(2)电流源IS2的电流为多少？
(3)要使开光打在1位置时，电流表读数为0，电流源IS2的电流为多少？
例题4.电路如图所示，(1)用戴维南定理求电流I1；(2)计算电阻R4消耗的功率；(3)求恒流源IS的功率。
例题5.开关S置位置1时电压表读数为4V，求开关S置位置2时电压表的读数。
例题6.将图(a)所示电路等效成图(b)所示的电压源。
要求
(1)计算等效电压源的Uou，Rab；
(2)若在ab之间接入一个电流表，计算电流表读数(不考虑电流表内阻对电路的影响)；
(3)若在ab之间接入一个电阻R，当R获得最大功率时，计算R的值和最大功率Pmax。
例题7.电路如图(a)所示。
已知图(b)所示电路中，电流表的读数是2A；图(c)(d)所示电路中的电流I1、I2分别是0.5A和1A。
求
(1)A部分电路的等效电源参数Uso、Ro的值；
(2)R和Is的值；
(3)图(a)电路中5欧姆电阻的功率。
戴维宁定理七种例题
对于任何一个含源二端网络都可以用一个电源来代替,其电源电动势E等于其含源二端网络的开路电压,其内阻R等于含源二端网络内所有电动势为零时的输入电阻,这就是戴维南定理.","force_purephv":"0","gnid":"92556239629d7cecd","highlight":{"ab_ta g_A":{"src":"kuaizixun_keywords_A","words":[{"index":50,"word":"内阻"},{"index":39,"word":"二端网络"},{"index":30,"word":"电动势"},{"index":21,"word":"电源"}]},"ab_tag_B":{"src":"kuaizixun_keywords_B","words":[{"index":50,"word ":"内阻"},{"index":39,"word":"二端网络"},{"index":30,"word":"电动势"},{"index":21,"word":"电源"}]}},"img_data":[{"flag":2,"img":[]}],"pat":"mass_model_adver,art_src_6,fts 2,sts0","powerby":"pika","pub_time":1574885731610,"rawurl":"http://zm. /ece8b7f69391c355ce27de98cb114a3b","redirect":0,"rptid": "611f0af7fbc1e915","src":"文学旅游生活","tag":[],"title":"戴维南定理的内容是什么?戴维南定理的例题_ ：可将任一复杂的集总参数含源线性时不变二端网络等效为一个简单的二端网络的定理. 对于任意含独立源,线性电阻和线性受控源的单口网络(二端网络),都可以用一个电压源与电阻相串联的单口网络(二端网络)来等效.这个电压源的电压...戴维南定理例题：戴维南定理是一个很实用的定理.虽然这样的题,你可以一步一步简化这个电路图,最终得到最简的形式求得所需的电压值.(这题这样做样还简单一些)但是如果这个电路更复杂类似桥式电路,就无法用化简的方法直接求答案了,只能用戴维...用戴维南定理求习题7-20图所示电路中的电流I0. - 上学吧找答案：首先,找Rth(也就是R0)当找Rth时.所有线性时不变的电压源,视为短路(一条直线).R不考虑,因为R是负载,戴维南定律只看出了负载以外的电路.所以,当把48V和60V 换成直线之后,可以看到12ohm和6ohm的电阻成并联,并联求出...求助.戴维南定理解题步骤._ ：运用戴维南定理解题的步骤概括为:1、分2、求E 3、求r 4、合分别配以相应的图形步骤(1) 把电路分为待求支路和有源二端网络两部分.(2) 把待求支路移开,求出有源二端网络的开路电压Uab (3) 将网络内各电源除去,仅保留电源内阻,求出网络两端的等效电阻Rab (4) 画出有源二端网络的等效电路,等效电路中电源的电动势E0=Uab,电源的内阻r0=Rab,然后在等效电路两端接入待求支路,则待求支路的电流为I= E0/( r0+R)【戴维南定理的内容以及解题步骤】：在计算戴维南等效电路时,必须联立两个由电阻及电压两个变量所组成的方程式,这两个方程式可经由下列步骤来获得: 1. 在AB两端开路(在没有任往外电流输出,亦即当AB点之间的阻抗无限大)的状况下计算输出电压VAB,此...戴维南定理是什么,解题步骤是哪些_ ：戴维南等效是关于电压源的等效:故此:第一步:将待求电路与外电路断开,求待求电路等效端口处的开路电压;第二步:将待求电路中所有电压源短路(直接用导线短接代替),将所有电流源开路(直接断开),化解纯电阻电路,求得内阻.(注:含受控源可参考百度文档:应用戴维南定理求解线性含受控源电路) 第三步:根据求得的开路电压和内阻画出等效电路即可.戴维南定理题?_ ：开路电压就是R0与R1分压, Uo=Us*R1/(R0+R1),等效电阻就是R0//R1,有了这个戴维南等效,计算I2和U就太容易了.。
戴维南定理基础练习题(打印版)
戴维南定理基础练习题（打印版）# 戴维南定理基础练习题## 一、理论回顾戴维南定理（Thevenin's Theorem）是电路理论中的一个重要定理，它提供了一种将复杂电路简化为等效电路的方法。
根据戴维南定理，任何线性双端网络都可以用一个电压源和内阻串联的等效电路来代替。
### 1. 定理内容戴维南定理指出，对于任何线性双端网络，当其两端开路时，等效电压源的电压等于开路电压；当其两端短路时，等效内阻等于短路电流除以开路电压。
### 2. 应用条件- 电路必须是线性的。
- 电路两端可以是任意的两个节点。
## 二、基础练习题### 练习题1：开路电压与短路电流的计算题目描述：给定一个简单的电路，包含一个电压源Vs，一个电阻R1，和一个并联电阻R2。
计算开路电压和短路电流。
电路参数：- Vs = 10V- R1 = 1kΩ- R2 = 2kΩ解答：开路电压等于电压源的电压，即Voc = Vs = 10V。
短路电流Isc可以通过计算总电阻Rt得到：\[ R_t = \frac{R_1 \times R_2}{R_1 + R_2} = \frac{1k\Omega \times 2k\Omega}{1k\Omega + 2k\Omega} = 0.6667k\Omega \]\[ I_{sc} = \frac{V_s}{R_t} = \frac{10V}{0.6667k\Omega}\approx 15.01mA \]### 练习题2：等效电路的构建题目描述：在练习题1的基础上，构建等效电路，并计算当负载电阻RL = 3kΩ时的输出电压。
解答：等效电路由10V的电压源和0.6667kΩ的内阻串联组成。
当连接负载电阻RL时，总电阻为：\[ R_{total} = R_{th} + R_L = 0.6667k\Omega + 3k\Omega = 3.6667kΩ \]输出电压Vout可以通过欧姆定律计算：\[ V_{out} = I_{load} \times R_{total} \]\[ I_{load} = \frac{V_{oc}}{R_{total}} =\frac{10V}{3.6667k\Omega} \approx 2.73mA \]\[ V_{out} = 2.73mA \times 3.6667k\Omega \approx 10V \]### 练习题3：电路参数的调整题目描述：如果将练习题1中的R1改为2kΩ，重新计算开路电压和短路电流。
戴维南定理专题
戴维南定理专题83．利用戴维南定理求解如题83图（a）中的电流I。
解：（1）将1A恒流源和10Ω电阻同时去掉后如（b）图,则开路电压U O＝V；（4分）（2）将(b)中除源后，等效电阻R O＝Ω；（3分）（3）(a)中的电流I＝A。
（5分）(a)(b)题83图83.利用戴维南定理求解如题83图中的电流I。
（1）断开待求支路,则开路电压U O＝V；(5分)（2）等效电阻R O＝Ω；（4分）（3）电流I＝ A。
（3分）题83图84．如题84图所示电路，利用戴维南定理求解如题84图（a）中的电流I。
（本题共11分）解：（1）将4Ω电阻去掉后如题84（b）图，则开路电压U ab= V；（4分）（2）将题84（b）图中除源后，等效电阻R ab= Ω；（3分）（3）题84（a）图中的电流I = A。
（4分）如题84图所示电路，试求：⑴电流I；⑵A点电位V A。
（用戴维南定律解）（12分）83.(12分)试分析计算：(1)利用戴维南定理求出题83(a)图的等效电路。
(8分)(2)若在题83(a)图中a、b两端接上题83(b)图，则R L两端的电压U L为多少？(2分)(3)若在题83(a)图中a、b两端接上题83(c)图，则I1、I2分别为多少？(设二极管为理想二极管)(2分)题83（a）题83（b）题83（c）解：(1)利用戴维南定理求解过程：第一步：求出题83(a)图中的开路电压U ab＝____________V。
第二步：将题83(a)图电路除源，画出无源二端网络如下：则无源二端网络的等效电阻R ab＝______________Ω。
第三步：画出题83（a)图的等效电路如下：(2)计算如下：(3)计算如下：83．如题83图所示，（1）若R L =1Ω，求电阻R L 中电流I L ；(10分)（2）当R L 为多大时，R L 能获得最大功率，并求出最大功率。
(2分) 解：据题意，移去R L 支路，电路如下图所示：U AB =___________________________________； R AB =___________________________________；根据戴维宁定理，原电路的等效电路如右图： （1）若R L =1Ω，I L =__________________________； （2）当R L =__________时，R L 能获得最大功率； PLmax =__________________________________。
戴维南定理基础练习题
戴维南定理基础练习题一、选择题1. 戴维南定理适用于下列哪种电路？A. 任何线性电路B. 只有无源元件的电路C. 含有独立源的电路D. 含有受控源的电路2. 戴维南等效电路中，等效电压源的内阻等于原电路的什么参数？A. 输入电阻B. 输出电阻C. 电源内阻D. 负载电阻A. 计算开路电压B. 计算等效电阻C. 将负载短路D. 将电源断路二、填空题1. 戴维南定理是将一个复杂的_______电路简化为一个等效的_______电路。
2. 在求解戴维南等效电路时，需要计算原电路的_______电压，然后计算等效电阻。
3. 戴维南等效电路中的等效电压源内阻等于原电路在_______电压处的等效电阻。
三、计算题1. 如图1所示电路，求电阻R4的戴维南等效电路参数。
2. 已知电路如图2所示，求电阻R3的戴维南等效电路参数。
3. 在图3所示电路中，求电阻R2的戴维南等效电路参数，并用其计算电流I。
四、分析题1. 分析下列电路，说明如何使用戴维南定理求解电流I。
2. 试分析图5所示电路，使用戴维南定理求解电阻R5的电压。
3. 在图6所示电路中，分别求出电阻R1和R2的戴维南等效电路参数，并分析电路中的电流分布。
五、判断题1. 戴维南定理可以用来求解电路中的任意一条支路电流。
（）2. 戴维南等效电路中的等效电压源电压方向与原电路中的电源电压方向相同。
（）3. 在计算戴维南等效电阻时，需要将所有独立源替换为它们的内阻。
（）4. 戴维南定理不适用于含有受控源的电路。
（）六、简答题1. 简述戴维南定理的基本原理。
2. 使用戴维南定理求解电路问题时，需要遵循哪些步骤？3. 为什么在计算戴维南等效电阻时，要将独立源置零？4. 请解释戴维南等效电路中的等效电压源内阻的物理意义。
七、应用题1. 给定如图7所示的电路，使用戴维南定理求电阻R4上的电压U。
2. 在图8所示的电路中，使用戴维南定理求电流源Is的电流值。
3. 如图9所示电路，使用戴维南定理求电阻R3上的功率P。
戴维南定理补充练习共18页文档
谢谢！
36、自己的鞋子，自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——得很慢，但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何，且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔，思而不学则殆。——孔子
戴维南定理补充练习
26、机遇对于有准备的头脑有特别的 亲和力 。 27、自信是人格的核心。
28、目标的坚定是性格中最必要的力 量泉源 之一， 也是成 功的利 器之一 。没有 它，天 才也会 在矛盾 无定的 迷径中 ，徒劳 无功。- -查士 德斐尔 爵士。 29、困难就是机遇。--温斯顿．丘吉 尔。 30、我奋斗，所以我快乐。--格林斯 潘。