混凝土结构周期折减系数取值分析
混凝土结构周期折减系数取值分析

混凝土结构周期折减系数取值分析摘要:简述周期折减的意义和重要性;通过估算结构中非结构构件与主体结构的刚度,找出周期折减系数取值的计算方法,并举例说明。
关键词:非结构构件;侧移刚度;周期与刚度Abstract: this cycle reduction of significance and meaning; Through the estimating structural components and central Africa the main structure of the stiffness, and find out the cycle reduction coefficient method, and give an example.Key words: the structure component; Lateral stiffness; Cycle and stiffness中图分类号:TU37文献标识码:A 文章编号:在进行多高层钢筋混凝土结构内力位移分析时,由于计算模型的简化,我们只考虑了主要结构受力构件(梁、柱、剪力墙和筒体等)的刚度,而没有考虑非承重结构的刚度,此时结构在弹性阶段的计算自振周期较实际自振周期偏长,按这一周期计算的地震力偏小。
因此在结构计算过程中,应根据具体情况,对计算自振周期进行折减,其目的是为了充分考虑非承重填充墙刚度对结构自振周期的影响。
因为自振周期小的结构,其刚度较大,相应吸收的地震力也较大。
若不做周期折减,则结构偏于不安全。
根据《全国民用建筑工程设计技术措施》(结构)第8.8节规定,当考虑填充墙对结构周期的影响时,周期折减系数ψT可按下列规定取值:框架结构0.6~0.8;框架-剪力墙结构0.7~0.9;剪力墙结构0.9~1.0。
《高层建筑混凝土结构技术规程》3.3.17条的条文说明中描述:设计人员应根据实际工程情况(填充墙的数量和刚度大小)来取值。
周期折减系数

大家都知道:对于周期折减系数:
2 框架-剪力墙结构可取0.7~0.8;
3 剪力墙结构可取0.9~1.0。
考虑周期折减系数主要目的是为了考虑结构的填充墙的刚度,本人第一次接触到周期折减系数时,一直认为既然考虑了填充墙的刚度,那么结构总体的刚度就是变大,然后在地震来的时候,填充墙可以吸收
的地震力作用变小,这样,会使得结构构件配筋变小,更容易满足,这是我一个错误的理解,不知道大家有没有和我一样的。
实则不然,继续以框架结构为列,其基本自振周期T1(s)可按下式计算:T1=1.7ψT(uT)1/2
注:uT假想把集中在各层楼面处的重力荷载代表值Gi作为水平荷载而算得的结构顶点位移;ψT结构基本自振周期考虑非承重砖墙影响的折减系数。
这样的话,考虑了结构的填充墙的刚度之后,T1会减小
根据抗震规范第5.1.5条
水平地震力影响系数为α1 =(Tg/T1)0.9аmax
FEK总=α1Geq=α10.85GE
可以得出T1减小,α1变大,会导致FEK变大,地震力作用变大,然而这部分地震力由框架(梁柱)承担,结构配筋变大,结构偏于安全。
那么,填充墙的刚度在这里面充当什么角色那?在计算自振周期的时候,考虑了他的刚度,导致结构自振周期减小了,然后就导致了地震力放大,当地震力放大之后,填充墙不考虑了,这部分地震力全由框架承担,假若这种情况下,框架都能承担的住的话,那结构真的来地震了,不就没问题了,也就是结构偏于安全了。
借用鲁烟的一句话,就是“填充墙引起地震力增大,但是墙这孙子只点火不灭火,增大的地震力还是梁柱框架承担啊”,再次谢谢鲁烟给我的帮助,解决了我的困惑,也希望大家能发表自己的看法。
自振周期折减系数

自振周期折减系数1 概念由于计算模型的简化和非结构因素的作用,导致多层钢筋混凝土框架结构在弹性阶段的计算自振周期(下简称“计算周期”)比真实自振周期(下简称“自振周期”)偏长。
因此,无论是采用理论公式计算还是经验公式计算;无论是简化手算还是采用计算机程序计算,结构的计算周期值都应根据具体情况采用自振周期折减系数(下简称“折减系数”)加以修正,经修正后的计算周期即为设计采用的实际周期(下简称“设计周期”),设计周期=计算周期×折减系数。
如果折减系数取值不恰当,往往使结构设计不合理,或造成浪费、或甚至产生安全隐患。
诚然,折减系数是钢筋混凝土框架结设计所需要解决的一个重要问题。
2 影响自振周期因素影响自振周期因素是诸多方面的,加之多层钢筋混凝土框架结构实际工程的复杂性,抗震规范没有、也不可能对折减系数给出一个确切的数值。
许多文献中给出,当主要考虑填充墙的刚度影响时,折减系数可0.6~0.7[2];根据填充墙的多少、填充墙开洞情况,其对结构自振周期影响的不同,可取0.50~0.90。
这些都是以粘土实心砖为填充墙的经验值,不言而喻,采用不同填充墙体材料的折减系数是不相同的。
当采用轻质材料或空心砖作填充墙,当然不应该套用实心砖为填充墙的折减系数。
对于粘土实心砖外的其它墙体可根据具体情况确定折减系数。
结构计算分析总是要进行简化的,简化程度取决于当时的计算工具;简化是有条件的,而关键是简化模型尽可能符合真实受力模型。
多层钢筋混凝土框架结构的计算周期往往与其自振周期有较大出入,笔者认为,此偏差主要来自计算模型的简化,没有计入那些难于准确计算的因素造成的。
一分为二的说,没有计入的那些因素,常常使计算周期比自振周期长,在一定条件下也会使计算周期比自振周期短,主要表现为以下几方面:3 计算周期长的原因1.填充墙的刚度影响大多数多层钢筋混凝土框架结构的设计计算中,并没有计算填充墙、装修(饰)材料、支撑、设备等非结构构件的刚度。
轻钢混凝土混合结构周期折减系数研究

轻钢混凝土混合结构周期折减系数研究轻钢混凝土混合结构是一种结构材料组合方式,将轻钢骨架与混凝土相结合,形成一种新型的结构系统。
该结构既具有轻钢的优点,又能发挥混凝土的优势,具有较好的抗震性能。
抗震设计是建筑结构设计的重要内容之一。
为了研究轻钢混凝土混合结构的抗震性能,需要了解其周期折减系数。
周期折减系数是指结构在地震作用下的振动周期与其静力等效周期之比,可以反映结构的柔度。
通过研究周期折减系数,可以评估结构的抗震性能。
本文以轻钢混凝土混合结构为研究对象,对其周期折减系数进行研究。
对轻钢混凝土混合结构的抗震性能进行了分析,包括其优势和不足之处。
然后,介绍了周期折减系数的计算方法,并对其影响因素进行了讨论。
接着,通过实例分析了不同参数对周期折减系数的影响,包括轻钢比例、混凝土强度等。
总结了轻钢混凝土混合结构周期折减系数的研究成果和展望未来的研究方向。
研究结果表明,轻钢混凝土混合结构的周期折减系数与许多因素有关,包括结构的刚度、轻钢比例、混凝土强度等。
轻钢比例是影响周期折减系数的重要因素之一。
随着轻钢比例的增加,结构的刚度会降低,周期折减系数也会增大。
混凝土强度也会影响周期折减系数,当混凝土强度增加时,周期折减系数会减小。
本文的研究结果对于轻钢混凝土混合结构的抗震设计具有一定的参考价值。
在实际工程中,可以根据结构的具体要求和地震区域的地震烈度等级,确定合适的轻钢比例和混凝土强度,以达到设计要求。
本文的研究还存在一些不足之处。
采用的实例数据较少,只是对一些参数进行了分析,对于整个结构的周期折减系数研究还不够完善。
本文只进行了理论分析,缺乏实际工程的验证和实践经验的总结。
未来的研究可以进一步完善这些不足,提高轻钢混凝土混合结构的抗震性能。
轻钢混凝土混合结构的周期折减系数研究具有重要的理论和实际意义。
通过对其影响因素进行研究,可以提高结构的抗震性能,保证结构的安全可靠性。
未来的研究可以进一步深入探讨轻钢混凝土混合结构的抗震性能,为其在实际工程中的应用提供更好的理论基础。
混凝土框架结构的周期折减系数合理性探寻

混凝土框架结构的周期折减系数合理性探寻混凝土框架结构的周期折减系数是指在考虑地震作用下,结构在周期减振过程中,其振动周期的相对减少程度。
周期折减系数一般用于确定结构的设计地震烈度,并用于计算结构的地震响应。
合理的周期折减系数能够准确地反映结构的减震能力,对保证结构的地震安全性具有重要意义。
混凝土框架结构的周期折减系数通常通过试验和理论计算相结合的方法确定。
试验方法是通过模拟地震实验,测量结构的地震反应,然后按照设计工况进行计算,得出结构的周期折减系数。
理论计算方法则是基于结构的动力特性和振动理论,通过计算相应的结构频率和阻尼比,推导出周期折减系数。
在确定周期折减系数时,需要考虑以下几个方面的因素:1.结构的材料特性:混凝土框架结构的周期折减系数受到结构材料的影响,包括混凝土和钢筋的强度、刚度和阻尼等特性。
不同材料的耗能能力和抗震性能会影响结构的减震效果。
2.结构的减振措施:在设计过程中,可以通过采取一些减振措施来提高结构的抗震性能,例如添加减震装置、降低结构刚度等。
这些减振措施会直接影响结构的周期折减系数。
3.设计地震动参数:周期折减系数还受到设计地震动参数的影响,包括地震峰值加速度、地震持时和地震波形等。
设计地震动参数的确定需要根据地震地区的地质条件和结构的设计要求进行合理选择。
4.结构的尺寸和形状:结构的尺寸和形状也会对周期折减系数产生一定的影响。
较大的结构在地震作用下可能具有较低的周期折减系数,而相同材料和形状的结构,在不同的尺寸下可能具有不同的周期折减系数。
综上,混凝土框架结构的周期折减系数的确定需要考虑结构的材料特性、减振措施、设计地震动参数和结构的尺寸和形状等因素。
只有综合考虑这些因素,才能得出合理的周期折减系数,准确评估结构的地震安全性。
因此,在实际工程设计中,需要进行详细的分析和计算,确保周期折减系数的合理性。
轻钢混凝土混合结构周期折减系数研究

轻钢混凝土混合结构周期折减系数研究轻钢混凝土混合结构是指在建筑结构中同时使用轻钢结构和混凝土结构的一种构造形式。
轻钢结构以其自重轻、强度高、施工速度快等优点被广泛应用于建筑领域,而混凝土结构则具有良好的抗震性能和耐久性。
将两者结合起来,能够发挥各自的优势,使得建筑结构既能满足强度和稳定性要求,又能达到轻质化和经济节能的目的。
在进行抗震设计时,结构的周期是一个十分重要的参数。
结构的周期是指结构在水平地震作用下的重复周期。
结构的周期越大,振动的周期越慢,抗震性能越好。
周期折减系数的研究对于轻钢混凝土混合结构的抗震设计具有重要意义。
周期折减系数是指实际结构的周期与理论周期之间的比值。
理论周期是指结构初始刚性状态下在无阻尼情况下的振动周期。
实际结构的周期受到结构的各种形式和尺寸参数的影响,因此需要通过周期折减系数来修正理论周期,得到实际结构的周期。
对于轻钢混凝土混合结构而言,其周期折减系数与结构的几何形态、材料性能、刚度布置等因素密切相关。
研究轻钢混凝土混合结构周期折减系数的方法和影响因素,对于准确评估结构的抗震性能具有重要意义。
目前,关于轻钢混凝土混合结构周期折减系数的研究还比较有限。
研究人员通常采用理论计算方法和试验验证方法来确定周期折减系数。
理论计算方法主要是基于结构的弹性模量、刚度矩阵和质量矩阵等参数,通过计算得到结构的理论周期,然后根据试验数据对理论周期进行修正,得到实际结构的周期。
试验验证方法则是通过在实际结构上进行振动试验,测得结构的实际周期。
在轻钢混凝土混合结构周期折减系数的研究中,还需要考虑结构的非线性特性和耗能能力。
由于混凝土结构具有较好的延性和耗能能力,而轻钢结构相对较脆弱,因此在考虑周期折减系数时需要综合考虑两者的特性。
结构设计各种调整系数
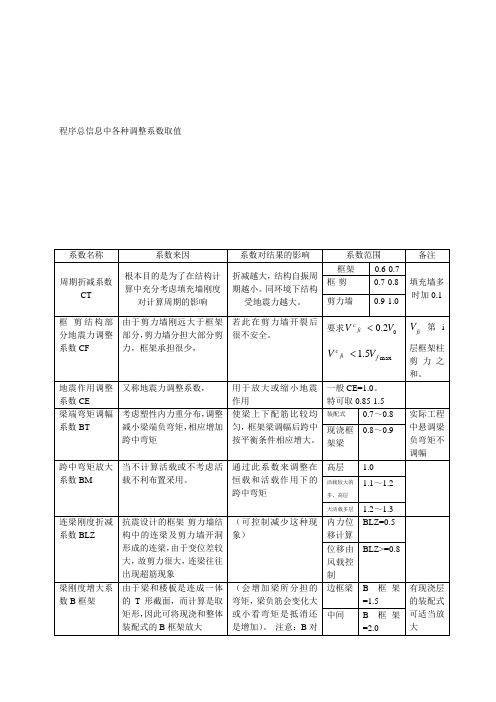
程序总信息中各种调整系数取值
《建筑结构荷载规范》(GB5009-2001)
《建筑抗震设计规范》(GB50011-2001)
《混凝土结构设计规范》(GB50010-2002)
《高层建筑混凝土结构技术规程》(JGJ3-2002)
选自《建筑结构设计新规范综合应用手册》朱炳寅编。
有自己的整理不算盗板吧?表一:
注:此表是本人自己整理,括号内文字是本人自加,此注仅对表一。
表二:
非抗震结构及抗震结构通用性的内力增大和调整
表三:
注:1.括号内数字用于角柱。
2.框支柱在转换层顶截面的内力放大系数是相对底层柱的放大.
3. 框支柱、框支梁内力的放大仅是对水平地震作用下的单工况内力的放大。
*对于特一级和一级的剪力墙,其加强区的设计弯矩取底层墙底截面组合弯矩。
4.本表大致规律是四级抗震按其他部系数据调整,三级抗震系数为基础,其他在其上又乘系数。
5.上注只对表三,此表数据全来自《建筑结构设计新规范综合应用手册》P110-112,本人数便校对敬请放心使用,如对数据来因有疑问请查看本书。
混凝土结构抗震设计自振周期折减系数的讨论

混凝土结构抗震设计自振周期折减系数的讨论采用结构动力学的方法计算结构周期,一般均未考虑结构填充墙的作用,未考虑填充墙对结构刚度的贡献,通常采用将计算周期乘以折减系数进行地震作用计算,周期作用折减系数对地震力计算影响较大,取值时应充分考虑填充墙的多少,影响实际自振周期的其他因数,合理确定周期折减系数。
标签:混凝土结构;抗震设计;自振周期;折减系数1 前言采用结构动力学的方法计算结构周期,一般均未考虑结构填充墙的作用,未考虑填充墙对结构刚度的贡献,同时由于在结构计算过程中,对计算模型进行了简化,致使混凝土结构的计算周期长于实际自振周期,大量工程实测周期表明:实际建筑物自振周期短于计算周期,尤其是有实心砖填充墙的框架结构,由于实心砖填充墙的刚度大于框架柱的刚度,其影响更为显著,实测周期约为计算周期的50%~60%;剪力墙结构中,由于砖墙数量较少,其刚度又远小于钢筋混凝土墙的刚度,实测周期与计算周期比较接近。
2 影响结构自振周期的因素2.1 填充墙的刚度与分布根据结构结构动力学原理,结构的自振周期主要与结构的质量与分布、结构的刚度与分布有关,填充墙的质量一般都以荷载的形式输入,而混凝土结构设计计算中,并未计入填充墙(含装饰材料、设备、支撑等非结构构件)的刚度,实际工程中,由于未考虑填充墙的刚度,而使计算周期比实测周期大许多,而填充墙的刚度又与填充墙的材料性能、数量、墙体完整性、与主体结构的连接情况等密切联系。
各种填充墙材料,由于其自身的刚度、延性的不同,其对结构的空间刚度贡献亦不同,如填充墙采用接近实心粘土砖的实心砌体,其对结构空间刚度贡献则大,若采用轻型砌体,则其对空间结构刚度的贡献小,同时填充墙的数量多、填充墙单片长度长、墙體开洞小、与主体结构连接紧密,则其对结构空间的贡献亦大,反之则小。
2.2 结构自身的变形以及外界干扰力的大小结构构件及非结构构件在随结构变形增加、裂缝开展的过程中,其刚度将逐渐衰减,从而使结构自振周期发生变化;另外,钢筋混凝土结构的自振周期,在大振幅振动与微幅振动下是不同的,对同一结构来说,地震作用由小至大,其自振周期也由短变长,如北京饭店东楼横向基本实测周期,在地震前(脉动法实测值)、海城地震时、唐山地震时分别测得其自振周期为0.90秒、0.95秒、1.40秒,而且,结构并未进入明显的塑性变形,震后仅有填充墙轻微开裂,也就是说,结构构件进入塑性变形之前,建筑物的抗侧移刚度已经明显降低,自振周期比微幅振动时(脉动法实测值)已经增加了许多。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
混凝土结构周期折减系数取值分析
摘要:简述周期折减的意义和重要性;通过估算结构中非结构构件与主体结构的刚度,找出周期折减系数取值的计算方法,并举例说明。
关键词:非结构构件;侧移刚度;周期与刚度
Abstract: this cycle reduction of significance and meaning; Through the estimating structural components and central Africa the main structure of the stiffness, and find out the cycle reduction coefficient method, and give an example.
Key words: the structure component; Lateral stiffness; Cycle and stiffness
中图分类号:TU37文献标识码:A 文章编号:
在进行多高层钢筋混凝土结构内力位移分析时,由于计算模型的简化,我们只考虑了主要结构受力构件(梁、柱、剪力墙和筒体等)的刚度,而没有考虑非承重结构的刚度,此时结构在弹性阶段的计算自振周期较实际自振周期偏长,按这一周期计算的地震力偏小。
因此在结构计算过程中,应根据具体情况,对计算自振周期进行折减,其目的是为了充分考虑非承重填充墙刚度对结构自振周期的影响。
因为自振周期小的结构,其刚度较大,相应吸收的地震力也较大。
若不做周期折减,则结构偏于不安全。
根据《全国民用建筑工程设计技术措施》(结构)第8.8节规定,当考虑填充墙对结构周期的影响时,周期折减系数ψT可按下列规定取值:框架结构0.6~0.8;框架-剪力墙结构0.7~0.9;剪力墙结构0.9~1.0。
《高层建筑混凝土结构技术规程》3.3.17条的条文说明中描述:设计人员应根据实际工程情况(填充墙的数量和刚度大小)来取值。
应该注意的是:周期折减系数不改变结构的自振特征,只改变地震影响系数,折减系数视填充墙的多少而定。
如果折减系数取值不恰当,往往使结构设计不合理,或造成浪费、或甚至产生安全隐患。
所以,周期折减系数是钢筋混凝土结构设计所需要解决的一个重要问题。
焀响自振周期因素是诸多方面的,加之多层钢筋混凝土结构实际工程的复杂性,规范没有、也不可能对折减系数给出一个确切的数值。
本文主要针对当主要考虑填充墙的刚度影响时,结构周期折减系数取值的计算方法。
1.主体结构的侧移刚度
使用程序计算时,在模型中输入主体结构主要构件截面,程序可以计算出结构每层的侧移刚度K0i。
2.砖墙的侧移刚度
无洞口砖墙的弹性刚度
不考虑砖墙的弯曲变形,仅计算其剪切变形,砖墙的柔度δbw=εh/GwAw=3h/EWAW
则无洞口砖墙弹性侧移刚度为Kbw=1/δbw=EWAW/3h(式一.1)
H—砖墙高度;Aw—砖墙横截面面积;ε—剪应变不均匀系数,矩形截面为1.2;
Gw—砖墙剪变模量,Gw=0.4EW;EW—砖墙弹性模量。
(2)小洞口砖墙的弹性刚度
当洞口面积与墙体面积比值不大于0.16,即a=(bd/lh)1/2≤0.4,有洞砖墙侧移刚度可取无洞砖墙侧移刚度乘以开洞折减系数。
Kbw1=(1-1.2a)Kbw (式一.2)
b—洞口宽度;d—洞口高度;l—墙体长度;
(3)大洞口砖墙的弹性刚度
当洞口面积与墙体面积比值大于0.16,即a=(bd/lh)1/2>0.4,
Kbw2=1/Σδi=1/Σ3hi/EWAWi (式一.3)
δi—墙体开洞后分块柔度;hi—墙体开洞后分块高度;AWi—墙体开洞后分块面积。
3.结构考虑砖墙后的刚度增加
Ki=λKbwi+K0i(式二.1)
ηi=Ki/K0i=(λKbwi+K0i)/K0i=1+ λKbwi/K0i(式二.2)
η=Σ(λKbwi+K0i)/ΣK0i=ΣηiK0i /ΣK0i(式二.3)
ηi—考虑砖墙后的层刚度增加系数;η—考虑砖墙后的结构刚度增加系数;
λ—砖墙在地震作用下会先于主体结构开裂,其刚度会退化降低,根据抗规7.2.5条在结构考虑砖墙刚度时,普通砖砌体刚度应予折减。
当主体为框架结构,取折减系数λ=0.2;主体为框架-剪力墙结构,取折减系数λ=0.46;主体为剪力墙结构,取折减系数λ=0.67。
4.结构周期与刚度的关系
根据折算质量法,结构的周期和刚度符合下式:T=2π(Meq/K)1/2
ψT= T1/T0=2π(Meq/Σ(Kbwi+K0i))1/2/2π(Meq/ΣK0i)1/2
=(ΣK0i/ΣηiK0i)1/2=1/η1/2(式三.1)
ψT —周期折减系数;T1—考虑填充墙刚度后的周期;T0—结构初始周期;
Meq—结构有效质量。
5.举例说明
例一:某3层商业,框架结构,层高分别为5.1m、4.2 m、4.2 m,建筑平面如图所示。
在PKPM中建立模型,输入墙体荷载,周期折减系数取1.0(不折减),周期和楼层刚度计算结果见下表。
例二:某18层高层住宅,剪力墙结构,层高为2.9m,标准层建筑平面如图所示。
在PKPM中建立模型,输入墙体荷载,周期折减系数取1.0(不折减),周期和楼层刚度计算结果见下表。
2、3层与4~18层平面相同,混凝土强度不同。
该工程周期折减系数ψT可取0.95,用程序输入折减系数0.95,重新计算并进行下一步设计。
结论和建议1.由于结构计算模型未考虑非结构构件的刚度,目前,通过经验系数对计算周期进行折减,适当增大结构抵御地震作用的能力是必要的,也是可行的。
抗震设计时,设计周期=计算周期×折减系数。
折减系数可按本文所提供的方法估算。
2.折减系数的取值同样必须遵循概念设计原则,使用者必须首先弄明白,折减系数与哪些因素相关,哪些是该工程的主要影响因素。
各因素在不同的实际工程、不同的变形阶段中的影响程度是不同的,应具体情况具体分析。
3.当主要考虑填充墙的刚度影响时,如折减系数按本文所提供的方法估算结果与规范要求相差过大,应根据填充墙的材料特性、开洞情况、沿竖向分布和在平面分布特点等综合考虑。
在特定情况下,考虑填充墙的不利影响,关键是把握住结构的真实刚度变化对结构的动力反映不利影响,并从真实情况进行结构设计、分析,对于保证结构安全,减轻震害,是十分必要的。
通过笔者的粗浅分析和工程实践摸索,指出影响自振周期的主要因素,并对折减系数的取值提出计算方法,供结构工程师参考。
参考文献:《建筑抗震设计规范》(GB50011-2010)
《高层建筑混凝土结构技术规程》(JGJ3-2010)
《全国民用建筑工程设计技术措施(结构)》2007版
注:文章内所有公式及图表请以PDF形式查看。
