材料力学第五版刘鸿文主编第三章ppt[63P][14.4MB]
合集下载
材料力学(刘鸿文_第5版)

第十四章 习题
2012年11月5日星期一
常州大学机械学院力学教研室
第五章 习题
第六章 弯曲变形
§6-1、工程中的弯曲变形问题 §6-2、挠曲线的微分方程 §6-3、用积分法求弯曲变形 6.1和连续性条件 6.3(a) Page 196 §6-4、用叠加法求弯曲变形 6.9(a) 6.10(b) Page 200 §6-5、简单超静定梁 Page 208 6.36 §6-6、提高弯曲刚度的一些措施
第十三章 习题
§13-1、概述 §13-2、杆件应变能的计算104 Page §13-3、应变能的普遍表达式 §13-4、互等定理 Page 106 §13-5、卡氏定理 Page 107 §13-6、虚功原理 §13-7、单位载荷法 Page 109 莫尔积分 §13-8、计算莫尔积分的图乘法 Page 109
第一章 绪论
§1-1、材料力学的任务 §1-2、变形固体的基本假设 §1-3、外力及其分类 §1-4、内力、截面法和应力的概念 §1-5、变形与应变 §1-6、杆件变形的基本形式
第一章 绪论习题
Page 11 1.2 Page 11 1.4 1.6
第二章 拉伸、压缩与剪切 第二章 习题
§2-1、轴向拉伸与压缩的概念和实例 §2-2、轴向拉伸与压缩时横截面上的内力和应力 2.2 Page 53 2.1(a)(c) §2-3、直杆轴向拉伸或压缩时斜截面上的应力 Page 54 2.6 §2-4、材料拉伸时的力学性能 §2-5、材料压缩时的力学性能 §2-7、失效、安全因数与强度计算54 2.7 Page 54 2.12 Page §2-8、轴向拉伸或压缩时的变形 58 2.19 Page 61 2.30 Page
附录 I 平面图形的几何性质
刘鸿文主编-材料力学课件

各向同性假设
总结词
各向同性假设认为材料在不同方向上具有相同的性质 和行为。
详细描述
各向同性假设是材料力学中的另一个重要假设。它意味 着材料在不同方向上具有相同的性质,如弹性模量、泊 松比等。这一假设使得我们可以用统一的数学模型来描 述材料的性质和行为,简化计算过程。在实际应用中, 对于一些各向同性较好的材料,可以采用统一的标准来 近似获得其整体性质。需要注意的是,各向同性材料并 不是指所有方向上的性质都完全相同,而是在一定范围 内可以近似认为各向同性。
机械零件设计
材料力学在机械领域中应用于各 种机械零件的设计,如轴、轴承
、齿轮等。
设备强度分析
对机械设备的强度进行分析,确保 设备在各种工况下的安全运行。
疲劳寿命预测
利用材料力学知识,预测机械零件 的疲劳寿命,提高设备的使用寿命 。
航空航天领域
飞行器结构分析
材料力学在航空航天领域 中应用于飞行器的结构分 析,确保飞行器的安全性 和稳定性。
详细描述
弹性力学理论是材料力学的基本理论之一,主要研究材料在弹性范围内受力时的变形和内力关系。该 理论基于胡克定律,即材料在弹性范围内受力时发生的形变与外力成正比,并引入了应变和应力等概 念来描述材料的变形和受力情况。
塑性力学理论
总结词
描述材料在超过弹性极限后发生塑性形 变时的应力-应变关系。
VS
根据船舶的工作环境和要求,选择具 有优良力学性能的材料。
05
材料力学的未来发展
新材料的研发
高强度轻质材料
如碳纤维复合材料、钛合金等, 在航空、汽车、体育器材等领域
有广泛应用前景。
智能材料
如形状记忆合金、压电陶瓷等, 具有自适应、自修复等特性,可 用于制造智能传感器、执行器等
材料力学刘鸿文第五版第三章扭转

例 传动轴,已知转速 n=300r/min,主动轮A输入功 率PA=45kW,三个从动轮输出功率分别为PB=10kW, PC=15kW,PD=20kW。试绘轴的扭矩图.
解: (1)计算外力偶矩 由公式 M e 9549P / n
(2)计算扭矩 (3) 扭矩图
T3 M A 1432N m
a
d
b
c
C、剪(切)应力大小
(1)由于沿圆周线方向各点的 变形相同,同一圆周线上各点 的 r相同,故可认为剪应力沿圆 周线处处相等。
(2)又因壁厚很薄,又可近似的认为沿壁厚方向均匀 分布。
因此认为剪应力在横截面均匀分布
由 d A r T A
根据应力沿壁厚 均匀分布可知
r0
PkW 103 60 2πnrpm
9549
PkW nrpm
§3.2 外力偶矩的计算 扭矩和扭矩图
2.扭矩和扭矩图 用截面法研究横 截面上的内力
T = Me T:截面上的扭矩
§3.2 外力偶矩的计算 扭矩和扭矩图
扭矩正负规定
右手螺旋法则 右手大拇指指向横截面外法线方向为正,反之为负
2(1 )
先看实验
圆轴扭转时的应力
一、实验与假设
1、实验现象
﹢各圆周线的形状、大小,两 圆周线间的距离都没有发生变化, 但都绕轴转过了不同的角度。
﹢纵线仍近似为直线,但都倾斜了一个角度,使原来的矩形都变 成了平行四边形。
2、平面假设
平面假设:圆轴扭转时,各横截面如同刚性平面一样绕轴转
动,即:假设圆轴各横截面在变形过程中,始终保持为平面, 其形状和大小不变,半径仍为直线。
Tmax 1432N m
材料力学ppt刘鸿文版

目录
§2.7 失效、安全因数和强度计算
例题2.5
AC为50×50×5的等边角钢,AB为10 号槽钢,〔σ〕=120MPa。确定许可载荷F。
解:1、计算轴力(设斜杆为1杆,水平杆 为2杆)用截面法取节点A为研究对象 Fx 0 FN1 cos FN 2 0
F
y
0
FN1 sin F 0
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
例题2.1
A
1 B
11=10kN;F2=20kN; F3=35kN;F4=25kN;试画 出图示杆件的轴力图。
F1 F1 F1
FN kN
F3
3
F4
解:1、计算各段的轴力。 AB段
FN1 FN2 F2
F F
x
x
0
FN1 F1 10kN
在图示结构中,设横梁AB的 变形可以省略,1,2两杆的横截 面面积相等,材料相同。试求1, 2两杆的内力。 解: 1、列出独立的平衡方程
1
例题2.8
2
l
3F 2FN 2 cos FN1 0
2、变形几何关系
A
B
a
l1
a
l2
a
l2 2l1 cos
3、物理关系
4、补充方程
b } F n
例题3-2
FS
h
nn
n
b
l
O Me
Fbs Abs bs
d
O
Me
0.5h
(a)
(b)
nF n S
(c)
目录
§2-13 剪切和挤压的实用计算
解:(1)校核键的剪切强度
Fs A bl d d 由平衡方程 M o 0 得 Fs bl M e
§2.7 失效、安全因数和强度计算
例题2.5
AC为50×50×5的等边角钢,AB为10 号槽钢,〔σ〕=120MPa。确定许可载荷F。
解:1、计算轴力(设斜杆为1杆,水平杆 为2杆)用截面法取节点A为研究对象 Fx 0 FN1 cos FN 2 0
F
y
0
FN1 sin F 0
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
例题2.1
A
1 B
11=10kN;F2=20kN; F3=35kN;F4=25kN;试画 出图示杆件的轴力图。
F1 F1 F1
FN kN
F3
3
F4
解:1、计算各段的轴力。 AB段
FN1 FN2 F2
F F
x
x
0
FN1 F1 10kN
在图示结构中,设横梁AB的 变形可以省略,1,2两杆的横截 面面积相等,材料相同。试求1, 2两杆的内力。 解: 1、列出独立的平衡方程
1
例题2.8
2
l
3F 2FN 2 cos FN1 0
2、变形几何关系
A
B
a
l1
a
l2
a
l2 2l1 cos
3、物理关系
4、补充方程
b } F n
例题3-2
FS
h
nn
n
b
l
O Me
Fbs Abs bs
d
O
Me
0.5h
(a)
(b)
nF n S
(c)
目录
§2-13 剪切和挤压的实用计算
解:(1)校核键的剪切强度
Fs A bl d d 由平衡方程 M o 0 得 Fs bl M e
刘鸿文版材料力学课件全套3
13
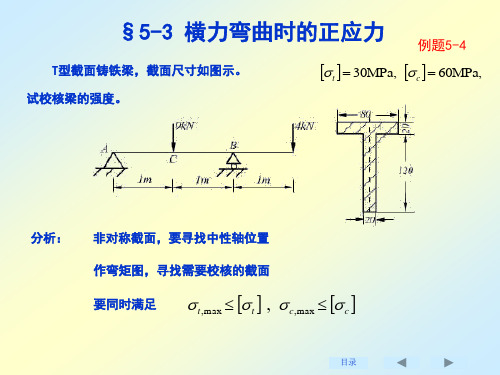
§5-4 弯曲切应力
切应变
Fs h2 2 ( y ) G 2I z G 4
P P
横力弯曲截面发生翘曲 若各截面 Fs 相等,则翘曲程度相同,纵向纤维长度不变,对 无影响。
计算
若各截面Fs不等(如有q作用),则翘曲程度不同,各纵向纤维长度发 生变化,对 计算有影响。但这种影响对 梁常可忽略。
2)写出x截面的弯矩方程
)
A
x
l
yB
F B
B
x
M ( x ) F (l x ) F ( x l )
3)列挠曲线近似微分方程并积分
d2y EI 2 M ( x ) F ( x l ) dx
积分一次
再积分一次
dy 1 2 EI EI F ( x l ) C dx 2 1 EIy F ( x l ) 3 Cx D 6
yA
y AL y AR
y AL y AR
A 0
-弹簧变形
AL AR
目录
~
~
A AA A A
~
~
~
~
A
A A A
A
~
§6-3 用积分法求弯曲变形
例1 求梁的转角方程和挠度方程,并求最大转角和最大挠度,梁的EI已知。
解
1)由梁的整体平衡分析可得:
y
FAx 0, FAy F (), M A Fl (
d M ( x) 2 dx EI z
目录
由上式进行积分,就可以求出梁横截面的转角 和挠度。
挠曲轴微分方程与边界条件
d 2w M ( x ) dx 2 EI
刘鸿文材料力学第五版课件
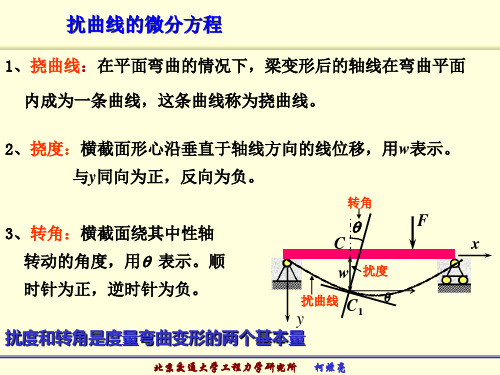
Fl 2 2 Fl 2 5Fl 2 = + = 2 EI EI 2 EI
(顺时针) 顺时针)
北京交通大学工程力学研究所
柯燎亮
§6-3 用叠加法求弯曲变形-例4 用叠加法求弯曲变形由叠加原理求图示弯曲刚度为EI的外伸梁 截面的挠度和转角以 由叠加原理求图示弯曲刚度为 的外伸梁C截面的挠度和转角以 的外伸梁 截面的挠度。 及D截面的挠度。 截面的挠度
qa(2a ) qa(2a ) wD1 = θ B1 = − 48EI 16 EI 截面的挠度和B截面右端的转角为 图d中D截面的挠度和 截面右端的转角为: 中 截面的挠度和 截面右端的转角为:
3 2
wD 2
2qa =− 16 EI
4
θ B2
qa 3 = 3EI
柯燎亮
北京交通大学工程力学研究所
§6-3 用叠加法求弯曲变形-例4 用叠加法求弯曲变形将相应的位移进行叠加,即得: 将相应的位移进行叠加,即得:
q B
(θ B )q
θ A = (θ A)q + (θ A)Me
Mel ql =( + ) ( 24EI 3EI
3
(wC )q
l
) Me
B
(θ B ) M e
θB = (θB)q + (θB)Me A (c) (θ A ) C (wC )M ql 3 Mel ( ) = − + l 24EI 6EI 北京交通大学工程力学研究所 柯燎亮
qa 4 wCq = 8EI
θ Cq
qa 3 = 6 EI
柯燎亮
北京交通大学工程力学研究所
§6-3 用叠加法求弯曲变形-例4 用叠加法求弯曲变形原外伸梁C端的挠度和转角也可按叠加原理求得, 原外伸梁 端的挠度和转角也可按叠加原理求得,即: 端的挠度和转角也可按叠加原理求得
材料力学1第五版刘鸿文主编
2
2
FN 2 A2
150000 0.37 0.37
C
1.1 106 N/m2 1.1MPa
50kN 150kN
结论: max 在柱的下段,其
值为1.1MPa,是压应力.
240
例题3 简易起重设备中,AC杆由两根 80807等边角钢组 成,AB杆由两根 10号工字钢组成. 材料为Q235钢,许用应
(2)当 = 45°时,
max
2
F
(3)当 = -45° 时,
min
2
(4)当 = 90°时, 0, 0
n
k
x
k
三、强度条件(Strength condition)
杆内的最大工作应力不超过材料的许用应力 1.数学表达式(Mathematical formula)
k
F
p
F A
F cos
A
cos
Fα
k pα
k
将应力 pα分解为两个分量:
F
F
沿截面法线方向的正应力
k
p cos cos2
n
沿截面切线方向的切应力
k
F
x
p
sin
2
sin2
k pα
pα
2.符号的规定(Sign convention) F (1)α角
section is called the Normal Stress)
lim ΔFN dFN p
ΔA0 ΔA dA
材料力学第五版(刘鸿文主编)课后答案解析
幻灯片295
幻灯片296
幻灯片297
幻灯片298
幻灯片299
幻灯片300
幻灯片301
幻灯片302
幻灯片303
幻灯片304
幻灯片305
幻灯片306
幻灯片307
幻灯片308
幻灯片309
幻灯片310
幻灯片311
幻灯片312
幻灯片313
幻灯片314
幻灯片315
幻灯片316
幻灯片317
幻灯片318
幻灯片319
幻灯片93
幻灯片94
幻灯片95
幻灯片96
幻灯片97
幻灯片98
幻灯片99
幻灯片100
幻灯片101
幻灯片102
幻灯片103
幻灯片104
幻灯片105
幻灯片106
幻灯片107
幻灯片108
幻灯片109
幻灯片110
幻灯片111
幻灯片112
幻灯片113
幻灯片114
幻灯片115
幻灯片116
幻灯片117
幻灯片118
幻灯片119
幻灯片220
幻灯片221
幻灯片222
幻灯片223
幻灯片224
幻灯片225
幻灯片226
幻灯片227
幻灯片228
幻灯片229
幻灯片230
幻灯片231
幻灯片232
幻灯片233
幻灯片234
幻灯片235
幻灯片236
幻灯片237
幻灯片238
幻灯片239
幻灯片240
幻灯片241
幻灯片242
幻灯片243
幻灯片244
幻灯片145
幻灯片146
幻灯片147
幻灯片296
幻灯片297
幻灯片298
幻灯片299
幻灯片300
幻灯片301
幻灯片302
幻灯片303
幻灯片304
幻灯片305
幻灯片306
幻灯片307
幻灯片308
幻灯片309
幻灯片310
幻灯片311
幻灯片312
幻灯片313
幻灯片314
幻灯片315
幻灯片316
幻灯片317
幻灯片318
幻灯片319
幻灯片93
幻灯片94
幻灯片95
幻灯片96
幻灯片97
幻灯片98
幻灯片99
幻灯片100
幻灯片101
幻灯片102
幻灯片103
幻灯片104
幻灯片105
幻灯片106
幻灯片107
幻灯片108
幻灯片109
幻灯片110
幻灯片111
幻灯片112
幻灯片113
幻灯片114
幻灯片115
幻灯片116
幻灯片117
幻灯片118
幻灯片119
幻灯片220
幻灯片221
幻灯片222
幻灯片223
幻灯片224
幻灯片225
幻灯片226
幻灯片227
幻灯片228
幻灯片229
幻灯片230
幻灯片231
幻灯片232
幻灯片233
幻灯片234
幻灯片235
幻灯片236
幻灯片237
幻灯片238
幻灯片239
幻灯片240
幻灯片241
幻灯片242
幻灯片243
幻灯片244
幻灯片145
幻灯片146
幻灯片147
刘鸿文版材料力学课件全套5ppt课件
尺寸因数
1 试样的疲劳极限
3.表面加工质量的影响——表面质量因数
( 1 ) 1
1 磨削加工(试样) 1 其他加工
一般情况下,构件的最大应力发生于表层,疲劳裂纹也多于表层生成。表面 加工的刀痕、擦伤等将引起应力集中,降低持久极限。所以表面加工质量对 持久极限有明显的影响。
看表11.2 不同表面粗糙度的表面质量因数
6E I
B
1 EI
ml 2
2 3
ml
逆时针
3E I
例:试用图乘法求所示悬臂梁自由端B的 挠度和转角。
CL12TU35
解:
wB
1 EI
l 3
ql 2 2
3l 4
ql 2
ql4
2
8E I
B
1 EI
l
3
ql 2 2
1
ql 2
ql3 顺时针
2
6E I
例:试用图乘法求图示悬臂梁中点C处的 铅垂位移。
ql 3 12
a 2
0
F ql 3 8a(l a)
(2) ql 2 / 8
C
1 EI
Fal 2
2 3
Fa2 2
1
ql 3 12
1 2
0
F ql 3 4a(2l 3a)
例:图示梁的抗弯刚度为EI,试求D点的 铅垂位移。
CL12TU38
解:
C
3 EI
Pa2 2
2a 3
Pa 3 EI
例:图示开口刚架,EI=const。求A、B两 截面的相对角位移 θAB 和沿P力作用线方向的 相对线位移 ΔAB 。
定理:
Fi i F11 F2 2 Fi i
所以:V Fi i
1 试样的疲劳极限
3.表面加工质量的影响——表面质量因数
( 1 ) 1
1 磨削加工(试样) 1 其他加工
一般情况下,构件的最大应力发生于表层,疲劳裂纹也多于表层生成。表面 加工的刀痕、擦伤等将引起应力集中,降低持久极限。所以表面加工质量对 持久极限有明显的影响。
看表11.2 不同表面粗糙度的表面质量因数
6E I
B
1 EI
ml 2
2 3
ml
逆时针
3E I
例:试用图乘法求所示悬臂梁自由端B的 挠度和转角。
CL12TU35
解:
wB
1 EI
l 3
ql 2 2
3l 4
ql 2
ql4
2
8E I
B
1 EI
l
3
ql 2 2
1
ql 2
ql3 顺时针
2
6E I
例:试用图乘法求图示悬臂梁中点C处的 铅垂位移。
ql 3 12
a 2
0
F ql 3 8a(l a)
(2) ql 2 / 8
C
1 EI
Fal 2
2 3
Fa2 2
1
ql 3 12
1 2
0
F ql 3 4a(2l 3a)
例:图示梁的抗弯刚度为EI,试求D点的 铅垂位移。
CL12TU38
解:
C
3 EI
Pa2 2
2a 3
Pa 3 EI
例:图示开口刚架,EI=const。求A、B两 截面的相对角位移 θAB 和沿P力作用线方向的 相对线位移 ΔAB 。
定理:
Fi i F11 F2 2 Fi i
所以:V Fi i
刘鸿文材料力学第五版课件
z A 1kN· m 5kN C 1kN· m B D x
z
5kN A CC 10kN B 3.64kN D
D
x
y
1.82kN 300mm
300mm
100mm
3.64kN
1 kN· m使轴产生扭转
y 1.82kN 10kN
§8-4 扭转与弯曲的组合
(3)绘制轴的内力图
z 5kN
3.64kN
1kN· m B D x
第八章 组合变形
§8-3 偏心压缩 §8-4 扭转与弯曲的组合
北京交通大学工程力学研究所
柯燎亮
§8-3 偏心压缩
一、偏心拉(压)
1.定义 当外力作用线与杆的轴线平行但不重合时, 将引起轴向 拉伸(压缩)和平面弯曲两种基本变形. 例如钻床的立柱、厂房中支承吊车梁的柱子。 F
F2
F1
O1
z A(yF,zF) y
M max 20kN m
πD W (1 4 ) 32
3
15kN· m
+
扭矩
20kN· m
-
r3
M2 T2 157.26MPa [ ] W
弯矩
§8-4 扭转与弯曲的组合
例题2 传动轴如图所示.在A处作用一个外力偶矩Me=1kN· m,皮 带轮直径D=300mm,皮带轮紧边拉力为F1,松边拉力为F2.且 F1=2F2,l=200mm,轴的许用应力[]=160MPa.试用第三强度理论设 y 计轴的直径
§8-3 偏心压缩
2. (外力分析)以横截面具有两对称轴的等直杆受偏心拉力 F 为例
(1)将外力向截面形心简化,使每个力(或力偶)只产生一种 基本变形形式 轴向拉力 F 力偶矩 M = F e,
z
5kN A CC 10kN B 3.64kN D
D
x
y
1.82kN 300mm
300mm
100mm
3.64kN
1 kN· m使轴产生扭转
y 1.82kN 10kN
§8-4 扭转与弯曲的组合
(3)绘制轴的内力图
z 5kN
3.64kN
1kN· m B D x
第八章 组合变形
§8-3 偏心压缩 §8-4 扭转与弯曲的组合
北京交通大学工程力学研究所
柯燎亮
§8-3 偏心压缩
一、偏心拉(压)
1.定义 当外力作用线与杆的轴线平行但不重合时, 将引起轴向 拉伸(压缩)和平面弯曲两种基本变形. 例如钻床的立柱、厂房中支承吊车梁的柱子。 F
F2
F1
O1
z A(yF,zF) y
M max 20kN m
πD W (1 4 ) 32
3
15kN· m
+
扭矩
20kN· m
-
r3
M2 T2 157.26MPa [ ] W
弯矩
§8-4 扭转与弯曲的组合
例题2 传动轴如图所示.在A处作用一个外力偶矩Me=1kN· m,皮 带轮直径D=300mm,皮带轮紧边拉力为F1,松边拉力为F2.且 F1=2F2,l=200mm,轴的许用应力[]=160MPa.试用第三强度理论设 y 计轴的直径
§8-3 偏心压缩
2. (外力分析)以横截面具有两对称轴的等直杆受偏心拉力 F 为例
(1)将外力向截面形心简化,使每个力(或力偶)只产生一种 基本变形形式 轴向拉力 F 力偶矩 M = F e,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
Me
n
Me • x
n
截面的位置;用垂直于杆轴线的
坐标 T 表示横截面上的扭矩,正
的扭矩画在 x 轴上方,负的扭矩画在 x 轴下方. T T +
_
x
(Torsion) 例题1 一传动轴如图所示,其转速 n = 300 r/min ,主动轮A输 入的功率为P1 = 500 kW . 若不计轴承摩擦所耗的功率,三个从
(Torsion)
§3-1 扭转的概念及实例 (Concepts and example problem of torsion )
一、工程实例(Example problems)
(Torsion)
(Torsion)
二、受力特点(Character of external force)
杆件的两端作用两个大小相等、方向相反、 且作用平面垂直于杆件轴线的力偶.
IP —为横截面对圆心的 极惯性矩
(Torsion)
max 的计算(Calculation of max ) 2、
max
T max T T Ip Ip Wt
dA T O ρ dA
max
max
ρ ρ
r
(Maximum Shear-Stress Formula)
Wt
Ip
动轮输出的功率分别为P2 = 150 kW 、P3 = 150 kW 及 P4 = 200kW. 试做扭矩图 Me1 Me2Me3
n
Me4
B
C
A
D
(Torsion)
Me1
Me2 Me3 n Me4
B 解:计算外力偶矩
C
A
D
P M e 9549 n M e1 15900 N m
M e 2 M e 3 4780 N m M e 4 6379 N m
在 AD 段内
T3 M e 4 6370 N m
注意:若假设扭矩为正值,则
扭矩的实际符号与计算符号相同.
作出扭矩图 从图可见,最大扭矩 在 CA段内. _
4780 N· m
9560 N· m 6370 N· m
+
Tmax 9560 N m
(Torsion)
1 薄壁圆筒:壁厚 t r0(r0—圆筒的平均半径) 10 一、应力分析(Analysis of stress)
G
该式称为材料的剪切胡克律. (Hooke’s law for shear) G –剪切弹性模量 弹性模量E,剪切弹性模量G与泊松比μ的 关系 O
E G 2(1 )
O
(torsion) (Torsion) 思考题:指出下面图形的切应变
切应变为
2
切应变为
0
(Torsion)
三、变形特点( Character of deformation )
杆件的任意两个横截面都发生绕轴线的相对转动.
Me
Me
(Torsion)
§3-2 扭转的内力的计算 (Calculating internal force of torsion )
一、外力偶矩的计算 (Calculation of external moment)
P M e 9549 (N m) n Ps M e 7024 (N m) n
Me2
Me1
n
Me3
从动轮
主动轮
从动轮
Me—作用在轴上的力偶矩( N ·m ) P—轴传递的功率(kW)
n—轴的转速( r/min ) Ps —轴传递的功率(PS)
(Torsion)
二、内力的计算 (Calculation of internal force)
1.实验前 1)画纵向线,圆周线; 2)施加一对外力偶. 2.实验后 ① 圆筒表面的各圆周线的形状、大小和间 Me 距均未改变,只是绕轴线作了相对转动; ② 各纵向线均倾斜了同一微小角度 ; ③ 所有矩形网格均歪斜成同样大小的平行四边形.
§3-3 薄壁圆筒的扭转 (Torsion of thin—walled cylindrical Vessels)
由图所示的几何关系得到
Me
Me
r l
式中, r 为薄壁圆筒的外半经.
l
薄壁圆筒的扭转试验发现,当外力偶 Me 在某一范围内时,与 Me (在数值上等于 T )成正比.
(torsion) (Torsion)
T 2 2πr t
的线性关系.
r l
T
从 T 与 之间的线性关系,可推出 与 间
(Torsion)
§3-5 圆杆在扭转时的变形 · 刚度条件 (Torsional deformation of circular bars & stiffness condition) §3-6 密圈螺旋弹簧的应力和变形 (Calculation of the stress and deformation in close-coiled helical springs) §3-7 非圆截面杆的扭转 (Torsion of noncircular prismatic bars) §3-8 开口和闭合薄壁截面杆的自由扭转 (Free torsion of open and closed thinwalled members)
由剪切胡克定律
G
d G G dx
同一圆周上各点剪应力
a A T
ρ O1
ρ
b
D G T d O2 G' D
dx b
a
均相同 ,且其值与
成正比, 与半径垂直.
(Torsion)
三、静力关系 (Static Relationship)
1、公式的建立(Establish the formula) dA T O ρ dA
x
dx
Me
(Torsion)
3、推论(Inference)
1) 横截面上无正应力,只 有切应力; 2) 切应力方向垂直半径或与 圆周相切.
Me
Me
圆周各点处切应力的方向于圆周相切, 且数值相等,近似的认为沿壁厚方向
A
D
各点处切应力的数值无变化.
B C
dx
t
(Torsion) 4、推导公式 (Derivation of formula)
max
Wt 称作抗扭截面系数,单位为 mm3 或 m3.
(Torsion) 3、极惯性矩和抗扭截面系数的计算
I p dA
2 A
Wt
(1)实心圆截面 (Solid circular section)
max
IP
dA 2π (d )
2
d
4
ρ
O
dρ
结果为负号,说明T 2 应是负值扭矩 同理,在 BC 段内
B Me2
T1 M e 2 4780 N m
T1
x
(Torsion) 同理,在 BC 段内
Me2 1 Me3
B 1 C Me2 T1
Me1 3 Me4 A T3 3 D Me4
T1 M e 2 4780 N m
1、在单元体左、右面(杆的横截面)上
只有切应力,其方向于 y 轴平行.
由平衡方程
y
Fy 0
可知,两侧面的内力元素 dy dz 大小相等,方向相反,将组成 一个力偶。 其矩为( dy dz) dx dy z
τ
dx
τ
x
(Torsion)
2、 要满足平衡方程
y
M z 0 Fx 0
Examine the deformation then propose the hypothesis
变形的分布规律
Distribution regularity of deformation
应力的分布规律
static relation
Distribution regularity of stress
建立公式
Establish the formula
(Torsion)
一、变形几何关系(Geometrical Relationship of Deformation)
1、变形现象 (Deformation phenomenon) 1) 轴向线仍为直线,且长度不变; 2) 横截面仍为平面且与轴线垂直;
ρ
a A T
E
b
O1 dx
ρ
a
D G T d O2 G' D' b
经过半径 O2D 上任一点G的纵向线EG 也倾斜了一个角度
ρ,它也就是横截面半径上任一点E处的切应变
GG' d tg EG dx
(torsion) (Torsion) 二、 物理关系(Physical Relationship)
3) 径向线保持为直线,只是绕轴
线旋转.
2、平面假设(Plane assumption)
变形前为平面的横截面 ,变形 后仍保持为平面.
(Torsion)
3、几何关系 (Geometrical relationship) 倾角 是横截面圆周上任一
点A 处的切应变, d 是 b-b 截面相对于a-a 截面象刚性 平面一样绕杆的轴线转动的 一个角度.
单元体两个相互垂直平面上的切 应力同时存在,且大小相等,都 指相(或背离)该两平面的交线. dy
τ
dx
τ
x
z
纯剪切单元体:
(Element in pure shear )
单元体平面上只有切应力而无正应力,则称为纯剪切单元体.
Me
n
Me • x
n
截面的位置;用垂直于杆轴线的
坐标 T 表示横截面上的扭矩,正
的扭矩画在 x 轴上方,负的扭矩画在 x 轴下方. T T +
_
x
(Torsion) 例题1 一传动轴如图所示,其转速 n = 300 r/min ,主动轮A输 入的功率为P1 = 500 kW . 若不计轴承摩擦所耗的功率,三个从
(Torsion)
§3-1 扭转的概念及实例 (Concepts and example problem of torsion )
一、工程实例(Example problems)
(Torsion)
(Torsion)
二、受力特点(Character of external force)
杆件的两端作用两个大小相等、方向相反、 且作用平面垂直于杆件轴线的力偶.
IP —为横截面对圆心的 极惯性矩
(Torsion)
max 的计算(Calculation of max ) 2、
max
T max T T Ip Ip Wt
dA T O ρ dA
max
max
ρ ρ
r
(Maximum Shear-Stress Formula)
Wt
Ip
动轮输出的功率分别为P2 = 150 kW 、P3 = 150 kW 及 P4 = 200kW. 试做扭矩图 Me1 Me2Me3
n
Me4
B
C
A
D
(Torsion)
Me1
Me2 Me3 n Me4
B 解:计算外力偶矩
C
A
D
P M e 9549 n M e1 15900 N m
M e 2 M e 3 4780 N m M e 4 6379 N m
在 AD 段内
T3 M e 4 6370 N m
注意:若假设扭矩为正值,则
扭矩的实际符号与计算符号相同.
作出扭矩图 从图可见,最大扭矩 在 CA段内. _
4780 N· m
9560 N· m 6370 N· m
+
Tmax 9560 N m
(Torsion)
1 薄壁圆筒:壁厚 t r0(r0—圆筒的平均半径) 10 一、应力分析(Analysis of stress)
G
该式称为材料的剪切胡克律. (Hooke’s law for shear) G –剪切弹性模量 弹性模量E,剪切弹性模量G与泊松比μ的 关系 O
E G 2(1 )
O
(torsion) (Torsion) 思考题:指出下面图形的切应变
切应变为
2
切应变为
0
(Torsion)
三、变形特点( Character of deformation )
杆件的任意两个横截面都发生绕轴线的相对转动.
Me
Me
(Torsion)
§3-2 扭转的内力的计算 (Calculating internal force of torsion )
一、外力偶矩的计算 (Calculation of external moment)
P M e 9549 (N m) n Ps M e 7024 (N m) n
Me2
Me1
n
Me3
从动轮
主动轮
从动轮
Me—作用在轴上的力偶矩( N ·m ) P—轴传递的功率(kW)
n—轴的转速( r/min ) Ps —轴传递的功率(PS)
(Torsion)
二、内力的计算 (Calculation of internal force)
1.实验前 1)画纵向线,圆周线; 2)施加一对外力偶. 2.实验后 ① 圆筒表面的各圆周线的形状、大小和间 Me 距均未改变,只是绕轴线作了相对转动; ② 各纵向线均倾斜了同一微小角度 ; ③ 所有矩形网格均歪斜成同样大小的平行四边形.
§3-3 薄壁圆筒的扭转 (Torsion of thin—walled cylindrical Vessels)
由图所示的几何关系得到
Me
Me
r l
式中, r 为薄壁圆筒的外半经.
l
薄壁圆筒的扭转试验发现,当外力偶 Me 在某一范围内时,与 Me (在数值上等于 T )成正比.
(torsion) (Torsion)
T 2 2πr t
的线性关系.
r l
T
从 T 与 之间的线性关系,可推出 与 间
(Torsion)
§3-5 圆杆在扭转时的变形 · 刚度条件 (Torsional deformation of circular bars & stiffness condition) §3-6 密圈螺旋弹簧的应力和变形 (Calculation of the stress and deformation in close-coiled helical springs) §3-7 非圆截面杆的扭转 (Torsion of noncircular prismatic bars) §3-8 开口和闭合薄壁截面杆的自由扭转 (Free torsion of open and closed thinwalled members)
由剪切胡克定律
G
d G G dx
同一圆周上各点剪应力
a A T
ρ O1
ρ
b
D G T d O2 G' D
dx b
a
均相同 ,且其值与
成正比, 与半径垂直.
(Torsion)
三、静力关系 (Static Relationship)
1、公式的建立(Establish the formula) dA T O ρ dA
x
dx
Me
(Torsion)
3、推论(Inference)
1) 横截面上无正应力,只 有切应力; 2) 切应力方向垂直半径或与 圆周相切.
Me
Me
圆周各点处切应力的方向于圆周相切, 且数值相等,近似的认为沿壁厚方向
A
D
各点处切应力的数值无变化.
B C
dx
t
(Torsion) 4、推导公式 (Derivation of formula)
max
Wt 称作抗扭截面系数,单位为 mm3 或 m3.
(Torsion) 3、极惯性矩和抗扭截面系数的计算
I p dA
2 A
Wt
(1)实心圆截面 (Solid circular section)
max
IP
dA 2π (d )
2
d
4
ρ
O
dρ
结果为负号,说明T 2 应是负值扭矩 同理,在 BC 段内
B Me2
T1 M e 2 4780 N m
T1
x
(Torsion) 同理,在 BC 段内
Me2 1 Me3
B 1 C Me2 T1
Me1 3 Me4 A T3 3 D Me4
T1 M e 2 4780 N m
1、在单元体左、右面(杆的横截面)上
只有切应力,其方向于 y 轴平行.
由平衡方程
y
Fy 0
可知,两侧面的内力元素 dy dz 大小相等,方向相反,将组成 一个力偶。 其矩为( dy dz) dx dy z
τ
dx
τ
x
(Torsion)
2、 要满足平衡方程
y
M z 0 Fx 0
Examine the deformation then propose the hypothesis
变形的分布规律
Distribution regularity of deformation
应力的分布规律
static relation
Distribution regularity of stress
建立公式
Establish the formula
(Torsion)
一、变形几何关系(Geometrical Relationship of Deformation)
1、变形现象 (Deformation phenomenon) 1) 轴向线仍为直线,且长度不变; 2) 横截面仍为平面且与轴线垂直;
ρ
a A T
E
b
O1 dx
ρ
a
D G T d O2 G' D' b
经过半径 O2D 上任一点G的纵向线EG 也倾斜了一个角度
ρ,它也就是横截面半径上任一点E处的切应变
GG' d tg EG dx
(torsion) (Torsion) 二、 物理关系(Physical Relationship)
3) 径向线保持为直线,只是绕轴
线旋转.
2、平面假设(Plane assumption)
变形前为平面的横截面 ,变形 后仍保持为平面.
(Torsion)
3、几何关系 (Geometrical relationship) 倾角 是横截面圆周上任一
点A 处的切应变, d 是 b-b 截面相对于a-a 截面象刚性 平面一样绕杆的轴线转动的 一个角度.
单元体两个相互垂直平面上的切 应力同时存在,且大小相等,都 指相(或背离)该两平面的交线. dy
τ
dx
τ
x
z
纯剪切单元体:
(Element in pure shear )
单元体平面上只有切应力而无正应力,则称为纯剪切单元体.
