1梅逊增益公式
梅森增益公式 自循环

梅森增益公式自循环
梅森增益公式是用来计算反馈系统的增益的公式,也被称为闭环增益公式。
该公式由美国控制工程师Richard Bellman和Rudolf Kalman在20世纪50年代提出。
梅森增益公式可以用于计算具有反馈的控制系统的增益,该增益可以决定系统的稳定性和性能。
这个公式采用了图论和网络分析的方法,将一个复杂的反馈系统转化为一个数学表达式,方便计算闭环系统的增益。
具体而言,在一个反馈系统中,梅森增益公式可以表示为:
G = G1 / (1 + G1 * H2 + G1 * H3 + ... + G1 * Hn)
其中,G是反馈系统的增益,G1是正馈通路的增益,H2、H3、...、Hn是反馈通路的传递函数。
自循环是指反馈系统中反馈信号直接或间接地重新输入到系统本身,从而影响系统的行为。
自循环可以通过梅森增益公式有效地计算闭环系统的增益。
通过梅森增益公式,可以分析反馈系统的稳定性和性能,并设计出适当的控制策略来实现所需的系统响应。
这对于控制工程和系统设计非常有用。
梅森增益公式三个互不接触的回路例题

梅森增益公式三个互不接触的回
路例题
梅森公式是梅森在创建流图时提出的一种计算传递函数的方法。
因为信号流程和框图没有本质区别,所以完全适用于框图。
它使传递函数的计算变得简单,过程完全格式化。
梅森增益公式三个互不接触的回路例题 1
如果两个回路之间没有共同点,则简称为两个非接触回路,否则称为接触,两个非接触回路的每个回路的增益的乘积称为两个非接触回路的增益。
同样,三个回路之间没有共同点,称为三个非接触回路,每个回路的增益的乘积称为三个非接触回路的增益。
如此类推,共计有n个回路的系统最多存在一个n个互不接触回路。
如果不存在b个互不接触回路,则一定不存在大于b的互不接触回路。
方框图是一种很有用的图示法,但对于复杂的控制系统,方框图的简化过程仍较复杂,且易出错.mason提出的倍号流图,既能及示系统的特点,而且还能直接应用梅森公式方便地写出系统的传递函数。
因此,信号流图在控制工程中也被广泛地应用。
信号流图是一种衣示线性化代数方程组变量间关系的图示方法,信号流图由节点和支路组成,每一个节点用符号“〇”表示系统的一个变量,而每两个节点间的支路用符号“一>” 连接,表示这两个变量之间信号的传输关系,信号流向由支路
上的箭头表示,而传输关系(增益、传递函数)则标注在支路上。
梅森增益公式适用范围.docx

梅森增益公式适用范围标题:梅森增益公式适用范围的阐述引言:梅森增益公式是电子电路设计中常用的一种分析工具,用于计算电路增益和频率响应。
然而,在实际应用中,梅森增益公式的适用范围有一定限制。
本文将就梅森增益公式的适用范围展开阐述,以帮助读者更好地理解和使用这一公式。
一、梅森增益公式简介梅森增益公式是一种基于网络理论的公式,用于计算复杂电路的总增益。
它是由美国电子工程师梅森提出的,一般用于线性、定常、时不变的电路分析。
二、适用范围的限制1. 线性电路要求梅森增益公式适用于线性电路,即电路的元件和信号是线性的。
对于非线性电路,例如包含二极管、晶体管等非线性元件的电路,梅森增益公式就不再适用。
2. 定常电路要求第1页/共6页梅森增益公式适用于定常电路,即电路的参数是固定的,不随时间变化。
对于具有非定常特性的电路,如含有开关、变阻器等可变元件的电路,梅森增益公式无法提供准确的结果。
3. 时不变电路要求梅森增益公式适用于时不变电路,即电路的参数与时间无关。
在实践中,例如考虑温度变化、电源变化等因素会导致电路参数发生改变,因此这些情况下梅森增益公式不能得到准确的结果。
三、梅森增益公式的优势尽管梅森增益公式存在一定的适用范围限制,但它仍然是电子电路设计中常用的工具。
以下是梅森增益公式的一些优势:1. 简单易用相比其他复杂的电路分析方法,梅森增益公式简单易懂,计算过程相对简单直观。
这使得它成为工程师们在电路设计、故障排除等方面的重要工具。
2. 可模块化分析梅森增益公式支持对电路进行模块化分析。
通过将复杂的电路划分为多个子电路,可以使用梅森增益公式计算每个子电路的增益,进而得到整个电路的总增益。
这种分析方法便于对电路进行优化和调试。
第2页/共6页3. 提供定量分析结果梅森增益公式给出的是数值化的增益结果,可以帮助工程师量化地评估和比较不同电路的性能。
这对于电路设计者来说非常重要,可以在设计初期对各个子电路进行评估和优化。
如何用梅逊公式求传递函数
• 通路传输(增益):通路中各支路传输的乘积称为通路传输或通 路增益。前向通路中各支路传输的乘积称为前向通路传输或前 向通路增益。
• 回路传输(增益):回路上各支路传输的乘积称为回路传输或回
路增益。
1/8/2024
如何用梅逊公式求传递函数
4
信号流图的等效变换
• 串联支路合并:
ab x1 x2 x3
8
例2: 已知结构图如下,可在结构图上标出节点,如上图所示。 然后画出信号流图如下图所示。
k
R(S) b
m
d
V1
l
g V3 e
V2
h
C(S)
f f
m
h
R1
Ⅰ
b
l
Ⅱ
V3
k
Ⅲ
Ⅳ
C
V1 d Ⅴ e V2 1
g
1/8/2024
如何用梅逊公式求传递函数
9
信号流图的绘制
例2: 按微分方程拉氏变换后
的代数方程所表示的变量间
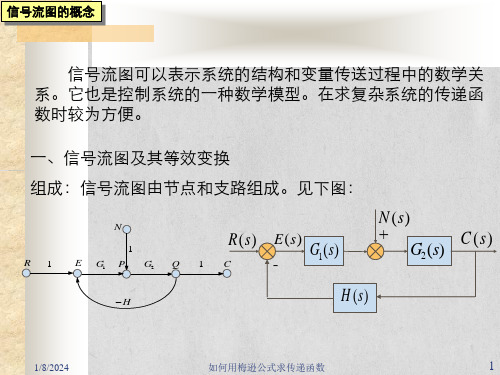
信号流图的概念
信号流图可以表示系统的结构和变量传送过程中的数学关 系。它也是控制系统的一种数学模型。在求复杂系统的传递函 数时较为方便。
一、信号流图及其等效变换
组成:信号流图由节点和支路组成。见下图:
R1
N
1
E G1 P
G2
Q
1
R(s)
C
E(s)
-
G1(s)
N (s)
+ G2(s) C (s)
H
H (s)
式中: La 流图中所有不同回路的回路传输之和;
LbLc 所有互不接触回路中,每次取其中两个回
路传输乘积之和;
LdLeLf 所有互不接触回路中,每次取其中三个
梅森增益公式

具有任意条前向通路及任意个单独回路和不接触回路的复杂信号流图,求取从任意源节点到任意阱节点之间传递函数的梅森增益公式记为
式中
——从源节点到阱节点的传递函数(或总增益);
——从源节点到阱节点的前向通路总数;
——从源节点到阱节点的第
条前向通路总增益;
——流图特征式
式中
——所有单路回路增益之和;
——所有互不接触的单独回路中,每次取其中两个回路的回路增益的乘积之和;
——所有互不接触的单独回路中,每次取其中三个回路的回路增益的乘积之和;
——流图余因子式,它等于流图特征式中除去与第
条前向通路相接触的回路增益项(包括回路增益的乘积项)以后的余项式。
[1]。
2.6信号流图与梅森公式
G2 ( s) H ( s) N ( s) N ( s) 1 G1 ( s)G2 ( s) H ( s)
N ( s)
7)系统的总输出 X o (s) i (s) X i (s) N (s) N (s)
8)系统的总偏差 (s) i ( s) X i ( s) N (s) N (s) 结论
练习 试化简下图所示系统的方框图,并求系 统传递函数。
可看出此题方框图化简较复杂,试用梅森公式化简.
• 两条前向通路 • 两条回路 • 主特征式
P G1G3G5 , P2 G2G4G5 1
L1 G3 H , L2 G4 H
1 ( L1 L2 ) 1 G3 H G4 H
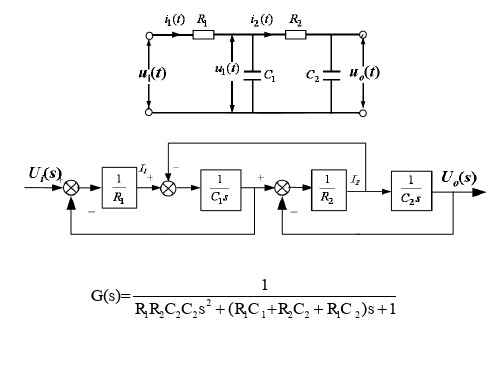
【例1】根据微分方程绘制信号流图
i1 (t ) 1 R1 [ui (t ) u A (t )]
1 u A (t ) [i1 (t ) i2 (t )]dt C1
1 i2 (t ) [u A (t ) uo (t )] R2
uo (t) 1 C2
i (t )dt
2
一般闭环控制系统的结构如下图所示
1)闭环系统的开环传递函数 将闭环控制系统主反馈 通道的输出断开,即 H(s)的输出通道断开 时,前向通道传递函数与反馈通道传递函数的乘积 G1(s)G2(s)H(s)称为该闭环控制系统的开环传递函数 ,记为GK(s)。
闭环系统的开环传递函数也可定义为反馈信 号B(s)和偏差信号ε(s)之间的传递函数,即:
X o ( s) G( s) G1 ( s)G2 ( s) ( s)
B( s) H ( s) X o (s)
4)输入信号作用下的闭环传递函数
令n(t)=0,此时在输入xi(t)作用下系统的闭环传 递函数为:
1梅逊增益公式

=1+ G1 +G2+G3 +2G1G2+G2G3 + G1 G3 + 2G1G2G3 6
G1 G1 R R 1 1 1 1
G2 G2 1 1
G3 G3
K K C C
1 1
前向通道:P1 = G1 G2G3 K P2 = G2G3 K P3 = G3 K P4 = G2 (1)G3 K
分别是:P1 = G1G2G3 ,1 = 1; P2 = G1G4 ,2= 1。
梅逊公式小结
梅逊公式同时适用于信号流图和结构图;
关键:数清楚前向通道数、单回环数、互不接触回环数; 注意:反馈环是正反馈还是负反馈;
bc
k , 在所有两两互不接触的 回环中,每次不重复取 其中的两个回环增益之 积之和; L PL — 第K条前向通路的传输;
其余的以此类推
3
例2-20 求图所示系统的信号流图输入x0至输出x8的总
传输P。 a
x0
b i
c
d j m
e
f
k
g
h x
8
解:
前向通道:1条, P1 = abcdefgh;
C(s)/R(s)=P=(P=1+1G G H 2 )/ +P2 +G G H 3、 特征式: 1
1 2 1 2 3
2、互不接触回环数: 0
2
+G1G2G3 + G4H2 + G1G4
=4、前向通道数:1G4 )/ (1+ G1G2H1 +G2G3H2 +G1G2G3 + G4H2 + G1G4 ) (G1G2G3 +G 2,
专题5-梅森增益公式

例 试用梅森公式求信号流图的传递函数C(s)/R(s) .
1
解: 单独回路有四个即
L
a
G1 G2 G3 G1G2
两个互不接触的回路有四组,即 Lb Lc G1G2 G1G3 G2G 3G1G2G3 三个互不接触的回路有一组,即
因此,系统的传递函数为
p2 G2G3 K , 2 1 G1 ; p4 G1G2G3 K , 4 1 .
p3 G1G3 K , 3 1 G2 ;
C ( s ) p11 p2 2 p3 3 p4 4 R( s ) G2G3 K (1 G1 ) G1G3 K (1 G2 ) 1 G1 G2 G3 2G1G2 G1G3 G2G3 2G1G2G3
L L L
d e
f
G1G2G3
1
则信号流图特征式为
1 La Lb Lc Ld Le L f 1 G1 G2 G3 2G1G2 G1G3 G2G3 2G1G2G3
前向通路共有四条,其增益及余因式分别为
p1 G1G2G3 K , 1 1 ;
C ( s) G1 ( s )G2 ( s ) ( s) R( s ) 1 G1 ( s )G2 ( s ) H ( s )
由 (s )可进一步求得输入信号作用下系统的输出量C(s)为
R( s ) 1 G1 ( s )G2 ( s ) H ( s )
1 n P pk k k 1
2.闭环系统的传递函数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 = 1 2 = 1 + G1 3 = 1 + G2 4 = 1
梅逊增益公式在方框图(结构图) 中的应用
能不能将梅逊公式直接应用到复杂方框图的传
递函数求解?答案是肯定的!!!
虽然,自控原理教材还没有明确给出公式,但
一篇文献上,已经进行了定义和说明。 参考文献:李平等,梅逊增益公式参数在方块图中的定义和
x P1 Δ1 abcdefgh P 8 两两不接触回环:3对,bidj , bifk , djfk x0 Δ 1 ( bi dj fk bcdefgm) ( bidj bifk djfk) bidjfk
单回环:4个, bi , dj , fk , bcdefgm 三个互不接触回环:1组, bidjfk
bc
k , 在所有两两互不接触的 回环中,每次不重复取 其中的两个回环增益之 积之和; L PL — 第K条前向通路的传输;
其余的以此类推
3
例2-20 求图所示系统的信号流图输入x0至输出x8的总
传输P。 a
x0
b i
c
d j m
e
f
k
g
h x
8
解:
前向通道:1条, P1 = abcdefgh;
C(s)/R(s)=P=(P=1+1G G H 2 )/ +P2 +G G H 3、 特征式: 1
1 2 1 2 3
2、互不接触回环数: 0
2
+G1G2G3 + G4H2 + G1G4
=4、前向通道数:1G4 )/ (1+ G1G2H1 +G2G3H2 +G1G2G3 + G4H2 + G1G4 ) (G1G2G3 +G 2,
=1 (bi + dj + fk + bcdefgm) + (bidj + bifk + djfk) bidjfk 1 = 1 0 = 1
4
例2-21 已知系统的信
d c a b e
号流图如下,求输入x1至
输出x2和x3的传输。 解:单回路: ac,abd,gi, ghj, aegf 2 x1 3
a b c d e f a bc def
Δ
— 信号流图的特征式;Δ 1 La Lb Lc Ld Le L f a bc def L 的回环之中,每次不重 复取其中三个回环增益乘积之和, LdLke —f ,在所有三个互不接触 余因子式(把第K条前向通道除去后的特征式) 。 def
说明,北京联合大学学报(自然科学版),2009,23(2):34-36.
梅逊公式求传递函数举例 例2-23 试求结构图中的传递函数C(s)/R(s)。
G4
R G1 -G1G2H1 H1 -G1G2G3 G2 G3 -G2G3H2 H2
C
解:1、单回环数: 5,-G1G2H1 -G2G3H2 -G1G2G3 -G4H2 - G1G4
x2 f
h j
g
i
x3 两两互不接触回路: ac与gi,ghj; abd与gi,ghj
x1到x2的传输: 3 P1 = 2ab 3
=1 (ac + abd + gi + ghj+aegf) + (acgi+acghj + abdgi + abdghj) 1 = 1 ( ac + abd ) (gi + ghj)
P2 = 3gfab 2ae
2 = 1
5
例2-22 试求信号流图中的传递函数C(s)/R(s) 。
G1 R 1 1 G2 1 G3 1 K C
解:
单回路: G1 ,G2 ,G3 ,G1G2 G2和G3 ,G1G2和G3
两两互不接触回路: G1和G2 , G1和G3 , 三个互不接触回路: G1 , G2和G3
Mason’s rule are named after him.
梅逊增益公式(Mason’s gain formula)
梅逊公式的一般表达式为
P
式中: P
a a
P Δ
k 1 k
nkຫໍສະໝຸດ Δ 1,表示所有不同单个回 环的增益之和; L n — 从输入节点至输出节点的前向通道总数;
b c
L L L L L L(增益); —输入输出节点间的总传输
分别是:P1 = G1G2G3 ,1 = 1; P2 = G1G4 ,2= 1。
梅逊公式小结
梅逊公式同时适用于信号流图和结构图;
关键:数清楚前向通道数、单回环数、互不接触回环数; 注意:反馈环是正反馈还是负反馈;
梅逊公式PPT课件
朱文兴
2.7.3梅逊增益公式简介
梅逊增益公式是一种求复杂信号流图传递函数的简
单方法。
它是美国的电子工程师萨穆埃尔· 杰斐逊· 梅逊推导
出来并以他的名字命名的。Samuel Jefferson Mason (1921–1974) was an American electronics engineer.
=1+ G1 +G2+G3 +2G1G2+G2G3 + G1 G3 + 2G1G2G3 6
G1 G1 R R 1 1 1 1
G2 G2 1 1
G3 G3
K K C C
1 1
前向通道:P1 = G1 G2G3 K P2 = G2G3 K P3 = G3 K P4 = G2 (1)G3 K
