奥数标数法练习 计数之标数法经典例题讲解
标数法: 用来解决计算最短路线问题的方法,在给出的图形中

“为什么蜈蚣出门要这么长时间呢?” “因为它要穿鞋呀… …”
7.
一只密蜂从 A 处出发, A 回到家里 B 处,每次只能从一个蜂房爬向右侧邻近的蜂房而 不准逆行,共有多少种回家的方法?
1 A 2 3 4 5 6 7 8 9 B
8. 在图中,用水平或垂直的线段连接相邻的字母,当沿着这些线段行走时,正好拼出 “ APPLE ”的路线共有多少条?
“为什么蜈蚣出门要这么长时间呢?” “因为它要穿鞋呀… …”
有问题跟我联系哦!wutong@ 【数学加油站答案】
1.
A E1 1 C 1 F2 3 1 D
3G 6 B
H
I
2. 首先明确三天所走的路线有什么不同?每天的路线有无限制条件?若有, 是什么?搞清 楚这些问题后,仍然用标数法求解.第一天(无限制条件)共有 16 条;第二天(必须 经过公园)共有 8 条;第三天(必须不经过公园)共有 8 条. 3. 因为 B 在 A 的右下方,由标号法可知,从 A 到 B 的最短路径上,到达任何一点的走法 数都等于到它左侧点的走法数与到它上侧点的走法数之和. 有积水的街道不可能有路线 经过,可以认为积水点的走法数是 0.接下来,可以从左上角开始,按照加法原理,依 次向下向右填上到各点的走法数.如右上图,从 A 到 B 的最短路线有 22 条.
“为什么蜈蚣出门要这么长时间呢?” “因为它要穿鞋呀… …”
标数法: 用来解决计算最短路线问题的方法,在给出的图形中 的每一个结点标出到达该点的方法 数,最后利用相加的原则求出到达目 的地的方法数。
从 A 到 B 的最短路线有多少条?
“为什么蜈蚣出门要这么长时间呢?” “因为它要穿鞋呀… …”
5. 用“标数”求出:从学校到养老院共 126 条.必经过市中心的 60 条,所以可行的路有: 126 60 66 (条) .
小学奥数 几何计数(三) 精选练习例题 含答案解析(附知识点拨及考点)

1.掌握计数常用方法;2.熟记一些计数公式及其推导方法;3.根据不同题目灵活运用计数方法进行计数.本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等,并渗透分类计数和用容斥原理的计数思想.一、几何计数在几何图形中,有许多有趣的计数问题,如计算线段的条数,满足某种条件的三角形的个数,若干个图分平面所成的区域数等等.这类问题看起来似乎没有什么规律可循,但是通过认真分析,还是可以找到一些处理方法的.常用的方法有枚举法、加法原理和乘法原理法以及递推法等.n 条直线最多将平面分成21223(2)2n n n ++++=++……个部分;n 个圆最多分平面的部分数为n (n -1)+2;n 个三角形将平面最多分成3n (n -1)+2部分;n 个四边形将平面最多分成4n (n -1)+2部分……在其它计数问题中,也经常用到枚举法、加法原理和乘法原理法以及递推法等.解题时需要仔细审题、综合所学知识点逐步求解.排列问题不仅与参加排列的事物有关,而且与各事物所在的先后顺序有关;组合问题与各事物所在的先后顺序无关,只与这两个组合中的元素有关.二、几何计数分类数线段:如果一条线段上有n +1个点(包括两个端点)(或含有n 个“基本线段”),那么这n +1个点把这条线段一共分成的线段总数为n +(n -1)+…+2+1条数角:数角与数线段相似,线段图形中的点类似于角图形中的边.数三角形:可用数线段的方法数如右图所示的三角形(对应法),因为DE 上有15条线段,每条线段的两端点与点A 相连,可构成一个三角形,共有15个三角形,同样一边在BC 上的三角形也有15个,所以图中共有30个三角形.ED CBA数长方形、平行四边形和正方形:一般的,对于任意长方形(平行四边形),若其横边上共有n 条线段,纵边上共有m 条线段,则图中共有长方形(平行四边形)mn 个.模块一、立体几何计数【例 1】 用同样大小的正方体小木块堆成如下图的立体图形,那么一共用了__________块小正方体。
计数第06讲_标数法(学生版)A4
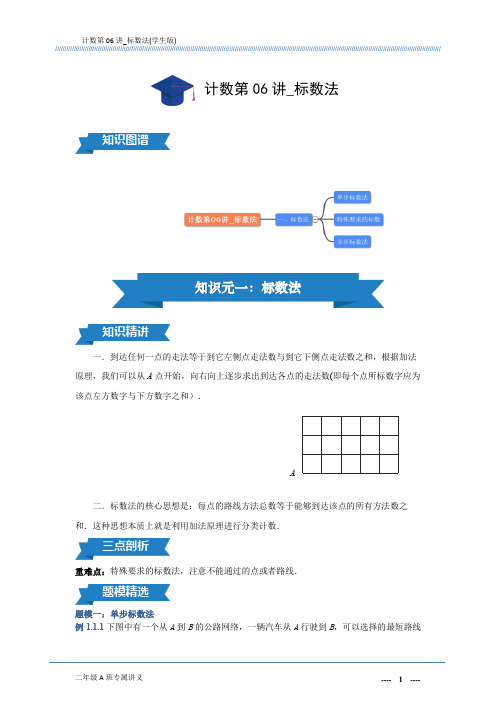
一.到达任何一点的走法等于到它左侧点走法数与到它下侧点走法数之和,根据加法原理,我们可以从A 点开始,向右向上逐步求出到达各点的走法数(即每个点所标数字应为该点左方数字与下方数字之和).二.标数法的核心思想是:每点的路线方法总数等于能够到达该点的所有方法数之和.这种思想本质上就是利用加法原理进行分类计数.重难点:特殊要求的标数法,注意不能通过的点或者路线.题模一:单步标数法例1.1.1下图中有一个从A 到B 的公路网络,一辆汽车从A 行驶到B,可以选择的最短路线计数第06讲_标数法A一共有________条?BA例1.1.2下图是一个街道的示意图,实线表示道路,从B到A,只能向右或向上或右斜上方沿着道路前进,则一共有_________种不同的走法.AB例1.1.3在图所示中,从“北”字开始,每次向下移动到一个相邻的字可以读出“北京奥运会”.那么一共有多少种不同的读法?北京京奥奥奥运运运运会会会会会题模二:特殊要求的标数例1.2.1在如图所示的街道示意图中,C处因施工不能通行,那么从A到B处的最短路线有________条.例 1.2.2有一只蚂蚁沿着下图中的方格线从A爬到B,每次只能向右爬一格或向上爬一格.图中画着黑点的地方必须通过,那么这只蚂蚁可以选择____________条不同的路线.例1.2.3如图,从A 出发经过十字路口D ,但不经过线段BC (不过点B 、C ),不同的最短路径有多少条?题模三:多步标数法例1.3.1如图所示,国际象棋中的棋子“皇后”从左下角走到右上角,每步只能向右、向上或者向右上移动任意多格,一共有多少种不同的走法?A .168B .178C .188D .198随练1.1如图,从A 点沿线段走到B 点,每次只能向上或向右走一步,共有多少种不同走法?DABCBA随练1.2在下图中,从A点沿线段走到B点,每次只能向上或向右走一步,共有多少种不同走法?BA随练1.3如图,从A出发经过十字路口D,但不经过线段BC(不过点B、C),不同的最短路径有多少条?DBCA随练1.4如图,从A出发经过十字路口D,但不经过线段BC(不过点B、C),不同的最短路径有多少条?DB CA随练1.5如图所示,亚瑟王要沿路线从A地前往B地拿去圣剑Excalibur,但路中有许多恶魔使得部分道路无法通行,那么亚瑟王现在要取得圣剑的最短路线共有_________条.(圆圈表示恶魔占据的地方)随练 1.6如图所示,国际象棋中的棋子“皇后”从左下角走到右上角,每步只能向右、向上或者向右上移动任意多格,一共有多少种不同的走法?作业1如图,有一个48 的棋盘,现将一枚棋子放在棋盘左下角格子A处,要求每一步只能向棋盘右上或右下走一步(如从C 走一步可走到D 或E ),那么将棋子从A 走到棋盘右上角B 处共有_______种不同的走法.作业2在下图中,从A 点沿线段走到B 点,每次只能向上或向右走一步,共有多少种不同走法?作业3一只兔子沿着方格的边从A 到B ,规定上只能往上或往右走,但是必须经过一座独木桥MN ,这只兔子有______________种不同的走法.ABABNM作业4一只甲虫沿着下图中的方格线从A 爬到B ,每次只能向右爬一格或向上爬一格.请问:(1)图中C 、D 两点必须都通过,那么这只甲虫可以选择多少条不同的路线?(2)图中C 、D 两点只通过其中的一个点,那么这只甲虫可以选择多少条不同的路线?图中C 、D 两点都不通过,那么这只甲虫可以选择多少条不同的路线?作业5如图,从A 处到B 的最短路线中,必通过十字路口C 和D 的,共有多少条?作业6一种蜂房编号如图所示,左上角有一只小蜜蜂,还不会飞,只会向相邻的蜂房爬行,且方向只能是向右、右上、右下方爬,它爬行到8号蜂房,共有____种路线.ABCDB AC D1 35 7 8642。
小奥四年级标数法

四年级计数问题:标数法难度:高难度如图,某城市的街道由5条东西向马路和7条南北向马路组成,现在要从西南角的处沿最短的路线走到东北角出,由于修路,十字路口不能通过,那么共有____种不同走法.解答:四年级计数问题:标数法难度:中难度如图为一幅街道图,从A出发经过十字路口B,但不经过C走到D的不同的最短路线有条.解答:计数习题标数法和加法原理的综合应用(★★★★)有20个相同的棋子,一个人分若干次取,每次可取1个,2个,3个或4个,但要求每次取之后留下的棋子数不是3或4的倍数,有()种不同的方法取完这堆棋子.【分析】把20、0和20以内不是3或4的倍数的数写成一串,用标号法把所有的方法数写出来:考点说明:本题主要考察学生对于归纳递推思想的理解,具体来说就是列表标数法的使用,难度一般,只要发现了题目中的限制条件,写出符合条件的剩余棋子数,然后进行递推就可以了。
<评价> :计数问题在各大考试中所占的分量越来越重,计数的知识也学习的比较早,标号法是加乘原理中加法原理的内容,在四年级以前已经学习过,但是灵活应用学习过的知识才是学习最重要的意义,六年级上(第十一级)第10讲会将计数问题与应用题或者最值问题进行综合学习,学习后能力会有进一步的提高。
计数方法与技巧(标数法例题1)计数方法与技巧(标数法例题2)计数方法与技巧(标数法例题3)1. 如图所示,小明家在A地,小学在B地,电影院在C地。
1.小明从家里去学校,走最短的线路,有多少种走法?2.小明从家里去电影院,走最短线路,有多少种走法?如图,从一楼到二楼有12梯,小明一步只能上1梯或2梯,问小明从1楼上到2楼有多少种走法?一只蜜蜂从A处出发,回到家里B处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?解答:蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”这意味着它只能从小号码的蜂房爬进相邻的大号码的蜂房。
明确了行走路径的方向,就可运用标数法进行计算。
小学奥数计数之标数法经典例题讲解【三篇】

小学奥数计数之标数法经典例题讲解【三篇】
解答:蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”
这意味着它只能从小号码的蜂房爬进相邻的大号码的蜂房。
明确了行
走路径的方向,就可使用标数法实行计算。
如图所示,小蜜蜂从A出发到B处共有89种不同的回家方法。
【第二篇】
例1.按图中箭头所指的方向行走,从A到I共有多少条不同的路线?
解答:
第1步:在起点A处标1。
再观察点B,要想到达点B,只有一个入口A,所以在B点也标1。
第2步:再观察点C,要想到达点C,它有两个入口A和B,所以在点
C处标1+1=2。
同理重复点F,点D,点E,点G,点H,点I
【第三篇】
分析:既然要走最短路线,自然是不能回头走,所以从A地到B地
的过程中只能向右或向下走.
我们首先来确认一件事,如下图
从A地到P点有m种走法,到Q点有n种走法,那么从A地到B地有多少种走法呢?
就是用加法原理,一共有m+n种走法.
这个问题明白了之后,我们就能够来解决这道例题了:
首先因为只能向右或向下走,那么最上面一行和最左边一列的每一个点都只能有一种走法,(因为不能够走回头路).
我们就在这些交点的旁边标记上一个数字,代表走到这个位置有多少种方法.。
奥数标数法练习 计数之标数法经典例题讲解

奥数标数法练习计数之标数法经典例题讲解【第一篇】一只蜜蜂从A处出发,回到家里B处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?如图所示,小蜜蜂从A出发到B处共有89种不同的回家方法。
【第二篇】例1.按图中箭头所指的方向行走,从A到I共有多少条不同的路线?解答:第1步:在起点A处标1。
再观察点B,要想到达点B,只有一个入口A,所以在B点也标1。
第2步:再观察点C,要想到达点C,它有两个入口A和B,所以在点C处标1+1=2。
同理重复点F,点D,点E,点G,点H,点I【第三篇】分析:既然要走最短路线,自然是不能回头走,所以从A地到B地的过程中只能向右或向下走.我们首先来确认一件事,如下图从A地到P点有m种走法,到Q点有n种走法,那么从A地到B地有多少种走法呢?就是用加法原理,一共有m+n种走法.这个问题明白了之后,我们就能够来解决这道例题了:首先因为只能向右或向下走,那么最上面一行和最左边一列的每一个点都只能有一种走法,(因为不能够走回头路).我们就在这些交点的旁边标记上一个数字,代表走到这个位置有多少种方法.【第四篇】有一个5位数,每个数字都是1,2,3,4,5中的一个,并且相临两位数之差是1.那么这样的5位数到底有多少个呢?(数字能够重复)这是一道数论的题目,但是我们也能够使用标数法来解答,并且非常直观.到第一站能够有5种选择,每种选择有一种走法,那么下一站,走1号门就只有一种走法(就是第一站走的2号门),走2号门就有2种走法(第一站走1号或3号门)走3号门也是2种走法(第一站走2号门或4号门)走4号门2种走法(第一站走3号门或者5号门)走5号门只有一种走法(第一站走的是4号门)我们发现在这个站经过某个门有多少种走法,正好等于他左上和右上的两个数字和.于是我们能够将数字标全.这道题的答案就是42种,虽然很多同学会用枚举法也能做出42种,但是一旦这道题给的不是5位数,而是7位数,9位数的话,枚举法就显得无力了.这种时候标数法是个不错的选择.能够用到标数法的问题有很多,大家掌握这种方法之后能够解决很多平时看起来很麻烦的题目。
标数法——精选推荐

标数法1、有20个相同的棋子,一个人分若干次取,每次可取1个,2个,3个或4个,但要求每次取之后留下的棋子数不是3或4的倍数,有()种不同的方法取完这堆棋子.【分析】把20、0和20以内不是3或4的倍数的数写成一串,用标号法把所有的方法数写出来:2、如图是某街区的道路图,C点正在修路不能通过,那么从A点到B点的最短路线有多少条?解答:使用标数法,C点不通用0表示,答案为110种。
插板法1、若有A、B、C、D、E五个人排队,要求A和B两个人必须不站在一起,则有多少排队方法?【解析】题目要求A和B两个人必须隔开。
首先将C、D、E三个人排列,有种排法;若排成DCE,则D、C、E“中间”和“两端”共有四个空位置,也即是:︺D︺C︺E︺,此时可将A、B两人插到四个空位置中的任意两个位置,有种插法。
2、在一张节目单中原有6个节目,若保持这些节目相对顺序不变,再添加进去3个节目,则所有不同的添加方法共有多少种?【解析】直接解答较为麻烦,可利用插空法去解题,故可先用一个节目去插7个空位(原来的6个节目排好后,中间和两端共有7个空位),有种方法;再用另一个节目去插8个空位,有种方法;用最后一个节目去插9个空位,有种方法,由乘法原理得:所有不同的添加方法为=504种。
3、一条马路上有编号为1、2、……、9的九盏路灯,为了节约用电,可以把其中的三盏关掉,但不能同时关掉相邻的两盏或三盏,则所有不同的关灯方法有多少种?【解析】若直接解答须分类讨论,情况较复杂。
故可把六盏亮着的灯看作六个元素,然后用不亮的三盏灯去插7个空位,共有种方法(请您想想为什么不是),因此所有不同的关灯方法有种。
捆绑法1、5个男生3个女生排成一排,3个女生要排在一起,有多少种不同的排法?分析此题涉及到的是排队问题,对于女生有特殊的限制,因此,女生是特殊元素,并且要求她们要相邻,因此可以将她们看成是一个元素来解决问题.解因为女生要排在一起,所以可以将3个女生看成是一个人,与5个男生作全排列,有种排法,其中女生内部也有种排法,根据乘法原理,共有种不同的排法.2、6个球放进5个盒子,每个盒子至少放一个球,有多少种不同的方法?其实,由抽屉原理可知,必然有两个球在一起。
计数篇(小学奥数计数必会题)

计数篇1.枚举与容斥计数枚举法:适用于数小,题目简单,就可以按照一定的顺序一一列举出来,如果数目较大,也可以用适当的标准,把问题分类,在每一类中进行枚举,枚举≠傻举,具有一定的特性。
要想在枚举中做到不重不漏需要满足四个规则:1.有序;2.分类;3.寻找规律;4.利用对称性;例1:政政有10块糖,如果每天至少吃3块,那么共有多少种不同的吃法吃完这10块糖?政政有10块糖,想分成三堆(不考虑顺序,且糖没有区别),每堆至少两块,有几种分法?(加加老师说:不要自己加限制条件,没有说多少天吃完。
)种种种天吃完种天吃完种天吃完4442 532 433 622.293513 334 343 433 35 37 46 55 64 73 21 10 1.1++++++++=+++++++++++++有1、2、3、4四张数字卡片,要求1不排在千位上,数2不排在百位上,数3不排在十位上,数4不排在个位上,那么用这四张卡片组成满足要求的四位数共有多少个?(全错位排序、递推公式、欧拉公式)93334321431241234 3431341231423 2413234121432=++⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧开头开头开头树形图(枚举树):枚举树状图是借助树状结构的分层特征来罗列所有的可能的一种方法,适用于层级结构鲜明的题型。
利用枚举树进行枚举的一般步骤和技巧1.明确条件:分析枚举对象满足的限制条件。
2.确定范围:根据限制条件缩小枚举的范围3.确定次序:一般按照由小到大、由少到多的原则,采用合适的分类保证枚举的完整,以求不重不漏。
4.逐一枚举:借助枚举树的分层特性,按照次序逐次画图枚举,最终求出问题的解。
甲乙两人进行乒乓球比赛,规定谁先胜三场,第一场甲胜。
问到决出最后胜负为止,共有几种不同的情形?其中甲胜的情形有几种?由树状图可得,比赛结果情况共10种,其中甲胜的情况有6种。
下图中6个点,9条线段。
一只蚂蚁从A点出发,要沿着图示的线段爬到C点,行进中,同一个点或者线段只能经过一次。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
奥数标数法练习计数之标数法经典例题讲解
解答:
第1步:在起点A处标1。
再观察点B,要想到达点B,只有一个入口A,所以在B点也标1。
第2步:再观察点C,要想到达点C,它有两个入口A和B,所以在点C处标1+1=2。
同理重复点F,点D,点E,点G,点H,点I
【第三篇】
分析:既然要走最短路线,自然是不能回头走,所以从A地到B地的过程中只能向右或向下走.
我们首先来确认一件事,如下图
从A地到P点有m种走法,到Q点有n种走法,那么从A地到B 地有多少种走法呢?
就是用加法原理,一共有m+n种走法.
这个问题明白了之后,我们就可以来解决这道例题了:
首先由于只能向右或向下走,那么最上面一行和最左边一列的每一个点都只能有一种走法,(因为不可以走回头路).
我们就在这些交点的旁边标记上一个数字,代表走到这个位置有多少种方法.
【第四篇】
有一个5位数,每个数字都是1,2,3,4,5中的一个,并且相临两位数之差是1.那么这样的5位数到底有多少个呢?(数字可以重复) 这是一道数论的题目,但是我们也可以使用标数法来解答,并且非常直观.
到第一站可以有5种选择,每种选择有一种走法,
那么下一站,
走1号门就只有一种走法(就是第一站走的2号门),
走2号门就有2种走法(第一站走1号或3号门)
走3号门也是2种走法(第一站走2号门或4号门)
走4号门2种走法(第一站走3号门或者5号门)
走5号门只有一种走法(第一站走的是4号门)
我们发现在这一站经过某个门有多少种走法,正好等于他左上和右上的两个数字和.于是我们可以将数字标全.
这道题的答案就是42种,
虽然很多同学会用枚举法也能做出42种,但是一旦这道题给的不是5位数,而是7位数,9位数的话,枚举法就显得无力了.这种时候标数法是个不错的选择.
可以用到标数法的问题有很多,大家掌握这种方法之后可以解决很多平时看起来很麻烦的题目。
