百分数的认识知识点
百分数的认识知识点

百分数的认识一、百分数的意义和写法1、百分数的意义:百分数表示一个数是另一个数的百分之几。
是指两个数的比,因此也叫百分率或百分比。
2、百分数的写法:百分数通常不写成分数形式,而在原来的分子后面加上“%”来表示。
3、百分数和分数的联系和区别:(1)联系:都可以表示两个数的倍比关系。
(2)区别:○1、百分数只表示两个数的倍比关系,不能表示具体的量,所以不能带单位,而分数既可以表示两个数的关系,又可以表示具体的量,所以表示具体的量时可以带单位。
○2、百分数的分子可以是整数,也可以是小数,而分数的分子只能是除0以外的自然数。
二、百分数和分数、小数的互化1、百分数与小数的互化(1)百分数化小数:把分子的小数点向左移动两位,同时去掉百分号。
(2)小数化百分数:把小数的小数点向右移动两位,同时添上百分号。
2、百分数与分数的互化(1)百分数化分数:先把百分数改写成分母是100的分数,能约分的要约成最简分数。
如果百分数的分子是小数时,在改写成分母是100的分数后,可根据分数的基本性质,化成分子是整数的分数,然后能约分的要约成最简分数。
(2)分数化百分数:○1、如果是常见的分数,可直接化成小数,再化成百分数。
○2、如果分母是100的因数,可根据分数的基本性质,化成分母是100的分数,再改写成百分数。
○3、根据分数和除法的关系,用分子除以分母,除不尽时保留三位小数,再化成百分数。
3、常见的分数、小数和百分数的互化21==50% 41==25% 43==75% 51==20% 52==40% 53==60% 54==80% 81==12 83==% 85==% 87==% 201==5% 4、在含有百分数、小数、分数的混合大小比较或解方程时,要根据题目的情况,把数据类型统一,以便于计算。
一般情况下,都要把百分数化成小数或分数。
三、用百分数解决问题1、常见的百分率的计算方法达标率=学生总人数达标学生人数×100% 发芽率=种子总数发芽种子数×100% 出勤率=学生总人数出勤人数×100% 合格率 =产品总数合格的产品数×100% 出粉率=小麦的重量粉的重量×100% 出油率=花生的重量油的重量×100% 出米率=稻谷的重量米的重量×100% 成活率=种植总数成活的数量×100% 命中率=投篮总数命中的次数×100% 含盐率=盐水的重量盐的重量×100% 2、“A 是B ”或“A 占B ”或“A 相当于B ”的百分之几列式均为:BA ×100%。
北师大版六年级数学百分数知识点:思维导图+知识梳理+例题精讲+易错专练
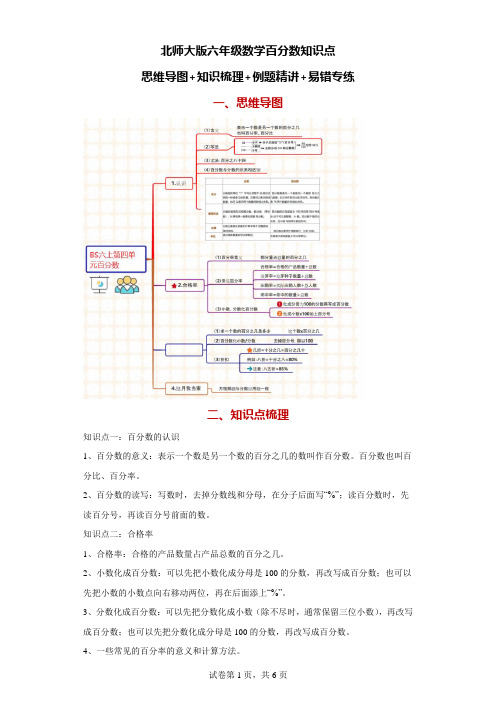
北师大版六年级数学百分数知识点思维导图+知识梳理+例题精讲+易错专练一、思维导图二、知识点梳理知识点一:百分数的认识1、百分数的意义:表示一个数是另一个数的百分之几的数叫作百分数。
百分数也叫百分比、百分率。
2、百分数的读写:写数时,去掉分数线和分母,在分子后面写“%”;读百分数时,先读百分号,再读百分号前面的数。
知识点二:合格率1、合格率:合格的产品数量占产品总数的百分之几。
2、小数化成百分数:可以先把小数化成分母是100的分数,再改写成百分数;也可以先把小数的小数点向右移动两位,再在后面添上“%”。
3、分数化成百分数:可以先把分数化成小数(除不尽时,通常保留三位小数),再改写成百分数;也可以先把分数化成分母是100的分数,再改写成百分数。
4、一些常见的百分率的意义和计算方法。
发芽率:发芽的种子数量占种子总数的百分之几。
发芽率=发芽种子数种子总数出米率:米的质量占稻谷质量的百分之几。
出米率=米的质量稻谷的质量出勤率:出勤人数占应出勤人数的百分之几。
出勤率=出勤人数应出勤人数及格率:及格人数占考试人数的百分之几。
及格率=及格人数考试人数知识点三:营养含量1、百分数化成小数:把百分号去掉,同时把小数点向左移动两位(位数不够时,用“0”补足)。
2、百分数化成分数:把百分数改写成分母是100的分数,能约分的要约成最简分数。
3、“求一个数的百分之几是多少”的问题的解题方法:与“求一个数的几分之几是多少”的问题的解题方法相同,都用乘法计算,即用这个数乘百分之几。
4、在计算时,要根据具体情况,先把百分数转化成分数或小数,再计算。
知识点四:这月我当家(解决实际问题)1、百分数的应用题与分数应用题的解题思路相同,都要找准单位“1”,单位“1”已知,求部分量,可以直接用乘法计算。
2、“已知一个数的百分之几是多少,求这个数”的解题方法:可以根据等量关系式“单位‘1’×百分之几=已知量”列方程解答。
3、“已知一个数的百分之几是多少,求这个数”也可以用除法计算。
北师大版六年级数学上册-第四章-百分数的认识--知识点总结+章节练习+单元测验

第四单元 百分数的认识知识点归纳:1、百分数的意义像84%,28%,2.5%……这样的数叫作百分数,表示一个数是另一个数的百分之几。
百分数也叫百分比、百分率。
百分数只表示两个数之间的关系,不能带单位名称,它表示的是一个比值。
2、百分数的读法和写法①百分数的读法:百分数的读法与分数的读法相同,但百分数读作“百分之几”,不读作“一百分之几”。
②百分数的写法:百分数相当于分母是100的分数,但百分数不能写成分数的形式,而是在分子的后面加上百分号(%)来表示.3、百分数和分数的区别①意义不同百分数只表示一个数是另一个数的百分之几。
它只能表示两个数之间的倍数关系,并不是表示某一个具体数量,所以百分数不能带单位。
分数不仅可以表示两个数之间的倍数关系,还可以表示一定的数量,所以分数表示数量时可以带单位.②写法不同百分数通常不写成分数形式,而在原来的分子后面加上百分号“%”来表示。
分数的最后结果中的分子只能是整数,计算结果不是最简分数的要化成最简分数。
百分数的最后结果中的分子可以是整数,也可以是小数。
如:18%,16.7%,180%4、小数、分数、百分数的互化①把小数化成百分数的方法:先把小数点向右移动两位,再在数的后面直接添上“%”,如0.25=25% ②把分数化成百分数的方法:可以先把分数化成分母是100的分数,再改写成百分数,如53=0.6=60%(除不尽的保留三位小数)。
③把百分数化成小数的方法:先把“%”去掉,同时把小数点向左移动两位,当移动的位数不够时,要添0补位。
第7页④把百分数化成分数的方法:先把百分数改写成分母是100的分数,能约分的要约分成最简分数.当百分数的分子是小数时,要要根据分数的基本性质把分子和分母同时扩大相同的倍数,把分子变成整数后能约分的再约分。
5、求一个数是另一个数的百分之几的方法求一个数是另一个数的百分之几的方法与求一个数是另一个数的几分之几的方法相同,就是用这个数除以另一个数,除不尽时通常保留三位小数,然后把小数点向右移动两位,再在数的后面加上%6、求百分率的方法:百分率一般是指部分占总体的百分之几。
百分数的知识点

百分数的知识点百分数作为数学学科中的一个重要知识点,是我们日常生活中经常用到的一种计算方式。
它表示的是某个数值与100的比值,通常用百分号“%”来表示。
百分数在我们的生活中应用极广,因此,掌握百分数的基本概念及其计算方法对于我们学习和工作是非常有必要的。
一、百分数的基本概念1.定义:百分数是一个分数,表示百分数与百分之一的关系。
2.百分数的百分数:百分数的百分数是原数值乘以100,表示为“%×%”。
3.数值的比较:比较两个数值的大小时,应该将它们都转化为百分数,然后再进行比较。
4.基数变化:当基数改变时,相应的百分数也会发生变化。
如果基数变为原来的a倍,则原来的百分数将变为原来的1/a倍。
5.计算规则:百分数的计算方法与百分数的“转化”相同,但是计算时需要根据公式进行处理。
具体方法如下:①将百分数分子中的数值除以分母100,得到一个小数。
②将这个小数乘以基数。
③得到的结果即为相应的百分数。
二、百分数的应用1.百分数的转化:当我们要将一个数值表示为百分数时,可以直接在数值后面加上一个百分号“%”。
2.利率计算:当我们要计算利率时,我们需要将利率转化为百分数。
例如,利率为5%,则转化为小数就是0.05。
3.增减比的计算:当我们要计算一个数的增加量或减少量时,可以将增加量或减少量与原数相除,然后再将结果乘以100,并加上一个正负号(正表示增加,负表示减少)就是相应的增减比。
4.百分数的均值:当我们要计算若干百分数的均值时,我们需要将这些百分数转化为原数,然后求出这些原数的平均值,最后再将平均值转化为百分数。
5.统计数据的百分数:当我们要计算统计数据的百分数时,我们需要将某一类别的数据数量除以总数,然后将结果乘以100,并保留小数后两位即可得到该类别的百分数。
三、常见的错误在计算百分数时,我们需要注意以下常见错误:1.在百分数的计算过程中,经常出现小数点位置错位的问题。
这时,我们需要注意小数点的位置,并将数值扩大或缩小以消除误差。
百分数知识点总结

百分数知识点总结百分数是我们生活中经常使用的一种表示方式,它能够准确地描述一定范围内的比例关系。
在学习和工作中,了解百分数的含义和应用十分重要。
本文将对百分数的定义、计算、应用以及常见的数学技巧进行总结和归纳。
一、百分数的定义百分数是以百为基数的比例,用百分号“%”表示。
百分数可以表示一个比例关系,即一个数与100的乘积。
例如,80%表示的是数80与100的乘积,即80% = 80/100 = 0.8。
二、百分数的计算1. 百分数转小数:将百分数除以100,得到的结果就是对应的小数。
例如,60% = 60/100 = 0.6。
2. 百分数转分数:将百分数的数值除以100并化为最简分数形式。
例如,25% = 25/100 = 1/4。
3. 小数转百分数:将小数乘以100,并在结果末尾加上百分号。
例如,0.75 = 0.75 × 100% = 75%。
4. 分数转百分数:将分数化为小数,然后再转化为百分数。
例如,3/5 = 0.6 = 0.6 × 100% = 60%。
三、百分数的应用1. 百分数在商业中的应用:百分数在销售、营销和金融领域中有着广泛的应用。
例如,折扣率可以用百分数表示,帮助消费者了解商品打折程度。
2. 百分数在统计中的应用:百分数可以用来描述一个群体中某种特征的比例。
例如,对某个调查对象的回答进行统计时,可以使用百分数来表示各个选项的比例。
3. 百分数在日常生活中的应用:百分数可以用来描述各种比例关系,例如考试成绩、人口增长率、物品的折旧率等等。
四、百分数的数学技巧1. 计算百分数的增长或减少量:如果需要求某个数的增长或减少量,可以先计算出增长或减少的百分比,然后再将该百分比应用到原始数值上,得到最终结果。
2. 计算百分数的乘除法:计算百分数的乘法可以简单地将原始数值乘以百分数所对应的小数;计算百分数的除法可以将原始数值除以100,再乘以百分数所对应的小数。
3. 百分数之间的比较:当需要比较两个百分数的大小时,可以将它们分别转化为小数,然后进行比较。
百分数的认识知识点

百分数的认识知识点 Prepared on 24 November 2020百分数的认识一、百分数的意义和写法1、百分数的意义:百分数表示一个数是另一个数的百分之几。
是指两个数的比,因此也叫百分率或百分比。
2、百分数的写法:百分数通常不写成分数形式,而在原来的分子后面加上“%”来表示。
3、百分数和分数的联系和区别:(1)联系:都可以表示两个数的倍比关系。
(2)区别:○1、百分数只表示两个数的倍比关系,不能表示具体的量,所以不能带单位,而分数既可以表示两个数的关系,又可以表示具体的量,所以表示具体的量时可以带单位。
○2、百分数的分子可以是整数,也可以是小数,而分数的分子只能是除0以外的自然数。
二、百分数和分数、小数的互化1、百分数与小数的互化(1)百分数化小数:把分子的小数点向左移动两位,同时去掉百分号。
(2)小数化百分数:把小数的小数点向右移动两位,同时添上百分号。
2、百分数与分数的互化(1)百分数化分数:先把百分数改写成分母是100的分数,能约分的要约成最简分数。
如果百分数的分子是小数时,在改写成分母是100的分数后,可根据分数的基本性质,化成分子是整数的分数,然后能约分的要约成最简分数。
(2)分数化百分数:○1、如果是常见的分数,可直接化成小数,再化成百分数。
○2、如果分母是100的因数,可根据分数的基本性质,化成分母是100的分数,再改写成百分数。
○3、根据分数和除法的关系,用分子除以分母,除不尽时保留三位小数,再化成百分数。
3、常见的分数、小数和百分数的互化21==50% 41==25% 43==75% 51==20% 52==40% 53==60% 54==80% 81==12 83==% 85==% 87==% 201==5% 4、在含有百分数、小数、分数的混合大小比较或解方程时,要根据题目的情况,把数据类型统一,以便于计算。
一般情况下,都要把百分数化成小数或分数。
三、用百分数解决问题1、常见的百分率的计算方法达标率=学生总人数达标学生人数×100% 发芽率=种子总数发芽种子数×100% 出勤率=学生总人数出勤人数×100% 合格率 =产品总数合格的产品数×100% 出粉率=小麦的重量粉的重量×100% 出油率=花生的重量油的重量×100% 出米率=稻谷的重量米的重量×100% 成活率=种植总数成活的数量×100% 命中率=投篮总数命中的次数×100% 含盐率=盐水的重量盐的重量×100% 2、“A 是B ”或“A 占B ”或“A 相当于B ”的百分之几列式均为:BA ×100%。
教学知识点百分数的概念和应用

教学知识点百分数的概念和应用百分数是数学中常用的一种表示形式,用来表示一个数相对于整体的占比或比率。
在教学中,掌握百分数的概念和应用是十分重要的。
本文将对百分数的概念进行解析,并探讨其在实际问题中的应用。
一、百分数的概念百分数是将一个数表示为百分之一的形式,通常用百分号“%”表示。
百分号可以理解为百分数的单位,它表示一个数与整体相比的千分之一。
例如,50%等于50/100,即1/2,表示整体中的一半。
百分数的计算很简单,只需将所表示的数除以100即可。
例如,75%等于75/100,即0.75。
二、百分数的应用1. 比例与百分数在比例中,百分数常常用来表示比例关系的大小。
例如,如果班级里男生有60人,女生有40人,我们可以用百分数来表示男女生的比例。
男生人数的百分数为60%,女生人数的百分数为40%。
2. 增减百分比百分数还可以用来表示数量的增减比例。
例如,某商品的价格在一年内上涨了20%,这意味着价格增加了原来的20%。
同样地,如果价格下降了20%,则表示价格减少了原来的20%。
3. 流量和比率在统计和调查中,百分数常用来表示各种现象的占比或比率。
例如,一份市场调查报告显示,85%的受访者表示满意,15%的受访者表示不满意。
这个百分数的结果可以帮助我们了解受访者的整体反馈。
4. 成绩和评级在学校教学中,百分数常用来表示学生的考试成绩和评级。
例如,一位学生的数学成绩是85分,这可以转化为85%的百分数来表示其在该门课程中的得分比例。
5. 利率和财务百分数还常用于表示利率和财务方面的数据。
例如,银行存款的年利率是3%意味着一年的利息收入是存款金额的3%。
三、百分数的计算方法计算百分数需要遵循一定的计算方法。
以下是两种常用的计算方式:1. 百分数到小数和分数的转换:将百分数除以100,得到的结果是相应的小数形式。
例如,25%可以转换为0.25或1/4。
2. 小数和分数到百分数的转换:将小数或分数乘以100,并加上百分号“%”。
小学数学百分数知识点总结

小学数学百分数知识点总结百分数是小学数学中的重要概念之一,它在日常生活和数学学习中都有着广泛的应用。
理解和掌握百分数的相关知识,对于提高数学素养和解决实际问题具有重要意义。
接下来,让我们一起深入学习小学数学百分数的知识点。
一、百分数的定义百分数表示一个数是另一个数的百分之几,也叫百分率或百分比。
百分数通常不写成分数的形式,而采用符号“%”(叫做百分号)来表示。
例如,45% 表示 45 是 100 的 45%。
二、百分数与分数、小数的互化1、百分数与小数的互化小数化成百分数:把小数点向右移动两位,同时在后面添上百分号。
例如,025 化成百分数是 25%。
百分数化成小数:把百分号去掉,同时把小数点向左移动两位。
例如,25% 化成小数是 025。
2、百分数与分数的互化分数化成百分数:通常先把分数化成小数(除不尽时,通常保留三位小数),再把小数化成百分数。
例如,3/4 化成小数是 075,再化成百分数是 75%。
百分数化成分数:把百分数写成分母是 100 的分数,再约分化简。
例如,75%可以写成 75/100,约分后是 3/4。
三、百分数的简单应用1、求一个数是另一个数的百分之几用一个数除以另一个数,再乘以 100%。
例如,甲数是 20,乙数是50,甲数是乙数的百分之几?列式为:(20÷50)×100% = 40%2、求一个数的百分之几是多少用这个数乘以百分数。
例如,50 的 20%是多少?列式为:50×20% = 103、已知一个数的百分之几是多少,求这个数用已知的数量除以对应的百分数。
例如,一个数的 30%是 15,求这个数。
列式为:15÷30% = 50四、百分数在生活中的应用1、折扣问题商品打折出售时,折扣是指现价是原价的百分之几。
几折就表示十分之几,也就是百分之几十。
例如,打八折出售,就是按原价的 80%出售。
2、税率问题纳税是根据国家税法的有关规定,按照一定的比率把集体或个人收入的一部分缴纳给国家。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
百分数的认识
一、百分数的意义和写法
1、百分数的意义:百分数表示一个数是另一个数的百分之几。
是指两个数的比,因此也叫百分率或百分比。
2、百分数的写法:百分数通常不写成分数形式,而在原来的分子后面加上“%”来表示。
3、百分数和分数的联系和区别:
(1)联系:都可以表示两个数的倍比关系。
(2)区别:
○
1、百分数只表示两个数的倍比关系,不能表示具体的量,所以不能带单位,而分数既可以表示两个数的关系,又可以表示具体的量,所以表示具体的量时可以带单位。
○
2、百分数的分子可以是整数,也可以是小数,而分数的分子只能是除0以外的自然数。
二、百分数和分数、小数的互化
1、百分数与小数的互化
(1)百分数化小数:把分子的小数点向左移动两位,同时去掉百分号。
(2)小数化百分数:把小数的小数点向右移动两位,同时添上百分号。
2、百分数与分数的互化
(1)百分数化分数:先把百分数改写成分母是100的分数,能约分的要约成最简分数。
如果百分数的分子是小数时,在改写成分母是100的分数后,可根据分数的基本性质,化成分子是整数的分数,然后能约分的要约成最简分数。
(2)分数化百分数:
○
1、如果是常见的分数,可直接化成小数,再化成百分数。
○
2、如果分母是100的因数,可根据分数的基本性质,化成分母是100的分数,再改写成百分数。
○
3、根据分数和除法的关系,用分子除以分母,除不尽时保留三位小数,再化成百分数。
3、常见的分数、小数和百分数的互化
21==50% 41==25% 4
3==75% 51==20% 52==40% 53==60% 5
4==80% 81==12 83==% 85==% 87==% 20
1==5% 4、在含有百分数、小数、分数的混合大小比较或解方程时,要根据题目的情况,把数据类型统一,以便于计算。
一般情况下,都要把百分数化成小数或分数。
三、用百分数解决问题
1、常见的百分率的计算方法
达标率=学生总人数达标学生人数×100% 发芽率=种子总数
发芽种子数×100% 出勤率=学生总人数出勤人数×100% 合格率 =产品总数
合格的产品数×100% 出粉率=小麦的重量粉的重量×100% 出油率=花生的重量
油的重量×100% 出米率=稻谷的重量米的重量×100% 成活率=种植总数
成活的数量×100% 命中率=
投篮总数命中的次数×100% 含盐率=盐水的重量盐的重量×100% 2、“A 是B ”或“A 占B ”或“A 相当于B ”的百分之几?列式均为:
B
A ×100%。
3、已知一个数的百分之几是A ,求这个数:A ÷百分之几。
4、求一个数比另一个数增加(或减少)百分之几的方法:
(1)先求出增加(或减少)的具体量,再除以单位“1”的量。
(2)如果是增加,用第一个量除以单位“1”的量,商再减去1。
如果是减少,用1减去第一个量除以单位“1”的量的商。
5、求增加(或减少)之后的数的方法: (1)先求出增加(或减少)的具体量,再用已知量加(或减)具体量。
(2)如果是增加,用已知量乘以1加百分率的和。
如果是减少,用已知量乘以1减百分率的差。
6、求增加(或减少)之前的数的方法:
如果是增加,用已知量除以1加百分率的和,如果是减少,用已知量除以1键百分率的差。
四、折扣、纳税、利率
(一)折扣
1、折扣:按原价的百分之几出售,叫做折扣,通称“打折”。
如八折就表示现价是原价的80%。
2、几折表示十分之几,也就是百分之几十。
如八折=10
8=80%,九五折==95%。
3、一成是十分之一,也就是10%,六成五就是十分之六点五,也就是65%。
4、现价=原价×折扣,原价=现价÷折扣。
