积和商的变化规律练习题
积和商的变化规律
例1 两个数相乘，一个 因数扩大3倍，要使积 扩大9倍，另一个因数 应该怎样变化？
例 2 两数相乘，如果一个 因数扩大3倍，另一个因
数缩小12倍，积将有什么 变化？
例3 两数相乘，积是48。如
果一个因数扩大2倍，另一 个因数相乘，如果一 个因数增加3，积就增加 36，另一个因数减少5， 积就减少100，问原来两 个乘数的积是多少？
例5 两数相除，被除数 扩大30倍，除数缩小6 倍，商将怎样变化？
例6 两数相除，如果被除数
扩大30倍，要使商扩大60 倍，除数应该怎样变化？
例7 两数相除，商是13，如 果被除数扩大10倍，除数缩 小6倍，商应该怎样变化？ 商变为多少？
例8 两数相除，商是6，余 数是30，如果被除数和除 数同时扩大10倍，商是多 少？余数是多少？
(完整版)和差积商的变化规律
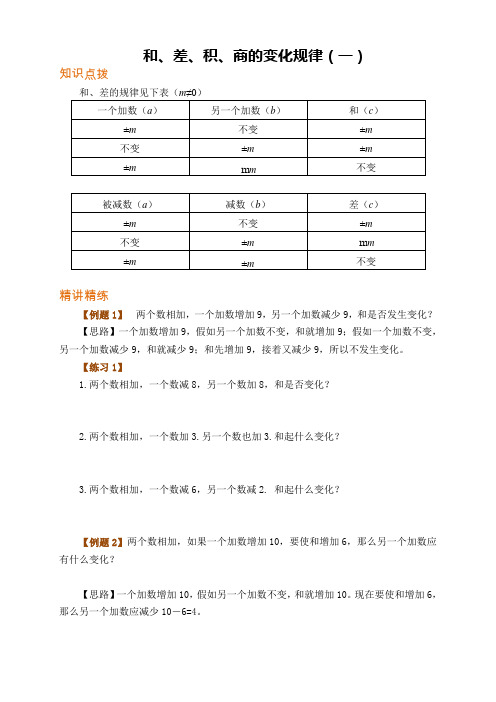
和、差、积、商的变化规律（一）知识点拨和、差的规律见下表（m≠0）精讲精练【例题1】两个数相加，一个加数增加9，另一个加数减少9，和是否发生变化？【思路】一个加数增加9，假如另一个加数不变，和就增加9；假如一个加数不变，另一个加数减少9，和就减少9；和先增加9，接着又减少9，所以不发生变化。
【练习1】1.两个数相加，一个数减8，另一个数加8，和是否变化？2.两个数相加，一个数加3.另一个数也加3.和起什么变化？3.两个数相加，一个数减6，另一个数减2. 和起什么变化？【例题2】两个数相加，如果一个加数增加10，要使和增加6，那么另一个加数应有什么变化？【思路】一个加数增加10，假如另一个加数不变，和就增加10。
现在要使和增加6，那么另一个加数应减少10－6=4。
【练习2】1.两个数相加，如果一个加数增加8，要使和增加15，另一个加数应有什么变化？2.两个数相加，如果一个加数增加8，要使和减少15，另一个加数应有什么变化？3.两个数相加，如果一个加数减少8，要使和减少8，另一个加数应有什么变化？【例题3】两数相减，如果被减数增加8，减数也增加8，差是否起变化？【思路】被减数增加8，假如减数不变，差就增加8；假如被减数不变，减数增加8，差就减少8。
两个数的差先增加8，接着又减少8，所以不起什么变化。
【练习3】1.两数相减，被减数减少6，减数也减少6，差是否起变化？2.两数相减，被减数增加12.减数减少12.差起什么变化？3.两数相减，被减数减少10，减数增加10，差起什么变化？【例题4】两数相乘，如果一个因数扩大8倍，另一个因数缩小2倍，积将有什么变化？【思路】如果一个因数扩大8倍，另一个因数不变，积将扩大8倍；如果一个因数不变，另一个因数缩小2倍，积将缩小2倍。
积先扩大8倍又缩小2倍，因此，积扩大了8÷2=4倍。
【练习4】1.两数相乘，如果一个因数缩小4倍，另一个因数扩大4倍，和是否起变化？2.两数相乘，如果一个因数扩大3倍，另一个因数缩小12倍，积将有什么变化？3.两数相乘，如果一个因数扩大3倍，另一个因数扩大6倍，积将有什么变化？【例题5】两数相除，如果被除数扩大4倍，除数缩小2倍，商将怎样变化？【思路】如果被除数扩大4倍，除数不变，商就扩大4倍；如果被除数不变，除数缩小2倍，商就扩大2倍。
人教版四年级上册《商的变化规律》
商的变化规律
复习导入
1、口算练习
60÷30＝2 400÷50＝ 8
100÷20＝ 5 80÷4＝ 20
250÷50＝5 320÷40＝8
2、你还记得积的变化规律吗？ 积的变化规律：两个数相乘，一个因数不变，另一个因数乘（或除以） 几（0除外），积也乘（或除以）几。
积不变的规律：两个数相乘，一个因数乘（或除以）几（0除外），另一 个数除以（或乘）相同的数，积不变。
20 ×20
什么数没有变化?什么数有变化?
÷2
÷2
③ 320 ÷ 8 = 40
被除数 乘 几， 商也 乘 几。 除数不变，
被除数 除以 几， 商也 除以几。
商的变化规律
规律一 除数不变，被除数乘或除以几(0除外)，商也乘或除以几。
被除数 ÷除数 = 商
扩大（×） 不 缩小（÷） 变
扩大（×） 缩小（÷）
你知道悟空为什么大笑吗？
商的变化规律
仔细观察这些算式：
从 ① 6÷3 = 2
上
×10 ×10
往 ② 60÷30 = 2
下
观
×10 ×10
察 ③ 600÷300 = 2
从 下 往 上 观 察
×10
×10
④ 6000÷3000 = 2
你发现了什么规律？
商的变化规律
1 从上往下观察：被除数和除数都乘一个相同的数，商（ 不变）。 2 从下往上观察：被除数和除数都除以一个相同的数，商（不变 ）。
悟空西天取经回来后，给孩儿们带来了礼物——桃子，分桃 子时，悟空说“把6个桃子平均分给3只猴子吧!”孩儿们连连 摇头“太少了!太少了!”孙悟空就说“那好吧，把60个桃子平均 分给30只猴子，怎么样？”小猴们还是不情愿，孙悟空就说 “干脆把600个桃子平均分给300只猴子吧？”猴儿们得寸进 尺，试探的说“大王，再多给点行不行啊？”悟空一拍胸脯， 显示出慷慨大度的样子“那就把6000个桃子平均分给3000只 猴子，你们总该满意了吧？”小猴子们笑了，孙悟空也笑了。
(完整版)商的变化规律练习题
积的变化规律练习题一、根据已知算式,直接写出下面各题的得数.18×24=432 105×45=4725（18÷2）×(24×2）= (105÷5)×（45×5）=（18×2）×（24÷2)= （105×3）×（45÷3）= 24×75＝1800 36×104＝3744（24○6）×（75×6)＝1800 （36×4）×（104○4）＝3744(24○3)×(75○□）＝1800 (36○□）×（104○□）＝374415×24=36015×72=( )30×24=（） 5×24=（ ) 15×12=( ）15×（24×）=3600 15×（24÷10）=（）12×20=240（12×6)×（20×5）=（ ) （12÷3）×（20÷4)=（）（12×）×（20×）=4800 （12÷）×（20÷）=40二、选择。
1．一个因数扩大5倍，另一个因数不变，积（）。
A、缩小5倍B、不变C、扩大5倍2．一个因数扩大5倍，另一个因数缩小5倍，积（）。
A、缩小5倍 B、不变 C、扩大5倍3．两数相乘，一个因数扩大2倍，另一个因数扩大3倍，那么积（）。
A、不变B、扩大5倍C、扩大6倍4．两个因数的积是60，这时一个因数缩小4倍，另一个因数不变,现在的积是( )A、240B、60C、155．一个长方形的面积为12平方米、把长扩大到原来的3倍，宽不变,扩大后的面积是（ )6．两个因数的积是100，把其中一个因数扩大到原来的3倍,另一个因数不变，积是（）7．一个正方形的面积为12平方米、把边长扩大到原来的3倍，，扩大后的面积是（ )8．两个因数的积是100，把其中一个因数扩大到原来的3倍，另一个因数也扩大到原来的3倍,积是（）9．两个因数的积是100，把其中一个因数扩大到原来的3倍,另一个因数也缩小到原来的3倍，积是（）10．一个因数不变,把其中另一个因数扩大到原来的3倍，积是90，原来两个因数的积是( )11．一个因数扩大到原来的3倍，另一个因数也扩大到原来的3倍,积是90，原来两个因数的积是（）12．一个因数扩大到原来的3倍，另一个因数缩小到原来的3倍，积是90,原来两个因数的积是（）。
积、商的变化规律(含答案)-
积、商的变化规律同学们好，在上一讲我们研究了和、差的变化规律，今天这一讲我们来研究，积、商的变化规律。
请同学们填出下表，说出什么发生了变化，积、商有没有发生变化，如果有变化是怎样变的，你能从中得出什么结论吗？规律：两个因数相乘，被乘数乘以（或除以）一个不为0的数，乘数不变，积也乘以（或除以）同一个数。
两个因数相乘，被乘数不变，乘数乘以（或除以）一个不为0的数，积也乘以（或除以）同一个数。
两个因数相乘，被乘数乘以（或除以）一个不为0的数，乘数同时除以（或乘以）同一个数，积不变。
规律：在除法里被除数乘以（或除以）一个不为0的数，除数不变，商也乘以（或除以）同一个数。
被除数不变，除数乘以（或除以）一个不为0的数，商反而除以（或乘以）同一个数。
被除数乘以（或除以）一个不为0的数，除数同时乘以（或除以）相同的一个数，商不变。
例1. 2584⨯=⨯⨯÷=⨯=()()254844100212100分析与解答：根据积的变化规律，一个因数扩大多少倍，另一个因数反而缩小相同的倍数，积不变的规律，使25×4，使84÷4，转化为100×21，这就很快计算出结果是2100。
例2. 12588⨯=⨯⨯÷=⨯=()()125888810001111000例3. 2250125÷=⨯÷⨯=÷=()()22508125818000100018分析与解答：根据商的变化规律，被除数和除数同时乘以或除以一个数（不为0）商不变的规律，可以使2250×8，使125×8，转化为18000÷1000，这样就能很快算出结果是18。
【模拟试题】（答题时间：45分钟）（一）尝试体验 1. 填一填1272244⨯⨯⨯⨯⨯⎫⎬⎪⎪⎪⎭⎪⎪⎪=÷÷÷÷÷⎫⎬⎪⎪⎪⎭⎪⎪⎪=()()()()()()()()()()()()()()()()()() 完成上面两组题后，每组后面的4个题与第一算式比较各部分是怎样变化的，才保证了使它们的和、差、积、商没发生变化？ 2. 利用积、商变化规律，计算下面各题。
四年级数学上册积和商的变化规律练习题
四年级数学上册积和商的变化规律练习题Prepared on 21 November 2021第16周周练积的变化规律一、填空题。
1.写得数并发现规律。
16×17=32×17=16×34=48×17=16×51=64×17=我发现了：一个因数相同，另一个因数（），积也（）。
请在上面的横线上举一个例子验证你的发现。
20×18=20×18=10×18=20×9=5×18=20×3=我发现了：一个因数相同，另一个因数（），积也（）。
请在上面的横线上举一个例子验证你的发现。
2.根据以上的发现填空。
（1）42×56=235242×112=（）21×56=（）42×28=（）7×56=（）（2）5×14=705×28=（）5×42=（）5×56=（）5×70=（）3.一个因数不变，另一个因数乘几或除以几（0除外），积也（）。
4.两个因数的积是360，如果一个因数除以3，另一个因数不变，积变为（）。
5.两个因数相乘，一个因数乘6，另一个因数不变，那么积（）。
6.两个因数相乘的积是5600，如果一个因数不变，另外一个因数除以10，那么积是（）。
7.两个数相乘是75，如果一个因数乘7，另一个因数除以7，积是（）。
8.已知A×B=400，如果A乘3，则积是（），如果B除以5，则积是（）。
9.两数相乘，如果一个因数缩小5倍，另一个因数扩大5倍，积()。
10.两数相乘，如果一个因数扩大8倍，另一个因数缩小2倍，积()。
11.两个数相乘，一个因数乘10，另一个因数也乘10，积（）。
12.两个因数的积是420，如果一个因数不变，另一个因数乘8，积是（）。
13.两个数相乘的积是160，如果一个因数除以2，另一个因数也除以2，积是（）。
积和商“变与不变”规律及练习(精品文档)_共5页
积和商“变与不变”规律㈠、积的变化规律：⑴、一个因数不变，另一个因数乘（或除以）几，积就相应的乘（或除以）几。
字母表示：如果a×b=c ，则(a×3)×b=c×3举例：a×b=12 如果(a×3)则积就是12×3=36.⑵、一个数乘一个比1大的数，积比原数大；⑶、一个数乘一个比1小的数，积比原数小。
㈡、积不变规律：一个因数乘（或除以）几，另一个因数相应的除以(或乘)几，积不变。
字母表示：如果a×b=c 则（a×5）×（b÷5）=c㈢、商的变化规律：⑴被除数不变，除数乘或除以几，商就相应的除以或乘几。
字母表示：如果a÷b=c ，则a÷（b×3）=c÷3本文档下载后根据实际情况可编辑修改使用举例：a÷b=12 如果(b×3)则商就是12÷3=4⑵除数不变，被除数乘或除以几，商就相应的乘或除以几。
字母表示：如果a÷b=c ，则(a×3)÷b=c×3举例：a÷b=12 如果(a×3)则商就是12×3=36.被除数大于除数，商就大于1；被除数小于除数，商就小于1.一个数除以一个比1大的数，商比被除数要小；一个数除以一个比1小的数，商比被除数要大。
㈣、商不变规律：被除数和除数同时乘或除以几，商不变。
1、根据78×12＝936，填写下面各题的结果。
7.8×12＝（） 0.78×12＝（） 7.8×0.12＝（） 0.78×（）＝936本文档下载后根据实际情况可编辑修改使用2、根据414÷18＝23，填写下面各题的结果。
4.14÷1.8＝（） 4140÷1.8＝（） 0.414÷0.18＝（） 41.4÷18＝（）3、根据45×63＝2835，填写下面各题的结果。
积和商的变化规律练习题
积和商的变化规律1、发现规律直接写得数。
16×17=272 32×17= 32×34=16×34= 48×17= 8×34=16×51= 64×17= 4×68=2、发现规律直接写得数。
2000÷25=80（2000×2）÷（25×2）= （2000×15）÷（25×15）=（2000÷5）÷（25÷5）= （2000÷18）÷（25÷18）=（2000÷5）÷25= （2000×20）÷25=2000÷（25÷5）= 2000÷（25×5）=（2000÷5）÷（25×2）= （2000×5）÷（25÷2）=（2000÷2）÷（25÷4）= （2000×2）÷（25×8）=3、两个因数的积是360，如果一个因数除以3，另一个因数不变，积变为（）。
4、两个因数相乘，一个因数乘6，另一个因数不变，那么积（）。
5、两个因数相乘的积是5600，如果一个因数不变，另外一个因数除以10，那么积是（）。
6、两个数相乘是75，如果一个因数乘7，另一个因数除以7，积是（）。
7、已知A×B=400，如果A乘3，则积是（），如果B除以5，则积是（）。
8、两个数相乘，一个因数乘10，另一个因数也乘10，积（）。
9、两个因数的积是420，如果一个因数不变，另一个因数乘8，积是（）。
10、两个数相乘的积是160，如果一个因数除以2，另一个因数也除以2，积是（）。
11、两数相除的商是15，如果被除数、除数同时扩大10倍，商是（）。
四年级数学上册积和商的变化规律练习题
第16周周练积的变化规律一、填空题。
1.写得数并发现规律。
16×17= 32×17=16×34= 48×17=16×51= 64×17=我发现了：一个因数相同，另一个因数（），积也（）。
请在上面的横线上举一个例子验证你的发现。
20×18= 20×18=10×18= 20×9=5×18= 20×3 =我发现了：一个因数相同，另一个因数（），积也（）。
请在上面的横线上举一个例子验证你的发现。
2.根据以上的发现填空。
（1）42×56=2352 42×112=（）21×56=（）42×28=（）7×56=（）（2）5×14=70 5×28=（）5×42=（）5×56=（）5×70=（）3.一个因数不变，另一个因数乘几或除以几（0除外），积也（）。
4.两个因数的积是360，如果一个因数除以3，另一个因数不变，积变为（）。
5.两个因数相乘，一个因数乘6，另一个因数不变，那么积（）。
6.两个因数相乘的积是5600，如果一个因数不变，另外一个因数除以10，那么积是（）。
7.两个数相乘是75，如果一个因数乘7，另一个因数除以7，积是（）。
8.已知A×B=400，如果A乘3，则积是（），如果B除以5，则积是（）。
9.两数相乘，如果一个因数缩小5倍，另一个因数扩大5倍，积( )。
10.两数相乘，如果一个因数扩大8倍，另一个因数缩小2倍，积( )。
11.两个数相乘，一个因数乘10，另一个因数也乘10，积（）。
12.两个因数的积是420，如果一个因数不变，另一个因数乘8，积是（）。
13.两个数相乘的积是160，如果一个因数除以2，另一个因数也除以2，积是（）。
14.芳芳在计算乘法时，把一个因数末尾多写了1个0，结果得到800，正确的积是应该是（）。
浙江省期末试题汇编—09商的变化规律、积的变化规律(试题)-五年级上册数学人教版
浙江省2022-2023学年期末试题汇编—09商的变化规律、积的变化规律（试题）-五年级上册数学人教版一．选择题（共4小题）1．（2022秋•上虞区期末）计算“7.65÷0.85”时，可以把除数转化成85，同时，把被除数扩大到原来的100倍。
这样算的依据是（ ）A．除法的性质B．小数的性质C．积不变规律D．商不变的性质2．（2022秋•瑞安市期末）下列算式中，与24×96结果不相等的是（ ）A．240×9.6B．2.4×960C．2.4×9.6D．（24×2）×（96÷2）3．（2022秋•平阳县期末）a÷0.8（a＞0）的商一定（ ）A．大于a B．小于a C．等于a D．无法确定4．（2022秋•慈溪市期末）下列算式中，如果△不为0，得数最大的是（ ）A．△÷1.5B．△÷0.5C．△×1.1D．△×0.9二．填空题（共10小题）5．（2022秋•上虞区期末）在横线里填上“＞”“＜”或“＝”。
（1）7 7.4（2）2.8÷1.5 2.8×1.5（3）2.4÷0.12 2.4÷1.2（4）3.72÷0.25 3.72×4 6．（2022秋•上虞区期末）根据214×46＝9844，可知2.14×4.6＝ ，984.4÷0.46＝ 。
7．（2022秋•嘉善县期末）根据78×25＝1950，直接写出下面算式的得数。
7.8×2.5＝ 19.5÷0.78＝ 1.95÷2.5＝ 8．（2022秋•奉化区期末）根据36×1.2＝43.2，直接写出下面各题的结果。
3.6×1.2＝ 360×0.12＝ 43.2÷3.6＝ 4.32÷0.12＝ 9．（2022秋•奉化区期末）比一比，在横线上填上“＞”、“＜”或“＝”。
积的变化规律和商的变化规律
一、积的变化规律1、一个因数不变，另一个因数乘几或除以几（0除外），积也乘几或除以几。
2、两个数相乘，一个因数乘或除以几（0除外），另一个因数除以或乘相同的数，则它们的乘积不变。
（1）42×5= （2）48×16=76842×15= （48×4）×（16÷4）=420×15= （48÷8）×（16×8）=840×15= （48×5）×（16○□）=768（3）7本作业本摞起来高25毫米，全班56本作业本摞起来有多高？（4）一个宽为9米的长方形菜地，面积是252平方米，如果把这块长方形菜地的宽增加到36米，长不变，扩建后的面积是多少？二、商的变化规律1、除数不变，被除数乘几或除以几（0除外），商也乘几或除以几。
2、被除数不变，除数乘几或除以几（0除外），商反而除以几或乘几。
3、被除数和除数都乘或除以一个相同的数（0除外），商不变。
（1）80÷16=（80○□）÷（16÷4）200÷40=（200÷20）÷（40○□）180÷15=（180×3）÷（15○□）（2）1400÷70，如果除数不变，被除数除以10，那么商应当（）。
被除数不变，除数乘3，商应当（）。
两个数的商是8，如果被除数不变，除数乘4，商就变成（）。
一个除法算式，被除数乘15，要使商不变，除数也要（）。
两个数相除的商是6，如果被除数和除数都除以12，商是（）。
一个除法算式的被除数、除数都除以3后，商是20，那么原来的商是（）。
.《除数是两位数的除法》1、商店里卖衣服，29元/件，49元/2件，王阿姨有185元，最多可以买多少件？还剩多少元？2、小李家距离学校520米，小李每分钟走65米，小红每分钟走60米，从家到学校小红比小李多走5分钟，小红家离学校多少米？3、每条裤子75元，商店推出优惠活动，买4条送一条，900元钱最多可以买几条这样的裤子？4、12箱蜜蜂一年可以酿900千克蜂蜜，林叔叔家养了8箱这样蜜蜂，一年可以酿多少千克蜂蜜？5、学校组织四年级的540名学生去植树，要分成9个植树点，每个植树点分成4个小组，平均每个小组有多少人？6、从山顶到山脚共998米，王林爬了14分钟，距山顶还有260米，他平均每分钟爬多少米？【下载本文档，可以自由复制内容或自由编辑修改内容，更多精彩文章，期待你的好评和关注，我将一如既. 往为您服务】。
积与商的变化规律
命题人：葛金韬★观察下列三组算式，你发现了什么?从上面的算式中可以看出：(1)一个因数不变，另一个因数扩大到它的几倍，积也扩大相同的倍数；(2)如果两个因数都扩大，那么积就扩大两个因数扩大的倍数的乘积；(3)如果一个因数扩大，另一个因数缩小，那么积就扩大(或缩小)两个因数扩大或缩小倍数的商。
例题1在乘法算式25×8中，如果一个因数扩大到它的2倍，另一个因数不变，那么积有什么变化?例题2在乘法算式510×360中，如果一个因数扩大到它的2倍，另一个因数扩大到它的3倍，那么积有什么变化?例题3在乘法算式510×360中，如果一个因数扩大到它的6倍，另一个因数缩小到原来的三分之一，那么积有什么变化?例题4在乘法算式510×360中，如果一个因数扩大到它的2倍，另一个因数缩小到原来的六分之一，那么积有什么变化?练习1．填空在乘法算式中，一个因数不变，另一个因数扩大到它的2倍，积( )；一个因数不变，另一个因数缩小到原来的三分之一，积( )；一个因数扩大到它的4倍，另一个因数扩大到它的3倍，积( )；一个因数缩小到原来的二分之一，另一个因数扩大到它的8倍，积( )。
2．先判断，再计算验证(1)在算式12×8中，如果一个因数不变，另一个因数扩大到它的3倍，积有什么变化?(2)在算式12×8中，如果一个因数不变，另一个因数缩小到原来的四分之一，积有什么变化?(3)在算式12×8中，如果一个因数不变，另一个因数缩小到原来的三分之一，积有什么变化?(4)在算式12×8中，如果一个因数缩小到它的三分之一，另一个因数缩小到它的四分之一，积有什么变化?(5)在算式12×8中，如果一个因数扩大到它的3倍，另一个因数扩大到它的4倍，积有什么变化?命题人：葛金韬★观察下列三组算式，你发现了什么?从上面的算式可以看出：(1)除数不变，被除数扩大到它的几倍，商也扩大相同的倍数；(2)被除数不变，除数扩大到它的几倍，商就缩小到原来的几分之一；(2)如果被除数、除数都扩大，那么商就扩大(或缩小)被除数与除数扩大(或缩小)倍数的商倍；(3)如果被除数扩大，除数缩小，那么商就扩大被除数扩大倍数与除数缩小倍数的乘积倍；(4)如果被除数缩小，除数扩大，那么商就缩小被除数缩小与除数扩大倍数的乘积分之一。
最新A4四年级上册积与商的变化规律专项练习题
积的变化规律练习题姓名一、根据已知算式，直接写出下面各题的得数。
18×24=432105×45=4725（18÷2）×（24×2）= （105÷5）×（45×5）=（18×2）×（24÷2）= （105×3）×（45÷3）=24×75＝180036×104＝3744（24○6）×（75×6）＝1800 （36×4）×（104○4）＝3744 （24○3）×（75○□）＝1800 （36○□）×（104○□）＝3744 15×24=36015×72=（）30×24=（）5×24=（）15×12=（）15×（24×）=3600 15×（24÷10）=（）12×20=240（12×6）×（20×5）=（）（12÷3）×（20÷4）=（）（12×）×（20×）=4800 （12÷）×（20÷）=40 二、选择。
1．一个因数扩大5倍，另一个因数不变，积（）。
A、缩小5倍B、不变C、扩大5倍2．一个因数扩大5倍，另一个因数缩小5倍，积（）。
A、缩小5倍B、不变C、扩大5倍3．两数相乘，一个因数扩大2倍，另一个因数扩大3倍，那么积（）。
A、不变B、扩大5倍C、扩大6倍4．两个因数的积是60，这时一个因数缩小4倍，另一个因数不变，现在的积是（）A、240 B、60 C、155．一个长方形的面积为12平方米、把长扩大到原来的3倍，宽不变，扩大后的面积是（）6．两个因数的积是100，把其中一个因数扩大到原来的3倍，另一个因数不变，积是（）7．一个正方形的面积为12平方米、把边长扩大到原来的3倍，，扩大后的面积是（）8．两个因数的积是100，把其中一个因数扩大到原来的3倍，另一个因数也扩大到原来的3倍，积是（）9．两个因数的积是100，把其中一个因数扩大到原来的3倍，另一个因数也缩小到原来的3倍，积是（）10．一个因数不变，把其中另一个因数扩大到原来的3倍，积是90，原来两个因数的积是（）11．一个因数扩大到原来的3倍，另一个因数也扩大到原来的3倍，积是90，原来两个因数的积是（）12．一个因数扩大到原来的3倍，另一个因数缩小到原来的3倍，积是90，原来两个因数的积是（）。
和差积商的变化规律
和.差,积、商的变化规律（一）知识点拨和、差的规律见下表（于0精讲精练【例题1】两个数相加，一个加数增加9,另一个加数减少9,和是否发生变化？【思路】一个加数增加9,假如另一个加数不变，和就增加9；假如一个加数不变，另一个加数减少9,和就减少9；和先增加9,接着又减少9,所以不发生变化。
【练习1】1.两个数相加，一个数减8,另一个数加8,和是否变化？2.两个数相加，一个数加3.另一个数也加3.和起什么变化？3.两个数相加，一个数减6,另一个数减2.和起什么变化？【例题2】两个数相加，如果一个加数增加10,要使和增加6,那么另一个加数应有什么变化？【思路】一个加数增加10,假如另一个加数不变，和就增加10。
现在要使和增加6,那么另一个加数应减少10 — 6=4。
【练习2】1.两个数相加，如果一个加数增加8,要使和增加15,另一个加数应有什么变化?2.两个数相加，如果一个加数增加8,要使和减少15,另一个加数应有什么变化?3.两个数相加，如果一个加数减少8,要使和减少8,另一个加数应有什么变化?【例题3】两数相减，如果被减数增加8,减数也增加8,差是否起变化？【思路】被减数增加8,假如减数不变，差就增加8；假如被减数不变，减数增加8, 差就减少8。
两个数的差先增加8,接着又减少8,所以不起什么变化。
【练习3】1.两数相减，被减数减少6,减数也减少6,差是否起变化？2.两数相减，被减数增加12.减数减少12.差起什么变化?3.两数相减，被减数减少10,减数增加10,差起什么变化?【例题4】两数相乘，如果一个因数扩大8倍，另一个因数缩小2倍，积将有什么变化？【思路】如果一个因数扩大8倍，另一个因数不变，积将扩大8倍；如果一个因数不变，另一个因数缩小2倍，积将缩小2倍。
积先扩大8倍又缩小2倍，因此，积扩大了 8 ・ 2=4 倍。
【练习4】1.两数相乘，如果一个因数缩小4倍，另一个因数扩大4倍，和是否起变化?2.两数相乘，如果一个因数扩大3倍，另一个因数缩小12倍，积将有什么变化?3.两数相乘，如果一个因数扩大3倍，另一个因数扩大6倍，积将有什么变化？【例题5】两数相除，如果被除数扩大4倍，除数缩小2倍，商将怎样变化？【思路】如果被除数扩大4倍，除数不变，商就扩大4倍；如果被除数不变，除数缩小2倍，商就扩大2倍。
人教版四年级数学上册期末 积、商的变化规律及其应用 专项试卷附答案
人教版四年级数学上册方法技能分类评价4.积、商的变化规律及其应用一、认真审题，填一填。
(每小题4分，共20分)1.两个因数的积是120，其中一个因数乘4，如果另一个因数不变，这时积是( )，如果另一个因数乘2，积是( )。
2.两个数相乘，一个因数除以4，要使积不变，另一个因数应该( )。
3.两数相除，商是60，如果被除数除以2，除数乘2，商是( )；如果被除数除以2，除数除以2，商是( )。
4.两数相除，被除数乘8，要使商不变，除数应( )。
5.已知482÷6＝80……2，那么4820÷60＝( )……( )。
二、仔细推敲，选一选。
(每小题4分，共20分)1.480÷60和48÷6的商( )。
A.相等B.不相等C.无法确定2.两数相除，商是12，若被除数除以2，要使商不变，除数要( )。
A.除以2B.乘2C.不变3.一个除法算式，被除数不变，除数乘5，要使算式仍成立，商应( )。
A.除以5B.乘5C.无法判断4.A×B＝380，若A扩大到原来的10倍，则积是( )。
A.38B.3800C.380005.下列说法错误的是( )。
A. 被除数扩大到原来的10倍，除数扩大到原来的5倍，则商扩大到原来的2倍B. 两数相乘，一个因数扩大到原来的10倍，另一个因数扩大到原来的2倍，积扩大到原来的5倍C. 除法算式中，被除数除以4后，商是30，原来的商是120三、细心的你，算一算。
(共35分)1.计算出每组中第一题的结果，直接写出下面两题的结果。
(每小题1分，共9分)63÷9＝80÷5＝15×6＝630÷90＝240÷5＝15×12＝6300÷900＝480÷15＝45×12＝2.根据△÷□＝72，求出下列算式的结果。
(每空1分，共6分) (△×5)÷□＝( )△÷(□×6)＝( )(△×12)÷(□×12)＝( )(△÷72)÷(□÷72)＝( )(△×4)÷(□÷2)＝( )(△÷4)÷(□×2)＝( )3.根据规律做一做。
四年级奥数 第10讲 变化规律(2)
第10讲 变化规律（二）专题简析：积商的变化规律如下图所示（m ≠0）：例1:两数相乘，一个乘数扩大3倍，要使积扩大9倍，另一个乘数应该怎样变化？练习：1 、两数相乘，一个乘数缩小至原来的16，要使积扩大3倍，另一个乘数应该怎样变化？2、两数相乘，一个乘数扩大8倍，要使积缩小至原来的12，另一个乘数应该怎样变化？3、两数相乘，一个乘数缩小至原来的15，要使积缩小至原来的110，另一个乘数应该怎样变化？例2:两数相乘，积是96.如果一个乘数缩小至原来的14，另一个乘数扩大3倍，那么积是多少？练习：1、两数相乘，积是70.如果一个乘数扩大2倍，另一个乘数缩小至原来的15，那么积是多少？2、两数相乘，积是56.如果一个乘数缩小至原来的12，另一个乘数扩大3倍，那么积是多少？3、两数相乘，积是60.如果一个乘数扩大6倍，另一个乘数也扩大6倍，那么积是多少？例3:两数相除，如果被除数缩小至原来的13，除数扩大2倍，商将怎样变化？练习：1、两数相除，被除数扩大25倍，除数缩小至原来的115，商将怎样变化？2、 两数相除，被除数缩小至原来的15，除数缩小至原来的110倍，商将怎样变化？3、 两数相除，被除数扩大3倍，除数扩大15倍，商将怎样变化？例4:两数相除，被除数扩大30倍，要使商扩大60倍，除数应该怎样变化？练习：1、 两数相除，被除数缩小至原来的18，要使商扩大 2倍，除数应该怎样变化？2、两数相除，除数扩大9倍，要使商缩小至原来的13，被除数应该怎样变化？3、 两数相除，被除数缩小至原来的112，要使商缩小 至原来的12，除数应该怎样变化？例5:两数相除，商是4，余数是10.如果被除数和除数同时扩大50倍，商是多少？余数是多少？练习：1、两数相除，商是5，余数是15.如果被除数和除数同时扩大20倍，商是多少？余数是多少？2、两数相除，商是7，余数是3.如果被除数和除数同时扩大100倍，商是多少？余数是多少？3、两数相除，商是12，余数是120.如果被除数和除数同时缩小至原来的110，商是多少？余数是多少？课后练习1、两数相乘，一个因数扩大5倍，要使积缩小到原数的15，另一个因数应怎样变化？2、两数相乘，一个因数扩大到原数的12倍，要使积扩大到原数的3倍，另一个因数应怎样变化3、两数相乘，积是72，若一个因数缩小到原数的14，另一个因数缩小到原数的12，那么积是多少?4、两数相乗，积是150，若一个因数缩小到原数的110，另一个因数扩大到原数的6倍，那么积多少?5、两数相除，被除数打扩大到原数的3倍除数缩小到原数的14，商将怎样变化?6、两数相除，被除数着小到原数的120，除数缩小到原数的15，商会怎样变化?提优练习1、两数相除，被除数扩大15倍，要使商缩小到原数的13，除数应怎样变化?2、两数相除，除数缩小到原数的12，要使商缩小到原数的14，被除数应怎样变化?3、两数相除，被除数扩大5倍，要使商扩大10倍，除数应怎样变化?4、两数相除，商是24，余数是24。
人教版2023-2024学年五年级数学上册典型例题系列之期中专项练习：积和商的规律(原卷版)+(解析
2023-2024学年五年级数学上册典型例题系列之期中专项练习：积和商的规律（原卷版）1．两个因数的积是42.6，如果一个因数扩大到原来的100倍，另一个因数缩小到原来的110，那么积是( )。
2．5.21×1.87中，如果因数5.21扩大到原数的10倍，要使积不变，因数1.87应改为( )。
3．两个数相除的商是1.34，如果被除数扩大到原来的100倍，除数缩小到原来的1100，那么商是( )。
4．根据145×18＝2610在括号里填上适当的数。
14.5×( )＝2.61 ( )×0.18＝2.61 145×( )＝261( )×1.8＝26.1 1.45×( )＝2.61 ( )×18＝2.615．根据18×64＝1152，可知1.8×0.64＝( )，0.18×6.4＝( )。
6．已知9.18×a＝b，当a等于( )时，b＞9.18；当a等于( )时，b＜9.18；当a等于( )时，b＝9.18；当a等于( )，b＝0。
7．两个因数的积是17.8，若将其中一个因数扩大到原来的100倍，另一个因数缩小到原来的1100，则积为( )。
8．在（）中填上“＞”“＜”或“＝”。
4.92×0.01( )4.925.43×0.85( )5.436.18×1.01( )6.187.89×1.5( )78.9×0.159．两个因数相乘的积是47.5，如果一个因数扩大10倍，另一个因数不变，积就扩大( )倍，结果是( )。
10．3.7×a＝b，当a( )时，b小于3.7；当a( )时，b大于3.7。
11．两个因数相乘的积是27.5，如果一个因数扩大10倍，另一个因数扩大100倍，积就扩大（），结果是（）。
12．两个因数的积是12.05，其中一个因数不变，另一个因数缩小到它的1 100，积是( )。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
奖 励 卡 因积变化、商不变 规律
1
1.根据15×24=360，直接写出下面各题的得数。
15×72=（ ） 30×24=（ ） 5×24=（ ） 15×12=（ ） 15×（24× ）=3600 15×（24÷10）=（ ）
1、一个因数扩大5倍，另一个因数不变，积（ ）。
2、一个因数扩大5倍，另一个因数缩小5倍，积（ ）。
3、两数相乘，一个因数扩大2倍，另一个因数扩大3倍，那么积（ ）。
4、两个因数的积是60，这时一个因数缩小4倍，另一个因数不变，现在的积是（ ）
5、一个长方形的面积为12平方米、把长扩大到原来的3倍，宽不变，扩大后的面积是（ ）
6两个因数的积是100，把其中一个因数扩大到原来的3倍，另一个因数不变，积是（ ） 7一个正方形的面积为12平方米、把边长扩大到原来的3倍，，扩大后的面积是（ ） 8、一个长方形的长扩大到原来的5倍，宽扩大到原来的2倍，面积扩大到原来的（ ）倍。
9、两个因数的积是420，如果一个因数不变，另一个因数乘8，积是（ ）。
10、两个数相乘的积是160，如果一个因数除以2，另一个因数也除以2，积是（ ）。
11、两数相除的商是15，如果被除数、除数同时扩大10倍，商是（ ）。
如果被除数不变，只把除数扩大5倍，商是（ ）。
12、150÷30，如果被除数增加300，要使商不变，除数应该（ ）。
13、两数相除，如果被除数扩大5倍，要使商不变，除数应该（ ）。
14、1400÷70，如果除数不变，被除数除以10，那么商应该（ ）。
15、被除数不变，除数乘3，商应当（ ）。
16、两个数的商是6，如果被除数与除数都除以2，商是（ ）。
17、两数相除，商是80，如果去掉除数个位上的0，商是（ ）。
18、两个数的商是12，如果被除数除以3，除数不变，则商是（ ）。
19、被除数和除数同时乘6，商（ ）。
20、在一个除法算式里，除数除以5，要使商不变，被除数应该（ ）。
21、在一道除法算式里，如果被除数除以20，除数（ ），商不变。
22、两数相乘，如果一个因数缩小5倍，另一个因数扩大5倍，积( )。
23、两数相乘，如果一个因数扩大8倍，另一个因数缩小2倍，积( )。
24、两数相除，如果被除数扩大4倍，除数扩大4倍，商( )。
25、两数相除，如果被除数扩大4倍，除数缩小2倍，商( )。
26、两数相除，如果被除数缩小2倍，除数扩大4倍，商( )。
27、两数相除，被除数缩小12倍，除数缩小2倍，商（ ）。
28、小科在计算除法时，把除数末尾的0漏写了，结果得到的商是70，正确的商应该是（ ）。