队列的定义
队列的定义(精)

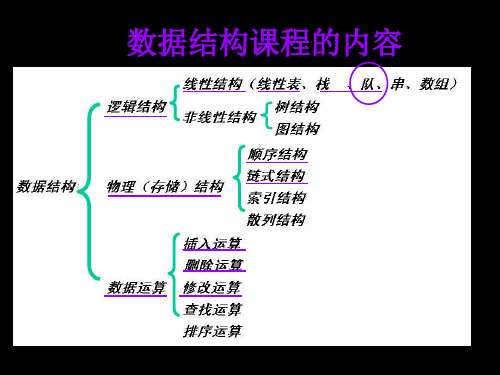
三、队列1.队列的定义队列(Queue)简称队,它也是一种运算受限的线性表,其限制是仅允许在表的一端进行插入,而在表的另一端进行删除。
我们把进行插入的一端称作队尾(rear),进行删除的一端称作队首(front)。
向队列中插入新元素称为进队或入队,新元素进队后就成为新的队尾元素;从队列中删除元素称为离队或出队,元素离队后,其后继元素就成为队首元素。
由于队列的插入和删除操作分别是在各自的一端进行的,每个元素必然按照进入的次序离队,所以又把队列称为先进先出表(First In First Out, 简称FIFO)。
在日常生活中,人们为购物或等车时所排的队就是一个队列,新来购物或等车的人接到队尾(即进队),站在队首的人购到物品或上车后离开(即出队),当最后一人离队后,则队列为空。
例如,假定有a,b,c,d四个元素依次进队,则得到的队列为(a,b,c,d),其中字符a为队首元素,字符d为队尾元素。
若从此队中删除一个元素,则字符a出队,字符b成为新的队首元素,此队列变为(b,c,d);若接着向该队列插入一个字符e,则e成为新的队尾元素,此队列变为(b,c,d,e);若接着做三次删除操作,则队列变为(e),此时只有一个元素e,它既是队首元素又是队尾元素,当它被删除后队列变为空。
2. 队列的存储结构队列的存储结构同线性表和栈一样,既可以采用顺序结构,也可以采用链接结构。
(1) 队列的顺序存储结构队列的顺序存储结构需要使用一个数组和两个整型变量来实现,利用数组来顺序存储队列中的所有元素,利用两个整型变量来分别存储队首元素和队尾元素的下标位置,分别称它们为队首指针和队尾指针。
假定存储队列的数组用queue[QueueMaxSize]表示,队首和队尾指针分别用front和rear表示,则元素类型为ElemType的队列的顺序存储类型可定义为: ElemType queue[QueueMaxSize];int front, rear;其中QueueMaxSize为一个整型全局常量,需事先通过const语句定义,由它确定顺序队列(即顺序存储的队列)的最大长度,即最多能够存储的元素个数。
queue的数据结构

queue的数据结构在计算机科学中,队列是最常见的数据结构之一。
队列是一种线性数据结构,使用先进先出的规则,即最先进入队列的元素将最先从队列中取出来。
在队列中,元素只能在队尾添加,只能从队头移除。
下面是围绕“队列的数据结构”分讲队列的相关知识。
1. 队列的定义队列是一种抽象数据类型,用于保存按照特定顺序排列的元素。
它是一种线性的、连续的、存储有序的数据结构,具有先进先出(FIFO)的特点。
2. 队列的操作队列的主要操作包括入队和出队。
入队操作:将元素添加到队列的末尾。
出队操作:从队列的头部删除一个元素并返回其值。
除此之外,队列还有其他一些常用的操作,如:队列初始化操作:用于创建一个空的队列。
队列长度操作:用于获取队列中元素的数量。
队列查找操作:用于查找队列中是否存在某个元素。
队列清空操作:用于清空队列中存储的所有元素。
3. 队列的应用队列在计算机科学中有着广泛的应用。
它经常用于实现异步任务处理、消息队列、多线程任务调度等场景。
在异步任务处理中,任务会被添加到队列中,异步任务处理程序会从队列中依次取出任务并执行。
这样可以使任务处理更高效,减少了重复的等待时间。
在消息队列中,队列用于保存需要传递的信息。
当消息到达队列的头部,消费者程序将该消息从队列中读取并处理。
在多线程任务调度中,队列用于保存需要执行的任务。
任务分发程序会将任务添加到队列中,线程池中的线程会从队列中获取任务并执行。
4. 队列的实现队列可以使用数组或链表实现。
使用数组实现队列时,需要维护两个指针,分别指向队列的头部和尾部。
使用链表实现队列时,每个元素都包含一个指向下一个元素的指针。
无论使用数组还是链表实现队列,都需要保证队列元素的顺序,以便快速执行出队操作。
同时,还需要注意到队列的空间限制,避免在添加元素时队列溢出。
5. 队列的效率队列的效率取决于其实现方式。
在数组实现中,入队和出队操作的时间复杂度为O(1);在链表实现中,入队和出队操作的时间复杂度也是O(1)。
(完整版)《队列》知识点总结

(完整版)《队列》知识点总结队列知识点总结
1. 队列的定义和特点
队列是一种常用的数据结构,它遵循先进先出(FIFO)的原则。
具体定义为:在队列中,元素的插入和删除操作分别发生在队尾和
队首。
队列的特点包括:
- 插入操作(入队)只能在队尾进行
- 删除操作(出队)只能在队首进行
- 队列中元素按照插入的顺序排列,先插入的元素在队列中靠
前
2. 队列的应用场景
队列常见的应用场景包括:
- 广度优先搜索(BFS):在图中使用队列来实现广度优先搜索算法
- 任务调度:多线程环境下,使用队列来调度任务并按照顺序执行
- 缓冲区:在生产者-消费者模型中,使用队列作为缓冲区来协调生产者和消费者的速度差异
3. 队列的实现方式
队列的实现可以有多种方式,常见的包括使用数组和使用链表两种方法。
- 数组实现队列:使用数组来存储队列中的元素,通过维护队列头部和尾部的指针来实现入队和出队操作。
- 链表实现队列:使用链表来存储队列中的元素,通过维护链表的头节点和尾节点来实现入队和出队操作。
4. 队列的时间复杂度分析
队列中常见的操作包括入队和出队,它们的时间复杂度如下:
- 入队操作的时间复杂度为O(1)
- 出队操作的时间复杂度为O(1)
5. 队列的相关算法
常见的与队列相关的算法包括:
- 循环队列:使用数组实现的队列,通过循环利用数组空间来提高队列的效率
- 双端队列:允许在队列的两端进行插入和删除操作的队列,具有队列和栈的特性
- 优先队列:插入操作可以按照优先级进行排序的队列,常用于解决相关的调度问题
以上为队列的知识点总结,希望对您有所帮助!。
队列研究的实施步骤有哪些

队列研究的实施步骤有哪些引言在计算机科学领域,队列是一种常用的数据结构。
队列研究的实施步骤涉及队列的定义、基本操作、应用场景等方面。
本文将介绍队列研究的实施步骤,以帮助读者更好地理解和应用队列。
步骤一:定义队列队列是一种先进先出(First-In-First-Out,FIFO)的数据结构,它只允许在队尾插入元素,在队头删除元素。
队列可以用数组、链表或其他数据结构实现。
在队列的定义中,需要明确队列的数据类型和容量限制。
步骤二:实现基本操作队列的基本操作包括入队(enqueue)和出队(dequeue)操作。
入队操作将元素插入队列的队尾,出队操作删除队列的队头元素。
除此之外,还包括其他常用操作,如获取队头元素(getFront)、获取队列长度(getSize)等。
常见的队列操作实现有顺序队列、循环队列、链式队列等。
选择合适的实现方式,根据需求和性能要求来决定。
步骤三:分析队列的性质和特点队列的性质和特点对于深入理解和应用队列起到关键作用。
队列的性质包括FIFO特性、队列是否为空、队列是否已满等。
队列的特点有序性、高效性、稳定性等。
分析队列的性质和特点可以帮助研究者更好地理解和优化队列的应用。
步骤四:研究队列的应用场景队列作为一种常用的数据结构,在各个领域都有广泛的应用。
研究队列的应用场景可以帮助开发人员解决实际问题。
常见的队列应用场景包括任务调度、消息队列、缓冲区等。
步骤五:比较队列与其他数据结构的优劣队列作为一种数据结构,与其他数据结构如栈、链表、树等都有不同的特点和应用场景。
比较队列与其他数据结构的优劣可以帮助研究者更好地选择适合的数据结构来解决问题。
步骤六:性能分析和优化队列的性能分析和优化是队列研究的重要内容。
通过对队列的性能参数如入队和出队的时间复杂度进行分析,可以评估队列的性能指标。
对队列的性能进行优化可以提高算法和系统的效率。
常见的队列性能优化技术包括改进队列实现方式、调整队列参数、优化队列的存储结构等。
queue 的用法

queue 的用法一、什么是队列1.1 定义队列(Queue)是一种常见的线性数据结构,它按照先进先出(FIFO)的原则管理数据。
队列有两个基本操作:入队和出队,即将元素从队列的一端插入,从另一端删除。
1.2 特点•元素在队列尾部入队,从队列头部出队;•队列的大小是动态变化的,可以根据需求进行扩容;•队列的查找和删除操作只能在队列的头部进行,插入操作只能在队列的尾部进行。
二、队列的实现方式2.1 静态数组实现使用静态数组实现队列需要提前确定队列的最大长度,当队列满时无法继续入队,而且在出队操作后需要移动队列中的元素,使队列保持连续的内存空间。
2.2 动态数组实现动态数组实现的队列可以根据需要调整队列的大小,当元素数量超过了队列的容量时,可以进行动态扩容。
2.3 链表实现链表实现的队列不需要提前确定队列的最大长度,每个元素通过指针连接,插入和删除操作相对简单。
链表实现的队列适用于频繁的插入和删除操作。
三、队列的应用场景3.1 线程池任务调度在多线程编程中,线程池负责管理工作线程,而任务调度就是通过队列来实现的。
当一个任务需要执行时,将其加入任务队列,由工作线程从队列中取出任务并执行。
3.2 网络请求的处理在处理网络请求时,队列常用于存储待处理的请求。
后台会按照请求的顺序,逐个处理队列中的请求,将结果返回给请求方。
3.3 操作系统进程调度操作系统中的进程调度也可以使用队列来实现。
每个进程的状态会被存储在队列中,按照一定的调度算法从队列中选取下一个要执行的进程。
3.4 消息队列消息队列是一种异步通信机制,数据传递的方式是通过队列来进行的。
发送方将消息放入队列中,接收方从队列中取出消息进行处理。
消息队列可以实现解耦和流量控制。
四、常见的队列操作4.1 入队操作入队操作是向队列尾部添加一个元素。
如果队列已满,则无法入队,此时需要考虑扩容操作。
4.2 出队操作出队操作是从队列头部删除一个元素。
如果队列为空,则无法出队,需要考虑如何处理空队列的情况。
队列及其表示方法教案

队列及其表示方法教案一、概述队列是一种常见的数据结构,它具有先进先出(FIFO)的特性。
本教案旨在介绍队列的基本概念和表示方法,帮助学生理解和应用队列。
二、队列的定义队列是一种有序的线性表,只允许在表的一端(队尾)进行插入操作,在另一端(队头)进行删除操作。
插入操作又称为入队(enqueue),删除操作又称为出队(dequeue)。
三、队列的基本操作1. 入队操作入队操作将元素添加到队列的队尾。
具体步骤如下:1. 判断队列是否已满,若已满则报错(队列溢出)。
2. 将待插入元素添加到队列的队尾。
3. 修改队尾指针。
2. 出队操作出队操作将队头元素从队列中删除并返回。
具体步骤如下:1. 判断队列是否为空,若为空则报错(队列为空)。
2. 返回队头元素。
3. 修改队头指针。
四、队列的表示方法队列有多种表示方法,常见的有顺序存储表示和链式存储表示。
1. 顺序存储表示顺序存储表示使用数组来存储队列元素。
采用两个指针front 和rear分别指向队头和队尾元素。
当队列为空时,front和rear指向同一个位置。
2. 链式存储表示链式存储表示使用链表来存储队列元素。
每个节点包含一个元素值和指向下一个节点的指针。
头指针指向队头节点,尾指针指向队尾节点。
五、总结队列是一种常用的数据结构,具有先进先出的特性。
本教案介绍了队列的定义、基本操作和表示方法,希望能够帮助学生掌握队列的基本概念和应用。
注意:本文档中的内容仅供参考,具体操作请根据实际情况进行调整和实施。
队列
例1: 一循环队列如下图所示,若先删除4个元素,接着再 插入4个元素,请问队头和队尾指针分别指向哪个位置? front front 1
2
J2
J3 J4 J5
front
J8
J9
front
0
J1
3
front
J7 J6 J5
rear
rear 解:由图可知,队头和队尾指针的初态分别为front=0 和rear=5。maxsize=6 删除4个元素后front=4;再插入4个元素后,r=(5+4)%6=3
16
链队列示意图
rear Q front p
a1 (队首) a2
a3 ^
(队尾)
讨论:
① 空队列的特征? front=rear
front
rear
^
② 队列会满吗?一般不会,因为删除时有free动作。除非内存不足! ③ 怎样实现入队和出队操作? 入队(尾部插入):rear->next=S; rear=S; 出队(头部删除):front->next=p->next;
2
1. 定
义
只能在表的一端进行插入运算,在表的另 一端进行删除运算的线性表 (头删尾插)
与同线性表相同,仍为一对一关系。 顺序队或链队,以循环顺序队更常见。
2. 逻辑结构 3. 存储结构
4. 运算规则
只能在队首和队尾运算,且访问结点时依 照先进先出(FIFO)的原则。
5. 实现方式 关键是掌握入队和出队操作,具体实现依顺序
14
5
4
front
例2 :数组Q[n]用来表示一个循环队列,f 为当前队列头元
素的前一位置,r 为队尾元素的位置。假定队列中元素的个 数小于n,计算队列中元素的公式为: (A) r-f (B)(n+f-r)% n (C)n+r-f (D) (n+r-f)% n
队列的定义、表示、实现

根据队列的大小,预先分配一定的存储空间,以 减少动态内存分配的开销。
3
设置队头和队尾指针
初始化队头和队尾指针,指向队列的起始位置。
队列的入队操作
检查队列是否已满
在执行入队操作之前,需要检查队列是否已 满,如果已满则无法再添加元素。
添加元素
将新元素添加到队列的末尾,更新队尾指针。
调整指针
将队尾指针指向新添加的元素。
使用Java实现队列
01
queue.add(1);
02
queue.add(2);
03
queue.add(3);
使用Java实现队列
System.out.println(queue.poll()); // 输出 1
System.out.println(queue.peek()); // 输出 2
使用Java实现队列
q.pop(); // 移除元素2
cout << q.size() << endl; // 输 出2
使用C实现队列
return 0;
}
谢谢观看
队头,最后一个元素为队尾。
插入操作
在数组存储结构的队尾插入元素时, 需要将新元素存储到数组的最后一 个位置,并将队尾指针向前移动一 位。
删除操作
在数组存储结构的队头删除元素时, 需要将队头指针向后移动一位,并 从数组中删除该位置的元素。
队列的顺序存储结构
顺序存储结构
队列的顺序存储结构使用连续的 内存空间来实现,每个元素包含 数据域和下标。数据域用于存储 数据,下标表示元素在队列中的 位置。
04
队列的效率分析
队列的入队效率
总结词
入队效率指的是向队列中添加元素的速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Linked queues
Append and Serve:
练习
试用一个bool变量区分队列空与不空(不使 用count)实现循环队列 • 写出 队列的class定义; • 说明队列空和队列满的条件分别是什么; • 完成队列的实现。
队列
演示与测试
Demonstration and testing
Testing and debugging
• A classic book on testing, now also online: The art of software testing, Glenford Myers • Read chapter 7 about debugging to reduce
good.
Circular Queue
Circular arrays(循环数组)
• 将数组设想为一个循环的,而非线性的; • 用两个下标front和rear记录队头和队尾位置; • 添加元素时,rear右移,将元素置于rear位
置。当rear等于max时(last index), rear 置 0. • 元素出队时,删除位于front位置的元素,然
class Extended_queue:public Queue { public: bool full() const; int size() const; void clear(); Error_code serve_and_retrieve(Queue_entry &item); };
队列
• Testing is the process of executing a program with the intent of finding errors.
• Errors: valid input produces invalid output. • Choosing those inputs which are likely to go
• Alternatively, we can automate the testing: generate a sequence of operations and compare two queues (one is assumed to be the standard) to see if they have the same state after each operation (See lab notes).
Definition of Queues
Queue Operations
设 QБайду номын сангаасeue_entry 表示队列元素的类型。
Constructor
Insertion (入队)
Queue Operations (2)
Deletion 出队
Get the front 取队头元素
Queue Operations (3)
your effort on debugging.
int main() /*Post: Accept commands from user and execute them */ {
Extended_queue <int> test_queue; introduction();// instructions for the user while (do_command(get_command(), test_queue)); }
后front右移. 当front 等于 max时, 置 front 为 0。
Boundary conditions
rear
front
No difference
rear
front
remove
empty after deletion
rear insert
front
Full after addition
Circular Implementation of Queues
template <class T> class Queue { public: Queue(); bool empty() const; Error_code serve(); Error_code append(const T &item); Error_code retrieve(T &item) const; protected: unsigned maxqueue; int count; int front,rear; T entry[maxqueue]; };
bool do_command(char c, Extented_queue <int> &test_queue)
Pre: c is a valid command Post: Perform the given command c on
test_queue. Return false if c ==‘q’ (quit), otherwise, return true
void get_command() Post: Get a valid command from the user and reurn it.
bool do_command(char c, Extended_queue<int> & test_queue) /*Post: perform the given commands. return true if c != 'q'. */{
bool continue_input = true; int x; switch(c) { case 'a'://append an item
if (test_queue.full()) cout <<"full!"<<endl; else {
cout << "input an integer:"<<endl; cin >> x; test_queue.append(x); }; break; case …. } return continue_input; }
the front is removed. Poor!
Linear implementation(线性实现)
• Two indices(下标) to keep track of both the front and the rear of the queue
• To serve an entry, take the entry and increase the front by one
• To verify the methods, we write a demonstration program.
• The program interactively accepts commands and prints the results, a kind of black box testing.
• To append an entry to the queue, increase the rear by one and put the entry in that position
• Problem: cannot reuse the discarded space • When the queue is regularly emptied, this is
}
Implementations
template <typename T> Queue <T>::Queue() /*post: the queue is initialized to be empty*/ {
count =0; rear = maxqueue -1; // rear is just before the front position //when it is empty front = 0; }
Check emptiness 检查队是否空
The Queue class
• The ADT Queue class:
class Queue { public: Queue();
Add more to make it a safe class. Write the data part and implement ADT
char get_command(){ char command; bool waiting = true; cout <<"select a command and press enter:"<<endl; while (waiting) { cin >> command; command = tolower(command); if (command == 'a' || command == 'q' || command == 's' || command == 'r')
wrong, especially the boundary cases.
1. Easy values. Test the program with data that are easy to check.
2. Typical, realistic values. Always try a program on data chosen to represent how the program will be used.
rear
front
Boundary conditions
• 问题:无法区分满队列与空队列。 • 解决方法: 1. 在数组中空一个位置; 2. 使用一个布尔量表示队列是否满。当
rear刚好到达front之前时,置 此标志为 true. 3. 使用一个计数器( counter)以记录队列 中的元素个数。
