最新沪科版八年级数学上第12章小结与复习ppt公开课优质课件
合集下载
八年级数学上册 第12章 全等三角形小结与复习课件上册数学课件

∠BAP=180 °,
求证:PA=PC.
E
【分析】由角平分线的性质易想到过点
A
P向∠ABC的两边作垂线段PE、PF,构
1 2
B
造角平分线的基本(jīběn)图形.
N P
FC
12/11/2021
第二十六页,共三十三页。
【证明(zhèngmíng)】过点P作PE⊥BA,PF⊥BC,垂足分别为E,F.
∵∠1=∠2,PE⊥BA,PF⊥BC,垂足(chuí zú)分别为E,F. ∴PE=PF, ∠PEA=∠PFC=90 °.
条件可知AB=AC,AD⊥BC.
12/11/2021
第二十一页,共三十三页。
B
D
C
解:相等(xiāngděng),理由如下:
∵AD⊥BC,
∴∠ADB=∠ADC=90°. 在Rt△ADB和Rt△ADC中,
AD=AD,
AB=AC,
B
∴ Rt△ADB ≌ Rt△ADC(HL). ∴BD=CD.
12/11/2021
E B
12/11/2021
第十八页,共三十三页。
A
G
F
D
C
方法总结
利用全等三角形证明角相等,首先(shǒuxiān)要找到两个角所 在的两个三角形,看它们全等的条件够不够;有时会用到等角转 换,等角转换的途径很多,如:余角,补角的性质、平行线的性
质等,必要时要想到添加辅助线.
12/11/2021
第十九页,共三十三页。
全等三角形的对应(duìyìng)边相等,对应(duìyìng)角
相等.
A
D
B
CE
F
应用格式: 如图:∵△ABC≌△DEF, ∴AB=DE,BC=EF,AC=DF
沪科版八年级数学上册第12章教学课件:12.1 第1课时 变量与函数(共23张PPT)

典例精析
例1 指出下列事件过程中的常量与变量注意:π是一个确 定的数,是常量
(1)某水果店橘子的单价为5元/千克,买a千橘子的总 价为m元,其中常量是 5 ,变量是 a,m ;
(2)周长C与圆的半径r之间的关系式是C=2πr,其中常 量是 2,π ,变量是 C, r ;
(3)三角形的一边长5cm,它的面积S(cm2)与这边上的高
第12章 一次函数
12.1 函数
第1课时 变量与函数
学习目标
1.联系自己的学习、生活实际,通过具体情境 领悟函数的概念,了解常量、变量,知道自变量 与函数,能写出简单的函数表达式;
2.探究变量的发现和函数概念的形成,提高学 生分析、解决问题的能力.
导入新课
情境引入
万物皆变
行星在宇宙中的位置随时间而变化
例2 阅读并完成下面一段叙述: ⒈某人持续以a米/分的速度用t分钟时间跑了s米,其中 常量是 a ,变量是 t,s .
⒉s米的路程不同的人以不同的速度a米/分各需跑的时间 为t分,其中常量是 s ,变量是 a,t .
3.根据上面的叙述,写出一句关于常量与变量的结论: 在不同的条件下,常量与变量是相对的 .
(2)y 是n的函数,其中n是自变量. (3)y 不是x的函数.
例如,到原点的 距离为1的点对 应实数1或-1,
课堂小结
常量与变量:在一个变化过程中, 数值发生变化的量为变量,数值 始终不变的量为常量.
变量与函数
函数:一般地,在一个变化过程 中,如果有两个变量x与y,并且 对于x的每个确定值,y都有唯一确 定的值与其对应,那么我们就说x 是自变量,y是x的函数.
自我发生变化的量__t_________; 因别人变化而变化的量___h_______.
沪科版数学八年级上册全册复习课件(PPT共276张)

(2)△ABC 的面积为 3×3-12×3×1-12× 3×1-12×2×2=4, 所以这个平行四边形的面积为 4×2=8.
数学·沪科版(HK)
第11章 |复习
方法技巧 我们以前就已经知道,平行四边形的两组对边平行 且相等,而线段平移后得到的线段与原线段平行且相 等,于是我们可以利用平移求平行四边形第四个顶点的 坐标;求平面直角坐标系中多边形的面积时,一般采用 补形法,即将所求图形的面积转化成若干个特殊的四边 形和三角形的面积的和与差,如本题中求△ABC 的面积, 就是转化为一个正方形的面积与三个三角形面积的差 来求解.
数学·沪科版(HK)
第11章 |复习 针对第15题训练
在坐标轴上,距离原点 5 个单位长度的点的坐标是 ___(_5_,0_)_,_(_0,_5_),__(-__5_,0_),__(0_,__-_5_)_______________________.
数学·沪科版(HK)
第12章复习(一)
数学·沪科版(HK)
数学·沪科版(HK)
第11章 |复习
►考点二 确定图形平移后的点的坐标
例 2 在平面直角坐标系中,已知线段 MN 的两个端 点的坐标分别是 M(-4,-1)、N(0,1),将线段 MN 平移 后得到线段 M′N′,点 M、N 的对应点分别为 M′、N′, 若点 M′的坐标为(-2,2),则点 N′的坐标为___(2_,4_)___.
,通
常把横坐标写在纵坐标的前面,这样坐标平面内的点
与 有序实数对 之间一一对应.
数学·沪科版(HK)
第11章 |复习
3.点的坐标特点
(1)各象限内的点的坐标符号特征:第一象限 (+,+) ,第 二象限 (-,+) ,第三象限 (-,-) ,第四象限 (+,-) .
数学·沪科版(HK)
第11章 |复习
方法技巧 我们以前就已经知道,平行四边形的两组对边平行 且相等,而线段平移后得到的线段与原线段平行且相 等,于是我们可以利用平移求平行四边形第四个顶点的 坐标;求平面直角坐标系中多边形的面积时,一般采用 补形法,即将所求图形的面积转化成若干个特殊的四边 形和三角形的面积的和与差,如本题中求△ABC 的面积, 就是转化为一个正方形的面积与三个三角形面积的差 来求解.
数学·沪科版(HK)
第11章 |复习 针对第15题训练
在坐标轴上,距离原点 5 个单位长度的点的坐标是 ___(_5_,0_)_,_(_0,_5_),__(-__5_,0_),__(0_,__-_5_)_______________________.
数学·沪科版(HK)
第12章复习(一)
数学·沪科版(HK)
数学·沪科版(HK)
第11章 |复习
►考点二 确定图形平移后的点的坐标
例 2 在平面直角坐标系中,已知线段 MN 的两个端 点的坐标分别是 M(-4,-1)、N(0,1),将线段 MN 平移 后得到线段 M′N′,点 M、N 的对应点分别为 M′、N′, 若点 M′的坐标为(-2,2),则点 N′的坐标为___(2_,4_)___.
,通
常把横坐标写在纵坐标的前面,这样坐标平面内的点
与 有序实数对 之间一一对应.
数学·沪科版(HK)
第11章 |复习
3.点的坐标特点
(1)各象限内的点的坐标符号特征:第一象限 (+,+) ,第 二象限 (-,+) ,第三象限 (-,-) ,第四象限 (+,-) .
八年级数学上册课件(沪科版):第12章一次函数复习课件

思考
y=k xn +b为一次函数的条件是什么? 一. 指数n=1
二. 系数 k ≠0
1.下列函数中,哪些是一次函数?
(1) y 2x
(2) y
1 (3) y x 1(4) y x
x2
答: (1)是 (2)不是 (3)是 (4)不是
2m2 :函数y=(m +2)x+(m² -4)为正比例
函数,则m为何值__m__=_2___
思考:下面2个图形中,哪个图象是y关于x的函数.
图1
图2
练习 1、一辆客车从杭州出发开往上海,设客 车出发t小时后与上海的距离为s千米, 下列图象能大致反应s与t之间的函数关 系的是( A )
A
B
C
D
2.小明骑自行车上学,开始以正常速度匀速 行驶,但行至中途自行车出了故障,只好停下 来修车。车修好后,因怕耽误上课,他比修车 前加快了骑车速度匀速行驶。下面是行驶路程 s(米)关于时间t(分)的函数图像,那么符合这个 同学行驶情况的图像大致是 ( C )
0=-2k+b
①
-1=b
②
把 b= -1 代入①,得:
y
k= - 0.5
a
-2
o
x
所以,其函数解析式为y=
-
0.5
-1
x-1
点评:求一次函数y=kx+b的解析式,可由已知条件给出的两 对x、y的值,列出关于k、b的二元一次方程组。由此求出k、 b的值,就可以得到所求的一次函数的解析式。
2、已知y与x-1成正比例,x=8时,y=6,写
(3) ∵图象与y轴的交点在轴的下方 ∴m-3﹤0 ∴m﹤3
怎样画一次函数y=kx+b的图象?
y=k xn +b为一次函数的条件是什么? 一. 指数n=1
二. 系数 k ≠0
1.下列函数中,哪些是一次函数?
(1) y 2x
(2) y
1 (3) y x 1(4) y x
x2
答: (1)是 (2)不是 (3)是 (4)不是
2m2 :函数y=(m +2)x+(m² -4)为正比例
函数,则m为何值__m__=_2___
思考:下面2个图形中,哪个图象是y关于x的函数.
图1
图2
练习 1、一辆客车从杭州出发开往上海,设客 车出发t小时后与上海的距离为s千米, 下列图象能大致反应s与t之间的函数关 系的是( A )
A
B
C
D
2.小明骑自行车上学,开始以正常速度匀速 行驶,但行至中途自行车出了故障,只好停下 来修车。车修好后,因怕耽误上课,他比修车 前加快了骑车速度匀速行驶。下面是行驶路程 s(米)关于时间t(分)的函数图像,那么符合这个 同学行驶情况的图像大致是 ( C )
0=-2k+b
①
-1=b
②
把 b= -1 代入①,得:
y
k= - 0.5
a
-2
o
x
所以,其函数解析式为y=
-
0.5
-1
x-1
点评:求一次函数y=kx+b的解析式,可由已知条件给出的两 对x、y的值,列出关于k、b的二元一次方程组。由此求出k、 b的值,就可以得到所求的一次函数的解析式。
2、已知y与x-1成正比例,x=8时,y=6,写
(3) ∵图象与y轴的交点在轴的下方 ∴m-3﹤0 ∴m﹤3
怎样画一次函数y=kx+b的图象?
沪科版八年级上册数学课件(第12章 一次函数)

1 C.S,h是变量,
2
2 1 D.S,h,a是变量, 2源自a是常量 是常量34
如果用总长为60 m的篱笆围成一个长方形场地,设长方形的
面积为S(m2),周长为p(m),一边长为a(m),那么S,p,a 中 是变量的是( A . S和 p ) B . S和 a C . p和 a D . S, p, a
知1-练
1
在圆的周长C=2πR中,常量与变量分别是( 2 3 4 5 A.2是常量,C、π、R是变量 B.2π是常量,C、R是变量 C.C、2是常量,R是变量 D.2是常量,C、R是变量
)
知1-练
2 3 4
5
6 7
1 在三角形的面积公式S= ah,a=2 cm中,下列说法正确 2 的是( ) 1 A.S,a是变量, h是常量 12 B.S,h是变量, 是常量
知1-导
(1) 这个问题中,涉及哪几个量? 观察上表,热气球在升空的过程中平均每分上升多少米? 你能求出上升后3 min和6 min时热气球到达的海拔高度吗?
问 题(二)
S市某日自动测量仪记下的用电 负荷曲线如图所示: 看图回答: (1)这个问题中,涉及哪几个量? (2)给出这天中的某一时刻,如4.5 h, 20 h, 能找到这 一时刻的负荷y(×103兆瓦) 是多少吗?你是怎么找到的? 找到的值是唯一确定的吗?
知1-导
知识点
1
常量与变量
问 题(一)
用热气球探测髙空气象,设热气球从海拔 1 800 m处的某地升 空(下图),在一段时间内,它匀速上 升.它上升过程中到达的海拔高 度h m与上升时间t min的 关系记录如下表:
时间 t/min 海拔高 度 h/m 0 1800 1 1830 2 1860 3 1890 4 1920 5 1950 6 1980 7 2010 … …
2
2 1 D.S,h,a是变量, 2源自a是常量 是常量34
如果用总长为60 m的篱笆围成一个长方形场地,设长方形的
面积为S(m2),周长为p(m),一边长为a(m),那么S,p,a 中 是变量的是( A . S和 p ) B . S和 a C . p和 a D . S, p, a
知1-练
1
在圆的周长C=2πR中,常量与变量分别是( 2 3 4 5 A.2是常量,C、π、R是变量 B.2π是常量,C、R是变量 C.C、2是常量,R是变量 D.2是常量,C、R是变量
)
知1-练
2 3 4
5
6 7
1 在三角形的面积公式S= ah,a=2 cm中,下列说法正确 2 的是( ) 1 A.S,a是变量, h是常量 12 B.S,h是变量, 是常量
知1-导
(1) 这个问题中,涉及哪几个量? 观察上表,热气球在升空的过程中平均每分上升多少米? 你能求出上升后3 min和6 min时热气球到达的海拔高度吗?
问 题(二)
S市某日自动测量仪记下的用电 负荷曲线如图所示: 看图回答: (1)这个问题中,涉及哪几个量? (2)给出这天中的某一时刻,如4.5 h, 20 h, 能找到这 一时刻的负荷y(×103兆瓦) 是多少吗?你是怎么找到的? 找到的值是唯一确定的吗?
知1-导
知识点
1
常量与变量
问 题(一)
用热气球探测髙空气象,设热气球从海拔 1 800 m处的某地升 空(下图),在一段时间内,它匀速上 升.它上升过程中到达的海拔高 度h m与上升时间t min的 关系记录如下表:
时间 t/min 海拔高 度 h/m 0 1800 1 1830 2 1860 3 1890 4 1920 5 1950 6 1980 7 2010 … …
八年级数学上册 第十二章全等三角形小结与复习课件2_6-10
∵∠ACB=∠ECD,CB=CD,
∠ABC=∠EDC, ∴△EDC≌△ABC(ASA).
CD
∴DE=BA.
E
答:测出DE的长就是A、B之间的距离.
花瓶里的纸花与笔筒中毛笔同时被主人摆放在案桌上。之后,蚂蚁逢人便说:“当你遇到无法逾越的障碍时,不妨换一种方式。玛茨亚很机灵,不过还是被吓了一跳。 电影在线观看 /tv/29.html 它倒还能挺直身子走路。
AD=AD, AB=AC,
∴ Rt△ADB ≌ Rt△ADC(HL). ∴BD=CD.
A
B
D
C
方法总结
利用全等三角形可以测量一些不易测量的距离和长度,还可对某些 因素作出判断,一般采用以下步骤: (1)先明确实际问题;
(2)根据实际抽象出几何图形;
(3)经过分析,找出证明途径; (4)书写证明过程.
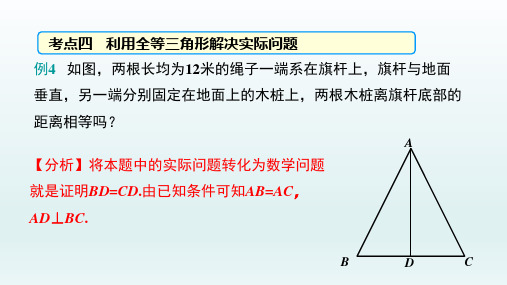
考点四 利用全等三角形解决实际问题 例4 如图,两根长均为12米的绳子一端系在旗杆上,旗杆与地面 垂直,另一端分别固定在地面上的木桩上,两根木桩离旗杆底部的 距离相等吗?
A
【分析】将本题中的实际问题转化为数学问题
就是证明BD=CD.由已知条件可知AB=AC,
AD⊥BC.
B
D
C
解:相等,理由如下:
∵AD⊥BC, ∴∠ADB=∠ADC=90°. 在Rt△ADB和Rt△ADC中,
针对训练
5.如图,有一湖的湖岸在A、B之间呈一段圆弧状,A、B间的距离不 能直接测得.你能用已学过的知识或方法设计测量方案,求出A、B间 的距离吗?
解:要测量A、B间的距离,可用如下方法:
D=BC,
再作出BF的垂线DE,使A、C、E在一条直
线上,
“现在我再来匀一匀。,
沪科版八年级数学上册第12章一次函数PPT教学课件
中”,一个量在某一变化过程中是常量,而在另一个
变化过程中,它可能是变量;如在s=vt中,当s一定
时,v、t为变量,s为常量;当t一定时,s、v为变量,
t为常量.
2.易错警示:
知1-讲
(1)判断一个量是常量还是变量,应先看它是否在一 个变化过程中,若在,则看它在这个变化过程中 数值是否发生改变. (2)常量与变量不是绝对的,而是对一个变化过程而 言的. (3)指出一个变化过程中的常量时,应连同它前面的 符号.
1
课堂讲解
列表法 解析法
2
课时流程
逐点 导讲练
自变量的取值范围
课堂 小结
课后 作业
表示函数关系主要有下列三种方法:列表法、解
析法、图象法.
知识点 1
列表法
列表法
知1-讲
通过列出自变量的值与对应函数值的表格来表 示函数关系的方法叫做列表法.
知1-讲
例1 一个小球在一个斜坡上由静止开始向下运动,
通过仪器观察 得到小球滚动的距离s(米)与时间
t(秒)的数据如下表: t s 1 2 2 8 3 18 4 32 „ „
请写出s与t的函数表达式.
知1-讲
解:因为t=1时,s=2;t=2时,s=8=2×4=2×22;
t=3时,s=18=2×9=2×32;
t=4时,s=32=2×16=2×42,
所以s与t的函数表达式为s=2t2.
(3)对于自变量的每一个确定的值,函数有且只有一个
值与之对应.
知2-讲
例2 下列关于变量x,y的关系式:①3x-2y=5;②y
=|x|;③2x-y2=10中,y是x的函数的是( B )
A.①③
B.①②
C.②③
八年级数学上册第12章一次函数12.1函数(第2课时)教学课件(新版)沪科版
(1)y=21x+4; (3)y=x 2 ;
(2)x y3=-2x2; (4)
y= . 解(1)当x=3时,y=2x+4=2×3+4=10.
(2)当x=3时,y=-2x2=-2×32=-18.
(3)当x=3时,y=
1=
x2
1 =1.
32
(4)当x=3时,y= x 3 = 3 3 =0.
二、新课讲解
罐头盒等圆柱形的物体常常如下图那样堆放. 随着层数的增加,物体的总数是如何变的?
填写下表:
层数n
12
物体总数y 1 3
3 4 5 …… 6 10 15 ……
函数的表示法: 列表法
二、新课讲解
一定质量的气体在体积不变时,假若温度降低到273℃,则气体的压强为零.因此,物理学把-273℃作 为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃) 之间有如下数量关系:T=t+273,T≥0.
二、新课讲解
例1 求下列函数中自变量x的取值范 围
(1)y=21x+4;
x2
(3)y=
解:(1)x为全体实数 (2)x为全体实数 (3)x≠2 (4)x≥3
(2)x y3=-2x2;
(4)y=
在用表达式表示 函数时,要考虑
自变量的取值必
须使函数表达式 有意义
二、新课讲解
例2 当x=3时,求下列函数的函数 值.
所以,当x=6时,到甲、乙两个商店购买费用相同;
当4≤x﹤6时,到甲商店购买合算;
当6﹤x≤10时,到乙商店购买合算.
五、布置作业 习题12.1ຫໍສະໝຸດ 本课结束三、归纳小结
1、列表法; 2、解析法; 3、解析法在实际应用中要 注意自变量的取值范围.
八年级数学上册第12章一次函数本章复习课件沪科版.ppt
【解】因为直线y=(m+2)x-4经过第二、四象限, 则有m+2<0,得m<-2,即m的取值范围是m<-2.
4.确定函数表达式 常常以选择和填空的形式出现,或出现在大
题的第一问. 做这一类题关键在于求出k和b的值. 给出两点,求一次函数表达式
例4.已知一次函数的图象经过A(-2,-3),B (1,3)两点. (1)求这个一次函数的解析式; (2)试判断点P(-1,1)是否在这个一次函数 的图象上?
的A种笔记本的数量要少于B种笔记本数量的
2 3
,但又
不少于B种笔记本数量的
1 3
,如果设他们买A种笔记
本n本,买这两种笔记本共花费w元.
①请写出w(元)关于n(本)的函数关系式,并求 出自变量n的取值范围; ②请你帮他们计算,购买这两种笔记本各多少时,
花费最少,此时的花费是多少元?
【解】(1)设能买A种笔记本x本,则能买B种 笔记本(30-x)本 依题意得:12x+8(30-x)=300,解得x=15. 因此,能购买A,B两种笔记本各15本.
(2)①依题意得:w=12n+8(30-n),
即w=4n+240,
且 n < 2(30 - n) 和 n 1(30 本)的函数关系式 为:w=4n+240,
自变量n的取值范围是
15 n < 12 2
,n为
整数.
n=___3__.
【分析】常以填空题的形式出现.比较容易忽略限制条件k≠0. 这个在考试中往往一紧张就忘了,所以说我们在平时就应当 注意错解:因为y=(n+3)x|n|-2是一次函数,所以|n|-2=1,且 n+3≠0,解得n=3.
2.考查图象 两种形式:第一,基础题(选择题)给出表达式, 选图象; 第二,综合题(选择)与反比例函数和二次函数的 图象结合考查,后边复习时再讲.
4.确定函数表达式 常常以选择和填空的形式出现,或出现在大
题的第一问. 做这一类题关键在于求出k和b的值. 给出两点,求一次函数表达式
例4.已知一次函数的图象经过A(-2,-3),B (1,3)两点. (1)求这个一次函数的解析式; (2)试判断点P(-1,1)是否在这个一次函数 的图象上?
的A种笔记本的数量要少于B种笔记本数量的
2 3
,但又
不少于B种笔记本数量的
1 3
,如果设他们买A种笔记
本n本,买这两种笔记本共花费w元.
①请写出w(元)关于n(本)的函数关系式,并求 出自变量n的取值范围; ②请你帮他们计算,购买这两种笔记本各多少时,
花费最少,此时的花费是多少元?
【解】(1)设能买A种笔记本x本,则能买B种 笔记本(30-x)本 依题意得:12x+8(30-x)=300,解得x=15. 因此,能购买A,B两种笔记本各15本.
(2)①依题意得:w=12n+8(30-n),
即w=4n+240,
且 n < 2(30 - n) 和 n 1(30 本)的函数关系式 为:w=4n+240,
自变量n的取值范围是
15 n < 12 2
,n为
整数.
n=___3__.
【分析】常以填空题的形式出现.比较容易忽略限制条件k≠0. 这个在考试中往往一紧张就忘了,所以说我们在平时就应当 注意错解:因为y=(n+3)x|n|-2是一次函数,所以|n|-2=1,且 n+3≠0,解得n=3.
2.考查图象 两种形式:第一,基础题(选择题)给出表达式, 选图象; 第二,综合题(选择)与反比例函数和二次函数的 图象结合考查,后边复习时再讲.
2023年沪科版数学八年级上册第12章 小结与复习课件优选课件
取值范围; (5)若这个函数图象过点(1,4),求这个函数的解析式.
【分析】(1)由函数图象经过原点得m-3=0且2m+1≠0; (2)函数图象在y轴的截距为﹣2,即m-3=2;(3)由两 直线平行得2m+1=3;(4)一次函数中y随着x的增大而减 小,即2m+1<0;(5)代入该点坐标即可求解.
解:(1)∵函数图象经过原点,∴m﹣3=0,且2m+1≠0,
解得m=3;
(2)∵函数图象在y轴的截距为﹣2,∴m﹣3=﹣2,
且2m+1≠0,解得m=1;
(3)∵函数的图象平行于直线y=3x﹣3,∴2m+1=3,
解得m=1;
(4)∵y随着x的增大而减小,∴2m+1<0,解得m<
1 2
.
(5)∵该函数图象过点(1,4),代入得2m+1+m-3=4,
解得m=2,∴有下列函数:① y 6x 5 , ② y = 2 x ,
③ y x 4 , ④ y 4x 3 . 其中过原点的直
线是__②___;函数y随x的增大而增大的是_①__、__②__、__③__;函 数y随x的增大而减小的是__④____;图象在第一、二、三象 限的是__③___.
10· · O· s5·=2x 1·(00≤x≤5) x(秒)
课堂小结
变
函
量
数
解析法 列表法 图象法
一次函数y=kx+b(k,b为常数, 且k≠0),特例y=kx(k为常 数,且k≠0).
一次函数与一元一次 方程、一元一次不等式
一次函数与二 元一次方程
用待定系数 法求一次函 数的解析式
1. 设所求的一次函数表达式为y=kx+b; 2. 根据已知条件列出关于k、b的方程组; 3. 解方程,求出k、b; 4. 把求出的k,b代回表达式即可.
【分析】(1)由函数图象经过原点得m-3=0且2m+1≠0; (2)函数图象在y轴的截距为﹣2,即m-3=2;(3)由两 直线平行得2m+1=3;(4)一次函数中y随着x的增大而减 小,即2m+1<0;(5)代入该点坐标即可求解.
解:(1)∵函数图象经过原点,∴m﹣3=0,且2m+1≠0,
解得m=3;
(2)∵函数图象在y轴的截距为﹣2,∴m﹣3=﹣2,
且2m+1≠0,解得m=1;
(3)∵函数的图象平行于直线y=3x﹣3,∴2m+1=3,
解得m=1;
(4)∵y随着x的增大而减小,∴2m+1<0,解得m<
1 2
.
(5)∵该函数图象过点(1,4),代入得2m+1+m-3=4,
解得m=2,∴有下列函数:① y 6x 5 , ② y = 2 x ,
③ y x 4 , ④ y 4x 3 . 其中过原点的直
线是__②___;函数y随x的增大而增大的是_①__、__②__、__③__;函 数y随x的增大而减小的是__④____;图象在第一、二、三象 限的是__③___.
10· · O· s5·=2x 1·(00≤x≤5) x(秒)
课堂小结
变
函
量
数
解析法 列表法 图象法
一次函数y=kx+b(k,b为常数, 且k≠0),特例y=kx(k为常 数,且k≠0).
一次函数与一元一次 方程、一元一次不等式
一次函数与二 元一次方程
用待定系数 法求一次函 数的解析式
1. 设所求的一次函数表达式为y=kx+b; 2. 根据已知条件列出关于k、b的方程组; 3. 解方程,求出k、b; 4. 把求出的k,b代回表达式即可.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、一次函数与一元一次方程、一元一次不等式 1.一次函数与一元一次方程
求ax+b=0(a,b是
常数,a≠0)的解.
x为何值时, 从“数”的角度看 函数y= ax+b的值为0?
求ax+b=0(a, b是 常数,a≠0)的解. 从“形”的角度看
求直线y= ax+b, 与 x 轴交点的横坐标.
2.一次函数与一元一次不等式 x为何值时, 解不等式ax+b>0(a, b是常数,a≠0) . 从“数”的角度看 函数y= ax+b的值大于0? 求直线y= ax+b在 x轴上
小,即2m+1<0;(5)代入该点坐标即可求解.
解:(1)∵函数图象经过原点,∴m﹣3=0,且2m+1≠0, 解得m=3; (2)∵函数图象在y轴的截距为﹣2,∴m﹣3=﹣2, 且2m+1≠0,解得m=1;
(3)∵函数的图象平行于直线y=3x﹣3,∴2m+1=3,
1 (4)∵y随着x的增大而减小,∴2m+1<0,解得m< . 2
4.描点法画图象的步骤:列表、描点、连线 5.函数的三种表示方法: 列表法
解析式法
图象法.
二、一次函数、正比例函数及分段函数的相关概念与性质
1.一次函数与正比例函数的概念
一次函数 一般地,如果y= k x+b (k、b是常数, k≠0),那么y叫做x的一次函数.
0 时,一次函数 特别地,当b=____ 正比例函数 y=k x+b变为y= ___(kx k为常数,k≠0), 这时y叫做x的正比例函数. 2.分段函数 当自变量的取值范围不同时,函数的解析式也不同, 这样的函数称为分段函数.
【答案】D
方法总结 利用函数的图象解决实际问题,正确理解函数图象横纵坐 标表示的意义,理解问题的过程,能够通过图象得到函数问题 的相应解决.
针对训练
1.下列变量间的关系不是函数关系的是( C ) A.长方形的宽一定,其长与面积
B.正方形的周长与面积
C.等腰三角形的底边长与面积 D.圆的周长与半径
2.函数 y
3.一次函数与正比例函数的性质 字母取 值 ( k>0 )
函数
图象
经过的象限
第一、二、三象限 第一、三象限 第一、三、四象限
函数 性质
b>0
y=kx+b (k≠0) b=0 b<0
y随x 增大 而 增大
函数
字母取值 ( k<0 ) b>0
图象
经过的象限 第一、二、四象限 第二、四象限 第二、三、四象限
函数 性质
y=kx+b (k≠0)
b=0 b<0
y随x增 大而 减小
4.由待定系数法求一次函数的表达式 求一次函数表达式的一般步骤:
(1)先设出函数表达式;
(2)根据条件列关于待定系数的方程(组);
(3)解方程(组)求出表达式中未知的系数;
(4)把求出的系数代入设的解析式,从而具体写出这 个解析式.这种求表达式的方法叫待定系数法.
三 象限. 4.一次函数y=-5x+2的图象不经过第______
5.点(-1,y1),(2,y2)是直线y=2x+1上两点,则y1____ < y2 .
6. 填空题: 有下列函数:① y 6 x 5 , ③ y x4 ② y = 2x ,
考点二 一次函数的图象、性质及表达式的求法
例2 已知函数y=(2m+1)x+m﹣3; (1)若函数图象经过原点,求m的值; (2)若函数图象在y轴的截距为﹣2,求m的值; (3)若函数的图象平行直线y=3x﹣3,求m的值; (4)若这个函数是一次函数,且y随着x的增大而减小,求m的 取值范围; (5)若这个函数图象过点(1,4),求这个函数的解析式. 【分析】(1)由函数图象经过原点得m-3=0且2m+1≠0; (2)函数图象在y轴的截距为﹣2,即m-3=2;(3)由两 直线平行得2m+1=3;(4)一次函数中y随着x的增大而减
解不等式ax+b>0(a,
Байду номын сангаас
方的部分(射线)所对 从“形”的角度看 b是常数,a≠0) . 应的横坐标的取值范 围.
四、一次函数与二元一次方程 一般地,任何一个二元一次方程都可以转化为一次函
数y=kx+b(k、b为常数,且k≠0)的形式,所以每个二元一
次方程都对应一个一次函数,也对应一条直线. 利用图象法解二元一次方程组的一般步骤: ①两个方程分别转化为一次函数 ②在同一坐标系中画出两个函数图象 ③找出图象交点坐标 ④写出方程组的解
考点讲练
考点一 函数的概念与图象
例1 (2016春•蓬溪县期中)王大爷饭后出去散步,从家中走20 分钟到离家900米的公园,与朋友聊天10分钟后,用15分钟返回 家中.下面图形表示王大爷离家时间x(分)与离家距离y(米) 之间的关系是( D )
O
O
O
O
A
B
C
D
【分析】对四个图依次进行分析,符合题意者即为所求.
2 中,自变量x的取值范围是( B ) 3 x
A.x>3 B.x<3 C.x≤3 D.x≥-3 3.(2016•滑县模拟)星期天下午,小强和小明相约在某公交 车站一起乘车回学校,小强从家出发先步行到车站,等小明到 了后两人一起乘公共汽车回到学校.图中折线表示小强离开家 的路程y(千米)和所用的时间x(分)之间的函数关系.下列 说法错误的是( C ) A.小强从家到公共汽车站步行了2千米 B.小强在公共汽车站等小明用了10分钟 C.公交车的平均速度是34千米/小时 D.小强乘公交车用了30分钟 x(分) y(千米)
解得m=1;
(5)∵该函数图象过点(1,4),代入得2m+1+m-3=4,
解得m=2,∴该函数的解析式为y=5x-1.
方法总结 一次函数与y轴的交点就是y=kx+b中b的值,两条直线平行, 其函数表达式中的一次项系数k相等,当k>0时,y随x的增大而 增大;当k<0时,y随x的增大而减小.
针对训练
第12章 一次函数
小结与复习
要点梳理
考点讲练
当堂练习
课堂小结
要点梳理
一、函数
1.
数值发生变化的量 数值始终不变的量
叫变量,
叫常量.
2.函数定义: 在一个变化过程中,如果有两个变量x与y,并且 对于x的每一个确定的值,y都有唯一确定的值与其
对应,那么我们就说x是自变量,y是x的函数.
3.函数的图象:对于一个函数,如果把自变量与函 数的每对对应值分别作为点的横坐标和纵坐标,那 么坐标平面内由这些点组成的图形,就是这个函数 的图象. (所用方法:描点法)
