蒙卡
蒙卡剂量算法(XVMC)在胸部肿瘤调强放射治疗计划设计中的临床价值

n r n ado a g
ark ( A )Reut: h ie n e e e ne al a o t a d ii i e c em grh w s in cn. t s O R . sl T e f r c t n i s d e b we Mo tC o l rh n n t StP n i a f o tm a gi at r gi m F e e l B l i s f i
刘吉平 ,王彬 冰 , 杨 静 ,白 雪 ,张 莉 ( 浙江省肿瘤医院 放射物理室, 浙江 杭州 302) 102
摘要 : 目的 : 比较 蒙卡 剂 量算 法 ( neC r ) 笔形 柬剂 量 算 法 (ii i P niB a 在 胸 部 肿 瘤调 强 放 射治 疗 计 划 Mo t al 和 o Fnt St ec em) e e l
果 相差 较 大 。 论 : 于组 织 密 度 差 异较 大 的 胸部 肿 瘤 病例 , 别 是使 用 调 强 放射 治 疗 技 术 时 , XV 结 对 特 用 MC 剂量 算 法评 估
放射 治疗 计 划 更准 确 。
关键 词 : 卡剂 量 算 法 ; 强 放 射治 疗 蒙 调 D 编 码 : o:03 6 ̄i n10 - 0 X2 1.5 0 OI d i1. 9 .s.0 5 22 .0 0 . 4 9 s 00
一款低放液体活度监测仪响应的蒙卡分析

一款低放液体活度监测仪响应的蒙卡分析发布时间:2021-06-02T05:59:34.342Z 来源:《中国电业》(发电)》2021年第4期作者:平建晓1,连琦2,曲广卫2,陈宇轩2,赵江斌2,杨中中2,孙世敏2 [导读] 根据实际需求,计算了反应堆二次水污染监测时常选用的典型核素24Na和16N核素的响应因子,其中对24Na衰变的特殊性,考虑了其真符合加出效应。
(1 三门核电有限公司,浙江三门 317112;2 陕西卫峰核电子有限公司,陕西西安 710118)摘要:本文以卫峰设计的一款WF-LL-810B型LaBr3:Ce低放液体活度监测仪为研究对象,用蒙特卡罗软件MCNP仿真计算了对137Cs溶液的全谱及全能峰的响应因子并与实验值进行了对比,结果均符合较好,证明采用的计算模型合理、可靠。
根据实际需求,计算了反应堆二次水污染监测时常选用的典型核素24Na和16N核素的响应因子,其中对24Na衰变的特殊性,考虑了其真符合加出效应。
关键词:低放液体;蒙特卡罗方法;LaBr3:Ce;24Na;16N MCNP Simulation of Low-level Radioactivity Liquid Monitor Ping Jian-xiao, Lian Qi, Qu Guang-wei, Chen Yu-xuan, Zhao Jiang-bin, Yang Zhong-zhong, Sun Shi-min (Sanmen Nulcear Power Co., Ltd. Zhejiang Sanmen, 317112 Shaanxi WeiFeng Nuclear Instrument Inc., Shaanxi Xi’an, 710118) Abstract:Monto Carlo software MCNP has been applied to simulate the designed WF-LL-810B LaBr3:Ce low level radioactivity liquid monitor responses for 137Cs liquid. Both the simulated 137Cs full spectrum and full energy peak responses agree well with experiment results,which proves that the model is reasonable and reliable. Responses for nuclides of 24Na and 16N which are common in reactor secondary water contamination monitoring have been simulated, in which true coincidence of 24Na has been accounted for due to its special decay pattern. Keywords:Low level liquid activity; Monto Carlo simulation; LaBr3:Ce; 24Na; 16N1 引言核电站反应堆在运行中可能发生轻微放射性释放而产生放射性废液,泄漏的放射性废液经放射性废液系统收集和处理,在满足排放标准后进行排放。
蒙卡方法模拟 -回复

蒙卡方法模拟-回复什么是蒙特卡罗方法模拟?蒙特卡罗方法模拟(Monte Carlo simulation)是一种使用概率和统计方法来解决问题的计算机模拟技术。
它通过随机取样(Random Sampling)和重复试验(Repetitive Trial)的方式,模拟系统的行为,并根据得到的随机结果进行推断和决策。
蒙特卡罗方法模拟的原理是基于概率统计的思想。
它将问题转化为一个或多个随机变量的分布,并通过大量的模拟实验来估计变量的期望值、分布、方差等统计指标。
蒙特卡罗方法模拟的步骤如下:1. 定义问题:明确需要解决的问题和目标,并了解问题的特点和约束条件。
2. 建立数学模型:将问题转化为数学模型,包括确定输入变量和输出变量,并定义它们之间的关系。
3. 设定随机数生成器:选择合适的随机数生成器,以产生随机样本,并设置样本的数量。
4. 生成随机样本:根据概率分布函数和相关参数,使用随机数生成器生成一系列的随机样本。
5. 运行模拟实验:将生成的随机样本输入到数学模型中,通过模拟实验来模拟系统的行为,并记录输出变量的值。
6. 统计分析和推断:根据模拟实验得到的结果,进行统计分析,计算输出变量的期望值、分布、方差等统计指标,并进行推断和决策。
7. 验证和优化:对模拟结果进行验证和优化,与实际数据进行比较,检查模型的准确性和可靠性,并对模型进行调整和改进。
蒙特卡罗方法模拟的应用非常广泛,例如:- 金融领域:投资组合管理、期权定价、风险管理等。
- 工程领域:可靠性分析、设计优化、系统仿真等。
- 自然科学领域:天气预测、生物模拟、物理实验模拟等。
- 经济学领域:市场研究、经济预测、政策决策等。
总结一下,蒙特卡罗方法模拟是一种基于概率统计的计算机模拟技术。
通过随机取样和重复试验的方式,模拟系统的行为,并根据随机结果进行推断和决策。
它的步骤包括定义问题、建立数学模型、设定随机数生成器、生成随机样本、运行模拟实验、统计分析和推断、验证和优化。
蒙卡三维独立剂量验证系统技术要求

-支持按照关键字如加速器、验证结果是否通过等进行筛选
-将患者验证数据进行分类,并将结果导出到Excel
同一患者多治疗计划合并
-支持同一患者不同治疗计划的独立分析
-支持同一患者不同治疗计划的合并分析
-当同一患者多个治疗计划存在时,可以删除冗余计划
批准与取消批准
-支持对整个计划进行批准
调整剂量网格大小
-支持使用TPS网格
-支持根据床结构自动外扩网格
自定义三个方向网格体素大小
-对于核磁加速器支持在剂量网格中自动生成上下线圈
多剖面结果显示
-支持任意位置的剂量剖线值
-支持水平剖线图显示剂量剖线值
-支持竖直剖线图显示剂量剖线值
5
分次剂量验证
分次治疗评价结果图表展示
-支持图表显示已治疗分次伽马值
支持对计划检查、QA检查和分次检查进
行独立批准
4
治疗计划独立计算剂量验证
剂量体积直方图(DVH)对比分析
支持对感兴趣体积的DVH按绝对值或者相对值进行显示或者隐藏
临床目标模板及自动分析
-支持按照计划类型设定临床目标集合
-支持自动使用匹配成功的临床目标集合对当前计划进行检查分析
靶区覆盖率对比分析
支持通过设定平均剂量差异阈值进行评估
-支持以机器、日期、病人名称和ID等方式对DlCOM文件进行分组存放,方便查找
自动将计划和剂量加载到对应的QA模体上进行舱证
通过计划文件自动判断是否为基于验证模体的QA计划并自动将计划和剂量加载到正确的QA模体上,自动完成验证
3
数据管理
病人管理功能
病人管理区域,提供了病人列表显示、刷新、搜索、删除等功能
6
python蒙卡遗传算法

python蒙卡遗传算法Python蒙特卡洛遗传算法介绍蒙特卡洛遗传算法(Monte Carlo Genetic Algorithm)是一种基于概率和随机性的优化算法。
它结合了蒙特卡洛模拟和遗传算法的思想,用于解决复杂的优化问题。
Python作为一种强大的编程语言,提供了丰富的库和工具,使得实现蒙特卡洛遗传算法变得简单且高效。
基本原理蒙特卡洛遗传算法通过模拟随机事件来估计问题的最优解。
它使用遗传算法中的进化过程来搜索解空间,并使用蒙特卡洛模拟来评估每个个体的适应度。
1. 初始化种群:随机生成初始种群,其中每个个体代表一个可能的解。
2. 评估适应度:对每个个体进行适应度评估,即计算其在问题空间中的目标函数值。
3. 选择操作:根据适应度值选择父代个体进行交叉和变异操作。
4. 交叉操作:对选定的父代个体进行交叉操作,生成子代个体。
5. 变异操作:对子代个体进行变异操作,引入新的基因组合。
6. 更新种群:将子代个体与父代个体合并,形成新的种群。
7. 重复步骤2-6,直到满足停止条件(达到最大迭代次数或找到满意的解)。
Python实现下面是一个简单的Python代码示例,演示了如何使用蒙特卡洛遗传算法解决一个简单的优化问题。
```pythonimport random# 目标函数:计算x^2 + y^2 的最小值def objective_function(x, y):return x**2 + y**2# 初始化种群def initialize_population(population_size):population = []for _ in range(population_size):x = random.uniform(-10, 10)y = random.uniform(-10, 10)population.append((x, y))return population# 计算适应度值def calculate_fitness(population):fitness_values = []for individual in population:x, y = individualfitness_values.append(objective_function(x, y))return fitness_values# 选择操作:轮盘赌选择def selection(population, fitness_values):total_fitness = sum(fitness_values)probabilities = [fitness / total_fitness for fitness infitness_values]selected_population = []for _ in range(len(population)):selected_individual = random.choices(population, probabilities)[0]selected_population.append(selected_individual)return selected_population# 交叉操作:单点交叉def crossover(parent1, parent2):crossover_point = random.randint(1, len(parent1) - 1)child1 = parent1[:crossover_point] + parent2[crossover_point:] child2 = parent2[:crossover_point] + parent1[crossover_point:] return child1, child2# 变异操作:随机变异def mutation(individual, mutation_rate):mutated_individual = []for gene in individual:if random.random() < mutation_rate:mutated_gene = random.uniform(-10, 10)mutated_individual.append(mutated_gene)else:mutated_individual.append(gene)return tuple(mutated_individual)# 更新种群def update_population(selected_population, population_size, mutation_rate):new_population = []while len(new_population) < population_size:parent1, parent2 = random.sample(selected_population, 2) child1, child2 = crossover(parent1, parent2)mutated_child1 = mutation(child1, mutation_rate)mutated_child2 = mutation(child2, mutation_rate)new_population.extend([mutated_child1, mutated_child2]) return new_population[:population_size]# 主函数def main():population_size = 100max_iterations = 1000mutation_rate = 0.01population = initialize_population(population_size)for iteration in range(max_iterations):fitness_values = calculate_fitness(population)selected_population = selection(population, fitness_values) population = update_population(selected_population, population_size, mutation_rate)best_solution = min(population, key=lambda individual: objective_function(*individual))print("Best solution:", best_solution)```总结蒙特卡洛遗传算法是一种强大的优化算法,通过结合蒙特卡洛模拟和遗传算法的思想,可以解决各种复杂的优化问题。
基于MCNP蒙卡软件的并行运算性能研究
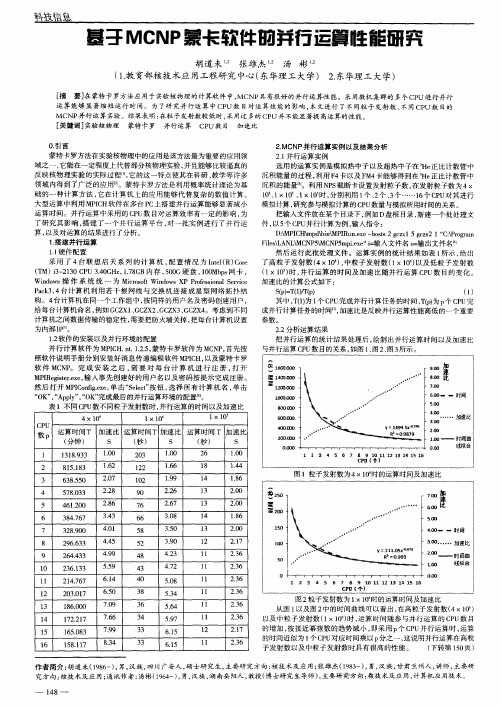
然后 打开 M P I C o n i f g . e x e , 单击“ S e l e c t ” 按钮, 选择 所有计 算机 名 , 单击 “ O K ” , “ A p p l y ” , “ O K ” 完成最后 的并行运算环境的配置 。 表 1不同 C P U 数不同粒子发射数时 , 并行运算 的时间 以及加速 比
1 . 2软件 的安装 以及并行环境 的配置 并行计算 软件为 M P I C H . n t . 1 . 2 . 5 , 蒙 特卡罗软件为 MC N P , 首先 按 照软件说 明手 册分别安装好 消息传 递编程软件 MP I C H, 以及蒙特 卡罗 软件 M C N P 。完成安装之后 , 需要 对 每 台 计 算 机 进 行 注 册 , 打 开 M P I R e g i s t e r . e x e , 输人事先创 建好 的用户 名以及密码按 提示完成注册 。
D: \ MP I CH\ mp d k b i n \ MPI Ru n . e x e— h o s t s 2 g c z xБайду номын сангаас1 5 g e z x 2 1” C: L P r o g r a m
F i I e s \ L AN L \ MC N P 5 \ MC N P 5 m p i . e x e ” i - 输入文件名 0 = 输 出文件名 然 后运行此批处 理文件 。运算 实例 的统计 结果如表 1 所示 , 给出
基孑 MC NP 蒙卡软件的并行 运算性雒研奔
胡道 未 张雄 杰 1 , 2 汤 彬1 , 2 ( 1 . 教 育部 核技 术应 用工程研 究 中心 ( 东华理 工 大学 ) 2 . 东华理 工大 学)
[ 摘 要] 在 蒙特卡 罗方 法应 用于实验核物理 的计算软件 中, MC N P 有很好的并行运算性能。采用微机集群的 多个 c P u进行并行 运 算能够显 著缩短运行 时间。 为了z q -  ̄ 并行运 算 中C , P U数 目对运 算性能的影响 , 本文进行 了不同粒子 发射数 、 不 同C P U¥  ̄目的 MC NP 并行运算 实验。结果表明 : 在粒 子发射数较低 时, 采用过多的C P U并不能显著提 高运 算的性能。 [ 关键词 ] 实验核物理 蒙特 卡罗 并行运算 c P u数 目 加速比
蒙卡方法模拟
蒙卡方法模拟
蒙卡方法模拟(Monte Carlo Simulation)是一种统计模拟方法,基于概率理论和随机数生成来实现对复杂系统的建模和模拟。
它通过对系统的一系列随机样本进行抽样,并利用这些样本的统计特性来估计系统的性能和输出结果。
蒙卡方法模拟的基本步骤包括:
1.定义问题:明确模拟的目标和问题,确定模拟的输入参数和输出结果。
2.建立模型:根据问题的实际情况,建立合适的数学模型或物理模型,将实
际问题转化为数学问题。
3.随机抽样:根据模型的随机性,生成一定数量的随机样本,用于模拟系统
的运行。
4.模拟运行:根据模型和随机样本,模拟系统的运行过程,记录每个样本的
运行结果。
5.统计处理:对模拟运行的结果进行统计分析,计算所需的性能指标和输出
结果。
蒙卡方法模拟具有以下几个特点:
1.适合处理高维问题:对于高维空间的问题,蒙卡方法模拟可以通过抽样来
近似求解,避免了复杂的解析求解。
2.可视化分析:通过图形化界面可以直观地展示模拟结果,便于分析问题原
因和找到改进方案。
3.需要大量计算资源:蒙卡方法模拟需要生成大量的随机样本,并进行复杂
的运算和处理,因此需要强大的计算资源。
4.对随机性敏感:蒙卡方法模拟的结果具有一定的随机性,因此需要设置足
够的样本数量以保证结果的稳定性和准确性。
蒙卡方法模拟在许多领域都有应用,如金融、能源、制造、医疗等。
它可以帮助人们更好地理解复杂系统的行为和性能,预测系统的未来趋势,并制定更好的决策和优化方案。
1。
蒙特卡洛往事
蒙特卡洛被誉为法网的风向标,其实,它在某种意义上是整个红土王朝的写照,它是费德勒至今未能征服的唯一一项ATP1000赛事,更是纳达尔时代的开启之地……
2005 科里亚的悲伤
阿根廷球员奎勒莫·科里亚算得上是
蒙特卡洛往事文/耶加雪啡
其中就包括了蒙特卡洛、罗马、罗兰·加洛斯,连续三站红土决赛被纳达尔三连杀的无奈经历。
其实在这之前,费德勒在蒙卡赛最好的战绩也不过是1/4决赛。
然而2006年的费天王,真是人挡杀人,佛挡杀佛,携澳网夺冠之势,对蒙卡冠军志在必夺。
决赛中,费德勒完全发挥出自己全德勒就已经在做了。
然而,当人们用崇拜的眼神期待着
瑞士天才再次奉献美妙表演时,纳达尔
用自己钢铁般的斗志和不懈的奔跑覆盖
了每一寸场地,一点一点将费德勒的作品
撕成碎片。
这时,包括费德勒本人在内的
每个人才意识到,西班牙人不只是一位战
神,他更是一头猛兽,随时都能够摧毁网
特卡洛、法网被决赛双杀;2008年双方交
手4次,费德勒0胜4负,蒙特卡洛、法网、
温网被决赛三杀。
当然,持续的攒人品还
是换来了巨大回报。
2009年费德勒终于
在索德林的“助攻”下夺得唯一的一个法
网桂冠,凑足了自己的全满贯事业。
从2009年起,费德勒一共参加了5次
蒙特卡洛大师赛,却再也没有在签表中与
乔科维奇。
上海蒙卡商务咨询有限公司企业信用报告-天眼查
4.4 企业业务
截止 2018 年 10 月 23 日,根据国内相关网站检索及天眼查数据库分析,未查询到相关信息。不排除因信 息公开来源尚未公开、公开形式存在差异等情况导致的信息与客观事实不完全一致的情形。仅供客户参 考。
4.5 竞品信息
截止 2018 年 10 月 23 日,根据国内相关网站检索及天眼查数据库分析,未查询到相关信息。不排除因信 息公开来源尚未公开、公开形式存在差异等情况导致的信息与客观事实不完全一致的情形。仅供客户参 考。
五、风险信息
5.1 被执行人信息
截止 2018 年 10 月 23 日,根据国内相关网站检索及天眼查数据库分析,未查询到相关信息。不排除因信 息公开来源尚未公开、公开形式存在差异等情况导致的信息与客观事实不完全一致的情形。仅供客户参 考。
5.2 失信信息
截止 2018 年 10 月 23 日,根据国内相关网站检索及天眼查数据库分析,未查询到相关信息。不排除因信 息公开来源尚未公开、公开形式存在差异等情况导致的信息与客观事实不完全一致的情形。仅供客户参 考。
2,550
4
企业名称
注册时间
上海元坤医疗科技发展有 限公司
2013-12-12
注册资本
状态 法定代表人
10376.04 万人民 存续(在 刘蒙
币
营、开
业、在
册)
投资数额(万 元)
1,500
四、企业发展
4.1 融资历史
截止 2018 年 10 月 23 日,根据国内相关网站检索及天眼查数据库分析,未查询到相关信息。不排除因信 息公开来源尚未公开、公开形式存在差异等情况导致的信息与客观事实不完全一致的情形。仅供客户参 考。
DPM蒙卡方法在放疗剂量计算中的应用研究
万方数据
一l&42一
中国医学物理学杂志
第27卷第3期
2010年5月
dpm.in程序,按提示修改后,程序运行测试通过,说明 按此种方法解决了DPM与加速器能谱接口问题并可 以进行剂量计算,但需对其计算的准确性进行验证。 1.2组织模体的建立
笔者在DPM子程序genvoxel.in中构建了含低 密度肺和水材料的非均匀组织模型,DPM在该模体 中用6 MV—X线计算了九个规则射野的剂量;并用 PTWUNIDOSE型号剂量仪实际测量了相同深度处 的剂量;将模体CT扫描数据网络传输至拓能TOP. SLANE(TPSl)和医科达PrecisePlan(TPS2)两套TPS 中并计算了模体下相同深度的剂量,三者的计算结果 进行了对比分析。用以研究DPM计算的准确性。我们 所构建的模体见图2。其中实际测量中水为固体水 (其中一块带电离室探头插孔),密度为1.0 g/cm3,肺 为等效材料。物理密度为0.29 g/cm3。
商业化放射治疗计划系统(TPS)投入临床使用 体现着临床放射治疗技术发展的水平。目前TPS在 组织剂量分布计算方法上主要有经验模型、陈化扩散 模型以及基于笔形束和点核的卷积/叠加(Convolu. tion/Superposition)方法的模型等,而其优化模块则普 遍使用共轭梯度、模拟退火和遗传等优化算法对照射 野的剂量分布进行优化。通过反复优化搜索出满足处 方剂量和剂量限制的最优计算计划。治疗计划系统中 对于加速器的源部分只是根据测量加速器在标准水 箱中的剂量分布反推几个参数带人公式中,只能在某 些能量段和特定介质中才能保证足够的计算精度,不 能准确地表达出加速器出束的全部信息,此方法主要 特点是计算速度快.均匀组织中计算误差能控制在 l%以内。但在计算非均匀介质中的剂量沉积会有较 大的误差,特别是在软组织与空气或骨骼交界面附近 可达30%左右【2】。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章Monte Carlo 法§8.1 概述Monte Carlo 法不同于前面几章所介绍的确定性数值方法,它是用来解决数学和物理问题的非确定性的(概率统计的或随机的)数值方法。
Monte Carlo 方法(MCM),也称为统计试验方法,是理论物理学两大主要学科的合并:即随机过程的概率统计理论(用于处理布朗运动或随机游动实验)和位势理论,主要是研究均匀介质的稳定状态[1]。
它是用一系列随机数来近似解决问题的一种方法,是通过寻找一个概率统计的相似体并用实验取样过程来获得该相似体的近似解的处理数学问题的一种手段。
运用该近似方法所获得的问题的解in spirit更接近于物理实验结果,而不是经典数值计算结果。
普遍认为我们当前所应用的MC技术,其发展约可追溯至1944年,尽管在早些时候仍有许多未解决的实例。
MCM的发展归功于核武器早期工作期间Los Alamos(美国国家实验室中子散射研究中心)的一批科学家。
Los Alamos 小组的基础工作刺激了一次巨大的学科文化的迸发,并鼓励了MCM在各种问题中的应用[2]-[4]。
“Monte Carlo”的名称取自于Monaco(摩纳哥)内以赌博娱乐而闻名的一座城市。
Monte Carlo 方法的应用有两种途径:仿真和取样。
仿真是指提供实际随机现象的数学上的模仿的方法。
一个典型的例子就是对中子进入反应堆屏障的运动进行仿真,用随机游动来模仿中子的锯齿形路径。
取样是指通过研究少量的随机的子集来演绎大量元素的特性的方法。
例如,)f在b(x<上的平均值可以通过间歇性随机选取的有xa<限个数的点的平均值来进行估计。
这就是数值积分的Monte Carlo 方法。
MCM 已被成功地用于求解微分方程和积分方程,求解本征值,矩阵转置,以及尤其用于计算多重积分。
任何本质上属随机组员的过程或系统的仿真都需要一种产生或获得随机数的方法。
这种仿真的例子在中子随机碰撞,数值统计,队列模型,战略游戏,以及其它竞赛活动中都会出现。
Monte Carlo 计算方法需要有可得的、服从特定概率分布的、随机选取的数值序列。
§8.2 随机数和随机变量的产生[5]-[10]全面的论述了产生随机数的各类方法。
其中较为普遍应用的产生随机数的方法是选取一个函数)(x g ,使其将整数变换为随机数。
以某种方法选取0x ,并按照)(1k k x g x =+产生下一个随机数。
最一般的方程)(x g 具有如下形式:m c ax x g mod )()(+=(8.1)其中=0x 初始值或种子(00>x ) =a 乘法器(0≥a )=c 增值(0≥c )=m 模数对于t 数位的二进制整数,其模数通常为t 2。
例如,对于31位的计算机m 即可取1312-。
这里a x ,0和c 都是整数,且具有相同的取值范围0,,x m c m a m >>>。
所需的随机数序{}n x 便可由下式得m c ax x n n m od )(1+=+ (8.2)该序列称为线性同余序列。
例如,若70===c a x 且10=m ,则该序列为7,6,9,0,7,6,9,0…… (8.3)可以证明,同余序列总会进入一个循环套;也就是说,最终总会出现一个无休止重复的数字的循环。
(8.3)式中序列周期长度为4。
当然,一个有用的序列必是具有相对较长周期的序列。
许多作者都用术语乘同余法和混合同余法分别指代0=c 和0≠c 时的线性同余法。
选取c a x ,,0和m 的法则可参见[6,10]。
这里我们只关心在区间)1,0(内服从均匀分布的随机数的产生。
用字符U 来表示这些数字,则由式(8.2)可得mx U n 1-=(8.4)这样U 仅在数组{}m m m m /)1(,......,/2,/1,0-中取值。
(对于区间(0,1)内的随机数,一种快速检测其随机性的方法是看其均值是否为0.5。
其它检测方法可参见[3,6]。
)产生区间),(b a 内均匀分布的随机数X ,可用下式U a b a X )(-+= (8.5)用计算机编码产生的随机数(利用式(8.2)和(8.4))并不是完全随机的;事实上,给定序列种子,序列的所有数字U 都是完全可预测的。
一些作者为强调这一点,将这种计算机产生的序列称为伪随机数。
但如果适当选取c a ,和m ,序列U 的随机性便足以通过一系列的统计检测。
它们相对于真随机数具有可快速产生、需要时可再生的优点,尤其对于程序调试。
Monte Carlo 程序中通常需要产生服从给定概率分布)(x F 的随机变量X 。
该步可用[6],[13]-[15]中的几种方法加以实现,其中包括直接法和舍去法。
直接法(也称反演法或变换法),需要转换与随机变量X 相关的累积概率函数)()(x X prob x F ≤=(即:)(x F 为x X ≤的概率)。
1)(0≤≤x F 显然表明,通过产生(0,1)内均匀分布随机数U ,经转换我们可得服从)(x F 分布的随机样本X 。
为了得到这样的具有概率分布)(x F 的随机数X ,不妨设)(x F U =,即可得)(1U F X -= (8.6)其中X 具有分布函数)(x F 。
例如,若X 是均值为μ呈指数分布的随机变量,且∞<<-=-x e x F x 0,1)(/μ (8.7)在)(x F U =中解出X 可得)1ln(U X --=μ(8.8)由于)1(U -本身就是区间(0,1)内的随机数,故可简写为U X ln μ-= (8.9)有时(8.6)式所需的反函数)(1x F -不存在或很难获得。
这种情况可用舍去法来处理。
令dx x dF x f )()(=为随机变量X 的概率密度函数。
令b x a >>时的0)(=x f ,且)(x f 上界为M (即:M x f ≤)(),如图8.1所示。
我们产生区间(0,1)内的两个随机数),(21U U ,则11)(U a b a X -+= M U f 21=(8.10)分别为在(a,b)和(0,M)内均匀分布的随机数。
若)(11X f f ≤ (8.11)则1X 为X 的可选值,否则被舍去,然后再试新的一组),(21U U 。
如此运用舍去法,所有位于)(x f 以上的点都被舍去,而位于)(x f 上或以下的点都由11)(U a b a X -+=来产生1X 。
图8.1 舍去法产生概率密度函数为)(x f 的随机变量例8.1 设计一子程序使之产生0,1之间呈均匀分布的随机数U 。
用该程序产生随机变Θ,其概率分布由下式给定πθθθ<<-=0),cos 1(21)(T解:生成U 的子程序如图8.2所示。
该子程序中,,0,21474836471221==-=c m 且1680775==a 。
应用种子数(如1234),主程序中每调用一次子程序,就会生成一个随机数U 。
种子数可取1到m 间的任一整数。
0001C**********************************************************0002 C PROGRAM FOR GENERATING RANDOM V ARIABLES WITH0003 C A GIVEN PROBABILITY DISTRIBUTION0004C**********************************************************00050006 DOUBLE PRECISION ISEED 00070008 ISEED=1234.D00009 DO 10 I=1,1000010 CALL RANSOM(ISEED,R)0011 THETA=ACOSD(1.0-2.0*R)0012 WRITE(6,*)I,THETA0013 10 CONTINUE0014 STOP0015 END0001C********************************************************* *0002 C SUBROUTINE FOR GENERATING RANDOM NUMBERS IN0003 C THE INTERV AL (0,1)0004C********************************************************* *00050006 SUBROUTINE RANDOM (ISEED,R)0007 DOUBLE PRECISION ISDDE,DEL,A0008 DATA DEL,A/2147483647.D0,16807.D0/00090010 ISDDE=DMOD(A*ISDDE,DEL) 0011 R=ISDDE/DEL0012 RETURN0013 END图8.2 例8.1的随机数生成器图8.2的子程序只是为了说明本章所介绍的一些概念。
大多数计算机都有生成随机数的子程序。
为了生成随机变量Θ,令)cos 1(21)(Θ-=Θ=T U则有 )21(cos )(11U U T -==Θ--据此,一系列具有给定分布的随机变量Θ便可由图8.2所示主程序中生成。
§8.3 误差计算Monte Carlo 程序给出的解按大量的检测统计都达到了平均值。
因此,该解中包含了平均值附近的浮动量,而且不可能达到100%的置信度。
要计算Monte Carlo 算法的统计偏差,就必须采用与统计变量相关的各种统计方法。
我们只简要介绍期望值和方差的概念,并利用中心极限定理来获得误差估计[13,16]。
设X 是随机变量。
则X 的期望值或均值x 定义为⎰∞∞-=dx x xf x )((8.12)这里)(x f 是X 的概率密度分布函数。
如果从)(x f 中取些独立的随机样本N x x x ,...,,21,那么的x 估计值就表现为N 个样本值的均值。
∑==N n n xN x 11ˆ(8.13)x 是X 的真正的平均值,而xˆ只是x 的有着准确期望值的无偏估计。
虽然xˆ的期望值等于x ,但x x ≠ˆ。
因此,我们还需要x ˆ的值在x 附近的分布测度。
为了估计X 以及xˆ在x 附近的的值的分布,我们需要引入X 的方差,其定义为X 与x 差的平方的期望值,即⎰∞∞--=-==dx x f x x x x x Var )()()()(222σ(8.14) 由2222)(x x x x x x +-=-,故有⎰⎰⎰∞∞-∞∞-∞∞-+-=dx x f x dx x xf x dx x f x x )()(2)()(222σ(8.15)或者 222)(x x x -=σ (8.16)方差的平方根称为标准差,即 2/122)()(x x x -=σ (8.17)标准差给出了x 在均值x 附近的分布测度,并由此给出了误差幅度的阶数。
