单轴晶体和双轴晶体
非线性光学复习总结

一.非线性基本概念线性极化率的基本概念:一、电场的复数表示法:E(r,t)=1/2E(r,ω)exp(-iωt)+c.c. (1)E(r,t)=Re{E(r,ω)exp(-iωt)} (2)E(r,t)=1/2E(r,ω)exp(-iωt) (3)以上三者物理含义是一致的,其严格数学表示是(1)式。
(注意是数学表达式,所以这种表示法主要还是为了运算的方便,具体那些系数、共轭神马的物理意义是其次的,不用太纠结。
)称为复振幅,代表频率为的简谐振动,的频率仅是数学描述,物理上不存在。
1/2是归一化系数。
对于线性算符,可采用(3)式进行简化计算,然后加c.c.或Re{ }即可对非线性算符,必须采用(1)式的数学形式计算二、因果性原理:某时刻的电场只能引起在此时刻以后介质的响应,而对此时刻以前的介质响应没有贡献。
也可以这样说,当光在介质中传播时,t时刻介质所感应的极化强度P(t)不仅与t时刻的光电场有关,也与此前的光电场有关。
(先有电场E,后有极化P)与此相关的是时间不变性原理:在某时刻介质对外电场的响应只与此前所加电场的时间差有关,而与所取的时间原点无关。
于是,极化强度表达的思路即是先找到时刻t之前附近的一段微小时间t-τ=dτ内电场的作用,再对从电场产生开始以来的时间进行积分,求得总的效应。
τ时刻电场,影响其后的极化:t时刻的极化,来自其前面时刻的电场贡献:或t时刻的极化,来自前面时刻的电场贡献:三、线性极化率:其中四、介电常数(各向同性介质):五、色散:由于因果性原理,导致必然是频率的函数,即介质的折射率和损耗都随光波长变化,称为色散现象。
正常色散:折射率随波长增加而减小。
六、KK关系:以上两式为著名的KK色散关系,由K-K关系课件,只要知道极化率的实部和虚部中任何一个与频率的函数关系(光谱特性)就可通过此关系求出另外一个。
线性极化率张量同样满足真实性条件:,所以,这两式是线性极化率的KK关系。
七、极化率的一维谐振子经典模型:没希望考了。
晶体的名词解释

晶体的名词解释我不得不承认晶体是奇妙的,是美丽的,它使无数的艺术家为之着迷。
晶体的名词解释:(1)异常晶体:指晶格中某一原子被异常电子或空穴占据而造成晶体缺陷时形成的晶体,也就是非整比化合物。
如碳钢的共析组织、过共析组织和亚共析组织。
(2)另类晶体:指除了具有晶体结构外,还具有单轴晶体的某些特征的晶体,如低温蜡,高温玻璃。
4.等轴晶体:晶体中相邻各晶面互相平行。
2.单轴晶体:指几何对称性一致的晶体,即同一个晶体内的所有晶面都在一个平面内,没有两个完全重合的晶面。
3.单形晶体:由一种原子组成的晶体称为单形晶体,如Na, Rb。
3.复形晶体:由多种原子组成的晶体称为复形晶体,如Ca。
2.位错晶体:晶体中由于晶体滑移(切变),原子的密度沿其滑移面方向发生变化而形成的晶体称为位错晶体,如Ba。
2.面心立方晶体:具有简单立方结构的单质是面心立方晶体,如金刚石。
2.简单立方晶体:由立方结构的金属组成的晶体称为简单立方晶体,如铝。
2.六方晶系:空间点阵类型属于六方晶系,其晶体中所有相同的晶面与晶向在空间上都呈正交关系。
(1)一轴晶体:指几何对称性一致的晶体,其空间点阵具有如下对称性:具有一个平行于{001}-{010}的一条完整的公共棱,具有两个互相垂直的面,它们互相垂直,具有三个互相垂直的棱。
(2)两轴晶体:几何对称性一致的晶体,但它不是任意的三维晶体,而是处于两个特定的空间点阵类型之间,在三个特定的空间点阵类型中,它们彼此间的差别表现在不同方向的两个基本对称性上。
两轴晶体又分为简单两轴晶体和复杂两轴晶体,前者是指具有一个平行于{001}-{010}的一条完整的公共棱,而后者则是具有两个互相垂直的面。
(3)三轴晶体:几何对称性一致的晶体,且空间点阵具有如下对称性:具有一个平行于{001}-{010}的三条完整的公共棱,具有三个互相垂直的面,它们互相垂直,而且彼此平行。
一个六方晶系点群,其中每个晶胞可以用30个三个轴互相垂直的矢量来表示,三个矢量的空间指向为( -1,0, 0)。
郑州大学电子线路非线性部分复习总结

郑州大学电子线路非线性部分复习总结第一篇:郑州大学电子线路非线性部分复习总结第一章1.(变压器乙类推挽乙类互补推挽)2.乙类互补推挽放大电路工作原理【乙类工作时,为了在负载上合成完整的正弦波,必须采用两管轮流导通的推挽电路】3.实际电路问题(小题)(交越失真产生的原因及补救的措施)【由于导通电压的影响,造成传输电路传输特性的起始段弯曲,在正弦波的激励下,输出合成电压波形将在衔接处出现严重失真,这种失真称为交越失真】【在输入端为两管加合适的正偏电压,使它们工作在甲乙类状态】4.互补推挽电路提出的原因,解决了什么样的问题【当乙类功率管工作时,只在半个周期导通为了在负载上合成完整的正弦波,必须采用两管轮流导通的推挽电路】5.单电源供电的互补推挽电路中,电容起到了什么作用,怎么等效成双电源供电【与双电源供电电路比较,仅在输出负载端串接一个大容量的隔直流电容Cl,VCC 与两管串接,若两管特性配对,则VO = VCC/2,CL 实际上等效为电压等于 VCC/2 的直流电源】6.传输线变压器传输信号的时候采用了什么样的方法【传输线变压器,低频依靠变压器磁耦合方式传输信号,高频依靠传输线电磁能交换方式传输信号,所以高频受限于传输线长度,低频受限于初级绕组电感量】 7.整流器的作用【整流器:电网提供的50Hz交流电—直流电。
整流电路的功能是将电力网提供的交流电压变换为直流电压】8.计算:利用传输线变压器,端电压相等,两端电流大小相等方向相反这样的准则计算传输线变压构成的阻抗变换器的阻抗比第二章丙类谐振功率放大器 1.电路结构【ZL ——外接负载,呈阻抗性,用 CL 与 RL 串联等效电路表示Lr 和 Cr ——匹配网络,与 ZL 组成并联谐振回路调节 Cr 使回路谐振在输入信号频率VBB——基极偏置电压,设置在功率管的截止区,以实现丙类工作】2.偏置条件【基极偏置电压,是静态工作点设置在功率管的截止区,以实现丙类(导通小于半个周期)工作】 3.工作原理【输入完整正余弦波形,ib和ic为脉冲波形,要求输出为同频率正余弦电压,所以在输入、输出端要有谐振回路,使ib和ic电流变为基波电压,实现无失真输出】 4.谐振回路的作用【选频:利用谐振回路的选频作用,可将失真的集电极电流脉冲变换为不失真的输出余弦电压阻抗匹配:调节 Lr 和 Cr , 谐振回路将含有电抗分量的外接负载变换为谐振电阻Re,实现阻抗匹配】5.直流供电【因为丙类功率谐振放大器是放大高频信号,对于高频信号的直流供电来说,应该引入高频扼流圈和滤波电容,进行高低频信号隔离,提高稳定性】 6.谐振功率放大器工作状态【欠压、临界和过压状态(波形形貌)】7.谐振功率放大器外部特性【负载特性放大特性(可以构成线性放大器,作为线性功放和振幅限幅器)调制特性(运用到基极、集电极调制电路,实现调幅作用)】第三章1.正弦波振荡器【反馈振荡器、负阻振荡器】 2.反馈振荡器结构组成【由主网络和反馈网络构成的闭合环路】3.闭合环路成为反馈振荡器的三个条件【(1)起振条件——保证接通电源后从无到有地建立起振荡(2)平衡条件——保证进入平衡状态后能输出等幅持续振荡(3)稳定条件——保证平衡状态不因外界不稳定因素影响而受到破坏】 4.三点式正弦波振荡器组成法则【交流通路中三极管的三个电极与谐振回路的三个引出端点相连接,其中,与发射极相接的为两个同性质电抗,而另一个(接在集电极与基极间)为异质电抗】 5.判断能否产生正弦振荡的方法【(1)是否可能振荡——首先看电路供电是否正确;二是看是否满足相位平衡条件(2)是否起振——看是否满足振幅起振条件(3)是否产生正弦波——看是否有正弦选频网络】6.3.2.3例题(不看例2)7.对于各个类型的振荡电路的优势【晶体振荡器优势:将石英谐振器作为振荡器谐振回路,就会有很高的回路标准性,因此有很高的频率稳定度】8.实现负阻振荡器利用的是什么【平均负增量电导】9.平均负增量电导在正弦波振荡器当中实现的作用【当正弦电压振幅增加时,相应的负阻器件向外电路提供的基波功率增长趋缓。
2020年高中物理竞赛—基础光学10双折射:晶体的光轴(共12张PPT)

( 垂直光轴截面 )
二. 单轴晶体中的波面 ( 惠更斯作图法(ve>vo) )
1. 光轴平行入射面,自然光斜入射负晶体中
B
•
A
B'
•
•
光轴
•
• 方解石
光轴
••
•
o光 e光
•
2. 光轴平行入射面,自然光垂直入射负晶体中
光轴
• •
方解石
•
光轴
• •
o光
e光
o光 e光
3. 光轴平行晶体表面,自然光垂直入射
负晶体 no ne
o光 ie,o
••
e光
加拿大树胶
••
e
o
•
• e光 o光
3. 波晶片(光轴平行于表面且厚度均匀的晶体)
自然光垂直入射波晶片后, o 光, e 光传播速度不同, 产生的相位不同 。
波晶片
出射 o 光 e 光的相差为
d
•
2π λ
(no
ne
)d
• •
e光 o光
波晶片分类
(no ne )d λ 4 (no ne )d λ 2 (no ne )d λ
π 2 π 2π
1 4 波片 半波片 全波片Leabharlann 光轴·o光
o 光的
·
主平面
光轴
e光
e 光的
主平面
(o光振动垂直o 光主平面)
(e 光振动在e 光主平面内)
光轴在入射面时,o 光主平面和e 光主平面重合,此时o 光振动和e 光振 动相互垂直。一般情况下,两个主平面夹角很小,故可认为o 光振动
和e 光振动仍然相互垂直。
5. 正晶体、负晶体
晶体光学

k
2 x0
k
2 y0
k
2 z0
0(2.3-5)
1 n2
1
xr
1 n2
1
yr
1 n2
1
zr
单轴晶体中 的传播规律
九.波矢菲涅耳方程的解
定义三个主折射率
nx xr , ny yr , nz zr
对于单轴晶体
z
ko kzo
oθ
kyo
y
xr yr nx ny no
0n2k0
k0
E
(2.2-13)
利用 A BC B AC C A B 上式写成
D 0n2 E k0 k0 E
(2.2-14)
菲涅耳方程
将基本方程 D 0n2 E k0 k0 E 写成分量形式
光 在 晶 体 中 的 传 播 规 律
晶体中 E和 D 的关系
由(2.2-4)式可以得到
k H D
D
1
H k
(2.2-12)
将(2.2-3)代入(2.2-12)当中得到 k E 0 H
D
1
0
2
k
Ek
no2 n22
cos2 Ey
Ex 0
n22 sin
cosEz
0
n22 sin
cosE y
ne2
第七章 光在晶体中的传播

合振动是正椭圆偏振态。
y E0 y
E0 x
右 旋
y E0 y
左 旋
E x E0 x Ex O E Px O E Px
Ay
右旋: / 2
Ay
左旋: / 2
E0 x E0 y E0时,椭圆偏振态退化为圆偏振态。
y
右 旋
左 旋
y
O
E P x
O
E P x
/ 2
6)单轴晶体和双轴晶体 单轴晶体:只有一个光轴方向的晶体, 如冰洲石和石英等。 双轴晶体:具有两个光轴方向的晶体, 如云母、蓝宝石和硫磺等。 7)单轴晶体的波面 (1)v o:o 光沿各个方向的传播速度, e 光沿光轴方向的传播速度。 (2)v e: 光沿垂直光轴方向的传播速度 e (3) ve vo
3)相位差 o光和 e光在晶体中经历的光程:
Lo no d , Le ne d
刚入射时相位相同,刚出射与刚入射 相比的相位落后量分别为:
,
o
2
刚出射时 o光与 e光相比的相位落后量为:
no d ,
e
2
2
ne d
o e
(no ne )d
4)刚出射时的振动表达式 (1)坐标架: (2)振动表达式:
4)平行光斜入射到光轴垂直入射面 的晶体上,求晶体中的折射光线?
作图步骤:
(1)过A点做边缘光线的垂线 AB t BB '/ c , (2)以A为中心、v e t 和 v t o 为半径做两个圆形波面 ' ' (3)过 B 点做切线,切点分别为 Ao 和 Ae '
' (4)连接 AAo两点,即为 o 光的折射光线
晶体的双折射现象(精)
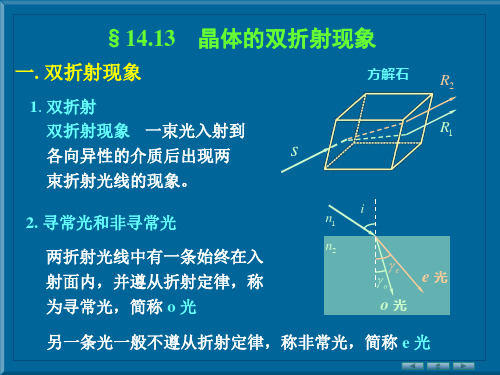
方解石
光轴
o光
e光
o光
e光
3. 光轴平行晶体表面,自然光垂直入射
o光
e光
e光
o光
此时,o, e 光传播方向相同,但传播速度不同。从晶体出 射后,二者产生相位差。
三. 晶体偏振器 1. 尼科耳棱镜 2. 渥拉斯顿棱镜
no (1.658) n(1.55) ne (1.486)
光轴
v o t
v e t
( 平行光轴截面 )
( 平行光轴截面 )
ve
vo
( 垂直光轴截面 )
ve
vo
( 垂直光轴截面 )
二. 单轴晶体中的波面 ( 惠更斯作图法(ve>vo) )
1. 光轴平行入射面,自然光斜入射负晶体中 B
光轴
A
光轴
B'
方解石
o光 e光
2. 光轴平行入射面,自然光垂直入射负晶体中
光轴
o光
负晶体 no ne
加拿大树胶
o光 e光
e光 o光
o光 ie,o e光
e光
e
上述两种棱镜得到的偏振光 质量非常好,但棱镜本身价 格很高,因而使用较少。
o
o光
3. 波晶片 (光轴平行于表面且厚度均匀的晶体) 自然光垂直入射波晶片后, o 光, e 光传播速度不同, 产生的相位不同 。 出射 o 光 e 光的相差为
5.1-晶体的光学各向异性

21
22
23
3 1 3 2 3 3
11 0 31
0
22 0
3 1 0 3 3
11 0 0
0
22
0
0 0 3 3
双轴
11 0 0
0
11
0
0 0 3 3
单轴
11 0 0
0
11
0
0 0 1 1
各向同性
赠送精美图标
1、字体安装与设置
在新坐标系 O-x1x2x3 中,该张量的表示式为[Tij].
O -x1x2x3 O -x1 x2x3 Tij Tij
2. 张量的变换 则当原坐标系 O-x1x2x3 与新坐标系 O-x1x2x3的坐标变
换矩阵为 [aij] 时,[Tij] 与 [Tij] 的关系为
T11T12T13 a11a12a13T11T12T13a11a21a31 T21T22T23a21a22a23T21T22T23a12a22a32 (9) T31T32T33 a31a32a33T31T32T33a13a23a33
A1 a11 a12 a13A1 A2a21 a22 a23A2 A3 a31 a32 a33A3
(12)
其分量变换公式为
A i a i j A j i ,j 1 ,2 ,3( 1 3 )
3. 对称张量
一个二阶张量 [Tij],如果有 Tij=Tji,称为对称张量,它 只有六个独立分量。
T11 T12 T13
1 0 0
0
2
0
0 0 3
5.1.2 晶体的介电张量 (Dielectric tensor of crystals)
不同晶体的结构具有不同的空间对称性,自然界中存 在的晶体按其空间对称性的不同,分为七大晶系:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单轴晶体和双轴晶体
晶体是由原子、离子或分子按照一定的周期性排列而成的固体物质,具有明显的晶格结构和晶面。
晶体可以根据其晶格结构的特征分为单轴晶体和双轴晶体两类。
一、单轴晶体
单轴晶体,也称为各向同性晶体,指晶体在任何方向上的物理性质都相同,而且对于光的传播方向没有特殊的限制。
单轴晶体大多数具有四方晶系和六方晶系,晶体结构是各向同性的,具有一些重要的光学性质,例如对光波的转动或移相,折射率和衍射等。
单轴晶体是常见的晶体,如石英、方解石等都是典型的单轴晶体。
二、双轴晶体
双轴晶体,也称为各向异性晶体,指晶体在不同方向的物理性质不同,而且对于光的传播方向也有明显的限制。
双轴晶体有三种晶系,包括正交晶系、单斜晶系和三斜晶系。
在双轴晶体中,光线射入时在不同的方向上会有明显的偏离,甚至存在一些有趣的视觉效果。
例如,光线穿过双轴晶体时会产生颜色的分离现象,成为偏光现象。
三、单轴晶体和双轴晶体的区别
1. 物理性质
单轴晶体在任何方向上的物理性质都相同,而双轴晶体在不同方向上的物理性质差异很大。
2. 光学特性
单轴晶体对光波的转动或移相、折射率和衍射等作用有非常明显的表现,而双轴晶体会产生偏振现象和颜色分离效应。
3. 晶体结构
单轴晶体大多数具有四方晶系和六方晶系,结构各向同性,而双轴晶体有三种晶系,具有各向异性。
4. 典型例子
单轴晶体有许多典型例子,如石英、方解石等,而双轴晶体的代表性示例则包括云母、柿子石、电气石等。
总体而言,单轴晶体和双轴晶体在物理、光学、结构等方面的特征有很大差异。
两类晶体也各具特色,在不同的应用中都有着广泛的用途。
