在单轴晶体中
单轴各向异性晶体中寻常光和非寻常光的关系

Re a i n hi e we n — d n r n x r 0 di a y b a s l to s p b t e o i a y a d e t a r n r e m r i n a i l n s t o i r sa s n u i x a l a io r p c c y t l y
Absr c : Ac o d n t t e e t r h o y f p o g to i u i x a l a i o r p i c sa , t e e a i n ta t c r i g o h v c o t e r o r pa a i n n n a i l y n s t o y c r t l h r l t y o
是 否存 在 可行性 解,即问题 转化成 了一个数 学问题 ;模拟 了高斯光 束在 单轴 各 向异 性 晶体传 播 的情
键词 :单轴各 向异性 晶体 ; 能 量 交换 ; 传播 ; 矢量 理论 ; 傍 轴传播 ; 模 拟
L a in e, o Qin 。 i i o g Kay n io Ta h Ga o g,L u We n ia g ,S
( .De at n f M ah mais n y is n omain En ie rn ie st 1 p rme to te t a d Ph sc ,I fr t g n eig Unv riy,Z e g h u 45 0 ,Ch n ; c o h n z o 0 01 i a 2 Colg fP oo ee to ce c a d En ie rn l e o h tn—lcrn S in e n gn eig,Nain l iest fDee e Te h oo y,Ch n s a 41 0 3,Chn ) e t a Unv riy o fns c n lg o agh 0 7 ia
单轴晶体 走离角

单轴晶体走离角
单轴晶体是指只有一个主光轴的晶体,一般具有高度的各向异性。
在
光学中,对单轴晶体要进行走离角的计算和分析。
走离角是指光线穿过单轴晶体时,入射光线与振动方向之间的角度差,也可以理解为折射光线振动面与入射光线振动面的夹角。
单轴晶体中
的走离角非常关键,可以用于研究单轴晶体的光学性质,特别是光线
折射方向的确定。
单轴晶体的走离角与其光学特性密切相关,光线在单轴晶体中传播时
会被分成两个振动方向,分别为快轴和慢轴。
走离角是指入射光线的
振动方向与快轴或慢轴的夹角,根据走离角的大小和快慢轴的位置关系,可以决定出折射光线的方向和振动方向。
对于入射光线接近快轴或慢轴的情况,走离角会非常小,光线折射时
的偏转角度也会很小。
如果入射光线的振动方向与快轴或者慢轴夹角
为45度,走离角将达到最大值。
此时折射光线将垂直于晶体表面传播,这种情况也被称为正交偏振。
在单轴晶体中,走离角的大小和方向与折射光线的传播方向密切相关。
如果走离角过大,光线偏转角过大,将对光学性能产生很大影响。
因
此,对于单轴晶体的光学研究和应用,需要对走离角的计算和分析有深入的了解和研究。
总之,走离角是单轴晶体中非常重要的光学参数之一,可以用于研究单轴晶体的光学性质,特别是光线折射方向的确定。
对于单轴晶体的光学研究和应用,走离角的计算和分析具有重要意义。
光通过单轴晶体时的双折射现象ppt课件
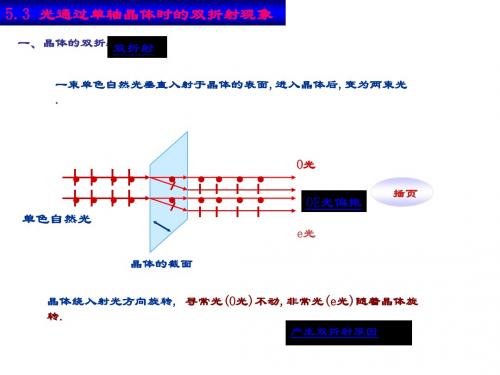
3、o光和e光的振动方向 o 光和 e光都是线偏振光,其振动方向如何?
o 光轴
e 光轴
o 光主截面
e 光主截面
用检偏器检验知
o 光的振动垂直 o光的主截面 e 光的振动在 e 光的主截面内
光轴在入射面内时, 两条光线的主截面就是入射面 o光的振动垂直入射面 两光偏振方向垂直 e光的振动在入射面内
4、o光和e光的主折射率(仅讨论单轴晶体) 光轴 o光的主折射率 两个主折射率
注意:在晶体内光轴是一个方向 实验上怎么操作呢?令入射表面垂直光轴,光线沿光轴方向入射,光线在晶体内 部传播不发生双折射。
光轴方向
空气
方解石 不发生双折射
方解石晶体的光轴(方向)
两钝隅连线方向为 光轴方向
101°52′
78°8′
78°8′
三个角度均为 101°52′的顶点 称为钝隅
单轴晶体 单轴晶体(uniaxis crystal) 只有一个光轴方向: 方解石 (冰洲石)、石英(quartz)、红宝石 人工拉制单轴晶体、ADP(磷酸二氢氨)、铌酸锂(LiNiO3) 方解石晶体的演示 双轴晶体(biaxis crystal)
方解石 晶体
纸面
双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面
双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面
双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面
双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石晶体实物照 片 纸面
光在单轴晶体中的传播与惠更斯作图法
H
,
由 ( 9
)
,
1 0 ( )
、
,
1 1 ( ) S
三 式可 知
,
在 各向 异 性介 质 中
,
因 刀 与 D 方 向一 般不 一 致
k 之
.
,
D
、
丫
k
与E
H
、
各组成 一 组右 旋 正 交 矢 量
而
k
S
与
间夹角等 于
刃
与 D 之 间夹 角
a
能 量传 播方 向 S 与等位 相 面 即 波 面 传 播方 向 波面 传播 速度 就 是 相 速
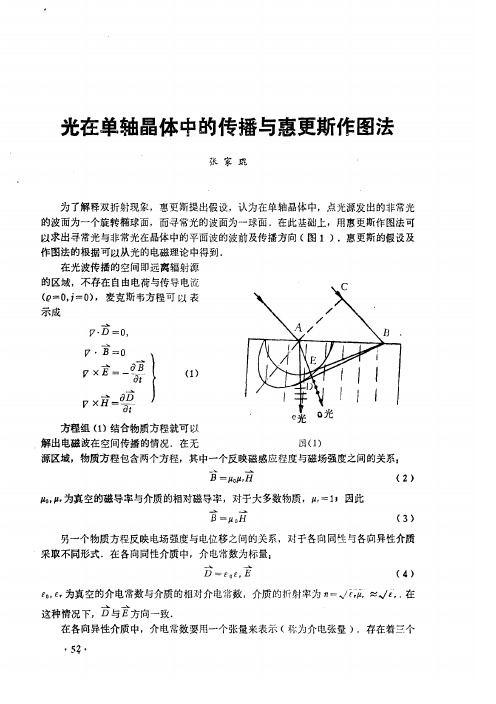
光 在 单 轴 晶 体 中的 传 播 与惠 更 斯 作 图 法
张 字 砚
为 了解释 双 折 射现 象 的波面为 一个旋 转椭球面
,
惠更 斯提 出假 设
,
认 为在单 轴晶体 中
.
,
点 光 源发 出 的 非常 光
,
,
而寻 常光 的 波面为 一 球面
.
在 此基础上
用 惠更 斯 作图 法 可
.
以 求 出寻 常光 与非常光在 晶体 中的平 面 波 的 波前 及 传播方 向 ( 图 1 )
:
= 、/ 若 币
r
二
扩
£
,
.
在
这种情 况 下
D
与 E 方 向一 致
,
.
在 各向异性 介质 中
5名
介 电常数 要 用一 个张量 来表示
( 称 为介 电 张 量 )
.
存在着 三 个
特 殊方 向
,
以 这 些 方 向为 坐 标轴 ( 主 轴 )
夕 . 了 了D .
第五章光的偏振晶体内o光和e光

负晶体是椭球面包球面。 光轴
光轴 vet
本节结束
vot
•
子波源
vot• vet
子波源
正晶体 (vo > ve)
负晶体 (vo < ve )
光学
5.5 光在晶体中的传播
1.惠更斯原理的表述
①光扰动同时到达的空间曲面被称为波面或波前;
②任何时刻波面上的每一点都可作为次波的波源,各 自发出球面次波;
惠更斯的这个假设,虽然没有深入到光与物质相互作用
的本质,而且缺乏理论上的严格性,但可对双折射现象作出 初步说明,其结果与电磁理论及实验事实是相符合的,并具 有简单、直观的优点。在此我们介绍惠更斯的方法。
根据惠更斯原理,在各向同性介质中,一子波源发出的
光波沿各方向传播的速度均为υ=c/n,是和光的传播方向、 光矢量振动方向无关的常数。经t后,形成的波面是一个半 径为υt的球面。因此在各向同性介质中光波的波面是球面。
的波面一样是球面。
o光的光矢量垂直于o光的主平面,
❖ e光的子波面
对e光,其光振动在包含光轴的平面内,振动方向与光轴 的夹角随传播方向而改变,e光不遵守折射定律,其折射率也 不是一个常数,
因而 ne c ve 常数
所以e光的传播速度随方向而变化。可见e光的波面不是球面。 惠更斯设想,它是环绕光轴的旋转椭球面,实际也是如此。
ne
c
e
ne为一常数。 称为晶体对e光 的主折射率。
A
B
C 空气
晶体
光轴
o
eo
e
15
对于正晶体, 对于负晶体,
o e o e
no ne no ne
光通过单轴晶体时的双折射现象
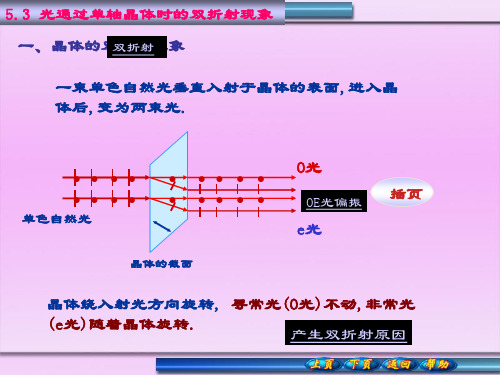
非常光( 非常光 extraordinary light e光): 光 (1) 是振动面平行于自己的主平面的线偏振光 是振动面平行于自己的主平面的线偏振光; (2) 一般不符合折射定律 在垂直于光轴的方向 一般不符合折射定律,在垂直于光轴的方向 传播时符合折射定律. 传播时符合折射定律 (3) 沿不同的方向折射率不同 传播速度不同 沿不同的方向折射率不同, 传播速度不同. 沿光轴的方向折射率和速度与O光相同 沿光轴的方向折射率和速度与 光相同. 光相同 光和e光的主平面相互平行时 两光的振动面互相垂直. 当o光和 光的主平面相互平行时 两光的振动面互相垂直 光和 光的主平面相互平行时,两光的振动面互相垂直 对于e光 沿垂直于光轴的方向的折射率称为主折射率,记为 记为n 对于 光, 沿垂直于光轴的方向的折射率称为主折射率 记为 e.
o
e
晶体主 截面 O
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
o e
晶体主 截面 O
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
o
e
O
晶体主 截面
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
o
e
O
晶体主 截面
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
方解石晶体实 物照片 纸面 方解石晶体 CaCO3
折射现 双 折射现 象
1、双折射现象 用眼睛观看发光点, 会看到两个像点,透 过方解石晶体,纸面 上的字成了的双字
O光和e光
自然光进入各向异性晶体中,光线怎样传播?
两束折射光
▲ 服从折射定律寻常光线
ordinary ray— O光 extra —e光
对单轴晶体中光的性质和双折射问题的几点讨论

eky′= 0 , e2kz′= e2k′= 1
1) 对于 o 光 , n = n1 = no ,由式 (19) 得到 :
( no2 - no2) Ex′= 0
( no2 - no2) Ey′= 0
20
n
2 e
Ez′=
0
式 (20) 的最后一式给出 Ez′= 0 ; 而前两式分别得出 非零解 : Ex′≠0 和 Ey′≠0.
同方向 、以不同的速度传播. 在单轴晶体中光的偏 振 、传播等问题的复杂性正是由上述原因所致 , 而 e 光的光线方向与它的波阵面不正交也正是由于 e 光 的相位和能量传播方向不同 、矢量 D 与 E 相分离的 结果[1 ] . 3. 1 对晶体中属于同一波矢 k 的两光矢量方向 Eo
⊥Ee的证明 由基本的电磁理论及物质方程容易推出 ,平面 简谐波在无源各向异性晶体中传播时电矢量 D 与 光矢量 E 的关系为
(19)
n2 eky′ekz′Ey′+
(
n
2 e
-
n2 e2ky′) Ez′= 0
根据式 (19) 即可全面分析 o 、e 两光的偏振方向及其
相互关系.
下面先讨论两个特殊方向 ,即波矢 k′沿光轴方
向和垂直于光轴方向的情况 , 然后再对一般情况予
以讨论.
3. 1. 1 波矢 k′沿光轴方向
当 k′沿光轴方向时 ,有 :
得两坐标系的变换关系为 :
图 2 坐标变换
x = x′cos θ+ y′sin θ
y = - x′sin θ+ y′cos θ
9
对应的波矢方向 ek 和光矢量 E 的变换式为 : ekx = eky′sin θ
eky = eky′cos θ
晶体的光轴

晶体的光轴晶体是由具有周期性排列的原子、离子或分子组成的固体材料。
晶体中的原子、离子或分子的排列方式决定了晶体的物理性质。
晶体的光学性质是其中一种重要的物理性质,它与晶体内部的光轴有着密切的联系。
光轴是晶体中具有特殊方向的轴线,沿着光轴方向的光具有特殊的传播性质。
不同晶体具有不同的光轴,可以分为单轴晶体和双轴晶体。
单轴晶体是指晶体中只有一个光轴。
在单轴晶体中,沿着光轴方向的光传播速度与晶体中其他方向的光传播速度不同,这种差异导致了光在晶体中的折射和偏振现象。
单轴晶体有着许多特殊的光学性质,例如双折射和光轴偏振等。
双轴晶体是指晶体中存在两个不同的光轴。
在双轴晶体中,沿着两个光轴方向的光传播速度与晶体中其他方向的光传播速度不同,这种差异导致了光在晶体中的折射和偏振现象。
双轴晶体的光学性质比单轴晶体更为复杂,光的传播方向和偏振状态会发生变化,因此在双轴晶体中通常需要考虑更多的光学参数。
晶体的光轴对于光的传播和偏振具有重要影响。
在光传播过程中,如果光线的传播方向与光轴方向平行,则光线不会发生偏振现象,即光线的偏振状态保持不变。
而当光线的传播方向与光轴方向垂直时,光线会发生偏振现象,即光线的偏振状态发生改变。
光在晶体中的传播速度与晶体的折射率有关。
晶体中的折射率可以通过光线沿晶体不同方向传播的速度比值来描述。
对于单轴晶体来说,折射率通常有两个值,一个是沿着光轴方向的折射率,另一个是沿着与光轴垂直的方向的折射率。
而对于双轴晶体来说,折射率则有三个值,分别对应于两个光轴方向和与两个光轴垂直的方向。
晶体的光轴还与晶体的偏振性质密切相关。
偏振是指光波中电场矢量在空间中的振动方向。
当光线传播方向与光轴方向平行时,光线的偏振状态保持不变,称为“平行光”。
而当光线传播方向与光轴方向垂直时,光线的偏振状态发生改变,称为“垂直光”。
晶体对平行光和垂直光的传播速度和折射率也会有差异,这种差异导致了光的偏振现象。
晶体的光轴是决定晶体光学性质的重要因素之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.设晶片的厚度为d,在晶片同o光e光的折射率为 no ne,则通过晶片后两束光的位相差为:
2 ( n o n e )d
4.波片:有一定厚度的晶片,或者说有特殊厚度的晶片
⑴ 4 片(四分之一波片) 若晶片厚度d满足 (n o - n e )d (2k 1) 4
⑷从D点分别作o光、e光次波面的切面 (包络面)就是o光和e光折射线的波 面,这样得到两个切点O和E。 ⑸从A点连接到切点o、E的方向,便分 别是o光和e光折射线的方向,(作图 法我们选择晶体的主截面作为入射面)
讨论几个有重要实际意义的特例:
二.单轴晶体的主折射率
1.晶体对o光的折射率 no: n O 2.e光折射率:在光轴垂直于入射面的特殊情况下,e 光也遵从折射定律,真空中的光速c与e光在垂直于 c 光轴方向的传播速度Ve之比 n e 叫做晶体对e e 光的主折射率。 3.no ne 均称为单轴晶体的主 折射率 正晶体:no< ne ( νo>νe) 负晶体: no>ne ( νo<νe) 两个主折射率之差(n e-no) 称为最大双折射率.
§5.4 光在晶体中的波面
一.单轴晶体中的波面
1.在各向同性介质中,点光源的波阵面是球面,单 轴晶体中,o光的波面也是球面。 2.在单轴晶体中,e光的波面是以光轴为转轴的旋 转椭球面.即:e光沿各个方向的速度不同,沿光 轴方向的速度也为νO;沿垂直于光轴方向的速 度与vo差别最大,以νe表示;沿其它方向的光 速介于νo与νe之间。 3.把o光、e光在单轴晶体内的波面画在一起,则两 个波面在光轴方向处相切。(如图)
(a)
有两种类型的双折射晶体
⑴Vo>Ve,(垂轴之间的e光波速为Ve),则称 正晶体,以石英代表,在正晶体内,椭球波 面内切于球面波面之内。 ⑵vo<ve,称负晶休,以冰洲石(方解石)为 代表,在负晶体内,椭球波面外切于球面波 面之外。
§5.5光在晶体中的传播方向
一.单轴晶体内o光与e光的传播方向:
2 或: ( n0 ne)d (2k 1) 2
即:振动方向垂直的o光、e光的光程差等于 4 的 奇数倍,位相差等于 的奇数倍的晶片, 2 称 片。4⑵ Nhomakorabea
2 片(半波片)
晶片厚度满足
2 ( n o n e )d ( 2k 1) 或:
(n o - n e )d (2k 1) 2
o光、e光程差若等于 2 奇数倍,位相差等于π 的奇数倍的晶片,称半波片。 线偏振光垂直入射到半波片,透射光仍为线偏 振光,假如入射时振动面和主截面之间的夹角为θ, 则透射出来的线偏振光的振动面从原来的方位向 转轴方向转过2θ.
⑶全波片:
(no - n e )d k
λ
或: Δ 2 ( )d 2k n0 ne (4)其它任意厚度d,
2 ( n o n e )d 习惯上称晶片.
4.存在缺点:
①制造时加工困难,价格昂贵。 ②不适用于会聚或发散光束,只适用于 平行入射光。 ③出射光对入射光要发生侧向位移,给测量 带来困难, ④不适用对紫外线研究
二.沃拉斯顿棱镜
1.构成(如图):由两块方解石磨制的直 角三棱镜构成,两者光轴方向互相垂直, 且光轴都平行于前后通光面。 2.作用:将一束光分解为互相分开的,振 动方向互相垂直的平面偏振光。又称棱镜 分束镜。
c O
§5.6偏振元件
一.尼科耳棱镜
1.构造:沿着与晶体主截面垂直的方向将方解面 切成两块直角棱镜,剖面磨成光学平面,再用加 拿大橡胶粘合起来便做成一个尼科耳棱镜。 2.作用:只让e光通过,且e光的偏振方向在主截 面内,这种棱镜叫尼科耳棱镜。 3.使用时注意:为保证让o光全反射,只让e光通 过,则入射光在第一端面上的入射角不得大于 15º 。 (如下图)
三.波晶片
1.晶片:一块表面平行的单轴晶体,其光轴与晶体表
面平行时,o光与e光沿同一方向传播,把这样的 晶体叫波晶片。 2.作用:入射线偏振光(要求入射的线偏振光的振 动方向不与晶体光轴平行或垂直),出射两束传 播方向相同的,振动方向互相垂直的,具有一定 的位相差的线偏振光,从而合成为椭圆偏振光或 圆偏振光,或者用于检验偏振光的偏振状态 。 或者说当一束偏振光正入射时,光在晶片内部产生 隐含双折射(o光e光传播方向相同,不分开,但 速度不同,振动方向正交)出射光变成传播方向 相同,振动方向正交,有恒定位相差的线偏振光, 两者一般合成为椭圆振光。
如作图法:
惠更斯作图法步骤(有五步):
⑴.画出平行的入射光束,标出两边缘光线与晶体 界面的交点(A、D) ⑵.由光到晶体界面的交点(如A点)作另一边缘入 射光线的垂线(AB),它便是入射线的波面(平面 波的波面),求出B到D的时间 BD
t C
(C为真空或空气中光速) ⑶.以A为中心,先以voΔt为半径,(Vo为o光在晶 体中的光速)作半圆(实际上是半球面亦即 o光的 次波面);再作与它在光轴方向相切的半椭球面, 令其另一个半长轴为voΔt,此半椭球面即为e光的 次波面。
