六年级.圆与扇形知识总结及练习
扇形知识点总结六年级
扇形知识点总结六年级扇形是初中数学中常见的一个几何图形，也是考试中常考的一个知识点。
本文将对扇形的定义、性质以及相关计算公式进行总结，帮助六年级的同学们更好地理解这一知识点。
1. 扇形的定义扇形是指以一个圆心为顶点，在圆内部取一段弧和两个半径所夹的图形。
扇形通常用字母O表示圆心，字母A表示交角的两条半径，字母θ表示弧所对的圆心角。
2. 扇形的性质①扇形的圆心角等于弧所对的端点所在的圆的幅角，即θ =∠AOB。
②扇形的面积公式为S = (θ/360°) × πr²，其中r为扇形所在圆的半径（或称为弦长）。
③扇形的周长公式为L = 2r + s，其中s为弧长。
④扇形与圆的关系：扇形的面积等于对应圆的面积乘以圆心角所占的比例，即S = (θ/360°) × πr²。
3. 扇形的计算方法在计算扇形的面积和周长时，需要根据已知条件选择适当的公式，并将已知量代入计算。
①已知扇形的圆心角θ和半径r，可以直接利用面积公式计算出面积S。
②已知扇形的弧长s和半径r，可以先根据弧长公式求得圆心角θ，然后再根据面积公式计算出面积S。
③已知扇形的面积S和半径r，可以先根据面积公式求得圆心角θ，然后再根据周长公式计算出周长L。
4. 扇形的常见例题例题1：已知扇形的圆心角为60°，半径为5 cm，求扇形的面积和周长。
解析：根据面积公式可知，S = (60°/360°) × π × 5² = 13.09 cm²。
根据周长公式可知，L = 2 × 5 + 60°/360° × 2 × 3.14 × 5 = 23.14 cm。
例题2：已知扇形的半径为8 cm，面积为25 cm²，求扇形的圆心角和周长。
解析：根据面积公式可知，25 = θ/360° × π × 8²，解得θ ≈146.52°。
六年级数学知识点 圆和扇形知识点_知识点总结
六年级数学知识点圆和扇形知识点_知识点总结圆和扇形是六年级数学中的重要知识点。
掌握圆和扇形的概念、性质以及相关计算方法对于解决与几何形体相关的问题尤为关键。
本文将对六年级数学中的圆和扇形知识点进行总结，帮助同学们更好地理解和掌握。
一、圆的概念圆是平面上一组距离中心点相等的点的集合。
其中，距离中心点相等的线段称为半径，中心点到圆上任意一点的距离称为半径。
圆上任意两点之间的线段称为弦。
二、圆的性质1. 圆的直径：通过圆心且在圆上的一条线段，其两个端点在圆上。
直径的长度是半径的两倍。
2. 圆的弧：两个端点在圆上的一条曲线。
3. 弧长：弧长是弧所对的圆心角所对应的圆周的长度。
如下图所示，弧AB所对应的圆周长度即为弧长。
4. 圆周角：以圆心为顶点的角。
任意两个在圆周上的点，以这两点为端点所得的圆心角都是一个圆周角。
三、扇形的概念扇形是由圆心、圆上的一个点和圆上的一条弧所确定的图形。
其中，圆心角是扇形的一条边所对应的圆心角。
四、扇形的性质1. 扇形的弧长：扇形的弧长是以圆心角所确定的扇形所对应的圆周的长度。
计算扇形的弧长使用的公式为：弧长 = （圆心角 / 360°） ×圆周长。
2. 扇形的面积：扇形的面积是以圆心角所确定的扇形所对应的圆的面积。
计算扇形的面积使用的公式为：面积 = （圆心角 / 360°） ×圆的面积。
五、圆和扇形的应用圆和扇形的概念和性质在实际中有广泛的应用。
以下是一些常见的应用情景：1. 钟面设计：钟面通常由多个扇形组成，掌握扇形的计算方法可以帮助我们设计出精美的钟表。
2. 构造轮胎：轮胎是由多个圆环组成的，掌握圆的性质可以帮助我们选择合适的尺寸和材料。
3. 日常生活中的圆物体：在生活中，我们经常会遇到圆形的物体，比如水杯、盘子等。
了解圆的概念和性质，可以帮助我们更好地理解和应用这些物体。
六、总结本文对六年级数学中的圆和扇形知识点进行了总结。
通过掌握圆和扇形的概念、性质以及应用，同学们可以更好地解决与几何形体相关的问题。
六年级数学专题思维训练—圆与扇形(含答案及解析)
六年级数学专题思维训练—圆与扇形1、分别以一个边长为2厘米的等边三角形的三个顶点为圆心，以2厘米为半径画弧，得到下图．那么，阴影图形的周长是厘米．（取3. 14）2、有7根直径都是5分米的圆柱形木头，现用绳子分别在两处把它们捆绑在一起，其切面如下图所示，至少需要绳子分米．（取3.14）3、把同一段铁丝围成一个正方形后，又改围成一个圆形，发现按照面积公式得出的二者面积之比为4：5，那么在计算圆面积时，圆周率丌的取值为。
4、如下图所示，已知圆环的面积是141.3平方厘米，那么阴影部分的面积是平方厘米．(取3. 14)5、如下图所示，弧IFD与JED是分别以A、B为圆心、以AD、BD为半径的圆弧，已知AD1=DB=DC=4厘米，且AGDHB、AFC与BEC分别是三条直线段．线段IA、FG、CD、EH、JB都分别垂直于AB.请问图中阴影部分的面积是多少？（取）6、如下图所示的半圆的直径BC=8厘米，AB=AC，D是AC的中点，则阴影部分的面积是．(取3. 14)7、如下图所示，ABCD是边长为10厘米的正方形，且AB是半圆的直径，则阴影部分的面积是平方厘米．（取3. 14）8、下图中正方形ABCD及DCEG的面积均为64平方厘米，EFG则为一半圆，F是弧EFG的中点．请问阴影部分的面积为多少平方厘米？（3.14）9、半径为10、20、30的三个扇形如下图放置，是的倍，10、如下图所示，图中的曲线是用半径长度的比为2：1.5：o．5的6条半圆曲线连成的，问：涂有阴影的部分与未涂阴影的部分的面积比是多少？11、有三个同心圆，它们的半径之比是3：4：5，如果大圆的面积是100平方厘米，那么中圆与小圆所构成的圆环的面积是A．20平方厘米 B．28平方厘米 C．36平方厘米 D．60平方厘米12、下图是两个圆，它们的面积之和为1991平方厘米，小圆的周长是大圆周长的90%.问：大圆的面积是多少？13、下图中五个相同的圆的圆心连线构成一个边长为10厘米的正五边形．求五边形内阴影部分的面积. =3. 14）14、如下图所示，已知圆心是O，半径r=9厘米，∠1 =∠2=15°，那么阴影部分的面积是平方厘米。
六年级圆的面积计算与扇形的认识练习题及答案解析
圆——面积计算与扇形的认识一、知识装备1、圆的面积公式推导过程：把圆平均分成若干份，可以拼成一个近似（ ），这个近似长方形的长相当于（ ）（r π），宽相当于（ ）（r ），因为长方形的面积等于圆的面积，所以圆的面积是（ ）。
2、已知周长求面积：先求出半径()2r C π=÷÷，再根据半径求面积。
3、圆中特殊的比：（1）半径比=直径比=周长比；（2）面积比=半径的平方比（或直径的平方比，或周长的平方比）； 4、圆环的面积：圆环的面积=大圆的面积-小圆的面积 （1）22S R r ππ=-环 （2）()22S R r π=-环 *（3）()()S R r R r π=+-环 5、记住结论：（1）周长相等的长方形、正方形、三角形和圆，圆的面积最大，三角形的面积最小。
（2）面积相等的长方形、正方形、三角形和圆，三角形的周长最长，圆的周长最短。
（3）如下图，在一个正方形中画一个最大的圆形，再在圆形中画一个最大的正方形。
S 大正∶S 圆∶S 小正= 4∶π∶2r πr6、扇形一条弧和经过这条弧两端的两条半径所围成的图形叫做（）。
圆上A、B两点之间的部分叫做（），读作（）。
顶点在圆心的（）叫做圆心角。
二、经典例题例1、一个圆的周长是25.12厘米，它的面积是多少平方厘米？举一反三1：在距离地面2.5米的地方，用长31.4米的绳子去绕某一棵树的树干，正好可以绕10圈，这棵树的树干横截面的面积是多少平方米？例2、在直径8米的圆形花坛周围，铺一条2米宽的小路，这条小路的面积是多少平方米？举一反三2：一个圆形花坛，周长62.8米，如果在这个花坛周围铺上一条宽1米的环形小路。
这条小路的面积有多大？例3、若两个圆的半径比是2︰3，则它们的直径比是（），周长比是（），面积比是（）。
举一反三3：（1）一个圆的半径扩大到原来的4倍，直径扩大到原来的（）倍，周长扩大到原来的（）倍，面积扩大原来的（）倍。
（2）一个圆的半径缩小到原来的51，直径缩小到原来的（ ），周长缩小到原来的（ ），面积缩小到原来的（ ）。
圆和扇形(经典题汇总)
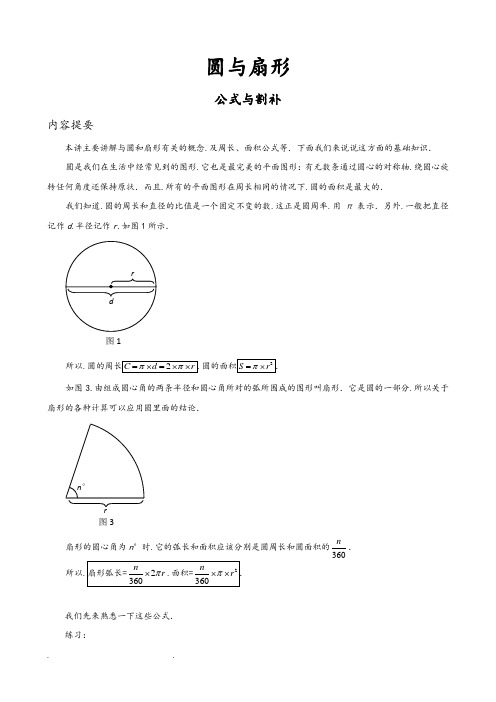
圆与扇形公式与割补内容提要本讲主要讲解与圆和扇形有关的概念.及周长、面积公式等．下面我们来说说这方面的基础知识． 圆是我们在生活中经常见到的图形.它也是最完美的平面图形：有无数条通过圆心的对称轴.绕圆心旋转任何角度还保持原状．而且.所有的平面图形在周长相同的情况下.圆的面积是最大的．我们知道.圆的周长和直径的比值是一个固定不变的数.这正是圆周率.用π表示．另外.一般把直径记作d .半径记作r .如图1所示．所以.如图3.由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫扇形．它是圆的一部分.所以关于扇形的各种计算可以应用圆里面的结论．扇形的圆心角为n °时.它的弧长和面积应该分别是圆周长和圆面积的360n． 所以我们先来熟悉一下这些公式． 练习：n °r 图3图11.半径是2的圆的面积和周长分别是多少？2.直径是5的圆的面积和周长分别是多少？3.周长是10π的圆的面积是多少？4.面积是9π的圆的周长是多少？例题一、基本公式运用例题1.已知扇形的圆心角为120°.半径为2.则这个扇形的面积和周长各是多少？（圆周率按3.14计算）例题2.已知扇形面积为18.84平方厘米.圆心角为60°.则这个扇形的半径和周长各是多少？（圆周率按3.14计算）60°随堂练习：1.已知一个扇形的弧长为0.785厘米.圆心角为45.这个扇形的半径和周长各是多少？2.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是多少？例题3.如图.直角三角形ABC 的面积是45.分别以B .C 为圆心.3为半径画圆．已知图中阴影部分的面积是35.58．请问：角A 是多少度？（π取3.14）二、 圆中方.方中圆例题4.如图.左下图和右下图中的正方形边长都是2.那么大圆、小圆的面积分别为________、________．随堂练习：1. 已知外面大圆的半径是4.里面小圆的面积是多少？（答案用π表示）二、割补法例题5. 求下列各图中阴影部分的面积（图中长度单位为厘米.圆周率按3.14计算）： （1） （2）随堂练习：求下图中阴影部分的面积（图中长度单位为厘米.圆周率按3.14计算）： （1） （2）例题6.求下列各图中阴影部分的面积（图中长度单位为厘米.圆周率按3.14计算）： （1） （2）例题7.已知图中正方形的边长为2.分别以其四个顶点为圆心的直角扇形恰好交于正方形中心.那么图中阴影部分的面积为________．（答案用 表示）例题8.根据图中所给数值.求下面图形的外周长和总面积分别是多少？（π取3.14）472随堂练习：1.根据下图中给出的数值.求这个图形的外周长和面积．（π取3.14）例题9.求图中阴影部分的面积．（圆周率 取3.14）思考题图中的4个圆的圆心是正方形的4个顶点.它们的公共点是该正方形的中心．如果每个圆的半径都是1厘米.那么阴影部分的总面积是多少平方厘米？作业：1.半径为4厘米的圆的周长是________厘米.面积是________平方厘米；2.半径为4厘米.圆心角为90︒的扇形周长是________厘米.面积是________平方厘米．（π取3.14）3.家里来客人了.淘气到超市买了4瓶啤酒.售货员阿姨将4瓶啤酒捆扎在一起（如下图所示）.捆4圈至少要用绳子________厘米．（π取3.14.接头处忽略不计）4.求下列各图中阴影部分的面积（图中长度单位为厘米.圆周率按3.14计算）：（1）（2）5.下列图形中的正方形的边长为2.则下图中各个阴影部分面积的大小分别为______、______．（π取3.14）6.用一块面积为36π平方厘米的圆形铝板下料.从中裁出了7个同样大小的圆铝板．问：所余下的边角料的总面积是多少平方厘米？圆与扇形旋转与重叠知识总结：学习如何利用割补法和包含排除的思想计算图形中特定部分的面积；学会分析几何图形的运动过程.并由此得出点的轨迹和图形扫过的区域．例题：一、 重叠问题例题1.下图中甲区域比乙区域的面积大57平方厘米.且半圆的半径是10厘米.那么其中直角三角形的另一条直角边的长度是多少？（圆周率π取3.14）例题2.下图中有一个等腰直角三角形ABC .一个以AB 为直径的半圆.和一个以BC 为半径的扇形．已知10AB BC ==厘米．图中阴影部分的面积为多少平方厘米？（π取3.14）随堂练习1. 如图17-13.以AB 为直径做半圆.三角形ABC 是直角三角形.阴影部分①比阴影部分②的面积小28平方厘米.AB 长40厘米．求BC 的长度．（π取3.14．）ABB例题3.如图.直角三角形的两条直角边分别为3和5.分别以三条边做了3个半圆（直角顶点在以斜边为直径的半圆上）.那么阴影部分的面积为______．例题4.图1是一个直径是3厘米的半圆.AB 是直径．如图2所示.让A 点不动.把整个半圆逆时针转60°.此时B 点移动到C 点．请问：图中阴影部分的面积是多少平方厘米？（π取3.14）二、 动态扫面积问题例题5.如图.正方形ABCD 边长为1厘米.依次以A 、B 、C 、D 为圆心.以AD 、BE 、CF 、DG 为半径画出四个直角扇形.那么阴影部分的面积为________平方厘米．（π取3.14）图1B图2例题6.如图所示.以等边三角形的B、C、A三点分别为圆心.分别以AB、CD、AE为半径画弧.这样形成的曲线ADEF被称为正三角形ABC的渐开线.如果正三角形ABC的边长为3厘米.那么此渐开线的长度为多少厘米.图中I、II、III三部分的面积之和是多少平方厘米？三、运动圆扫面积例题7.图中正方形的边长是4厘米.而圆环的半径是1厘米．当圆环绕正方形无滑动地滚动一周又回到原来位置时.其扫过的面积有多大？（π取3.14）随堂练习1.图中长方形的长是10厘米.宽是4厘米.而圆环的半径是1厘米．当圆环绕正方形无滑动地滚动一周又回到原来位置时.其扫过的面积有多大？（π取3.14）例题8.图中等边三角形的边长是3厘米.而圆环的半径是1厘米．当圆环绕等边三角形无滑动地滚动一周又回到原来位置时.其扫过的面积有多大？（π取3.14）思考题如图所示.一只小狗被拴在一个边长为4米的正五边形的建筑物的一个顶点处.四周都是空地．绳长刚好够小狗走到建筑物外墙边的任一位置．小狗的活动范围是多少平方米？（建筑外墙不可逾越.小狗身长忽略不计.π取3）作业：1. 图17-14由一个长方形与两个90︒角的扇形构成.其中阴影部分的面积是_______平方厘米．（π取3.14．）2. 图中有一个矩形和两个半径分别为5和2的直角扇形.那么两个阴影部分的面积相差为_______．（π取3.14）图17-14狗3.如图.直角三角形的两条直角边长分别是10cm和6cm.分别以直角边为直径作出两个半圆.这两个半圆的交点恰好落在斜边上.那么阴影部分的面积是_______cm2．（π取3.14）（17π-30）4.图1是一个直径是3厘米的半圆.AB是直径．如图2所示.让A点不动.把整个半圆逆时针转60°.此时B点移动到C点．请问：图中阴影部分的面积是_______平方厘米（π取3.14）5.图中正方形的边长是6厘米.而圆环的半径是1厘米．当圆环绕正方形无滑动地滚动一周又回到原来位置时.其扫过的面积有______．（π取3.14）6.图中等边三角形的边长是5厘米.圆形的半径是1厘米．当圆形绕等边三角形滚动一周又回到原来位置时.扫过的面积有________．（π取3.14）图1 B图26cm几何计数知识总结：例题：一、 枚举或分类解题利用枚举法以及分类的方法进行几何计数.特别是对于正方形和三角形的计数问题．通常按照面积的大小或者包含基本图形的多少来对图形进行分类．例题1.小杰瑞把巧克力棒摆成了如图所示的形状.其中每一条小短边代表一个巧克力棒．请问：（1）一共有多少个巧克力棒？（2）这些巧克力棒共构成了多少个三角形？（3）嘴馋的小杰瑞吃掉一个巧克力棒后（图中两端带有箭头的小边）.剩下的图形中还有多少个三角形？随堂练习 1. 图中共有_______个三角形；例题2.如图.它是由18个大小相同的小正三角形拼成的四边形.其中某些相邻的小正三角形可以拼成较大的正三角形．图中包含“*”的各种大小的正三角形一共有_______．*例题3.如图.AB .CD .EF .MN 互相平行.则图中三角形个数是_______．例题4.图中有多少个正方形？二、 与排列组合有关的计数利用排列组合的方法进行几何计数.特别是对于矩形和四边形的计数问题例题5.如图.线段AB .BC .CD .DE 的长度都是3厘米．请问：（1）图中一共有多少条线段？（2）这些线段的长度之和是多少厘米？随堂练习1. 求图中一共有多少条线段．3厘米3厘米 3厘米 3厘米 A BC D EB MAEF D N例题6.求图中一共有多少条线段．求图中一共有多少个矩形．随堂练习1. 如图.四条边长度都相等的四边形称为菱形．用16个同样大小的菱形组成如图的一个大菱形．数一数.图中共有多少个菱形？例题7.右图是一个长为9.宽为4的长方形网格.每一个小格都是一个正方形.那么：1）从中可以数出_______个矩形．2）从中可以数出_______个正方形．3）从中可以数出包含_______个.正方形有________个．随堂练习（1）图中包含★的长方形有_______个．包含☺的正方形又有_______个．（2）图中同时包含☺和★的长方形有_______个．三、与容斥原理有关的几何计数例题8.图中一共包含多少个矩形？多少个正方形？随堂练习1.图中有_______个矩形思考题用16个边长为1的等边三角形拼成一个边长为4的大等边三角形.那么组成的图形中可以找出多少个平行四边形？作业1.数一数图中一共有多少条线段？2.图中共有_______个三角形．【分析与解】按边长分类数.图中共有93113++=个三角形；平行四边形共有333215⨯+⨯=个．3. 在图中.包含※的长方形共有________个．4. 图中有_______个矩形._______个正方形．【分析与解】图中共有718+=个正方形.19个长方形．这道题适合按大小分类数．5. 图中有三角形_______个.梯形_______个．【分析与解】三角形有()312318⨯++=个.梯形有()()1212318+⨯++=个．6. 图中有_______个正方形._______个长方形．【分析与解】答案是38.144．长方形有()()()()123123452123123144++⨯++++⨯-++⨯++=⎡⎤⎣⎦ 个.正方形有()()352413294138⨯+⨯+⨯⨯-++=个（这里给出正方形的求法比较巧妙.如果不合适.请按正方形的边长分类枚举）．行程知识总结：本讲重点学习在小升初中和各个杯赛中的较复杂的行程问题.行程问题主要有三组共9个基本公式：（1） =⨯路程速度时间；=÷速度路程时间；=÷时间路程速度；（2） =⨯相遇路程速度和时间；=÷速度和相遇路程时间；=÷时间相遇路程速度和；（3） =⨯追及路程速度差时间；=÷速度差追及路程时间；=÷时间追及路程速度差．要会灵活运用公式.通过已知的条件求出未知的路程、速度或时间．此时.我们还经常需要用到以下这三个基本倍数关系：当运动的速度相同时.时间的倍数关系等于路程的倍数关系；当运动的时间相同时.速度的倍数关系等于路程的倍数关系；当运动的路程相同时.时间的倍数关系等于速度的倍数关系.但注意时间长的速度慢.时间短的速度快．例题1. （ ）甲、乙两地间的路程是600千米.上午8点客车以平均每小时60千米的速度从甲地开往乙地.货车以平均每小时50千米的速度从乙地开往甲地．要使两车在全程的中点相遇.货车必须在上午几点出发？例题2. （ ）某学校组织学生去春游.以2米/秒的速度前进.一名学生以4米/秒的速度从队尾跑到队头.再回到队尾.共用6分钟.那么队伍的总长为多少米？例题3. A 城在一条河的上游.B 城在这条河的下游．A 、B 两城的水路距离为396千米．一艘在静水中速度为每小时12千米的渔船从B 城往A 城开.一艘在静水中速度为每小时30千米的治安巡逻艇从A 城往B 城开．已知河水的速度为每小时6千米.从A 流向B ．两船在距离A 城180千米的地方相遇．巡逻艇在到达B 城后得到消息说他们刚才遇到的那艘渔船上有一名逃犯.于是巡逻艇立刻返回去追渔船．请问巡逻艇能不能在渔船到达A 城之前追上渔船？如果能的话.请问巡逻艇在距A 城多远的地方追上渔船；如果不能的话.请算出巡逻艇比渔船慢多少小时到A 城．例题4. 蜗牛沿着公路前进.对面来了一只兔子.他问兔子：“后面有乌龟吗？”.兔子回答说：“10分钟前我超过了一只乌龟”.接着蜗牛继续爬了10分钟.遇到了乌龟．已知乌龟的速度是蜗牛速度的10倍.那么兔子速度是乌龟速度的________倍．例题5.甲、乙二人相距100米的直路上来回跑步,甲每秒钟跑2.8米,乙每秒钟跑2.2米.他们同时分别在直路两端出发,当他们跑了30分钟时,这段时间内相遇了几次？例题6.甲乙两车同时从A、B两地出发相向而行.两车在距离B地64千米的地方第一次相遇.相遇后两车继续原速前进.并且在到达对方出发点之后.立即沿原路返回.途中在距离A点48千米处第二次相遇.问：两次相遇点距离是多少千米？例题7.甲、乙两车分别从A、B两地出发.在A、B之间不断往返行驶.已知甲车的速度是每小时15千米.乙车的速度是每小时35千米.并且甲、乙两车第三次相遇（这里特指面对面的相遇）的地点与第四次相遇的地点恰好相距120千米.那么.A、B两地之间的距离等于_________ 千米．例题8.快、中、慢3辆车同时从同一地点出发.沿同一公路追赶前面的一个骑车人．这3辆车分别用6分钟、10分钟、12分钟追上骑车人．现在知道快车每小时走24千米.中车每小时走20千米.那么.慢车每小时走多少千米？例题9.有甲乙丙三车各以一定的速度从A到B.乙比丙晚出发10分钟.出发后40分钟追上丙.甲比乙又晚出发10分钟.出发后60分钟追上丙.问.甲出发后多少分钟可以追上乙？思考题一次越野赛跑中.当小明跑了1600米时.小刚跑了1450米.此后两人分别以每秒a米和每秒b米匀速跑.又过100秒时小刚追上小明.200秒时小刚到达终点.300秒时小明到达终点.这次越野赛跑的全程为多少？作业1.现有两列火车同时同方向齐头行进.快车每秒行18米.慢车每秒行10米.行12秒后快车超过慢车．如果这两辆火车车尾相齐同时同方向行进.则9秒后快车超过慢车．那么快慢两车的车长分别是几米？2.一辆中巴车6点（24小时制）从A城出发.以每小时40千米的速度向B城驶去.3小时后一辆小轿车以每小时75千米的速度也从A出发到B．当小轿车到达B后.中巴车离B还有90千米．那么中巴车是几点几分到达B的？3.甲、乙两人从相距为46千米的A、B两地出发相向而行.甲比乙先出发一个小时．他们两人在乙出发后4小时相遇.又已知甲比乙每小时快2千米.那么乙的速度为每小时多少千米？4.甲、乙两人分别从南北两地相对而行．已知甲每分钟走50米.乙走完全程要30分钟．相对而行10分钟后.甲、乙仍相距100米．那么还要过多少秒钟.甲、乙第一次相遇？5.（第三届“走进美妙的数学花园”团体对抗赛第22题）一个和尚每天早晨都到河边去提一桶水.他提空桶时每秒走3米.提满桶时每秒2米.来回一趟需10分钟。
六年级上扇形知识点总结
六年级上扇形知识点总结扇形是初中数学学习中的一个重要概念，它是指由一个圆心角和弧所围成的图形。
在六年级上学期，我们学习了关于扇形的一些基本知识和性质，下面我们就来总结一下：1. 扇形的定义：扇形是由一个圆心角和弧所围成的图形。
圆心角是指由圆心两条射线所围成的角，它的顶点在圆心上。
弧是圆上的一段弯曲部分，连接了圆心角的两个端点。
2. 扇形的要素：扇形有三个基本要素：圆心、半径和圆心角。
圆心是扇形的中心点，半径是从圆心到圆上任意一点的距离，圆心角是由圆心和两条射线围成的角度。
3. 扇形的计算：扇形的面积可以通过圆心角的大小来计算。
扇形的面积公式为：扇形的面积 = (圆心角/360°) × πr²，其中r为扇形的半径。
4. 扇形的性质：(1) 对于相同的圆心角，当半径增大时，扇形的面积也会增大。
(2) 对于相同的半径，当圆心角增大时，扇形的面积也会增大。
(3) 扇形的面积最大值为半圆，当圆心角为180°时，扇形成为半圆，此时扇形的面积等于圆的面积的一半。
5. 扇形和圆的关系：扇形是圆的一部分，它占据了圆的一部分面积。
圆可以看作是由无数个扇形组成的，而扇形则是圆的一部分。
6. 扇形的应用：扇形的概念在日常生活和实际问题中有很多应用。
例如，在计算机图形学中，扇形被用来表示圆的一部分；在建筑设计中，扇形被用来设计弧形的门窗等。
通过以上总结，我们对六年级上学期关于扇形的相关知识有了更深入的了解。
掌握扇形的概念、计算方法和性质，对于解决与扇形相关的数学问题和实际应用具有重要的意义。
希望同学们能够在以后的学习中不断巩固扇形的知识，灵活运用，取得更好的成绩！。
六上数学知识整理——圆和扇形统计图
五、圆1、圆的认识用圆规画圆时，针尖所在的点叫做圆心，一般用字母O表示。
连接圆心和圆上任意一点的线段叫做半径，一般用字母r表示，半径的长度就是圆规两个脚之间的距离。
通过圆心并且两端都在圆上的线段叫做直径，一般用字母d表示。
（1）圆是轴对称图形，有无数条对称轴。
（2）一个圆里的半径有无数条，直径也有无数条。
（3）同一圆内，所有的半径都相等，所有的直径也都相等，直径长度是半径的两倍。
（4）圆心决定了圆的位置，半径决定了圆的大小。
（5）用圆可以设计出许多美丽的图案。
2、圆的周长任意一个圆的周长与它的直径的比值是一个固定的数，我们把它叫做圆周率，用字母π（pài）表示。
它是一个无限不循环小数。
π=3.1415926535……但在实际应用中常常只取它的近似值，例如: π≈3.14。
圆的周长=直径×π。
如果用C表示圆的周长，就有：C=∏d 或 C=2∏r把一个圆平均分成若干偶数份，剪开后，把这些小纸片拼成一个近似于四边形的图形，我们会发现，分的份数越多，每一份就越小，拼成的图形就会越接近于一个长方形。
从上图中可以看出长方形的长近似于∏r ，宽近似于r 。
因为长方形的面积=长×宽， 所以圆的面积=半径×∏×半径=半径的平方×∏如果用S 表示圆的面积，那么圆的面积的计算公式就是：S=∏r23、圆的面积C/2 (∏d)r外圆内方和外方内圆中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。
外方内圆阴影部分面积：S阴影=d－r ×∏外圆内方阴影部分面积：S阴影= r ×∏－rd4、扇形如左图，圆上A、B两点之间的部分叫做弧，读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
图中涂色部分就是扇形。
像∠AOB这样，顶点在圆心的角叫做圆心角。
在同一个圆中，扇形的大小与这个扇形的圆心角的大小有关。
扇形的面积公式：扇形面积=半径×∏×圆心角S=O∏r2 2222环形和扇环环形的面积公式：（大圆半径 －小圆半径 ）×∏ S=(R –r )∏扇环的面积公式:（大圆半径 －小圆半径 ）×∏×O S=(R –r )∏O七、扇形统计图1、我们可以用扇形统计图来表示各部分数量与总数之间的关系。
六年级.圆与扇形知识总结及练习
未来教育学科教师辅导讲义 学员姓名年 级 六年级 科 目 数学 授课时间段 学科教师 王晓芬 课时数2H 课 题 圆 教学目标及重难点教学内容 一、知识梳理1、圆的周长：d C π=或r C π2=2、弧长：l ＝180n πr 3、圆的面积：S=πR 24、圆环面积：22r R S S S ππ-=-=内圆外圆圆环5.扇形的面积： S 扇形＝360n πR 2，其中R 为扇形的半径，n 为圆心角． 引导学生理解公式：在应用扇形的面积公式S 扇形=2360r n π 进行计算时，要注意公式中n 的意义：n 表示1°圆心角的倍数，它是不带单位的。
6、弧长与扇形面积的关系：∵l ＝180n πR ， S 扇形＝360n πR 2， ∴360n πR 2＝12R ·180n πR ． ∴S 扇形＝12lR 二、例题讲解例1：有一圆形铁片，没有标明圆心，你能测出它的圆心吗？例2：圆形花坛的直径是20米，则其周长是多少米？小自行车得车轮直径是50厘米。
绕花坛一周车轮大约转动多少周？例3：已知圆的半径为3厘米，圆心角的度数为20度，计算圆心角所对的弧长度。
例4：钟面上的分针长6cm ，经过25分钟时间，分针的针尖走过的路径长为多少厘米。
例5：一个圆形蓄水池的周长是25.12m ，这个蓄水池的占地面积是多少？例6：一个圆环铁片，内圆半径是6cm ，环宽是4场面，求这个环形铁片的面积是多少？例7：已知扇形的圆心角120度，半径为3cm ，则这个扇形的面积是多少？例8：已知扇形的圆心角为270度，弧长为12π，求扇形的面积。
三、练习巩固1、下列语句中正确的是（ ）Ａ、因为圆周率表示圆的周长和直径的关系，所以圆周率随着圆的周长和直径的变化而变化Ｂ、圆心角相等，所对弧的长也相等Ｃ、圆的周长扩大６倍，半径就扩大３倍Ｄ、在一个圆中，圆心角是圆周角的61，那么圆心角所对的弧长是圆周长的61 2、 一个圆的半径增加２cm ，则它的周长增加 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
未来教育学科教师辅导讲义 学员姓名
年 级 六年级 科 目 数学 授课时间段 学科教师 王晓芬 课时数
2H 课 题 圆 教学目标及重难点
教学内容 一、知识梳理
1、圆的周长：d C π=或r C π2=
2、弧长：l ＝180
n πr 3、圆的面积：S=πR 2
4、圆环面积：22r R S S S ππ-=-=内圆外圆圆环
5.扇形的面积： S 扇形＝360
n πR 2，其中R 为扇形的半径，n 为圆心角． 引导学生理解公式：在应用扇形的面积公式S 扇形=2360
r n π 进行计算时，要注意公式中n 的意义：n 表示1°圆心角的倍数，它是不带单位的。
6、弧长与扇形面积的关系：
∵l ＝180n πR ， S 扇形＝360n πR 2， ∴360n πR 2＝12R ·180n πR ． ∴S 扇形＝12
lR 二、例题讲解
例1：有一圆形铁片，没有标明圆心，你能测出它的圆心吗？
例2：圆形花坛的直径是20米，则其周长是多少米？小自行车得车轮直径是50厘米。
绕花坛一周车轮大约转动多少周？
例3：已知圆的半径为3厘米，圆心角的度数为20度，计算圆心角所对的弧长度。
例4：钟面上的分针长6cm ，经过25分钟时间，分针的针尖走过的路径长为多少厘米。
例5：一个圆形蓄水池的周长是25.12m ，这个蓄水池的占地面积是多少？
例6：一个圆环铁片，内圆半径是6cm ，环宽是4场面，求这个环形铁片的面积是多少？
例7：已知扇形的圆心角120度，半径为3cm ，则这个扇形的面积是多少？
例8：已知扇形的圆心角为270度，弧长为12π，求扇形的面积。
三、练习巩固
1、下列语句中正确的是（ ）
Ａ、因为圆周率表示圆的周长和直径的关系，所以圆周率随着圆的周长和直径的变化而变化
Ｂ、圆心角相等，所对弧的长也相等
Ｃ、圆的周长扩大６倍，半径就扩大３倍
Ｄ、在一个圆中，圆心角是圆周角的61，那么圆心角所对的弧长是圆周长的6
1 2、 一个圆的半径增加２cm ，则它的周长增加 。
3、一根圆形钢管的外直径为２０cm ，在钢管上绕了５００圈钢丝，求钢丝长为多少？（π＝3.14）
4、 已知半圆Ｏ的直径ＡＢ＝２０cm ，求半圆Ｏ的弧长和周长（π取3.14）
5、扇形ＡＯＢ和扇形ＣＯＤ同圆，且弧ＡＢ的长度是弧ＣＤ长度的，3
1则扇形ＡＯＢ的面积是
扇形ＣＯＤ面积的（ ） π1
.91
.61
.31
.D C B A
6、从Ａ到Ｂ有甲、乙、丙三条路程，这三条路程都由半圆组成，则这三条路线是（ ）
Ａ、一样近 Ｂ、甲近 Ｃ、乙近 Ｄ、丙近
7、如图：ABC ∆是等腰直角三角形，以C 为圆心，CA 为半径，画弧交BC 于点E ，以B 为圆心，BA 为半径画弧交BC 于点D ，求阴影部分的面积。
8. 如图，半径ＯＡ＝６０cm ，∠ＢＡＯ＝３０°，求扇形ＡＯＢ的面积
四、课堂基础练习
一、填空题：
1、圆的半径为4厘米，它的周长为 厘米。
2、圆心角是0120的弧长是其所在圆周长的 。
3、一条弧长为9.42厘米，圆心角为0150，这条弧的半径为 厘米。
4、某种汽车轮胎的外直径是0.8米，滚动160周，汽车行驶了 米。
5、圆心角是045，半径是8厘米的扇形，它的周长是 厘米。
6、如果一个圆的周长是π2米，那么这个圆的面积是 平方米。
7、图中OAB ∆是等边三角形，阴影部分是一个扇形，
那么阴影部分的面积是 平方厘米。
8、一个圆环的面积是小圆面积的16倍，则大圆半径是小圆半径的 倍。
9、扇形的面积是157平方厘米，它所在的圆面积是1256平方厘米，则扇形的圆心角是 度。
10、已知圆心角为0120的扇形弧长为12.56厘米，则扇形的面积是 平方厘米。
11、若一个扇形的半径是2厘米，圆心角所对的弧长是8厘米，则这个扇形的面积为 平方厘米。
12、已知大扇形面积是小扇形面积的
4
9倍，如果它们的圆心角相等，那么小扇形半径是大扇形半径的 。
二、选择题：
1、若一个圆的半径扩大3倍，则它的周长与面积分别扩大了（ ）
A.3倍，3倍
B.3倍，6倍
C.6倍，3倍
D.3倍，9倍
2、在扇形统计图中，某扇形的面积占圆面积的60％，如果整个圆表示有50名学生，扇形表示精通电脑的学生，那么精通电脑的学生有（ ）
A.20人
B.30人
C.40人
D.50人
3、如果一个圆被分为3个扇形，其中两个扇形的面积分别占了整个圆面积的35%和25%，那么剩下扇形的圆心角（ ）
A. 216度
B.144度
C.180度
D.200度
4、一个扇形的半径扩大2倍，圆心角扩大3倍，则扇形的面积（ ）
A.扩大5倍
B.扩大6倍
C.扩大18倍
D.扩大12倍
5、把一个圆分成两个不等的扇形，且大扇形的面积是小扇形面积的411
倍，则小扇形的圆心角是（ ） 000072.90.160.288.D C B A
三、解答题
1、 若一段圆心角是0150的弧，长为48厘米，则这段弧所在的圆的周长是多少厘米？
2、 用48米的篱笆材料，在空地上围成一个绿化场地。
现有两种设计方案：一种是围成正方形场地，另一种是围成
圆形场地，试问：选用哪种方案围成的场地面积较大？并说明理由。
3、 投掷铅球的安全区，是弧长为 16米，圆心角为0120的扇形，问：安全区的面积是多少平方米？
4、 将一张圆形铝皮，沿半径剪开成A 、B 、C 三个扇形。
已知A 的面积比B 的面积小
31，B 的面积比C 的面积小4
1，求面积最小的扇形的圆心角的度数。
五、课后作业
一、填空题（每小题3分，满分36分）
1、圆的直径为30，则圆的周长＝ .
2、圆半径为2cm ，那么180°的圆心角所对的弧长l = cm.
3、如果圆的半径r ＝12cm ，那么18°的圆心角所对的弧长l ＝ cm.
4、把边长为2分米的正方形剪成一个最大的圆，则这个圆的面积＝ dm 2.
5、大圆的半径是小圆的半径的2倍，则大圆面积是小圆面积的 倍.
6、一个半圆面的半径是r ，则它的面积是 .
7、圆的面积扩大到原来的9倍，则它的半径扩大到原来的 倍.
8、一个圆的半径从2cm 增加到3cm ，则周长增加了 cm.
9、120°的圆心角所对的弧长是15.072米，弧所在的圆的半径是 米.
10、一个扇形面积是它所在圆面积的6
1，这个扇形的圆心角是 度. 11、一个圆环的外半径是5cm ，内半径是3cm,这圆环的面积是 cm 2.
12、把直径为18厘米的圆等分成9个扇形，每个扇形的周长是 厘米.
二、选择题（每题3分，满分12分）
13、下列结论中正确的是………………………………………………（ ）
(A)任何圆的周长与半径之比不是一个常数；
(B)任何两个圆的周长之比等于它们的半径之比；
(C)任何两个圆的周长之比是一个常数；
(D 称圆的周长与半径之比为圆周率.
14、下列判断中正确的是………………………………………………（ ）
(A)半径越大的弧越长；
(B)所对圆心角越大的弧越长；
(C)所对圆心角相同时，半径越大的弧越长；
(D)半径相等时，无论圆心角怎么改变弧长都不会改变.
15、下列判断中正确的是………………………………………………（ ）
(A)半径越大的扇形面积越大；
(B)所对圆心角越大的扇形面积越大；
(C)所对圆心角相同时，半径越大的扇形面积越大；
(D)半径相等时，所对圆心角越大的扇形面积越小.
16、一个圆的半径增加2cm，则这个圆………………………………（）
(A)周长增加4cm；(B)周长增加π4cm；(C)面积增加4cm2；(D)面积增加.π4cm2.
三、简答题（17～20每题5分，21～24每题6分，25题8分，满分52分）
π3,试计算这辆汽车的行驶速度为每小时多少千17、一辆汽车的轮子直径1米，若行驶时车轮转速为8周/秒，取≈
米？
π3，试计算当上述汽车以120千米/小时的速度行使时，车轮的转速是每秒多少周.（结果保留整数位）
18、取≈
19、小红用4根各长1米的绳子围成4个圆，小蓝用2根各长2米的绳子围成2个圆，小白用1根长4米的绳子围成1个圆，试求他们围得图形的面积之比.
四、学生对于本次课的评价：
○很满意○满意○一般○不太满意○很不满意
学生签字：教导处签字：。