6.1平面机构的动态静力分析
合集下载
第三章平面机构的运动分析及静力分析
令下式为零向量
(k ) (k ) (k ) A (x ) f ( x )
(k ) 的线性方程组，解出 (k ) 并代入下式 ，可 上式为 x x ( k 1) 得到改进后的解向量 x
( k 1) (k ) (k ) (k ) (k ) (k ) (k ) (k ) (k ) T x ( x1 x1 , x2 x2 , , xn xn ) x x
的一组值。这样在此点式 () 外均为已知，因而可以解此线性方程组，得到
[ A]( ) [ B](q)
中除
( k ) , ( k ) , , ( k ) ) (1 2 n
[ A]( ) [ B](q)
的瞬时值。再将式
看成微分方程组，可以写出各 ( )
点，也可能是一过度约束系统处于瞬时能动位置。如果系
统在任何位置都有上式存在，则为一存在过约束的机构。
§3-2 运动方程式的建立和求解
例3-1 作铰接四杆机构的位移、速度、加速度分析。
l1 l2 l3 l4
l1 cos1 l2 cos 2 l3 cos 3 l4 0 l1 sin 1 l2 sin 2 l3 sin 3 0
之间的关系。
§3-2 运动方程式的建立和求解
（2）n 杆的基本组可以与相关构件组成n/2个独立封闭形（图 中I、II、III表示封闭形的序号）。每个封闭形可建立一个矢 量环方程或两个标量方程。 n杆的基本组在运动分析中引入n个运动变量，可以建立 的独立方程数也为n个，在一般情况下可以得到确定解。
对于n个构件组成的杆组，可得n/2个如下形式矢量封闭方程
6. 机构结构理论： 平面低副机构可看作是由机架、主动件和一个或多个基本杆 组（Assur组）所组成的，这些基本杆组具有运动确定性和静力 确定性。
6.1平面机构的动态静力分析
写成矩阵的形式为
M3 C32 M32 ~rDCC32 R32 0
第六章 机构的动态静力分析
M3 C32 M32 ~rDCC32 R32 0
u03 c3
v03
s3c
23
M 3 s3s23
s3 c 3c 23 c3s23
0 u32
[C12
]s32
s21
0
0 0
c2 s2c12 s2s12 r32 r21
s2
c2c12
c
2s12
s32
s21
0
0
s12
c12 0 0
r32c2 s32s2c12 r21 0 r32s2 s32c2c12 s21 0 s32s12 0
r32c2 r21 0 r32s2 s21 0
第六章 机构的动态静力分析
6.1 平面机构的动态静力分析
6.1.1 构件的受力分析
非输入杆受力如图所示。 Fi — 主动力的主矢； Mi — 主动力的主矩； -Ri,j — 构件j对构件i的运动
副作用力，j<i， 例如 j=i-1, i-2,……； Rk,i — 构件k对构件i的运动 副作用力，k>i， 例如 k=i+1, i+2,……。
共有9个方程：
R10x R21x
F1x
m1G1x
R10 y R21y F1y m1G1y
r1y R10x r1x R10 y r1y R21x r1x R21y M1N M1 J11
R21x R32x F2x m2G2x R21y R32 y F2 y m2G2 y
构件2的力和力矩平衡方程为
R32 R21 m2G2
(d e3 ) R32 r2 R21 J22
M3 C32 M32 ~rDCC32 R32 0
第六章 机构的动态静力分析
M3 C32 M32 ~rDCC32 R32 0
u03 c3
v03
s3c
23
M 3 s3s23
s3 c 3c 23 c3s23
0 u32
[C12
]s32
s21
0
0 0
c2 s2c12 s2s12 r32 r21
s2
c2c12
c
2s12
s32
s21
0
0
s12
c12 0 0
r32c2 s32s2c12 r21 0 r32s2 s32c2c12 s21 0 s32s12 0
r32c2 r21 0 r32s2 s21 0
第六章 机构的动态静力分析
6.1 平面机构的动态静力分析
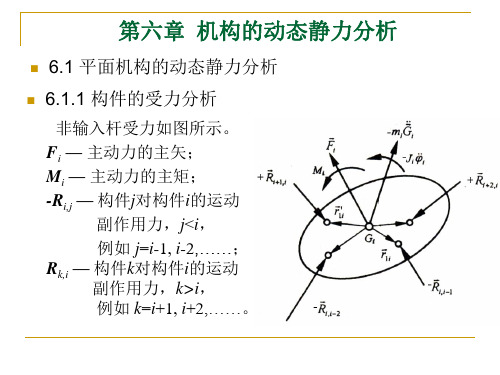
6.1.1 构件的受力分析
非输入杆受力如图所示。 Fi — 主动力的主矢； Mi — 主动力的主矩； -Ri,j — 构件j对构件i的运动
副作用力，j<i， 例如 j=i-1, i-2,……； Rk,i — 构件k对构件i的运动 副作用力，k>i， 例如 k=i+1, i+2,……。
共有9个方程：
R10x R21x
F1x
m1G1x
R10 y R21y F1y m1G1y
r1y R10x r1x R10 y r1y R21x r1x R21y M1N M1 J11
R21x R32x F2x m2G2x R21y R32 y F2 y m2G2 y
构件2的力和力矩平衡方程为
R32 R21 m2G2
(d e3 ) R32 r2 R21 J22
第一章机构的动态静力分析
其中A为系数矩阵
0 0 0 1 0 p3 y 1 0 q4 y 0 0 0 0 1 p3 x 0 1 q4 x 0 0 0 0 0 0 1 0 p4 y 0 0 0 0 0 0 0 1 p4 x 0 0 1 0 0 0 0 0 0
系数矩阵中的元素与各构件的质心位置有关。
Md为平衡力矩：
驱动力矩。
构件4：
4 F4 FR 4 FR3 m4 s 4 M 4 p4FR 4 q4FR3 J 4
构件2：
2 F2 FR 2 FR1m2 s 2 M 2 p2FR 2 q2FR1 Md J 2
凸轮作用于从动件的力：FR
FR cos 0 (a) G( FP 0 ks)fFR 2 x m s 从动件的平衡方程：FR 2 x FR sin 0 (b) FR (r0 s)sin FR 2 x H M 2 0 (c )
凸轮的平衡方程：
FR1 y FR cos 0 (d ) FR1x FR sin 0 (e) M d FR (r0 s)sin 0 ( f )
对质心的矩式平衡方程 pI FRi qI FRi1 M I J II 0
方程可改写为
I FRi FRi1FI mI s I pI FRi qI FRi1 M I J I
其中：pI , qI 为从质心至铰链 的矢径
二、平面连杆机构的动态静力分析
第i个构件的力平衡方程 FRi为第（i＋1）个构件作用在第i个构件上 的约束反力。
二、平面梁杆机构的动态静力分析
第I个构件在约束反力、主动力主矢、主矩、惯 性力、惯性力偶矩的共同作用下处于平衡状态。
列出矢量形式的平衡方程
二、平面连杆机构的动态静力分析
1-机构的动态静力分析
“二力杆”的受力，与运动构件的受力分析为什么不同？
Machinery Dynamics
静力分析是基础
加入惯性力，成为动态静力分析
力平衡是根本 矢量形式和标量形式是统一的； 力平衡和力矩平衡是独立的。 重视对机架的附加反动 摆动力和摆动力矩对机器的影响 研究平衡力矩的特性 在动态设计中的指导意义
Machinery Dynamics
机械动力学
Raymond Ding ©
Question 1
pi FRi qi FRi1 Mi Jii
vector equation & scalar equation
Machinery Dynamics
机械动力学
Raymond Ding ©
1 0 0 1 q2 y q2 x 0 0 0 A 0 0 0 0 0 0 0 0 0 1 0 p2 y 1 0 q3 y 0 0 0 0 1 p2 x 0 1 q3 x 0 0 0 0 0 0 1 0 p3 y 1 0 q4 y 0 0 0 0 1 p3 x 0 1 q4 x 0 0 0 0 0 0 1 0 p4 y 0 0 0 0 0 0 0 1 p4 x 0 0 1 0 0 0 0 0 0
FR1x FR1 y FR 2 x FR 2 y R FR 3 x FR 3 y FR 4 x FR 4 y Md
m2 s 2 F2 x x m2 s 2 F2 y y J 22 M 2 m3 s 3 F3 x x B m3 s 3 F3 y y J 33 M 3 m4 s 4 F4 x x m4 s 4 F4 y y J 44 M 4
Raymond Ding ©
平面连杆机构的动态静力分析
Machinery Dynamics
静力分析是基础
加入惯性力，成为动态静力分析
力平衡是根本 矢量形式和标量形式是统一的； 力平衡和力矩平衡是独立的。 重视对机架的附加反动 摆动力和摆动力矩对机器的影响 研究平衡力矩的特性 在动态设计中的指导意义
Machinery Dynamics
机械动力学
Raymond Ding ©
Question 1
pi FRi qi FRi1 Mi Jii
vector equation & scalar equation
Machinery Dynamics
机械动力学
Raymond Ding ©
1 0 0 1 q2 y q2 x 0 0 0 A 0 0 0 0 0 0 0 0 0 1 0 p2 y 1 0 q3 y 0 0 0 0 1 p2 x 0 1 q3 x 0 0 0 0 0 0 1 0 p3 y 1 0 q4 y 0 0 0 0 1 p3 x 0 1 q4 x 0 0 0 0 0 0 1 0 p4 y 0 0 0 0 0 0 0 1 p4 x 0 0 1 0 0 0 0 0 0
FR1x FR1 y FR 2 x FR 2 y R FR 3 x FR 3 y FR 4 x FR 4 y Md
m2 s 2 F2 x x m2 s 2 F2 y y J 22 M 2 m3 s 3 F3 x x B m3 s 3 F3 y y J 33 M 3 m4 s 4 F4 x x m4 s 4 F4 y y J 44 M 4
Raymond Ding ©
平面连杆机构的动态静力分析
3第三章 平面机构的静力分析
＝ － 0.2sin30º ＋0.3sin45º ＋0.5sin0－0.4 sin60º ＝ －0.234kN
第三章
平面机构的静力分析
合力的大小：
FR ( FR x )2 ( FR y )2 (1.085 )2 (0.234 )2 1.11kN
合力的方向：
tan
F F
平衡力系——作用于物体并使其保持平衡状态的 力系。
第三章
平面机构的静力分析
任何物体受力后都将或多或少地发生变形。
刚体——忽略受力后微小变形的力学模型。
F F´
F
F´
微小变形对零件或构件 的平衡问题影响甚微，作 静力分析时将其视为刚体。
第三章
平面机构的静力分析
变形体——不能忽略受力后微小变形的力学模型。
第三章
平面机构的静力分析
性质4 作用与反作用定律 ——作用力与反作用力总是大小相等、方向相 反、作用线相同，并分别作用在这两个构件上。 作用力与反作用力——两构件间相互作用的力。 性质5 合力投影定理
——力系的合力在某一 直角坐标轴上的投影，等 于力系中各分力在同一轴 上投影的代数和。
第三章
平面机构的静力分析
汽车刹车的操纵机构
第三章
平面机构的静力分析
解： 分析：此题如果直接由力矩定义式MB(F)=±Fd求 解，力臂d不容易确定，但题目已给出力F作用点A与 矩心B的铅直距离a＝0.25 m，水平距离b＝0.05 m， 因此，应用合力矩定理可方便地计算力矩。 （1）将力F分解为水平和铅直方向两分力Fx、Fy， 这两分力的力臂就是a和b，则： Fx= Fcosα= 300×cos30°= 260 N Fy= Fsinα= 300×sin30°=150 N （2）由合力矩定理可得： MB(F)=MB(Fx)+MB(Fy)=Fx a－Fyb =260×0.25－150×0.05=57.5 N· m
平面机构的力分析机械的摩擦与效率_真题-无答案
平面机构的力分析、机械的摩擦与效率(总分100,考试时间90分钟)一、填空题1. 作用在机械上的力按作用在机械系统的内外分为______和______。
2. 作用在机械上的功按对机械运动产生的作用分为______和______。
3. 机构动态静力分析时，把______视为一般外力加在机构构件上，解题的方法、步骤与静力分析完全一样。
4. 用速度多边形杠杆法可以直接求出作用在任意构件上的未知平衡力(平衡力矩)，此方法的依据是______原理。
5. 运动链的静定条件为______，______。
6. 矩形螺纹和梯形螺纹用于______，而三角形(普通)螺纹用于______。
7. 机构效率等于______功与______功之比，它反映了______功在机械中的有效利用程度。
8. 移动副的自锁条件是______，转动副的自锁条件是______，螺旋副的自锁条件是______。
9. 从效率的观点来看，机械的自锁条件是______；对于反行程自锁的机构，其正行程的机械效率一般小于______。
10. 槽面摩擦力比平面摩擦力大是因为______。
11. 提高机械效率的途径有______，______，______，______。
12. 机械发生自锁的实质是______。
二、选择题1. 传动用丝杠的螺纹牙形选择______。
A.三角形牙 B.矩形牙 C.三角形牙和矩形牙均可2. 单运动副机械自锁的原因是驱动力______摩擦锥(圆)。
A.切于 B.交于 C.分离3. 如果作用在轴颈上的外力加大，那么轴颈上摩擦圆______。
A.变大 B.变小 C.不变 D.变大或不变4. 机械出现自锁是由于______。
A.机械效率小于零B.驱动力太小 C.阻力太大 D.约束反力太大5. 两运动副的材料一定时，当量摩擦因数取决于______。
A.运动副元素的几何形状 B.运动副元素间的相对运动速度大小 C.运动副元素间作用力的大小 D.运动副元素间温差的大小6. 机械中采用环形支承的原因是______。
第一章_机构的动态静力分析课件
F21y (LS 2E )x J 2 2
对构件3：
T sin 3 Q cos3 F32x N43Q sin 3 N43P sin 3 m3aS3x
T cos3 Q sin 3 F32 y N43Q cos3 N43P cos3 F32x (LS3F ) y F32 y (LS3F )x N43Q[(LS 3Q ) y sin 3
从动件在凸轮廓线驱动下作上升 -停歇-下降-停歇的周期性运动， 其位移为s，即
（从最低位置——基园半径 r0
处算起）为凸轮转角 的函数，
是一个已知量。
凸轮和从动件的受力图 从动件所受的工作载荷为G，是 随凸轮转角而变化的一个已知量
封闭弹簧的刚度系数为k;
初压力为
F
（对应于下歇位置
p0
时的锁紧力）
T cos3 Q sin 3 F54 y F41y N43Q cos4 N43P cos4 m4 g m4aS 4 y
（1.3.4）
F54 y (LS 4C )x F54x (LS 4C ) y N43Q[(LS 4Q ) y sin 4
摆式飞剪机构简图
飞剪各构件受力图
对每个构件可写出其力和力矩的平衡方程如下：
对构件1：
F01x F21x F41x m1aS1x F01y F21y F41y m1g m1aS1y
F01x (LS1O )y F21x (LS1E )y F41x (LS1B )y （1.3.1）
F65x (LS 6D ) y F06x (LS 6O1) y M d 6 J6 6
（1.3.6）
【分析】平面机构的力分析
【关键字】分析第四章平面机构的力分析§4-1机构力分析的目的和方法1、作用在机械上的力驱动力：∠VS锐角（驱动力→原动力）作功生产阻力（有效阻力）（+、-）阻力: ∠VS钝角有害阻力常见的作用力：原动力、摩揩力、运动副反力、重力、“惯性力”2、机构力分析的目的和方法影响及其运动的动力性能→运转性能、调速、平衡、振动、功率分析力（力矩）后续机械设计重要参数→尺寸、机构、强度确定运动副反力→ 强度、摩揩磨损、效率任务（目的）确定机构的平衡力（或平衡力矩）→原动机功率？克服生产阻力？§4-2构件惯性力的确定假设已知构件质量、转动惯量（实际设计中可采用类比法，初估计，再逐步修正）及运动参数。
1、做平面复合运动构件两者可合二为一：力偶等效原理2、做平面移动构件3、绕定轴转动构件§4-3质量代换法1、静代换问题求解任取B、C为代换点：解得：代换质量2、动代换问题的求解解得结论：1）静代换简单容易，其代换点B、C可随意选取。
2）动代换只能随意选定一点，另外一点由代换条件确定。
3）使用静代换，其惯性力偶矩将产生误差：4）§4-3用图解法作机构的动态静力分析(不考虑摩揩力)（达朗贝尔原理在机构力分析中的应用）1、机构组的静定条件“未知力数目”= 平衡方程数目结论：1）求一个低副反力，需求解两个未知量，而高副则只需一个。
故有静定条件：即：仅有低副时：2）杆组即是静定结构。
（杆组中不含有未知的外力一定可求解）2、机构的动态静力学分析例题4-1 往复式运输机构简图及受力情况。
求应加在1构件上X—X方向上的平衡力。
（图、解）解：1、作出机构简图并作出运动分析2、确定各构件中的惯性力（矩），将其加在机构上3、 取出构件4、5进行力分析 平衡方程图解→45R 、65R的大小4、 取出构件2、3进行力分析2构件对C 点取矩，→求出τ12R 3构件对C 点取矩，→求出τ63R对2、3构件组有：图解可解出→n R 63 、n R 12的大小5、取构件2可直接求出32R6、取构件1（三力汇交）有：图解可解出：→b P 、61R的大小补充：茹可夫斯基杠杆法茹可夫斯基杠杆法是求解平衡力的一种简易方法，不必求运动副反力。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
写成矩阵的形式为
M3 C32 M32 ~rDCC32 R32 0
第六章 机构的动态静力分析
M3 C32 M32 ~rDCC32 R32 0
u03 c3
v03
s3c
23
M 3 s3s23
s3 c 3c 23 c3s23
0 u32
第六章 机构的动态静力分析
6.1 平面机构的动态静力分析
6.1.1 构件的受力分析
非输入杆受力如图所示。 Fi — 主动力的主矢； Mi — 主动力的主矩； -Ri,j — 构件j对构件i的运动
副作用力，j<i， 例如 j=i-1, i-2,……； Rk,i — 构件k对构件i的运动 副作用力，k>i， 例如 k=i+1, i+2,……。
GR F R G－1F
第六章 机构的动态静力分析
6.2 空间机构的动态静力分析
6.2.1 分析方法 ——单个示力副法
采用“一点突破，逐个求解”的思路。从单个运动副开始， 逐步暴露运动副反力，结合运动副的性质，消除不必要的未知量， 从而大大地减少了未知数的数量和方程的数目，简化计算。
该方法与“拆杆拆副法”及机构的“几何同一性条件”一起， 构成了空间机构学的一个新体系。
列构件3的力平衡方程为
F3 (R32 ) R03 0
即
0
r32 r03
0
[C23
]T
0
s03
0
F3
0 0
第六章 机构的动态静力分析
0
r32 r03
0
[C23
]T
Hale Waihona Puke 0s030
F3
0 0
0 c3
0
s
3c
23
F3 s3s23
s3 c 3c 23 c3s23
6.2.2 分析实例
已知：在图示的 RCCC机构中，输出杆3 上的工作阻力F3和阻力 矩M3，不计各构件的惯 性力。
求：各运动副反力 和输入杆的驱动力矩 M0 。
第六章 机构的动态静力分析
解：选取构件2和3之间的圆柱副 C为示力副。 C副中，构件3对构件2的反力为 R32 ，反力矩为 M32，
它们在坐标系2中可表示为
R10x , R10 y , R21x , R21y , R32x , R32 y , R03x , R03 y ,M1N
第六章 机构的动态静力分析
写成矩阵的形式为
1 0 1
0
1
0
0 1
0 0
0 0
0 0
0 0
0 R10x
0
R10
y
m1G1x m1G1y
F1x F1y
r1y 0
写成标量的形式为
R10x R21x F1x m1G1x R10 y R21y F1y m1G1y
r1y R10x r1x R10 y r1y R21x r1x R21y
M1N M1 J11
第六章 机构的动态静力分析
构件2的力和力矩平衡方程为
R21 R32 F2 m2G2
[C12
]s32
s21
0
0 0
c2 s2c12 s2s12 r32 r21
s2
c2c12
c
2s12
s32
s21
0
0
s12
c12 0 0
r32c2 s32s2c12 r21 0 r32s2 s32c2c12 s21 0 s32s12 0
r32c2 r21 0 r32s2 s21 0
s2 0 h2
0 h2
0
r32
0
0
u21 v21 0
0
u32c2 (v32 r32s2 )s2c12 u21 0 u32s2 (v32 r32s2 )c2c12 v21 0 (v32 r32s2 )s12 0
v32 r32s2
第六章 机构的动态静力分析
式中，r1i ,r2i ...为由质心Gi到
运动副反力Ri＋1,i, Ri＋2,i ,….作 用点的矢径；
r1i ,r2i ...为由质心Gi到
运动副反力-Ri＋1,i, -Ri＋2,i ,…. 作用点的矢径。
第六章 机构的动态静力分析
对以输入构件，其平衡方程为
(Ri1,i Ri2,i .....). (Ri,i1 Ri,i2 .....). Fi mGi FN 0
0
R10
y
m1G1x m1G1y
r1 0
y
r1x 0
r1y 1
r1x 0
0 1
0 0
1 0
R21x R21 y
＝mJ21G12
x
0 0
0 0
0 r2 y
1 r2x
0 dy
1 dx
0
R32
x
0 R32 y
mJ22G22y
0
0
0
0
ux
uy
0M1N
0
即 最后得
该方法的创始人为张启先院士，北航机构学学科及机器人所 的创始人。
示力副法——在单闭链空间机构中，假想拆开一个运动副， 用相应的运动副反力代替运动副的约束，以保持运动链或机构的 平衡状态，列运动链或机构的力平衡方程，求解获取运动副的反 力值。这个运动副就是示力副。
第六章 机构的动态静力分析
6.2 空间机构的动态静力分析
再选取构件1和2之间的圆柱副 B为示力副。 B副中，构件1对构件2的反力为 R21，反力矩为 M21 ，它 们在坐标系1中可表示为
R21 [r21, s21, 0]T
M21 [u21, v21, 0]T
第六章 机构的动态静力分析
列构件2的力平衡方程为
R32 R21 0
r32 r21
r1x 0
r1y 1
r1x 0
0 1
0 0
0 0
0 0
1 0
R21x R21y
J11
m2G2
M1 x F2
x
0 0 0 0
0 1 0 1 r2 y r2x r2y r2x
0 0
0 0
0
R32
x
0 R32 y
mJ22G22yMF22y
0 0 0 0
0 0
0 0
R32 [r32 , s32 , t32 ]T [r32 , s32 , 0]T M32 [u32 , v32 , w32 ]T [u32 , v32 , 0]T
t32=0和w32=0的 原因是因为 C 副为 圆柱副，构件2和3 相对可沿z2轴移动和 绕z2轴转动。
第六章 机构的动态静力分析
共有9个方程：
R10x R21x
F1x
m1G1x
R10 y R21y F1y m1G1y
r1y R10x r1x R10 y r1y R21x r1x R21y M1N M1 J11
R21x R32x F2x m2G2x R21y R32 y F2 y m2G2 y
求：各运动副的作用力和驱动力矩M1N以及连杆与摆动滑块之间 作用力距离摆块转动中心的距离e3 。
第六章 机构的动态静力分析
解：各构件的受力平衡图如下。
第六章 机构的动态静力分析
解：构件1的力平衡方程为
R21 R10 m1G1
r1 R21 r1 R10 M1N J11
第六章 机构的动态静力分析
s32 0
第六章 机构的动态静力分析
列构件2的力矩平衡方程为
M32 rBC R32 M21 0
写成矩阵的形式为
C12 (M32 ~rBC R32 ) M21 0
即
c2 s2
0
s2c12 c 2 c12
s12
s 2s12 c2s12
c12
u32
v32
0
0 s2 0
R32x R21x m2G2x R32 y R21y m2G2 y
d x R32 y d y R32x r2x R21y r2 y R21x J 22
ux R32x u y R32 y 0
第六章 机构的动态静力分析
表示成矩阵的形式为
1 0 1
0
1
0
0 1
0 0
0 0
0 R10x
(d e3) R32 r2 R21 J22 e3 R32 J33 J32
相加，得
d R32 r2 R21 (J2 J3 )2
摇块3的质心G3与铰链中心B0重合，所以G3 0
因此有
R03 R32
第六章 机构的动态静力分析
最后得到关于 R10 , R21, R32 , M1N 的方程组： R21 R10 m1G1
r2 R21 r2 R32 M 2 J22
即
R21x R32x F2x m2G2x R21y R32 y F2 y m2G2 y
r2 y R21x r2x R21y r2y R32x r2x R32 y M 2 J 22
第六章 机构的动态静力分析
构件3的力和力矩平衡方程为
构件2的力和力矩平衡方程为
R32 R21 m2G2
(d e3 ) R32 r2 R21 J22
第六章 机构的动态静力分析
构件3的力和力矩平衡方程为
R03 R32 m3G3
e3 R32 J33 J32
第六章 机构的动态静力分析
作用力R32垂直于移动副导路，则有
e3 R32 0 将构件2和3的力矩平衡方程
s2 0 h2
0 h2
0
r32
0
0
u21
v21
0
0
0 s2 0
式中， ~rBC s2
0
h2
0 h2 0
M3 C32 M32 ~rDCC32 R32 0
第六章 机构的动态静力分析
M3 C32 M32 ~rDCC32 R32 0
u03 c3
v03
s3c
23
M 3 s3s23
s3 c 3c 23 c3s23
0 u32
第六章 机构的动态静力分析
6.1 平面机构的动态静力分析
6.1.1 构件的受力分析
非输入杆受力如图所示。 Fi — 主动力的主矢； Mi — 主动力的主矩； -Ri,j — 构件j对构件i的运动
副作用力，j<i， 例如 j=i-1, i-2,……； Rk,i — 构件k对构件i的运动 副作用力，k>i， 例如 k=i+1, i+2,……。
GR F R G－1F
第六章 机构的动态静力分析
6.2 空间机构的动态静力分析
6.2.1 分析方法 ——单个示力副法
采用“一点突破，逐个求解”的思路。从单个运动副开始， 逐步暴露运动副反力，结合运动副的性质，消除不必要的未知量， 从而大大地减少了未知数的数量和方程的数目，简化计算。
该方法与“拆杆拆副法”及机构的“几何同一性条件”一起， 构成了空间机构学的一个新体系。
列构件3的力平衡方程为
F3 (R32 ) R03 0
即
0
r32 r03
0
[C23
]T
0
s03
0
F3
0 0
第六章 机构的动态静力分析
0
r32 r03
0
[C23
]T
Hale Waihona Puke 0s030
F3
0 0
0 c3
0
s
3c
23
F3 s3s23
s3 c 3c 23 c3s23
6.2.2 分析实例
已知：在图示的 RCCC机构中，输出杆3 上的工作阻力F3和阻力 矩M3，不计各构件的惯 性力。
求：各运动副反力 和输入杆的驱动力矩 M0 。
第六章 机构的动态静力分析
解：选取构件2和3之间的圆柱副 C为示力副。 C副中，构件3对构件2的反力为 R32 ，反力矩为 M32，
它们在坐标系2中可表示为
R10x , R10 y , R21x , R21y , R32x , R32 y , R03x , R03 y ,M1N
第六章 机构的动态静力分析
写成矩阵的形式为
1 0 1
0
1
0
0 1
0 0
0 0
0 0
0 0
0 R10x
0
R10
y
m1G1x m1G1y
F1x F1y
r1y 0
写成标量的形式为
R10x R21x F1x m1G1x R10 y R21y F1y m1G1y
r1y R10x r1x R10 y r1y R21x r1x R21y
M1N M1 J11
第六章 机构的动态静力分析
构件2的力和力矩平衡方程为
R21 R32 F2 m2G2
[C12
]s32
s21
0
0 0
c2 s2c12 s2s12 r32 r21
s2
c2c12
c
2s12
s32
s21
0
0
s12
c12 0 0
r32c2 s32s2c12 r21 0 r32s2 s32c2c12 s21 0 s32s12 0
r32c2 r21 0 r32s2 s21 0
s2 0 h2
0 h2
0
r32
0
0
u21 v21 0
0
u32c2 (v32 r32s2 )s2c12 u21 0 u32s2 (v32 r32s2 )c2c12 v21 0 (v32 r32s2 )s12 0
v32 r32s2
第六章 机构的动态静力分析
式中，r1i ,r2i ...为由质心Gi到
运动副反力Ri＋1,i, Ri＋2,i ,….作 用点的矢径；
r1i ,r2i ...为由质心Gi到
运动副反力-Ri＋1,i, -Ri＋2,i ,…. 作用点的矢径。
第六章 机构的动态静力分析
对以输入构件，其平衡方程为
(Ri1,i Ri2,i .....). (Ri,i1 Ri,i2 .....). Fi mGi FN 0
0
R10
y
m1G1x m1G1y
r1 0
y
r1x 0
r1y 1
r1x 0
0 1
0 0
1 0
R21x R21 y
＝mJ21G12
x
0 0
0 0
0 r2 y
1 r2x
0 dy
1 dx
0
R32
x
0 R32 y
mJ22G22y
0
0
0
0
ux
uy
0M1N
0
即 最后得
该方法的创始人为张启先院士，北航机构学学科及机器人所 的创始人。
示力副法——在单闭链空间机构中，假想拆开一个运动副， 用相应的运动副反力代替运动副的约束，以保持运动链或机构的 平衡状态，列运动链或机构的力平衡方程，求解获取运动副的反 力值。这个运动副就是示力副。
第六章 机构的动态静力分析
6.2 空间机构的动态静力分析
再选取构件1和2之间的圆柱副 B为示力副。 B副中，构件1对构件2的反力为 R21，反力矩为 M21 ，它 们在坐标系1中可表示为
R21 [r21, s21, 0]T
M21 [u21, v21, 0]T
第六章 机构的动态静力分析
列构件2的力平衡方程为
R32 R21 0
r32 r21
r1x 0
r1y 1
r1x 0
0 1
0 0
0 0
0 0
1 0
R21x R21y
J11
m2G2
M1 x F2
x
0 0 0 0
0 1 0 1 r2 y r2x r2y r2x
0 0
0 0
0
R32
x
0 R32 y
mJ22G22yMF22y
0 0 0 0
0 0
0 0
R32 [r32 , s32 , t32 ]T [r32 , s32 , 0]T M32 [u32 , v32 , w32 ]T [u32 , v32 , 0]T
t32=0和w32=0的 原因是因为 C 副为 圆柱副，构件2和3 相对可沿z2轴移动和 绕z2轴转动。
第六章 机构的动态静力分析
共有9个方程：
R10x R21x
F1x
m1G1x
R10 y R21y F1y m1G1y
r1y R10x r1x R10 y r1y R21x r1x R21y M1N M1 J11
R21x R32x F2x m2G2x R21y R32 y F2 y m2G2 y
求：各运动副的作用力和驱动力矩M1N以及连杆与摆动滑块之间 作用力距离摆块转动中心的距离e3 。
第六章 机构的动态静力分析
解：各构件的受力平衡图如下。
第六章 机构的动态静力分析
解：构件1的力平衡方程为
R21 R10 m1G1
r1 R21 r1 R10 M1N J11
第六章 机构的动态静力分析
s32 0
第六章 机构的动态静力分析
列构件2的力矩平衡方程为
M32 rBC R32 M21 0
写成矩阵的形式为
C12 (M32 ~rBC R32 ) M21 0
即
c2 s2
0
s2c12 c 2 c12
s12
s 2s12 c2s12
c12
u32
v32
0
0 s2 0
R32x R21x m2G2x R32 y R21y m2G2 y
d x R32 y d y R32x r2x R21y r2 y R21x J 22
ux R32x u y R32 y 0
第六章 机构的动态静力分析
表示成矩阵的形式为
1 0 1
0
1
0
0 1
0 0
0 0
0 R10x
(d e3) R32 r2 R21 J22 e3 R32 J33 J32
相加，得
d R32 r2 R21 (J2 J3 )2
摇块3的质心G3与铰链中心B0重合，所以G3 0
因此有
R03 R32
第六章 机构的动态静力分析
最后得到关于 R10 , R21, R32 , M1N 的方程组： R21 R10 m1G1
r2 R21 r2 R32 M 2 J22
即
R21x R32x F2x m2G2x R21y R32 y F2 y m2G2 y
r2 y R21x r2x R21y r2y R32x r2x R32 y M 2 J 22
第六章 机构的动态静力分析
构件3的力和力矩平衡方程为
构件2的力和力矩平衡方程为
R32 R21 m2G2
(d e3 ) R32 r2 R21 J22
第六章 机构的动态静力分析
构件3的力和力矩平衡方程为
R03 R32 m3G3
e3 R32 J33 J32
第六章 机构的动态静力分析
作用力R32垂直于移动副导路，则有
e3 R32 0 将构件2和3的力矩平衡方程
s2 0 h2
0 h2
0
r32
0
0
u21
v21
0
0
0 s2 0
式中， ~rBC s2
0
h2
0 h2 0