第三章 几何光学习题
《光学教程答案》word版

第三章几何光学1.证明反射定律符合费马原理证明:设界面两边分布着两种均匀介质,折射率为山和勺(如图所示)。
光线通过笫一介质中指泄的A点后到达同一介质中指左的B点。
(1)反正法:如果反射点为位于处轴与A和3点所著称的平面之外,那么在ox轴线上找到它的垂足点C"点,.由于AC > AC ,BC >BC\故光线AC B所对应的光程总是大于光线AC B所对应的光程而非极小值,这就违背了费马原理。
故入射面和反射面在同一平面内。
(2)在图中建立坐xoy标系,则指定点A,B的坐标分别为(和yj和(w),反射点C的坐标为(圮0)所以AC3光线所对应的光程为:△=厲[JCv—xj' + y; + >](x-x2)2 + y;]根据费马原理,它应取极小值,所以有空=" 也-①利(sin_sinE = O心yjix-x^ + y- y](x-x2y+y;即:L = i22.根据费马原理可以导出在近轴光线条件下,从物点发出并会聚到像点的所有光线的光程都相等。
EF证:如图所示,有位于主光轴上的一个物点S 发出的光束经薄透镜折射后成一个 明亮的实象点S'。
设光线SC 为电光源S 发出的任意一条光线,其中球面AC 是由点光 源S 所发出光波的一个波面,而球面DB 是会聚于象点S'的球面波的一个波面,所以有关系式SC = SA, SD = SB •因为光程\CEFl)s =SC + CE + nEF + FD + DS △$ MS = SA + I1AB + BS根据费马原理,它们都应该取极值或恒定值,这些连续分布的实际光线,在近轴 条件下其光程都取极大值或极小值是不可能的,唯一的可能性是取恒定值,即它们的光程相等。
3. 睛E 和物体PQ 之间有一 块折射率为1.5的玻璃平板,平 板的厚度d 为30cmo 求物体PQ 的像P0与物体P0之间的距离妁为多少?解:根据例题3.1的结果 PP n1 PP = 30x(1 ———)=10cm1.5n =1.5题3图4.玻璃棱镜的折射棱角A为60。
第三章 几何光学

第三章、几何光学的基本原理一、选择题1.如图,直角三角形ABC 为一透明介质制成的三棱镜的截面,且30=∠A 0,在整个AC 面上有一束垂直于AC 的平行光线射入,已知这种介质的折射率n>2,则( ) A .可能有光线垂直AB 面射出B .一定有光线垂直BC 面射出C .一定有光线垂直AC 面射出D .从AB 面和BC 面出射的光线能会聚一点 B2.如图所示,AB 为一块透明的光学材料左侧的端面。
建立直角坐标系如图,设该光学材料的折射率沿y 轴正方向均匀减小。
现有一束单色光a 从原点O 以某一入射角θ由空气射入该材料内部,则该光线在该材料内部可能的光路是下图中的哪一个 ( )A. B. C. D.3.如图,横截面为等腰三角形的两个玻璃三棱镜,它们的顶角分别为α、β,且α < β。
a 、b 两细束单色光分别以垂直于三棱镜的一个腰的方向射入,从另一个腰射出,射出的光线与入射光线的偏折角均为θ。
则ab 两种单色光的频率υ1、υ2间的关系是( )A 、 υ1 = υ2B 、 υ1 > υ2C 、 υ1 < υ2D 、 无法确定 D 、4、发出白光的细线光源ab ,长度为L ,竖直放置,上端a 恰好在水面以下,如图所示,现考虑线光源ab 发出的靠近水面法线(图中虚线)的细光束经水面折射后所成的像,由于水对光有色散作用,若以1L 表示红光成的像长度,2L 表示蓝光成的像的长度,则( ) A 、L L L <<21B 、L L L >>21C 、L L L >>12D 、L L L <<125、如图所示,真空中有一个半径为R ,质量分布均匀的玻璃球,频率为0υ的细激光束在真空中沿直线BC 传播,并于玻璃球表面C 点经折射进入玻璃球,且在玻璃球表面D 点又经折射进入真空中,0120=∠COD ,已知玻璃对该激光的折射率为3,则下列说法中正确的是( )A 、 一个光子在穿过玻璃球的过程中能量逐渐变小B 、 此激光束在玻璃球中穿越的时间cRt 3=(c 为真空中光速)C 、 改变入射角α的大小,细激光可能在玻璃球的内表面发生全反射D 、 图中的激光束的入射角045=α6、如图所示,两束单色光A 、B 自空气射向玻璃,经折射形成复合光束C ,则下列说法中正确的是:( )A 、 A 光子的能量比B 光子的能量大 B 、 在空气中,A 光的波长比B 光的波长短C 、 在玻璃中,A 光的光速小于B 光的光速D 、 玻璃对A 光的临界角大于对B 光的临界角7、如图所示,激光液面控制仪的原理是:固定的一束光AO 以入射角i 照射到液面上,反射光OB 射到水平的光屏上,屏上用一定的装置将光信号转变为电信号,电信号输入控制系统用以控制液面高度,如果发现光点B 在屏上向右移动了Δs 的距离到B ˊ,则可知液面升降的情况是( )A 、 升高了2S ∆·tan i B .降低了2S ∆·tan i D 、 升高了2S ∆·cot i D 、 降低了2S∆·cot i8.人类对光的本性的认识经历了曲折的过程。
第三章-几何光学
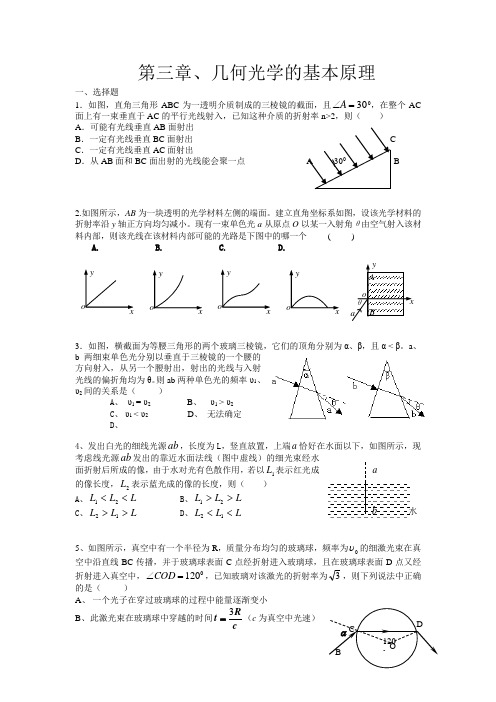
第三章、几何光学的基本原理一、选择题1.如图,直角三角形ABC 为一透明介质制成的三棱镜的截面,且30=∠A 0,在整个AC 面上有一束垂直于AC 的平行光线射入,已知这种介质的折射率n>2,则( ) A .可能有光线垂直AB 面射出 B .一定有光线垂直BC 面射出 CC .一定有光线垂直AC 面射出D .从AB 面和BC 面出射的光线能会聚一点 A 300 B2.如图所示,AB 为一块透明的光学材料左侧的端面。
建立直角坐标系如图,设该光学材料的折射率沿y 轴正方向均匀减小。
现有一束单色光a 从原点O 以某一入射角θ由空气射入该材料内部,则该光线在该材料内部可能的光路是下图中的哪一个 ( )A. B. C. D.3.如图,横截面为等腰三角形的两个玻璃三棱镜,它们的顶角分别为α、β,且α < β。
a 、b 两细束单色光分别以垂直于三棱镜的一个腰的方向射入,从另一个腰射出,射出的光线与入射光线的偏折角均为θ。
则ab 两种单色光的频率υ1、υ2间的关系是( )A 、 υ1 = υ2B 、 υ1 > υ2C 、 υ1 < υ2D 、 无法确定 D 、4、发出白光的细线光源ab ,长度为L ,竖直放置,上端a 恰好在水面以下,如图所示,现考虑线光源ab 发出的靠近水面法线(图中虚线)的细光束经水面折射后所成的像,由于水对光有色散作用,若以1L 表示红光成的像长度,2L 表示蓝光成的像的长度,则( ) A 、L L L <<21B 、L L L >>21C 、L L L >>12D 、L L L <<125、如图所示,真空中有一个半径为R ,质量分布均匀的玻璃球,频率为0υ的细激光束在真空中沿直线BC 传播,并于玻璃球表面C 点经折射进入玻璃球,且在玻璃球表面D 点又经折射进入真空中,0120=∠COD ,已知玻璃对该激光的折射率为3,则下列说法中正确的是( )A 、 一个光子在穿过玻璃球的过程中能量逐渐变小B 、 此激光束在玻璃球中穿越的时间cRt 3=(c 为真空中光速) 水 a b O CDB α1200y a θ xo A ByxoyxoyxoyxoC 、 改变入射角α的大小,细激光可能在玻璃球的内表面发生全反射D 、 图中的激光束的入射角045=α6、如图所示,两束单色光A 、B 自空气射向玻璃,经折射形成复合光束C ,则下列说法中正确的是:( )A 、 A 光子的能量比B 光子的能量大 B 、 在空气中,A 光的波长比B 光的波长短C 、 在玻璃中,A 光的光速小于B 光的光速D 、 玻璃对A 光的临界角大于对B 光的临界角7、如图所示,激光液面控制仪的原理是:固定的一束光AO 以入射角i 照射到液面上,反射光OB 射到水平的光屏上,屏上用一定的装置将光信号转变为电信号,电信号输入控制系统用以控制液面高度,如果发现光点B 在屏上向右移动了Δs 的距离到B ˊ,则可知液面升降的情况是( )A 、 升高了2S ∆·tan i B .降低了2S ∆·tan i D 、 升高了2S ∆·cot i D 、 降低了2S∆·cot i8.人类对光的本性的认识经历了曲折的过程。
几何光学课后部分习题答案

部分作业答案 几何光学部分第一章 几何光学基本定律与成像16、一束平行细光束入射到半径为30r mm =、折射率为 1.5n =的玻璃球上,求其会聚点的位置。
如果在凸面镀上反射膜,其会聚点应在何处?如果凹面镀反射膜,则反射光束在玻璃中的会聚点在何处?反射光束经前表面折射后,会聚点又在何处?解:玻璃球可以看作两个折射球面组合在一起,设凸面为第一面,凹面为第二面 (1)首先考虑光束射入玻璃球第一面时的状态,使用单折射球面物像关系公式1111111n n n n l l r ''--=' 由11111.5;1;;30n n l r mm '==→-∞=,得190l mm '=。
对于第二面,由于两球面顶点距离260d r mm ==,所以222121.0; 1.5;30;30n n l l d mm r mm ''===-==-,由物像关系 2222222n n n n l l r ''--=' 得215l mm '=,即会聚点位于第二面顶点右侧15mm 处。
(2) 将第一面镀膜,形成反射镜,就相当于凸面镜,则11111;1;;30n n l r m m '==-→-∞=,得到115l mm '=,即会聚点位于第一面顶点右侧15mm 处。
(3)光线经过第一面折射后第二面镀膜则22221.5; 1.5;30;30n n l mm r mm '==-==-,得到210l mm '=-,即反射光束在玻璃球内的会聚点位于第二面顶点左侧15mm 处。
(4)再经过第一面折射,将其记为第三面,则333231.5; 1.0;2106050;30n n l l r mm r mm ''===+=-+== 由物像关系3333333n n n n l l r ''--=' 得375l mm '=,即光束从玻璃球出来后的会聚点位于第一面顶点右侧75mm 处,也是第二面顶点右侧15mm 处。
(最新)第三章几何光学的基本原理2

29 一厚透镜的焦距为60mm ,其两焦点间的距离为125mm ,若(1)物点放在光轴上焦点左方20mm 处;(2)物点放在光轴上物方焦点右方20mm 处;(3)虚物落在光轴上象方主点右方20mm 处,问在这三种情况下象的位置各在何处?象的性质如何?并作光路图。
解:(1)将f =-60毫米,60='f 毫米,=1x -20毫米代入牛顿公式得: ),( 240180601802060)60(111实象毫米毫米P s x f f x '=+='=-⨯-='='其光路图如图所示。
(2)将f =-60毫米,60='f 毫米,=1x 20毫米代入牛顿公式得:),( 120601801802060)60(222虚象毫米毫米P s x f f x '-=+-='-=⨯-='='(3)将f=-60毫米,8520560,603=++=='x f 毫米毫米代入牛顿公式得: ),( 65.1735.426035.428560)60(333实象毫米毫米P s x f f x '=-='-=⨯-='='30 一个会聚透镜和一个发散透镜互相接触构成一复合光具组,,当物距为-80cm 时,实象距镜60cm ,若会聚透镜的焦距为10cm ,问发散透镜的焦距为多少?解:设会聚透镜的焦距1f ',发散透镜的焦距2f ',复合系统的焦距f ' 因复合光具组在物距为-80cm 时,实象距为60cm 由:ss f 111-'=',解出复合光具组的焦距:cm f 7/240=' 因两透镜互相接触,有:21111f f f '-'=',已知:cm f 101=' 解出发散透镜的焦距:cm f 1.142-='31 试述测定会聚透镜焦距的几种方法。
第三章__几何光学的基本原理

第三章 几何光学的基本原理3.眼睛E 和物体PQ 之间有一块折射率为1.5的玻璃平板(如图所示),平板的厚 度d 为30cm 。
求物体PQ 的像Q P ''与物体PQ 之间的距离2d 为多少? 已知:1=n ,51.='n ,cm d 30=求:?=2d 解:由图可知 12i QNQ Q d sin ='=,设x QN =,即光线横向的偏移,则 12i xd sin = (1)在入射点A 处,有 21i n i n sin sin '=在出射点B 处,有 12i n i n '='sin sin ,因此可得 11i i '= 即出射线与入射线平行,但横向偏移了x 。
由图中几何关系可得: ()()21221i i i di i AB x -=-=sin cos sin又因为 1i 和2i 很小,所以 12≈i cos , ()2121i i i i -≈-sin 而 21i n ni '= ,所以 1121i ni n ni '='=则 ()⎪⎭⎫ ⎝⎛'-=-=11211i n i d i i d x ,即 ⎪⎭⎫ ⎝⎛'-'=n n di x 11 (2) (2)式代入(1)式得 cm d d n n i i d d 1031511511112==⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛'-'≈.. 6.高5cm 的物体距凹面镜顶点12cm ,凹面镜的焦距是10cm ,求像的位置及高度,并作光路图。
已知:cm y 5=, cm s 12-=,cm f 10-=' 求:?='s ?='y 作光路图解:根据 f s s '='+111得601121101111-=+-=-'='s f s ,cm s 60-='∴又据 n ns s y y '⋅'=' ,而 n n -='所以得 cm y s s y 2551260-=⨯---='-=' 光路图(cm r cm rf 20102-=∴-==',)C为圆心。
第三章__几何光学的基本原理复习课程

第三章__几何光学的基本原理第三章几何光学的基本原理3.眼睛E和物体PQ之间有一块折射率为1.5的玻璃平板(如图所示),平板的厚度d为30cm。
求物体PQ的像QP''与物体PQ之间的距离2d为多少?已知:1=n,51.='n,cmd30=求:?=2d解:由图可知12iQNQQdsin='=,设xQN=,即光线横向的偏移,则12ixdsin=(1)在入射点A处,有21inin sinsin'=在出射点B处,有12inin'='sinsin,因此可得11ii'=即出射线与入射线平行,但横向偏移了x。
由图中几何关系可得:()()21221iiidiiABx-=-=sincossin收集于网络,如有侵权请联系管理员删除收集于网络,如有侵权请联系管理员删除又因为 1i 和2i 很小,所以 12≈i cos , ()2121i i i i -≈-sin 而 21i n ni '= ,所以 1121i ni n ni '='=则 ()⎪⎭⎫ ⎝⎛'-=-=11211i n i d i i d x ,即 ⎪⎭⎫ ⎝⎛'-'=n n di x 11 (2) (2)式代入(1)式得 cm d d n n i i d d 1031511511112==⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛'-'≈.. 6.高5cm 的物体距凹面镜顶点12cm ,凹面镜的焦距是10cm ,求像的位置及高度,并作光路图。
已知:cm y 5=, cm s 12-=,cm f 10-=' 求:?='s ?='y 作光路图解:根据 f s s '='+111得601121101111-=+-=-'='s f s ,cm s 60-='∴又据 n ns s y y '⋅'=' ,而 n n -='所以得 cm y s s y 2551260-=⨯---='-=' 光路图(cm r cm rf 20102-=∴-==',Θ)C为圆心。
chap3习题答案.

f 60cm
(1)当x1 20mm时,有
x1= f f x1
60 (60) 180mm 20
s1 f x 60 180 240mm (p ,实像)
(2)当x2 20mm时,有
x2= f f x2
60 (60) -180mm 20
s2
2
r
r
r
r
s2
nr n
n
nD 2(n
n)
1.57 20 6.05 (cm) 2 (1.53 1)
15.有两块玻璃薄透镜的两表面均各为凸球面及凹球面,其曲率半径为10cm. 一物点在主轴上距离20cm处,若物和镜均浸在水中,分别用作图法和计算法 求像点的位置.设玻璃的折射率为1.5,水的折射率为1.33.
1
f f1 f f 1
1
1
sf12sf sf1sf 1 1
1 s
s11s1s
1 f1
1 f
120120
3913.911.2120.00.0224444
s凸 s凸s1 s1404.902.92cmcm
解: n' n n' n s' s r
(1)s r s1' r
n n n n n s1 r r r
n n n n s s r
即s1 r
(2) s1
s2'
r
2
r
仍在原处(球心),物像重合
/2
n n n n 2n n n n n
n n n n
s3
r1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 几何光学习题
1、一个5cm 高的物体放在球面镜前10cm 处成1cm 高的虚像,则此镜是凸面镜还是凹面镜,
曲率半径为多少? ( )
(A) 凹面镜、5cm (B) 凸面镜、5cm
(C) 凹面镜、—5cm (D) 凸面镜、—5cm
2、 将折射率为n 1=1.50的有机玻璃浸没在油中,而油的折射率为n 2=1.10。
试问临界角为多
少? ( )
(A )arcsin(1.10/1.50) (B )1.10/1.50 (C )1.50/1.10 (D )arccos(1.10/1.50)
(E )arctan(1.50/1.10)
3、 一物体置于焦距为8cm 的薄凸透镜前12cm 处,现将另一焦距为6cm 的薄凸透镜放在
第一透镜右侧30cm 处,则最后成像的性质为 ( )
(A )一个倒立的实像 (B )一个放大的虚像 (C )一个放大的实像
(D )一个缩小的实像 (E )成像于无穷远处
4、说出产生光谱的两种光学元件( )、( )。
5、白光通过棱镜折射后,波长越长的光偏向角( )。
6、凹厚透镜的折射率为1.5,前后表面的曲率半径分别为20mm 和25mm ,中心厚度为20mm ,
后表面镀铝反射膜,在前表面左方40mm 处放置高度为5mm 的小物体。
求在傍轴条件下最后
成像的位置和高度,以及像的倒正、放缩和虚实情况?
7、将焦距为5cm 的薄凸透镜L 沿直径方向剖开,分成上、下两部分B A L L 、,
并将它们沿垂直于对称轴各平移0.01cm 。
其间空隙用厚度为0.02cm 的黑纸镶嵌。
这一装置
称为比累对切透镜。
若将波长为632.8nm 的点光源置于透镜左侧对称轴上10cm 处。
(1) 试分析P 点发出的光束经透镜后的成像情况。
若成像不止一个,计算像点间的距离。
(2) 若在透镜右侧cm a 110 处置一光屏DD ,试分析光屏DD 上能否观察到干涉花样。
若能观察到,试问相邻两条亮条纹的间距是多少?
8、如图所示,折射率为1.5的厚透镜上下表面的曲率半径均为3cm ,中心厚度为2cm 将其置于水面上,水的折射率为1.33,高度为2mm 的小物置于厚透镜下方水中的光轴上,小物与厚透镜下表面中心点的距离为4cm ,求最后成像的位置和高度,以及像的倒正、虚实和放缩情况?
9、如图所示,杨氏装置中的点光源S 发出波长为nm 600=λ的单色光波,间距为mm d 4.0=的双缝S 1和S 2对称分布于光轴两侧,衍射屏和观察屏的距离为cm 100r 0=,凸透镜L 的前后曲率半径相等,焦距为cm f 10=',置于衍射屏和观察屏之间,薄透镜与衍射屏的距离为cm A 10=,在薄透镜和观察屏之间充满折射率为1.33的水。
在傍轴条件下求观察屏DD 上干涉条纹的形状和间距?
10、光线经等腰棱镜折射后,偏向角δ与入射角i 的关系如图1,球棱镜顶角α和折射率。
图1
45° 30δi
11、对以下三种系统,入射光和出射光如图,试判断物、像的虚实。
(A)(B)(C)
解:(A)虚物,实像
(B)实物,虚像
(C)实物,虚像
12、如图所示,一块平凹薄透镜,凹面曲率半径为0.5m,玻璃折射率n=1.5,且在平面上涂一反射层。
在此系统左侧的主轴上放一物P,P距系统1.5m,试问最后成像在何处?大小有何?。
