第12章-弯曲变形
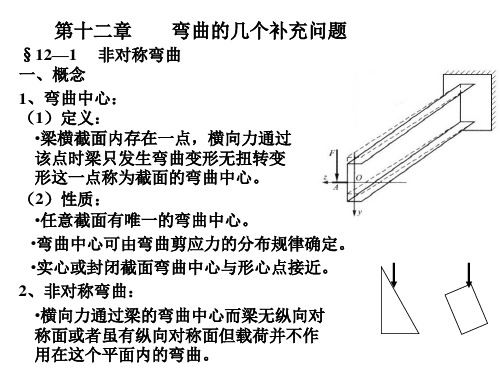
材料力学课件第十二章 弯曲的几个补充问题
Fy
Fl w= w +w = 3E
2 y 2 z
3
cos ϕ sin ϕ + I Iz y
2
2
(2)挠度方向 ) wz I z tanψ = = tan ϕ wy I y 挠度方向与F力不在同一平面内(因此称为斜弯曲)。 挠度方向与 力不在同一平面内(因此称为斜弯曲)。 力不在同一平面内
FSy az = ∫ rτ dA FSz a y = ∫ rτ dA
A A
FS
3、截面弯曲剪力的作用点为弯曲中心。 、截面弯曲剪力的作用点为弯曲中心。
二、截面弯曲中心的位置规律 1、具有两个对称轴或中心对称 、 截面,弯曲中心与形心重合。 截面,弯曲中心与形心重合。 2、具有一个对称轴截面, 弯曲中 、具有一个对称轴截面 心在该轴上。 心在该轴上。 3、由两个矩形组合的截面,弯曲 、由两个矩形组合的截面, 中心在交接处。 中心在交接处。 4、一侧开口截面弯曲中心在形 心的另一侧。 心的另一侧。
§12—2 开口薄壁杆件的剪应力 弯曲中心 一、开口薄壁杆件的剪应力 1、剪应力计算: 、剪应力计算: F (1) Sy对应的剪影力。 ) 对应的剪影力。 FSy S z∗ τ= I zδ F (2) Sz对应的剪影力。 ) 对应的剪影力。 ∗ FSz S y τ= I yδ 2、截面剪力作用点。 、截面剪力作用点。
Fz
Fy
ymax cos ϕ zmax sin ϕ = Fl + Iz Iy
σ Fy
σ Fz
2、杆端挠度 、 (1)数值计算 )
Fl 3 cos ϕ = wy = 3EI z 3EI z Fy l
3
Fz
Fz l 3 Fl 3 sin ϕ = 曲正应力计算 横向力作用在主惯性平面内: 1、横向力作用在主惯性平面内:
第十二章工程力学之组合变形方案

将T分解为沿AC杆轴线的分量Tx和垂直于轴线的分量Ty
Tx T cos 30 40
3 34.6KN 2
Ty
T
sin 30
40
1 2
20KN
可见, Tx和Fcx使AC产生轴向压缩,而Ty、P和Fcy产生弯曲变 形,所以AC杆实际发生的是轴向压缩与弯曲的组合变形。
32 M
d 3
4 15 103
d 2
32 6 103
d 3
根据强度条件 t max [ ]
有
4 15 103
d 2
32
6 103
d 3
35 106
由上式可求得立柱的直径 d≥122mm
例12-3:如图12-6(a)所示,电动机的功率为9kW,转速为 715r/m,皮带轮直径D=250mm,电动机主轴外伸部分长度为 l=120mm,直径d=40mm。求外伸部分根部截面A、B两点的应力。
二、叠加原理
杆在组合变形下的应力和变形分析,一般可利用叠加原理。
叠加原理: 实践证明,在小变形和材料服从虎克定律的前提下, 杆在几个载荷共同作用下所产生的应力和变形,等于每个载荷 单独作用下所产生的应力和变形的总和。
当杆在外力作用下发生几种基本变形时,只要将载荷简化为一 系列发生基本变形的相当载荷,分别计算杆在各个基本变形下 所产生的应力和变形,然后进行叠加,就得到杆在组合变形下 的应力和变形。
M
M max Wy
35 103 2 152 106
115106
115MPa
截面上的弯曲正应力分布如图12-4(c)所示。 (4) 组合变形下的最大正应力
材料力学练习-知识归纳整理
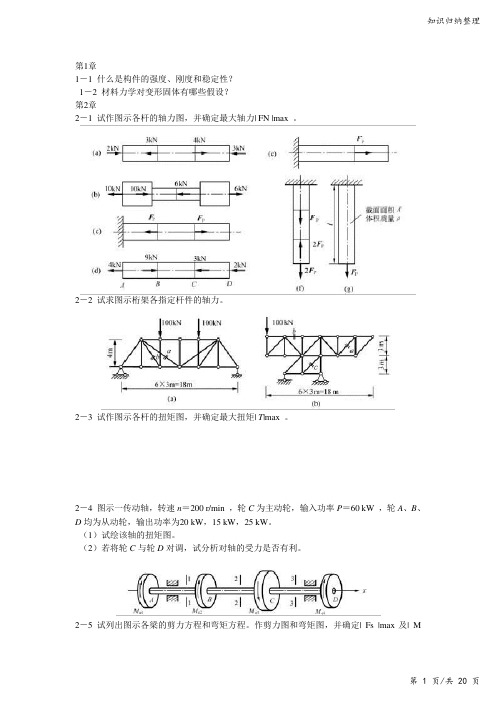
知识归纳整理第1章1-1 什么是构件的强度、刚度和稳定性?1-2 材料力学对变形固体有哪些假设?第2章2-1 试作图示各杆的轴力图,并确定最大轴力| FN |max 。
2-2 试求图示桁架各指定杆件的轴力。
2-3 试作图示各杆的扭矩图,并确定最大扭矩| T|max 。
2-4 图示一传动轴,转速n=200 r/min ,轮C为主动轮,输入功率P=60 kW ,轮A、B、D均为从动轮,输出功率为20 kW,15 kW,25 kW。
(1)试绘该轴的扭矩图。
(2)若将轮C与轮D 对调,试分析对轴的受力是否有利。
2-5 试列出图示各梁的剪力方程和弯矩方程。
作剪力图和弯矩图,并确定| Fs |max及| M求知若饥,虚心若愚。
|max 值。
2-6 试用简易法作图示各梁的剪力图和弯矩图,并确定| F s |max及| M|max值,并用微分关系对图形举行校核。
2-7 图示起重机横梁AB承受的最大吊重F P=12kN,试绘出横梁A B 的内力图。
2-8 图示处于水平位置的控制手柄,在自由端C处受到一铅垂向下的集中力F p作用。
试画出AB段的内力图。
千里之行,始于足下。
第3章3-1图示圆截面阶梯杆,承受轴向荷载F1=50kN与F2的作用,AB与BC段的直径分别为d1=20mm与d2=30mm,如欲使AB与BC段横截面上的正应力相同,试求荷载F2之值。
3-2变截面直杆如图所示。
已知A1=8cm2,A2=4cm2,E=200GPa 。
求杆的总伸长量。
3-3 在图示结构中,AB为刚性杆,CD为钢斜拉杆。
已知F P1=5kN ,F P2=10kN ,l=1m ,杆CD的截面积A=100mm2 ,钢的弹性模量E=200GPa 。
试求杆CD的轴向变形和刚性杆AB在端点B 的铅垂位移。
3-4 一木柱受力如图所示。
柱的横截面为边长200mm的正方形,材料可以为符合胡克定律,其弹性模量E=10GPa。
如不计柱的自重,试求:求知若饥,虚心若愚。
第十二章 弯曲刚度和变形讲解

定义混凝土开裂前的
M
截面刚度为初始刚度,
180 160 140
=1.27% =0.98%
B0
B1
B2
开裂后至割线刚度突 变结束时的割线刚度 为开裂后刚度
M (×106N.mm)
120 100
80 60 40 20
=0.81%
o
=0.66% =0.52% =0.40%
f =0.29%
0
-20 0
1.15 6E
1 3.5 f
= 1.1 0.65 ftk s sk te
在短期弯矩Msk=(0.5~0.7)Mu范围,三个参数、 和 中, 和 为常数,而 随弯矩增长而增大。
该参数反映了裂缝间混凝土参与受拉工作的情况,随着弯矩增 加,由于裂缝间粘结力的逐渐破坏,混凝土参与受拉的程度减
20
40
60
80
100
120
¦Õ (×10£ 6mm-1)
ª¿ ÑÁ óº Õ¸ ȶ /õ³ ʼ Õ¸ ȶ Ö¸ ½î üÇ þ·Ê±Õ¸ ȶ /õ³ ¼Ê Õ¸ ȶ
M
B0
B1
B2
o
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1
0 0
f
¼Æ Ëã Çú Ïß Äâ ºÏ Çú Ïß
小,平均应变增大, 逐渐趋于1.0,抗弯刚度逐渐降低。
等效惯性矩法 Branson建议
M B
EI0
EIcr
A
Ie
=
( Mcr M
)a I0
[1 ( Mcr M
)a ]Icr
o
ACI318-95取a=3,于是有:
I
第12章--构造运动及其形迹

第二节 构造变动
一、 新构造运动的证据
(一)地貌标志
地貌形态是内外地质作用相互制约的产物。
新构造运动的时间较近,形成的地貌形态保 留得较好,因此用地貌方法研究新构造运 动,是特别重要的方法。
– 如以上升运动为主的地区,常形成剥蚀地貌; – 以下降运动为主的地区,常形成堆积地貌。
1、新构造运动中地壳上升的证据
第一节 构造运动的一般特征
一、构造运动的方向性
水平运动 垂直运动
1、 水平运动 水平运动——地壳或岩石圈物质大致
沿地表切线方向的运动,也称造山 运动。
表现: 岩石水平方向的挤压和拉张,岩层褶
皱和断裂,形成褶皱山系和地堑、裂谷等。
现代水平运动的例证:
1970年云南通海地震,一条断裂,长60km, 水平位移量达2.2m。
– 岩层的上下界面叫层面,分别称顶面和底面。 – 岩层顶面和底面的垂直距离称为岩层的厚度。
尖灭 透镜体 夹层 互层
(一)岩层的产状类型
水平岩层 倾斜岩层 直立岩层 倒转岩层
◆岩层特征的变化 夹 层
尖灭
互 层
透镜体
1、水平岩层
原始产状水平或近于水平的岩层。
– 形成于广阔的海底、湖盆盆地中。 – 除新近形成的水平沉积层,几乎所有出露的水平岩
高出海面数米~几百米处有珊瑚礁。
– 如我国台湾高雄附近,在距今海面200— 350m高的地方发现有下更新统的珊瑚灰 岩。
山腰和山顶,有海蚀穴、海蚀阶 地、海蚀崖及蘑菇石等。
– 如山东荣城、厦门,海滩高出海 面20—40m。
– 连云港南云台山主峰——玉女峰 (625.3m)及周围也发现了大量海蚀阶 地、海蚀穴等。
海侵、海退剖面示意
(三)构造变形
材料力学第12章 能量法

范围内工作时,其轴线弯曲成为一段圆弧,如图12.5(a)所示。两端横截
面有相对转动,其夹角为θ ,由第7章求弯曲变形的方法可以求出
图12.5 与前面的情况相似,在线弹性范围内,当弯曲外力偶矩由零逐渐增加到M0时
,梁两端截面相对于转动产生的夹角也从零逐渐增加到θ ,M0与θ 的关系也
是斜直线,如图12.5(b)所示,所以杆件纯弯曲变形时的应变能为
dW在图12.2(a)中以阴影面积来表示。拉力从零增加到FP的整个加载过程
中所做的总功则为这种单元面积的总和,也就是说是△OAB的面积,即
可以将以上的分析推广到其他受力情况,因而静载荷下外力功的计算式可以
写为 式中的 F是广义力,它可以是集中力或集中力偶;Δ 是与广义力F相对应的
位移,称为广义位移,它可以是线位移或角位移。式(12.2)表明,当外力
在工程实际中,最常遇到的是横力弯曲的梁。这时梁横截面上同时有剪力和
弯矩,所以梁的应变能应包括两部分:弯矩产生的应变能和剪力产生的应变 能。在细长梁的情况下,剪切应变能与弯曲应变能相比,一般很小,可以不
计,常只计算弯曲应变能。另外,此时弯矩通常均随着截面位置的不同而变
化,类似于式(12.5)与式(12.9),梁的弯曲应变能为
表面上的剪力与相应的位移方向垂直,没有做功。因此,单元体各表面上的 剪切力在单元体变形过程中所做的功为
故单元体内积蓄的应变能为
则单元体内积蓄的应变比能为
下
这表明,vε 等于γ 直线
的面积。由剪切胡克定律=Gγ ,比能又可以写成下列形式
(3)扭转 如图12.4(a)所示的受扭圆轴,若扭转力偶矩由零开始缓慢增加到最终值T
,积蓄在弹性体内的应变能Vε 及能量耗损Δ E在数值上应等于载荷所做的功 ,既 如果在加载过程中动能和其他形式的能量耗损不计,应有
工程力学第12章弯曲变形
AC段 (0 ≤ x ≤ a) 段 BC段 (a ≤ x ≤ L) 段 Fb 2 Fb 2 F EIω1' = EIθ1 = x + C1, EIω2 ' = EIθ2 = x − (x − a)2 + C2 , 2L 2L 2 Fb 3 EIω1 = x + C1x + D , EIω2 = Fb x3 − F (x − a)3 + C2 x + D2 , 1 6L 6L 6 3、确定常数 、 边界条件: 边界条件:
θA 。
X
解:取参考坐标系Axy。 取参考坐标系 。 1、列出梁的弯矩方程 、
d 2ω M(x) 2、 、 2 = dx EIz
(0 ≤ x ≤ L)
1 2 EIω"= − qx 2 积分一次: 积分一次:EIω' = EIθ = − 1 qx3 + C(1) ) 1 46 积分二次: 积分二次: EIω = − qx + Cx + D (2) ) 24
2、积分常数的确定——边界条件和连续条件: 、积分常数的确定 边界条件和连续条件: 边界条件和连续条件 边界条件:梁在其支承处的挠度或转角是已知的,这样的 边界条件:梁在其支承处的挠度或转角是已知的, 已知条件称为边界条件。 已知条件称为边界条件。 连续条件:梁的挠曲线是一条连续、光滑、平坦的曲线。 连续条件:梁的挠曲线是一条连续、光滑、平坦的曲线。因 此,在梁的同一截面上不可能有两个不同的挠度 值或转角值,这样的已知条件称为连续条件。 值或转角值,这样的已知条件称为连续条件。
二、分段列出梁的挠曲线近似微分方程,并对其积分两次 分段列出梁的挠曲线近似微分方程, 1、对挠曲线近似微分方程积分一次,得转角方程: 、对挠曲线近似微分方程积分一次,得转角方程:
《弹性力学》第十二章薄板弯曲
4w q D
得:
C
q0
8D
3 a4
2 a 2b 2
3 b4
从而
w
q0 1
x2 a2
y2 b2
2
8D
3 a4
2 a 2b 2
3 b4
内力
M
x
D
2w x2
2w y 2
4CD
3x2 a4
xy
8CD1
xy a 2b 2
最大挠度为: wmax x0,y0 C
最大弯矩为(设a>b):
Mmax
My
x0, y b
8CD b2
其中
C
8D
3 a4
q0
2 a2b2
3 b4
,D
Et3
12 1 2
28
例2 试求图示四边简支,
承受均布载荷 q0 的矩形
o
q0
薄板之最大挠度。
x
z
解:取图示坐标系
设
w
m1
Ym
y
sin
mx
a
a
b
则在x=0及x=a边界上,边
o
2
界条件
w 0,
自然满足。
2w x 2
0
b
x
2
y
将w 的表达式代入弹性曲面微分方程
4w q D
29
得
Ym4
m1
材料力学第12章 能量方法
9
(2)剪切变形时的应变能及应变能密度 工程中的剪切变形,一般是与其他变形相伴存 在的,且横截面上的切应力是不均匀分布的。在计 算其应变能时,应以单元体为基础。
图12.3
10
剪切变形时的应变能密度为
可见,剪切变形的应变能密度在数值上等于三 角形OAB的面积。 杆件的剪切应变能为
11
(3)圆轴扭转时的应变能 圆轴扭转时,如果材料应力应变关系处于线弹 性范围,则扭矩MT与扭转角φ的关系也是一条直线 ,如图12.4(b)所示。仿照杆件拉伸应变能的证 明,则变形过程中扭矩所做的功在数值上等于三角 形OAB的面积。有
4
那么,在外力从F1增加到F1+dF1的过程中, 外力功的增量为 当外力从零开始逐渐增加到F值时,则外力功 为 代入 ,得
5
图12.1
6
根据功能原理公式(12.1),则应变能为
式(12.3)为等截面直杆在轴力为常量条件下 的应变能计算公式。如果杆件的轴力FN分段为常 量时,应变能应为各段应变能的总和,即
7
积分可得整个杆件的应变能Vε为 为了更全面地了解应变能,还要知道单位体积 内的应变能,即应变能密度(strainenergy dens ity)由式(a)得应变能密度vε
8
显然,应变能密度vε的数值等于如图12.1(c) 所示三角形oab的面积。这样,又可以将上式的应 变能密度和应变能式(12.5)改写为
第12章
第一节 概述
能量方法
在工程结构分析中,经常需要计算结构和构件 的变形。使用一般的方法(如积分法)进行变形计 算时,需要分析结构和构件的具体变形形式,计算 工作量大。特别是对于刚架、桁架和曲杆等变形复 杂的超静定结构,一般方法根本无法完成。工程上 通常采用能量原理完成结构和构件的变形分析。
材料力学课件第十三章弯曲的几个补充问题
(2) 绘制弯矩图 绘出 Mz (x)图 绘出 My(x) 图
A截面为梁的危险截面
y
F1=1kN
0.5m 0.5m
A z
B
C
x
F2=2kN
x
Mz = 1 kN·m
1kN·m
My= 1 kN·m
1kN·m
Mz使A截面上部受拉,下部受压
My使A截面前部受拉,后部受压
Mz(x)图
x My(x)图
(3) 应力分析
1.分解(Resolution) 将外载沿横截面的两个形心主轴分解,于是得到两个正交的
平面弯曲 2.叠加(Superposition)
对两个平面弯曲进行研究,然后将计算结果叠加起来
Fz
z
j
Fy F
y
A
z y
Bx
Fz
Fy
F
垂直纵向对称面
梁在垂直纵向对 称面 xy 面内发 生平面弯曲 。 z轴为中性轴
' My z
Iy
2.与 Mz 相应的正应力为(The bending normal stress corresponding to Mz)
'' M z y
Iz
C 点处的正应力(The normal stress at point C)
' '' M y z Mz y
Iy
Iz
m
z C ( y,z )
Fy 与均布荷载 q使梁在 xy平面内产生弯曲(z为中性轴)
Fz 使梁在 xz平面内产生弯曲(y为中性轴)
q
F 40° Fy
z
A
C
Fz B
a
a
y
(1) 画弯矩图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P
P
A
C
B
D
支点位移条件:
fA 0 fB 0
连续条件:
fC fC
fD 0 D 0
或写成 fC 左 fC 右
光滑条件: C C
或写成 C 左 C 右
讨论:
①适用于小变形情况下、线弹性材料、细长构件的平面弯曲。
②可应用于求解承受各种载荷的等截面或变截面梁的位移。
③积分常数由挠曲线变形的几何相容条件(边界条件、连续条
一、度量梁变形的两个基本位移量
1.挠度:横截面形心沿垂直于轴线方向的线位移。用w表示。
与 f 同向为正,反之为负。
C
P x 2.转角:横截面绕其中性轴转
w
动的角度。用 表示,顺时
f
C1
针转动为正,反之为负。
二、挠曲线:变形后,轴线变为光滑曲线,该曲线称为挠曲线。
其方程为:
w =f (x)
三、转角与挠曲线的关系: tg df
fmax
f (L) PL3 3EI
解:建立坐标系并写出弯矩方程 f
M
(x)
0
P(a
x)
(0 x a) (a x L)
a
P
L
x
写出微分方程的积分并积分
EIf
0
P(a
x)
(0 x a) (a x L)
EIf
1 2
P(a
x)2
C1
D1
EIf
1 6
P(a
x)3
C1x C2
D1x D2
应用位移边界条件求积分常数
f
EIf (0)
1 6
Pa3
C2
0
EI
(0)
1 2
Pa2
C1
0
a
P
L
x
(a ) (a ) C1 D1
f (a ) f (a )
C1a C2 D1a D2
C1
D1
1 2
Pa2
; C2
D2
1 6
Pa3
写出弹性曲线方程并画出曲线
f
(
x)
P 6EI
第十二章 弯曲变形
§12–1 引言 §12–2 挠曲轴近似微分方程 §12–3 计算梁位移的积分法 §12–4 计算梁位移的叠加法 §12–5 简单静不定梁 §12–6 梁的刚度条件与合理刚度设计
§12-1 引 言
研究范围:等直梁在对称弯曲时位移的计算。 研究目的:①对梁作刚度校核;
②解超静定梁(变形几何条件提供补充方程)。
(a
P
6 EI
a3
x)3 3a 2 x
3a2
x
a3
(0 x a) (a x L)
最大挠度及最大转角
m
a
x
(a)
Pa 2 2EI
f
a
P
L
x
fmax
f
(L)
Pa 2 6EI
a 3L
§12-4 计算梁位移的叠加法
一、叠加法 多个载荷同时作用于结构而引起的变形等于每个载荷单
独作用于结构而引起的变形的代数和。
P
q 例2 按叠加原理求A点转角和C点
A
B
挠度。
C
a
a
P
=
解、载荷分解如图 由梁的简单载荷变形表,
A
B
查简单载荷引起的变形。
+
PA
Pa 2 4EI
f
PC
Pa 3 6EI
q
A
B
qA
qa3 3EI
f
qC
5qL4 24 EI
A
P
q B
叠加
C
A PA qA
a
a
P
a2 (3P4qa) 12 EI
=
A
件)确定。
④优点:使用范围广,直接求出较精确; 缺点:计算较繁。
例1 求下列各等截面直梁的弹性曲线、最大挠度及最大转角。
解: 建立坐标系并写出弯矩方程
M (x) P(L x)
f P
L
x
写出微分方程的积分并积分 应用位移边界条件求积分常数
EIf M (x) P(L x)
EIf
1 2
P(L
物理方程——变形与力的关系
B
f
qL4 Bq8EI ; f BRB
RB L3 3EI
RB
补充方程
q0
qL4 RB L3 0 8EI 3EI
RB
3qL 8
B
求解其它问题(反力、应力、
变形等)
A L
f
A EI
L
A
=
=
C EA LBC
q0 x
B RB
q0 B RB
B RB
+
x)2
C1
EIf
1 6
P(L
x)3
C1x C2
EIf
(0)
1 6
PL3
C2
0
EI
(0)
EIf
(0)
1 2
PL2
C1
0
C1
1 2
PL2
;
C2
1 6
PL3
f
P
L
x
写出弹性曲线方程并画出曲线
f (x) P (L x)3 3L2x L3 6EI
最大挠度及最大转角
m
ax
ቤተ መጻሕፍቲ ባይዱ
(
L)
PL2 2EI
fqC fdPC
0.5L qb2 (3L2 4b3 )db qL4
0
24 EIL
240 EI
例4 按逐段分析求和法说明。
L1
L2
P
A
C
f
Bx f
f f1 f2
=
L1 A 刚化AC段C
L1
+
L2
P 等价
B
L2
P 等价
L2
P
C
Bx
f1
f
L1
P L2
A
C
B
A
C
M Bx
刚化BC段
f
f2
f A EI
B
fC f PC f qC
+
5qa4 Pa3
q
24 EI 6EI
A
B
例3 按叠加原理求C点挠度。 解:载荷无限分解如图
q0
b
C
x
dx
dPq(x)dx2bq0 db L
x
由梁的简单载荷变形表,
0.5L
0.5L
查简单载荷引起的变形。
f
f
dPC
(dP
)b(3L2 4b3 48 EI
)
叠加
qb2 (3L2 4b3 )db 24 EI
(2)
式(2)就是挠曲线近似微分方程。
对于等截面直梁,挠曲线近似微分方程可写成如下形式:
EIf (x) M (x)
§12-3 计算梁位移的积分法
1.微分方程的积分
EIf (x) M (x)
EIf (x) M (x)dx C1
EIf (x) M (x)dxdx C1x C2
2.位移边界条件
L
MA A L
A L
=
q0 Bx
§12-5 简单静不定梁
1、处理方法:变形协调方程、物理
方程与平衡方程相结合,求全部未
q0 知力。
B 解:建立相当系统
确定超静定次数,用反力
q0 代替多余约束所得到的结构—
B
—相当系统。
RB
A L
A A
+
=
q0 几何方程——变形协调方程
B RB
f B f Bq f BRB 0
(P1P2 Pn ) 1(P1 ) 2(P2 ) n (Pn )
f (P1P2 Pn ) f1(P1 ) f2 (P2 ) fn (Pn )
二、逐段分析求和法 要点:首先分别计算各梁段的变形在需求位移处引起的位 移,然后计算其总和(代数和或矢量和),即得需 求之位移。
小变形
f
(1)
dx
§12-2 挠曲轴近似微分方程
一、挠曲线近似微分方程 f M>0
f (x) 0
x
1 M z (x)
EI z
1
f (1
(x) f 2)
小变形
3 2
f (x)
f
M<0 f (x) 0
f ( x) M z ( x) EI z
x
f ( x) M z ( x) EI z
