南京航空航天大学结构力学课后习题答案
南京航空航天大学 结构力学 课后习题答案 第7章
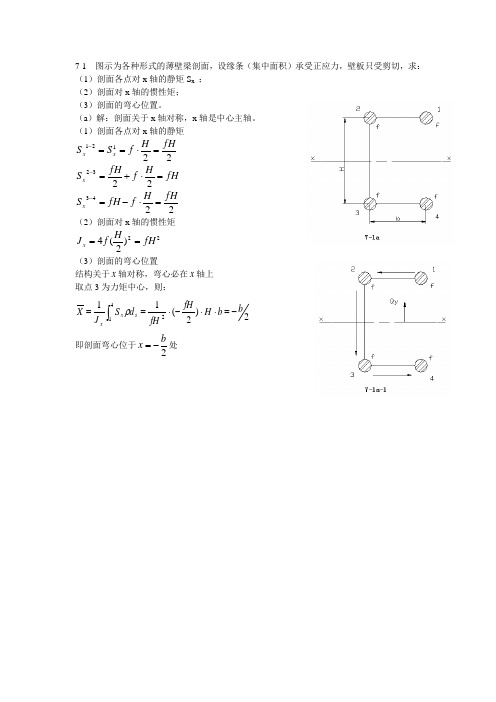
7-1 图示为各种形式的薄壁梁剖面,设缘条(集中面积)承受正应力,壁板只受剪切,求: (1)剖面各点对x 轴的静矩S x ; (2)剖面对x 轴的惯性矩; (3)剖面的弯心位置。
(a )解:剖面关于x 轴对称,x 轴是中心主轴。
(1)剖面各点对x 轴的静矩22121fHH f S S x x =⋅==- fH H f fH S x =⋅+=-2232 2243fHH f fH S x=⋅-=- (2)剖面对x 轴的惯性矩22)2(4fH H f J x == (3)剖面的弯心位置结构关于x 轴对称,弯心必在x 轴上 取点3为力矩中心,则:2)2(11241b b H fH fHd S J X s x x-=⋅⋅-⋅==⎰ρ 即剖面弯心位于2b x -=处(1)剖面各点对x 轴的静矩12233445563()28837828711828117()82873()828x x x x x H H S f fH H S fH f fH H S fH f fHH S fH f fH H S fH f fH -----=⋅-==+⋅==+⋅==+⋅-==+⋅-= 剪流沿1-2-3-4-5-6方向为正(2)剖面对x 轴的惯性矩2222412[()2()]28232x i i H H H J f y f f fH ==⋅-+⋅=∑ (3)剖面的弯心结构关于x 轴对称,弯心必在x 轴上设弯心在3-4杆左侧,距3-4杆的距离为X ,由弯心的定义可知当弯心处作用有y Q 时,结构上的剪流和y Q 在结构上任意一点的合力矩为零 现对x 轴和3-4杆交点处取矩,则1223455608228y H H H HQ X q b q b q b q b ----⋅-⋅⋅-⋅⋅-⋅⋅-⋅⋅= (1) 又知y x y xQ q S J =则(1)式可化为12234556131()822841x x x x x bH bH bH bH X S S S S b J ----=⋅+⋅+⋅+⋅=即结构弯心在x 轴上3-4杆左侧3141b 处题7-1b 图(1)剖面各点对x 轴的静矩12322545651221221122221()221()22x x x x x H S f fH H S f fH H S fH fH f H S f fHH S f fH-----=⋅==⋅==++⋅=⋅-=-=⋅-=- 剪流方向如图(2)剖面对x 轴的惯性矩22224()22()222x i i H HJ f y f f fH ==⋅+⋅⋅=∑(3)剖面的弯心结构关于x 轴对称,弯心必在x 轴上设弯心在2-5杆左侧,距2-5杆的距离为X ,由弯心的定义可知当弯心处作用有y Q 时,结构上的剪流和y Q 在结构上任意一点 的合力矩为零现对x 轴和2-5杆交点处取矩,则12234556022222222y b H b H b H b HQ X q q q q ----⋅+⋅⋅-⋅⋅+⋅⋅-⋅⋅= (1)又知y x y xQ q S J =则(1)式可化为122345561()04444x x x xx bH bH bH bH X S S S S J ----=-⋅+⋅-⋅+⋅= 即结构弯心在x 轴上与2-5杆相交处题7-1c 图(1)剖面各点对x 轴的静矩x S fR =(2)剖面对x 轴的惯性矩222x i i J f y fR ==∑(3)剖面的弯心结构关于x 轴对称,弯心必在x 轴上11Rx x xs X S ds fR ds J J πρρ=⋅=⋅⎰⎰(1)其中ρ为承受剪流的面积到x 轴的距离,取极坐标θ,记上缘条处0θ=,逆时针方向为正,则cos R ρθ=,代入(1)式得11cos cos 0RxxX fR R ds fR R Rd J J ππθθθ=⋅=⋅⋅=⎰⎰即剖面弯心在两缘条中心连线与x 轴的交点处题7-1d 图(1)剖面各点对x 轴的静矩122343355667871099714452424144515244225722227522221()441()44152()424x x x x x x x x x H S f fH fH H S f fHH S f fHH S fH fH f fHH S fH f fHH S fH f fHH S f fHH S f fHH S fH f fH---------=⋅==+⋅==⋅==++⋅==+⋅==-⋅==⋅-=-=⋅-=-=-+⋅-=- 剪流方向如图(2)剖面对x 轴的惯性矩2222134()62()224x i i H H J f y f f fH ==⋅+⋅⋅=∑ (3)剖面的弯心结构关于x 轴对称,弯心必在x 轴上设弯心在5-6杆右侧,距5-6杆的距离为X ,由弯心的定义可知当弯心处作用有y Q 时,结构上的剪流和y Q 在结构上任意一点的合力矩为零 现对x 轴和5-6杆交点处取矩,则1223433567()42422y H H H H HQ X q a b q a q b q b q b -----⋅-⋅⋅+-⋅⋅-⋅⋅-⋅⋅-⋅⋅ 7879910()0424H H Hq b q a q a b ----⋅⋅-⋅⋅-⋅⋅+= (1) 又知y x y xQ q S J =代入(1)式可得11(2)26X a b =+ 即结构弯心在x 轴上5-6杆右侧11(2)26a b +处 题7-1e 图7-2 题7-2图所示薄壁梁剖面,缘条承受正应力,其截面积为22cm f =。
结构力学课后习题答案
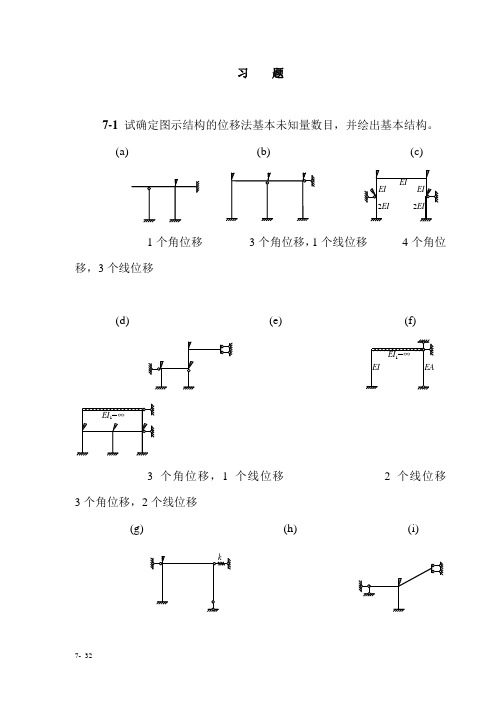
习题7-1 试确定图示结构的位移法基本未知量数目,并绘出基本结构。
(a) (b) (c)1个角位移3个角位移,1个线位移4个角位移,3个线位移(d) (e) (f)3个角位移,1个线位移2个线位移3个角位移,2个线位移(g) (h)(i)7- 327- 33一个角位移,一个线位移 一个角位移,一个线位移 三个角位移,一个线位移7-2 试回答:位移法基本未知量选取的原则是什么?为何将这些基本未知位移称为关键位移?是否可以将静定部分的结点位移也选作位移法未知量?7-3 试说出位移法方程的物理意义,并说明位移法中是如何运用变形协调条件的。
7-4 试回答:若考虑刚架杆件的轴向变形,位移法基本未知量的数目有无变化?如何变化?7-5 试用位移法计算图示结构,并绘出其内力图。
(a)解:(1)确定基本未知量和基本结构有一个角位移未知量,基本结构见图。
lll7- 34Z 1M 图(2)位移法典型方程11110pr Z R +=(3)确定系数并解方程iql Z ql iZ ql R i r p 24031831,821212111==-∴-==(4)画M 图M 图(b)4m4m 4m7- 35解:(1)确定基本未知量1个角位移未知量,各弯矩图如下1Z =1M 图32EIp M 图(2)位移法典型方程11110pr Z R +=(3)确定系数并解方程 1115,352p r EI R ==- 153502EIZ -=114Z EI=(4)画M 图()KNm M ⋅图(c)6m6m9m7- 36解:(1)确定基本未知量一个线位移未知量,各种M 图如下1M 图243EI 243EI 1243EI p M 图F R(2)位移法典型方程11110pr Z R +=(3)确定系数并解方程 1114,243p pr EI R F ==- 140243p EIZ F -=12434Z EI=(4)画M 图7- 3794M 图(d)解:(1)确定基本未知量一个线位移未知量,各种M 图如下11Z1111r 252/25EA a 简化a2a a2aa F P7- 38图1pR pp M(2)位移法典型方程11110pr Z R +=(3)确定系数并解方程 11126/,55p pr EA a R F ==-126055p EA Z F a -=13a Z EA=(4)画M 图图M(e)l7- 39解:(1)确定基本未知量两个线位移未知量,各种M 图如下图1=11211 EA r l r ⎛⇒=⎝⎭1M221EA r l ⎛=⎝⎭图12 0p p p R F R ⇒=-=p M p(2)位移法典型方程1111221211222200p p r Z r Z R r Z r Z R ++=++=(3)确定系数并解方程7- 4011122122121,1,0p p p EA r r r l EA r l R F R ⎛=== ⎝⎭⎛=+ ⎝⎭=-=代入,解得12p p lZ F EAlZ F EA=⋅=⋅(4)画M 图图M p7-6 试用位移法计算图示结构,并绘出M 图。
南京航空航天大学结构力学课后习题答案

第三章能量原理(习题解答)3-1写出下列弹性元件的应变能和余应变能的表达式。
(a )等轴力杆;(b )弯曲梁;(c )纯剪矩形板。
解:(a )等轴力杆 应变能 余应变能其中L 为杆的长度,f 为杆的截面积,△为杆的变形量,E 为材料的弹性模量。
(b ) 弯曲梁 应变能 余应变能(c ) 纯剪矩形板 应变能 余应变能3-2求图3-2所示桁架的应变能及应变余能,应力一应变之间的关系式为 (a) E (b)E,_解:取节点2进行受力分析,如图3-2a 所示 根据平衡条件,有U BdV fl dV联立(1)、(2)、(3)、(4),得到桁架的应变能为 联立(1)、(2)、(3)、(5),得到桁架的余应变能为(a ) E 时N 1 cos45 N 3COS 45N 1 si n45 N 3 sin 45PN 1p1BN1、2N巳P N 1 1f 13N 3f 3N ±3N 31Ef 1Ef 3 U v AdVfld(1)(2)(3) (4) (5)Nj 联立(1)、(2)、(4)、(6),得到桁架的应变能为 联立(1)、(2)、(5)、(6),得到桁架的应变能为3-3 一种假想的材料遵循如下二维的应力一应变规律 其中E 、G 和 是材料常数。
导出用这种材料做成的二维物体的应变能密度解:应变能密度 余应变能密度 总应变能密度 而 所以应变能密度为3-4试用虚位移原理或最小位能原理确定题3-4图所示平面桁架的节点 o的位置和各杆内力。
各杆材料相同,弹性常数为 E 。
P 1 104N ,P 2 5 103 N ,各杆截面积 f 1 1.5cm 2, f 2. 2cm 2,o-2 杆:系统位能 令 0,则——0,—— 0 ,从而:uv解得由N 旦^ ,得l3-5 试用最小位能原理导出承受均布载荷 q 的弯曲等截面梁(图3-5)的 平衡方程式。
解:由教科书例3-2知 悬臂梁的边界条件为: 在 x 0 处,w 0, dw 0dx在x l 处,剪力Q 0,弯矩M 0 又知u z 业(直法线假设)dx(b )3cm 2。
结构力学习题课后答案(高等教育版)

习 题8-1 试说出单元刚度矩阵的物理意义及其性质与特点。
8-2 试说出空间桁架和刚架单元刚度矩阵的阶数。
8-3 试分别采用后处理法和先处理法列出图示梁的结构刚度矩阵。
(a)解:(a )用后处理法计算 (1)结构标识(2)建立结点位移向量,结点力向量[]T44332211 θνθνθνθν=∆[]Ty M F M F M F M F F 4y43y32y211 =θ(3)计算单元刚度矩阵⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=2222322211211462661261226466126122EI 21 l l -l l l -l -l l -l l l l - l k k k k k ①①①①①⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=222233332232223 33 6 3632336 362EI 21 l l - l l l - l -l l -l l l -l l k k k k k ②②②②②lll⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=222234443343323 33 6 3632336 362EI 2 1 l l - l l l - l -l l -l l l -l l k k k k k ③③③③③(4)总刚度矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡++=222222222234443343333322322222112112 3300003 6 3 6 000 03403003601236000 0 3632600 363186120000 26460 0 0 06126122EI 0 0 00 0 0 4 3 2 1 4 3 2 1 l l -l l l - l - - l l -l l l l - l - - l l -l l -l l l l - -l -- l l -l l l l - l k k k k k k k k k k k k k ③③③③②②②②①①①①θ (5)建立结构刚度矩阵支座位移边界条件[][]00004311 θ θ θν=将总刚度矩阵中对应上述边界位移行列删除,得刚度结构矩阵。
南京航空航天大学 结构力学 课后习题答案 第7章

7-1 图示为各种形式的薄壁梁剖面,设缘条(集中面积)承受正应力,壁板只受剪切,求: (1)剖面各点对x 轴的静矩S x ; (2)剖面对x 轴的惯性矩; (3)剖面的弯心位置。
(a )解:剖面关于x 轴对称,x 轴是中心主轴。
(1)剖面各点对x 轴的静矩22121fHH f S S x x =⋅==- fH H f fH S x =⋅+=-2232 2243fHH f fH S x=⋅-=- (2)剖面对x 轴的惯性矩22)2(4fH H f J x == (3)剖面的弯心位置结构关于x 轴对称,弯心必在x 轴上 取点3为力矩中心,则:2)2(11241b b H fH fHd S J X s x x-=⋅⋅-⋅==⎰ρ 即剖面弯心位于2b x -=处(1)剖面各点对x 轴的静矩12233445563()28837828711828117()82873()828x x x x x H H S f fH H S fH f fH H S fH f fHH S fH f fH H S fH f fH -----=⋅-==+⋅==+⋅==+⋅-==+⋅-= 剪流沿1-2-3-4-5-6方向为正(2)剖面对x 轴的惯性矩2222412[()2()]28232x i i H H H J f y f f fH ==⋅-+⋅=∑ (3)剖面的弯心结构关于x 轴对称,弯心必在x 轴上设弯心在3-4杆左侧,距3-4杆的距离为X ,由弯心的定义可知当弯心处作用有y Q 时,结构上的剪流和y Q 在结构上任意一点的合力矩为零 现对x 轴和3-4杆交点处取矩,则1223455608228y H H H HQ X q b q b q b q b ----⋅-⋅⋅-⋅⋅-⋅⋅-⋅⋅= (1) 又知y x y xQ q S J =则(1)式可化为12234556131()822841x x x x x bH bH bH bH X S S S S b J ----=⋅+⋅+⋅+⋅=即结构弯心在x 轴上3-4杆左侧3141b 处题7-1b 图(1)剖面各点对x 轴的静矩12322545651221221122221()221()22x x x x x H S f fH H S f fH H S fH fH f H S f fHH S f fH-----=⋅==⋅==++⋅=⋅-=-=⋅-=- 剪流方向如图(2)剖面对x 轴的惯性矩22224()22()222x i i H HJ f y f f fH ==⋅+⋅⋅=∑(3)剖面的弯心结构关于x 轴对称,弯心必在x 轴上设弯心在2-5杆左侧,距2-5杆的距离为X ,由弯心的定义可知当弯心处作用有y Q 时,结构上的剪流和y Q 在结构上任意一点 的合力矩为零现对x 轴和2-5杆交点处取矩,则12234556022222222y b H b H b H b HQ X q q q q ----⋅+⋅⋅-⋅⋅+⋅⋅-⋅⋅= (1)又知y x y xQ q S J =则(1)式可化为122345561()04444x x x xx bH bH bH bH X S S S S J ----=-⋅+⋅-⋅+⋅= 即结构弯心在x 轴上与2-5杆相交处题7-1c 图(1)剖面各点对x 轴的静矩x S fR =(2)剖面对x 轴的惯性矩222x i i J f y fR ==∑(3)剖面的弯心结构关于x 轴对称,弯心必在x 轴上11Rx x xs X S ds fR ds J J πρρ=⋅=⋅⎰⎰(1)其中ρ为承受剪流的面积到x 轴的距离,取极坐标θ,记上缘条处0θ=,逆时针方向为正,则cos R ρθ=,代入(1)式得11cos cos 0RxxX fR R ds fR R Rd J J ππθθθ=⋅=⋅⋅=⎰⎰即剖面弯心在两缘条中心连线与x 轴的交点处题7-1d 图(1)剖面各点对x 轴的静矩122343355667871099714452424144515244225722227522221()441()44152()424x x x x x x x x x H S f fH fH H S f fHH S f fHH S fH fH f fHH S fH f fHH S fH f fHH S f fHH S f fHH S fH f fH---------=⋅==+⋅==⋅==++⋅==+⋅==-⋅==⋅-=-=⋅-=-=-+⋅-=- 剪流方向如图(2)剖面对x 轴的惯性矩2222134()62()224x i i H H J f y f f fH ==⋅+⋅⋅=∑ (3)剖面的弯心结构关于x 轴对称,弯心必在x 轴上设弯心在5-6杆右侧,距5-6杆的距离为X ,由弯心的定义可知当弯心处作用有y Q 时,结构上的剪流和y Q 在结构上任意一点的合力矩为零 现对x 轴和5-6杆交点处取矩,则1223433567()42422y H H H H HQ X q a b q a q b q b q b -----⋅-⋅⋅+-⋅⋅-⋅⋅-⋅⋅-⋅⋅ 7879910()0424H H Hq b q a q a b ----⋅⋅-⋅⋅-⋅⋅+= (1) 又知y x y xQ q S J =代入(1)式可得11(2)26X a b =+ 即结构弯心在x 轴上5-6杆右侧11(2)26a b +处 题7-1e 图7-2 题7-2图所示薄壁梁剖面,缘条承受正应力,其截面积为22cm f =。
结构力学课后习题答案

结构⼒学课后习题答案附录B 部分习题答案2 平⾯体系的⼏何组成分析2-1 (1)× (2)× (3)√ (4)× (5)× (6)×。
2-2 (1)⽆多余约束⼏何不变体系;(2)⽆多余约束⼏何不变体系;(3)6个;(4)9个;(5)⼏何不变体系,0个;(6)⼏何不变体系,2个。
2-3 ⼏何不变,有1个多余约束。
2-4 ⼏何不变,⽆多余约束。
2-5 ⼏何可变。
2-6 ⼏何瞬变。
2-7 ⼏何可变。
2-8 ⼏何不变,⽆多余约束。
2-9⼏何瞬变。
2-10⼏何不变,⽆多余约束。
2-11⼏何不变,有2个多余约束。
2-12⼏何不变,⽆多余约束。
2-13⼏何不变,⽆多余约束。
2-14⼏何不变,⽆多余约束。
5-15⼏何不变,⽆多余约束。
2-16⼏何不变,⽆多余约束。
2-17⼏何不变,有1个多余约束。
2-18⼏何不变,⽆多余约束。
2-19⼏何瞬变。
2-20⼏何不变,⽆多余约束。
2-21⼏何不变,⽆多余约束。
2-22⼏何不变,有2个多余约束。
2-23⼏何不变,有12个多余约束。
2-24⼏何不变,有2个多余约束。
2-25⼏何不变,⽆多余约束。
2-26⼏何瞬变。
3 静定梁和静定刚架3-1 (1) √;(2) ×;(3) ×;(4) √;(5) ×;(6) √;(7) √;(8) √。
3-2 (1) 2,下;(2) CDE ,CDE ,CDEF ;(3) 15,上,45,上;(4) 53,-67,105,下; (5) 16,右,128,右;(6) 27,下,93,左。
3-3 (a) 298AC M ql =-,Q 32AC F ql =;(b) M C = 50kN·m ,F Q C = 25kN ,M D = 35kN·m ,F Q D = -35kN ;(c) M CA = 8kN·m ,M CB = 18kN·m ,M B = -4kN·m ,F Q BC = -20kN ,F Q BD = 13kN ; (d) M A = 2F P a ,M C = F P a ,M B = -F P a ,F Q A = -F P ,F Q B 左 = -2F P ,F Q C 左 = -F P 。
南京航空航天大学 结构力学 课后习题答案 第6章

6-1 题6-1图所示平面桁架,各杆Ef 相同,求在载荷P 作用下桁架各杆的内力。
解:(1)解除约束:系统静不定度为K=1,故解除1-2杆的约束, 代之以约束力X 1,如图6-1a 所示。
(2)内力分析:求<<P>>状态下的内力N p 、 单位状态<<1>> 下的内力N 1,内力分别如图6-1b,6-1c 所示。
(3)求典型方程中的影响系数δ11和载荷系数△1PEfdEf l N i i )223(2111+===∑ δ EfPdEf l N N i i P P 2111-===∆∑(4)求解多余约束力X 1:由典型方程01111=∆+P X δ解得:PP d EfEf Pd X P 172.0)223()223(22/1111≈-=+=∆-=δ(5)用叠加原理11X N N N P +=求出各杆的内力PN N P N N P N N P N )12(;)222(;)22(;)223(45342414251312-==-==-==-=6-2 题6-2图所示平面桁架,杆长AD=DC=BC=1m,AC 杆和BD 杆的截面积A AC =A BD =200mm 2,A AD =A DC =A BC =150mm 2, 各杆材料均相同,E =200KN/mm 2,当C 点受垂直载荷P =100KN 作用时,求该结构各杆的内力。
解:(1)解除约束:系统静不定度为K=1,故解除CD 杆的约束, 代之以约束力X 1,如图6-2a 所示。
(2)内力分析:求<<P>>状态下的内力N p 、 单位状态<<1>>下的内力N 1,内力分别如图6-2b,6-2c 所示。
(3)求典型方程中的影响系数δ11和载荷系数△1P1150.0803342111≈+===∑ i i Ef l N δ4316.048093411-≈-===∆∑P Ef l N N i i P P (4)求解多余约束力X 1:由典型方程01111=∆+P X δ解得:755.3663437233480480934/1111≈--=+⨯--=∆-=P P X P δ(5)用叠加原理求出各杆的内力: 11X N N N P +=KN N C B 480.88=-KN N D B 252.3-=-748.46=-C A NKN N D A 877.1=-KN N D C 755.3=-如图6-2d 所示。
结构力学课后习题答案[1]
![结构力学课后习题答案[1]](https://img.taocdn.com/s3/m/8c0493dc80eb6294dd886c23.png)
)e( 移位线个 1�移位角个 3 移位角个 1
)d(
)c(
。构结本基出绘并�目数量知未本基法移位的构结示图定确试 1-7
)b(
) a(
题
习
33 -7
下如图矩弯各�量知未移位角个 1 m4 m4
量知未本基定确�1� �解 C IE
m4
D Nk01
IE
B
IE2 m/Nk5.2
A )b(
图M
42 lq 2 5
图矩弯终最画�4� 得解�入代
61.53
IE
3
0 � p 2 R , 0 3 � p 1R 6 � 2 2r IE � 1 2r � 2 1r , I E 2 � 1 1r
程方解并数系定确�3�
p2
11
1
0�
R � 2 Z 2 2r � 1 Z 1 2r R � 2 Z 2 1r � 1 Z 11r
N K 0 3 � � p 2 R , N K 0 3 � p 1R 4 � � 2 2r 0 � 1 2r � 2 1r , i1 1 � 1 1r
p2
得解�入代
i3
程方解并数系定确�3�
0�
R � 2 Z 2 2r � 1 Z 1 2r R � 2 Z 2 1r � 1 Z 11r
程方型典法移位�2�
程方型典法移位�2�
0�
p1
图p M
03 � p 1R � 0 � p 1R
03
04 -7
m2
m2 数常=IE F
B E
m2
m2
D
A
m2
Nk03
C )c(
90.92 55.43
图M
81.8 19.02 54.57 02
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 能量原理
(习题解答)
3-1 写出下列弹性元件的应变能和余应变能的表达式。
(a )等轴力杆;(b )弯曲梁;(c )纯剪矩形板。
解:(a )等轴力杆
应变能 余应变能
其中L 为杆的长度,f 为杆的截面积,Δ为杆的变形量,E 为材料的弹性模量。
(b )弯曲梁 应变能
余应变能 (c )纯剪矩形板 应变能 余应变能
3-2 求图3-2所示桁架的应变能及应变余能,应力—应变之间的关系式为 (a ) E σε= (b )
σ=
解:取节点2进行受力分析,如图3-2a 所示。
根据平衡条件,有
13213113cos 45cos 45sin 45sin 45N N P N N P N N ︒︒︒︒
⎧+=⎨=+⎩⇒== (1)
311313
N N
f f σσ== (2)
(a ) E σε=时
3
1131
3
N N Ef Ef εε=
=
(3) 0
V
U AdV fl d εσε==⎰⎰ (4) 0
V
U BdV fl d σ
εσ*
==⎰⎰ (5)
联立(1)、(2)、(3)、(4),得到桁架的应变能为 联立(1)、(2)、(3)、(5),得到桁架的余应变能为
(b )
σ=时
22
3113222213
N N E f E f εε== (6)
联立(1)、(2)、(4)、(6),得到桁架的应变能为 联立(1)、(2)、(5)、(6),得到桁架的应变能为 3-3 一种假想的材料遵循如下二维的应力—应变规律
其中E 、G 和μ是材料常数。
导出用这种材料做成的二维物体的应变能密度。
解:应变能密度 余应变能密度 总应变能密度 而
所以应变能密度为
3-4 试用虚位移原理或最小位能原理确定题3-4图所示平面桁架的节点o 的位置和各杆内力。
各杆材料相同,弹性常数为E 。
N P 4110=,N P 32105⨯=,各杆截面积215.1cm f =,222cm f =,233cm f =。
解:设o 点的位移为u 、v ,则各杆的变形量如下: o-1杆:)(2
2
sin cos 1v u v u +=+=∆θθ o-2杆:v =∆2
o-3杆:)(22
sin cos 3v u u +-=+-=∆θθ 系统位能 令0=∏δ,则0=∂∏∂u ,0=∂∏
∂v
,从而: 解得
由∆=
l
Ef
N ,得 3-5 试用最小位能原理导出承受均布载荷q 的弯曲等截面梁(图3-5)的平衡方程式。
解:由教科书例3-2知 悬臂梁的边界条件为:
在0x =处,0w =,0dw dx = 在x l =处,剪力0Q =,弯矩0M = 又知
dw
u z
dx
=-(直法线假设)
在x l =处,弯矩0M = 所以,当x l =时, 又知 所以
在x l =处,剪力0Q =
所以,当x l =时,330d w
dx
=
由以上,如果
则有受均布载荷悬臂梁的平衡方程为
44d w
EJ q dx
-=0
3-6 试用最小余能原理求解图3-6所示圆框的弯矩表达式,并给出弯矩图。
圆框的截面弯矩刚度为EJ 、sin P
q R
απ=。
解: 根据圆框的对称性可知,在图3-6a 的受力分析图中,只有轴力和弯矩,而无剪力。
取右半部分的一段进行受力分析如图3-6a 所示。
根据平衡条件,可得到弯矩表达式 余应变能 外力余能
故
根据最小余能原理
*0
0002
00
1
2
MRd M EJ
M N R PR π
αππ∂∏=⇒=∂⇒--=⎰
(1)
*0
00020(1cos )037
28
MRR d N EJ M N R PR π
ααππ∂∏=⇒-=∂⇒--=⎰ (2)
联立(1)、(2)解得
则圆框截面的弯矩为
3-7 试用瑞利—李兹法确定图3-7所示梁的点A 处横向挠度。
解:梁两端简支,其位移边界条件为
0202|0|0x x w d w dx ===⎧⎪⎨=⎪⎩, 2
2|0|0x L x L w d w
dx
===⎧⎪⎨=⎪⎩ 选取正弦函数为基函数,取前两项,则 梁的应变能为
梁的外力势能 梁的总位能
由最小位能原理 因此
当2
3
x L =时
3-8 沿直平面内的正方形薄板,边长为2a ,四边固定,只受重力g ρ作用,如图3-8所示。
设0μ=,试取位移分量的表达式为 用瑞利—李兹法或伽辽金法求解。
解:运用伽辽金法求解。
本题中的四边形薄板四边固支,因此是一个平面应力问题。
其基本方程为
()222222222222
1101221101221,2,3m m E u u v X u dxdy x y x y E v v u Y v dxdy y x x y m μμμμμμ⎡⎤
⎛⎫∂-∂+∂+++=⎢⎥ ⎪-∂∂∂∂⎝⎭⎣⎦
⎡⎤
⎛⎫∂-∂+∂+++=⎢⎥ ⎪-∂∂∂∂⎝⎭⎣⎦=⎰⎰⎰⎰L (1) 当只取1A 项和1B 项时,位移分量的表达式为
2222112242242222112
22222222211
2224
661,1221,133411,u y xy u x xy A A x a a y a a v y v x B B x a a y a a A u x y v xy
B x y a a a x y a ⎛⎫⎛⎫∂∂⎛⎫
⎛⎫
=--=-- ⎪ ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫∂∂⎛⎫
⎛⎫
=--=-- ⎪ ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭
⎝⎭⎝⎭⎛⎫⎛⎫∂∂=--= ⎪⎪∂∂∂∂⎝⎭⎝⎭ (2) 因为0,0,X Y g μρ===,所以(1)式可简化为
222122222
1221102211022a
a
a a a a a a u u v E u dxdy x
y x y v v u E g v dxdy y x x y ρ----⎛⎫
∂∂∂++= ⎪∂∂∂∂⎝⎭⎡⎤⎛⎫
∂∂∂+++=⎢⎥ ⎪∂∂∂∂⎝⎭⎣⎦
⎰⎰⎰⎰ (3)
将11,u v ,及(2)式代入(3)式,得
即 简化为 由此解得
代入位移表达式,得 由物理方程,得
3-9 用李兹法求解受均布载荷作用双简支梁的最大挠度和最大弯矩,挠度函数选下列两种形式,比较其计算结果。
(a )1()sin x
w x a l
π=
(b )133()sin
sin
x
x
w x a a l l
ππ=+
解:双简支梁两端的位移边界条件是
在0x x l ==处,22
00d w
w dx
== 弯矩的表达式为
(a )1()sin x
w x a l
π=时
梁的总位能
由最小位能原理0δ∏=有 所以挠度函数的表达式
最大挠度 最大弯矩
(b )133()sin sin
x x
w x a a l l
ππ=+时 梁的总位能
由最小位能原理0δ∏=有 所以挠度函数的表达式
最大挠度 最大弯矩
3-10 用李兹法求解受均布载荷悬臂梁的挠度,挠度函数选下列各种形式,并比较两种计算所得的最大挠度。
(a )2323()w x a x a x =+
(b )()(1cos )2x
w x A l
π=-
解:悬臂梁的边界条件是
在x=0处,00dw
w dx
==
(a )2323()w x a x a x =+时
梁的总位能
由最小位能原理0δ∏=有
232321
04603EJla EJl a ql a ∂∏=⇒+-=∂ (1) 2342331
061204EJl a EJl a ql a ∂∏=⇒+-=∂ (2) 联立(1)、(2)解得
所以挠度函数的表达式
最大挠度
(b )()(1cos
)2x
w x A l
π=-时
梁的总位能
δ∏=有根据最小余能原理0
所以挠度函数的表达式
最大挠度。
