单组分系统
单组分相图

二氧化碳的相图
BOA——固相面 → 固相区 AOC——液相面 → 液相区 BOC——气相面 → 气相区
O
A
C
OB——固体CO2蒸汽压曲线 OC——液体CO2蒸汽压曲线 OA——固体CO2熔点曲线
B
二氧化碳的相图
A
C
O点是三相点,干冰、 液体CO2、固体CO2三 相同时存在,呈平衡 状态。
B
O
二氧化碳的相图
单组分系统的相图
小组成员:冯顺承 王哲 李靖宇 刘永红 吕杰
单组分系统的相图 在研究多相平衡的系统时,整个系统 状态如何随温度、压强、组成等性质的改 变而发生变化,可以应用解析法、表格法、 图形法。更多应用图形法表示系统状态的 变化,而这种图形就是相图。
单组分系统的相图
单组分系统的两相平衡热力学方程 即克劳修斯-克拉贝龙方程
A
————→ O
C
↑ ▏
B
单组分系统的相图
水的相图和前面二氧 化碳的相图几乎是一样 的,因此我们就不再详 细讨论了
硫的相图
硫有四种相:单 斜硫、斜方硫、液态 硫、硫蒸汽 原因:单组分体 系最多只能有三相共 存,而硫却有单斜硫 和斜方硫两种固态, 因此硫的相图存在四 个三相点。
硫的相图
如图: 单相面(4个):OAC、 OAB、ABC、CBT 两相平衡线(6条) 三相点(3个):A、B、 C 亚稳三相点(1个): G
三相点O的温度 是液体CO2再起蒸汽压 力下的凝固点。物质 的熔点和凝固点相同, 在101325Pa下是正常 熔点。因此,CO2无正 常熔点,三相点的温 度就是熔点。
A
C
O
B
二氧化碳的相图
1.如果在图中作一条横 线,由箭头所示可知, 当压强p不变时,随温度 T的升高,CO2由固态变 为液态 2.如果在图中作一条纵 线,由箭头所示可知, 当温度T不变时,随压强 p的增大,CO2由气态变 为液态
物理化学相平衡知识点

物理化学相平衡知识点相平衡一、主要概念组分数,自由度,相图,相点,露点,泡点,共熔点,(连)结线,三相线,步冷(冷却)曲线,低共熔混合物(固相完全不互溶)二、重要定律与公式本章主要要求掌握相律的使用条件和应用,单组分和双组分系统的各类典型相图特征、绘制方法和应用,利用杠杆规则进行有关计算。
1、相律: F = C - P + n, 其中:C=S-R-R’(1) 强度因素T,p可变时n=2(2) 对单组分系统:C=1, F=3-P(3) 对双组分系统:C=2,F=4-P;应用于平面相图时恒温或恒压,F=3-P。
2、相图(1)相图:相态与T,p,x的关系图,通常将有关的相变点联结而成。
(2)实验方法:实验主要是测定系统的相变点。
常用如下四种方法得到。
12对于气液平衡系统,常用方法蒸气压法和沸点法;液固(凝聚)系统,通常用热分析法和溶解度法。
3、单组分系统的典型相图对于单组分系统C =1,F =C -P +2=3-P 。
当相数P =1时,自由度数F =2最大,即为双变量系统,通常绘制蒸气压-温度(p-T )相图,见下图。
pTlBC AOsgC 'pTlBCA Os gFGD单斜硫pT液体硫BCAO正交硫硫蒸气(a) 正常相图 (b) 水的相图(c) 硫的相图图6-1 常见的单组分系统相图4、二组分系统的相图类型:恒压的t -x (y )和恒温的p -x (y )相图。
相态:气液相图和液-固(凝聚系统)相图。
(1)气液相图根据液态的互溶性分为完全互溶(细分为形3成理想混合物、最大正偏差和最大负偏差)、部分互溶(细分为有一低共溶点和有一转变温度的系统)和完全不溶(溶液完全分层)的相图。
可以作恒温下的p -x (压力-组成)图或恒压下的t -x (温度-组成)图,见图5-2和图5-3。
t = 常数液相线气相线g + llgB Apx B (y B )t = 常数g + l液相线气相线g + llgB Apx B (y B )g + lg + lt = 常数液相线气相线lgBApx B (y B )(a) 理想混合物 (b) 最大负偏差的混合物 (c) 最大正偏差的混合物 图6-2 二组分系统恒温下的典型气液p -x 相图p = 常数液相线或泡点线气相线或露点线g + llgBAtx B (y B )p = 常数g + l液相线或泡点线气相线或露点线g + llg BAtx B (y B )g + lp = 常数液相线或泡点线气相线或露点线g + llgBAtx B (y B )(a) 理想或偏差不大的混合物 (b) 具有最高恒沸点(大负偏差) (c) 具有最低恒沸点(大正偏差)B在A液层中的溶解度线A在B液层中的溶解度线最高会溶点l 1 + l 2p = 常数lBAtx B最低会溶点B在A液层中的溶解度线A在B液层中的溶解度线最高会溶点l 1 + l 2p = 常数lBAtx B DCGFOgg + l g + ll 1 + l 2p = 常数lBAtx B (y B )(d) 有最高会溶点的部分互溶系统 (e)有最高和最低会溶点的部分互溶系统 (f) 沸点与会溶点分离4x B (y B )三相线COD ( l 1 +g + l 2)l 1DC GFOgg + lg + l l 1 + l 2p = 常数l 2B Atx B (y B )三相线COD ( g + l 1 + l 2)g + l 1l 1DC GFOgg + l 2l 1 + l 2p = 常数l 2BAtg + B(l )三相线COD [ A(l ) +g + B(l ) ]DCGFOgg + A(l )A(l ) + B( l )p = 常数BAtx B (y B )(g) 液相部分互溶的典型系统 (h)液相有转沸点的部分互溶系统 (i) 液相完全不互溶的系统图6-3 二组分系统恒压下的典型气液相图(2)液-固系统相图: 通常忽略压力的影响而只考虑t -x 图。
2.8 单组分体系相图

饱和蒸气压大于同温下的冰的饱和蒸汽压。
14 /28
即过冷水的化学势高于同温度下冰的化学
势,只要稍受外界因素的干扰(如振动或 有小冰块或杂质放入),立即会出现冰。
15 /28
2) OB线向左下 可延伸到无限
ቤተ መጻሕፍቲ ባይዱ接近绝对零度。
• 根据克-克方
程,冰-汽平
衡曲线符合:
8 /28
• 通过相律虽能得到水的相图的大致轮廓,
但相图中所有线和点的具体位置却不能由 相律给出,必须由实验来测定。
9 /28
OA线: 水-汽平衡线(即水的饱和蒸汽压T 曲线) OB线: 冰-汽平衡线(即冰的饱和蒸气压T曲线) OC线: 冰-水平衡线; “ O ” 点为冰-水-汽三相平衡的三相点。
情形,即 冰-水-汽 三相平衡,此时体系的自由度:
f=C+2=13+2=0
• 即三相平衡点的 T, p 均已确定,不能变更。
7 /28
• 因此,在相图上
有一个确定的点
代表三相平衡。
• 这个点 “ O ” 叫
作水的三相点。
显然,水在三相点时,固、液、汽三相两
两平衡,所以三相点应为三个两相平衡曲 线的交点。
§2.8 单组分系统相图
表示相平衡系统的性质(如沸点、熔点、蒸汽压、 溶解度)与条件(如温度、压力、组成等) 的函数关 系的图叫相平衡强度状态图,简称相图。 相 图: 体系的相、自由度随温度、压力等的变化规律 在状态空间中的描述。
按组分数: 单组分系统, 双组分系统, 三组分系统
按组分间相互溶解: 完全互溶,部分互溶,完全不互溶 按性质-组成: 蒸汽压-组成图, 沸点-组成图,熔点组成图, 温度-溶解度图
4.2单组分系统详解

二、克劳修斯-克拉珀龙方程
2. 固-气平衡
Hm=SubHm; Vm=Vm(g)-Vm(s),Vm(g)>>Vm(s) ; Vm Vm(g)=RT/p 只需要将液-气平衡式中的VapHm换成 SubHm
•冰点是在水中溶有空气和一定大 气压力下测定的数据。当大气压 力为105Pa时,冰点温度为273.15, 改变外压,冰点温度也随之改变。
A
冰点温度比三相点温度低0.01K是由两种因素造成的: (1)因外压增加,使凝固点下降0.00748K ; (2)因水中溶有空气,使凝固点下降0.00241K。
一、单组分系统相图
E
p
A
气
AD ——气-固两相平衡线 •即冰的升华曲线 •理论上组分系统相图
AE——液-固两相平衡线 •AE线的斜率为负值,说明当 压力增高时冰的熔点降低,即 增加压力有利于体积较小的水 的生成。 •当E点延长至压力大于 2108Pa时,有不同结构的冰 生成,相图变得复杂。
dG()=dG() dG=-SdT+Vdp
-S()dT+V()dp=-S()dT+V()dp
二、克劳修斯-克拉珀龙方程
[V()- V()] dp =[S() -S()]dT
dp = S (β ) - S (α ) = S m dT V (β ) -V (α ) V m
Sm和Vm分别是1mol物质由相变到相的熵变和体积变化. 对于可逆相变:
H m S m = T dp H m = dT TVm ——克拉珀龙方程
Hm为相变潜热,它表明了两相平衡时p-T关系.
二、克劳修斯-克拉珀龙方程
1. 液-气平衡
dp/dT:液体的饱和蒸气压和温度的关系 Hm=VapHm; Vm=Vm(g)-Vm(l); Vm(g)>>Vm(l) ; Vm Vm(g)=RT/p
第五章相平衡个

第五章 相平衡一、本章基本要求1.掌握相、组分数和自由度的意义;2.了解相律的推导过程及其在相图中的应用;3.了解克劳修斯-克拉珀龙方程式的推导,掌握其在单组分两相平衡系统中的应用;4.掌握各种相图中点、线及面的意义;5.根据相图能够画出步冷曲线,或由一系列步冷曲线绘制相图;6.掌握杠杆规则在相图中的应用;7.结合二组分气液平衡相图,了解蒸馏与精馏的原理;8.对三组分系统,了解水盐系统的应用,相图在萃取过程中的应用及分配定律的应用;二、 基本公式和内容提要一基本公式相律的普遍形式:f K n =-Φ+ 克拉珀龙方程:mm d ln d V T H T p ∆∆= 克劳修斯-克拉珀龙方程的各种形式:微分式: 2m vap d ln d RT H T p ∆= vap m H ∆与温度无关或温度变化范围较小vap m H ∆可视为常数, 定积分:vap m 211211ln ()H p p R T T ∆=- 不定积分式:vap mln H p C RT ∆=-+ 特鲁顿规则:K)J/(mol 88b mvap ⋅≈∆T H杠杆规则:以系统点为支点,与之对应的两个相点为作用点,有如下关系:1122()()n x x n x x -=-其中n 1 、n 2 分别表示平衡两相的摩尔数,x 、x 1、x 2分别表示系统的组成及其对应的平衡两相的组成;二内容提要1.单组分系统 单组分系统相律的一般表达式为:f =1-Φ+2=3-Φ图5-1 水的相图可见单组分系统最多只能有三相平衡共存,并且最多有两个独立变量,一般可选择温度和压力;水的相图为单组分系统中的最简单相图之一;图5-1中三条曲线将平面划分成固、液及气相三个区;单相区内f =2;AB 、AD 和AE 分别表示气液、气固和固液两相平衡线;两相共存时f =1;虚线AC 表示应该结冰而未结冰的过冷水与水蒸气平衡共存;A 点为三相点,这时f =0,水以气、液、固三相共存;水的三相点与水的冰点不同,冰点与压力有关;单组分系统两相平衡共存时T 与p 的定量关系式可由克拉珀龙方程式描述;对于有气相参与的纯物质气液两相或气固两相平衡,可用克劳修斯-克拉珀龙方程描述;特鲁顿规则是近似计算气化热或沸点的经验式;2.二组分双液系统 对于二组分系统, f =2-Φ+2=4-Φ;Φ=1时f =3,即系统最多有三个独立变量,这三个变量通常选择温度、压力和组成;若保持三者中的一个变量恒定,可得到p ~x 图、T ~x 图和p ~T 图;在这三类相图中,系统最多有3个相同时共存;1二组分完全互溶系统的气液平衡:这类系统的相图如图5-2;图中实线为液相线,虚线为气相线,气相线与液相线之间为气液二相共存区;靠近气相线一侧为气相区,靠近液相线一侧为液相区;其中Ⅰ为理想液态混合物系统;Ⅱ、Ⅲ分别为一般正、负偏差系统;Ⅳ、Ⅴ分别是最大正、负偏差系统;Ⅰ~Ⅲ类系统中易挥发组分在气相中的组成大于其在液相中的组成,一般精馏可同时得到两个纯组分;Ⅳ、Ⅴ类相图中极值点处的气相组成与液相组成相同,该系统进行一般精馏时可得到一个纯组分和恒沸混合物;二组分系统的两相平衡状态对应一个区域,用杠杆规则可以计算两相平衡共存区平衡二相的相对数量;图5-2 完全互溶系统的气液2部分互溶的二组分系统:因两种液体结构上有显著的差别,会出现一种液体在另一种液体中只有有限的溶解度,超过一定范围便要分成两个液层,即“部分互溶”,相图见图5-3;C点对应的温度称为“临界溶解温度”;温度超过C点,正丁醇与水两组分能以任何比例互溶;还存在另外两类溶解度图,分别见图5-4和图5-5,前者具有下临界溶解温度,后者同时具有上、下临界溶解温度;图5-3 水-正丁醇的溶解图图5-4 水-三乙基胺的溶解度图图5-5 水-烟碱的溶解度图图5-6 邻硝基氯苯、对硝基氯苯二元系统的冷却曲线a 和熔点组成图b3完全不互溶的双液系统:如果两种液体结构相差很大,彼此间的溶解度可以忽略不计,这样的系统可以看作完全不互溶的双液系统;在这类系统中任意液体在某一温度下的蒸气压与该液体同温度下单独存在时的蒸气压相同,与两种液体存在的量无关;总蒸气压**A B p p p =+,因此完全不互溶液体混合物的沸点低于任意纯组分的沸点,这是水蒸气蒸馏的基础;3.二组分固液系统1简单低共熔系统:常用热分析法或溶解度法绘制这类相图;利用“冷却曲线”绘制的邻硝基氯苯A 与对硝基氯苯B 的固液相图见图5-6;aE 和bE 线分别表示邻硝基氯苯与对硝基氯苯固体与熔化物平衡时液相组成与温度的关系曲线,也称为熔点降低曲线;E 点为最低共熔点,对应该温度的水平直线为三相平衡线两端点除外,共存的三相为固体邻硝基氯苯和对硝基氯苯及E 点对应的溶液,aE 、bE 及三相线将图形分成4个部分,各区域的相态分别注在图上;低共熔系统相图与药学密切相关,如利用冷却结晶过程分离提纯化合物;利用熔点变化检查药物或中间体纯度;指导药物配伍及防冻制剂的制备;改良与修饰剂型;与气-液相图联用,对混合物进行分离和提纯;2生成化合物系统:若A 与B 形成的化合物在固相和液相均是稳定的,并且熔化时固相和液相的组成相同,称为生成稳定化合物系统;若A 与B 间形成n 个稳定的化合物,则其固液相图相当于n +1个简单低共熔系统相图的拼合,若A 与B 间形成的化合物C,在加热到熔点之前,就分解成熔化物和另一种固体,熔化物与固态化合物C 的组成不同,称为生成不稳定化合物系统;其相图与前者有所不同;4.三组分系统 当温度和压力同时固定时,在平面上用等边三角形可表示三组分凝聚系统中各平衡系统的状态;其中三个顶点分别表示三个纯物质,三条边分别表示2个端点对应物质构成的二组分系统,三角形内任意一点表示三组分系统,二组分及三组分系统的组成可利用相图得到;三液体间可以是一对、二对甚至是三对部分互溶的,这类系统的相图在液-液萃取过程中有重要作用;除三液系统外,还有水盐系统,其相图对于粗盐提纯、分离具有指导作用;三、 概念题和例题一 概念题1.在一个抽空的容器中,放入过量的NH4Is并发生下列反应:NH4Is NH3g+HIg2HIg H2g+I2g系统的相数Φ= ;组分数K= ;自由度f= ;2.在一个抽空的容器中,放入过量的NH4HCO3s发生下列反应并达平衡:NH4HCO3s NH3g+H2Og+CO2g系统的相数Φ= ;组分数K= ;自由度f= ;3.在一个抽空容器中,放入足量的H2Ol,CCl4l及I2g;H2Ol和CCll完全不互4l中,容器上部的气相中同时含有I2g、H2Og及溶,I2g可同时溶于H2Ol和CCl4CCl4g;该平衡系统的相数Φ= ;组分数K= ;自由度f= ;4.含KNO3和NaCl的水溶液与纯水达渗透平衡,系统的相数Φ= ;组分数K= ;自由度f= ;5.在下列不同情况下,反应:2NH3 g N2 g +3H2 g 达平衡时,系统的自由度各为多少1反应在抽空的容器中进行;2反应在有N2的容器中进行;3反应于一定的温度下,在抽空的容器中进行;6.A和B两种液态物质微观角度讲要满足哪些条件才能形成理想液态混合物7.水的三相点与正常冰点有何不同8.液体的饱和蒸气压越高,沸点就越低;而由克劳修斯-克拉珀龙方程知,温度越高,液体的饱和蒸气压愈大;两者是否矛盾为什么9.对于具有最大正、负偏差的液-气平衡系统,易挥发组分在气相中的组成大于其在液相中的组成的说法是否正确为什么10.在一定压力下,若A、B二组分系统的温度-组成图中出现最高恒沸点,则其蒸气压对拉乌尔定律产生正偏差吗11.导出杠杆规则的基本依据是什么它能解决什么问题如果相图中横坐标为质量分数,物质的数量应取什么单位若横坐标为摩尔分数,物质的数量又应取什么单位二概念题答案1.2,1,12.2,1,13.3,3,24.3, 2, 45.1f=3-1-1-1+2 =2;2f=3-1-1+2=3;3 f=3-1-1-1+1=16.A和B两种液体分子的大小和结构十分接近,使得A-A分子之间、B-B 分子之间及A-B分子之间作用力近似相等时,可构成理想溶液;7.三相点是严格的单组分系统,水呈气、液、固三相共存时对应的温度为,压力为;而冰点是在水中溶有空气和外压为时测得的温度数据;首先,由于水中溶有空气,形成了稀溶液,冰点较三相点下降了;其次,三相点时系统的蒸气压低于冰点时的外压,由于压力的不同冰点又下降了,故冰点时的温度为;8.两者并不矛盾;因为沸点是指液体的饱和蒸气压等于外压时对应的温度;在相同温度下,不同液体的饱和蒸气压一般不同,饱和蒸气压高的液体,使其饱和蒸气压等于外压时,所需的温度较低,故沸点较低;克劳修斯-克拉珀龙方程是用于计算同一液体在不同温度下的饱和蒸气压的,温度越高,液体越易蒸发,故饱和蒸气压越大;9.不正确;因为具有最大正、负偏差系统的相图中有极值点,在极值点处液相组成与气相组成相同,用一般精馏不能将恒沸混合物分离;对于具有最大正、负偏差系统,题中的叙述应修正为适于理想或非理想液态混合物系统的柯诺瓦洛夫规则,即:在二组分溶液中,如果加入某一组分使溶液的总蒸气压增加即在一定压力下使溶液的沸点下降,则这个组分在气相中的组成将大于它在液相中的组成;10.产生负偏差;因为温度-组成图上有最高极值点,压力-组成图上必有最低极值点,故题中所给系统对拉乌尔定律产生最大负偏差;11.导出杠杆规则的基本依据是质量守恒定律,该规则具有普遍意义;可用于计算任意平衡两相的相对数量;相图中横坐标以质量分数表示时,物质的数量以质量为单位;横坐标以摩尔分数表示时,物质的数量以摩尔为单位;三例题例1 水的蒸汽压方程为:4885ln p A T=-, 式中A 为常数,p 的单位为Pa;将10g 水引入体积为10L 的真空容器中,问在323K 达到平衡后,容器中还剩多少水解:将T =,p =101325Pa 代入所给方程中,则:4885ln101325373.2A =- 得A = 于是蒸汽压方程为:Tp 488524.61ln -= 将T =323K 代入上式,得:p =因为 V l +V g =10L, V l V g , 故 V g ≈10L设蒸汽为理想气体,mol 0493.0gg ==RT pV n ,W g =0.888g故还剩水为:10-=9.112g例2 已知298K 时气相异构反应:正戊烷异戊烷的p K =,液态正戊烷和异戊烷的蒸气压kPa 与温度的关系式分别可用下列二式表示: 正戊烷:2002453145.9ln +-=T p 异戊烷:2252453002.9ln +-=T p 假定两者形成的溶液为理想液态混合物,计算298K 时液相异构反应的x K ;解:K p =**x p p K p p =异异正正图5-7 邻硝基氯苯A 与对 硝基氯苯B 的T -x 图 **x p p K K p =正异由已知条件知298K 时,2002453145.9ln +-=T p , *67.99kPa p =正 同理可求得*91.40kPa p =异,则:**67.9913.249.8591.40x p p K K p ==⨯=正异 例3 邻硝基氯苯A 与对硝基氯苯B 的温度-组成图如图5-7:1指出图中点、线、区的意义;2某厂对硝基氯苯车间的结晶器每次处理氯苯硝化料液×103kg,料液的组成为B W =66%,A W =33%间W =1%,可忽略不计,温度约为327K, 若将此料液冷却到290K 此时溶液中含B 35%,如R 点所示,问:1 每次所得对硝基氯苯的产量为多少kg2 平衡产率如何3 冷母液的组成如何冷母液中尚含对硝基氯苯及邻硝基氯苯各多少kg3画出图中f 、g 、h 三物系的步冷曲线;解:1Ⅰ区为邻硝基氯苯与对硝基氯苯二异构体所组成的溶液,为单相区;Ⅱ区为邻硝基氯苯固相与溶液两相平衡共存区;Ⅲ区为对硝基氯苯固相与溶液两相平衡共存区;Ⅳ区为对硝基氯苯固相与邻硝基氯苯固相两相共存区;ac 线为邻硝基氯苯凝固点降低曲线;bc 线为对硝基氯苯凝固点降低曲线;过c 点的水平线与温度坐标的两个交点除外为三相线,线上任意一点都表示邻硝基氯苯固相、对硝基氯苯固态及对应c 点组成溶液的三相平衡共存;a 点为纯邻硝基氯苯的凝固点,b 点为纯对硝基氯苯的凝固点,c 点为低共熔点,该点对应的温度称为低共熔温度;2将W A =33%,W B =66%,温度为323K m 点的系统冷却到190K,此时有大量对硝基氯苯固态析出,冷母液的组成为R 点所示,含对硝基氯苯W B =35%;此时析出的对硝基氯苯固体与溶液的质量比,可由杠杆规则确定,即:66.000.135.066.0B --=溶液m m 又:3B 7.810kg m m +=⨯溶液图5-8 f 、g 、h 三物系的冷却曲1联立以上两式解得:m B =×103kg 272.3%66.0108.71072.333=⨯⨯⨯=平衡产率 3冷母液的组成为含对硝基氯苯W B =35%,含对硝基氯苯的量为:333(7.810 3.7210)35% 1.42810 kg ⨯-⨯⨯=⨯冷母液中含邻硝基氯苯的量为3333(7.810 3.7210) 1.42810 2.62510 kg ⨯-⨯-⨯=⨯3三系统的冷却曲线见图5-8;例 4 下,苯和甲苯的沸点分别为和,摩尔蒸发热分别为30696J/mol 和31967J/mol 设摩尔蒸发热与温度无关;已知苯和甲苯可构成理想液态混合物,问:若使该溶液在,条件下沸腾,其组成应如何解:)11(ln 21m 12T T R H p p -∆= 苯:)2.37314.3531(314.830696101325ln 2-=p 2p = kPa, 甲苯:)2.37318.3831(314.831967101325ln 2-=p 2p = kPa**+p p x p x =苯苯甲苯甲苯176.30+76.10=101.325x x 苯甲苯=1x x +苯甲苯可得 苯x = , 甲苯x =例5 在温度T 时,纯Al 和纯Bl 的饱和蒸气压分别为40kPa 和120kPa;已知A 、B 两组分可形成理想液态混合物;1在温度T 下,将y B =的A 、B 混合气体于气缸中进行恒温缓慢压缩;求第一滴微小液滴不改变气相组成出现时系统的总压力及小液滴的组成x B 各为若干2若A 、B 液态混合物恰好在温度T 、100kPa 下沸腾,此混合物的组成x B 及沸腾时蒸气的组成y B 各为若干解:1设与y B =的气相成平衡的液相组成为x B 时,总压为p ,则有:*B B B **A B B Bp (1)p x y x p x =-+,代入已知数据得: x B =**A B A B B B (1)p p p p x p x =+=-+=40×1-+120×=2由题意知:100 =*A p 1-x B +*B p x B将*A40kPa p =,*B 120kPa p =代入上式得 x B =对应的气相组成: *B B B 0.900100p x y == 例6 在下,将9.0kg 的水A 与30.0kg 的醋酸B 形成的液态混合物加热到378K,达到气液两相平衡时,气相组成y B =,液相中x B =;求气液两相的质量各为多少千克解:由M A =18×10-3 kg/mol,MB=60×10-3 kg/mol 得:mol 500A A A ==M m n ,mol 500BB B ==M m n mol 1000B A =+=n n n 总 系统的总组成:B 0,B 0.500n n n ==总在T =378K 、p =达到气液平衡时,根据杠杆规则,可列出下列关系: g0.5440.5000.34650.5000.417n n -==-总 n g =总n =×1000=n l =总n -n g =1000-=气、液相的平均摩尔质量分别为:M g =Σy i M i =×18+×60×10-3=×10-2 kg/mol图5-9 水-异丁醇沸点-组成示意图 丁醇-水沸点-组成示意图M l =Σx i M i =×18+×60×10-3=×10-2 kg/mol气相的质量:m g =n g M g =××10-3=12.3kg液相的质量:m l = n l M l =××10-2=26.7kg例7 异丁醇-水是液相部分互溶系统,已知其共沸数据如下:共沸点为,共沸组成含异丁醇的质量分数是:气相%,液相中异丁醇层为%,水层为%;今有异丁醇-水液态混合物0.5kg,其中含异丁醇%,将此混合物在压力下加热;1作沸点-组成示意图;2温度接近时,此平衡系统中存在哪些相 各相重多少千克3当温度由刚有上升趋势时,平衡系统中存在哪些相 各相重多少千克解:1根据共沸数据画出相图如图5-9;2温度接近时,平衡系统中存在两个共轭液层,即异丁醇层和水层,设水层重为x kg,则异丁醇层重为-x kg;由上图可知: x 30-=-x 85-30解得: x = 0.36kg异丁醇层重为:-=0.14kg3刚有上升趋势时,系统中亦存在两相,即气相和水层相;设水层重y kg,则气相重为-y kg于是有:y 30-=-y 70-30y = 0.326kg,气相重为:- = 0.174kg四、习题解答1.指出下列平衡系统的组分数、自由度各为多少1NH 4Cls 部分分解为NH 3g 和HClg ;2若在上述系统中额外加入少量的NH 3g ;3NH 4HSs 和任意量的NH 3g 及H 2Sg 平衡;4Cs,COg,CO 2g,O 2g 在100℃时达平衡;解:1K =3-1-1=1, f =1-2+2=12K =3-1-0=2, f =2-2+2=23K =3-1-0=2, f =2-2+2=24K =4-2-0=2, f =2-2+1=12.在水、苯和苯甲酸的系统中,若指定了下列事项,试问系统中最多可能有几个相,并各举一例;1指定温度;2指定温度和水中苯甲酸的浓度;3指定温度、压力和水中苯甲酸的浓度;解:1f=3-Φ+1=4-Φ,f=0时,Φ=4,即最多可有4相共存,如气相、苯甲酸固体、苯甲酸的饱和水溶液及其饱和苯溶液;2f=2-Φ+1=3-Φ,f=0时,Φ=3,故最多可有三相共存,如苯甲酸的饱和水溶液相、苯甲酸的饱和苯溶液相和气相;3f=2-Φ+0=2-Φ,即系统最多可有两相共存,如苯甲酸苯溶液及苯甲酸水溶液;3.求下述系统的自由度数,如f≠0,则指出变量是什么;1在标准压力p下,水与水蒸气平衡;2水与水蒸气平衡;3在标准压力p下,I2在水中和CCl4分配已达到平衡,无I2s存在;4NH3g、H2g、N2g已达化学平衡;5在标准压力p下,NaOH水溶液与H3PO4水溶液混合后;6在标准压力p下,H2SO4水溶液与H2SO4·2H2O固已达平衡;解:1 f=1-2+1=0,即无变量系统2 f=1-2+2=1,即T或p3 f=3-2+1=2,即T和x4 f=2-1+2=3,即T、p和x5 f=3-1+1=3,即T、x1和x26 f=2-2+1=1,即T4.硫的相图如图5-10;图5-10 硫的相图1写出图中各线和点代表哪些相的平衡;2叙述系统的状态由X在恒压下加热至Y所发生的变化;解:1AB:正交与气相;BC:单斜与气相,CD:气相与液相;CE:单斜与液相;BE:过热正交硫的蒸气压曲线;BG:正交与气相;CG:液态与气态;GE:正交与液态;EF:过热正交硫的熔化曲线;B:正交、单斜与气相;C:单斜、液相与气相;E:正交、气相与液相;G:液相、单斜与正交2如图:X→a为正交硫的恒压升温过程,a点为正交硫与单斜硫两相平衡共存,a→b为单斜硫的恒压升温过程,b点为单斜硫与液态两相平衡共存,b→Y为液态硫的恒压升温过程;5.氯仿的正常沸点为外压为,试求氯仿的摩尔气化热及时的饱和蒸气压; 解:由特鲁顿规则知:Δvap H m = 88T b = 88×+ = kJ/mol将已知数据代入克-克方程:)11(ln 21m 12T T R H p p -∆= )15.313165.3341(314.829450325.101ln 2-=p 解得:kPa 0.492=p6.今把一批装有注射液的安瓿瓶放入高压消毒锅内加热消毒,若用的水蒸气进行加热,问锅内的温度有多少度已知Δvap H m = kJ/mol 解:vap m 211211ln ()H p p R T T ∆=- )115.3731(314.840670325.10199.151lnT-= T =385K7.某有机物的正常沸点为外压为,从文献上查得:压力减为 kPa 时,它的沸点为,问在时的沸点为多少 假定~范围内温度对气化热的影响可以忽略; 解:vap m 211211ln ()H p p R T T ∆=- vap m 0.26711ln ()101.3258.314503.15363.15H ∆=- Δvap H m = kJ/mol)115.5031(314.864442325.10133.1ln T-= T =393K8.氢醌的蒸气压实验数据如下: 压力/kPa求:1氢醌的升华热、蒸发热、熔化热设它们均不随温度变化; 2气、液、固三相共存时的温度与压力;3在500K 沸腾时的外压;解:1)11(ln 21m 12T T R H p p -∆= sub m 1.333411ln ()0.13338.314405.55436.65H ∆=-Δsub H m = kJ/molvap m 13.33411ln ()5.33278.314465.15489.65H ∆=- Δvap H m = kJ/molΔfus H m =Δsub H m -Δvap H m = kJ/mol2设三相平衡共存时的温度为T ,压力为p ,则有:sub m 11ln()0.13338.314405.55H p T ∆=- vap m 11ln ()5.33278.314465.15H p T∆=- 二式联立得:T =, p =3沸腾时蒸气压等于外压,即有:)500115.4651(314.8708333327.5ln -=p p =9.为了降低空气的湿度,让压力为的潮湿空气通过一冷却至的管道,试用下列数据,估计在管道出口处空气中水蒸气的分压;水在和时的蒸汽压分别为和,时冰的熔化热为kg 假设所涉及的热效应都不随温度而变;当此空气的温度回升到时压力仍为,问这时的空气相对湿度为若干解:)11(ln 21m 12T T R H p p -∆= vap m 1.22811ln ()0.61068.314273.15283.15H ∆=- vap m 44.93 kJ/mol H ∆=m fus m vap m sub H H H ∆+∆=∆=+××-3= kJ/mol设时冰的饱和蒸汽压为p ,时水的饱和蒸汽压为1p ,则有:)15.248115.2731(314.8509306106.0ln -=p kPa 064.0=p)15.293115.2731(314.8449306106.0ln 1-=pkPa 35.21=p 相对湿度为:%72.2%10035.2064.0=⨯ 10.两个挥发性液体A 和B 构成一理想溶液,在某温度时溶液的蒸气压为,在气相中A 的摩尔分数为,液相中为,求此温度下纯A 和纯B 的蒸气压; 解:由题意知: **AA B A (1)p x p x p +-= *A A A y p x p= 将54.1kPa p =,65.0A =x ,A 0.45y =代入以上二式,得:*A37.45 kPa p =,*B 85.01 kPa p = 11.由甲苯和苯组成的某一溶液含30%质量分数的甲苯,在时纯甲苯和纯苯的蒸气压分别为和,设该溶液为理想溶液,问时溶液的总蒸气压和分压各为多少解:30920.26730709278x ==+甲苯 4.870.267 1.300 kPa p =⨯=甲苯15.76(10.267)11.55 kPa p =⨯-=苯p =12.在下,HNO 3、H 2O 系统的组成为:t/K 373 383 393 395 393 388 383 373 x HNO 3液 y HNO 1画出此系统的沸点组成图;2将3mol HNO 3和2mol H 2O 的混合气冷却到387K,互相平衡的两相组 成为何 相对量为多少3将3mol HNO 3和2mol H 2O 的混合物蒸馏,待溶液沸点升高了4K 时,整个馏出物的组成为若干4将3mol HNO 3和2mol H 2O 的混合物进行精馏,能得到什么纯物质解:1系统的沸点-组成图如图5-11:图5-11 HNO 3-H 2O 系统的沸点-组成图 图5-12 水-异丁醇系统的沸点-组成图 2由图可得:系统点组成、气相组成及液相组成分别为、及,则有:n g -=n l -gl 60540.199260n n -==- 34纯HNO 313.水和异丁醇的气液平衡相图如图5-12;1指出各个相区存在的相态及自由度;2组成为w 1的稀溶液精馏后,在塔顶和塔釜分别得到什么3能根据此相图设计合理的工业分馏过程,完全分离水和异丁醇吗 如果能,请写出大致的分离流程;解:1各区域的相态及自由度分别如下:a 区:气相g,f =2;b 区:液相l 1与气相g 两相共存,f =1;c 区:液相l 2与气相g 两相共存,f =1;d 区:液相l 1与液相l 2两相共存,f =1;e 区:液相l 1,f =2; f 区:液相l 2,f =2;2组成为w 1的稀溶液精馏后,在塔顶和塔釜分别得到恒沸混合物和水;3先将此混合液精馏,在塔釜中得到纯水后,将塔顶得到的恒沸物冷却使其进入液-液两相区,利用分液漏斗将两个液相分离得到水层及异丁醇层,再分别进行精馏,于是在塔釜分别得到纯水及异丁醇;如此进行下去,则可完全分离水和异丁醇;14.已知液体A 与液体B 可形成理想溶液,液体A 的正常沸点为,其摩尔气化热为35 kJ/mol;由2mol A 和8mol B 形成的溶液在标准压力#p 下的沸点为;将x B =的溶液置于带活塞的气缸中,开始时活塞紧紧压在液面上,在下逐渐减小活塞上的压力;求:1出现第一个气泡时系统的总压和气泡的组成;2当溶液几乎全部气化,最后仅有一小滴液体时液相的组成和系统的总压; 解:1设时A 和B 的饱和蒸气压分别为*A p 和*B p ,则有:*A 3500011ln ()101.3258.314338.15318.15p =- *A46.41 kPa p = 由**A A B B 101.325p x p x +=,得*B115.05 kPa p =出现第一个气泡时,液相的组成近似为原溶液的组成,即x B =, x A =,则:A A 46.410.40.211846.410.4115.050.6p y p ⨯===⨯+⨯ 0.78820.21181B =-=y**A A B B 87.61 kPa p p x p x =+=2当溶液几乎全部气化,最后仅有一小滴液体时,气相的组成与原溶液的组成相同,即:y A =,y B = 则有:*A A*B B A Bp x y p p x y p= 解得:x A =,x B =*B 46.410.623072.28kPa 0.4p ⨯== 15.水和乙酸乙酯是部分互溶的,设在,两相互呈平衡,其中一相含有%酯,而令一相含水%都是质量分数;设Raoult 定律适用于各相的溶剂,在此温度时纯乙酸乙酯的蒸气压为,纯水的蒸汽压是;试计算:1酯的分压;2水蒸气分压;3总蒸气压; 解:酯相:0.161883.79100183.79183.79=-+=水x x 酯=1-=p 酯=×水相:0.0146186.75100886.75886.75=-+=酯x x 水=1-=p 水=× =p =p 酯+p 水=16.若在合成某有机化合物之后进行水蒸气压蒸馏,混合物的沸腾温度为;实验时的大气压为,的水饱和蒸汽压为;馏出物经分离、称重,知水的质量分数为%;试估计此化合物的分子量;解:222*H OH O H O *B B B 0.450.55W p M W p M ==图5-13 某二元凝聚系统相图 图5-14 各点对应系统的步冷曲222*H OH O B B *B H Op M W M p W = 2**B H O 99.2084.5314.67 kPa p p p =-=-=B 84.53180.55127 g/mol 14.670.45M ⨯⨯==⨯ 17.某二元凝聚系统的相图如图5-13;1试绘出分别从a 、b 、c 、d 、e 各点开始冷却的步冷曲线;2说明混合物d 和e 在冷却过程中的相变化;解:1a 、b 、c 、d 、e 各点对应系统的步冷曲线分别见图5-14;2d →d 1为液态混合物的恒压降温过程,d 1点开始析出固态B,d 1→d 2为固态B 与溶液二相共存,d 2点为固态B 、固态E 和溶液三相共存,d 2→d 3为固态E 与溶液二相共存,d 3以后为固态A 与固态E 二相共存;e →e 1为液态混合物的恒压降温过程,e 1点开始析出固态B,e 1 →e 2为固态B 与溶液二相共存,e 2点为固态B 、固态E 和溶液三相共存,e 2点以后为固态E 的恒压降温过程;18.下表列出邻-二硝基苯和对-二硝基苯的混合物在不同组成时的熔点数%,w/w K %,w/w K100 4090 3080 2070 1060 0501绘制x T -图,并求最低共熔点混合物的组成;2如果系统的原始组成分别为含对-二硝基苯75%和45%,问用结晶法能从上述混合物中回收得到纯对-二硝基苯的最大百分数为若干解: 1T -x 图如图5-15;图5-15 邻-二硝基苯和对-二硝基苯系统的T-x 图图5-15 邻-二硝基苯和对-二硝基苯系统的T-x 图由上图可知最低共熔混合物的组成为含对位化合物%;2设含对位化合物75%和45%的系统,冷却结晶可得到纯对位化合物的最大百分数分别为x 、y ,则:%7.675.221005.2275=--=x %0.295.221005.2245=--=y 19.图5-16是FeO n -Al 2O 3相图;请指出各相区相态;图5-16 FeO n -Al 2O 3相图解:1区:液相区;2区:浮士体+液相;3区:尖晶石+液相;4区:浮士体;5区:浮士体+尖晶石;6区:尖晶石+液相;7区:刚玉+ 液相;8区:尖晶石;9区:刚玉;10区:尖晶石+刚玉;图5-17 KNO 3-NaNO 3-H 2O 的相图 图5-18 水-乙醚-甲醇三组分系统相图 20.图5-17是三组分系统KNO 3-NaNO 3-H 2O 的相图,实线是298K 时的相图,虚线是373K 下的相图;一机械混合物含70%的KNO 3及30%的NaNO 3,请根据相图拟定分离步骤;解:设含70%KNO 3、30%NaNO 3的系统点在BC 线上的D 点;在298K 时向该系统中加水使其沿DA 线向A 点移动,直至进入KNO 3固体与KNO 3、NaNO 3水溶液二相共存区,此时NaNO 3全部溶解,剩余的固体是KNO 3,但其中可能混有不溶性杂质,这时加热至373K,在该温度时,系统点位于液相区,在高温下过滤除去杂质,再将滤液冷却至298K,即有KNO 3的晶体析出;21.KNO 3-NaNO 3-H 2O 系统在278K时有一三相点,在这一点无水KNO 3和无水NaNO 3同时与一饱和溶液达平衡;已知此饱和溶液含KNO 3为%质量分数,含NaNO 3为%质量分数;如果有一70g KNO 3和30g NaNO 3的混合物,欲用重结晶方法回收KNO 3,试计算在278K 时最多能回收KNO 3多少克解:最多可回收KNO 3为:30700.090463.4g 0.4101-⨯= 22.某温度时在水、乙醚和甲醇的各种三元混合物中二液层的组成如下:甲醇%质量分数 0 10 20 30水%质量分数 液层1 93 82 70 45 液层2 1 6 15 40根据以上数据绘制三组分系统相图,并指出图中各区相态;解:由已知数据绘制的三组分系统的相图及各区相态见图5-18;。
物理化学--相平衡状态图

φ =1,f=3 φ =2,f=2 φ =3,f=1 φ =4,f=0
最多3个独立变量(T, p, 该相组成) 最多4个相平衡共存(无变量)
指定温度, 则有压力-组成图 ; f ′ = 3- φ
指定压力, 则有温度-组成图 . f′= 3 - φ
9
二组分系统按液态互溶情况分类:
Hale Waihona Puke g(A+B) l(A+B)
气 O
C' B
0 0.01 100
• H2O的相图
• OA线是冰的熔点随压力变化曲线, 遵守克拉贝龙方程. 注意其斜率为 负值.
• 3个面分别是气, 液, 固单相区.
• 交点O是三相平衡点, 自由度数为0, 其温度比正常熔点高0.01K.
374.2• 从相图分析恒压变温和恒温变压 t/℃ 过程的相变化(见图).
两相平衡
三相平衡
水或冰的饱和蒸汽压/Pa 平衡压力 平衡压力
/MPa
/Pa
水⇔气 冰⇔气 冰⇔水 冰⇔水⇔气
⎯
103.4
199.6
⎯
(190.5)
165.2
161.1
⎯
285.8
295.4
115.0
⎯
421.0
410.3
61.8
⎯
611.0
611.0 611.0×10-6 611.0
2337.8
⎯
⎯
相平衡状态图
表示相平衡系统的性质(如沸点、熔点、蒸汽压、溶 解度)及条件(如温度、压力、组成等) 间函数关系 的图叫相平衡状态图,简称相图
按组分数: 单组分系统,双组分系统,三组分系统 按组分间相互溶解: 完全互溶,部分互溶,完全不互溶 按性质-组成: 蒸汽压-组成图, 沸点-组成图,熔点组成图,
单组分系统的相图
水和水蒸汽两相平衡。继续加压水蒸汽全部
变为水,到达f点,即一定温度和压力下的水。
4
2.单组分系统的相图
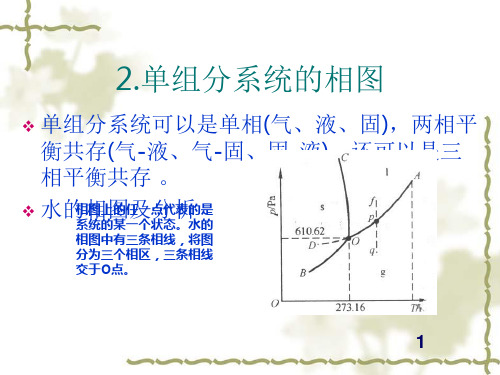
❖ 单组分系统可以是单相(气、液、固),两相平 衡共存(气-液、气-固、固-液),还可以是三 相平衡共存 。
❖ 水的相相图上图的任及一点分代析表ห้องสมุดไป่ตู้是 系统的某一个状态。水的 相图中有三条相线,将图 分为三个相区,三条相线 交于O点。
1
(1)相线分析
❖ OA线是水和水蒸汽的两相平衡线,即饱和蒸汽压线。该线 右液态端水终在止临于界水温的度临上界不点存(Tc在=6。4O7.A4K斜,率P大c=于2.2零1,×表10示4 水kP的a)蒸, 汽压随温度升高而增大,或说水的沸点随外压增大而升高。 OA可以延伸到O点以下为OD线。OD线在图中表示为虚线。 称为过冷水的饱和蒸汽压与温度的关系曲线。
❖ OB线是冰和水蒸汽的两相平衡线,即冰的升华压(蒸汽压)曲 线。理论上可延伸至0 K。OB线斜率也大于零,且大于OA 线斜率。说明温度对冰的蒸汽压影响比对水的影响大。
❖ OC线是冰和水的两相平衡线,即冰的熔点曲线。其斜率小 于零,说明压力增大,水的凝固点降低。
2
(2)相区分析
❖ 相图中的三条线将相图分为三个区域。气相 区(AOB)、液相区(AOC)和固相区(COB)。在 三个区域的一定范围内,任意改变温度或压 力,不会引起相变化。
(3)相点分析
❖ O点是三条两相平衡线的交汇点,称为三相
点。在该点三相平衡共存,温度和压力为一
固定值(273.16K,610.6Pa),不想水能一的想改三:相变点,与 否
物理两相公式

物理两相公式两相公式通常涉及物质在两个不同相态之间的平衡关系。
以下是一些基本的物理两相公式和概念:1. 相律:吉布斯相律是一个用于确定系统自由度数的重要公式,它表示为C=S-R-R',其中C 是组分的数量,S是相的数量,R是独立化学反应的数量,R'是独立约束条件的数量。
对于只受温度和压力影响的平衡系统,最常用的相律形式是F=C-P+2。
2. 两相平衡:在两相共存的情况下,例如液体和气体,存在一个平衡状态,其中两相的化学势相等。
这意味着μ1(T,p) = μ2(T,p),其中μ1和μ2分别是两相的化学势,T是温度,p 是压力。
3. 相变潜热:当物质从一个相转变为另一个相时,会吸收或释放潜热。
例如,水在沸腾时会吸收潜热,而在凝结时会释放潜热。
4. 临界点:在临界点,物质的两个相(如液相和气相)变得不可区分,此时满足\left(\frac{\partial p}{\partial V_m}\right)_T=0和\left(\frac{\partial ^2p}{\partial V_m^2}right)_T=0,其中p是压力,V_m是摩尔体积。
5. 杠杆规则:在两相区,物系点和相点之间的关系可以通过杠杆规则来描述,这是相图分析中的一个重要工具。
6. 单组分系统:在单组分系统中,不存在两相共存的区间,只有一个两相共存的曲线。
这是因为单组分系统的相图相对简单,只有一条表示相变的曲线。
7. 法拉第电磁感应定律:虽然不是直接关于两相平衡的公式,但法拉第电磁感应定律E=n ΔΦ/Δt描述了磁场变化产生的电动势,这在某些物理现象中与两相系统的动态变化有关。
综上所述,这些公式和概念是理解物质在不同相态之间如何平衡和转变的基础。
在实际应用中,这些公式可以帮助我们预测和控制物质的相变行为,从而在科学研究和工程实践中发挥作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p21.0131050.83678.48105 Pa
(2)ln 1.10105 226018(T2-373) 1.013105 8.314373T2 T2375K 即102C
二、克劳修斯-克拉珀龙方程
2. 固-气平衡
Hm=SubHm; Vm=Vm(g)-Vm(s) Vm(g)>>Vm(s) ; Vm Vm(g)=RT/p
一、水的相图
三相点与冰点的区别
A
一、水的相图
两相平衡线的斜率
三条两相平衡线的斜率均可
p
E
B
冰
水
由Clausius-Clapeyron方程或 Clapeyron方程求得。
AB线
d ln p H vap m
dT
RT 2
610.16Pa C
A气
D
273.16K
T
H vap m 0 斜率为正。
化合物
熔点/°C 熔点时的蒸气压/kPa
顺丁烯二酸酐
60
0.44
萘
79
0.9
苯甲酸
120
0.8
-萘酚
122
0.33
苯酐
131.6
0.99
水杨酸
159
2.4
-樟脑
179
49.3
二、克劳修斯-克拉珀龙方程
T, p T+dT,p+dp
G=0 相
dG() G=0
相
相 dG()
相
显然 dG()=dG() dG=-SdT+Vdp
或
d ln dT
p
Vap H RT 2
m
二、克劳修斯-克拉珀龙方程
• 此式称为克劳修斯-克拉佩龙方程的微分形式.当温度变化范 围不大时, VapHm或看成常数,积分可得:
ln p-VapH m K RT
• K为积分常数.lnp~1/T作图应为一直线,斜率为(- VapHm/R) • 如在T1~T2间作定积分
例题. 已知水在100oC时 p*=1.013105Pa, VapH=2260Jg-1,计算: (1)95oC时的p*水=? (2)p=1.10105Pa时水的沸点
解: (1) ln p2 VapH m (T2 -T1)
p1
R T1T2
2286.0311483(376383-63873)-0.1782
一、水的相图
p
E
B
冰
水
A
C
气
D T
一、水的相图
dp/dT=fusHm/fusVm
-20oC,
E 2.108Pa
p
冰
水
A
C
气
D
lnp~1/T
T1 0.0098oC
临界点
B 374oC,
2.23107Pa
T
一、水的相图
AB 是气-液两相平衡线,即水的蒸气压曲线。它不能任意 延长,终止于临界点。临界点p=2.2107Pa,T=647K,这时 气-液界面消失。高于临界温度,不能用加压的方法使气体 液化。
AD线
d ln p sub Hm
dT
RT 2
ssub Hm 0 斜率为正。
AE线
dp fusH m dT T V fus
fus H 0, fusV 0 斜率为负。
一、水的相图
其它相图例举:硫 的 相 图
p
正交
p
X
液 Y
气 T
一、水的相图
其它相图例举:CO2 相 图
一、水的相图
一些有机化全物在熔点时的蒸气压
B Y
T2 T
一、水的相图
两相平衡线上的相变过程
在两相平衡线上的任何一点都可能有三种情况。 如AB线上的P点: (1)处于f点的纯水,保持温度不变,逐步减小压力,在无 限接近于P点之前,气相尚未形成,系统自由度为2。用升压 或降温的办法保持液相不变。
一、水的相图
(2)到达P点时,气相出现,在气-液两相平衡时,f =1。压 力与温度只有一个可变。 (3)继续降压,离开P点时,最后液滴消失,成单一气相,f = 2。通常只考虑(2)的情况。
一、水的相图
三相点与冰点的区别
三相点是物质自身的特性,不能加以改变,如H2O的 三相点T=273.16K,p=610.62Pa。
冰点是在大气压力下,水、冰、气三相共存。当大气压 力为105Pa时,冰点温度为273.15,改变外压,冰点也随之改 变。
E
B
冰
水
p
610.16Pa C
A气
D
273.16K
ln p2 VapH m (T2-T1)
p1
RT1T2
二、克劳修斯-克拉珀龙方程
• 特鲁顿(Trouton)规则:
Vap Hm 88 J K -1 mol-1 Tb
Tb为正常沸点,此规则只适用于正常液体,即非极性液体,液 体分子不缔合液体,如液体苯,不适用于水(强极性液体).
二、克劳修斯-克拉珀龙方程
A点 是三相点(triple point),气-液-固三相共
存,=3,f=0。三相点的温
度和压力皆由系统自定。
E
B
冰
水
p
610.16Pa C
A气
D
273.16
T
H2O的三相点温度为273.16 K,压力为610.16 Pa。
一、水的相图
E
p
p 610.16Pa
冰
水
X NF M
A
C
气
D T1 273.16K
-S()dT+V()dp=-S()dT+V()dp
二、克劳修斯-克拉珀龙方程
[V()- V()] dp =[S() -S()]dT
dp dT
S (β V (β
)- S )-V
(α (α
) )
S V
m m
Sm和Vm分别是1mol物质由相变到相的熵变和体积变 化.对于可逆相变:
S
m
H T
m
dp dT
E
AD 是气-固两相平衡线, 即冰的升华曲线,理论上
p
B
冰
水
可延长至0 K附近。
610.16Pa C
A气
D
0.0098oC
T
AE 是液-固两相平衡线,当C点延长至压力大p=2108Pa时,
相图变得复杂,有不同结构的冰生成。
一、水的相图
AC是BA的延长线,是过冷水和水蒸气的介稳平衡线。因为在 相同温度下,过冷水的蒸气压大于冰的蒸气压,所以AC线在 AD线之上。过冷水处于不稳定状态,一旦有凝聚中心出现, 就立即全部变成冰。
H m TVm
Hm为相变潜热,它表明了两相平衡时p-T关系.
二、克劳修斯-克拉珀龙方程
1. 液-气平衡
dT/dp:液体的饱和蒸气压和温度的关系 Hm=VapHm; Vm=Vm(g)-Vm(l) Vm(g)>>Vm(l) ; Vm Vm(g)=RT/p
dp dT
Vap TVm
Hm (g)
Vap H m×p RT 2
单组分系统相律
• 单组分系统相律的一般表达式为:
f=1- +2=3-
• 单组分系统最多有三相共存,最多可有两个自由度,一般是温 度和压力.
• 最常见的二相平衡有: l g; s l; s g;
=2; f=1,
• 单组分系统两相平衡 时,温度和压力只有一个是独立的,它们 之间有函数关系.克-克方程就是讨论这种关系的.
