用于数字地图自动综合的多边形合并算法
本科第五章数字地图的自动综合

武汉大学资源与环境科学学院 吴凡
地图自动综合的目的与任务
数字环境下地图自动综合的特点
(1)地图自动综合在操作对象、主体、方式和结果等方面,有着与手工地图综合不同的特点。前者 地图自动综合在操作对象、主体、方式和结果等方面 地图自动综合在操作对象 的操作对象是数字地图,操作主体(操作者)是制图员与计算机的交互作用,操作方式是在计算机可 读的情况下通过编程来实现,操作结果是经过综合了的数字地图;而后者的操作对象是模拟地图 ,操作主体是制图员,操作方式是利用刻(绘)图工具在目视可读的情况下直接处理图形资料,其结 果仍是模拟地图。 (2)由于模拟地图具有目视可读的特点,所以手工地图综合过程中选取、化简、概括和位移等操作 由于模拟地图具有目视可读的特点, 由于模拟地图具有目视可读的特点 是一次(同时)完成的,而在数字地图环境下,只能是计算机可读 数字地图环境下, 数字地图环境下 只能是计算机可读,选取、化简和位移等操作是分别 独立进行的,其操作步骤具有很强的可分解性。从这个意义上说,地图综合过程中的操作步骤分 解越细(当然要合理),地图自动综合的实现就相对地越容易。 (3)模拟地图的自动综合其结果仍然是模拟地图 模拟地图的自动综合其结果仍然是模拟地图,在目视可读的情况下,地图综合的质量是可以目 模拟地图的自动综合其结果仍然是模拟地图 视检查的,当然也是可以目视修改的。数字地图综合的结果仍然是数字地图 数字地图综合的结果仍然是数字地图,计算机可读,但目 数字地图综合的结果仍然是数字地图 前计算机还无法判别综合结果是否符合要求,因此,还必须在图形交互编辑条件下,将综合结果 显示在屏幕上,由制图员进行检查并利用修改功能予以修改,当然许多情况下也是可以使用智能 启发式人机交互方式进行修改的。 (4)地图综合是一项复杂的创造性思维过程和繁重的劳动过程 地图综合是一项复杂的创造性思维过程和繁重的劳动过程,在模拟地图 模拟地图综合的情况下,这种复 地图综合是一项复杂的创造性思维过程和繁重的劳动过程 模拟地图 杂的创造性思维过程和繁重的劳动过程都是由制图人员人工完成的,综合质量取决于制图人员对 制图对象规律性的认识和对这些规律的表达能力;在数字地图综合 数字地图综合条件下,复杂的创作性思维过 数字地图综合 程由制图员完成,而繁重的重复劳动过程却是由计算机编程实现的,即使引用专家系统等人工智 能技术,计算机也只是模仿制图专家在综合过程中处理问题的思维方式,解决由制图专家才能处 理好的问题,综合质量取决于模型、算法、规则的合理性、完备性及智能化程度。综合的决策由 制图员做出,而决策的实现是由计算机完成的。
浅谈地图制图综合方法

浅谈地图制图综合方法在数字化时代的今天,地理信息系统已成为空间信息分析应用的主要工具,但空间信息在GIS中的最好表示方式仍然是地图。
本文以地图制图的理论为基础,提出了地图制图综合的几种方法,希望对相关人士有所帮助。
标签:地图自动综合概念模型模型算法1前言地图自动综合的研究从上世纪60 年代就开始了。
最初的研究内容是将地图目标看作简单的几何实体进行操作,如Douglas 和Peucker 进行的线目标化简算法;Topfer 和Pillewizer 的对点、面群目标的选取等。
这些算法使得地图综合的问题得到简化,使得计算的运算量大大的减少;但同时也带来了一些不可忽视的问题,例如不能反映制图综合的约束条件以及不能完全满足基于GIS 下的地图综合的需要。
此后,众多的制图学者进行了多方面的探讨,提出了许多有建设性的理论和方法。
2地图自动综合方法2.1交互式综合在交互式综合中,低层次的任务由软件执行,高层次的任务由人来实现和控制。
交互式方法基于友好的用户界面,用户可以在系统选项中轻松地漫游,选择要被综合的对象和综合所用到的工具。
一个交互式综合方法要成功,最重要的是它不仅仅代替了制图员的笔,而且真正使用户能够在一个高层次上对综合做出决策,也就是说,系统必须能够放大人类的智能。
因此这种方法又叫做“放大智能方法。
”2.2批处理式综合地图自动综合主要批处理方法:面向信息综合、滤波法、启发式综合和分形学方法、小波分析法等。
面向信息综合的基本思想:在原图上找出信息密度(单位面积信息量)太大且因此不能保证缩小后的地图的视觉易读性的位置。
通过在该处改变制图目标,使目标概率增加,从而使信息量减少。
面向信息的综合大都是研究地图的总体信息,甚至基本上只涉及关于一幅图的平均信息量,然而对于具体的综合操作来说,更为重要的是单个制图目标的信息。
滤波是对以周期振动为特征的一种现象的一定频率范围的减弱或抑制。
当低通滤波时,地图信息的局部高频被消除;当高通滤波时,地图信息的局部低频被消除。
fme多个多边形合并

fme多个多边形合并FME是一种功能强大的空间数据转换工具,它可以处理和合并多个多边形。
本文将介绍如何使用FME合并多个多边形,并探讨合并后的多边形的特点和应用。
我们需要了解多边形的基本概念。
多边形是由一系列有序的线段组成的封闭图形,它可以是简单多边形或复杂多边形。
简单多边形是不自交的多边形,而复杂多边形则可以是自交的。
在空间数据中,多边形常用于表示地物的边界或区域。
在FME中,可以使用多种方式合并多个多边形。
一种常用的方法是使用Union操作符,它可以将多个多边形合并为一个单一的多边形。
合并后的多边形将包含原始多边形的全部边界,并且不会有重叠或缺失的部分。
这种合并方式适用于简单多边形和复杂多边形。
除了Union操作符,FME还提供了其他一些操作符和功能,可以用于合并多个多边形。
例如,可以使用Buffer操作符将多个多边形扩展为缓冲区,然后使用Dissolve操作符将缓冲区合并为一个多边形。
这种方法适用于需要合并附近区域的情况。
合并多个多边形可以有多种应用场景。
首先,合并可以简化空间数据的管理和分析。
通过将多个多边形合并为一个,可以减少数据的复杂性,提高数据处理效率。
其次,合并可以用于创建新的地理区域。
例如,在城市规划中,可以将多个小区域合并为一个大区域,以便更好地管理和规划城市发展。
此外,合并还可以用于计算多个多边形的总面积或周长,以及进行空间分析和决策支持。
然而,需要注意的是,合并多个多边形可能会导致一些问题。
首先,合并后的多边形可能会变得非常复杂。
如果原始多边形的边界非常不规则或包含大量的顶点,合并后的多边形可能会变得非常复杂,使数据处理和分析变得困难。
其次,合并可能导致信息的丢失或歧义。
如果原始多边形之间存在重叠或相交的部分,合并后的多边形可能无法准确表示原始多边形的边界。
因此,在进行合并操作时,需要仔细考虑数据的特点和需求,并进行适当的处理和校验。
FME是一种强大的空间数据转换工具,可以用于合并多个多边形。
多重合并区域计算

多重合并区域计算
多重合并区域计算是指在二维平面上给定多个区域,并计算它们的合并结果。
常见的应用场景包括图像处理、地理信息系统等领域。
具体的计算方法可以根据需求选择不同的算法。
下面介绍几种常用的多重合并区域计算算法:
1. 基于边界的算法:首先计算每个区域的边界,并将边界进行合并。
合并的方法可以是简单的相交或者融合。
这种算法适用于区域边界明确的情况。
2. 基于像素的算法:将每个区域表示为二值图像,通过对图像进行像素级的操作实现合并。
常见的操作包括逻辑运算(如并、交、补等)、图像融合等。
这种算法适用于区域以像素为基本单位的情况。
3. 基于图的算法:将每个区域表示为图的节点,并通过图的遍历和连接操作实现合并。
常见的算法包括最小生成树、最大流、最短路径等。
这种算法适用于区域之间存在复杂连接关系的情况。
4. 基于分割的算法:将整个平面划分为若干个区域,并通过区域的分割和合并操作实现最终的合并结果。
常见的算法包括分层聚类、区域生长等。
这种算法适用于区域个数较多且结构复杂的情况。
无论采用哪种算法,其关键是确定合并的规则和条件,以及对结果的评估和优化。
这需要根据具体的应用场景和需求进行调整和改进。
数字地面模型分割合并算法流程

•
• •
按照夹角大小对点排序,若夹角相同,按照距离排序
依次链接所有顶点,得到多边形 根据“凸多边形的各顶点必在该多边形的任意一条边的同侧”定理,删除非凸壳 顶点,得到边界。
凸壳生成算法
分割采样点
凸壳生成算法
P2
1、构造子网边界 2、三角化子网
P4 P3
P5 P1 P0
分割合并算法
P3 P2
1、构造子网边界 2、三角化子网 3、类似构造另外一个子集
P5
P4 P3 P4
P2
4、底线和顶线的查找
P0
P1 P5
P1
P0
Xmax Xmin
分割合并算法
P3 P2
1、构造子网边界 2、三角化子网 3、类似构造另外一个子集
P5
P4 P3 P4
P2
4、底线和顶线的查找 5、合并三角形
分割合并算法
分割合并算法步骤
S1 将数据集以横坐标为主、纵坐标为辅按升序排序。 S2 如数据集中点数大于阀值,则继续将数据集化为点个数近似相等 的两个子集,并 对每个子集做如下工作: ① 获取每子集的凸壳; ② 以凸壳为数据边界进行三角化,并用LOP优化成D三角网; ③ 找出连接左右子集两个凸壳的底线和顶线; ④ 由底线到顶线合并两个三角网。 S3 如数据集中点数不大于阀值,则直接输出三角剖分结果。
分割合并算法要点:
1、数据点集采用递归分割快速排序法;
2、子集凸壳的生成可采用格雷厄姆算法; 3、子集三角化可采用任意方法,3或4个点可直接三角剖分;
4、子网合并则需先找出左右子集凸壳的底线和顶线;
5、逐步合并三角剖分得到最终D三角网(三角网的局部优化)。
多边形配准算法

多边形配准算法是指通过一定的算法和技巧,将两个或多边形进行对齐和匹配的过程。
在计算机视觉和图形处理领域,多边形配准是一项非常重要的技术,广泛应用于图像处理、计算机图形学、地理信息系统等领域。
多边形配准算法的目标是将两个多边形的顶点进行对应,使得它们的形状和位置尽可能相似或完全一致。
具体来说,多边形配准算法通常包括以下几个步骤:
1. 多边形表示:首先需要将多边形表示为数学模型,常用的表示方法有平面几何表示法和参数化表示法等。
2. 特征提取:提取多边形的特征点、线、面等几何特征,以便进行匹配。
常用的特征提取方法有SIFT、SURF、ORB等。
3. 特征匹配:根据提取出的特征点,进行特征匹配,找出两个多边形之间的对应关系。
常用的特征匹配方法有暴力匹配、RANSAC、最小二乘法等。
4. 变换模型估计:根据匹配的特征点,估计多边形的变换模型,包括平移、旋转、缩放等。
常用的变换模型估计方法有奇异值分解(SVD)、广义最小二乘法等。
5. 多边形配准:根据估计出的变换模型,对原始多边形进行变换,使其与目标多边形对齐和匹配。
常用的变换方法有仿射变换、透视变换等。
多边形配准算法的精度和稳定性对于实际应用非常重要。
为了提高精度和稳定性,可以采用更精确的特征提取和匹配方法、改进变
换模型的估计方法等技术手段。
同时,也需要针对具体的应用场景和需求,设计合适的算法和参数,以满足实际需求。
数字电子地图制作中的测绘技术与数据融合方法

数字电子地图制作中的测绘技术与数据融合方法数字电子地图制作是现代测绘技术与数据融合的产物。
测绘技术的发展使得地图的制作更加精确和高效,而数据融合方法则为地图中的信息提供了更多种类和更全面的表现形式。
在数字电子地图的制作过程中,测绘技术起着至关重要的作用。
传统的测绘方法主要依靠人工地面测量,这种方式耗时耗力且不精确。
而现代测绘技术采用了各种先进的设备和技术手段,如全站仪、卫星定位系统等,大大提高了地图制作的效率和精度。
其中,全站仪是测绘中最常用的仪器之一。
全站仪通过激光测距仪和角度测量系统,能够准确测量目标点的坐标和角度,从而生成地图所需的基本数据。
全站仪的高精度和高效率使其成为现代地图制作过程中的重要工具。
除了测绘技术外,数据融合方法也是数字电子地图制作不可或缺的一部分。
数据融合方法可以将多个不同来源的数据进行整合和合并,以获得更加全面和准确的地图信息。
数据融合方法有多种形式,其中一种常见的方法是图像融合。
图像融合通过对不同分辨率、不同传感器获取的图像进行处理和融合,得到更清晰、更全面的地图。
这种方法在卫星图像处理和遥感技术中得到广泛应用。
此外,地理信息系统(GIS)也是数字电子地图制作中常用的工具之一。
GIS能够将各种地理数据进行整合、分析和展示,为地图制作提供更多功能和应用场景。
通过GIS,地图制作者可以将不同类型的数据融合在一起,形成更为丰富和有价值的地图产品。
在数据融合方法的应用过程中,需要考虑数据的质量和一致性。
不同数据来源可能存在误差和偏差,因此在数据融合过程中,需要进行数据质量评估、数据配准和精度控制等工作,以保证地图的准确性和可靠性。
此外,随着人工智能技术的不断发展,数据融合方法在数字电子地图制作中的应用也在不断扩展。
利用深度学习等人工智能技术,可以实现对多源数据的智能融合和分析,从而得到更加精确和全面的地图信息。
综上所述,数字电子地图制作中的测绘技术与数据融合方法具有重要意义。
指南四:多边形叠合
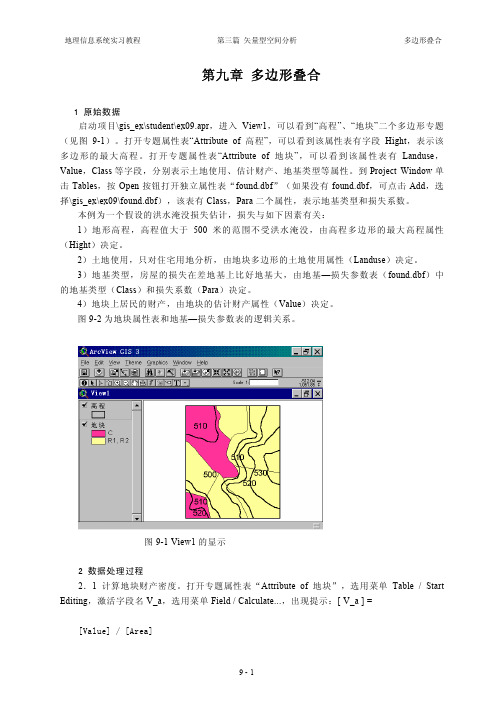
第九章 多边形叠合1 原始数据启动项目\gis_ex\student\ex09.apr,进入View1,可以看到“高程”、“地块”二个多边形专题(见图9-1)。
打开专题属性表“Attribute of 高程”,可以看到该属性表有字段Hight,表示该多边形的最大高程。
打开专题属性表“Attribute of 地块”,可以看到该属性表有Landuse,Value,Class等字段,分别表示土地使用、估计财产、地基类型等属性。
到Project Window单击Tables,按Open按钮打开独立属性表“found.dbf”(如果没有found.dbf,可点击Add,选择\gis_ex\ex09\found.dbf),该表有Class,Para二个属性,表示地基类型和损失系数。
本例为一个假设的洪水淹没损失估计,损失与如下因素有关:1)地形高程,高程值大于500米的范围不受洪水淹没,由高程多边形的最大高程属性(Hight)决定。
2)土地使用,只对住宅用地分析,由地块多边形的土地使用属性(Landuse)决定。
3)地基类型,房屋的损失在差地基上比好地基大,由地基—损失参数表(found.dbf)中的地基类型(Class)和损失系数(Para)决定。
4)地块上居民的财产,由地块的估计财产属性(Value)决定。
图9-2为地块属性表和地基—损失参数表的逻辑关系。
图9-1 View1的显示2 数据处理过程2.1 计算地块财产密度。
打开专题属性表“Attribute of 地块”,选用菜单Table / Start Editing,激活字段名V_a,选用菜单Field / Calculate...,出现提示:[ V_a ] =[Value] / [Area]按OK键结束,可以看到字段V_a被赋值。
选用菜单 Table / Stop Editing,对随后的提示回答yes,保存所作的编辑,结束专题属性表“Attribute of 地块”的编辑状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
) 在合并的凸包两相邻不同多边形顶点之间 插入离这两顶点连线距离较近的多边形凸顶点 , 可 获取较合理的两多边形邻近部位的初步形态 ( 如图 所示 )。 此时数组中的顶点序列变为# $%+%,$%&
2,$%& ,$2&2 ,$2& ,$2&’,$2&(,$%&,,$%&%-,
图 . 多边形的最终合并结果
O5P
,算 法 相 对 简 单,但 合 并 得 到 的 多 边 形 的 形 态 不
很理想 。 基于 NeGaunay 三角网的多边形合并 , 主要 是利用三角网确定多边形顶点 、 边之间的空间关 系 ,由 于 构 网 算 法 相 对 复 杂,本 文 试 图 从 计 算 几
.1‘.
测
绘
工
程 即线段 mv 的长度 。
A 的所有顶点到 B 的最小距离 D1,B 的所有顶点 到 A 的最小距离 D2, 多边形间的距离为 min (D1, D2)。 4 ) 多边形间邻近边的投影长度 : 构成多边形
邻近边的条件是多边形两边之间端点到相对边距 离的最大值不大于规定的距离尺度 ( 本文考虑为地 图上符号间的距离尺度 ), 且两边的夹角在许可的 范 围 之 内 ( 如 图 1- 甲 中 的 边 de 和 边 mn 为 邻 近 边 )。 两边中一条边的投影长度指这条边在邻近边
图 1 邻近边间投影和多边形间的邻近度
2.2 "凸包演化 " 算法的基本步骤 1 ) 分别将待合并的两多边形的顶点通过去重
复点 、调整坐标串为同时针方向 、建立凸包 、 坐标排 序 ( 按 : 或 ; 坐标值 )、 分析每个顶点的凸凹特征 等操作表示为如下数据结构中的顶点数组 :
<=>ede? @<ABC< <DEFeA<eG H in< in< mIiJDK 88 顶点 JD 88 顶点所属多边形 JD 88 是否已被使用 mIiPLM=ELnJDK
L2 , 则多边形 P1 和 P2 之间的邻近度可表示为 N = (L1!C18C2 9 L2!C28C1 )8 (C19C2)。 图 1-丙中 A 、B 两个多边形的邻近度比图 1- 乙中的邻近度要
大 , 可见邻近度不仅反映了多边形间的距离邻近 , 也反映了方位邻近关系 。
a e m q p ! v o ! ! b c d n B B A A
形顶点之间的形态 ,这对合并的多边形形态是否合 理起重要作用 , 就是在这两顶点之间是否插入边与 对应多边形的交点或用交点替换某一顶点 。 这一操 作的判断条件要视多边形合并的形态要求而定 , 如
图 2 多边形凸包的合并
街区合并需突出其直角化特征 ,而植被面的合并则 可能将面积改变量大小作为重要参考 。 具体计算涉 及距离 、 角度 、 面积 、 转折方向等 , 得到两多边形的
!"# $%&’()*"+ ,’( $&&(-&$*)’. ’, /’%0&’. $//%)-1 *’ $2*’+$*)3 +$/ &-.-($%)4$*)’.
WAN Hui_lian1, WU Fang1, WAN Bao_shan2, DEN Hong_yan1 (1. Institute of Surveying and Mapping, Information Engineering University, ABengCBou 450052, DBinaE 2. Fenan PoGyteHBniH University, IiaoCuo 454000, DBina) Abstract: It presents a neJ aGgoritBm named KDonveL FuGG EvoGutionK for aggregation of poGygons on tBe Masis of Homputation geometry. It is praHtiHaG in tBe softJare of automatiH map generaGiCation. Key words: automatiH map generaGiCationE Homputation geometryE aggregation of poGygonsE HonveL BuGG evoGutionE spatiaG reGationsBipE reGation HBaraHter MetJeen poGygons
2.1 算法相关定义
为了便于后面算法的描述和理解 , 将本文中几 个自定义的概念予以集中解释 。
BNNL mIOJ@P@edK
BNNL mIOJ@BBME=K88QRPS 为凸包上顶点 TUALVS 则不是 BNNL mIOJ@LLCDMBBME=K 88QRPS 则 为 多 边 形 局 部 凸 顶
第 14 卷 第 3 期
测 绘 工 程
2005 年 Q 月
10230114302 56 784+19302 :0; <:==302
+,-.14/ 0,.3 SEP./ 2005
用于数字地图自动综合的多边形合并算法
王辉连 1,武 芳 1, 王宝山 2, 邓红艳 1
(1. 信息工程大学 测绘学院 , 河南 郑州 450052 ; 2. 河南理工大学 , 河南 焦作 454000 ) 摘要 : 从计算几何出发 , 实现了能考虑到空间关系和形态要求的一种新的多边形合并算法 -" -- 凸包演化 " 算 法 , 并用于自动综合软件中 , 取得了较好的效果 。 关键词 : 自动制图综合 ; 计算几何 ; 多边形合并 ; 凸包演化 ; 空间关系 ; 多边形相关特征 中图分类号 :P208 文献标识码 : 文章编号 :1006-7949(2005)03-0015边形合并算法
多边形合并的难点应在获取待合并的两多边
形之间的相关特征上 。 所谓相关特征 , 即两多边形 之间的距离 、 邻近边的方向和投影关系 、 点到多边 形的距离 、 轮廓局部的凸凹等特征 。 有了这些信息 , 才能对相应轮廓点做出取舍 , 得到合理的新轮廓 点 。 笔者曾尝试仅通过多边形之间的边边关系和点 边关系去描述多边形间的相关特征 , 并在此基础上 进行多边形合并 ,实验表明此方法在轮廓点的顺序 判断和生成新的轮廓点序列方面有所不足 。 由于在 计算机内部多边形表现为一个序列化的坐标串 , 串 行化和顺序既是其数据上的特点 , 也是一种空间结 构特征 , 多边形的合并必须基于此特征进行 ; 而且 从数据的角度看 ,两多边形合并就是将两个有序坐 标串打散 , 再形成一个新坐标串的过程 , 是对于点 集的分析处理 。 凸包作为一个点集的最小凸多边 形 , 既是其空间分布范围的边界 , 也是其外轮廓的 近似 ,且有很好的空间顺序特征 。 因此 , 本文算法选 择了基于凸包通过 " 逐步求精 " 的方法来得到合并 后的新多边形 , 为体现这一特点 , 将算法命名为 " 凸 包演化 "多边形合并算法 。
112.^, ^_.^)。 2) 建立一个新的顶点数组用来表示合并后的
第
期
王辉连等: 用于数字地图自动综合的多边形合并算法
4%05
多边形 ,首先提取前一步中两多边形顶点数组中的 凸包顶点为一点集 , 在此基础上重新生成一个凸 包 , 将凸包顶点存入数组 , 即为两多边形凸包合并 的结果 ,见图 2 。 此时数组中的顶点序列为#$%&%,
0
引言
多边形合并是计算几何中研究比较多的一个
1
自动综合中的多边形合并
在数字地图生产中 , 不论是采用手工交互编绘
方面 。多边形形态复杂 ,合并时涉及到点线关系 、 点 面关系 、 线线关系 、 线面关系及面面关系的分析与 处理 ,因而开发一种好的多边形合并算法是具有挑 战性的工作 。 多边形合并在视觉直观看来较容易解 决 , 根据格式塔心理学原理 , 通过人的视觉感知能 积极组织并获取图形的结构化信息 , 能根据待合并 的多边形各部分之间的相近 、 相似或连续等特征很 快得到一个 " 好的格式塔 ", 即好的多边形合并结果 图形 。 但通过计算机来解决多边形合并 ,要分析多 边形之间的邻近边 、 结合部的凸凹性 , 多边形边之 间的方位关系和连续性等 , 根据分析结果确定合并 方案 ,需要通过计算几何的相关算法经过大量运算 才能得到 。 多边形合并算法的关键也在于如何获取 多边形的形态特征和它们之间的各种空间关系 , 本 文在这方面作了一些实验和探索 , 实现了一个较好 的有实用价值的多边形合并算法 。
从上面的顶点数据结构中 , 通过分析得到顶点 的多项属性 , 即已分析了多边形轮廓的基本形状和 空间序列特征 ,而且轮廓中隐含凸包 。 如图 2 所示 , 得到的两多边形顶点数组中的顶点序列如图中编 号 , 以顶点 F1-5 为例 , 其数据结构中的各项值可 能 为 (5,1,UALVS ,UALVS ,QRPS ,UALVS ,QRPS ,
合并结果如图 . 所示 。 要注意的是 ,上述步骤中多个步骤都是可迭代 的 , 迭代条件视具体要求而适当调整 。 在自动综合
图 两多边形邻近部位的初步处理
中图形的尺度是很重要的因素 ,其大小将直接影响 多边形的细节特征 。 如图 . 中的合并结果就忽略了 顶点 $%+. 、$%+( 、$%+0 之间的细节 , 这个结果可 能在制图综合中是一种较优选择 。
收稿日期 :2005-04-05 项目来源 : 国家自然科学基金资助项目 (404R1115 ) 作者简介 : 王辉连 >1QR1*? , 男 , 信息工程大学测绘学院硕士研究生 。
还是自动综合 , 都涉及较多的面状目标合并的操 作 ,特别是在大比例尺地图生产时 。 植被 、水域的合 并在某些地区的地图生产中可能会比较多 , 但更多 的是居民地建筑物或街区的合并 。 不同地物的面合 并各有其特点和要求 , 传统数字地图编绘较多地依 赖制图员的经验 ,面状地物合并的多边形形态也取 决于视觉综合的结果 , 通过重新采集边线数据得到 合并后的多边形数据 。 由于自动综合的需要 , 关于 多边形合并的方法研究也较多 , 其中比较有代表性 的是利 用 NeGaunay 三 角 网 进 行 合 并 O1*3P, 合 并 效 果 不 错 ; 有 基 于 扫 描 线 技 术 的 多 边 形 合 并 O4P, 主 要 用 于处理相交多边形的合并 ;有基于栅格数据的合并
