第三章 两个自由度系统振动
合集下载
第六讲--多自由度系统振动-2

解: 1)求柔度系数
m
31
k/5
m
21
k/3
P=1
2m k
11
32 4
P=1
22 4 12
P=1
33 9
23 4 13
11 1/ k 21 31 11
22
1 k
1 k /3
4
22
1 k
1 k/3
1 9
k /5
3.3.1 柔度法
1 1 1
柔度矩阵: [ ] 1 4 4
1 4 9
2)求频率
2 0 0
质量矩阵: [M] m 0 1 0
0 0 1
由频率方程: M I 0
2 1 1 m 2 4 4 0 ,
2 4 9
展开式为: 3 15 2 42 30 0
1 m m2
方程三个根为: 1 11.601 2 2.246 3 1.151
三个频率为:
1 0.2936
k m
4Y
4 4
3.4.1 主振型矩阵与正则坐标
(2)正则坐标 任意一个质点的位移 y 都可按主振型来组合:
y1 1Y11 2Y12 3Y13 y2 1Y21 2Y22 3Y23
yi 1Yi1 2Yi2 3Yi3
yn 1Yn1 2Yn2 3Yn3
nY1n nY2n
y1
y2
Y1 Y121
Y YYY132111
Y2 1
Y2 2
Y32
Y3 1
Y3 2
Y33
Y14 Y4
2
Y34
Y41
Y2 4
Y3 4
Y44
主 振
型 矩 阵
第一振型
1
机械振动学(第三章)-多自由度振动系统

装备制造学院
College of Equipment Manufacture
利用直接法,对下图所示的三自由度振动系统建立微分方程。。
装备制造学院
College of Equipment Manufacture
解:1)受力分析 选取 m1, m2和m3离开平衡位置的坐标x1, x2和 x3 为3 个独立 坐标。受力分析如图所示 2)建立振动微分方程 (c c ) x c x ( k k ) x k x p (t ) x m1: m 2 2 2 2 2 ( c 2 c 3 ) x 2 c2 x 1 c 3 x 3 ( k 2 k 3 ) x 2 k 2 x1 k 3 x 3 p 2 ( t ) x m2: m 2 2 2 2 3 c 3 x 3 c3 x 2 k 3 x3 k 3 x 2 p 3 (t ) x m3: m 3
装备制造学院
College of Equipment Manufacture
本章结束
装备制造学院 College of Equipment Manufacture
3 )如果将应为能量耗散函数 D 引起的阻尼力也从其他的非势 力的广义力中分离出来,并使Qi仅代表外部作用的广义激振力, 则可将非保守系统的拉格朗日方程改为:
d dt ( T i q ) T i q U qi D i q Q i ( i 1, 2 , 3 ,...., n )
车 身 车 轮 二 自 由 度 振 动 问 题
装备制造学院
College of Equipment Manufacture
装备制造学院
College of Equipment Manufacture
两自由度系统-振动力学
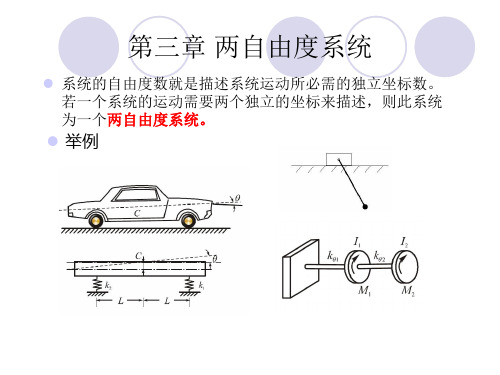
振幅比、主振型、固有振型
1
A21 A11
k11
n21m1
k12
k22
k12
n21m2
2
A22 A12
k11 n22m1
k12
k12
k22 n22m2
1 1
特征向量、振型向量、模态向量
1
,
2
A 1
A11 A21
A11
1
1
,
A 2
A12 A22
A12
1
2
模态参数包括:
3K t I
系统按第二阶固有振型做简谐振动
x10 x0,x20 0,x10 x20 0
解得:A11 A12 x0 / 2,1 2 900
作业:3-1,3-2,3-4
x1 0.5x0 cos
K / I t 0.5x0 cos
3K t I
x2 0.5cos
K / I t 0.5x0 cos
于是有
k11 n2m1
k12
0
(7)
k21
k22 n2m2
m1m2n4 (m1k22 m2k11)n2 k11k22 k122 0
(8)
方程有两个正实根
n 1,2
m1k22 m2k11
(m1k22 m2k11)2 4m1m2 (k11k22 k122 ) 2m1m2
(9)
[K]:刚度矩阵。
{x}:位移向量
第一节 无阻尼自由振动
分析{x0},{x0}引起的自由振动
微分方程的一般形式:
m1
0
0 m2
x1 x2
k11 k 21
k12 k 22
x1 x2
0 0
第三章 两自由度系统

k12 x1 F sin t k 22 x 2 0
M x K x F sin t
三.方程求解
令方程的解为
jt xt X e
X1 X X 2
k 2 L x3 0 2 k 2 L 0
方程含有静耦合和动耦合
结论:
1. 2. 3. 4. 5. 描述一个两自由度系统的运动,所需要的独立坐标数是 确定的、唯一的,就是自由度数2。但为描述系统运动 可选择的坐标不是只有唯一的一组。 对于同一个系统,选取的坐标不同,列出的系统运动方 程的具体形式也不同,质量矩阵和刚度矩阵对不同的坐 标有不同的具体形式。 如果系统的质量矩阵和刚度矩阵的非对角元有非零的元 素,则表明方程存在坐标耦合。坐标耦合决定于坐标的 选取,不是系统的固有性质。 方程中存在耦合,则各个方程不能单独求解。 同一个系统,选取不同的坐标来描述其运动,不会影响 到系统的性质,其固有特性不变。
2 随
变化的曲线
§3.3无阻尼吸振器
一.物理模型
二.数学模型
m1 x1 k1 x1 k 2 x2 x1 F sin t m2 x2 k 2 x2 x1 0
m1 0 x1 k1 k2 k2 x1 F sin t 0 m x k k2 x2 0 2 2 2
可以解出两自由度系统的两个固有频率。
§3.4有阻尼振动
一.自由振动
1.物理模型
2.数学模型
m1 x1 c1 c2 x1 k1 k 2 x1 c2 x2 k 2 x2 0
机械振动二自由度讲解
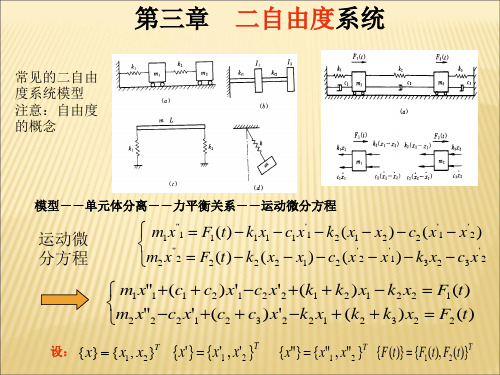
动能、势能和能量耗散函 数均是非负的。也就是说, 对任意的位移,任意的速 度,必然有
ET
1 {x'}T [M ]{x'} 0 2
U 1 {x}T [K ]{x} 0
2
D 1 {x'}T [C]{x'} 0
2
由此可知,质量矩阵、阻尼矩阵和刚度矩阵均是正定或半正定矩阵。一般说来,
工程振动问题中遇到的质量矩阵一般都是正定矩阵。对于静定和超静定结构,刚度矩
U
1 2
k1x12
1 2
k2 (x2
x1 ) 2
1 2
k3 x22
1 2 {x1,
x2}T
k1 k2
k2
k2 k2 k3
xx12
1 2
{x}T
[K
]{x}
系统的能量 耗散函数
D
1 2
c1x'12
1 2
c2
(x'2
x'1
)2
1 2
c3 x'22
U
1 2
[k1
y
2 A
k2( yA
Lq )2 ]
1 2
{
y
A
,q
}k1k2 Lk2
mL1 mL12
Ic
y'
q
A
'
k2L k2 L2
yA
q
yA和q下的运动微分方程为
示例:
第三章(多自由度系统的振动)

固有振型的正交性
加权正交性的简洁表示
T r M s 0, r s
M s M r , r s
T r
rT M s M r rs
rs
def
1, r s 0, r s
rT K s 0, r s
rT K s K r , r s
x
x1 1
节点
x3 1
3 2
k m
x2 1
理解固有振型
理解固有振型
理解固有振型
返回
固有振型的正交性
1.固有振型的归一化
2 r 1 3 2 r 1 3
都是固有振型向量 ① 按某一自由度的幅值归一化
k m
理解固有振型
3k k 0 m 0 0 1 0 k 2k k 2 0 m 0 2 0 0 k 3k 0 0 m 3 0
u(t ) sin(t )
对任意时间都成立
( M ) 0, 2
特征方程 特征值
det( K M ) 0
r (r 1, 2, N )
有非零
r (r 1, 2, N )
特征向量
u(t ) ψa sin(t ) φ sin(t )
结论: 系统存在形如 形式的同步振动。
u(t ) φ sin(t )
多自由度系统的固有振动
2.多自由度系统的固有振动
Mu(t ) Ku(t ) 0
( K 2 M ) sin(t ) 0
第r阶模态质量
固有振型关于刚度矩阵加权正交性 T 当 rs 时 r K s 0 T r K s K r 当 rs时
二自由度系统振动的理论解析

质量矩阵的求解
对如下图所示的系统,质量为m的刚性杆,由刚度 为 k1和k2 的弹簧分别之于A点和D点。A点支座的约束只 允许刚性杆在x-y平面内运动,而限制沿x轴方向的平动。
C点为刚性杆的质心,JC 表示绕通过C点z轴(垂直于纸
面,未标出)的转动惯量。B点是满足 k1l4 k2l5 的特殊 点,如果在B点作用有沿y轴方向的力,系统产生平动而 无转动。如果在B点作用有力矩,系统只产生转动而无
二自由度系统的振动微分方程一般包括两个互相耦合 的二阶常微分方程组,二自由度系统的运动形态要由两个 独立的坐标确定。
建立振动微分方程最常用的方法有:牛顿第二定律 法、动静法、拉格朗日法等。
3.2 二自由度系统振动方程
建立运动微分方程的方法和单自由度系统基本一样, 但难度更大。
3.2.1 作用力方程的一般形式及其矩阵表达式
二自由度系统作用力方程的一般形式:
一般矩阵形式:
[M ]{x} [C]{x) [K]{x} {F(t)}
由此可得:
m1x1 F1(t) k1x1 c1x1 k2 (x1 x2 ) c2 (x1 x2 )
m2 x2 F2 (t) k3 x2 c3 x2k2 (x1 x2 ) c2 (x1 x2 )
)
[R]({F} [M ]{x} [C]{x})
这就是系统振动方程的位移形式。
柔度意为弹簧受单位作用力而产生的变形。 柔度影响系数 Rij 的力学意义是:在j坐标处作用单位 广义力,引起i坐标处的广义位移。由柔度影响系数就可 以形成系统的柔度矩阵 [R]。 由材料力学的位移互等定理可知 Rij Rji ,即柔度矩 阵是对称的。
量),将系统中的小刀架、工件、砂轮及砂轮架等视为
集中质量,再忽略存在于系统中的阻尼,就可以把这些 系统近似简化成图(d)所示的两自由度振动系统的动 力学模型。
第三章二自由度系统

为了完全确定物体的位置而选定的任意一组彼此独立的 坐标参数,称为这个物体的广义坐标。在选定坐标时,除去 直角坐标X、Y、Z之外,我们也可以用角度φ、θ及从物体 中的一点到某些固定点的距离等参数来确定物体在空间的位 置。
二自由度系统振动 / 不同坐标系的运动微分方程
以汽车的二自由度振动模型为例
汽车板簧以上部分被简化成为一根刚性杆,具有质量m和绕质心 的转动惯量Ic。质心位于C 点。分别在A点和B点与杆相联的弹性 元件k1、k2为汽车的前,后板簧。
若系统有 n 个自由度,则各项皆为 n 维矩阵或列向量
二自由度系统振动 / 运动微分方程
式中:
[M
]
m11 m21
m12
m22
m1
0
0
m2
[K
]
k11 k 21
[C]
c11 c21
k12
k
22
k1 k2
k2
c12
c22
2 ET x1x1
2 ET x12
m1
m12
2 ET x1x2
2 ET x2x1
m21
0
m22
2ET x2x2
2 ET x22
m2
[M
]
m11 m21
m12
m22
m1
0
0
m2
二自由度系统振动 / 能量法
(t ) (t)
如同在单自由度系统中所定义的,在多自由度系统中 也将质量、刚度、位移、加速度及力都理解为广义的。
二自由度系统振动 / 不同坐标系的运动微分方程
以汽车的二自由度振动模型为例
汽车板簧以上部分被简化成为一根刚性杆,具有质量m和绕质心 的转动惯量Ic。质心位于C 点。分别在A点和B点与杆相联的弹性 元件k1、k2为汽车的前,后板簧。
若系统有 n 个自由度,则各项皆为 n 维矩阵或列向量
二自由度系统振动 / 运动微分方程
式中:
[M
]
m11 m21
m12
m22
m1
0
0
m2
[K
]
k11 k 21
[C]
c11 c21
k12
k
22
k1 k2
k2
c12
c22
2 ET x1x1
2 ET x12
m1
m12
2 ET x1x2
2 ET x2x1
m21
0
m22
2ET x2x2
2 ET x22
m2
[M
]
m11 m21
m12
m22
m1
0
0
m2
二自由度系统振动 / 能量法
(t ) (t)
如同在单自由度系统中所定义的,在多自由度系统中 也将质量、刚度、位移、加速度及力都理解为广义的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x [ M ]{ɺɺ} + [ K ]{ x} = {F }
(3)
式中: 分别叫作质量矩阵 式中:[M],[K]分别叫作质量矩阵、刚度矩阵,且都为实 分别叫作质量矩阵、刚度矩阵, T T 对称矩阵,即 [ 对称矩阵 即:M ] = [ M ] , [ K ] = [ K ]
x {ɺɺ} , { x} , {F }-分别为加速度列向量、位移列向量、 分别为加速度列向量 位移列向量、 加速度列向量、
激振力列向量
2.固有模态振动 固有模态振动 图示自由振动方程为: 图示自由振动方程为:
m1 0 x 0 ɺɺ1 k11 ɺɺ + k m2 x2 21 k12 x1 x = {0} k22 2
(4)
ɺ 受初始扰动 { x0 } , { x0 } 后,系统如何发生运动
k1a1 − k2b1 x1 0 = 2 2 k1a1 + k2b1 θ 0
(2)选 x2 , θ 为坐标描述系统运动,且k1a2 = k2b2 )
x m − me ɺɺ2 k1 + k2 − me J θ + 0 ɺɺ 0 0 x2 0 = 2 2 k1a2 + k2b2 θ 0
第二节 无阻尼强迫振动
一、本节研究内容
x m11 m12 ɺɺ1 k11 k12 x1 F 研究 ɺɺ + k x = 0 sin ωt m21 m22 x2 21 k22 2
的解具有的一般性。 的解具有的一般性 根据线性叠加原理:
即含有动力 耦合 又含有静力 耦合
m − ma 1
− ma1 ɺɺ3 k1 + k 2 x θ + −k L J A ɺɺ 2
− k 2 L x3 0 = 2 k 2 L θ 0
结论: 结论:
k1 x1 m1 m1 ɺɺ1 x
k1
F1 ( t )
x1
m1
kc
F2 ( t )
x2
m2
k2
F1 ( t )
k c ( x2 − x1 )
F2 ( t )
m2
k 2 x2 m2 ɺɺ2 x
∑ F = 0 得:
x
m1ɺɺ1 + ( k1 + k2 ) x1 − kc x2 = F1 x m2 ɺɺ2 − kc x1 + ( kc + k2 ) x2 = F2 x
a1
m, J c
b1
m1ɺɺ1 + k11 x1 + k12 x2 = F1 x m2 ɺɺ2 + k21 x1 + k22 x2 = F2 x
(1)取质心C在垂直方向的运动 )取质心 在垂直方向的运动 x1 ( t ) ,车身绕质心 的 车身绕质心C的 车身绕质心 转动θ ( t ) 作为描述系统转动的坐标。
4 n 2 n 2 12
方程的两个根,即特征值为
ω n21 , 2
1 m k + m 2 k 11 = [ 1 22 ∓ m1 m 2 2
2 m 1 k 22 + m 2 k 11 2 k 11 k 22 − k 12 ( ) −4 ] m1 m 2 m1 m 2
ω n1 〈ω n 2 , 分 别 叫 系 统 第 一 阶 固 频 、 第 二 阶 固 频
F1 sin ω1t F1 0 1. = sin ω1t + sin ω2t F2 sin ω2t 0 F2
(6)
A,B有非零解的条件为: 有非零解的条件为: 有非零解的条件为 2 k11 − m1ωn k12 = 0 (7) 2 k21 k22 − m2ωn
频率方程
2 k11 − m1ωn
k12 k22 − m2ω
2 n
k21
= 0 (7)
频率方程
展开后
m1m2ω − ( m1k22 + m2k11 )ω + k11k22 − k = 0
根据∑ Fx = 0, ∑ M c = 0可得:
k1
c
k2
2.坐标耦合产生的原因 以例说明: 坐标耦合产生的原因: 以例说明: 坐标耦合产生的原因
θ
x1
ɺɺ mx1
cJ θ ɺɺ
c
k1 ( x1 + a1θ )
k2 ( x1 − b1θ )
静力耦合 弹性耦合
m 0
0 ɺɺ1 k1 + k2 x θ + k a − k b J c ɺɺ 1 1 2 1
动力耦合 惯性耦合
a2
b2
e
a1
g
ℓ
c θ cJ θ ɺɺ
c
x2 c
( )
d
(3)选 x3 , θ )
ɺɺ m ɺɺ2 − eθ k ( x − b θ ) x 2 2 2 k1 ( x2 + a2θ )ຫໍສະໝຸດ θ ɺɺ Jcθx3
k1x3
ɺɺ m(ɺɺ3 − a1θ ) k ( x −ℓθ ) x 2 3
第三章 两个自由度系统振动 内容重点: 内容重点:
1.运动方程建立 运动方程建立 2.模态频率、模态振型 模态频率、 模态频率 3.广义座标与座标耦合 广义座标与座标耦合 4.动力减振 动力减振
第一节 无阻尼自由振动
内容重点: 内容重点: 1.固有模态及其振动 固有模态及其振动 2.对初始条件响应 对初始条件响应 3.广义坐标与坐标耦合 广义坐标与坐标耦合 一、固有模态振动 1.运动微分方程 运动微分方程 由
x1 = A sin (ωnt + ϕ ) 设: x2 = B sin (ωnt + ϕ )
2 k11 − m1ωn k21
(5)
( 5)代入(4)得: )代入( )
A 0 = 2 k22 − m2ωn B 0 k12
2 k11 − m1ωn 将ωn1,ωn 2分别代入(6)式 k 21
A 0 k12 = 2 k22 − m2ωn B 0
得:
k11 − ω n21 m1 B1 k12 u r1 = =− =− = 21 A1 k12 k 22 − ω n21 m 2 u11 (8)
1 A2 = r2 − r1
( r2 x10 − x20 )
2
ɺ ɺ ( r2 x10 − x20 ) +
ωn21
( −r1 x10 + x20 )
ɺ ɺ r2 x10 − x20
2
+
ɺ ɺ ( −r1 x10 + x20 )
2 ωn 2
2
tgϕ1 =
ωn1 ( r2 x10 − x20 )
tgϕ 2 =
方程通解( ) 方程通解(12)中 A1 , A2 , ϕ1 , ϕ 2由初始条件确定: 设t=0时:x1 ( 0 ) = x10 x2 ( 0 ) = x20
ɺ ɺ x1 ( 0 ) = x10
ɺ ɺ x2 ( 0 ) = x20
2
将初始条件代入方程(12)可得: 将初始条件代入方程( )可得
1 A1 = r2 − r1
(1)
写成矩阵方程: 写成矩阵方程:
m1 0 0 ɺɺ1 k1 + kc x ɺɺ + − k m2 x2 c −kc x1 F1 x = F (2) kc + k 2 2 2
一般形式: 一般形式:
k1
x1
m1
kc
x2
m2
k2
x m 0 ɺɺ1 2k − k x1 0 运动方程: 解:运动方程 ɺɺ + − k 3k x = 0 0 2m x2 2 2 2k − mωn −k =0 频率方程: 频率方程: 2 −k 3k − 2mωn x1 k1 2 4 2 2 kc 2m ωn − 7 mkωn + 5k = 0 m1
(1)描述系统运动坐标选择不唯一; )描述系统运动坐标选择不唯一; (2)对同一系统,坐标不同,运动方程形式也不同; )对同一系统,坐标不同,运动方程形式也不同; (3)坐标耦合决定于坐标选择,不是系统固有性质; )坐标耦合决定于坐标选择,不是系统固有性质; 4)若方程存在耦合,则方程不能单独求解; (4)若方程存在耦合,则方程不能单独求解; (5)选取不同坐标,不会影响系统的性质,其固有特 )选取不同坐标,不会影响系统的性质, 性不变。 性不变。 模态坐标可使方程解耦下章讨论
1 = r1
1 A1 sin (ω n1t + ϕ1 ) A sin ω t + ϕ r2 2 ( n2 2 )
(12)
分析:系统自由振动是系统两个固有模态振动的线性组合 只有 分析:系统自由振动是系统两个固有模态振动的线性组合,只有 在某些特定条件下,系统才会只作某个固有频率的自由振动。 在某些特定条件下,系统才会只作某个固有频率的自由振动 例:对于图示系统,设:m1 = m, m2 = 2m, k1 = kc = k , k2 = 2k 对于图示系统, 试求系统的固有模态。 试求系统的固有模态
ωn 2 ( r1 x10 − x20 )
ɺ ɺ r1 x10 − x20
三、广义坐标与坐标耦合 1.什么叫坐标耦合 什么叫坐标耦合
x m1 0 ɺɺ1 k11 k12 x1 F + = 1 0 m ɺɺ k k x F 2 x2 21 22 2 2
