安徽省马鞍山二中2014-2015学高一上学期期中考试 数学 扫描版含答案
2014-2015学年上学期高一期中测试数学试题(含答案)

2014-2015学年上学期高一期中测试数学试题(含答案)第I 卷(选择题共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每个小题给出的四个选项中,只有一项是符合要求的)1.下列函数中,既是偶函数又在+∞(0,)单调递增的函数是( ) A .3y x = B . 1y x =+ C .21y x =-+ D . 2x y -= 2.在同一坐标系中,表示函数log a y x =与y x a =+的图象正确的是( )A B C D 3.若1log 12a<,则a 的取值范围是( ) A .1(0,)(1,)2+∞ B .1(,1)2 C .(1,)+∞ D .1(,1)(1,)2+∞4.已知函数f (x )为定义在R 上的奇函数,当x ≥0时, ()22x f x x m =++ (m 为常数),则(1)f -的值为( )A .-3B .-1C .1D .3 5.设全集U =R ,{}|0P x f x x ==∈R (),,{}|0Q x g x x ==∈R (),,{}|0S x x x ϕ==∈R (),,则方程220f x x x ϕ=()+g ()()的解集为( )A . P Q SB .P QC .P Q S ()D . P Q S u (C )5.设9.0log 5.0=a ,9.0log 1.1=b ,9.01.1=c ,则c b a , ,的大小关系为( ) A .c b a << B .c a b << C .a c b << D .b c a << 6.设}3 2, ,21,31 ,1{-∈α,若函数αx y =是定义域为R 的奇函数,则α的值为( ) A .3 ,31 B .3 ,31 ,1- C .3 ,1- D .31 ,1-7.已知函数)(x f 是奇函数,当0>x 时,)1 ,0( )(≠>=a a a x f x ,且3)4(log 5.0-=f ,则a 的值为( )A .3B .3C .9D .23 8.已知函数⎪⎩⎪⎨⎧>-≤=-)1( )23(log )1( 2)(2x x x x f x ,若4)(=a f ,则实数=a ( )A .2-或6B .2-或310 C .2-或2 D .2或310 9.方程021231=⎪⎭⎫⎝⎛--x x 的解所在的区间为( ) A .) 1 ,0 ( B .) 2 ,1 ( C .) 3 ,2 ( D .) 4 ,3 (10.已知函数bx ax y +=2和xbay =|)| || ,0(b a ab ≠≠在同一直角坐标系中的图象不可能... 是( )11.已知函数)3(log 221a ax x y +-=在区间) ,2[∞+上是减函数,则a 的取值范围是( )A .)4 ,(-∞B .]4 ,4[-C .]4 ,4(-D .]4 ,(-∞12.若在直角坐标平面内B A ,两点满足条件:①点B A ,都在函数)(x f y =的图象上;②点B A ,关于原点对称,则称B A ,为函数)(x f y =的一个“黄金点对”.那么函数=)(x f ⎪⎩⎪⎨⎧>≤-+)0( 1)0( 222x x x x x 的“黄金点对”的个数是( ) A .0个 B .1个 C .2个 D .3个第Ⅱ卷(非选择题,共90分)二、填空题:本题共4小题,共20分.13.已知集合}06|{2=--=x x x M ,}01|{=+=ax x N ,且M N ⊆,则由a 的取值组成的集合是 .14.若x x f =)(log 5,则=-)9log 2(log 255f .15.已知定义在R 上的偶函数)(x f 满足0)1(=-f ,并且)(x f 在)0 ,(-∞上为增函数.若0)( <a f a ,则实数a 的取值范围是 .16.已知函数()x f 的定义域是}0|{≠∈=x R x D ,对任意D x x ∈21 ,都有:=⋅)(21x x f)()(21x f x f +,且当1>x 时,()0>x f .给出结论:①()x f 是偶函数;②()x f 在()∞+ ,0上是减函数.则正确结论的序号是 .三、解答题:本大题共6小题,共70分,解答应写出必要的文字说明、证明过程及演算步骤。
2014-2015学年度高一数学期中试卷(含答案解析)

第1页 共10页 ◎ 第2页 共10页绝密★启用前2014-2015学年度期中卷高一数学考试范围:必修一;考试时间:120分钟;命题人: 注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明一、选择题(题型注释)1.已知集合{}1,2,3M =,{}2,3,4N =,则 ( ) A .M N ⊆ B .N M ⊆ C .{}1,4MN = D .{}2,3M N =【答案】D【解析】解:因为根据已知 的集合,可以判定集合间的关系,以及集合的运算,那么显然选项D 成立。
2.设集合}1,0,1{-=M ,},{2a a N =,则使M∩N=N 成立的a 的值是( ) A .1 B .0 C .-1 D .1或-1 【答案】C 【解析】试题分析:由于集合中的元素互不相同,所以20,1a a a a ≠⇒≠≠.又因为M∩N=N ,所以1a =-. 考点:集合的特征及集合的基本运算. 3.设,则( )A .﹣2<x <﹣1B .﹣3<x <﹣2C .﹣1<x <0D .0<x <1 【答案】A【解析】因为y=3x在R 上单调递增,又,故﹣2<x <﹣1故选A4.若0.90.48 1.54,8,0.5a b c -===则( )A .c b a >> B. a c b >> C.b a c >> D.b c a >> 【答案】D【解析】0.9 1.80.48 1.44 1.5 1.542,82.(0.5)2.-===函数2x y =是增函数,1.8 1.5 1.44,>>所以.a c b >>故选D5.函数()f x =的定义域是 A. {x ︱34x >} B. {01x x <≤} C. {1x x ≥} D. {x ︱314x <≤} 【答案】D 【解析】略6.设函数))((R x x f ∈为奇函数,),2()()2(,21)1(f x f xf f +=+=则=)5(f ()A.0B .1C .25D .5【答案】C【解析】令x=-1可得(1)(1)(2)(1)(2),(2)2(1)1,f f f f f f f =-+=-+∴==13(3)(1)(2)122f f f ∴=+=+=,35(5)(3)(2)122f f f =+=+=.7.某同学家门前有一笔直公路直通长城,星期天,他骑自行车匀速前往旅游,他先前进了a km ,觉得有点累,就休息了一段时间,想想路途遥远,有些泄气,就沿原路返回骑了b km(b <a ), 当他记起诗句“不到长城非好汉”,便调转车头继续前进. 则该同学离起点的距离s 与时间t 的函数关系的图象大致为 ( )【答案】C【解析】分析:本题根据运动变化的规律即可选出答案.依据该同学出门后一系列的动作,匀速前往对应的图象是上升的直线,匀速返回对应的图象是下降的直线,等等,从而选出答案. 解答:解:根据他先前进了akm ,得图象是一段上升的直线,DCBA第3页 共10页 ◎ 第4页 共10页由觉得有点累,就休息了一段时间,得图象是一段平行于t 轴的直线,由想想路途遥远,有些泄气,就沿原路返回骑了bkm (b <a ),得图象是一段下降的直线, 由记起诗句“不到长城非好汉”,便调转车头继续前进,得图象是一段上升的直线, 综合,得图象是C , 故选C .点评:本小题主要考查函数的图象、运动变化的规律等基础知识,考查数形结合思想.属于基础题. 8.函数的单调增区间为( )A .B .(3,+∞)C .D .(﹣∞,2)【答案】D【解析】由题意知,x 2﹣5x+6>0∴函数定义域为(﹣∞,2)∪(3,+∞),排除A 、C , 根据复合函数的单调性知的单调增区间为(﹣∞,2),故选D9.若函数()1(0,1)1x mf x a a a =+>≠-是奇函数,则m 为 A.1- B.2 C.1 D.2-【答案】B 【解析】 试题分析:111111x a(),()()xxxm m mf x f x aaa --=+=+-=-+--- 由于函数是奇函数,()(),f x fx ∴-=-即x a (1)1(1)2111x x x x m m m a a a a -+=-+∴=--- 所以2m =,故选:B.考点:函数的奇偶性10. 下列每组中两个函数是同一函数的组数共有( ) (1)2()1f x x =+和2()1f v v =+(2) y =和y =(3) y=x 和321x xy x +=+ (4) y=和y(A) 1组 (B) 2组 (C) 3组 (D) 4组 【答案】C【解析】根据同意哈函数的定义可知选项A 中定义域和对应关系相同,成立,选项B 中,定义域相同,对应关系相同,选项C 中,相同,选项D 中,定义域不同,故是同一函数的 组数有3组,故选C 11.已知1a >,函数x y a =与log ()a y x =-的图像可能是( )【答案】B【解析】试题分析:因为根据1a >,可知指数函数递增函数,排除C ,D 选项,同时在选项A,B 中,由于对数函数log ()a y x =-的图像与log a y x =的图像关于y 轴堆成,那么可知.排除A.正确的选项为B.考点:本题主要是考查同底的指数函数与对数函数图像之间的关系的运用。
安徽省马鞍山二中2014届高三上学期期中考试数学理试题(附答案)

马鞍山二中2014届高三年级第一学期期中考试试题数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分150分,考试时间120分钟第Ⅰ卷一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={0,m 2},B={1,2},则“m=1”是“A ∪B={0,1,2}”的( )2.已知点()1,3A ,()4,1B -则与AB 同方向的单位向量是( ) A . 34,55⎛⎫-⎪⎝⎭ B . 43,55⎛⎫- ⎪⎝⎭ C . 34,55⎛⎫- ⎪⎝⎭D . 43,55⎛⎫-⎪⎝⎭3.已知点(),a b 在圆221x y +=上,则函数()2cos sin cos 12af x a x b x x =+--的最小正周期和最小值分别为( ) A . 32,2π- B . 3,2π- C . 5,2π- D . 52,2π-4.已知函数()21f x +的定义域为12,2⎛⎫- ⎪⎝⎭,则()f x 的定义域为( )A . 31,24⎛⎫- ⎪⎝⎭B . 31,2⎛⎫- ⎪⎝⎭ C .()3,2-D . ()3,3-5.实数5lg 24lg 81log 22723log 322++∙- 的值为( )6.已知角x 的终边上一点坐标为55sin ,cos 66ππ⎛⎫⎪⎝⎭,则角x 的最小正值为( ) A .56π B . 53π C . 116π D . 23π7.设复数z 满足(1)62z i i ⋅+=-,则复数z 的共轭复数是( ).A .24i - B. 24i + C .44i + D.44i -8.已知向量()2,8a b +=-,()8,16a b -=-,则a 与b 夹角的余弦值为( ) A . 6365 B . 6365- C . 6365± D . 5139.设分程220xx ++=和方程2log 20x x ++=的根分别为p 和q ,函数()()()2f x x p x q =+++,则( )A . ()()()203f f f =<B . ()()()023f f f <<C . ()()()302f f f <=D . ()()()032f f f <<10.已知函数,若方程f (x )=x+a 有且只有两个不相等的实数根,则实数a 的取值范围是( )第Ⅱ卷二、填空题(本大题共5个小题,每小题5分,共25分)11.已知f (x )=2x 3+ax 2+b ﹣1是奇函数,则a ﹣b= .13.函数y =tan ⎝⎛⎭⎫π4x -π2的部分图象如图所示,则(O B →-OA →)·OB →=14.设两个向量a =(λ+2,λ2-cos 2α)和b =(m ,m2+sin α),其中λ,m ,α为实数.若a =2b ,则λm 的取值范围是___________.15.设M 为平面内一些向量组成的集合,若对任意正实数t 和向量M a ∈ ,都有M a t ∈,则称M 为“点射域”.现有下列平面向量的集合: ①2{(,)|}x y x y ≥;②0(,)|0x y x y x y ⎧-≥⎫⎧⎨⎨⎬+≤⎩⎩⎭;③22{(,)|20}x y x y x +-≥;④22{(,)|3260}x y xy +-<;上述为“点射域”的集合的有 (写正确的标号)马鞍山二中2014届高三年级第一学期期中考试试题数学(理科)解答本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分150分,考试时间120分钟第Ⅰ卷一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={0,m 2},B={1,2},则“m=1”是“A ∪B={0,1,2}”的( B )2.已知点()1,3A ,()4,1B -则与AB 同方向的单位向量是( A ) A . 34,55⎛⎫-⎪⎝⎭ B . 43,55⎛⎫- ⎪⎝⎭ C . 34,55⎛⎫- ⎪⎝⎭D . 43,55⎛⎫-⎪⎝⎭3.已知点(),a b 在圆221x y +=上,则函数()2cos sin cos 12af x a x b x x =+--的最小正周期和最小值分别为( B ) A . 32,2π- B . 3,2π- C . 5,2π- D . 52,2π-4.已知函数()21f x +的定义域为12,2⎛⎫- ⎪⎝⎭,则()f x 的定义域为( C )A . 31,24⎛⎫- ⎪⎝⎭B . 31,2⎛⎫- ⎪⎝⎭ C .()3,2-D . ()3,3-5.实数5lg 24lg 81log 22723log 322++∙- 的值为(D )6.已知角x 的终边上一点坐标为55sin ,cos 66ππ⎛⎫⎪⎝⎭,则角x 的最小正值为( B ) A .56π B . 53π C . 116π D . 23π 7.设复数z 满足(1)62z i i ⋅+=-,则复数z 的共轭复数是( B ).A .24i - B. 24i + C .44i + D.44i -8.已知向量()2,8a b +=-,()8,16a b -=-,则a 与b 夹角的余弦值为( B ) A . 6365 B . 6365- C . 6365± D . 5139.设分程220xx ++=和方程2log 20x x ++=的根分别为p 和q ,函数()()()2f x x p x q =+++,则( A )A . ()()()203f f f =<B . ()()()023f f f <<C . ()()()302f f f <=D . ()()()032f f f <<10.已知函数,若方程f(x)=x+a有且只有两个不相等的实数根,则实数a的取值范围是(D)解:函数第Ⅱ卷二、填空题(本大题共5个小题,每小题5分,共25分) 11.已知f (x )=2x 3+ax 2+b ﹣1是奇函数,则a ﹣b= ﹣1 .解析:因为a -2b 与3a +kb 共线,所以存在实数λ使得a -2b =λ(3a +kb ), 整理得(3λ-1)a +(k λ+2)b =0,又因为向量a 、b 不共线,所以⎩⎪⎨⎪⎧3λ-1=0k λ+2=0,∴⎩⎪⎨⎪⎧λ=13k =-6. 答案:-613.函数y =tan ⎝⎛⎭⎫π4x -π2的部分图象如图所示,则(O B →-OA →)·OB →= 4解析:由题意知A (2,0),B (3,1),所以(OB →-OA →)·OB →=(1,1)·(3,1)=414.设两个向量a =(λ+2,λ2-cos 2α)和b =(m ,m2+sin α),其中λ,m ,α为实数.若a =2b ,则λm 的取值范围是_______________.解析:根据已知条件得2b =(2m ,m +2sin α),又a =2b ,所以λ+2=2m ,λ2-cos 2α=m +2sin α,于是2λ2-2cos 2α=λ+2+4sin α,即2λ2-λ=-2sin 2α+4sin α+4=-2(sin α-1)2+6,故-2≤2λ2-λ≤6,即⎩⎪⎨⎪⎧2λ2-λ≤62λ2-λ≥-2,解得-32≤λ≤2,故λm =λλ2+1=2-4λ+2∈[-6,1]. 答案:[-6,1]15.设M 为平面内一些向量组成的集合,若对任意正实数t 和向量M a ∈ ,都有M a t ∈ ,则称M 为“点射域”.现有下列平面向量的集合: ①2{(,)|}x y x y ≥;②0(,)|0x y x y x y ⎧-≥⎫⎧⎨⎨⎬+≤⎩⎩⎭;③22{(,)|20}x y x y x +-≥;④22{(,)|3260}x y x y +-<; 上述为“点射域”的集合的有 ② (写正确的标号)17.(本小题满分12分)如图,A ,B 是海面上位于东西方向相距5(3+3)海里的两个观测点,现位于A 点北偏东45°,B 点北偏西60°的D 点有一艘轮船发出求救信号,位于B 点南偏西60°且与B 点相距203海里的C 点的救援船立即前往营救,其航行速度为30海里/时,该救援船到达D 点需要多长时间?解:由题意知AB =5(3+3)(海里),∠DBA =90°-60°=30°,∠DAB =90°-45°=45°, ∴∠ADB =180°-(45°+30°)=105°. 在△DAB 中,由正弦定理得 DB sin ∠DAB =ABsin ∠ADB,∴DB =AB ·sin ∠DABsin ∠ADB=+3sin105°=+3sin45°cos60°+cos45°sin60°=533+3+12=103(海里).又∠DBC =∠DBA +∠ABC =30°+(90°-60°)=60°, BC =203(海里), 在△DBC 中,由余弦定理得CD 2=BD 2+BC 2-2BD ·BC ·cos ∠DBC=300+1200-2×103×203×12=900,∴CD =30(海里),则需要的时间t =3030=1(小时).即该救援船到达D 点需要1小时.18.(本小题满分12分)已知A ,B ,C 的坐标分别为A (3,0),B (0,3),C (cos α,sin α),α ∈ ⎝⎛⎭⎫π2,3π2.(1)若|AC →|=|BC →|,求角α的值;⎪x 2-+23,⎦⎤,12=xx 2+1,+1x≥2(=x x 2+1=1+1x∈⎦⎤,12⎦⎤,12⎦⎤,12+23,+23,+2,≤1.⎦⎤,12+23,⎝⎛⎭⎫12+76,⎝⎛⎭⎫12⎭⎫-14⎩⎝⎛⎭⎫12≤14,g ,14<a ≤12,⎩3a +23,14<a ≤12.∴f f(0)。
2014-2015学年上学期高一期中测试数学试题(含答案)

2014-2015学年上学期高一期中测试数学试题(含答案) 第I 卷(选择题共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每个小题给出的四个选项中,只有一项是符合要求的)1.下列函数中,既是偶函数又在+∞(0,)单调递增的函数是( )A .3y x =B . 1y x =+C .21y x =-+D . 2x y -=2.在同一坐标系中,表示函数log a y x =与y x a =+的图象正确的是( )A B C D3.若1log 12a<,则a 的取值范围是( ) A .1(0,)(1,)2+∞ B .1(,1)2 C .(1,)+∞ D .1(,1)(1,)2+∞4.已知函数f(x)为定义在R 上的奇函数,当x≥0时, ()22xf x x m =++ (m 为常数),则(1)f -的值为( )A .-3B .-1C .1D .35.设全集U =R ,{}|0P x f x x ==∈R (),,{}|0Q x g x x ==∈R (),,{}|0S x x x ϕ==∈R (),,则方程22f x x x ϕ=()+g ()()的解集为( )A . P Q SB .P QC .P Q S ()D . P Q S u (C )5.设9.0log 5.0=a ,9.0log 1.1=b ,9.01.1=c ,则c b a , ,的大小关系为( )A .c b a <<B .c a b <<C .a c b <<D .b c a <<6.设}3 2, ,21 ,31 ,1{-∈α,若函数αx y =是定义域为R 的奇函数,则α的值为( )A .3 ,31B .3 ,31 ,1- C .3 ,1- D .31,1- 7.已知函数)(x f 是奇函数,当0>x 时,)1 ,0( )(≠>=a a a x f x,且3)4(log 5.0-=f ,则a的值为( )A .3B .3C .9D .238.已知函数⎪⎩⎪⎨⎧>-≤=-)1( )23(log )1( 2)(2x x x x f x ,若4)(=a f ,则实数=a ( ) A .2-或6 B .2-或310 C .2-或2 D .2或3109.方程21231=⎪⎭⎫ ⎝⎛--x x 的解所在的区间为( )A .) 1 ,0 (B .) 2 ,1 (C .) 3 ,2 (D .) 4 ,3 (10.已知函数bx ax y +=2和xb a y =|)| || ,0(b a ab ≠≠在同一直角坐标系中的图象不可能 是( )11.已知函数)3(log 221a ax x y +-=在区间) ,2[∞+上是减函数,则a 的取值范围是( )A .)4 ,(-∞B .]4 ,4[-C .]4 ,4(-D .]4 ,(-∞12.若在直角坐标平面内B A ,两点满足条件:①点B A ,都在函数)(x f y =的图象上;②点B A ,关于原点对称,则称B A ,为函数)(x f y =的一个“黄金点对”.那么函数=)(x f ⎪⎩⎪⎨⎧>≤-+)0( 1)0( 222x x x x x 的“黄金点对”的个数是( )A .0个B .1个C .2个D .3个 第Ⅱ卷(非选择题,共90分)二、填空题:本题共4小题,共20分.13.已知集合}06|{2=--=x x x M ,}01|{=+=ax x N ,且M N ⊆,则由a 的取值组成的集合是 .14.若x x f =)(log 5,则=-)9log 2(log 255f .15.已知定义在R 上的偶函数)(x f 满足0)1(=-f ,并且)(x f 在)0 ,(-∞上为增函数.若0)( <a f a ,则实数a 的取值范围是 .16.已知函数()x f 的定义域是}0|{≠∈=x R x D ,对任意D x x ∈21 ,都有:=⋅)(21x x f)()(21x f x f +,且当1>x 时,()0>x f .给出结论:①()x f 是偶函数;②()x f 在()∞+ ,0上是减函数.则正确结论的序号是 .三、解答题:本大题共6小题,共70分,解答应写出必要的文字说明、证明过程及演算步骤。
安徽省马鞍山二中、安师大附中2015届高三数学上学期统一考试试题 文

2015届安师大附中、马鞍山二中统一考试试卷数学试题〔文科〕一.选择题〔本大题有10小题,每一小题5分,共50分,在每一小题给出的四个选项中,只有一项为哪一项符合题目要求的,请将答案写在答题卷上〕1.复数z 满足(1)1(z i i i +=-是虚数单位〕,如此复数z 的虚部为 ( ▲) A .1 B.i - C. i D.1-2. 集合2{|430},{|0},2xA x x xB x x =-+>=≤-如此A B =〔▲〕A .{|12}x x <<B .{|123}x x x <<>或C .{|01}x x ≤<D .{|013}x x x ≤<>或3.在数列{n a }中,假设11=a ,且对所有n N *∈, 满足212n a a a n ⋅⋅⋅=,如此=+53a a (▲)A .1625 B . 1661 C .925 D .15314. ,a b 是两个非零向量,给定条件:||||||;p a b a b ⋅=条件:,q t R ∃∈使得a tb =,如此p 成立是q 成立的 (▲)A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件5.34120341204250x y x y x y -+≥⎧⎪+-≥⎨⎪--≤⎩,如此22x y +的最小值是 (▲)A .3B .254C .125D .144256. 在ABC △中,内角,,A B C 所对的边长分别是,,a b c 。
假设cos (2)cos c a B a b A -=-,如此ABC △的形状为〔 〕A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形 7.函数()sin(2),()sin(2)33f x xg x x ππ=+=-,如下说法正确的答案是 (▲)A. ()f x 的图象可以由()g x 的图象向左平移23π个单位得到 B. ()f x 的图象可以由()g x 的图象向右平移3π个单位得到C. ()f x 的图象可以由()g x 的图象关于直线2x π=对称变换而得到 D. ()f x 的图象可以由()g x 的图象关于直线4x π=对称变换而得到8. 某几何体的三视图如下列图,如此该几何体的体积为 ( ▲ )A.643 B.803 C.163D.4339.函数()f x 满足()(1)(2),f x f x f x x R =+-+∈. 当()0,3x ∈时,2()f x x =,如此(2014)f = ( ▲ )A.5 B .5- C .1- D .110.函数()f x 是定义在R 上的奇函数,当0x ≥时,2221()(|||2|3)2f x x a x a a =-+--,假设x R ∀∈,都有(1)()f x f x -≤,如此实数a 的取值范围为 ( ▲ )A.11[,]66-B.66[,]66-C.11[,]33- D.33[,]33- 二.填空题〔本大题有5小题,每一小题5分,共25分,请将答案写在答题卷上〕 11. 在△ABC 中,假设54b B π=,∠=,t a nA=2, 如此a = ▲ .12. 下表给出一个“直角三角形数阵〞满足每一列成等差数列,从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i 行第j 列的数为(i j i j i a ≥,、j ∈N )*,如此83a 等于 ▲ .141124, 3334816,, ……13. (0,3)x ∈,如此函数143y x x=+-的最小值为 ▲ .B14.函数x x x x f ln 4321)(2+--=在[,1]t t +上不单调,如此实数t 的取值范围是 ▲. 15.如图正方形BCDE 的边长为a ,AB =,将ABE ∆沿BE 边折起,折起后A 点在平面BCDE 上的射影为D 点,如此翻折后的几何体中有如下描述: ①AB 与DE ; ② AB ∥CE ;③B ACE V -的体积是216a ;④ 平面ABC ⊥平面ADC ;⑤ 直线EA 与平面ADB 所成角为30. 其中正确的有 ▲ .〔填写你认为正确的序号〕三、解答题〔本大题共6 道题,总分为75分〕 16.〔此题总分为12分〕集合2{(,)|2},{(,)|10,02}A x y y x mx B x y x y x ==++=-+=≤≤.假设A B ≠∅,求实数m 的取值范围.17.〔此题总分为12分〕函数()y f x =满足:,,,a b R a b ∀∈≠都有()()a f a b f b +>()().a f b b f a +(1) 用定义证明:()f x 是R 上的增函数; (2)设,x y 为正实数,假设494,x y+=试比拟()f x y +与(6)f 的大小.A18.〔此题总分为12分〕 向量2(3sin,1),(cos ,cos ).444x x x m n == (1)假设1m n ⋅=,求2cos()3x π-的值; (2)记()f x m n =⋅,在ABC ∆中,角,,A B C 的对边分别是,,a b c 且满足:(2)cos cos .a c B b C -=求函数()f A 的取值范围.19.〔此题总分为12分〕25,a a 是方程212270x x -+=的两根,数列{n a }是公差为正的等差数列,数列{n b }的前n 项和为n T ,且11(2n n T b n =-∈N )*.(1)求数列{n a },{n b }的通项公式;(2)记n n n c a b =,假设数列{n c }的前n 项和n S ,求证: 2.n S <20. 〔此题总分为13分〕 在四棱锥P ABCD -中,,,,AB BC AC CD AB BC ⊥⊥=60ADC ∠=〔即:底面是一幅三角板拼成〕〔1〕假设PA 中点为,E 求证:BE ∥面PCD 〔2〕假设3,PA PB PC PD ===与面PAC成30角,求此四棱锥的体积.21. 〔此题总分为14分〕函数2()ln (0),()min{,4,21}xf x x ax ag x x x =->=--,min {,}s t 是取,s t 中较小者.〔1〕求()f x 的单调区间和极值;〔2〕假设对于任意1(1,)x ∈+∞,都存在2(0,)x ∈+∞,使得12()()0f x g x -=,求实数a 的取值范围.2015届安师大附中马鞍山二中统一考试文科数学参考答案一、1. A 2. C 3. B 4. C 5. D 6. D 7. D 8. B 9. C 10. B 二、11.210 12.1213. 3 14. (0,1) 15. ①③④⑤三、16.【解】 由2221(1)10x mx x x m x ++=+⇒+-+=,[02]x ∈,, 由题设知2()(1)1,[02]f x x m x x =+-+∈,必有零点.所以: (1)假设在[0,2]只有一个零点,如此(2)0f m <⇒<32-. 或2(1)4011022m m m⎧--=⎪⇒=-⎨-≤≤⎪⎩---------------- 6分 (2)假设在[0,2]有两个零点,如此 (2)010220f m ≥⎧⎪-⎪<-<⎨⎪∆>⎪⎩312m ⇒-≤<-. -------- 11分由(1)(2)知:1m ≤-.------------------------------------------------------------- 12分17.【解】 (1)1212,,,x x R x x ∀∈<由题意11221221()()()()x f x x f x x f x x f x +>+⇒1212()[()()]0x x f x f x -->因为12120()()0x x f x f x -<⇒-<即12()().f x f x <故()f x 为R 上的递增函数. ------------------------- 6分(2)由491491494()[()][49]44y x x y x y x y x y x y+=⇒+=++=+++ 1492500,[132]44y x x y x y x y >,>∴+≥+⋅=〔当且仅当49y x x y =时,取等〕 即:515,24x y ==时,min 25()64x y +=> ()f x 是R 上的增函数,因此()(6).f x y f +>---------- 12分18.【解】 (1)3m n ⋅=sin4x cos 4x +2cos 4x 32=1sin cos 22x +122x +=1sin()262x π++.--------3分 ∵1m n ⋅=, ∴1sin()262x π+=, cos()123x π+=-21sin ()262x π+=,2cos()cos 3x π-=-1()32x π+=-. -------------------- 6分(2)∵(2)cos cos .a c B b C -=由正弦定理得(2sin sin )cos sin cos .A C B B C -= ∴2sin cos sin().A B B C =+sin()sin ,sin 0.A B C B C A A π++=∴+=≠∴1cos 23B B π=⇒=. ------------------------------- 9分 ∴203A π<<.∴1sin 62622A πππ<+<,⇒<()126A π+<. 又∵1()sin()262x f x m n π=⋅=++,∴1()sin()262A f A π=++.故函数()f A )的取值范围是3(1)2,.---------------- 12分19.【解】 (1)由25251227a a a a +=,=, 且0d <得2539a a =,=. ∴521213a a d a -==,=.∴21(n a n n =-∈N )*. ---------------- 3分 在112n n T b =-中,令1n =,得123b =.当2n ≥时11111122n n n n T b T b --,=-,=-, 两式相减得11122n n n b b b -=-.∴11(2)3nn b n b -=≥.∴1212()(333n n nb n -==∈N )*.---------------- 6分 422(2)(21)33n n nn c n -=-⋅=, ∴233512(333n S =+++21)3nn -+,① 23312(333n S =++12321)33n n n n +--++. ② ① - ②得2321112[2(3333n S =+++1211)]33n n n +-+- --------------------- 9分 11112(1)932112[]31313nn n -+⨯--=+-- 11214411142()333333nn n n n ++-+=+--=-.FE GADBCP∴22223n nn S +=-<. ------------------ 12分20【解】〔1〕设,AC AD 的中点分别为,.G F易证,,B G F 三点共线BF ∴∥CD BF ⇒∥面PCDEF ∥PD EF ⇒∥面PCD得:面BEF ∥面PCDBE ∴∥面PCD ---------------- 6分〔2〕PA PB PC PG ==⇒⊥面ABCD , 如此有.PG CD ⊥又AC CD CD ⊥⇒⊥面PACPC ∴是PD 在面PAC 内的射影,所以30.CPD ∠= ------------ 10分由3332333PC CD AC PG AB BC =⇒=⇒=⇒===93342ABCD S ∴=+ 1933339()(23).34228V ∴=⋅+⋅= ------------- 13分21.【解】〔1〕2112()2,0,0.ax f x ax x a x x-'=-=>> ()f x ∴的减区间是1,);2a +∞ 增区间是1(0,).2a----------- 4分 11()=()(1ln 2);().22f x f a f x a =-+极大值极小值无 ------------ 6分〔2〕依题意:设{()|1},{()|0}A f x x B g x x A B =>=>⇒⊂21,01(),1 2.(,2]4,2x x g x x x B x x ⎧-<<⎪=≤≤∴=-∞⎨⎪->⎩----------------------- 9分①1>,在11(1,),()(,ln 2)22x f x a A B ∈+∞∈-∞--=⊂5111ln 22222a a e -∴--≤⇒≥故511[,)22a e -∈;②假设01,<≤在(1,),()(,(1))(,2],x f x f A ∈+∞∈=-∞=⊂-∞ (1)2f a =-≤ 显然成立,故12a ≥符合题意 综合得:51.2a e -≥ ----------------------------------------------------- 14分。
XXX2014-2015学年高一上学期期中考试数学试题 Word版含解析

XXX2014-2015学年高一上学期期中考试数学试题 Word版含解析没有明显有问题的段落需要删除,只需修改格式错误和语言表达不清的地方。
XXX2014-2015学年第一学期期中考试高一数学试题第Ⅰ卷选择题(共30分)一、选择题(本题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项符合题目要求。
)1、已知集合$S=\{x|x+1\geq2\}$,$T=\{-2,-1,0,1,2\}$,则$S\cap T=$()A。
$\{2\}$。
B。
$\{1,2\}$。
C。
$\{0,1,2\}$。
D。
$\{-1,0,1,2\}$解题思路】:题目给出了集合$S$和$T$,需要先求出它们的具体表达内容,再求它们的交集。
$S$是一次函数不等式的解,$S=\{x|x\geq1\}$;$S\cap T=\{1,2\}$,故选B。
2、用阴影部分表示集合$C\cup A\cup B$,正确的是()解题思路】:题目给出了四个图形,需要判断哪个图形表示$C\cup A\cup B$。
利用XXX求解,A中阴影部分表示$C\cup(A\cup B)$,B中阴影部分表示$(C\cup A)\cap B$,C中阴影部分表示$A\cap B$,D中阴影部分表示$C\cup A\cup B$,故选D。
3、函数$y=\log_{\frac{1}{2}}(x-1)$的定义域是()A。
$(1,+\infty)$。
B。
$[1,+\infty)$。
C。
$(0,+\infty)$。
D。
$[0,+\infty)$解题思路】:题目给出了函数$y=\log_{\frac{1}{2}}(x-1)$,需要求出它的定义域。
由$\log_{\frac{1}{2}}(x-1)>0$得$x-1>0$,即$x>1$,故选A。
4、下列函数中,在其定义域内既是奇函数又是减函数的是()A。
$y=-|x|$。
B。
$y=x$。
C。
$y=|x|$。
【真题】15年安徽省马鞍山二中高三(上)数学期中试卷含答案(文科)

2014-2015学年安徽省马鞍山二中高三(上)期中数学试卷(文科)一、选择题(每小题5分,共计50分)1.(5分)=()A.﹣1﹣i B.﹣1+i C.1+i D.1﹣i2.(5分)已知集合P={x|x2≤1},M={a}.若P∪M=P,则a的取值范围是()A.(﹣∞,﹣1]B.[1,+∞)C.[﹣1,1]D.(﹣∞,﹣1]∪[1,+∞)3.(5分)若,则cosα的范围是()A. B. C.D.4.(5分)设函数f(x)=,若f(a)=4,则实数a=()A.﹣4或﹣2 B.﹣4或2 C.﹣2或4 D.﹣2或25.(5分)若tanα=3,则sin2α+sin2α的值等于()A.2 B.1 C.D.6.(5分)若“∀x∈R,∃x0∈R,f(x)>g(x0)”,则有()A.f(x)max>g(x)min B.f(x)max>g(x)max C.f(x)min>g(x)max D.f(x)>g(x)minmin7.(5分)设的夹角为θ,若|||﹣|||=|+|,则()A.cosθ=﹣1 B.cosθ=1C.﹣1<cosθ<0 D.0<cosθ<18.(5分)若定义在R上的偶函数f(x)在(﹣∞,0)上是减函数,且f()=2.那么不等式f()>2的解集为()A.B.C. D.(2,+∞)9.(5分)对于函数y=f(x),x∈R,“y=|f(x)|的图象关于y轴对称”是“y=f(x)是奇函数”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件10.(5分)如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若.(λ,μ∈R),则λ+μ的取值范围是()A.(﹣1,0)B.(﹣1,+∞)C.(﹣∞,﹣1)D.(﹣1,0)∪(0,1)二、填空题(每小题5分,共计25分)11.(5分)已知平面向量=(1,﹣3),=(4,﹣2),λ+与垂直,则λ=.12.(5分)等差数列{a n}中,a1+a2+a3=﹣24,a18+a19+a20=78,则此数列前20项和等于.13.(5分)设sin(+θ)=,则sin2θ=.14.(5分)已知f(x)是定义在R上的偶函数,并且f(x+2)=﹣,当2≤x≤3时,f(x)=x,则= .15.(5分)以下给出五个命题,其中真命题的序号为①函数f(x)=3ax+1﹣2a在区间(﹣1,1)上存在一个零点,则a的取值范围是a<﹣1或a>;②“菱形的对角线相等”的否定是“菱形的对角线不相等”;③∀x∈(0,),x<tanx;④若0<a<b<1,则lna<lnb<a b<b a;⑤“b2=ac”是“a,b,c成等比数列”的充分不必要条件.三、解答题(16~18题每题12分,19~21题每题13分,共计75分)16.(12分)已知命题p:关于x的方程x2﹣ax+4=0有实根;命题q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数,若“p或q”是真命题,“p且q”是假命题,求实数a的取值范围.17.(12分)已知函数f(x)=2sinx(sinx+cosx).(1)求函数f(x)的最大值及相应的x值;(2)试叙述:函数y=f(x)的图象可由函数y=sinx的图象经过怎样的变换而得到.18.(12分)在△ABC中,角A,B,C,所对的边分别为a,b,c.已知sinA+sinC=psinB (p∈R).且ac=b2.(Ⅰ)当p=,b=1时,求a,c的值;(Ⅱ)若角B为锐角,求p的取值范围.19.(13分)已知函数f(x)=﹣alnx,若函数y=f(x)的图象在点P(2,f (2))处的切线方程为l:y=x+b.(1)求出实数a,b的值;(2)当时,不等式f(x)<k恒成立,求实数k的取值范围.20.(13分)在数列{a n}中,a1=1,a2=2,且a n+1=(1+q)a n﹣qa n﹣1(n≥2,q≠0).(1)设b n=a n+1﹣a n(n∈N*),证明{b n}是等比数列;(2)求数列{a n}的通项公式.21.(13分)已知数列{a n}的前n项和S n=n2,n∈N*.(1)若b n=,求数列{b n}的前n项和P n;(2)若c n=,求数列{c n}的前n项和T n.2014-2015学年安徽省马鞍山二中高三(上)期中数学试卷(文科)参考答案与试题解析一、选择题(每小题5分,共计50分)1.(5分)=()A.﹣1﹣i B.﹣1+i C.1+i D.1﹣i【解答】解:====﹣1+i.故选:B.2.(5分)已知集合P={x|x2≤1},M={a}.若P∪M=P,则a的取值范围是()A.(﹣∞,﹣1]B.[1,+∞)C.[﹣1,1]D.(﹣∞,﹣1]∪[1,+∞)【解答】解:∵P={x|x2≤1},∴P={x|﹣1≤x≤1}∵P∪M=P∴M⊆P∴a∈P﹣1≤a≤1故选:C.3.(5分)若,则cosα的范围是()A. B. C.D.【解答】解:∵cosα在(﹣,0]上是单调递增的,在[0,]上是单调递减的,故cosαmax=cos0=1;又cos(﹣)=>cos=,故有cosαmin=cos=.故选:C.4.(5分)设函数f(x)=,若f(a)=4,则实数a=()A.﹣4或﹣2 B.﹣4或2 C.﹣2或4 D.﹣2或2【解答】解:当a≤0时若f(a)=4,则﹣a=4,解得a=﹣4当a>0时若f(a)=4,则a2=4,解得a=2或a=﹣2(舍去)故实数a=﹣4或a=2故选:B.5.(5分)若tanα=3,则sin2α+sin2α的值等于()A.2 B.1 C.D.【解答】解:∵tanα=3,∴sin2α+sin2α====.故选:D.6.(5分)若“∀x∈R,∃x0∈R,f(x)>g(x0)”,则有()A.f(x)max>g(x)min B.f(x)max>g(x)max C.f(x)min>g(x)max D.f(x)>g(x)minmin【解答】解:∵“∀x∈R,∃x0∈R,f(x)>g(x0)”,即对∀x∈R,∃x0∈R,使f(x)>g(x0)成立,∴f(x)min>g(x)min.故选:D.7.(5分)设的夹角为θ,若|||﹣|||=|+|,则()A.cosθ=﹣1 B.cosθ=1C.﹣1<cosθ<0 D.0<cosθ<1【解答】解:由于|||﹣|||=|+|,则两边平方得,+﹣2||=++2,则有=﹣||=||cosθ,即有cosθ=﹣1,故选:A.8.(5分)若定义在R上的偶函数f(x)在(﹣∞,0)上是减函数,且f()=2.那么不等式f()>2的解集为()A.B.C. D.(2,+∞)【解答】解:根据题意画出函数f(x)的示意图,不等式f()>2转化为>或<﹣,∴原不等式的解集为,故选:B.9.(5分)对于函数y=f(x),x∈R,“y=|f(x)|的图象关于y轴对称”是“y=f(x)是奇函数”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【解答】解:例如f(x)=x2﹣4满足|f(x)|的图象关于y轴对称,但f(x)不是奇函数,所以,“y=|f(x)|的图象关于y轴对称”推不出“y=f(x)是奇函数”当“y=f(x)是奇函数”⇒f(﹣x)=﹣f(x)⇒|f(﹣x)|=|f(x)|⇒y=|f(x)|为偶函数⇒,“y=|f(x)|的图象关于y轴对称”所以,“y=|f(x)|的图象关于y轴对称”是“y=f(x)是奇函数”的必要而不充分条件故选:B.10.(5分)如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若.(λ,μ∈R),则λ+μ的取值范围是()A.(﹣1,0)B.(﹣1,+∞)C.(﹣∞,﹣1)D.(﹣1,0)∪(0,1)【解答】解:如图所示:∵,可得λ<0,μ<0,故λ+μ<0,故排除B,D.∵|OC|=|OB|=|OA|,∴由=λ2+μ2+2λμcos∠AOB=1,当∠AOB=120°时,由(λ+μ)2=1+3λμ>1,可得λ+μ<﹣1;故选:C.二、填空题(每小题5分,共计25分)11.(5分)已知平面向量=(1,﹣3),=(4,﹣2),λ+与垂直,则λ=﹣1.【解答】解:,()⇒(λ+4)×1+(﹣3λ﹣2)×(﹣3)=0⇒λ=﹣1,故答案为﹣1.12.(5分)等差数列{a n}中,a1+a2+a3=﹣24,a18+a19+a20=78,则此数列前20项和等于180.【解答】解:由a1+a2+a3=﹣24,a18+a19+a20=78,得得a 1+a20==18所以S20==180故答案为:18013.(5分)设sin(+θ)=,则sin2θ=﹣.【解答】解:∵sin(+θ)=,即+=,平方可得+sin2θ=,解得sin2θ=﹣,故答案为﹣.14.(5分)已知f(x)是定义在R上的偶函数,并且f(x+2)=﹣,当2≤x≤3时,f(x)=x,则= .【解答】解:∵f(x+2)=﹣,∴f(x+4)=﹣=f(x),则函数是周期为4的周期函数,∵f(x)是定义在R上的偶函数,∴f()=f(﹣)=f(4﹣)=f(),∵当2≤x≤3时,f(x)=x,∴f()=,故答案为:15.(5分)以下给出五个命题,其中真命题的序号为①③④①函数f(x)=3ax+1﹣2a在区间(﹣1,1)上存在一个零点,则a的取值范围是a<﹣1或a>;②“菱形的对角线相等”的否定是“菱形的对角线不相等”;③∀x∈(0,),x<tanx;④若0<a<b<1,则lna<lnb<a b<b a;⑤“b2=ac”是“a,b,c成等比数列”的充分不必要条件.【解答】解:①,∵f(x)=3ax+1﹣2a在区间(﹣1,1)上存在一个零点,∴f(﹣1)•f(1)=(1﹣5a)(a+1)<0,解得a<﹣1或a>,故①正确;②,“菱形的对角线相等”的否定是“菱形的对角线不都相等”,故②错误;③,由图可知,x=,tanx=BA(正切线),∀x∈(0,),x<tanx,正确;④,∵0<a<b<1,y=lnx为增函数,y=a x、y=b x均为减函数,∴lna<lnb<0<a b<b b<b a,故④正确;⑤“b2=ac”是“a,b,c成等比数列”的必要不充分条件,故⑤错误.综上所述,①③④正确,故答案为:①③⑤.三、解答题(16~18题每题12分,19~21题每题13分,共计75分)16.(12分)已知命题p:关于x的方程x2﹣ax+4=0有实根;命题q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数,若“p或q”是真命题,“p且q”是假命题,求实数a的取值范围.【解答】解:若p真:则△=a2﹣4×4≥0∴a≤﹣4或a≥4(4分)若q真:,∴a≥﹣12(8分)由“p或q”是真命题,“p且q”是假命题得:p、q两命题一真一假(10分)当p真q假时:a<﹣12;当p假q真时:﹣4<a<4(12分)综上,a的取值范围为(﹣∞,﹣12)∪(﹣4,4)(14分)17.(12分)已知函数f(x)=2sinx(sinx+cosx).(1)求函数f(x)的最大值及相应的x值;(2)试叙述:函数y=f(x)的图象可由函数y=sinx的图象经过怎样的变换而得到.【解答】解:(1)f(x)=2sin2x+2sinxcosx=1﹣cos2x+sin2x=,∴函数f(x)的最大值为.此时;(2)第一步,将y=sinx的图象向右平移单位,得的图象;第二步,将的图象上的各点横坐标变为原来的(纵坐标不变),得的图象;第三步,将的图象上的各点纵坐标变为原来的倍(横坐标不变),得的图象;第四步,将的图象向上平移1个单位得的图象;18.(12分)在△ABC中,角A,B,C,所对的边分别为a,b,c.已知sinA+sinC=psinB (p∈R).且ac=b2.(Ⅰ)当p=,b=1时,求a,c的值;(Ⅱ)若角B为锐角,求p的取值范围.【解答】(Ⅰ)解:由题设并利用正弦定理得故可知a,c为方程x2﹣x+=0的两根,进而求得a=1,c=或a=,c=1(Ⅱ)解:由余弦定理得b2=a2+c2﹣2accosB=(a+c)2﹣2ac﹣2accosB=p2b2﹣b2cosB ﹣,即p2=+cosB,因为0<cosB<1,所以p2∈(,2),由题设知p∈R,所以<p<或﹣<p<﹣又由sinA+sinC=psinB知,p是正数故<p<即为所求19.(13分)已知函数f(x)=﹣alnx,若函数y=f(x)的图象在点P(2,f (2))处的切线方程为l:y=x+b.(1)求出实数a,b的值;(2)当时,不等式f(x)<k恒成立,求实数k的取值范围.【解答】解:(1)∵f(x)=﹣alnx,∴f',∴f'.∴.∵点P坐标满足,∴f(2)=2﹣2ln2,∵点P在直线l上,∴b=﹣2ln2,∴a=2,b=﹣2ln2;(2)由(1)知.∴,由f'(x)=0⇒舍去).∴当x∈时,f(x)为减函数,当x∈[]时,f(x)为增函数.又,故当时,函数y=f(x)的最大值为,∴.20.(13分)在数列{a n}中,a1=1,a2=2,且a n+1=(1+q)a n﹣qa n﹣1(n≥2,q≠0).(1)设b n=a n+1﹣a n(n∈N*),证明{b n}是等比数列;(2)求数列{a n}的通项公式.【解答】解:(1)证明:由题设a n=(1+q)a n﹣qa n﹣1(n≥2),得+1a n+1﹣a n=q(a n﹣a n﹣1),即b n=qb n﹣1,n≥2.又b1=a2﹣a1=1,q≠0,所以{b n}是首项为1,公比为q的等比数列.(2)由(1)可得数列{b n}的通项公式b n=q n﹣1,∵b n=a n+1﹣a n,=q n﹣2,∴a n﹣a n﹣1…a2﹣a1=1,把上述各式相加,得到a n﹣a1=q n﹣2+q n﹣3+…+q∴a n=21.(13分)已知数列{a n}的前n项和S n=n2,n∈N*.(1)若b n=,求数列{b n}的前n项和P n;(2)若c n=,求数列{c n}的前n项和T n.【解答】解(1)由S n=n2,得a1=S1=1,当n≥2时,,验证n=1时成立,∴a n=2n﹣1,∴P n=b1+b2+…+b n=..两式作差得:,∴,则;(2)c n==.,,两式作差得:,∴,,则.赠送—高中数学知识点【1.3.1】单调性与最大(小)值(1)函数的单调性①定义及判定方法②在公共定义域内,两个增函数的和是增函数,两个减函数的和是减函数,增函数减去一个减函数为增函数,减函数减去一个增函数为减函数.③对于复合函数[()]y f g x=,令()u g x=,若()y f u=为增,()u g x=为增,则[()]y f g x=为增;若()y f u=为减,()u g x=为减,则[()]y f g x=为增;若()y f u=为增,()u g x=为减,则[()]y f g x=为减;若()y f u=为减,()u g x=为增,则[()]y f g x=为减.(2)打“√”函数()(0)af x x ax=+>的图象与性质()f x分别在(,-∞、)+∞上为增函数,分别在[、上为减函数.(3)最大(小)值定义①一般地,设函数()y f x=的定义域为I,如果存在实数M满足:(1)对于任意的x I∈,都有()f x M≤;(2)存在x I∈,使得()f x M=.那么,我们称M是函数()f x的最大值,记作yxomax ()f x M =.②一般地,设函数()y f x =的定义域为I ,如果存在实数m 满足:(1)对于任意的x I ∈,都有()f x m ≥;(2)存在0x I ∈,使得0()f x m =.那么,我们称m 是函数()f x 的最小值,记作max ()f x m =.【1.3.2】奇偶性(4)函数的奇偶性②若函数()f x 为奇函数,且在0x =处有定义,则(0)0f =.③奇函数在y 轴两侧相对称的区间增减性相同,偶函数在y 轴两侧相对称的区间增减性相反.④在公共定义域内,两个偶函数(或奇函数)的和(或差)仍是偶函数(或奇函数),两个偶函数(或奇函数)的积(或商)是偶函数,一个偶函数与一个奇函数的积(或商)是奇函数.。
安徽省马鞍山二中学高二上学期期中考试 数学 扫描版含
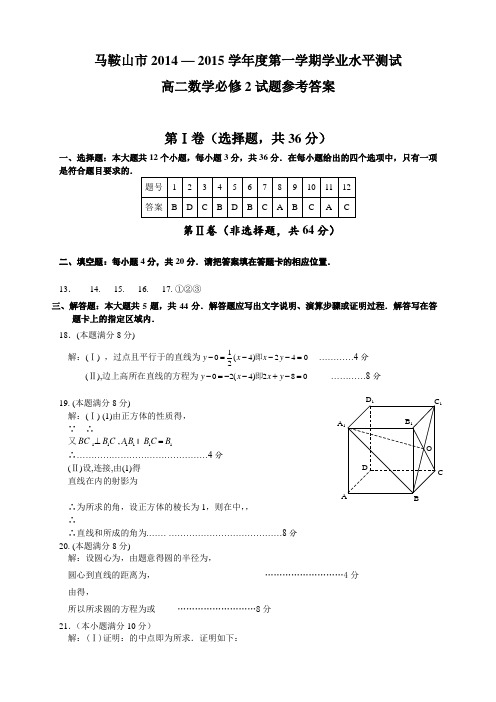
马鞍山市2014 — 2015学年度第一学期学业水平测试高二数学必修2试题参考答案第Ⅰ卷(选择题,共36分)一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.第Ⅱ卷(非选择题,共64分)二、填空题:每小题4分,共20分.请把答案填在答题卡的相应位置.13. 14. 15. 16. 17. ①②③三、解答题:本大题共5题,共44分.解答题应写出文字说明、演算步骤或证明过程.解答写在答题卡上的指定区域内.18.(本题满分8分)解:(Ⅰ) ,过点且平行于的直线为10(4)2402y x x y -=---=即 …………4分(Ⅱ),边上高所在直线的方程为02(4)280y x x y -=--+-=即 …………8分19. (本题满分8分)解:(Ⅰ) (1)由正方体的性质得, ∵ ∴又111111,BC B C A B B C B ⊥= ∴………………………………………4分(Ⅱ)设,连接,由(1)得直线在内的射影为∴为所求的角,设正方体的棱长为1,则在中,,∴∴直线和所成的角为.…… …………………………………8分20. (本题满分8分)解:设圆心为,由题意得圆的半径为, 圆心到直线的距离为, ………………………4分由得,所以所求圆的方程为或 ………………………8分21.(本小题满分10分)解:(Ⅰ)证明:的中点即为所求.证明如下:O AB C D A 1C 1D 1B 1取的中点∵分别为,的中点 ,∴, ,∴∥平面 …………………………………5分(Ⅱ)∵,又11312242BEF S BF EF BC AD =⨯=⨯⨯=∴13B PEF P BEF BEF V V S PA --==⨯= …………………10分 22.(本小题满分10分) 解:(Ⅰ)根据题意,设直线的方程为: 代入圆方程得:,显然,设则12121,1y y x x +=+=∴点的坐标为 …………………………4分 (Ⅱ)假设存在这样的直线联立圆的方程并整理得:222(22)440x b x b b ++++-=当24(69)033b b b ∆=-+->⇒--<< 设,则234341(1),(44)2x x b x x b b +=-+=+-∴∵以为直径的圆经过原点,所以3344(,),(,)OE x y OF x y ==∴234340,340x x y y b b +=+-=即均满足∴均满足.∴直线的方程为:或. …………………………10分 法二:可设圆系方程22244()0x y x y x y b λ+-+-+-+=24(,)22λλ---则圆心坐标为,圆心在直线上,且该圆过原点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
马鞍山市2014―2015学年度第一学期期中素质测试
数学必修 ① 试题 答案
二、填空题(本题共5小题,每小题4分,共20分.)
13. [4,5)(5,)+∞ 14. 7- 15. 10 16. (,4][10,)-∞+∞ 17. ①③④.
三、解答题:(本题共5小题,共44分.解答题应写出文字说明、演算步骤或证明过程)
18. (本小题满分8分)
已知集合{|240}A x x =-<,{|05}B x x =≤<,全集U =R .
求:(Ⅰ)A B ; (Ⅱ)()U A B ð.
【命题意图】考查集合的表示法以及集合的交、并、补运算,简单题.
【答案】(Ⅰ){|2}A x x =<,{}|5A B x x =<;
……4分 (Ⅱ)(){|05}U B x x x =<≥或ð,(){|0}U A B x x =<ð.
……8分
19. (本题满分8分)
求下列各式的值:
(Ⅰ)1lg lg 254-; (Ⅱ)1212[(1](1--+.
【命题意图】考查指数、对数的基本运算,简单题.
【答案】
(Ⅰ)()1lg lg 25lg 4lg 25lg 425lg10024
-=--=-⨯=-=-; ……4分
(Ⅱ)1
212[(1](111)0
--==-=. ……8分
20. (本小题满分9分)
已知函数()log (1)a f x x =+,()log (1)a g x x =-,其中0a >且1a ≠,设()()()h x f x g x =-.
(Ⅰ)求函数()h x 的定义域;
(Ⅱ)判断函数()h x 的奇偶性,并说明理由;
(Ⅲ)解关于x 的不等式()0h x >.
【命题意图】考查函数性质的综合应用,中档题.
【答案】
(Ⅰ)()()()log (1)log (1)a a h x f x g x x x =-=+--,由1010x x +>⎧⎨->⎩
,解得11x -<<,所以函数()h x 的定义域为(1,1)-; ……3分 (Ⅱ)由(Ⅰ)可知定义域关于原点对称,
()log (1)log (1)()a a h x x x h x -=--+=-,所以()h x 为奇函数; ……6分 (Ⅲ)由()()()0h x f x g x =->得()()f x g x >,即log (1)log (1)a a x x +>-,
当1a >时,则有1111x x x +>-⎧⎨-<<⎩
,解得()0,1x ∈; 当01a <<时,则有1111x x x +<-⎧⎨
-<<⎩,解得()1,0x ∈-. ……………………9分
21. (本小题满分9分) 已知函数()a f x x x
=+,且(1)10f =. (Ⅰ)求a 的值;
(Ⅱ)试判断函数()f x 在[3,)+∞上的单调性,并用定义加以证明;
(Ⅲ)求函数()f x 在区间[3,6]上的最大值与最小值.
【命题意图】考查函数单调性的判定以及利用单调性求最值,中档题.
【答案】(Ⅰ)由(1)110f a =+=得9a =. ……2分 (Ⅱ)9()f x x x
=+在[3,)+∞上是增函数,证明如下: ……4分 任取12,[3,)x x ∈+∞,且12x x <,
1212121212999()()()()()1f x f x x x x x x x x x ⎛⎫-=+-+=-- ⎪⎝⎭
, ∵123x x ≤<,∴120x x -<,129x x >,12910x x -
>, ∴12()()0f x f x -<,即12()()f x f x <,
所以()f x 在[3,)+∞上是增函数. ……7分 (Ⅲ)由(Ⅱ)可知,()f x 在[3,6]上是单调递增,所以最大值为15(6)2
f =,最小值为(3)6f =. ……9分
22. (本小题满分10分)
设函数()(,,)n f x x bx c n N b c R +=++∈∈
(Ⅰ)若2n =时,()f x 为偶函数,且函数()f x 的值域为[3,)+∞,求()f x 的解析式;
(Ⅱ)设2n ≥,1,1b c ==-,证明:()f x 在区间1(,1)2
内存在唯一的零点; (Ⅲ)在(Ⅱ)条件下,当3n =时,这个零点更靠近12
与1中的哪一个值? 【命题意图】考查函数的基本性质与二次函数的基础知识,以及函数零点存在性定理的考查,较难题.
【答案】
(Ⅰ)当2n =时,又()f x 为偶函数,所以有()()f x f x -=,从而可求出0b =, 此时2()f x x c =+ ……2分
结合值域为[3,)+∞可知3c =.故解析式为2()3f x x =+;
……3分 (Ⅱ)()1n f x x x =+-,因为11111()()1()022222
n n f =+-=-<,(1)11110n f =+-=>,所以1()(1)02f f ⋅<,所以()f x 在区间1(,1)2内存在零点. ……5分
由于函数(2)n y x n N n +=∈≥,和1y x =-在1(,1)2内单调递增,所以()1n f x x x =+-在1(,1)2
内单调递增,从而()f x 在区间1(,1)2内存在唯一的零点. ……7分
(Ⅲ)当3n =时,3()1f x x x =+-,结合(Ⅱ)的结论可知,()f x 在区间1(,1)2
内存在唯一的零点,又因为3111()()10222f =+-<,(1)10f =>,3333()()10444
f =+->,所以这个零点在区间13(,)24内,故这个零点更靠近12. ……10分。
