线段、直线和射线
直线、射线、线段(知识点总结、例题解析)

第四章 几何图形初步4.2 直线、射线、线段一、知识考点知识点1【直线】1、直线:把线段向两端无限延伸形成的图形叫做直线。
2、特点:是直的;无粗细之分;无端点;不可以度量;不可以比较长短,无限长。
3、基本性质:经过两点有且只有一条直线(两点确定一条直线);4、直线有两种表示方法:(1)用直线上任意两点的大写字母,如:表示为直线AB 或直线BA 。
(2)也可以用一个小写字母表示,如:直线l5、直线和点的位置关系:(1)在直线上:点O 在直线l 上,或者说说直线l 经过点O(2)点在直线外:点P 在直线l 外,或者说说直线l 不经过点P6、交点:当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做他们的交点。
O Pl知识点2【射线】1、射线:将线段向一个方向无限延长,就形成了射线,射线有一个端点。
2、特点:是直的,有一个端点,不可以度量,不可以比较长短,无限长。
3、射线有两种表示方法:(1)可以用两个大写英文字母表示,其中一个是射线的端点,另一个是射线上除端点外的任意的一点,端点写在前面。
(如图:可以记作射线OM,但不能记作射线MO) (2)可以用一个小写英文字母表示,比如:射线OM也可以记为射线l。
4、射线的画法:画射线一要画出射线端点,二要画出射线经过一点,并向一旁延伸的情况。
知识点3【线段】1、线段:直线上两个点和它们之间的部分叫做线段,这两个点叫做线段的端点。
2、特点:线段是直的,它有两个端点,他的长度是有限的,可以度量的,可以比较长短。
3、基本性质:(1) 线段公理:两点之间的所有连线中,线段最短(两点之间,线段最短)(2) 两点之间的距离:两点之间线段的长度,叫做这两点之间的距离。
注意:两点间的距离是指线段的长度,是一个数值,而不是指线段本身。
(3) 线段的中点到两端点的距离相等。
(4) 线段的大小关系和它们的长度的大小关系是一致的4、线段有两种表示方法:(1)可以用它的两个端点的大写英文字母来表示,如线段AB(或线段BA)(2)可以用一个小写字母来表示,如线段a5、线段的画法:用直尺和尺规作图(尺规作图)已知:线段a(如图所示),用直尺和圆规画一条线段,使它等于已知线段a第一步:任意画一条射线AC第二步:用圆规量取已知线段a的长度。
直线,射线,线段

C
D
5
【例题 7】如图,已知线段 a,b,c,画一条线段,使它等于 a+b-c(用尺规法).
【例题 8】如图,线段 AB=8 cm,点 C 是 AB 的中点,点 D 在 CB 上且 DB=1.5 cm, 求线段 CD 的长度.
【例题 9】平面上有 n 个点(n≥2) ,且任意三个点不在同一条直线上,过这些点能作 多少条不同的直线?
4.已知线段 AB,在 BA 的延长线上取一点 C,使 CA=3AB,则 CB=_______AB,CA=_______CB. 5.如图所示,射线 OA 表示的方向是_______,射线 OB 表示的方向是_______·
6.如图,下列说法,正确说法的个数是(
A B 图1 C A B 图2 C D
考点 2
射线
(1)射线的概念:直线上的一点和它一旁的部分叫做射线,这个点叫做射线的端 点。 (2)射线的表示方法:用射线的端点和射线上任一点来表示,如图 1 中的射线记 做射线 OA 或射线 l . 注意:①表示端点的字母一定要写在前面,使字母的顺序与射线延伸的方向一致, 如图 1 射线 OA 不能表示成射线 AO; ②同一条射线是指射线的端点相同,而延伸方向也相同的射线。如图 2, 射线 OA 与射线 OB 表示同一条射线; ③两条不同射线是指端点不同的射线,或者是指端点相同但延伸方向不同 的射线,如图 2 中,射线 OB 与射线 AB 不是同一射线.
5 BC ,则线段 BC 等于( 3
(D) 3.5cm
)
4.如图,已知 AB=8,AP=5,OB=6,则 OP 的长是( A.2 B.3 C.4 D.5
5.已知 1 条直线能将平面分成两部分,2 条直线能将平面分成 3 和 4 部分,则 3 条直线最多能将平面 分成( A.4 部分 ) B.6 部分 C.7 部分 D.8 部分 )
直线、射线、线段

基本平面图形一、线段、射线、直线1、线段、射线、直线的定义(1)线段:线段可以近似地看成是一条有两个端点的崩直了的线。
线段可以量出长度。
(2)射线:将线段向一个方向无限延伸就形成了射线,射线有一个端点。
射线无法量出长度。
(3)直线:将线段向两个方向无限延伸就形成了直线,直线没有端点。
直线无法量出长度。
2、线段、射线、直线的表示方法(1)线段的表示方法有两种:一是用两个端点来表示,二是用一个小写的英文字母来表示。
(2)射线的表示方法只有一种:用端点和射线上的另一个点来表示,端点要写在前面。
(3)直线的表示方法有两种:一是用直线上的两个点来表示,二是用一个小写的英文字母来表示。
3、直线公理:过两点有且只有一条直线。
简称两点确定一条直线。
4、线段的比较(1)叠合比较法;(2)度量比较法。
5、线段公理:“两点之间,线段最短”。
连接两点的线段的长度,叫做这两点的距离。
6、线段的中点:如果线段上有一点,把线段分成相等的两条线段,这个点叫这条线段的中点。
1AB或AB=2AC=2BC。
若C是线段AB的中点,则:AC=BC=2二、角1、角的概念:(1)角可以看成是由两条有共同端点的射线组成的图形。
两条射线叫角的边,共同的端点叫角的顶点。
(2)角还可以看成是一条射线绕着他的端点旋转所成的图形。
2、角的表示方法:角用“∠”符号表示(1)分别用两条边上的两个点和顶点来表示。
(顶点必须在中间)(2)在角的内部写上阿拉伯数字,然后用这个阿拉伯数字来表示角。
(3)在角的内部写上小写的希腊字母,然后用这个希腊字母来表示角。
(4)直接用一个大写英文字母来表示。
3、角的度量:会用量角器来度量角的大小。
4、角的单位:角的单位有度、分、秒,用°、′、″表示,角的单位是60进制与时间单位是类似的。
度、分、秒的换算:1°=60′,1′=60″。
5、锐角、直角、钝角、平角、周角的概念和大小(1)平角:角的两边成一条直线时,这个角叫平角。
线段,射线,直线的关系

线段,射线,直线的关系
线段、射线和直线是平面几何中三种不同的线,它们之间有一定的关系。
线段是一种有端点的线。
线段上存在两个端点,称为线段的起点和终点。
如果把一些线段连接起来,就能构成折线。
射线是没有端点的线,它只有一个起点,并且从起点一直延伸下去,永远不会终止,可以理解为如箭头般一直延伸的线。
直线也是一种没有端点的线,它不仅在一个方向上没有端点,而且在任何方向上都没有端点,可以理解为平行的线。
从上面可以看出,线段是有端点的,射线和直线都是无端点的,射线只有一个起点永远不会终止,而直线没有端点,在任何方向上都没有。
- 1 -。
线段、直线、射线

猜一猜,画一画,从一点出发可以画多少条射线?
从一点出发可以画无数条射线。
线段、直线、射线的区别
直线、线段和射线有什么相同和不同之处呢? 小组讨论一下,把你们的发现填在ቤተ መጻሕፍቲ ባይዱ格中。
图形 相同点 端点个数 延长情况
线段
都 是 直 直 的 线 2
长度
不能延长 可测量
射线
直线
1
0
一端无限 延长 不可测量
两端无限 延长 不可测量
联系:线段和射线都是直线的一部分。
神奇夺宝之旅
准备好了吗?开始吧!
火眼金睛
下面哪些是线段,哪些是直线,哪些是射线。
(1) 线段: 直线: 射线 :
(2) (3) (1) (5) (2) (6)
(3)
(4)
(5)
(6)
第一关
辨断对错
1.直线没有端点,射线有一个端点,线段有 两个端点。 (√ ) 2.一条射线长8米。 ( ×) 3.一条直线长5米。 ( ×) 4. 一条射线比一条直线短。 ( × )
猜一猜,经过一点可以画多少条直线?
经过一点可以画无数条直线。
画一画,经过两点可以画多少条直线?
经过两点只能画一条直线
发现之旅:
设想1: 把线段向一端无限延伸,那会是个什么图
形?
射线(AB)
射线
:把线段向一端无限延伸,就得到一条射
线。
注意:不能表示为射线BA。必须把 表示端点的字母 放在前面。
第二关
end
猜一猜:
(打一线的名称)
有 始 有 终 ( 线段 )
有 始 无 终 (射线 ) 无 始 无 终 (直线 )
课后作业:
第39页做一做。
直线 射线 线段
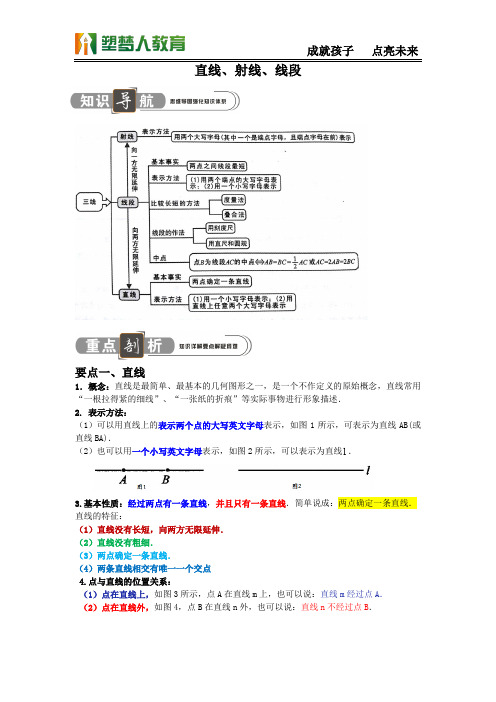
直线、射线、线段要点一、直线1.概念:直线是最简单、最基本的几何图形之一,是一个不作定义的原始概念,直线常用“一根拉得紧的细线”、“一张纸的折痕”等实际事物进行形象描述.2. 表示方法:(1)可以用直线上的表示两个点的大写英文字母表示,如图1所示,可表示为直线AB(或直线BA).(2)也可以用一个小写英文字母表示,如图2所示,可以表示为直线l.3.基本性质:经过两点有一条直线,并且只有一条直线.简单说成:两点确定一条直线.直线的特征:(1)直线没有长短,向两方无限延伸.(2)直线没有粗细.(3)两点确定一条直线.(4)两条直线相交有唯一一个交点4.点与直线的位置关系:(1)点在直线上,如图3所示,点A在直线m上,也可以说:直线m经过点A.(2)点在直线外,如图4,点B在直线n外,也可以说:直线n不经过点B.要点二、线段1.概念:直线上两点和它们之间的部分叫做线段.2.表示方法:(1)线段可用表示它两个端点的两个大写英文字母来表示,如图所示,记作:线段AB 或线段BA .(2)线段也可用一个小写英文字母来表示,如图5所示,记作:线段a .3. “作一条线段等于已知线段”的两种方法:法一:用圆规作一条线段等于已知线段.例如:下图所示,用圆规在射线AC 上截取AB =a .法二:用刻度尺作一条线段等于已知线段.例如:可以先量出线段a 的长度,再画一条等于这个长度的线段.4.基本性质:两点的所有连线中,线段最短.简记为:两点之间,线段最短.如图6所示,在A ,B 两点所连的线中,线段AB 的长度是最短的.要点剖析:(1)线段是直的,它有两个端点,它的长度是有限的,可以度量,可以比较长短. (2)连接两点间的线段的长度,叫做这两点的距离. (3)线段的比较:①度量法:用刻度尺量出两条线段的长度,再比较长短.②叠合法:利用直尺和圆规把线段放在同一条直线上,使其中一个端点重合,另一个端点位于重合端点同侧,根据另一端点与重合端点的远近来比较长短.5.线段的中点:把一条线段分成两条相等线段的点,叫做线段的中点.如图7所示,点C 是线段AB 的中点,则12AC CB AB ==,或AB =2AC =2BC .要点剖析:若点C 是线段AB 的中点,则点C 一定在线段AB 上图6 图71.概念:直线上一点和它一侧的部分叫射线,这个点叫射线的端点.如图8所示,直线l 上点O 和它一旁的部分是一条射线,点O 是端点.l2.特征:是直的,有一个端点,不可以度量,不可以比较长短,无限长. 3.表示方法:(1)可以用两个大写英文字母表示,其中一个是射线的端点,另一个是射线上除端点外的 任意一点,端点写在前面,如图8所示,可记为射线OA .(2)也可以用一个小写英文字母表示,如图8所示,射线OA 可记为射线l . 要点剖析:(1)端点相同,而延伸方向不同,表示不同的射线.如图9中射线OA ,射线OB 是不同的射线.(2)端点相同且延伸方向也相同的射线,表示同一条射线.如图10中射线OA 、射线OB 、射线OC 都表示同一条射线.要点四、直线、射线、线段的区别与联系1.直线、射线、线段之间的联系(1)射线和线段都是直线上的一部分,即整体与部分的关系.在直线上任取一点,则可将直线分成两条射线;在直线上取两点,则可将直线分为一条线段和四条射线.(2)将射线反向延伸就可得到直线;将线段一方延伸就得到射线;将线段向两方延伸就得到直线.2.三者的区别如下表要点剖析:图8 图9 图10(1)联系与区别可表示如下:(2)在表示直线、射线与线段时,勿忘在字母的前面写上“直线”“射线”“线段”字样.命题点一:计算图形中的直线、射线、线段的条数例1.如图,(1)能用字母表示的直线有_____条,它们是___________________________(2)能用字母表示的线段有_____条,它们是___________________________(3)在直线EF上能用字母表示的射线有_____条,它们是_______________________例2。
线段射线与直线的概念与判断知识点总结
线段射线与直线的概念与判断知识点总结线段、射线和直线是几何学中常见的概念,它们在图形分析和问题解决中起着重要的作用。
本文将对线段、射线和直线的概念进行总结,并介绍它们的判断方法。
1. 线段的概念线段是由两个不同点A和B确定的有限部分。
通常用直线上的两个点A和B来表示线段,记作AB。
线段AB的长度可以通过测量两个端点之间的距离来确定。
线段的长度是有限的,因此在直线上有起点A和终点B。
2. 射线的概念射线是由一个起点A和一个经过该点的方向确定的无限延伸部分。
射线通常用一个起点A和一个经过该点的方向线段来表示,记作→AB。
射线的长度是无限的,因此在直线上只有一个起点A,没有终点。
3. 直线的概念直线是由无数个点沿着同一方向无限延伸而成的。
直线通常用一个大写字母表示,如直线L。
直线上的任意两个点可以确定一条直线,也可以通过给定一点和一条经过该点的方向来确定一条直线。
4. 判断线段、射线和直线要判断一个几何图形是线段、射线还是直线,可以根据以下方法进行判断:4.1 判断线段:如果在直线上给出两个不同的点A和B,并且这两个点之间有明显的起点和终点,那么这个几何图形就是线段。
线段的长度是有限的,可以通过测量两个端点之间的距离得到。
4.2 判断射线:如果在直线上给出一个点A和一个经过该点的方向,且这个方向与直线上其他点的连接方向不同,那么这个几何图形就是射线。
射线的长度是无限的,只有一个起点,没有终点。
4.3 判断直线:如果一个几何图形上的所有点都沿着同一方向无限延伸,那么这个几何图形就是直线。
直线上的任意两个点可以确定一条直线。
通过以上判断方法,我们可以正确地区分线段、射线和直线,并在几何图形分析和问题解决中应用它们。
再次强调,线段有明确的起点和终点,射线只有一个起点且无终点,而直线上的点可以无限延伸。
总结:线段、射线和直线在几何学中具有不同的定义和特征。
- 线段由两个不同点确定,有明确的起点和终点。
- 射线由一个起点和经过该点的方向确定,只有一个起点且无终点。
线段、射线、直线知识点总结及习题
线段、射线、直线知识点总结及习题线段、射线、直线是几何学中的基本概念,它们在解决几何问题中起到了核心的作用。
本文将对线段、射线、直线的定义、特性以及常见习题进行总结,帮助读者更好地理解和掌握相关知识。
一、线段的定义与特性线段是由两个端点所确定的一段直线,具有以下特性:1. 线段的长度是有限的,可以通过两个端点的距离来计算。
2. 线段是有方向的,从一个端点指向另一个端点。
3. 线段可以任意延长,但是延长后的部分不再属于原来的线段。
二、射线的定义与特性射线是由一个起点和一个方向确定的一段直线,具有以下特性:1. 射线只有一个起点,但是没有终点。
2. 射线是无限延伸的,可以一直延伸出去。
3. 射线只有一个确定的方向,无法逆转。
三、直线的定义与特性直线是由无数个点连成的轨迹,具有以下特性:1. 直线是无限延伸的,没有起点和终点。
2. 直线上的任意两点可以确定一条直线,直线上的所有点都在同一直线上。
3. 直线没有宽度,是一维的。
四、习题示例1. 以下图形中,哪些是线段、哪些是射线、哪些是直线?(插入图示:线段AB、射线CD、直线EF)解答:线段AB是一段有限长度的直线,射线CD是由一个起点C 和一个方向确定的直线,直线EF是一条无数个点连成的轨迹,没有起点和终点。
2. 两个线段的长度分别是5cm和8cm,它们的和是多少?(插入图示:线段AB=5cm,线段CD=8cm)解答:线段AB和CD的长度分别是5cm和8cm,它们的和是5cm+8cm=13cm。
3. 从一个点出发,向两个不同的方向延伸的直线叫做什么?(插入图示:起点O,向左延伸的直线AB,向右延伸的直线CD)解答:从一个点出发,向两个不同的方向延伸的直线称为射线。
在图中,直线AB是一条由起点O向左延伸的射线,直线CD是一条由起点O向右延伸的射线。
通过以上习题,我们可以加深对线段、射线、直线的理解,并能够熟练运用相关知识解决几何问题。
总结:线段、射线、直线是几何学中的重要概念,它们的定义和特性对于解决几何问题至关重要。
射线直线线段
● 线的认识:1、直线没有端点,可以向两端无限延长。
射线有一个端点,可以向一端无限延长。
线段有两个端点,不能延长。
2、射线和线段都可以看成是直线的一部分;线段可以量出长度,而直线不能。
3、由一点可以引出无数条射线;经过一点可以画无数条直线直线;经过两点只能画一条直线。
● 平行与垂直:4、在同一平面内不相交的两条直线叫做平行线,也可以说这两条直线互相平行。
如果这两条直线相交成直角,这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
5、在同一平面内,两条直线的位置关系只有两种:一、平行;二、相交。
当两条直线相交成直角时,这两条直线互相垂直,它们的交点叫做垂足。
6、如果两条直线相交有一个角是直角,其它三个角也是直角。
7、两条直线都和一条直线平行,这两条直线互相平行。
8、与一条直线平行的线有无数条,与一条直线垂直的有无数条。
9、右图中,L1是L2的平行线,L3是L1的垂线,也是L2的垂线。
10、我们可以用三角尺画垂线,用直尺和三角尺画平行线。
11、从直线外一点到这条直线所画的垂直线段最短,它的长度叫做这点到直线的距离。
12、从直线外一点到这条直线可以画无数条线段,垂线段最短。
13、过直线外一点可以画一条直线与这条直线垂直,可以画无数条直线与这条直线相交。
14、两条平行线之间的距离:处处相等并且互相平行。
15、长方形的对边是互相平行的,邻边是互相垂直的。
● 角的分类、度量、画24、角可以分为:锐角、直角、钝角、平角、周角五大类。
按从小到大的顺序排列是:锐角〈 直角 〈 钝角 〈 平角 〈 周角锐角——小于90度;直角——等于90度;钝角——大于90度,小于180度;平角——等于180度;周角——等于360度。
25、1周角= 2平角= 4直角 = 8个45度13、用直尺和三角尺画平行线的一般步骤:(1)固定三角尺,沿一条直角边先画一条直线;(2)用直尺紧靠三角尺的另一条直角边,固定直尺,然后平移三角尺;(3)再沿第一步中的直角边画出另一条直线。
直线、射线和线段有什么区别和联系
直线、射线与线段的区别和联系
直线是最基本的线,现实生活中我们看不到完整的直线,我们只能想象,想象直线是可以向两方无限延伸的,没有粗细的,只存于我们头脑中的抽象的线。
几何中直线没有端点,不可度量,谈不上长度。
我们平时画直线实际只是画出了直线的一部分,尽管画的是有限部分,但必须想象它是无限延伸的,因此,画直线时,所画部分两头不要形成大圆点。
射线可以看做直线的一部分,射线有一个端点,并可以向一方无限延伸。
射线也没有长度,不能度量。
直线上两点间的部分叫做线段,线段有两个端点,可以度量。
线段有长度,能比较大小,进行计算。
线段、射线与直线是部分与整体关系,也就是说线段、射线是直线的一部分。
在直线上取一点把直线分成两条射线,取两点把直线分成一条线段和两条射线,把射线反向延长或线段向两方延长就可以得到直线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线段的一端无限延长后就是一条射线,射线只有 一个端点。
说一说:
在生活中还看到过哪些射线?
手电筒的光线可以看成射线。
探照灯的光线可以看成射线。
汽车的灯光也可以看作是射线。
画一画: 过一点能画多少条射线?
过一点能画无数条射线
如果把线段的两端无限延长 请问: (1)这条线有几个端点? (2)这条线可以画完吗? (3)这条线是否可以度量?
线段的两端无限延长后就是一条直线,直线 没有端点。
说一说:
在生活中还看到过哪些直线?
画一画
过一点可以画多少条直线? 过两点又可以画多少条直线?
过一点可以画无数条直线。 过两点只能画一条直线。
议一议
线段、射线、直线有什么区别?
线段、射线和直线之间的区别 端点 个数 2 1 可否无限延长
两端不可以无限延长 一端可以无限延长
线段、直线和射线
能把这些线分成两类吗?
直的
弯的
黑板的一边可以看成是一条线段,线段有两个端点。
说一说:
在生活中还看到过哪些线段?
画一画: 两点间还可以怎样画线?
在两点之间可以画出很多条线,其中线段最短, 线段的长度就是这两点间的距离。
如果把线段的一端无限延长, 请问: (1)这条线有几个端点? (2)这条线可以画完吗? (3)这条线是否可以度量?
小结
今天,你收获了什么?
思考题
在下面图中可以数出几条线段?
10条线段
作业(做在书上)
• 课本P62,练习十二,1,2,3题。
图形
可否度量 可度量 不可度量
以无限延 长
不可度量
1. 在下图中,哪些是线段?哪些是直线?哪些是射线?
直线
射 线
线段
线段
射线
2. 判断下列说法对不对。如果有错,请指出错在哪里。 (1)直线只有一个端点。(× ) (2)把线段两端无限延长后是一条射线。( × ) (3)一条射线长5cm 。 ( × ) (4)直线比射线长。 (×) 3. 画一画。 (1)画一条3cm长的线段。 (2)以下面的点为端点画两条射线。
