第2章轴对称图形题型专项训练-苏科版八年级数学上册期末复习
八年级数学上册第2章轴对称图形章末回顾与整合提升习题课件新版苏科版
解：如图，点 P 即为所求.
1
2
3
4
5
6
7
8
9
10
11
12
线上.∴ AD 垂直平分 EF .
1
2
3
4
5
6
7
8
9
10
11
12
判定2角平分线的判定
9. 【新考法·构造全等三角形法】如图， CB ＝ CD ，∠ D ＋
∠ ABC ＝180°， CE ⊥ AD 于点 E . 若∠ BAD ＝40°，
则∠ CAB 为
20° .
1
2
3
4
5
6
7
8
9
10
11
12
判定3等腰(等边)三角形的判定
性质3角平分线的性质
5. [2024苏州立达中学月考]如图，在△ ABC 中， AD 平分
∠ BAC ， DE ⊥ AB 于点 E ， S△ ABC ＝21， DE ＝3， AB ＝
6，则 AC 的长是
1
2
.
8
3
4
5
6
7
8
9
10
11
12
性质4等腰三角形的性质
6. [2023高邮一模]如图， AB ＝ AC ＝ AD ，若 AD ∥ BC ，
第2章
轴对称图形
章末回顾与整合提升
考点1
两个概念
概念1轴对称图形
1. [2023连云港]在美术字中，有些汉字可以看成是轴对称图
形.下列汉字中，是轴对称图形的是(
A. 我
B. 爱
C. 中
D. 国
1
苏科版数学八年级上册第2章轴对称图形章末重难点题型(举一反三)(原卷版)
轴对称图形章末重难点题型汇编【举一反三】【苏科版】【考点1 判断轴对称图形】【方法点拨】掌握轴对称图形的概念：把一个图形沿着某一条直线翻折，如果直线两旁的部分能够互相重合，那么称这个图形是轴对称图形，这条直线就是对称轴。
注意：理解轴对称图形的定义应注意两点：（1）轴对称图形是一个图形，反映的是这个图形自身的性质。
（2）符合要求的“某条直线”可能不止一条，但至少要有一条。
【例1】（2019春•相城区期中）下列图形中，不是轴对称图形的是（）A．B．C．D．【变式1-1】（2018秋•思明区校级期中）如图，四个手机应用图标中是轴对称图形的是（）A．B．C．D．【变式1-2】（2018秋•开封期中）下列四个图形中，不是轴对称图形的是（）A．B．C．D．【变式1-3】（2018秋•宜兴市校级期中）下列图形中，不是轴对称图形的有（）A．1个B．2个C．3个D．4个【考点2 角平分线的应用】【方法点拨】掌握角平分线的性质定理：角平分线上的点到角两边的距离相等牢记：（1）角平分线的性质是证明线段相等的一个比较简单的方法；（2）当遇到有关角平分线的问题时，通常过角平分线上的点向角的两边作垂线，构造相等的线段。
【例2】（2019春•港南区期中）如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于D，DE ⊥AB于E，若AB＝6cm，则△DBE的周长是（）A．6 cm B．7 cm C．8 cm D．9 cm【变式2-1】（2018秋•九龙坡区校级期中）如图，AD是△ABC的角平分线，DE⊥AB于E，已知△ABC的面积为28．AC＝6，DE＝4，则AB的长为（）A．6B．8C．4D．10【变式2-2】（2018秋•思明区校级期中）如图，△ABC中，AB＝6，AC＝4，AD平分∠BAC，DE⊥AB于点E，BF⊥AC于点F，DE＝2，则BF的长为（）A．3B．4C．5D．6【变式2-3】（2018秋•西城区校级期中）如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC ＝24，DE＝4，AB＝7，则AC长是（）A．3B．4C．6D．5【考点3 线段垂直平分线性质的应用】【方法点拨】掌握线段垂直平分线的性质定理：线段垂直平分线上的点到线段两端的距离相等注意：（1）这里的距离指的是点与点之间的距离，也就是两点之间线段的长度。
苏科版八年级上册数学第二章 轴对称图形 含答案
苏科版八年级上册数学第二章轴对称图形含答案一、单选题(共15题，共计45分)1、如图，有一张直角三角形纸片，两直角边AC＝6cm，BC＝8cm，将△ABC折叠，使点B与点A重合，折痕为DE，则CD等于( )A. cmB. cmC. cmD. cm2、下列各图经过折叠不能围成一个正方体的是（）A. B. C. D.3、以下国产新能源电动车的车标图案不是轴对称图形的是（）A. B. C. D.4、如图，∠XOY＝90°，OW平分∠XOY，PA⊥OX，PB⊥OY，PC⊥OW．若OA＋OB ＋OC＝1，则OC＝（）A.2－B. －1C.6－D. －35、如图，等边△ABC的边长为3，P为BC上一点，且BP＝1，D为AC上一点，若∠APD＝60°，则CD的长为（）A. B. C. D.6、如图，有一块Rt△ABC的纸片，∠ABC= ，AB＝6，BC＝8，将△ABC沿AD折叠，使点B落在AC上的E处，则BD的长为( )A.3B.4C.5D.67、在螳螂的示意图中，AB//DE，△ABC是等腰三角形，∠ABC＝124°，∠CDE＝72°，则∠BCD＝（）A.16°B.28°C.44°D.45°8、如图，已知中，DE、FG分别是AB，AC边上的垂直平分线，，，则的度数是（）A.10°B.20°C.30°D.40°9、将矩形纸片ABCD按如图所示的方式折叠，AE、EF为折痕，∠BAE＝30°，BE＝1，折叠后，点C落在AD边上的C处，并且点B落在EC1边上的B1处．则1EC的长为（）A. B.2 C.3 D.210、已知实数满足，则以的值为两边的等腰三角形的周长是（）A.10B.8或10C.8D.以上都不对11、如图，在△ABC中，点D在AB上，且CD=CB，点E为BD的中点，点F为AC的中点，连结EF交CD于点M，连接AM．若∠BAC=45°，AM=4，DM=3，则BC 的长度为（）A.8B.7C.6D.512、如图，AB是⊙O的直径，点E是AB上一点，过点E作CD⊥AB，交⊙O于点C，D，以下结论正确的是（）A.若⊙O的半径是2，点E是OB的中点，则CD＝B.若CD＝，则⊙O的半径是1 C.若∠CAB＝30°，则四边形OCBD是菱形 D.若四边形OCBD是平行四边形，则∠CAB＝60°13、如图，在矩形ABCD中，AB＝6，BC＝8，E是BC边上一点，将矩形沿AE折叠，点B落在点B'处，当△B'EC是直角三角形时，BE的长为（）A.2B.6C.3或6D.2或3或614、如图，在矩形ABCD中，E是CD边的中点，且BE⊥AC于点F，连接DF，则下列结论错误的是（）A.△ADC∽△CFBB.AD＝DFC. ＝D. ＝15、如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于AB的长为半径画弧，两弧相交于C，D，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是（）A.矩形B.菱形C.正方形D.等腰梯形二、填空题(共10题，共计30分)16、如图，把一张上下两边平行的纸条沿EF折叠，若∠2=132°，则∠1=________.17、如图，等腰三角形中，，是底边上的高，则AD=________.18、若等腰三角形的底角等于15°,腰长为4cm,则等腰三角形的面积为________.19、如图，在△ABC中，，，AD是BC边上的中线，将△ACD沿AD折叠，使点C落在点F处，DF交AB于点E，则∠DEB＝________.20、如图，在同一平面内，将边长相等的正三角形和正六边形的一条边重合并叠在一起，则∠1的度数为________．21、如图，在△ABC中，AB=AC=3cm，AB的垂直平分线交AC于点N，△BCN的周长是5cm，则BC的长等于________ cm．22、如图，∠A=15°，∠C=90°，DE垂直平分AB交AC于E，若BC=4cm，则AC=________cm．23、如图，在△ABC中，∠ACB=90°，CD是△ABC的中线，若∠DCB=40°，则∠A的度数为________ °．24、如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE．将△ADE沿AE 对折至△AFE，延长EF交边BC于点G，连接AG、CF．下列结论：①△ABG≌△=3．其中正确结论的是________．AFG；②BG=GC；③AG∥CF；④S△FGC25、如图，将一张长方形的纸片ABCD沿AF折叠，点B到达点B′的位置．已知AB′∥BD，∠ADB=20°，则∠BAF=________．三、解答题(共5题，共计25分)26、已知：如图，在△ABC中，AB=AC，点D，E在边BC上，且BD=CE．求证：AD=AE．27、在Rt△ABC中，∠C=90°，DE是AB的垂直平分线，且∠BAD：∠BAC=1：3，求∠B的度数．28、如图所示，沿AE折叠矩形，点D恰好落在BC边上的点F处，已知AB=8cm，BC=10cm，求EC的长．29、如图，在等腰△ABC中，AB=AC，AH⊥BC，点E是AH上一点，延长AH至点F，使FH=EH,求证：四边形EBFC是菱形.30、（1）如图1，△ABC中，∠C=90°，AB的垂直平分线交AC于点D，连接BD．若AC=2，BC=1，求△BCD的周长为；（2）O为正方形ABCD的中心，E为CD边上一点，F为AD边上一点，且△EDF 的周长等于AD的长．①在图2中求作△EDF（要求：尺规作图，不写作法，保留作图痕迹）；②在图3中补全图形，求∠EOF的度数；③若，求的值参考答案一、单选题(共15题，共计45分)1、C2、D3、C4、B5、B6、A7、A8、B9、B10、A11、B12、C13、C14、C15、B二、填空题(共10题，共计30分)16、17、19、20、21、23、24、25、三、解答题(共5题，共计25分)26、27、29、。
苏科版八年级上册数学第二章 轴对称图形含答案(满分必备)
苏科版八年级上册数学第二章轴对称图形含答案一、单选题(共15题，共计45分)1、下列命题是真命题的是（）．A.有两条边、一个角相等的两个三角形全等。
B.等腰三角形的对称轴是底边上的中线。
C.全等三角形对应边上的中线相等。
D.有一个角是60°的三角形是等边三角形。
2、如图所示，△ABC是等边三角形，且BD＝CE，∠1＝15°，则∠2的度数为（）A.15°B.30°C.45°D.60°3、有一张平行四边形纸片ABCD，已知，按如图所示的方法折叠两次，则的度数等于（）A.55°B.50°C.45°D.40°4、到△ABC三个顶点距离相等的点是△ABC的（）A.三条角平分线的交点B.三条中线的交点C.三条高的交点D.三条垂直平分线的交点5、在下列汽车标志中，既是轴对称图形，又是中心对称图形的是（）A. B. C. D.6、如图，在△ABC中，AB＞AC，分别以点B和点C为圆心，大于BC一半的长为半径作圆弧，两弧相交于点M和点N，作直线MN交AB于点D；连结CD.若AB＝7，AC＝5，则△ACD的周长为（）A.2B.12C.17D.197、剪纸是我国传统的民间艺术，下列剪纸作品中，是轴对称图形的为（）A. B. C. D.8、△BDE和△FGH是两个全等的等边三角形，将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长，则只需知道（）A.△ABC的周长B.△AFH的周长C.四边形FBGH的周长D.四边形ADEC的周长9、如图，C、D在以线段AB为直径的⊙O上，若CA=CD，且∠ACD=40°，则∠CAB=（）A.10°B.20°C.30°D.40°10、已知AB=8cm，小红在作线段AB的垂直平分线时操作如下：分别以A和B 为圆心，5cm的长为半径画弧，两弧相交于C、D，则直线CD即为所求，根据此种作图方法所得到的四边形ADBC的面积是（）A.12cm 2B.24cm 2C.36cm 2D.48cm 211、如图，AB∥CD，AB＝AC，∠1＝40°，则∠ACE的度数为（）A.80°B.100°C.120°D.160°12、如图，把一矩形纸片OABC放入平面直角坐标系xoy中，使OA，OC分别落在x轴、y轴上，现将纸片OABC沿OB折叠，折叠后点A落在点A'的位置，若OA=1，OB=2，则点A'的坐标为（）A. B. C.（） D.（）13、将AD与BC两边平行的纸条ABCD按如图所示折叠，则∠1的度数为（）A.72°B.45°C.56°D.60°14、如图，△ABC中，∠ABC＝45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，DH⊥BC于H交BE于G.下列结论：①BD＝CD；②AD+CF＝BD；③CE＝BF；④AE＝BG.其中正确的个数是（）A.1个B.2个C.3个D.4个15、如图，等边的边长为3，点D在边上，，线段在边上运动，，有下列结论：① 与可能相等；② 与可能相似；③四边形面积的最大值为；④四边形周长的最小值为.其中，正确结论的序号为（）A.①④B.②④C.①③D.②③二、填空题(共10题，共计30分)16、某同学从平面镜里看到镜子对面的电子钟的示数如图所示，这时的实际时间是________.17、如图，在△ABC中，已知∠B=∠C，则可判定AB=AC的依据是________；18、如图，矩形ABCD中，把△ACD沿AC折叠到△ACD′，AD′与BC交于点E，若AD=8，DC=6，则BE的长为________．19、在矩形ABCD中，AB＝8，BC＝10，E是AB上一点，将矩形ABCD沿CE折叠后，点B落在AD边的点F上，则折痕CE的长为________.20、已知点在直线上，点在直线上，与关于y轴对称．则和的交点坐标为________．21、如图，矩形纸片ABCD，AD=2AB=4，点F在线段AD上，将△ABF沿BF向下翻折，点A的对应点E落在线段BC上，点M，N分别是线段AD与线段BC上的点，将四边形CDMN沿MN向上翻折，点C恰好落在线段BF的中点C'处，则线段MN的长为________．22、如图，BE⊥AC，垂足为D，且AD＝CD，BD＝ED.若∠ABC＝54°，则∠E＝________°.23、如图，△ABC中，已知AB=5，AC=4，AD平分∠BAC交BC于D，DE⊥AC交AC于点E，若DE=2，则△ABC的面积为________．24、如图，在⊙O中，半径为5，∠AOB=60°，则弦长AB=________．25、把一张长方形纸条按如图方式折叠，若∠1＝40°，则∠2的度数是________．三、解答题(共5题，共计25分)26、如图所示，△ABC和△AEF为等边三角形，点E在△ABC内部，且E到点A，B，C的距离分别为3，4，5，求∠AEB的度数．27、如图，在长方形ABCD中，已知AB=8cm，BC=10cm，将AD沿AF折叠，使点D落在BC上的点E处.求BE及CF的长.28、作图题：（要求保留作图痕迹，不写作法）（1）作△ABC中BC边上的垂直平分线EF（交AC于点E，交BC于点F）；（2）连结BE，若AC=10，AB=6，求△ABE的周长．29、如图，在中，AB＝AC，点D是BC上一点，点E是AC上一点，且DE⊥AD.若∠BAD＝55°，∠B＝50°，求∠DEC的度数.30、如图，△ABC中，AB＝AC，∠BAC＝120°，AD⊥AC交BC于点D，求证：BC ＝3AD．参考答案一、单选题(共15题，共计45分)1、C2、D3、B4、D5、A6、B7、D8、A9、B10、B11、B12、B13、C14、C15、D二、填空题(共10题，共计30分)16、17、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)28、。
八年级数学上册第2章轴对称图形专题训练4三线合一知一推二习题课件新版苏科版
专题训练4
轴对称图形
三线合一
知一推二
一
等腰＋中点
1. 如图，在△ ABC 中， AB ＝ AC ， D 是 BC 的中点， BE ⊥
AC 于点 E . 求证：∠ BAC ＝2∠ EBC .
证明：∵ AB ＝ AC ， D 是 BC 的中点，
∴ AD ⊥ BC ，∠ BAC ＝2∠ DAC ，
∴∠ ADC ＝90°，∵ BE ⊥ AC ，
∴∠ BEC ＝90°，∴∠ DAC ＝∠ EBC ，
∴∠ BAC ＝2∠ EBC .
1
2
3
4
5
6
7
8
2. 如图，在△ ABC 中， AB ＝ AC ，点 D 是 BC 的中点，过
点 A 作 EF ∥ BC ，且 AE ＝ AF . 求证：
(1) DE ＝ DF ；
∴△ BDG ≌△ CDH (ASA)，∴ BG ＝ CH .
1
2
3
4
5
678二源自等腰＋高3. 如图，△ ABC 中， AB ＝ AC ， AD ⊥ BC ，垂足为点 D ，
DE ∥ AC ，求证： AE ＝ DE .
证明：∵ AB ＝ AC ， AD ⊥ BC ，
∴∠ BAD ＝∠ CAD .
∵ DE ∥ AC ，∴∠ EDA ＝∠ CAD .
1
2
3
4
5
6
7
8
证明：(1)如图，连接 AD ，∵ AB ＝
AC ，点 D 为 BC 的中点，∴ AD ⊥
BC ，∴∠ ADB ＝90°，∵ EF ∥ BC ，
∴∠ DAF ＝∠ ADB ＝90°，∴ AD ⊥
EF ，∵ AE ＝ AF ，∴ AD 垂直平分
苏科版八年级上册第2章轴对称图形基础证明题专项训练(Word版,无答案)
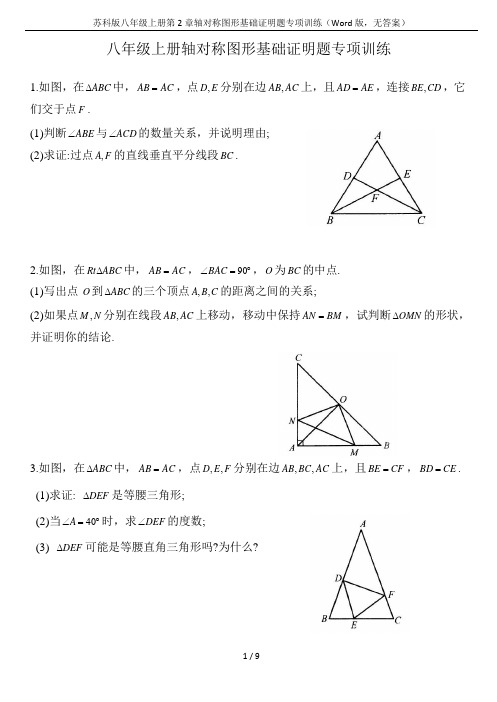
苏科版八年级上册第2章轴对称图形基础证明题专项训练（Word版，无答案）八年级上册轴对称图形基础证明题专项训练1.如图，在∆ABC 中，AB =AC ，点D, E 分别在边AB, AC 上，且AD =AE ，连接BE,C D ，它们交于点F .(1)判断∠ABE 与∠ACD 的数量关系，并说明理由;(2)求证:过点A, F 的直线垂直平分线段BC .2.如图，在Rt∆ABC 中，AB =AC ，∠BAC =90︒，O 为BC 的中点.(1)写出点O 到∆ABC 的三个顶点A, B,C的距离之间的关系;(2)如果点M , N 分别在线段AB, AC 上移动，移动中保持AN =BM ，试判断∆OMN 的形状，并证明你的结论.3.如图，在∆ABC 中，AB =AC ，点D, E, F 分别在边AB,BC,AC 上，且BE =CF ，BD =CE .(1)求证:∆DEF 是等腰三角形;(2)当∠A = 40︒时，求∠DEF 的度数;(3) ∆DEF 可能是等腰直角三角形吗?为什么?4.如图，设∠BAC =α ( 0︒<α<90︒)，用一些等长的小木棒，从点A1开始，向右依次摆放在两射线之间，并使小木棒的两端恰好分别落在射线AB, AC 上，其中A1A2为第一根小木棒，且AA1=A1 A2(1)若已经摆放了3 根小木棒，则α2= (用含α的式子表示);(2)若只能摆放4 根小木棒，求α的取值范围.5.如图，在∆ABC 中，AB =AC,AB 的垂直平分线DE 交AC 于点E,C E 的垂直平分线正好经过点B ，与AC 相交于点F ，求∠A 的度数.6.如图，在四边形ABCD 中，AD // BC ，E 是AB 的中点，连接DE 并延长交CB 的延长线于点F ，点G 在边BC 上，且∠GDF =∠ADF .(1)求证: ∆ADE ≅∆BFE ;(2) 连接EG ，判断EG 与DF 的位置关系并说明理由.7.如图，在∆ABC 中，AB =AC,D,E 是边BC 上的点，连接AD, AE ，以∆ADE 的边AE 所在直线为对称轴作∆ADE 的轴对称图形∆AD'E ，连接D'C，若BD =CD'.(1)求证: ∆ABD ≅∆ACD' ;(2) 若∠BAC =120︒，求∠DAE 的度数.8.如图①，在等腰三角形ABC 中，AB =AC ，∠BAC <60︒，D 为∆ABC 外部的一点.在AB 的右侧作∠ABD =60︒，且∠ADB =∠ACB .(1)探究线AB 段、CD 和BD 的数量关系.(2)如图②，若将“∠A <60︒”改为“∠A >60︒”.(1)中的结论是否还成立?若成立.给出证明；若不成立，给出正确的结论.并简要说明理由.9.如图，在∆ABC 中，∠C =90︒，AB 的垂直平分线DE 交AC 于点D ，垂足为E ，连接BD ，若∠A =30︒，CD = 3 .求:(1) ∠BDC 的度数(2) AC 的长度.10.如图，在∆ABC 中，AB =AC ，D 是BC 边上一点，DE ⊥AB 于点E ，FD ⊥BC ，交AC 于点F ，G 是FC 的中点，连接GD .求证: GD ⊥DE .11.如图，在∆ABC 中，AB =AC ，BD 、CD 分别平分∠EBA 、∠ECA，BD 交AC 于点F ，连接AD .(1)直接写出∠BDC 与∠BAC 之间的关系式;(2)求证: ∆ABD 为等腰三角形;(3)当∠EBA的大小满足什么条件时，以A 、B 、F 为顶点的三角形为等腰三角形?12.如图，△ABC、△CDE 均为等边三角形，连接BD、AE 交于点O，BC 与AE 交于点P．求证：（1）求证：AE=BD；（2）求∠AOB 的度数．13.已知：如图，在 Rt △ACB 中，∠ACB=90°，点 D 是 AB 的中点，且 CD= 12AB ，点 E 是 CD 的中点，过点 C 作 CF ∥AB 交 AE 的延长线于点 F ．（1）求证：△ADE ≌△FCE ；（2）若∠DCF=120°，DE=2，求 BC 的长．14.如图，在 ∆ABC 中，∠C = 90︒ ，AD 是∠BAC 的平分线，DE ⊥ AB 于点 E ，点 F 在 AC 上，BD = DF .求证:(1) CF = EB . (2) AB = AF + 2EB .15.如图，在 ∆ABC 中， BA = BC ，点 D 在边CB 上，且 DB = DA = AC . (1)如图①，填空∠B =，∠C =(2)若 M 为线段 BC 上的点，过 M 作直线 MH ⊥ AD 于点 H ，交直线 AB 、 AC 与点 N 、 E ，如图②.①求证: ∆ANE 是等腰三角形.②试写出线段 BN 、CE 、CD 之间的数量关系，并加以证明.16.如图，在∆ABC 中，AB =AC ，点D 、E 、F 分别在边AB 、BC 、AC 上，且BD =CE ，BE =CF ，如果点G 为DF 的中点，那么EG 与DF 垂直吗?17.如图，在∆ABC 中，AB =AC , D 、E 是BC 边上的点，连接AD 、AE ，以∆ADE 的边AE所在直线为对称轴作∆ADE 的轴对称图形∆AD'E ，连接D'C，若BD =CD'.(1)求证: ∆ABD ≅∆ACD' .(2)若∠BAC = 120︒，求∠DAE 的度数.18.如图①，∆ABC 和∆CDE 均为等腰三角形，AC =BC ，CD =CE ，AC >CD ，∠ACB =∠DCE 且点A 、D 、E 在同一直线上，连接BE .(1)若∠ACB = 60︒，则∠AEB 的度数为;线段AD 、BE 之间的数量关系是.(2)若∠ACB =n︒，用n 表示∠AEB 并说明理由.(3)如图②，若∠ACB =∠DCE =90︒, M 是DE 的中点.若CM =7，BE =10 ，试求AE 的长.(请写全必要的证明和计算过程)19.如图，∠ABC=90°，D，E 分别在BC，AC 上，A D⊥DE，且AD=DE，点F 是AE 的中点，FD 与AB 相交于点M．(1) 求证：∠FMC=∠FCM .(2) AD 与MC 垂直吗? 请说明理由．20.在△ABC 中，已知AC=BC，∠ACB=90°，点D 是AB 的中点，点E 是AB 边上一点(1) BF 垂直CE，垂足为点F，交CD 于点G (图1)，求证：AE=CG；(2) AH 垂直CE 的延长线，垂足为点H，交CD 的延长线于点M (图2)，找出图中与BE 相等的线段，并加以证明．21.如图，在R t△ABC 中，∠ACB=90°，AC=BC，D 为边BC 的中点，C E⊥AD，垂足为点E，BF∥AC 交CE 的延长线于点F，连接DF．求证：AB 垂直平分DF．22.如图，在△ABC 中，AB=AC，AD⊥BC，C E⊥AB，AE=CE．求证：(1) △AEF≌△CEB；(2) AF=2CD．。
第2章+轴对称图形+综合提优练习2024-2025学年苏科版八年级数学上册+
第2章《轴对称图形》综合提优练习一、选择题1．△ABC中，BC＝10，AB的垂直平分线与AC的垂直平分线分别交BC于点D，E，且DE ＝4，则AD+AE的值为（）A．6B．14C．6或14D．8或122．如图，在△ABC中，∠BAC＞90°，D为BC的中点，点E在AC上，将△CDE沿DE 折叠，使得点C恰好落在BA的延长线上的点F处，连接AD、CF，则图中所有的等腰三角形的个数为（）A．1B．2C．3D．43．如图，AD∥BC，点E是线段AB的中点，DE平分∠ADC，BC＝AD+2，CD＝7，则BC2﹣AD2的值等于（）A．14B．9C．8D．54．如图，四边形ABCD中，AB＝AD，BC＝BD，若∠ABD＝∠BAC＝α，则∠BDC的度数为（）A．2αB．45°+αC．90°﹣αD．180°﹣3α5．如图，∠BAC＝30°，AP平分∠BAC，GF垂直平分AP，交AC于F，Q为射线AB上一动点，若PQ的最小值为3，则AF的长为（）A．3B．6C．3D．96．如图，等腰直角三角形ABC中，∠BAC＝90°，D、E分别为AB、AC边上点，AD＝AE，AF⊥BE交BC于点F，过点F作FG⊥CD交BE的延长线于点G，交AC于点M．以下四个结论：①△ADC≌△AEB；②∠AEG＝∠CDB；③△EGM是等腰三角形；④BG＝AF+FG；恒成立的结论有（）A．①②③④B．①③C．②③④D．①②④二、填空题7．如图，AE是∠CAM的角平分线，点B在射线AM上，DE是线段BC的中垂线交AE于E，过点E作AM的垂线交AM于点F．若∠ACB＝28°，∠EBD＝25°，则∠AED ＝°．8．如图，在△ABC中，∠C＝60°，AC＝5，BC＝4，点D为CB延长线上一点．当点D 在CB延长线上运动时，AD﹣BD的最小值为．9．如图，线段OM⊥ON，O为垂足，一把角尺的直角顶点A在线段OM上，端点B在线段ON上，已知ON＝AB＝4，AC＝2，当点B在从点O运动到点N的过程中，点C也随着运动，当线段OC最长时，∠BAO的度数为．10．如图，在Rt△ABC中，∠ACB＝90°，点D为斜边AB上的一点，连接CD，将△BCD 沿CD翻折，使点B落在点E处，点F为直角边AC上一点，连接DF，将△ADF沿DF 翻折，点A恰好与点E重合，则∠CEF的度数为．11．如图，∠ABC＝60°，AB＝4，动点P从点B出发，以每秒1个单位长度的速度沿射线BC运动，设点P的运动时间为t秒（t＞0），当△ABP为锐角三角形时，t的取值范围是．12．如图，AD是△ABC的中线，∠ADC＝60°，BC＝6，把△ADC沿直线AD折叠后，点C落在点E的位置上，连接BE，则BE的长是．13．如图，△ABC的边AB、AC的垂直平分线m、n相交于点D，连接CD，若∠1＝39°，则∠BCD的大小是度．14．如图，在△ABC中，∠ACB＝90°，S△ABC＝14，BC＝4，P是AB边上的动点（不与点B重合），将△BCP沿CP所在的直线翻折，得到△B′CP，连接B′A，则B′A长度的最小值是．三、解答题15．如图，已知线段a、b，请用无刻度的直尺和圆规作出特定的三角形：（1）求作一个等腰三角形，使得它的腰长为b，底边上的高为a．（2）求作一个三角形，使得它的两边长分别为a、b，第三边上的中线为c．16．如图，在等边三角形ABC中，D是AB上的一点，E是CB延长线上一点，连接CD、DE，已知∠EDB＝∠ACD．（1）求证：△DEC是等腰三角形．（2）当∠BDC＝5∠EDB，EC＝8时，求△EDC的面积．17．已知：A、B两点在直线l的同侧，试分别画出符合条件的点M．（不用写作法）（1）如图①，在l上求作一点M，使得AM+BM最小；（2）如图②，在l上求作一点M，使得|AM﹣BM|最小；（3）如图②，在l上求作一点M，使得|AM﹣BM|最大．18．如图钢架中，∠A＝20°，焊上等长的钢条来加固钢架，若AP1＝P1P2，问这样的钢条至多需要多少根？（1）请补充完整如下解答：解：由题意可知，P1P2＝P2P3＝P3P4＝P4P5＝…∵∠A＝20°，AP1＝P1P2，∴∠AP2P1＝．∴∠P2P1P3＝∠P1P3P2＝40°，同理可得，∠P3P2P4＝∠P2P4P3＝60°，∠P4P3P5＝∠P4P5P3＝．∴∠P5P4B＝100°＞90°，∴对于直线P4B上任意一点P6（点P4除外），P4P5＜P5P6，∴这样的钢条至多需要根．（2）继续探究：当∠A＝15°时，这样的钢条至多需要多少根？19．在探索三角形全等的条件时，老师给出了定长线段a，b，且长度为b的边所对的角为n°（0＜n＜90°）小明和小亮按照所给条件分别画出了图1中的三角形，他们把两个三角形重合在一起（如图2），其中AB＝a，BD＝BC＝b，发现它们不全等，但他们对该图形产生了浓厚兴趣，并进行了进一步的探究：（1）当n＝45时（如图2），小明测得∠ABC＝65°，请根据小明的测量结果，求∠ABD 的大小；（2）当n≠45时，将△ABD沿AB翻折，得到△ABD′（如图3），小明和小亮发现∠D′BC的大小与角度n有关，请找出它们的关系，并说明理由；（3）如图4，在（2）问的基础上，过点B作AD′的垂线，垂足为点E，延长AE到点F，使得EF＝（AD+AC），连接BF，请判断△ABF的形状，并说明理由．20．定义：如果1条线段将一个三角形分割成2个等腰三角形，我们把这条线段叫做这个三角形的“双等腰线”．如果2条线段将一个三角形分成3个等腰三角形，我们把这2条线段叫做这个三角形的“三等腰线”．如图1，BE是△ABD的“双等腰线”，AD、BE是△ABC的“三等腰线”．（1）请在图2三个图中，分别画出△ABC的“双等腰线”，并做必要的标注或说明．（2）如果一个等腰三角形有“双等腰线”，那么它的底角度数是．（3）如图3，△ABC中，∠C＝∠B，∠B＜45°．画出△ABC所有可能的“三等腰线”，使得对∠B取值范围内的任意值都成立，并做必要的标注或说明．（每种可能用一个图单独表示，如果图不够用可以自己补充）。
苏科版八年级数学上册第二章轴对称图形压轴题练习
2. 在 △ ������������������中,
,������������ = ������������,经过点 C 的直线 l 与 AB 平行,点 D 为直线 l 上
的动点(不与点 C 重合),作射线 DA,过点 D 作射线������������ ⊥ ������������,交直线 BC 于点 E．
(2) 如图 3,若������������ ≠ ������������,
,
BN 与 AB 的位置关系,并说明理由．
,点 M 在线段 AB 上运动,请判断
7. 如图在等腰▵������������������中,������������ = ������������ = 20������������,������������ = 16������������,
5. 在 △ ������������������中,������������ = ������������,
交直线 BC 于点 Q．
,P 为直线 AC 上一点,过点 A 作������������ ⊥ ������������于点 D,
(1)如图 1,当 P 在线段 AC 上时,求证：������������ = ������������；
������→������→������方向运动,且速度为每秒 2cm,它们同时出发,设出发的时间为 t 秒．
(1)出发 2 秒后,求 △ ������������������的面积；
(2)当点 Q 在边 BC 上运动时,出发几秒钟后, △ ������������������能形成等腰三角形？
(3)当点 Q 在边 CA 上运动时,求能使 △ ������������������成为等腰三角形的运动时间．
且在 CM 的下方(沿 CM 顺时针方向)作等腰直角三角形 CMN,
苏科版八年级数学上册 第二章 2.2 轴对称的性质练习题
苏科版八年级数学上册上册第二章 2.2 轴对称的性质一、单选题1.下列说法错误的是（）A. 关于某直线成轴对称的两个图形一定能完全重合B. 线段是轴对称图形C. 全等的两个三角形一定关于某直线成轴对称D. 轴对称图形的对称轴至少有一条2.如图，△ABC和△A′B′C′关于直线L对称，下列结论中符合题意的有（）⑴△ABC≌△A′B′C′⑵∠BAC=∠B′A′C′⑶直线L垂直平分CC′⑷直线BC和B′C′的交点不一定在直线L上．A. 4个B. 3个C. 2个D. 1个3.将一长方形纸片，按右图的方式折叠，BC，BD为折痕，则∠CBD的度数为( )A. 60°B. 75°C. 90°D. 95°4.如图,在△ABC中,AB=8，BC=6，AC=5，点D在AC上,连结BD,将△ABC沿BD折叠后,若点C恰好落在AB边上的点E处,则△ADE的周长为( )A. 5B. 6C. 7D. 85.如图，把一个正方形经过上折、右折、下方折三次对折后沿虚线剪下，则所得图形是（）A. B. C. D.6.如图，在△ABC中，∠C＝40°，将△ABC沿着直线l折叠，点C落在点D的位置，则∠1－∠2的度数是（）A. 40°B. 80°C. 90°D. 140°7.如图，把一长方形纸片ABCD沿EG折叠后，点A，B分别落在A′、B′的位置上，EA′与BC相交于点F，已知∠1=130°，则∠2的度数是（）A. 40°B. 50°C. 65°D. 80°8.如图，方格纸上有2条线段，请你再画1条线段，使图中的3条线段组成一个轴对称图形，最多能画（）条线段．A. 1B. 2C. 3D. 49.如图，图1是AD∥BC的一张纸条，按图1→图2→图3，把这一纸条先沿EF 折叠并压平，再沿BF折叠并压平，若图3中∠CFE=18°，则图2中∠AEF的度数为（）A.120°B.108°C.126°D.114°10.如图，在四边形 ABCD 中，∠C=70°，∠B=∠D=90°，E、F 分别是 BC、DC 上的点，当△AEF 的周长最小时，∠EAF 的度数为（）A. 30°B. 40°C. 50°D. 70°二、填空题11.如图，ΔABC是一个三角形纸片，其中AB=AC，∠A=36°，沿DE 折叠纸片，使点A落在点B处，则∠BEC= ________.12.将一个矩形纸片沿BC折叠成如图所示的图形，若∠ABC=27°，则∠ACD的度数为________．13.如图，点D、E分别在ΔABC的AB、AC边上，沿DE将ΔADE翻折，点A的对应点为点A′，∠A′EC=α，∠A′DB=β，且α<β，则∠A等于________(用含α、β的式子表示).14.如图,点P是直线AC外的一点,点D,E分别是AC,CB两边上的点,点P关于CA的对称点P1恰好落在线段ED上,P点关于CB的对称点P2落在ED的延长线上,若PE=2.5,PD=3,ED=4,则线段P1P2的长为________.15.如图，等边△ABC的边长为1cm，D、E分别是AB、AC上的点，将△ADE 沿直线DE折叠，点A落在点F处，且点F在△ABC外部，则阴影部分图形的周长为________cm.16.如图，△ABC的内部有一点P，且D，E，F是P分别以AB，BC，AC为对称轴的对称点.若△ABC的内角∠BAC＝70°，∠ABC＝60°，∠ACB＝50°，则∠ADB ＋∠BEC＋∠CFA＝________°.17.如图，在△ABC中，将∠C沿DE折叠，使顶点C落在△ABC内C′处，若∠A=75°，∠B=65°，∠1=40°，则∠2的度数为________．18.如图，在Rt△ABC中，∠C=90°，AB=5，AC=4，CB=3，点D是BC边上的点，将△ADC沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则△PEB的周长的最小值是________．19.如图，在三角形纸片ABC中，∠C＝90°，∠B＝30°，点D(不与B，C重合)是BC上任意一点，将此三角形纸片按如图的方式折叠，若EF的长度为a，则△DEF 的周长为________(用含a的式子表示)．20.如图，△ABC是边长为1的等边三角形，BD为AC边上的高，将△ABC折叠，使点B与点D重合，折痕EF交BD于点D1，再将△BEF折叠，使点B于点D1重合，折痕GH交BD1于点D2，依次折叠，则BDn= ________．三、综合题21.作出已知图形△ABC 关于给定直线 l 的对称图形△A'B'C'.22.如图,在△ABC中,AB=AC,DE是△ABE的对称轴,△BCE的周长为14,BC=6,求AB 的长.23.探索归纳：（1）如图1，已知△ABC为直角三角形，∠A=90°，若沿图中虚线剪去∠A，则∠1+∠2等于________；（2）如图2，已知△ABC中，∠A=40°，剪去∠A后成四边形，则∠1+∠2=________；（3）如图2，根据（1）与（2）的求解过程，请你归纳猜想∠1+∠2与∠A的关系是________；（4）如图3，若没有剪掉，而是把它折成如图3形状，试探究∠1+∠2与∠A的关系并说明理由.24.如图1，在△ABC中，∠A＜90°，P是BC边上的一点，P1， P2是点P关于AB、AC的对称点，连结P1P2，分别交AB、AC于点D、E.（1）若∠A＝52°，求∠DPE的度数；（2）如图2，在△ABC中，若∠BAC＝90°，用三角板作出点P关于AB、AC的对称点P1、P2，（不写作法，保留作图痕迹），试判断点P1， P2与点A是否在同一直线上，并说明理由.25.ABCD是长方形纸片的四个顶点，点E、F、H分别是边AB、BC、AD上的三点，连结EF、FH．（1）将长方形纸片的ABCD按如图①所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B′、C′、D′，点B′在F C′上，则∠EFH的度数为________；（2）将长方形纸片的ABCD按如图②所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B′、C′、D′（B′、C′的位置如图所示），若∠B′FC′=18°，求∠EFH的度数；（3）将长方形纸片的ABCD按如图③所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B′、C′、D′（B′、C′的位置如图所示），若∠EFH=β°，求∠B′FC′的度数为________．26.如图（1）如图1，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，①写出图中一对全等的三角形，并写出它们的所有对应角；②设∠AED的度数为x ，∠ ADE的度数为y，那么∠1，∠2的度数分别是多少？（用含有x或y的代数式表示）③∠A与∠1、∠2之间有一种数量关系始终保持不变，请找出这个规律．（2）如图2，把△ABC纸片沿DE折叠，当点A落在四边形BCDE外部时，∠A与∠1、∠2的数量关系是否发生变化？如果发生变化，求出∠A与∠1、∠2的数量关系；如果不发生变化，请说明理由.答案解析部分一、单选题1.【答案】 C【考点】轴对称的性质，轴对称图形解：A、关于某直线成轴对称的两个图形一定能完全重合，符合题意，故本选项不符合题意；B、线段是轴对称图形，符合题意，故本选项不符合题意；C、全等的两个三角形不一定关于某直线成轴对称，但关于某直线成轴对称的两个三角形一定全等，故本选项符合题意；D、轴对称图形的对称轴至少有一条，符合题意，故本选项不符合题意．故答案为：C．【分析】根据轴对称的概念以及性质对各选项分析判断即可得解．2.【答案】 B【考点】轴对称的性质解：∵△ABC和△A′B′C′关于直线l对称，∴①△ABC≌△A′B′C′，符合题意；②∠BAC=∠B′AC′，∴∠BAC+∠CAC′=∠B′AC′+∠CAC′，即∠BAC′=∠B′AC符合题意；③l垂直平分CC′，符合题意；④应为：直线BC 和B′C′的交点一定在l上，故本小题不符合题意．综上所述，结论正确的是①②③共3个．故答案为：B．【分析】轴对称的性质：①成轴对称的两个图形全等，②成轴对称的两个图形，对称点的连线被对称轴垂直平分，据此逐一判断即可.3.【答案】 C【考点】翻折变换（折叠问题）解：∵一张长方形纸片沿BC、BD折叠，∴∠ABC=∠A′BC，∠EBD=∠E′BD，而∠ABC+∠A′BC+∠EBD+∠E′BD=180°，=90°，∴∠A′BC+∠E′BD=180°× 12即∠CBD=90°.故答案为：C.【分析】根据折叠的性质得到∠ABC=∠A′BC，∠EBD=∠E′BD，再根据平角的定义有∠ABC+∠A′BC+∠EBD+∠E′BD=180°，易得A′BC+∠E′BD=180°× 12 =90°，则∠CBD=90°。
(黄金题型)苏科版八年级上册数学第二章 轴对称图形含答案
苏科版八年级上册数学第二章轴对称图形含答案一、单选题(共15题，共计45分)1、若线段AD，AE分别是△ABC的BC边上的中线和高线，则（）A.AD≥AEB.AD＞AEC.AD≤AED.AD＜AE2、如图，正三角形ABC的边长为3+ ，在三角形中放入正方形DEMN和正方形EFPH，使得D，E，F在边AB上，点P、N分别在边CB、CA上，设两个正方形的边长分别为m，n，则这两个正方形的面积和的最小值为（）A. B. C.3 D.3、下列图形“线段、角、等腰三角形、平行四边形、圆”，其中既是轴对称图形，又是中心对称图形的有（）A.2个B.3个C.4个D.5个4、下列篆字中，轴对称图形的个数有（）A.1个B.2个C.3个D.4个5、如图，点A在双曲线y=上，且OA=4，过A作AC⊥x轴，垂足为C，OA的垂直平分线交OC于B，则△ABC的周长为（）A.2B.4C.D.56、如图，Rt△ABC中，∠ABC的平分线交于，若，则点到的距离是（）A.5cmB.4cmC.3cmD.2cm7、如图，已知△ABC中，∠ABC＝45°，F是高AD和BE的交点，∠CAD＝30°，CD＝4，则线段BF的长度为（）A.6B.7C.8D.98、如图，Rt△ABC中，∠C=90°，∠B=45°，AD是∠CAB的平分线，DE⊥AB于E，AB=a，CD=m，则AC的长为（）A.2mB.a-mC.aD.a+m9、等腰三角形的周长为，其中一边长为，则该等腰三角形的底边长为（）A. 或B. 或C.D.10、如图，在中，，为的平分线，，则等于（）A. B. C. D.11、如图，矩形中，，，将此矩形折叠，使点B与点D 重合，折痕为，则的面积为（）A.12B.10C.8D.612、如图，△A BC是等边三角形，点D是BC边上任意一点，DE⊥AB于点E，DF⊥AC于点F，若等边三角形的高为4，则DE+DF＝（）A.1B.2C.3D.413、如图，AB=AC，BE⊥AC于点E，CF⊥AB于点F，BE、CF相交于点D，则①△ABE≌△ACF；②△BDF≌△CDE；③点D在∠BAC的平分线上．以上结论正确的是（）A.①B.②C.①②D.①②③14、下列图形中是轴对称图形,又是中心对称图形的是（）A. B. C. D.15、如图，在△ABC中，BD,CD分别平分∠ABC,∠ACB，过点D作直线平行于BC，交AB,AC于点E,F，当∠A的位置及大小变化时，线段EF和BE+CF的大小关系为（）A.EF＞BE+CFB.EF=BE+CFC.EF＜BE+CFD.不能确定二、填空题(共10题，共计30分)16、如图△ABC中，AD平分∠BAC，AB=4，AC=2，且△ABD的面积为3，则△ACD 的面积为________．17、如图，三角形纸片ABC中，AB＝AC，∠BAC＝120°，BC＝14cm，折叠纸片，使点C和点A重合，折痕与AC，BC交于点D和点E；则折痕DE的长为________.18、如图，O是等边△ABC内一点，OA=3，OB=4，OC=5，以点B为旋转中心，将线段BO逆时针旋转60°得到线段BO′，连接AO′.则下列结论：①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到；②连接OO′，则OO′=4；③∠AOB=150°；=6+4 .④S四边形AOBO′其中正确的结论是________.19、如图，△ABC与△A'B'C'关于直线l对称，且∠A=105°，∠C'=30°，则∠B的度数为________20、如图，将一张等边三角形纸片沿中位线剪成4个小三角形，称为第一次操作：然后，将其中的一个三角形按同样方式再剪成4个小三角形，共得到7个小三角形，称为第二次操作；再将其中一个三角形按同样方式再剪成4个小三角形，共得到10个小三角形，称为第三次操作；…根据以上操作，①第七次操作共得到________个三角形；②若要得到220个小三角形，则需要操作的次数是________．21、如图，在6×8的网格纸中，每个小正方形的边长都为1，动点P、Q分别从点D、A同时出发向右移动，点P的运动速度为每秒2个单位，点Q的运动速度为每秒1个单位，当点P运动到点C时，两个点都停止运动.运动时间t 为________秒时，△PQB成为以PQ为腰的等腰三角形.22、如图，把三角形纸片折叠，使点、点都与点重合，折痕分别为，，得到，若厘米，则的边的长为________厘米.23、已知，如图 AB=AC，∠BAC=40°，D 为 AB 边上的一点，过 D 作DF⊥AB，交 AC 于 E，交 BC 延长线于点 F 则∠F=________°.24、若二次函数的图像经过（2，0），且其对称轴为直线x=-1，则当函数值y>0成立时，x的取值范围是________.25、如图所示，在△ABC中，∠C = 90°，边AB的垂直平分线分别交AB，AC 边于点D,E,连结BE.若AB = 10，BC = 6，则△ACE的周长是 ________ .三、解答题(共5题，共计25分)26、如图，点M，N分别在正三角形ABC的BC，CA边上，且BM=CN，AM，BN交于点Q．求证：∠BQM=60°．27、已知，如图，BC>AB，AD=DC，BD平分∠ABC，求证：∠ A+∠ C=180°28、如图，已知AB=AC=AD，且AD∥BC，求证：∠C=2∠D．29、在△ABC中，∠C=90°，DE垂直平分斜边AB，分别交AB、BC于D、E，若∠CAE=∠B+30°，求∠AEC的度数。
苏科版八年级上册数学第二章 轴对称图形 含答案
苏科版八年级上册数学第二章轴对称图形含答案一、单选题(共15题，共计45分)1、已知二次函数y=－x2+x+6及一次函数y=－x+m,将该二次函数在x轴上方的图像沿x轴翻折到x轴的下方，图像的其余部分不变，得到一个新图像（如图所示）.当直线y=－x+m与新图像有4个交点时，m的取值范围是（）A. B. C. D.2、已知等腰三角形的一个角是100°，则它的底角是（）A.40°B.60°C.80°D.40°或100°3、如图，在▱ABCD中，CE平分∠BCD，交AB于点E，EA＝3，EB＝5，ED＝4.则CE的长是（）A.5B.6C.4D.54、如图，等圆⊙O1和⊙O2相交于A、B两点，⊙O1经过⊙O2的圆心O2，连接AO1并延长交⊙O1于点C，则∠ACO2的度数为（）A.60°B.45°C.30°D.20°5、已知坐标平面内一点A(2，1)，O为原点，B是x轴上一个动点，如果以点B，O，A为顶点的三角形是等腰三角形，那么符合条件的动点B的个数为（）A.2个B.3个C.4个D.5个6、如图，把一个长方形的纸片对折两次（折痕互相垂直），然后剪下一个角，为了得到一个锐角为60°的菱形，剪口与折痕所成的角的度数应为（）A.30°B.60°C.120°D.30°或60°7、观察下列图案，是轴对称而不是中心对称的是（）A. B. C. D.8、已知直线y=﹣x+3与坐标轴分别交于点A，B，点P在抛物线y=﹣（x ﹣）2+4上，能使△ABP为等腰三角形的点P的个数有（）A.3个B.4个C.5个D.6个9、如图，在△ABC中，AB=CB，∠B=120°，AC=8，AB边的垂直平分线交AB于D，交AC于E，BC边的垂直平分线交BC于F，交AC于G，则EG的长是（）A.8B.C.4D.10、下列图形中，既是轴对称图形又是中心对称图形的是( )A. B. C. D.11、如图，在△ABC中，BD是角平分线，∠A=∠CBD36°，则图中有等腰三角形（）A.3个B.2个C.1个D.0个12、下列图形中不是轴对称图形的是（）A. B. C. D.13、下列图形中，既是轴对称图形又是中心对称图形的是（）A. B. C. D.14、如图，在菱形OABC中，点B在x轴上，点A的坐标为（2，2 )，将菱形绕点O旋转，当点A落在x轴上时，点C的对应点的坐标为（）A. 或B.C.D.或15、腰长为10，一条中线长为6的等腰三角形的底边长为（）A.16B.8C.8或D.16或二、填空题(共10题，共计30分)16、如图，将菱形纸片ABCD折叠，使点A恰好落在菱形的对称中心O处，折痕为EF，若菱形ABCD的边长为2cm，∠A=120°，则EF=________cm．17、一个等腰三角形的两边长分别为3和7，这个三角形的周长是________．18、若（a﹣5）2+|b﹣9|＝0，则以a、b为边长的等腰三角形的周长为________.19、已知等腰三角形的一个外角为130°，则它的顶角的度数为________.20、如图为正三角形ABC与正方形DEFG的重叠情形，其中D、E两点分别在AB、BC上，且BD=BE．若AC=18，GF=6，则F点到AC的距离为________．21、等腰三角形一腰上的高与另一腰的夹角为，则这个等腰三角形的底角度数为________.22、如图，是斜边上的高，将沿折叠，点恰好落在边的中点处，则等于________．23、如图，在中，，，的垂直平分线分别交，于，，，则的长为________.24、如图，将长方形ABCD沿着对角线BD折叠，点C落在C'处，BC′交AD于点E.若AB=4cm，AD=8cm，则△BDE的面积等于________.25、在四边形ABCD中，∠A＝∠ABC＝90°，△BCD为等边三角形，且AD＝2,则四边形ABCD的周长为________三、解答题(共5题，共计25分)26、如图，在中，，点在边上，且，连接，若，求的度数．27、如图，在△ABC中，点D，E，F在边BC上，点P在线段AD上，若PE ∥AB，∠PFD=∠C，点D到AB和AC的距离相等．求证：点D到PE和PF的距离相等．28、如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，求△BCE的面积．29、（1）如图1，△ABC中，∠C=90°，AB的垂直平分线交AC于点D，连接BD．若AC=2，BC=1，求△BCD的周长为；（2）O为正方形ABCD的中心，E为CD边上一点，F为AD边上一点，且△EDF 的周长等于AD的长．①在图2中求作△EDF（要求：尺规作图，不写作法，保留作图痕迹）；②在图3中补全图形，求∠EOF的度数；③若，求的值30、已知如图，四边形中，，，求证：.参考答案一、单选题(共15题，共计45分)1、D2、A3、C5、C6、D7、A8、A9、D10、C11、A12、D13、B14、D15、D二、填空题(共10题，共计30分)16、17、18、19、21、22、23、24、25、三、解答题(共5题，共计25分)27、28、29、30、。
八年级数学上册第2章轴对称图形专题训练5等腰三角形角度计算的技巧习题课件新版苏科版
B1 C ，连接 BB1，设 CB1交 AB 于点 D ， A1 B1分别交
AB 、 AC 于点 E 、 F .
(1)在图中不再添加其他任何线段的情况下，请你找出一
对全等的三角形，并加以证明(△ ABC 与△ A1 B1 C 全等
分类讨论求角度
6. [2024张家港期末]等腰三角形一腰上的高与底边的夹角为
140° .
70°，则顶角的度数为
1
2
3
4
5
6
7
8
9
10
11
7. [2024无锡新吴区期末]在△ ABC 中， AB ＝ AC ， AB 的垂
直平分线与 AC 所在直线相交所得的锐角为30°，则底角
∠ B 的度数是
60°或30°
除外)；
1
2
3
4
5
6
7
8
9
10
11
解：(1)△ CBD ≌△ CA1 F . 理由如下：∵ AC ＝ BC ，
∠ ACB ＝90°，∴∠ A ＝∠ CBA ＝45°.
∵△ ABC 绕点 C 逆时针旋转α角(0°＜α＜90°)，得到
△ A1 B1 C ，∴ CA ＝ CA1，∠ A ＝∠ A1，∠ ACA1＝
∠ CDE ＝60°，∴∠ DAE ＝∠ DEA ＝60°，
∴△ ADE 是等边三角形.
1
2
3
4
5
6
7
8
9
10
11
(2)若 AD ＝ AE ，试求α与β之间的关系.
解：(2)∵ AB ＝ AC ，∴∠ B ＝∠ C ＝90°－ ∠ BAC .
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
苏科版八年级上册期末复习训练2：轴对称图形知识导图： I |成轴叶称的网个囲彫金爭| ~［点轴叶称的网个出审中•时应矗的遑銭就叶你轴•克年疋I 2.小亮同学以四种不同的方式连接正六边形ABCDEF 的两条对角线，连接后的情形如选 项中的图形所示，其中不是轴对称图形的是〔〕轴对称的性质 T 线段的对称性卜 轴对称图形-几种根本的轴对称图形 -1线段枪直平分线的性质T 线J 殳垂直平分线的抑定 应鱼习孑分线是它的对称轴I15亘五平分线上的点列线找两鵡的吧离相等I 应亟応丽相等的点在线段的參立平分线E ］ 角的对称性I ---- 〔用平分线所在直线是它的对丽 — 角平分线的硕］~隔平分线上的点到角两边的距诵耳］ I~I 角平分线的对乏］I 角的内部到角两边^离相茅的点在角的平分瓦上1 -等腰三角形的对称性_ —I 等腰亍角喊］——I 等腰三角形的性质I-［黑I L_|等腰三角形的判定|_|等角对等还 • 三角彩虑址L 的宁线、高峥顶角平分銭互相珂 T 等边三角形的对称性|~［^3条对称轴 等边三角形的杜质 L#等边三角形的判定|一 等边三角形的各内角都等于60。
| 三个用都相等的三角形是等边三角形| 有一个命爭于60。
的等腰三角形是寻边三用疝 ｛直角三角形的性质定理II 直角三用形斛边上的中线茅于斜边的一* 设计轴对称图案 专题一：轴对称和轴对称图形 1 •如下图的图标，是轴对称图形的是〔 〕3•如图，将AABC 沿直线DE 折叠后，使点A 与点C 重合，己知BC 二6, ABCD 的周长为4•如图，在AABC 中，AC 的垂直平分线分别交AC 、BC 于E 、D 两点，EC 二4, AABC 的 周长为23,那么ZiABD 的周长为〔〕 A. 13 B. 15 5•如图，在AABC 中，AB 二BC, ZABC=110° , AB 的垂直平分线DE 交AC 于点D,连接 BD,贝IJZABD 二 _____ ° •6.如图，在ZXABC 中，DE 是BC 的垂直平分线，垂足为E,交AC 于点D,假设AB 二6, AC 二9, 那么Z\ABD 的周长是 _ .专题三：等腰三角形的性质与判定A AA DB DC ADD7. ____________________________________ 在AABC中，ZA二40°,当ZC二时，AANC 为等腰三角形.8. 如图，己知三角形ABC为等边三角形，D为BC的中点，DE丄AC于点E,假设BC=4cm,那么CE的长为 __ cm.D C随堂小练习9. 己知P是AABC内点，连接PA、PB、PC,且PA二PB二PC,那么点P—定是〔〕A. AABC的三条中线的交点B. AABC的三条内角平分线的交点C. AABC的三条高的交点D. AABC的三边的中垂线的交点10. 以下命题：①两个全等三角形合在一起是一个轴对称图形；②等腰三角形对称轴是底边上的中线所在直线；③等边三角形一边上的高就是这边的垂直平分线；④一条线段可以看成是以它的垂直平分线为对称轴的轴对称图形.其中正确的命题有〔〕.A. 1个个个个12.ZAOB=30°，点P在ZAOB的内部，点R与P关于OA对称，点P?与点P关于OB对称，那么△ROP?是〔〕•A. 含30°角的直角三角形B. 顶角是30°的等腰三角形C. 等边三角形D. 等腰直角三角形22.如图，CD与BE互相垂直平分，AD丄DB, ZBDE二70。
,那么ZCAD二___13.如图，等边三角形ABC两条中线，BD、CE交于点6那么ZBOC二____14•如图，在正方形网格上有一个ADEF (顶点在格点上).(1) 画ADEF关于直线HG的轴对称图形；(2) 画ADEF的边EF上的高所在直线；(3) 假设网格上的最小正方形边长为1，求ADEF的面积•15.如图，等边三角形ABC中，D是AC的中点，E是BC延长线上的一点，且CE二CD, DF —BE,垂足为F,求证:BF=EF.26.如图，在AABC中，AB二AC, AD是Z^ABC的角平分线，EF垂直平分AC,分别交AC、AD、AB 于点E、0、F.假设ZCAD二20°,求ZOCD 的度数.17.如图，在11X11的正方形网格中，每个小正方形的边长都为2，网格中有一个格点AABC (即AABC的顶点都在格点上).(1)在图中作出AABC关于直线/对称的(要求A与B与B\, C与C|相对应)；(2)在直线/上找一点P，使得PA+PB最小.28.如图，在直角梯形ABCD中，ZABC=90° , AD〃BC, AB=BC, E是AB的中点，CE丄BD.(1) 求证：BE二AD；(2) 求证：AC是线段ED的垂直平分线；(3) ADBC是等腰三角形吗？并说明理由.19•最短路径问题:例：如下图，要在街道旁修建一个奶站，向A、B提供牛奶，奶站应建在什么地方, 才能使A、B到它的距离之和最短.居民区H解：只有A关于/的对称点A'与C、B在一直线上时，才能使AC+BCA关于直线“街道〞的对称点Z ,然后连接Z B,交“街道〞于点C,那么点C就是所求的点，如以下图.应用：如下图，点A是锐角ZMON内部任意一点，在ZMON的两边OM、ON上各取一点B、C,组成三角形，使三角形周长最小.〔1〕借助直角三角板在图中找出符合条件的点B和C；求三角形的最小周提优特训：最短路问题类型：运用轴对称性求解:L如图，ZAOB二—点P是ZAOC内的一定点，点M. N分别在OA、0B上移动，当厶PMN的周长最小时，ZMPN的值为〔〕C.180°-aD.18(T-2tz2.如图，在锐角三角形ABC中，ZACB二30° , AB=5, ZiABC的面积为23.〔1〕假设点P在AB边上且CP二3価，D、E分别为边AC、BC上的动点，求APDE 周长的最小值；〔2〕假设一只羊在AABC区域内，从路边AB某点出发跑到水沟边AC喝水，然后跑向路边BC吃草，再跑回出发点处休息，直接写出小羊所跑的最短路程.3.(1)如图(!■),在AB直线一侧有C、D两点，在AB上找一点P,使C、D、P三点组成的三角形周长最短，找出此点；(2) 如图(2),在ZAOB内部有一点P,是否在OA、0B上分别存在点E、F,使得E、F、P三点组成的三角形周长最短，找岀E、F两点；(3) 如图(3),在ZAOB内部有两点M、N,是否在OA、0B上分别存在点E、F, 使得E、F、M、N四点组成的四边形的周长最短，找出E、F两点.(2)0• MNAB(3)参考答案1. D2. D3. 94. B5. 356. 157. 40°或70°或100°8. 19. D10. B11. C12. 70°13. 12014. 〔1〕略〔2〕略〔3〕315. 在等边三角形ABC中，D是AC的中点，A ZDBC=-ZABC =- X60° =30° , ZACB=60° .2 2TCE 二CD,A ZCDE=ZETCE 二CDZCDE=ZE=30°/.BD=ED, ABDE为等腰三角形,又DF丄BE,・・・F是BE的中点，・•・ BF=EF.16. TAB二AC, AD是ZXABC的角平分线，/.AD 丄BC.VZCAD=20° ,・•・ ZACD二70°•・・EF垂直平分AC,・・・AO二CO,A ZACO=ZCAD=20° ,・•・ ZOCD=ZACD-ZACO=50°17. 略18. (1)如图，V ZABC=90° , BD±EC,A Zl+Z3=90° , Z2+Z3二90〞 ,Z1=Z2.TZABC二ZDAB二90° , AB二BC,・・・AD二BE.(2)如图，V ZABC=90° , AB=BC, A Z6=ZACB=45° . TE是AB的中点，/. EB=EA.由AD二BE,得AE=AD.VAD//BC,Z7=ZACB=45° ,•・・Z6二45° ,A Z6=Z7.由等腰三角形的性质，得EM二MD, AM丄DE.故AC是线段ED的垂直平分线.〔3〕ADBC是等腰三角形〔CD二BD〕.理由如下：由〔2〕得CD二CE.由〔1〕得CE二BDACD=BD•••△DCB是等腰三角形.19. 〔1〕作点A关于0M端点对称点A',关于ON的对称点A",连接A' A",与OM、ON相交于B、C两点，连接AB、AC, AABC即为所求.〔2〕此时线段A' A〃的长度即为周长的最小值，连接OA、OA‘、OA".由对称性知：ZA‘ OA" =60° .OA二OA'二OA" =10.A"为等边三角形，A' A"二OA'二OA" =10.・•・三角形的最小周长为10.提优特训：1. D2. 〔2〕如图〔2〕分别作点P关于AC的对称点G,关于BC的对称点H,连接GH分别交AC、BC于点D、E,连接PD、PE、CG、CH,那么APDE的周长的最小值GH的长. •・•点P、G关于AC对称A ZCCA=ZPCA, CG二CP•・•点P、H关于BC对称・•・ ZBCH二ZPCB, CH二CP・•・ CG 二CP 二CH 二3価ZACB 二30°A ZHCG=60°•••△CGH是等边三角形.•.CH=CG=3vl0•••△PDE的周长最小值为3価.〔2〕如图〔2〕,易知小羊所跑的路程即为的周长由〔1〕可知，△〞“!＜的周长的最小值为CM的长度当CM1AB时，CM的长度最小，那么△MNK的周长最小・••小羊所跑的最短路程为CM =乩=竺.AB 53. 〔1〕如图〔2〕,作点C关于直线AB的对称点C，,连接C' D交AB于点P,那么点P就是所要求的点.〔2〕如图〔2〕,作点P关于P关于0A的对称点C,关于OB的对称点D.,连接CD, 交OA 于点E, 0B于点F,那么点E、F就是所要求作的点.〔3〕如图〔3〕,作点M关于0A的对称点C,作点N关于0B的对称点D,连接CD, 交0A 于点E, 0B与点F,那么点E、F就是所要求作的点.。