编译原理第二章习题解答
编译原理第二版作业答案_第2章
第二章 文法和语言p48 4、6（6）、11、 12（2）（6）、18（2）4 证明文法G=（{E,O}，{(，)，+，*，v ，d}，P ，E ）是二义的,其中P 为 E → EOE | (E) | v | d O → + | * 证明：因为E=〉 EOE =〉EOEOE =〉EOEOv =〉EOE+v=〉EOv+v =〉E*v+v =〉v*v+v ， 句子v*v+v 有两棵不同的语法树所以文法G 是二义的。
问题：1）只有文字说明，比如v*v+v 有两棵语法树，但没有画出语法树或者最左（最右）推导过程2）给出的是不同句子（v*v+d v+v*d ）的语法树 6、已知文法G ：EEEE OO v*v+ vE EE E O O v+v* v〈表达式〉∷=〈项〉|〈表达式〉+〈项〉〈项〉∷=〈因子〉|〈项〉*〈因子〉〈因子〉∷=（〈表达式〉）| i试给出下述表达式的推导及语法树（6）i+i*i推导过程：〈表达式〉=〉〈表达式〉+〈项〉E=〉E+T =〉〈表达式〉+〈项〉*〈因子〉=〉E+ T*F=〉〈表达式〉+〈项〉* i =〉E+ T*i=〉〈表达式〉+ 〈因子〉* i =〉E+F*i=〉〈表达式〉+ i* i =〉E+i*i=〉〈项〉+ i* i =〉T +i*i=〉〈因子〉+ i* i =〉F +i*i=〉i +i*i =〉i +i*i 共8步推导语法树：〈表达式〉+〈因子〉〈项〉i 〈因子〉i〈项〉〈项〉〈因子〉i*11、一个上下文无关文法生成句子abbaa的推导树如下：（1）给出该句子相应的最左推导和最右推导（2）该文法的产生式集合P可能有哪些元素？（3）找出该句子的所有短语、简单短语、句柄。
（1）最左推导：S=〉ABS=〉aBS=〉aSBBS=〉aBBS=〉abBS=〉abbS =〉abbAa=〉abbaa最右推导：S =〉ABS=〉ABAa=〉ABaa=〉ASBBaa=〉ASBbaa=〉ASbbaa=〉Abbaa=〉abbaa（2）该文法的产生式集合P可能有下列元素：S→ABS | Aa|εA→a B→SBB|b（3）因为字符串中的各字符有相对的位置关系，为了能相互区别，给相同的字符标上不同的数字。
(完整word版)编译原理课后答案
第二章 高级语言及其语法描述4．令+、*和↑代表加，乘和乘幂，按如下的非标准优先级和结合性质的约定，计算1+1*2↑2*1↑2的值：（1） 优先顺序（从高至低）为+，*和↑，同级优先采用左结合。
（2） 优先顺序为↑，+，*，同级优先采用右结合。
解：（1）1+1*2↑2*1↑2=2*2↑1*1↑2=4↑1↑2=4↑2=16 （2）1+1*2↑2*1↑2=1+1*2*1=2*2*1=2*2=46．令文法G6为 N →D|NDD →0|1|2|3|4|5|6|7|8|9 （1） G6 的语言L （G6）是什么？（2） 给出句子0127、34和568的最左推导和最右推导。
解：（1）L （G6）=｛a|a ∈∑+,∑=﹛0,1,2,3,4,5,6,7,8,9｝｝（2）N ＝＞ND ＝＞ NDD ＝＞ NDDD ＝＞ DDDD ＝＞ 0DDD ＝＞ 01DD ＝＞ 012D ＝＞ 0127 N ＝＞ ND ＝＞ N7＝＞ ND7＝＞ N27＝＞ ND27＝＞ N127＝＞ D127＝＞ 0127 N ＝＞ ND ＝＞ DD ＝＞ 3D ＝＞ 34 N ＝＞ ND ＝＞ N4＝＞ D4 ＝＞34N ＝＞ ND ＝＞ NDD ＝＞ DDD ＝＞ 5DD ＝＞ 56D ＝＞ 568 N ＝＞ ND ＝＞ N8＝＞ ND8＝＞ N68＝＞ D68＝＞ 5687．写一个文法，使其语言是奇数集，且每个奇数不以0开头。
解：A →SN, S →+|-|∑, N →D|MDD →1|3|5|7|9, M →MB|1|2|3|4|5|6|7|8|9 B →0|1|2|3|4|5|6|7|8|9 8. 文法：E T E T E T TF T F T F F E i→+-→→|||*|/()| 最左推导:E E T T TF T i T i T F i F F i i F i i i E T T F F F i F i E i E T i T T i F T i i T i i F i i i ⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒⇒⇒⇒⇒⇒+⇒+⇒+⇒+⇒+⇒+********()*()*()*()*()*()*()最右推导:E E T E TF E T i E F i E i i T i i F i i i i i E T F T F F F E F E T F E F F E i F T i F F i F i i i i i ⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒⇒⇒⇒⇒+⇒+⇒+⇒+⇒+⇒+⇒+**********()*()*()*()*()*()*()*()语法树：/********************************EE FTE +T F F T +iiiEEFTE-T F F T -iiiEEFT+T F FTiii*i+i+ii-i-ii+i*i*****************/9．证明下面的文法是二义的：S → iSeS|iS|I解：因为iiiiei 有两种最左推导，所以此文法是二义的。
编译原理教程课后习题答案第二章
第二章 词法分析2.1 完成下列选择题：(1) 词法分析器的输出结果是。
a. 单词的种别编码b. 单词在符号表中的位置c. 单词的种别编码和自身值d. 单词自身值(2) 正规式M1和M2等价是指。
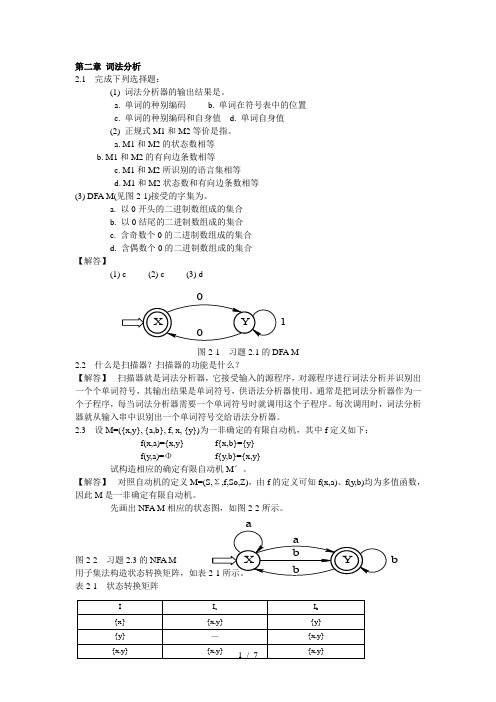
a. M1和M2的状态数相等b. M1和M2的有向边条数相等c. M1和M2所识别的语言集相等d. M1和M2状态数和有向边条数相等(3) DFA M(见图2-1)接受的字集为。
a. 以0开头的二进制数组成的集合b. 以0结尾的二进制数组成的集合c. 含奇数个0的二进制数组成的集合d. 含偶数个0的二进制数组成的集合【解答】(1) c (2) c (3) d图2-1 习题2.1的DFA M2.2 什么是扫描器？扫描器的功能是什么？【解答】 扫描器就是词法分析器，它接受输入的源程序，对源程序进行词法分析并识别出一个个单词符号，其输出结果是单词符号，供语法分析器使用。
通常是把词法分析器作为一个子程序，每当词法分析器需要一个单词符号时就调用这个子程序。
每次调用时，词法分析器就从输入串中识别出一个单词符号交给语法分析器。
2.3 设M=({x,y}, {a,b}, f, x, {y})为一非确定的有限自动机，其中f 定义如下：f(x,a)={x,y} f {x,b}={y}f(y,a)=Φ f{y,b}={x,y}试构造相应的确定有限自动机M ′。
【解答】 对照自动机的定义M=(S,Σ,f,So,Z)，由f 的定义可知f(x,a)、f(y,b)均为多值函数，因此M 是一非确定有限自动机。
先画出NFA M 相应的状态图，如图2-2所示。
图2-2 习题2.3的NFA M 用子集法构造状态转换矩阵，如表表2-1 状态转换矩阵1b将转换矩阵中的所有子集重新命名，形成表2-2所示的状态转换矩阵，即得到 M ′=({0,1,2},{a,b},f,0,{1,2})，其状态转换图如图2-3所示。
表2-2 状态转换矩阵将图2-3所示的DFA M ′最小化。
《编译原理》课后习题答案第二章
有代表性的符号串:a,a0,aa,a00,a0a,aa0
习题2
3.(1)E T T/F F/F (E)/F (E+T)/F (T+T)/F (F+F)/F (i+i)/i
(2)E E+T E+T+T E+T*F+F E+T*F+i E+T*T*F+i
M:M(0,a)=1 M(0,b)=2
M(1,a)=1 M(1,b)=4
M(2,a)=1 M(2,b)=3
M(3,a)=3 M(3,b)=2
M(4,a)=0 M(4,b)=5
M(5,a)=5 M(5,b)=1
化简：
1.分化
① {0,1} {2,3,4,5}
② {0,1} {2,4} {3,5}
2.合并
=M(M(D,1),1011)
=M(M(C,1),011)
=M(M(F,0),11)
=M(M(E,1),1)
=M(C,1)
=F
∴DFA D能接受字符串0011011
8.解：将状态转换图列表，即：
由左图可知，该状态转换图直接对应的是确定有穷状态自动机DFA
DFA D=（{0,1,2,3,4,5},{a,b},M,0,{0,1}）
A::=bc|bAc
(2)Z::=AB
A::=ab|aAb
B::=b|Bb
7. 解:题中要求文法是:
Z::=1|3|5|7|9|Z1|Z3|Z5|Z7|Z9|A1|A3|A5|A7|A9
A::=2|4|6|8|A0|A2|A4|A6|A8|Z0|Z2|Z4|Z6|Z8
编译原理第二版作业答案_第2章
第二章 文法和语言p48 4、6（6）、11、 12（2）（6）、18（2）4 证明文法G=（{E,O}，{(，)，+，*，v ，d}，P ，E ）是二义的,其中P 为 E → EOE | (E) | v | d O → + | * 证明：因为E=〉 EOE EOE = =〉EOEOE EOEOE==〉EOEOv EOEOv = =〉EOE+v=〉EOv+v EOv+v==〉E*v+v E*v+v = =〉v*v+v ， 句子v*v+v 有两棵不同的语法树所以文法G 是二义的。
问题：1）只有文字说明，比如v*v+v 有两棵语法树，但没有画出语法树或者最左（最右）推导过程2）给出的是不同句子（v*v+d v+v*d ）的语法树 6、已知文法G ：E E EE E OO v*v+ vE E E E E O O v+v* v〈表达式〉∷=〈项〉|〈表达式〉+〈项〉〈项〉 ∷=〈因子〉|〈项〉*〈因子〉〈因子〉 ∷=（〈表达式〉）| i试给出下述表达式的推导及语法树（6）i+i*i推导过程：〈表达式〉=〉〈表达式〉+〈项〉 E=〉E+T =〉〈表达式〉+〈项〉*〈因子〉 =〉E+ T*F=〉〈表达式〉+〈项〉* i =〉E+ T*i=〉〈表达式〉+ 〈因子〉* i =〉E+F*i=〉〈表达式〉+ i* i =〉E+i*i=〉〈项〉+ i* i =〉T +i*i=〉〈因子〉+ i* i =〉F +i*i=〉i +i*i =〉i +i*i 共8步推导语法树：〈表达式〉〈表达式〉+〈因子〉 〈项〉i 〈因子〉i〈项〉〈项〉 〈因子〉i*11、一个上下文无关文法生成句子abbaa 的推导树如下：（1）给出该句子相应的最左推导和最右推导 （2）该文法的产生式集合P 可能有哪些元素？ （3）找出该句子的所有短语、简单短语、句柄。
（1）最左推导：S=〉ABS=〉aBS=〉aSBBS=〉aBBS =〉abBS=〉abbS =〉abbAa=〉abbaa最右推导：S =〉ABS=〉ABAa=〉ABaa=〉ASBBaa =〉ASBbaa=〉ASbbaa=〉Abbaa=〉abbaa（2）该文法的产生式集合P 可能有下列元素：S →ABS | Aa|e A →a B →SBB|bSABSS B B a 1 a 3b 2 b 1 eAa 2（3）因为字符串中的各字符有相对的位置关系，为了能相互区别，给相同的字符标上不同的数字。
编译原理习题解答(第2-3章)_吴蓉
P41 27. 给 出 一 个 产 生 下 列 语 言 L （ G ） ＝ {W|W∈{a,b}*且W中含a的个数是b个数两倍的前 后文无关文法。 解：文法G=({S, A, B}, {a, b}, P, S) P: S::=AAB|ABA|BAA|ε A::=aS B::=bS 或者 S::=Saab|aSab|aaSb|aabS|Saba|aSba|abSa|abaS|Sbaa |bSaa|baSa|baaS|ε 或者 S::=aaB|aBa|Baa|ε B:？ 先构造其转换系统：
0 0 ε Z’ Z 1 A 0 S ε S’
根据其转换系统可得状态转换集、状态子集转换矩阵如下表 所示：(其中S’可以忽略，结果是一样的) I I0 I1 S 0 2 2 1 Ф 1
{S’, S}
{A} {A, Z, Z’}
{A}
{A, Z, Z’} {A, Z, Z’}
P41 29. 用扩充的BNF表示以下文法规则： (1) Z::=AB|AC|A (2) A::=BC|BCD|AXZ|AXY (3) S::=aABb|ab (4) A::=Aab|ε 解: (1) Z::=A（B|C|ε）::=A[B|C] (2) A::=BC （ ε|D ） |{X （ Z|Y ） }::= BC[D]|{X （ Z|Y ）} (3) A::=a((AB|ε)b) ::= a[AB]b (4) A::={ab|ε}::={ab}
DFA=（{S，A，Z}，{0，1}，M，S，{Z}） 其中M： M（S，0）=Z M（S，1）= A M（A，0）=Z M（Z，0）=Z M（Z，1）=A
该语言的正规文法G[Z]为： 右线性文法：//S :: =0|1A|0Z 左线性文法： A :: =0|0Z A :: =1|Z1 Z :: =0|1A|0Z Z :: =0|A0|Z0 若终止状态只引入不引出则适合构造右线性文法 ，若开始状态只引出不引入则适合构造左线性文 法，若终态和初态均既有引入又有引出，则构造 文法要注意。
编译原理习题解答(第2-3章)_吴蓉
P39 12.试分别构造产生下列语言的文法： 试分别构造产生下列语言的文法： 试分别构造产生下列语言的文法 （1）{ abna | n=0，1，2，3……} ） ， ， ， （3）{ aban | n≥1} ） （5）{ anbmcp | n，m，p≥0} ） ， ， 解： （1）G＝{VN，VT，P，S}，VN＝{S，A }，VT＝ ） ＝ ， ， ， ， {a，b}， ， ， P：S∷＝aAa ： ∷ 或 S∷＝aB ∷ A∷＝bA |ε B∷＝bB | a ∷ ∷ （3）G＝{VN，VT，P，S}，VN＝{S，A }，VT＝ ） ＝ ， ， ， ， {a，b}， ， ， P：S∷＝abA ： ∷ 或 S∷＝Sa | aba ∷ A∷＝aA | a ∷
P41 27. 给 出 一 个 产 生 下 列 语 言 L （ G ） ＝ {W|W∈{a,b}*且W中含 的个数是 个数两倍的前 中含a的个数是 ∈ 且 中含 的个数是b个数两倍的前 后文无关文法。 后文无关文法。 解：文法G=({S, A, B}, {a, b}, P, S) 文法 P: S::=AAB|ABA|BAA|ε A::=aS B::=bS 或者 S::=Saab|aSab|aaSb|aabS|Saba|aSba|abSa|abaS|Sbaa |bSaa|baSa|baaS|ε 或者 S::=aaB|aBa|Baa|ε B::=SbS
1 0 S 0
A
0 Z 0
1
解题思路二： 写出其正规表达式 解题思路二 ： 写出其正规表达式(0|10)*(10|0|1)【 如果仅有 【 (0|10)*的话推导不出 ，因为是连接关系，后面缺了 的话 的话推导不出1，因为是连接关系，后面缺了10的话 的话推导不出 就会以1结尾 同样的道理还要推导出0， 结尾， 就会以 结尾 ， 同样的道理还要推导出 ， 所以得到此正规 画出转换系统，然后根据转换系统来推导出文法。 式 】 ， 画出转换系统 ， 然后根据转换系统来推导出文法 。 也可以根据正规表达式直接写文法，例如正规表达式 (0|10)*(10|0|1)可以看成是 可以看成是a*b，推导出 可以看成是 ，推导出A::= (0|10)A|10|0|1， ， 即A::= 0A|1B|10|0|1，其中 ，其中B::=0A，但是 此项不符合正规 ，但是10此项不符合正规 文 法 的 选 项 ， 可 以 进 行 改 写 从 而 得 到 A::= 0A|1B|0|1 B::=0A|0。 。
编译原理教程(第二版)胡元义课后答案第二章
第二章 词法分析 对图2-21的DFA进行最小化。首先将状态分为非终态 集和终态集两部分：{0,1,2,5}和{3,4,6,7}。由终态集 可知，对于状态3、6、7，无论输入字符是a还是b的下一 状态均为终态集，而状态4在输入字符b的下一状态落入 非终态集，故将其化为分 {0,1,2,5}, {4}, {3,6,7} 对于非终态集，在输入字符a、b后按其下一状态落 入的状态集不同而最终划分为
重新命名
图2-9 习题2.5的状态转换矩阵
第二章 词法分析
a 0 a 1 b 2
b b 3
a a 4
图2-10 习题2.5的最简DFA
第二章 词法分析 2.6 有语言L={w|w∈(0,1)+，并且w中至少有两个
1，又在任何两个1之间有偶数个0}，试构造接受该语
言的确定有限状态自动机(DFA)。
M′=({0,1,2},{a,b},f,0,{1,2})，其状态转换图如图
2-3所示。
第二章 词法分析 表2-2 状态转换矩阵
f 状态 0 1 2 字符
a 2 — 2
b 1 2 2
第二章 词法分析 将图2-3所示的DFA M′最小化。首先，将M′的状 态分成终态组{1,2}与非终态组{0}。其次，考察{1,2}，
0 0 0 1 1 0 2 0 3 1 4 0 5 1 0 0 6
图2-13 习题2.6的最简DFA
第二章 词法分析 2.7 已知正规式((a|b)*|aa)*b和正规式(a|b)*b。
(1) 试用有限自动机的等价性证明这两个正规式
是等价的；
(2) 给出相应的正规文法。 【解答】 图2-14所示。 (1) 正规式((a|b)*|aa)*b对应的NFA如
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
部分习题解答
© 西安电子科技大学 ·软件学院
难点
第2章习题
1. 根据模式，写出正规式 2. 依据 NFA/DFA，写出正规式
计算量大
3. 正规式NFA 4. NFADFA： ε_闭包，smove 5. DFA最小化
© 西安电子科技大学 ·软件学院
2
1. 根据模式写出正规式
一般思路：（1）分析题意 （2）列举一些最简单的例子 （3）寻找统一规律*,考虑所有可能情况**
© 西安电子科技大学 ·软件学院
13
其它
习题2.9 构造 10*1 的最小DFA
解： 活用 Thompson 算法
(1) 分解为三部分：1，0*，1；
(2) 画出三者的状态转换图：
1
0
1
0 2
1
3
4
(3) 连接运算：子图首尾相连
1
0 1
0
11
4
这已经是最小的DFA
© 西安电子科技大学 ·软件学院
14
11
其它
关于：正规式 -> NFA -> DFA -> DFA最小化： 说明：（一般）逐步计算 正规式->NFA： （1）呆板Thompson算法:
自上而下分解正规式—— 语法树， 自下而上构造NFA —— 后续遍历; 特点：每个运算对应一次构造，繁琐！ （2）活用Thompson算法： 分解正规式：得到若干规模适中的子正规式； 为每个子正规式：画出其最简的状态转换图（子图）； 按Thompson算法，将子图组合，得到完整的图。
长度为4：0011, 1100,
？ 0101, 0110, 1001, 1010
b) 前4个串： 由00和11组成的串 正规式B*, B= 00 | 11
A = (B*|C*)* = (00 | 11|01|10)*
c) 后4个串： 由01和10组成的串
正规式C*, C= 01|10
考虑：0001
d) 修改正规式C为D：
D = (01|10) (00|11)* (01|10)
最终A = (B|D)* = ( (00|11) | (01|10) (00|11)* (01|10) )*
© 西安电子科技大学 ·软件学院
4
1. 根据模式写出正规式
习题2.4 (2) 所有不含有子串 011 的01串
思路1：简单例子，观察规律 (1) 最简单的串： 0 , 1, 11, 00, 10, 01, 010, … (2) 上述各串重复： (0 | 00 | 01 | 010 )* = (01 | 0)* (3) 再考虑：仅由1组成的串，或 若干1打头的串。
a 0
a,c 1
b,c b
a 2
b,c
该DFA从初态到终态有三条路径：0b2，0c2，0a1b2 用正规式表示为： b | c | a(a|c)*b，
而且是这三条路径均至少重复一次， 故最终的正规式为：(b|c|a(a|c)*b)+
© 西安电子科技大学 ·软件学院
10
其它
习题2.9 用自然语言给出下述正规式所描述的语言，并构造
© 西安电子科技大学 ·软件学院
12Байду номын сангаас
其它
关于：正规式 -> NFA -> DFA -> DFA最小化：
说明：（一般）逐步计算 NFA->DFA（子集法）：关键点:
(1) ε_闭包（{NFA初态}）, 即DFA的初态； (2) 计算 DFA的状态转移（同时得到DFA的其它状态）；
** 借助状态转换矩阵登记：DFA状态、状态转移。 (3) DFA终态：包含NFA终态的状态集。 DFA最小化：关键点: (1) 初始划分：终态组，非终态组； (2) 结合状态转换矩阵，分裂每个状态组； (3) 选代表：修改状态转换矩阵，删除重复的行； (4) 结合新的状态转换矩阵，画状态图，删死/不可达状态.
描述
识别
正规式
有限自动机
正规式、FA是从两个不同的侧面表示一个集合(即正 规集)。所以，根本的方法是以正规集为桥梁，
- 先分析清楚 FA 识别的集合之结构特征， - 然后再设计此集合的正规式。
© 西安电子科技大学 ·软件学院
8
2.依据NFA/DFA，给出正规式
思路2：根据FA直接写出对应的正规式。其考查重点、步骤: 考查“FA之状态图的结构与正规式运算的关系”
(1) 从同一状态出发的 多条边/路径：
(2) 同一个状态的入边 和 出边：
a|b ab
(3) 环：
重复0次或多次： *，至少重复1次： +
然后据上，考查每条从初态到终态的路径，综合正规式即可。
© 西安电子科技大学 ·软件学院
9
2.依据NFA/DFA，给出正规式
习题2.10 (2) 用正规式描述 DFA 所接受的语言；
A1A | A0A1A0A
** 关键：如何构造正规式 A ?
© 西安电子科技大学 ·软件学院
3
1. 根据模式写出正规式
(1) 分析题意
习题2.4 (1) 由偶数个0和奇数个1构((23成))列 寻的举 找0一 规1些 律串最,考简虑单所的有例可子能情况
③ 构造正规式 A(偶数个0/偶数个1)
a) 长度为2: 00, 11
② 其中插入若干个0 （注意11之间应至少插入1个0）， 即可不出现“011”， 正规式为： (0+1) (0+1) 0*
即：每个1前面至少1个0，正规式化简为： (01 | 0)* ③ 再考虑：仅由1组成的串，或 若干1打头的串。
最终的正规式： 1*(01|0)*
© 西安电子科技大学 ·软件学院
6
以上情况 进行或运算，可得：/* ( [^*] | *[^*/]/])*)**/*/
④ 考虑：中间可有若干连续 *，可得最终正规式：
"/*" ([^*]|**[^*/])* ** "*/"
© 西安电子科技大学 ·软件学院
7
2.依据NFA/DFA，给出正规式
思路1： 回顾“正规式 与 FA的关系”
正规集
他们的最小DFA：
10*1
(0|1)*011(0|1)*
说明：所谓用自然语言描述就是解释字符串的特点。 注意：绝对不允许用正规式表示，因为正规式是已知条件. 解：
10*1：首尾是1、中间有零或若干个0的01串。 (0|1)*011(0|1)* ：至少含一个011的01串。
© 西安电子科技大学 ·软件学院
习题2.4 (1) 由偶数个0和奇数个1构成的01串
解：① 最简单的串有 0个0和1个1组成的串： 1 2个0和1个1组成的串：010 ，001，100
② 在上述串的中间、两头添加偶数个0和/或偶数个1，即可 得到满足题意的其他串。
设偶数个0/偶数个1组成的串，可用正规式 A 表示，则最 终正规式：
最终的正规式： 1* | 1*(01|0)* = 1*(01|0)*
© 西安电子科技大学 ·软件学院
5
1. 根据模式写出正规式
习题2.4 (2) 所有不含有子串 011 的01串
思路2：考虑包含 011 的串，然后构造没有011的串 ① 含有 子串 011 的最简单的串：
0* 0 0* 1 0*0 1 0*
1. 根据模式写出正规式
习题2.4 (4) 块注释 /* … */ 。其中 … 中不含有 子串 */ 。
思路：简单例子，观察规律。 关键：注释中若出现 *：若紧跟的是/则结束注释，
否则仍然是注释。
① 注释为空：
/* ε */
② 考虑没有 * 的注释： /* [^*]* */
③ 考虑含 * 的注释： /* (*[^/])* */