精华:特殊平行四边形知识归纳和题型精讲
特殊平行四边形知识点归纳

特殊平行四边形知识点归纳1.对角线:特殊平行四边形的对角线分别连接了两对相对顶点,它们相交于一个点,并且该交点将对角线分为两个相等的部分。
2.平行线性质:特殊平行四边形的两对边分别是平行的。
根据平行线的性质,可以推论出特殊平行四边形的一些重要性质,如对边相等和内角和为180度。
3.对角线性质:特殊平行四边形的对角线相等,即对角线BD=AC。
这个性质可以通过两个相似三角形的性质证明得出。
4.垂直线性质:特殊平行四边形的对角线相交于一个垂直点,即∠BOC=90度。
这个性质可以通过垂直线的性质证明得出。
5.邻补角性质:特殊平行四边形的邻补角(共享一条边且内角和为180度的两个角)之和为180度。
这个性质可以通过平行线的性质证明得出。
6.夹角性质:特殊平行四边形的夹角(相邻且共享一条边的两个内角)之和为180度。
这个性质也可以通过夹角的定义和平行线的性质证明得出。
7.对角线中点连线性质:特殊平行四边形的对角线的中点分别连接,即中点E和F相连,则EF平行于对边AB和CD,并且EF=AB=CD。
这个性质可以通过对角线中点连线构造等腰直角三角形的性质证明得出。
特殊平行四边形的这些性质和概念在几何学中有着广泛的应用。
例如,在解决平行四边形的面积、周长、角度和边长等问题时,可以利用这些性质来求解。
特殊平行四边形还与三角形、四边形和多边形等几何图形的关系密切相关,在几何证明和问题求解中起着重要的作用。
总之,特殊平行四边形是一个重要的几何概念,它具有一系列的重要性质和应用。
通过深入理解这些知识点,并善于运用它们来解决问题,可以提高我们的几何学思维能力和分析问题的能力。
初中数学特殊平行四边形知识点总结

特殊的平行四边形一、平行四边形(复习):中心对称图形,非轴对称图形平行四边形的定义:两组对边分别平行的四边形叫做平行四边形平行四边形的性质(1)平行四边形的对边平行且相等。
(对边)(2)平行四边形相邻的角互补,对角相等(对角)(3)平行四边形的对角线互相平分。
(对角线)(4)平行四边形是中心对称图形,对称中心是对角线的交点。
补充:(1)若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段的中点是对角线的交点,并且这条直线二等分此平行四边形的面积。
(2)推论:夹在两条平行线间的平行线段相等。
(3)平行线分线段成比例定理:两条直线被一组平行线所截,截得的对应线段的长度成比例。
推论:平行于三角形一边的直线,截其他两边(或两边延长线)所得的对应线段成比例平行四边形的判定(1)定义:两组对边分别平行的四边形是平行四边形。
(对边)(2)定理1:两组对边分别相等的四边形是平行四边形。
(对边)(3)定理2:一组对边平行且相等的四边形是平行四边形。
(对边)(4)定理3:两组对角分别相等的四边形是平行四边形。
(对角)(5)定理4:对角线互相平分的四边形是平行四边形。
(对角线)两条平行线的距离:两条平行线中,一条直线上的任意一点到另一条直线的距离,叫做这两条平行线的距离。
注意:平行线间的距离处处相等。
平行四边形的面积:S平行四边形=底边长×高=ah二、菱形:特殊平行四边形,有平行四边形一切性质菱形的定义:有一组邻边相等的平行四边形叫做菱形菱形的性质(1)菱形的四条边相等,对边平行。
(边)(2)菱形的相邻的角互补,对角相等。
(对角)(3)菱形的对角线互相垂直平分,并且每一条对角线平分一组对角。
(对角线)(4)菱形既是中心对称图形又是轴对称图形;对称中心是对角线的交点(对称中心到菱形四条边的距离相等);对称轴有两条,是对角线所在的直线。
菱形的判定(1)定义:有一组邻边相等的平行四边形是菱形。
(2)定理1:四边都相等的四边形是菱形。
平行四边形及特殊的平行四边形知识点归纳总结

平行四边形及特殊的平行四边形知识点归纳总结平行四边形,就像是数学世界里的一个灵动的精灵,总是充满着各种奇妙的特点和变化。
先来说说平行四边形的定义吧。
两组对边分别平行的四边形就是平行四边形。
这就好比两个人,各自朝着不同的方向前进,但是步伐始终保持平行,是不是很有趣?平行四边形的性质那可不少。
它的对边相等,这就像双胞胎一样,长得一模一样,不分彼此。
对边平行就更不用说啦,一直朝着相同的方向延伸,不离不弃。
还有啊,它的对角相等,邻角互补。
这就好像是好朋友,有相同的兴趣爱好,也能互相补足。
平行四边形的判定方法也很重要哦。
两组对边分别平行的四边形,这是定义判定,就像一把最直接的钥匙打开大门。
两组对边分别相等的四边形,这不就像是找到了两个一模一样的拼图块,拼在一起就是完整的图形嘛。
一组对边平行且相等的四边形,这就好比一个人既有前进的方向,又有足够的实力,肯定能到达目的地。
对角线互相平分的四边形,就像两个人共同分享一个宝贝,公平分配,和谐共处。
说完平行四边形,咱们再来瞧瞧特殊的平行四边形。
菱形,那可是有棱有角的美。
菱形的四条边都相等,这不就像是四个一样高的小伙伴手拉手站成一圈。
菱形的对角线互相垂直且平分,各自都有自己的职责,又能互相配合。
矩形呢,方方正正,有规有矩。
矩形的四个角都是直角,就像是四个坚定的战士,昂首挺胸,威风凛凛。
矩形的对角线相等,仿佛是两条实力相当的巨龙,不分上下。
正方形就更厉害啦,它既是菱形又是矩形,集两家之长。
正方形的四条边相等,四个角都是直角,对角线互相垂直平分且相等。
这就如同一个全能的超人,无所不能。
掌握这些知识点,就像是拥有了一把打开数学宝藏的钥匙。
当你在数学的海洋中遨游时,这些知识能让你如鱼得水,轻松应对各种难题。
难道你不想拥有这样的能力吗?还不赶紧把这些知识装进你的脑袋里,让它们成为你攻克数学难题的有力武器!总之,平行四边形及特殊的平行四边形的知识点就像是一个丰富多彩的宝藏库,等待着我们去探索、去挖掘、去运用。
特殊平行四边形知识点总结材料及题型
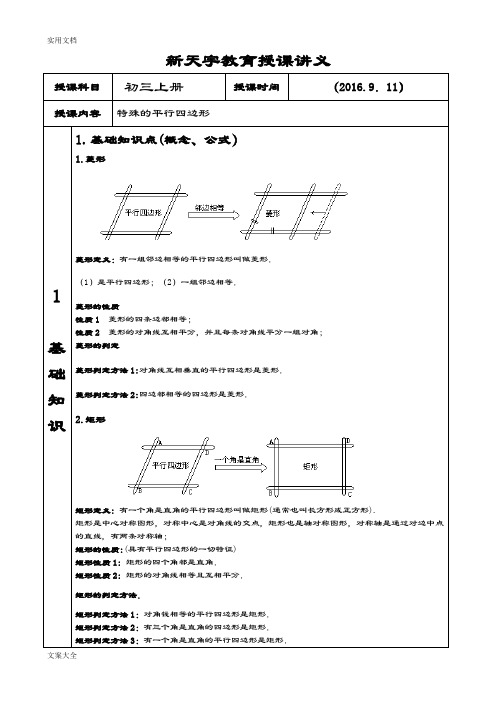
新天宇教育授课讲义授课科目初三上册授课时间(2016.9.11)授课内容特殊的平行四边形1基础知识1.基础知识点(概念、公式)1.菱形菱形定义:有一组邻边相等的平行四边形叫做菱形.(1)是平行四边形;(2)一组邻边相等.菱形的性质性质1菱形的四条边都相等;性质2 菱形的对角线互相平分,并且每条对角线平分一组对角;菱形的判定菱形判定方法1:对角线互相垂直的平行四边形是菱形.菱形判定方法2:四边都相等的四边形是菱形.2.矩形矩形定义: 有一个角是直角的平行四边形叫做矩形(通常也叫长方形或正方形).矩形是中心对称图形,对称中心是对角线的交点,矩形也是轴对称图形,对称轴是通过对边中点的直线,有两条对称轴;矩形的性质:(具有平行四边形的一切特征)矩形性质1: 矩形的四个角都是直角.矩形性质2: 矩形的对角线相等且互相平分.矩形的判定方法.矩形判定方法1:对角钱相等的平行四边形是矩形.矩形判定方法2:有三个角是直角的四边形是矩形.矩形判定方法3:有一个角是直角的平行四边形是矩形.矩形判定方法4:对角线相等且互相平分的四边形是矩形.2.正方形正方形是在平行四边形的前提下定义的,它包含两层意思:①有一组邻边相等的平行四边形(菱形②有一个角是直角的平行四边形(矩形)正方形不仅是特殊的平行四边形,并且是特殊的矩形,又是特殊的菱形.正方形定义:有一组邻边相等.....叫做正方形.正方形是中心对称.......的平行四边形......并且有一个角是直角图形,对称中心是对角线的交点,正方形又是轴对称图形,对称轴是对边中点的连线和对角线所在直线,共有四条对称轴;因为正方形是平行四边形、矩形,又是菱形,所以它的性质是它们性质的综合,正方形的性质总结如下:边:对边平行,四边相等;角:四个角都是直角;对角线:对角线相等,互相垂直平分,每条对角线平分一组对角.注意:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;正方形的两条对角线把它分成四个全等的等腰直角三角形,这是正方形的特殊性质.正方形具有矩形的性质,同时又具有菱形的性质.正方形的判定方法:(1)有一个角是直角的菱形是正方形;(2)有一组邻边相等的矩形是正方形.注意:1、正方形概念的三个要点:(1)是平行四边形;(2)有一个角是直角;(3)有一组邻边相等.2、要确定一个四边形是正方形,应先确定它是菱形或是矩形,然后再加上相应的条件,确定是正方形.2.本节课的重点、难点(1)对平行四边形和特殊的几种图形的性质要注意理解(2)对证明特殊平行四边形的方法进行掌握3.学生容易混淆的知识点(1)各种四边形对角线的特点。
特殊的平行四边形知识梳理

【学习目标】1. 掌握平行四边形、矩形、菱形、正方形的概念, 了解它们之间的关系.2. 探索并掌握平行四边形、矩形、菱形、正方形的有关性质和常用判别方法, 并能运用这些知识进行有关的证明和计算.3. 掌握三角形中位线定理. 【要点梳理】 要点一、平行四边形1.定义:两组对边分别平行的四边形叫做平行四边形. 2.性质:(1)对边平行且相等; (2)对角相等;邻角互补; (3)对角线互相平分; (4)中心对称图形. 3.面积:4.判定:边:(1)两组对边分别平行的四边形是平行四边形; (2)两组对边分别相等的四边形是平行四边形; (3)一组对边平行且相等的四边形是平行四边形. 角:(4)两组对角分别相等的四边形是平行四边形; (5)任意两组邻角分别互补的四边形是平行四边形. 边与角:(6)一组对边平行,一组对角相等的四边形是平行四边形;对角线:(7)对角线互相平分的四边形是平行四边形. 要点诠释:平行线的性质:高底平行四边形⨯=S(1)平行线间的距离都相等; (2)等底等高的平行四边形面积相等.要点二、矩形1.定义:有一个角是直角的平行四边形叫做矩形. 2.性质:(1)具有平行四边形的所有性质;(2)四个角都是直角; (3)对角线互相平分且相等;(4)中心对称图形,轴对称图形. 3.面积:4.判定:(1) 有一个角是直角的平行四边形是矩形.(2)对角线相等的平行四边形是矩形.(3)有三个角是直角的四边形是矩形. 要点诠释:由矩形得直角三角形的性质: (1)直角三角形斜边上的中线等于斜边的一半;(2)直角三角形中,30度角所对应的直角边等于斜边的一半. 要点三、菱形1. 定义:有一组邻边相等的平行四边形叫做菱形. 2.性质:(1)具有平行四边形的一切性质; (2)四条边相等;(3)两条对角线互相平分且垂直,并且每一条对角线宽=长矩形 S平分一组对角;(4)中心对称图形,轴对称图形.3.面积:4.判定:(1)一组邻边相等的平行四边形是菱形;(2)对角线互相垂直的平行四边形是菱形; (3)四边相等的四边形是菱形.要点四、正方形1. 定义:四条边都相等,四个角都是直角的四边形叫做正方形.2.性质:(1)对边平行; (2)四个角都是直角;(3)四条边都相等;(4)对角线互相垂直平分且相等,对角线平分对角; (5) 两条对角线把正方形分成四个全等的等腰直角三角形;(6)中心对称图形,轴对称图形.3.面积:边长×边长=×对角线×对角线 4.判定:(1)有一个角是直角的菱形是正方形;(2)一组邻边相等的矩形是正方形; (3)对角线相等的菱形是正方形;2对角线对角线高==底菱形⨯⨯S =S 正方形12(4)对角线互相垂直的矩形是正方形;(5)对角线互相垂直平分且相等的四边形是正方形;(6)四条边都相等,四个角都是直角的四边形是正方形.【知识网络】例1、菱形具有而一般平行四边形不具有的性质是()A.对边相等 B.对角相等C.对角线互相平分D.对角线互相垂直例2、如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于()A.B.C.5 D.4例3、如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为()A.2 B.3C.D.2例4、如图,菱形ABCD的对角线AC、BD相交于点O,AC=8,BD=6,过点O作OH ⊥AB,垂足为H,则点O到边AB的距离OH等于()A.2 B.C.D.例5、如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个锐角为60°的菱形,剪口与折痕所成的角a的度数应为.例1、如图,在矩形ABCD中,点O为对角线AC、BD的交点,点E为BC上一点,连接EO,并延长交AD于点F,则图中全等三角形共有()A.3对B.4对C.5对D.6对例2、如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2,DE=2,则四边形OCED的面积()A.2 B.4C.4D.8例3、如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE =S△COE,其中正确结论有()A.1个 B.2个C.3个D.4个例4、如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点,则DC和EF的大小关系是()A.DC>EF B.DC<EFC.DC=EF D.无法比较例5、如图,在Rt△ABC中,∠ACB=90°,将边BC沿斜边上的中线CD折叠到CB′,若∠B=50°,则∠ACB′=.例1、下列说法正确的是()A.对角线相等且互相垂直的四边形是菱形B.对角线互相垂直平分的四边形是正方形C.对角线互相垂直的四边形是平行四边形D.对角线相等且互相平分的四边形是矩形例2、已知:如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,面积记作S1;再作第二个正方形A2B2C2A3,面积记作S2;继续作第三个正方形A3B3C3A4,面积记作S3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第6个正方形的面积S6是()A.256 B.900 C.1024 D.4096例3、如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则正方形的边长为()A.4 B.3 C.2+ D.例4、如图,正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,连接BF,DF.则BE:CF的值为.例5、如图,正方形ABCD中,以对角线BD为边作菱形BDFE,使B,C,E三点在同一直线上,连接BF,交CD与点G.(1)求证:CG=CE;(2)若正方形边长为4,求菱形BDFE的面积.。
特殊平行四边形知识点总结及题型

特殊平行四边形知识点总结及题型特殊平行四边形知识点总结及题型特殊平行四边形是几何学中的重要概念,它包括矩形、菱形和正方形。
这些特殊平行四边形具有一些独特的性质和特征,它们在几何学、晶体学和工程学等领域都有广泛的应用。
本文将总结特殊平行四边形的定义、性质、判定方法和典型题型,以帮助读者更好地理解和掌握这些知识。
一、定义1、矩形:一个内角为直角的平行四边形叫做矩形。
2、菱形:一个内角为锐角的平行四边形叫做菱形。
3、正方形:内角均为直角的平行四边形叫做正方形。
二、性质1、对边平行且相等。
2、对角线互相平分且相等。
3、四个内角均为90度。
4、邻角互补。
5、对角线与邻边组成的三角形为等腰直角三角形。
三、判定方法1、矩形 (1) 内角为直角。
(2) 对边平行且相等。
2、菱形 (1) 内角为锐角。
(2) 对边平行且相等。
3、正方形 (1) 内角均为直角。
(2) 对边平行且相等。
四、典型题型1、求特殊平行四边形的角度和周长。
2、证明特殊平行四边形的性质和判定方法。
3、解决与特殊平行四边形相关的实际问题。
五、扩展知识1、空间几何中的特殊平行四边形,如空间双面平行四边形等。
2、立体几何中的特殊平行四边形,如平行六面体等。
3、相关知识点,如三角函数、向量等在特殊平行四边形中的应用。
总之,特殊平行四边形是一个具有丰富内容和广泛应用的知识点。
理解和掌握这些特殊形状的特点和性质,对于解决相关问题以及进一步学习几何学、物理学等学科都具有重要意义。
希望读者通过阅读本文,能够对这些特殊平行四边形的定义、性质、判定方法和典型题型有更深入的理解和掌握,为进一步学习打下坚实的基础。
平行四边形知识点总结平行四边形知识点总结一、定义平行四边形是一种几何图形,具有两条相互平行的对边和两条对角线。
它是人类生活中常见的形状,具有广泛的应用价值。
二、性质1、平行四边形的对边平行且相等。
2、平行四边形的对角相等。
3、平行四边形的内角和为360度。
初二数学特殊的平行四边形知识点的归纳

初二数学特殊的平行四边形知识点的归纳初二数学特殊的平行四边形知识点的归纳【菱形】1.菱形的定义:有一组邻边相等的平行四边形叫做菱形。
2.菱形的性质:(1)菱形的性质有:①平行四边形的一切性质;②四条边都相等;③对角线互相垂直,并且每一条对角线平分一组对角;④菱形是对称轴图形,它有2条对称轴,分别为它的两条对角线所在的直线。
(2)菱形面积=底×高=对角线乘积的一半。
3.菱形的判定:(1)用定义判定(即一组邻边相等的平行四边形是菱形)。
(2)对角线互相垂直的平行四边形是菱形。
(3)四条边都相等的四边形是菱形。
综上可知,判定菱形时常用的思路:四条边都相等菱形菱形四边形平行四边形有一组邻边相等菱形【矩形】1.矩形的定义:有一个角是直角的平行四边形叫做矩形。
2.矩形的性质:(1)具有平行四边形的一切性质;(2)矩形的`四个角都是直角;(3)矩形的四个角都相等。
4.矩形的判定方法:(1)用定义判定(即有一个角是直角的平行四边形是矩形);(2)三个角都是直角的四边形是矩形;(3)对角线相等的平行四边形是矩形。
综上可知,判定矩形时常用的思路:【正方形】1.正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形。
2.正方形的性质:正方形具有平行四边形、矩形、菱形的一切性质。
(1)边:四条边相等,邻边垂直且相等,对边平行且相等。
1(2)角:四个角都是直角。
(3)对角线:对角线相等且互相垂直平分,每条对角线平分一组对角。
3.正方形的判定(1)根据定义判定;(2)对角线相等的菱形是正方形;(2)有一个角是直角的菱形是正方形;(3)有一组邻边相等的矩形是正方形;(4)对角线互相垂直的矩形是正方形。
4.特殊的平行四边形之间的关系矩形、菱形是特殊的平行四边形,正方形是更特殊的平行四边形,它既是矩形,又是菱形,它们之间的关系如图所示:5.依次连接四边形各边中点所得到的四边形的形状:(1)依次连接任意四边形各边中点所得到的四边形是平行变形;(2)依次连接对角线相等的四边形各边中点所得到的四边形是菱形;(3)依次连接对角线垂直的四边形各边中点所得到的四边形是矩形;(4)依次连接对角线垂直且相等的四边形各边中点所得到的四边形是正方形;陕西人民教育出版答案_陕西人民教育出版社初二数学课堂练习册答案【四篇】12.2第1课时正比例函数的图象和性质答案课前自主预习知识要点1y=kx+b≠0y=kx≠0自我检测1一次正比例一次知识要点2原点直线y=kx上升增大下降减小陡自我检测201增大课堂达标训练1、B2、33、y=-6x+20是4-6:BCD7、a8、列表:描点并画出图象略,课后巩固提升1-3:CBC4、答案不,只要k>0即可,如y=2x5、≠1-16、-2第二、四7、m>1/28、(1)s=100t(0≤t≤20);(2)图略;(3)当s=1000时,1000=100t,解得t=10.故第10分钟时他恰好走了一半的路程.9、把x=-2代人y=-3x中,得y=6,所以点P的坐标为(-2,6),那么PA=6,OA=2,则Rt△POA的面积为1/2PA•OA=1/2×6×2=610、(1)图略;(2)A(2,2),图略;(3)(2,0)或(4,0).12.2第2课时一次函数的图象和性质答案课前自主预习知识要点1截距b自我检测1-3-1知识要点2lbl上下自我检测2y=2x+3y=2x-4知识要点3增大上升减小下降自我检测3C课堂达标训练1-4:DADA5、由y=-x+3可列表:图略,与x轴的交点坐标为(3,0),与y轴的交点坐标为(0,3).6、B7、A课后巩固提升1-4:CDDA5、(0,2)或(0,-4)6、y=-2x+17、(1)由题意可得0=m×0+lm-1l,即lm-1l=0,解得m=1;(2)由题意可得lm-1l=2,∴m-1=2或m-1=-2,解得m=3或m=-1∵y随x的增大而增大,∴m>0,∴m=39、(1)①填表如下:②如图所示;(2)①y=lxl的图象位于第一、二象限,在第一象限y随x的增大而增大,在第二象限y随x的增大而减小;②函数有最小值,最小值为0;(3)函数y=lxl的图象向右平移2个单位得到函数y=lx-2l的图象.12.2第3课时用待定系数法求一次函数的解析式答案课前自主预习知识要点2(1)y=kx+b(2)方程(组)1-2y=x-2课堂达标训练1-3:BBD4、55、y=3x-56、47、(1)设一次函数解析式为y=kx+b,∵一次函数的图象经过(2,5)和(-1,-1)两点,一次函数解析式为y=2x+1;(2)当x=0时,y=1;当y=0时,2x+1=0,解得x=-1/2,∴此函数图象与坐标轴的交点坐标为(0,1)(-1/2,0),∴此函数图象与坐标轴围成的三角形面积为1/2××1/2=1/4课后巩固提升1-3:BAD4、y=3/2x-25、2/36、y=-1/3x+27、y=-x+58、y=x+2或y=-x+29、y=x-210、(1)y=-2-x+3(2)与x轴交点为(3/2,0),与y轴交点为(0,3).11、由题意知k=-3,则y=-3x+b,将(2,-1)代人得-3×2+b=-1,解得b=5,则y=-3x+512、设B点坐标为(m,0),故m=4,当m=4时,由直线y=kx+b过点A(1,2),B(4,0),此时直线的解析式为y=2/3x+8/3;当m=-4时,由直线y=kx+b过点A(1,2),B(-4,0),此时直线的解析式为y=2/5x+8/5,综上所述,该直线的解析式为y=-2/3x+8/3或y=2/5x+8/513、设该一次函数的关系式是y=kx+b.当k>0时,y随x的增大而增大,此时,当x=-1时,y=3;当x=2时,y=6则这个函数的解析式是y=x+4;当k<0时,y随x的增大而减小,此时,当x=-1时,y=6;当x=2时,y=3则这个函数的解析式是y=-x+5.综上所述,这个一次函数的解析式是y=x+4或y=-x+5.12.2第4课时分段函数答案课前自主预习知识要点分段函数自我检测51.2(x-2)+5课堂达标训练1、D2、C3、(1)2(2)64、y=2xy=x+506、16课后巩固提升1、B2、C4、225、①②③6、(1)∵CD∥x轴,(2)设直线AC的解析式为y=kx+b(是≠0),∵直线经过点A(O,6),B(30,12),所以,直线AC的解析式为y=1/5x+6(0≤x≤50).当x=50时,y=1/5×50+6=16即该植物长16cm.7、(1)由题意,三口之家应缴购房款为0.3×3×30+0.5×30=42(万元);(2)当0≤x≤30时,y=0.3×3r=0.9x;当30当x>m时,y=0.3×3×30+0.5×3×(m-30)+0.7×3×(x-m)=2.1x-18-0.6m.(3)当50≤m≤60时,y=1.5×50-18=57(舍去);当45≤m<50时,y=2.1×50-0.6m-18=87-0.6m,当y=58.2时,解得m=48.相关热词搜索:初二数学第四章知识点初二数学第四章知识点一、四边形的相关概念1、四边形在同一平面内,由不在同一直线上的四条线段首尾顺次相接组成的图形叫做四边形。
人教八年级数学特殊平行四边形相关知识归纳总结与例题精讲

人教八年级数学特殊平行四边形相关知识归纳总结与例题精讲龙文学校-----您值得信赖的专业个性化辅导学校特殊平行四边形相关知识的归纳和常见题型精讲附件:矩形菱形广场的性能及判定汇总边性角质对角线矩形对边平行且相等四个角都是直角互相平分且相等有三个角是直角;是平行四边形且有一个角是直角;是平行四边形且两条对角线相等.菱形对边平行,四边相等对角相等互相垂直平分,且每条对角线平分一组对角正方形对边平行,四边相等四个角都是直角互相垂直平分且相等,每条对角线平分一组对角判定四边相等的四边形;是平行四边形且有一是矩形,且有一组邻边相等;组邻边相等;是菱形,且有一个角是直角。
是平行四边形且两条对角线互相垂直。
既是轴对称图形,又是中心对称图形对称性一.矩形矩形的定义:具有直角的平行四边形称为矩形(通常也称为矩形或正方形)矩形是中心对称图形,对称中心是对角线的交点,矩形也是轴对称图形,对称轴是通过对边中点的直线,有两条对称轴;矩形的性质:(具有平行四边形的所有特征)矩形性质1:矩形的四个角都是直角.矩形属性2:矩形的对角线相等且等分如图,在矩形abcd中,ac、bd相交于点o,由性质2有11ac=BD。
因此,我们可以得到直角三角形的一个性质:直角三角形22形斜边上的中线等于斜边的一半.ao=bo=co=do=矩形的判定方法.矩形的确定方法1:对角线相等的平行四边形为矩形。
矩形确定方法2:三个角为直角的四边形为矩形龙文学校-----您值得信赖的专业个性化辅导学校矩形确定方法3:直角平行四边形为矩形矩形判定方法4:(4)对角线相等且互相平分的四边形是矩形.例1:如图所示,矩形ABCD长8cm,对角线比AD边长4cm。
求出AD的长度以及a点到BD的距离AE例2已知:如图,矩形abcd中,e是bc上一点,df⊥ae于f,若ae=bc.求证:ce=ef.例3。
如图所示,在矩形ABCD中,e是ad上的点,f是AB上的点,EF⊥ EC,EF=EC,de=4cm,矩形ABCD的周长为32cm,计算AE的长度例4、如图,在abcd中,e为bc的中点,连接ae并延长交dc的延长线于点f.(1)验证:ab=CF;(2)当bc与af满足什么数量关系时,四边形abfc是矩形,并说明理由.acbefd龙文学校-----您值得信赖的专业个性化辅导学校二、钻石菱形定义:有一组邻边相等的平行四边形叫做菱形.【重点】钻石(1)是一个平行四边形;(2)一组相邻的边是相等的菱形的性质属性1钻石的四边相等;性质2菱形的对角线互相平分,并且每条对角线平分一组对角;钻石的测定菱形判定方法1:对角线互相垂直的平行四边形是菱形.注意,这种方法包括两个条件:(1)它是一个平行四边形;(2)这两条对角线互相垂直菱形判定方法2:四边都相等的四边形是菱形.例1:如图所示,四边形ABCD是菱形,f是AB上的一个点,DF与E中的AC相交。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级平行四边形相关知识归纳和常见题型精讲性质和判定总表矩形菱形正方形的矩形菱形正方形性质边对边平行且相等对边平行,四边相等对边平行,四边相等角四个角都是直角对角相等四个角都是直角对角线互相平分且相等互相垂直平分,且每条对角线平分一组对角互相垂直平分且相等,每条对角线平分一组对角判定·有三个角是直角;·是平行四边形且有一个角是直角;·是平行四边形且两条对角线相等.·四边相等的四边形;·是平行四边形且有一组邻边相等;·是平行四边形且两条对角线互相垂直。
·是矩形,且有一组邻边相等;·是菱形,且有一个角是直角。
对称性既是轴对称图形,又是中心对称图形一. 矩形矩形定义: 有一个角是直角的平行四边形叫做矩形(通常也叫长方形或正方形).矩形是中心对称图形,对称中心是对角线的交点,矩形也是轴对称图形,对称轴是通过对边中点的直线,有两条对称轴;矩形的性质:(具有平行四边形的一切特征)矩形性质1:矩形的四个角都是直角.矩形性质2:矩形的对角线相等且互相平分.如图,在矩形ABCD中,AC、BD相交于点O,由性质2有AO=BO=CO=DO=21AC=21BD.因此可以得到直角三角形的一个性质:直角三角形斜边上的中线等于斜边的一半.矩形的判定方法.矩形判定方法1:对角钱相等的平行四边形是矩形. 矩形判定方法2:有三个角是直角的四边形是矩形. 矩形判定方法3:有一个角是直角的平行四边形是矩形.矩形判定方法4: (4)对角线相等且互相平分的四边形是矩形.例1已知:如图 ,矩形 ABCD ,AB 长8 cm ,对角线比AD 边长4 cm .求AD 的长及点A 到BD 的距离AE 的长.例2 已知:如图,矩形ABCD 中,E 是BC 上一点,DF ⊥AE 于F ,若AE=BC . 求证:CE =EF .例3.如图,已知矩形ABCD 中,E 是AD 上的一点,F 是AB 上的一点,EF ⊥EC ,且EF =EC ,DE =4cm ,矩形ABCD 的周长为32cm ,求AE 的长.例4、中,E 为BC 的中点,连接AE 并延长交DC 的延长线于点F .(1)求证:AB=CF ;(2)当BC 与AF 满足什么数量关系时,四边形ABFC 是矩形,并说明理由.FEDCBA二.菱形菱形定义:有一组邻边相等的平行四边形叫做菱形.【强调】菱形(1)是平行四边形;(2)一组邻边相等.菱形的性质性质1菱形的四条边都相等;性质2 菱形的对角线互相平分,并且每条对角线平分一组对角;菱形的判定菱形判定方法1:对角线互相垂直的平行四边形是菱形.注意此方法包括两个条件:(1)是一个平行四边形;(2)两条对角线互相垂直.菱形判定方法2:四边都相等的四边形是菱形.例1已知:如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.求证:∠AFD=∠CBE.例2已知:如图ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.求证:四边形AFCE是菱形.例3、如图,在ABCD中,O是对角线AC的中点,过点O 作AC的垂线与边AD、BC分别交于E、F,求证:四边形AFCE是菱A DE1例4、已知如图,菱形ABCD 中,E 是BC 上一点,AE 、BD 交于M ,若AB=AE,∠EAD=2∠BAE 。
求证:AM=BE 。
例5. (10湖南益阳)如图,在菱形ABCD 中,∠A =60°,AB =4,O 为对角线BD 的中点,过O 点作OE ⊥AB ,垂足为E .(1)求线段BE 的长.例6、(2008四川自贡)如图,四边形ABCD 是菱形,DE⊥AB 交BA 的延长线于E ,DF⊥BC,交BC 的延长线于F 。
请你猜想DE 与DF 的大小有什么关系?并证明你的猜想例7、(2008山东烟台)如图,菱形ABCD 的边长为2,BD=2,E 、F 分别是边AD ,CD 上的两个动点,且满足AE+CF=2.(1)求证:△BDE≌△BCF;(2)判断△BEF 的形状,并说明理由; (3)设△BEF 的面积为S ,求S 的取值范围.BM ADCEDBO60三.正方形正方形是在平行四边形的前提下定义的,它包含两层意思: ①有一组邻边相等的平行四边形 (菱形) ②有一个角是直角的平行四边形 (矩形)正方形不仅是特殊的平行四边形,并且是特殊的矩形,又是特殊的菱形. 正方形定义:有一组邻边相等......并且有一个角是直角.......的平行四边形.....叫做正方形. 正方形是中心对称图形,对称中心是对角线的交点,正方形又是轴对称图形,对称轴是对边中点的连线和对角线所在直线,共有四条对称轴;因为正方形是平行四边形、矩形,又是菱形,所以它的性质是它们性质的综合,正方形的性质总结如下:边:对边平行,四边相等; 角:四个角都是直角;对角线:对角线相等,互相垂直平分,每条对角线平分一组对角.注意:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;正方形的两条对角线把它分成四个全等的等腰直角三角形,这是正方形的特殊性质.正方形具有矩形的性质,同时又具有菱形的性质.正方形的判定方法:• (1)有一个角是直角的菱形是正方形; • (2)有一组邻边相等的矩形是正方形. • 注意:1、正方形概念的三个要点:• (1)是平行四边形; • (2)有一个角是直角; • (3)有一组邻边相等.2、要确定一个四边形是正方形,应先确定它是菱形或是矩形,然后再加上相应的条件,确定是正方形.例1 已知:如图,正方形ABCD 中,对角线的交点为O ,E 是OB上的一点,DG⊥AE 于G ,DG 交OA 于F . 求证:OE=OF .例2 已知:如图,四边形ABCD 是正方形,分别过点A 、C 两点作l 1∥l 2,作BM ⊥l 1于M ,DN ⊥l 1于N ,直线MB 、DN 分别交l 2于Q 、P 点.求证:四边形PQMN 是正方形.例3、(2008海南)如图,P 是边长为1的正方形ABCD 对角线AC 上一动点(P 与A 、C不重合),点E 在射线BC 上,且PE=PB . (1)求证:① PE=PD ; ② PE ⊥PD ; (2)设AP =x , △PBE 的面积为y .① 求出y 关于x 的函数关系式,并写出x 的取值范围; ② 当x 取何值时,y 取得最大值,并求出这个最大值.例4.(2006年河南省)如图,梯形ABCD 中,AD ∥BC ,AB=AD=DC ,E 为底边BC 的中点,且DE ∥AB ,试判断△ADE 的形状,并给出证明.AB CPDE图 5E D C BA例5:(2008深圳)如图,在梯形ABCD 中,AB ∥DC , DB 平分∠ADC ,过点A 作AE ∥BD ,交CD 的延长线于点E ,且∠C =2∠E . (1)求证:梯形ABCD 是等腰梯形.(2)若∠BDC =30°,AD =5,求CD 的长.例题讲解例一.分析:(1)因为矩形四个角都是直角,因此矩形中的计算经常要用到直角三角形的性质,而此题利用方程的思想,解决直角三角形中的计算,这是几何计算题中常用的方法.解:设AD=xcm ,则对角线长(x+4)cm ,在Rt △ABD 中,由勾股定理:222)4(8+=+x x ,解得x=6. 则 AD=6cm .(2)“直角三角形斜边上的高”是一个基本图形,利用面积公式,可得到两直角边、斜边及斜边上的高的一个基本关系式: AE×DB= AD×AB,解得 AE = 4.8cm .例二分析:CE 、EF 分别是BC ,AE 等线段上的一部分,若AF =BE ,则问题解决,而证明AF =BE ,只要证明△ABE ≌△DFA 即可,在矩形中容易构造全等的直角三角形. 证明:∵ 四边形ABCD 是矩形,∴ ∠B=90°,且AD ∥BC . ∴ ∠1=∠2. ∵ DF ⊥AE , ∴ ∠AFD=90°. ∴ ∠B=∠AFD .又 AD=AE , ∴ △ABE ≌△DFA (AAS ). ∴ AF=BE . ∴ EF=EC .此题还可以连接DE ,证明△DEF ≌△DEC ,得到EF =EC .菱形 例1 证明:∵ 四边形ABCD 是菱形,∴ CB=CD , CA 平分∠BCD . ∴ ∠BCE=∠DCE .又 CE=CE , ∴ △BCE ≌△COB (SAS ). ∴ ∠CBE=∠CDE .∵ 在菱形ABCD 中,AB ∥CD , ∴∠AFD=∠FDC ∴ ∠AFD=∠CBE .例2 证明:∵ 四边形ABCD 是平行四边形,∴AE∥FC.∴∠1=∠2.又∠AOE=∠COF,AO=CO,∴△AOE≌△COF.∴EO=FO.∴四边形AFCE是平行四边形.又EF⊥AC,∴AFCE是菱形(对角线互相垂直的平行四边形是菱形).例6、解:DE=DF证明如下:连结BD∵四边形ABCD是菱形∴∠CBD=∠ABD(菱形的对角线平分一组对角)∵DF⊥BC,DE⊥AB∴DF=DE(角平分线上的点到角两边的距离相等)例7 、正方形例1 分析:要证明OE=OF,只需证明△AEO≌△DFO,由于正方形的对角线垂直平分且相等,可以得到∠AOE=∠DOF=90°,AO=DO,再由同角或等角的余角相等可以得到∠EAO=∠FDO,根据ASA可以得到这两个三角形全等,故结论可得.证明:∵ 四边形ABCD 是正方形,∴ ∠AOE=∠DOF=90°,AO=DO (正方形的对角线垂直平分且相等). 又 DG ⊥AE , ∴ ∠EAO+∠AEO=∠EDG+∠AEO=90°.∴ ∠EAO=∠FDO .∴ △AEO ≌△DFO .∴ OE=OF .例2 分析:由已知可以证出四边形PQMN 是矩形,再证△ABM ≌△DAN ,证出AM=DN ,用同样的方法证AN=DP .即可证出MN=NP .从而得出结论.证明:∵ PN ⊥l 1,QM ⊥l 1,∴ PN ∥QM ,∠PNM=90°.∵ PQ ∥NM ,∴ 四边形PQMN 是矩形.∵ 四边形ABCD 是正方形∴ ∠BAD=∠ADC=90°,AB=AD=DC (正方形的四条边都相等,四个角都是直角). ∴ ∠1+∠2=90°.又 ∠3+∠2=90°, ∴ ∠1=∠3.∴ △ABM ≌△DAN .∴ AM=DN . 同理 AN=DP .∴ AM+AN=DN+DP即 MN=PN .∴ 四边形PQMN 是正方形(有一组邻边相等的矩形是正方形).例3 (1)证法一:① ∵ 四边形ABCD 是正方形,AC 为对角线,∴ BC=DC , ∠BCP =∠DCP=45°.∵ PC =PC ,∴ △PBC ≌△PDC (SAS ).∴ PB = PD , ∠PBC =∠PDC .又∵ PB = PE ,∴ PE =PD .② (i )当点E 在线段BC 上(E 与B 、C 不重合)时, ∵ PB =PE ,∴ ∠PBE =∠PEB ,∴ ∠PEB =∠PDC ,∴ ∠PEB +∠PEC =∠PDC +∠PEC =180°,∴ ∠DPE =360°-(∠BCD +∠PDC +∠PEC )=90°, ∴ PE ⊥PD . )(ii )当点E 与点C 重合时,点P 恰好在AC 中点处,此时,PE ⊥PD .(iii )当点E 在BC 的延长线上时,如图.∵ ∠PEC =∠PDC ,∠1=∠2,∴ ∠DPE =∠DCE =90°, A B C D P E1 2 H∴ PE ⊥PD .综合(i )(ii )(iii ), PE ⊥PD .(2)① 过点P 作PF ⊥BC ,垂足为F ,则BF =FE .∵ AP =x ,AC =2,∴ PC =2- x ,PF =FC =x x 221)2(22-=-. BF =FE =1-FC =1-(x 221-)=x 22. ∴ S △PBE =BF ·PF =x 22(x 221-)x x 22212+-=. 即 x x y 22212+-= (0<x <2). ② 41)22(21222122+--=+-=x x x y . ∵ 21-=a <0, ∴ 当22=x 时,y 最大值41=. (1)证法二:① 过点P 作GF ∥AB ,分别交AD 、BC 于G 、F . 如图所示. ∵ 四边形ABCD 是正方形, ∴ 四边形ABFG 和四边形GFCD 都是矩形, △AGP 和△PFC 都是等腰直角三角形. ∴ GD=FC =FP ,GP=AG =BF ,∠PGD =∠PFE =90°. 又∵ PB =PE ,∴ BF =FE , ∴ GP =FE ,∴ △EFP ≌△PGD (SAS ).∴ PE =PD .② ∴ ∠1=∠2.∴ ∠1+∠3=∠2+∠3=90°.∴ ∠DPE =90°.∴ PE ⊥PD .(2)①∵ AP =x , ∴ BF =PG =x 22,PF =1-x 22. ∴ S △PBE =BF ·PF =x 22(x 221-)x x 22212+-=. 即 x x y 22212+-= (0<x <2). ② 41)22(21222122+--=+-=x x x y . ∵ 21-=a <0, A B C P D E F A B C P D E F G 1 2 3∴ 当22=x 时,y 最大值41=. (注:用其它方法求解参照以上标准给分.)例4 【解析】△ADE 是等边三角形.理由如下:∵AB=CD ,∴梯形ABCD 为等腰梯形,∵∠B=∠C .∴E 为BC 的中点,∵BE=CE .在△ABE 和△DCE 中,∵,,AB DC B C BE CE =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△DCE .∵AE=DE .∴AD ∥BC ,DE ∥AB ,∴四边形ABCD 为平行四边形.∴AB=DE∵AB=AD ,∴AD=AE=DE .∴△ADE 为等边三角形.例5:(1)证明:∵AE ∥BD, ∴∠E =∠BDC∵DB 平分∠ADC ∴∠ADC =2∠BDC又∵∠C =2∠E∴∠ADC =∠BCD∴梯形ABCD 是等腰梯形(2)解:由第(1)问,得∠C =2∠E =2∠BDC =60°,且BC =AD =5∵ 在△BCD 中,∠C =60°, ∠BDC =30°∴∠DBC =90°∴DC =2BC =10完如有侵权请联系告知删除,感谢你们的配合!。
