中学知识点交大优立方
杨浦区春季补习班 新王牌初中数学靳T老师知识点汇总
杨浦新王牌新王牌初中数学靳T老师知识点汇总一线段、角1）经过两点有一条直线，并且只有一条直线。
2）两点之间线段最短二相交线、平行线1）经过直线外或直线上一点，有一条而且只有一条直线与已知直线垂直2）经过已知直线外的一点，有一条直线而且只有一条直线与已知直线平行三平行四边形平行四边形两组对边分别平行平行四边形的对角相等1）平行四边形的性质平行四边形的对边相等平行四边形的对角线互相平分平行四边形是中心对称图形，两条对角线的交点是对称中心两组对边分别平行的四边形平行四边形两组对边分别相等的四边形是平行四边形2）平行四边形的判定一组对边分别相等的四边形是平行四边形对角线互相平分的四边形是平行四边形两组对角分别相等的四边形是平行四边形四菱形、矩形、正方形（具有平行四边形所有的性质）矩形的性质矩形的四个角都是直角矩形的对角线相等矩形的判定有三个角是直角的四边形是矩形对角线相等的平行四边形是矩形菱形的四条边都相等菱形的性质菱形的对角线互相垂直，且每一条对角线平分一组对角菱形的面积等于它的两条对角线的积的一半菱形的判定四条边相等的四边形是菱形对角线互相垂直的平行四边形是菱形正方形四个角是直角正方形的性质正方形的对角线相等且互相垂直平分正方形四条边相等正方形每一条对角线平分一组对角正方形的判定有一个角是直角的菱形是正方形有一组邻边相等的矩形是正方形菱形、矩形、正方形是中心对称图形，对称中心是对角线的交点五梯形等腰梯形的同一底边上的两个内角相等等腰梯形的性质等腰梯形是轴对称图形，经过两底中点的直线是它的对称轴等腰梯形的两条对角线相等等腰梯形的判定：在同一条底边上的两个内角相等的梯形是等腰梯形对角线相等的梯形是等腰梯形梯形的中位线：梯形的中位线平行于两底，并且等于两底和的一半梯形的面积：中位线×高（上底+下底）×高÷2六三角形①三角形的概念1）三角形的三个内角和等于180°2）三角形的一个外角等于和它不相邻的两个内角和3）三角形的一个外角大于任何一个和它不相邻的内角4）三角形的任何两边的和大于第三边②等腰三角形的性质：(1)等腰三角形的两腰相等(2)等腰三角形的两个底角相等. (等边对等角)(3)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(等腰三角形三线合一.)(4)等腰三角形是轴对称图形，顶角平分线（底边上的中线、底边上的高）所在的直线是它的对称轴 .③等腰三角形的判定:(1)有两条边相等的三角形是等腰三角形.(定义)(2)有两个角相等的三角形是等腰三角形.(等角对等边)④等边三角形的性质:(1)等边三角形的三条边都相等.(2)等边三角形的三个内角都相等，并且每一个内角都等于60°(3)等边三角形是轴对称图形，有三条对称轴.⑤等边三角形的判定:(1)有三条边相等的三角形是等边三角形.(定义)(2)三个角都相等的三角形是等边三角形.(3)有一个角是60°的等腰三角形是等边三角形⑥直角三角形的性质:(1)直角三角形的两个锐角互余.(2)直角三角形斜边上的中线等于斜边的一半.(3)在直角三角形中，30°角所对的直角边等于斜边的一半.(4)在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30° (5)勾股定理:直角三角形两条直角边的平方和等于斜边的平方.⑦直角三角形的判定:(1)有一个角是直角的三角形是直角三角形.(定义)(2)较小两边的平方和等于较大边的平方的三角形是直角三角形.(勾股定理的逆定理) 七 相似三角形 ①比例线段，若dcb a =（或a ∶b =c ∶d ），则四条线段a 、b 、c 、d 叫做比例线段. 比例基本性质：若dcb a =，则ad =bc .在比例中运用设k 法.②相似多边形，对应边成比例，对应角相等.）③相似三角形的相似比（当k =1时,得特殊的相似三角形，称为全等三角形）. ④相似三角形的判定定理：(1)如果一个三角形的两角分别与另一个三角形的两角对应相等，那么两个三角形相似；(2)如果一个三角形的两边分别与另一个三角形的两边对应成比例，并且夹角对应相等，那么两个三角形相似；(3)如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么两个三角形相似； (4)如果两个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似． ⑤相似三角形的性质定理：(1)若两个三角形相似，则这两个三角形的对应边成比例，对应角相等.(2)若两个三角形相似，它们对应中线的比，角平分线的比，高的比都等于相似比. (3)若两个三角形相似，它们周长比等于相似比，面积比等于相似比的平方. ⑥重心：三角形的重心与顶点的距离等于它与对边中点的距离的两倍八 圆1、 圆的定义：圆是平面上到定点的距离等于定长的点的集合。
陕西省渭南市杜桥中学高三数学考前回归基础复习
杜桥中学2009年高三考前回归基础复习2009-5第一部分: 基础知识集合、简易逻辑1.集合中的元素具有三个性质:无序性、确定性和互异性. 注意: ①集合元素的互异性.②对集合A 、B, A∩B=∅时, 要注意: A=∅ 或B=∅ ;求集合的子集时要注意∅是任何集合的子集, ∅是任何非空集的真子集.③交集的补集等于补集的并集, 即U (A∩B )=U A ∪U B;并集的补集等于补集的交集,即U (A ∪∩B)=U A∩U B;④对于含有n 个元素的有限集合M, 其子集、真子集、非空子集、非空真子集的个数依次为,2n、21n -,22n -.2.四种命题, 原命题: p ⇒q, 逆命题: q ⇒p ,否命题: p ⌝⇒q ⌝; 逆否命题: q ⌝⇒p ⌝.原命题等价于逆否命题,但原命题与逆命题、否命题都不一定不等价. 注意: ①两个命题互为逆命题,它们有相同的真假性;②两个命题为互逆命题或互否命题,它们的真假性没有关系; ③一个命题的在逆命题与它的否命题,具有相同的真假性;④在判断一些命题的真假时,如果不容易直接判断,可以反向判断其逆否命题的真假.3. "或命题"的真假特点是"一真即真,要假全假";"且命题"的真假特点是"一假即假, 要真全真";"非命题"的真假特点是:"一真一假".4.充要条件 ①定义法,正、反方向推理,若p ⇒q, p 就是q 的充分条件,反过来,q 就是p 的必要条件; 若p ⇒q 且q ⇒ p, 则p 是q 的充分非必要条件(或q 是p 的必要非充分条件);②利用集合间的包含关系,例如: 若A B ⊆, 则A 是B 的充分条件(B 是A 的必要条件);若A=B,则A 是B 的充要条件.注意: 要善于构造命题的逆命题来判断命题的充要关系,也就是说若原命题的充要关系不易判定时,可考虑它的等价命题－－逆否命题,进而化难为易.函数1.函数的概念: 设A 、B 是非空集合,如果按照某种确定的对应关系f, 使对于集合A 中的任意一个数x, 在集合B 都有唯一确定的数f(x)和它对应,那么就称f: A→B,为从集合A 到集合B 的函数,记作y=f(x), x ∈A, 其中,x 叫做自变量,x 的取值X 围A 叫做函数的定义域;与x 的值对应的y 的值叫做函数值,函数值的集合{f(x)|x ∈A}叫做函数的值域.对应关系,定义域和值域是函数的三个要素.注意: ①函数图像与x 轴上的垂线至多一个公共点,但与y 轴上的垂线的分共点可能没有,也可任意个;②函数图像一定是坐标系中的曲线,但坐标系中的曲线不一定能成为函数图像. 2.单调性和奇偶性1.奇函数在关于原点对称的区间上若有单调性,则其单调性完全相同;偶函数在关于原点对称的区间上若有单调性,则其单调性恰恰相反.注意: ①确定函数的奇偶性,务必先判定函数定义域是否关于原点对称; ②对于偶函数而言: f(－x)=f(x)=f(|x|);③若奇函数定义域中有0, 则必有f(0)=0, 但f(0)=0是f(x)为奇函数的必要非充分条件.2.定义在关于原点对称的区间上的任意一个函数,都可表示成"一个奇函数与一个偶函数的和(或差)".3.图象变换①函数图像的平移、伸缩变换中,图像的特殊点、特殊线与作相应的变换.②图像变换就重视将所研究的函数与常见函数(正比例函数、反比例函数、一次函数、二次函数、对数和指数函数、三角函数)的相互转化. 4.指数与对数:①ba N =⇔log ab N =⇒log a NaN =(对数恒等式: log a N a N =, a>0,且a≠1, N>0)②换底公式: log log log m a m NN a=(a>0,且a≠1, m>0,且m≠1, N>0)③换底公式推论: log log m na a nb b m=(a>0,b>0,n>0,m≠0, 且a≠1,b ≠1) 5.指数函数与对数函数的图象与性质: 单调性与特殊点是什么?,你能从图中说出函数的性质吗?注意: ①指数函数与对数函数, 当a>1时,都是其定义域上的单调增函数, 当0<a<1,都是定义域上的单调减函数;指数函数的图象都过点(0,1),对数函数的图象都过点(1,0).②设函数2()log ()m f x ax bx c =++(a≠0), 记24b ac ∆=-,若f(x)的定义域为R, 则a>0,且0∆<,若f(x)的值域为R,则a>0, 且0∆≥. 6.幂函数: 由下图能说出幂函数的性质.注意：幂指数大于0时,幂函数在(0,+∝)上单调递增;幂指数小于0时,幂函数在(0,+∞)上单调递减,所有幂函数的图象都过点(1,1).7.互为反函数的两个函数的关系: 1()()f a b fb a -=⇔=不等式1.不等式的性质: (1)a>b,b>c ⇒a>c; (2)a>b,c>0 ⇒ac>bc, a>b,c<0⇒ac<bc; (3) a>b ⇒a+c>b+c(4)a>b,c>d ⇒ a+c>b+d; (5) a>b>0,c>d>0, ⇒ ac>bd(6) a>b>0, n ∈N, n>1 ⇒nna b >；>2.一元二次不等式 20ax bx c ++>(或<0) (20,40a b ac ≠∆=->), 如果a 与2ax bx c ++同号,则其解集在两根之外;如果a 与2ax bx c ++异号,则其解集在两根之间,简言之: 同号两根之外, 异号两根之间.3.(1) ||x a <⇔22x a <⇔ －a<x<a ; ||x a >⇔22x a >⇔x>a 或x<－a ; (2)绝对值三角不等式: |a |－|b |≤|a ±b |≤|a |+|b |. 4.利用重要不等式 a +b ≥2ab 以及变式2()2a b ab +≤等求函数的最值时,务必注意a 、b ∈R +, 且"等号成立"时的条件是ab 或a+b 其中之一应是定值(一正二定三相等)5.常用不等式有: b a ab +2≤ab ≤2ba +≤222b a +(a,b R +); a 2+b 2+c 2≥ab+bc+ca(当且仅当a=b=c 时,取等号).6.极值定理: 已知x,y 是正数, 则有①若积xy 是定值p, 则当x=y 时和x+y 有最小值; ②若和x+y 是定值s, 则当x=y 是积xy 有最大值214s . ③已知a,b,x,y ∈R+ , 若ax+by=1, 则有1111()()by axax by a b x y x y x y+=++=+++≥a+b+2ab = (a+ b)2. ④a,b,x,y ∈R+ , 若1a b x y+=则有x+y=(x+y)(a x + b y )=a+b+ ay x + bxy ≥a+b+2ab = (a+ b)2. 7.比较大小的方法主要有: 作差比较法,作商比较法,函数性质法,放缩法等.注意 ①比较两个实数的大小时,只需考查它们差的符号或它们商与"1"的大小关系; ②使用不等式的性质时要注意性质成立的条件.8.给定区间上含参数的不等式恒成立(或有解)的条件依据:(1)在给定区间(－∞,+∞)的子区间L (形如[α,β], (－∞,β], [α,+ ∞)等)上含参数的不等式f(x)≥t (t 为参数)恒成立的充要条件是f(x)min ≥t (x ∈L)(2) 在给定区间(－∞,+∞)的子区间L 上含参数的不等式f(x)≤t (t 为参数)恒成立的充要条件是f(x)max ≤ t (x ∈L)(3) 在给定区间(－∞,+∞)的子区间L 上含参数的不等式f(x) ≥t (t 为参数)有解的充要条件是f(x)max ≥ t (x ∈L)(4) 在给定区间(－∞,+∞)的子区间L 上含参数的不等式f(x)≤t (t 为参数) 有解的充要条件是f(x)min ≤ t (x ∈L)数列1.(1){a n }与a n 是不同的: {a n }表示数列a 1,a 2,a 3,…, a n ,…,而a n 只表示这个数列的第n 项.(2)对于一个确定的数列,其通项公式并不是一定唯一. 2.等差数列{a n }中:(1)a n =a+(n －1)d=a m +(n －m)d; p+q=m+n ⇒ a p +a q =a m +a n . (2){ka n +b}也成等差数列(3)a 1+a 2+…+a m , a k +a k+1+…+a k+m －1,…仍成等差数列. (4)S n =n(a 1+a n )2 , S n =na 1+ n(n －1)2 d , S n = d 2n 2+(a 1－d2)n (5)a p =q,a q =p (p ≠q) ⇒ a p+q =0; S p =q,S q =p (p ≠q) ⇒ S p+q =－(p+q); S m+n =S m +S n +mnd3.等比数列{a n }中;(1)a n =a 1q n －1=a m q n －m ; m+n=r+s, a m ·a n =a r ·a s(2)a 1+a 2+…+a m , a k +a k+1+…+a k+m －1,…仍成等比数列(4) 111 (1)(1) (1)11n n n na q S a a q a q q q q =⎧⎪=--⎨=≠⎪--⎩= 111(1) (1)11n n na q S a a q q q q =⎧⎪=⎨-+≠⎪--⎩ 注意:①a n －b n =(a －b)(a n －1+a n －2b+a n －3b 2+…+ab n －2+b n －1)②S m+n =S m +q m S n =S n +q n S m .③并非任何两数总有等比中项.仅当实数a,b 同号时,实数a,b 才存在等比中项,且同号两实数a,b 的等比中项不仅存在,而且有一对为±ab, 也就是说,两实数要么没有等比中项(非同号时),如果有,必有一对(同号时).4.等差数列与等比数列的联系(1)如果数列{a n }成等差数列, 那么数列{n aA }(n aA 总有意义)必成等比数列. (2)如果数列{a n }成等比数列, 那么数列{log ||a n a }(a>0,a≠1)必成等差数列.(3)如果数列{ a n }既成等差数列也成等比数列,那么数列{ a n }是非零常数数列; 数列{a n }是常数数列仅是数列既成等差数列又成等比数列的必要非充分条件.(4)如果两等差数列有其公共项,那么由它们的公共项顺次组成的新数列也是等差数列,且新等差数列的公差是原两等差数列公差的最小公倍数.(5)如果一个等差数列与一个等比数列由其公共项顺次组成新数列,那么常选用"由特殊到一般的方法"进行研讨,且以其等比数列的项为主,探求等比数列中哪些项是它们的公共项,构成什么样的新数列.注意: 公共项仅是公共的项,其在各自数列中所处位置不一定相同,即研究的是a n =b m , 但也有少数问题中研究a n =b n ,这时既要求项相同,也要求在各自数列中所处位置相同. 5.数列求和的常用方法.(1)公式法: ①等差数列求和公式, ②等比数列求和公式 ③常用公式: 1+2+3+…+n=12n(n+1) , 12+22+32+…+n 2=16n(n+1)(2n+1), 1+3+5+…+(2n －1)=n 2(2)分组求和法: 在直接运用公式法求和有困难时,常将"和式"中"同类项"先合并在一起,再运用公式法求和.(3)倒序相加法: 在数列求和中,若和式中到首尾距离相等的两项和有其共性,则常考虑选用倒序相加法,发挥其共性的作用求和.(4)错位相减法: 如果数列的通项是由一个等差数列的通项与一个等比数列通项相乘构成,那么常选用错位相减法,将其和转化为"一个新的等比数列的和"求解".(5)裂项相消法: 如果数列的通项可"分裂成两项差"的形式,且相邻项分裂后相关联,那么常选用裂项相消法求和,常用裂项形式有: ①111(1)1n n n n =-++②1111()()n n k k n n k=-++ ③2211111()1211k k k k <=---+; 21111111(1)1k k k k k k k -<<=-+-- ④1111[](1)(2)2(1)(1)(2)n n n n n n n =-+++++⑤11(1)!!(1)!n n n n =-++⑥<< ⑦ a n =S n －S n －1 (n≥2) 注意:运用等比数列求和公式时,务必检查其公比与1的关系,必要时应分类讨论. 6.数列的通项的求法:(1)公式法: 等差、比数列的通项公式.(2)已知S n (即a 1+a 2+…+a n =f(n)) , 求a n , 用作差法: 11 (1)(2)n n n S n a S S n -=⎧=⎨-≥⎩(3)已知a 1·a 2·…·a n =f(n) , 求a n , 用作商法: (1) (1)() (2)(1)n f n a f n n f n =⎧⎪=⎨≥⎪-⎩(4)若a n+1－a n =f(n) ,求a n ; 用累加法: a n =(a n －a n －1)+(a n －1－a n －2)+…+(a 2－a 1)+a 1 (n ≥2) (5)已知1()n n a f n a +=,求a n ; 用累乘法: 321121nn n aa a a a a a a -=(n≥2) (6)a n =ka n －1+b, a n =ka n －1+b n (k,b 为常数)的递推数列都可以用待定系数法,先将问题转化为公比为k 的等比数列后, 再求a n . (7) 形如 11n n n a a ka b--=+的递推数列都可以用倒数法求通项.注意: ①对通项公式中含有(－1)n 的一类数列,在求S n 时, 要注意讨论n 的奇偶性; ②在用等比数列前n 项和公式时,一定要分q=1和q ≠1两种情况来讨论;③用a n =S n －S n －1求数列的通项公式时,你注意到此等式成立的条件了吗?(n ≥2,当n=1时,a 1=S 1); ④一般地,当已知条件中含有a n 与S n 的混合关系时,常需运用关系式a n =S n －S n －1, 先将已知条件转化只含a n 或S n 的关系式,然后现求解. ⑤当遇到a n+1－a n －1=d 或11n n a q a +-=(n ≥2)时,要分奇数项偶数项讨论,其结果多是分段形式. 三角函数1.弧长分式: ||l r α=, 扇形面积公式: S=12lr 21||2r α=. 其中l 为弧长, r 为圆的半径, α为圆心角的弧度数.2.三角函数诱导公式的本质是: 奇变偶不变,符号看象限.3.同角三角函数关系: sin 2α+cos 2α=1ααcos sin =tan α； tan αcot α=1. 4.三角函数的性质、图象及其变换:(1)y=sinx,y=cosx,y=tanx 的定义域,值域,单调性,奇偶性,有界性和周期性.注意: 绝对值对三角函数周期性有影响,一般说,某一周期函数解析式加绝对值或平方,其周期是: 弦减半,切不变.既是周期函数又是偶函数的函数自变量加绝对值,其周期性不变.其他不定,如y=sin 2x,y=|sinx|的周期是π, y=|tanx|的周期不变. (2)函数y=Asin(ωx+ϕ):①图象是由五点法作出来的,这五个点是满足: ωx+ϕ=0, 2π, π, 32π,2π的五个x 的值,对应y 值分别是0,A,0,－A,0;②这个函数的最小正周期是2πϖ.注意: 用"五点法"作正余弦函数的图象要注意必须先将解析式化为y= Asin(ωx+ϕ)或y= Acos(ωx+ϕ)的形式,要关注: ω>0的限制条件,当题目没有这个限制条件时要注意最小正周期是2||πϖ, 应特别注意其对单调性的影响.5.三角恒等变换的主要公式: cos （α±β）=cos αcos β sin αsin β. sin(α±β）=sin αcos βcos αsin βtan tan tan()1tan tan αβαβαβ±±=sin2α=2sinαcosα co s2α=cos 2α－sin 2α=2cos 2α－1=1－2sin 2α.注意: 如下公式的运用: tan tan tan()(1tan tan )αβαβαβ±=±22tan sin 21tan ααα=+221tan cos 21tan ααα-=+, 22tan tan 21tan ααα=- sin 2α=22cos 1α-，cos 2α=22cos 1α+sin 1cos tan 21cos sin ααααα-==+ 6.三角恒等变换方法:(1)角的变换主要有: 如α=(α+β)－β=(α－β)+β, 2α=(α+β)+ (α－β), 2α=(β+α)－(β－α),α+β=2·α+β2 , α+β2 = (α－β2)－(α2－β)等.(2)三角式变换主要有: 三角函数名互化(切化弦)、三角函数次数的降升(降次、升次),运算结构的转化,解题时应本着"三看"的基本原则来进行, 即"看角、看函数、看特征", 基本技巧有: 巧变角,分式变形使用, 化切为弦,用倍角公式将高次降次.注意: 三角恒等式的证明方法灵活多样,可总结如下:①从一边开始直接推证,得到另一边,一般地,如果所证等式一边比较繁而另一边比较简时多采用此法,即由繁到简.②左右归一法,即将所证恒等式左、右两边同时推导变形,直接推得左右两边都等于同一个式子. ③比较法, 即设法证明: "左边－右边=0" 或"左右=1"; ④分析法,从被证的等式出发,逐步探求使等式成立的充分条件,一直推到已知条件或显然成立的结论成立为止,则可以判断原等式成立. 7.内角和定理:(1)三角形的三角之和为π, 任意两角和与第三个角总互补,任意两半角和与第三角的半角总互余. (2)锐角三角形 ⇔ 三内角都是锐角 ⇔ 三内角的余弦值为正值 ⇔ 任意两角和都是钝角 ⇔ 任意两边的平方和大于第三边的平方. 8.正弦定理:sin sin sin a b cA B C===2R (R 为三角形外接圆的半径). 注意: ①已知三角形两边一对角,求解三角形时,若运用正弦定理,则务必注意可能有两解. ②正弦定理之变式: a:b:c=sinA:sinB:sinC, a=2RsinA, b=2RsinB,c=2RsinC,sin sin sin a b c A B C ===sin sin sin a b cA B C++++ ③ 三角形的内切圆半径: 2ABCS r a b c∆=++9.余弦定理: a 2=b 2+c 2－2bccosA, 222cos 2b c a A bc +-==22()12b c abc+-- 注意: 正弦定理、余弦定理并不是孤立的,解题时要根据具体题目合理选用,有时还要交替运用. 10.面积公式: 111sin sin sin 222ABC S ab C bc A ac B ∆=== 11.在△ABC 中, tanA+tanB+tanC=tanAtanBtanC, tan tan tan tan tan tan 1222222A B B C A C ++=平面向量1.几个概念: 零向量、单位向量(与AB 共线的单位向量是±||ABAB ,特别地 (||||AB AC AB AC +)⊥(||||AB AC AB AC -)(菱形的对角线垂直)、平行(共线)向量(无传递性,是因为有0)、相等向量(有传递性)、相反向量、向量垂直以及一个向量在另一向量上的投影(a 在b 上的投影是:||cos ,||a ba ab b <>=∈R) 2.两个非零向量平行(共线)的充要条件: a ∥b ⇔a =λb .两个非零向量垂直的充要条件: a ⊥b ⇔a ·b =0 ⇔ |a +b |=|a －b | 注意: ①零向量和任何向量共线②零向量不能作为基底,两个非零向量共线时,不能作为平面的一组基底,给定向量沿基底的分解是唯一的.③向量夹角与直线的夹角区分开,向量共线时,夹角有为0°或180°两种情况 3.平面向量基本定理: 如果1e , 2e 是同一平面内的两个不共线向量,那么对于该平面内的任一向量a ,有且仅有一对实数λ1,λ2,使a =λ11e +λ22e .4.三点A 、B 、C 共线⇔AB 、AC 共线,向量PA 、PB 、PC 中三终点A 、B 、C 共线⇔存在实数α、β使得PA =αPB +βPC 且α+β=1.5.向量的数量积:设a =（x 1，y 1），b =（x 2，y 2），则 |a |2=(a )2=a ·a （1）a ·b =| a |·| b |cosθ= x 1x 2+y 1y 2；（2）|a |=2121y x +； （3）cos 〈a ，b 〉=||||a ba b =222221212121y x yx y y x x +⋅++；a 在b 上的投影为||cos ,||a b a a b b <>==（4）a ⊥b ⇔a ·b =0⇔x 1x 2+y 1y 2=0.注意: ①<a ,b >为锐角 ⇔a ·b >0且a 、b 不同向; <a ,b >为直角⇔a ·b =0且a 、b ≠0; <a ,b >为钝角 ⇔a ·b <0且a 、b 不反向; a ·b <0是<a ,b >为钝角的必要非充分条件. ②对于一个向量等式,可以移项,两边平方、两边同乘以一个实数,两边同时取模,两边乘以一个向量,但不能两边同除以一个向量,即两边不能约去一个向量; 向量的"乘法"不满足结合律,即()()a b c a b c ≠,切记两向量不能相除(相约)6.向量的运算律: (1)交换律: a b b a +=+, a b b a =(2)结合律: ()()a b c a b c ++=++, ()a b c a b c --=-+, λ(μa )=(λμ) a ,(λa )·b =λ(a ·b )=a ·(λb ); (3)分配律: (λ+μ) a =λa +μa , λ(a +b )=λa +λb , (a +b )·c =a ·c +b ·c注意: ①向量加法的三角形法则适用于任意两个非零向量相加,并且可以推广到两个以上的非零向量相加.②向量减法是加法的逆运算.③向量平行(共线)与直线平行是有区别的,直线平行不包括重合的情况. 7.线段的定比分点坐标公式设P 1(x 1,y 1),P 2(x 2,y 2),P(x,y)是线段P 1P 2的分点,λ是实数, 且1PP =λ2PP ,则121211x x x y y y λλλλ+⎧=⎪⎪+⎨+⎪=⎪+⎩⇔121OP OP OP λλ+=+⇔12(1)OP tOP t OP =+- (t= 11+λ)中点坐标公式: 121222x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩⇔122MP MP MP+=⇔ P 为P 1P 2的中点. 三角形重心坐标公式: △ABC 三个顶点的坐标分别为A(x 1,y 1)、B(x 2,y 2)、C(x 3,y 3)则△ABC 的重心坐标是G(1233x x x ++,1233y y y ++). 8.三角形四心的向量形式: 设O 为△ABC 所在平面上一点, 角A 、B 、C 所对边长分别是a 、b 、c,则 (1)O 为△ABC 的外心 ⇔2OA =2OB =2OC (2)O 为△ABC 的重心⇔OA +OB +OC =(3) O 为△ABC 的垂心⇔OA ·OB =OB ·OC =OA ·OC (4) O 为△ABC 的内心⇔ a OA +b OB +c OC =0 9.按向量平移的几个结论:(1)点P(x,y)按向量a =(h,k)平移后得到点P'(x+h,y+k)..(2)函数y=f(x)的图象C 按向量a =(h,k)平移后得到图象C', 则C'的函数解析式为y=f(x －h)+k. (3)图象C'按向量a =(h,k)平移后得到C, 若C 的解析式y=f(x),则C' 的函数解析式y=f(x+h)－k. (4)曲线C: f(x,y)=0按向量a =(h,k)平移后得到图象C' , 则C' 的方程为f(x －h,y －k)=0. (5)向量m =(x,y)按向量a =(h,k)平移后得到的向量仍然为m =(x,y).直线和圆的方程1.直线的倾斜角与斜率: 直线倾斜角的X 围是[0,π), 经过两点P 1(x 1,y 1), P 2(x 2,y 2),斜率公式为:2121y y k x x -=-2.直线方程的五种形式:(1)点斜式为: y －y 1=k(x －x 1)(直线过点P 1(x 1,y 1), 且斜率为k,不包括y 轴和平行于y 轴的直线). (2)斜截式为: y=kx+b (b 为直线l 在y 轴上的截距,且斜率为k, 不包括y 轴和平行于y 轴的直线) (3)两点式为:112121y y x x y y x x --=--(y 1≠y 2)(直线过点P 1(x 1,y 1),P 2(x 2,y 2),且x 1≠x 2,y 1≠y 2,不包括坐标轴和平行于坐标轴的直线) (4)截距式为:1x ya b+=(a 、b 分别为直线的横、纵截距,且a≠0、b≠0,不包括坐标轴,平行于坐标轴和过原点的直线)(5)一般式Ax+By+C=0(其中A 、B 不同时为0)注意: 应用直线方程的点斜式、斜截式设直线方程时,一般可设直线的斜率为k, 但要注意到直线垂直于x 轴时,即斜率k 不存在的情况.3,知直线纵截距b,常设其方程为y=kx+b 或x=0; 知直线横截距x 0, 常设其方程为x=my+x 0, (直线的斜率k 存在时,m 为k 的倒数)或y=0.知直线过点(x 0,y 0),常设其方程为y=k(x －x 0)+y 0或x=x 0.注意: 直线在坐标轴上的截距可正、可负、也可为0, 直线两截距相等⇔ 直线的斜率为－1或直线过原点；直线两截距互为相反数⇔ 直线的斜率为1或直线过原点;直线两截距绝对值相等⇔ 直线的斜率为±1或直线过原点.4.距离公式: (1)点P(x 0,y 0)到直线l: Ax+By+C=0的距离:d =(2)两平行线间的距离公式: Ax+By+C 1=0, Ax+By+C 2=0之间的距离d =(3)夹角公式和到角公式 夹角公式: ① 2121tan ||1k k k k α-=+(l 1: y=k 1x+b 1,;y=k 2x+b 2,k 1k 2≠－1);②12211212tan ||A B A B A A B B α-=+(l 1: A 1x+B 1y+C 1=0,l 2: A 2x+B 2y+C 2=0, A 1A 2+B 1B 2≠0)直线12l l ⊥时,直线1l 与2l 的夹角为2π l 1到l 2的角公式: ①2121tan 1k k k k α-=+(l 1: y=k 1x+b 1,;y=k 2x+b 2,k 1k 2≠－1);②12211212tan A B A B A A B B α-=+(l 1: A 1x+B 1y+C 1=0,l 2: A 2x+B 2y+C 2=0, A 1A 2+B 1B 2≠0)直线12l l ⊥时,直线1l 到2l 的夹角为2π 5.圆的方程有: 标准方程222()()x a y b R -+-=;一般式方程: 220x y Dx Ey F ++++=(2240D E F +->);以A(x 1,y 1),B(x 2,y 2)为直径的两端点的圆的方程是(x －x 1)(x －x 2)+(y －y 1)(y －y 2)=0; 圆的参数方程是cos cos x a r y b r θθ=+⎧⎨=+⎩(θ为参数)注意: 解决直线与圆的位置关系问题有"函数方程思想"和数形结合思想"两种思路,等价转化求解,重要的是发挥"圆的平面几何性质(如半径、半弦长、弦心距构成直角三角形,切线长定理,割线定理,弦切角定理等)的作用.6.(1)过圆222x y R +=上一点P(x 0,y 0)的切线方程是200xx yy R +=(2)过圆222()()x a y b R -+-=上一点P(x 0,y 0)的切线方程是200()()()()x a x a y a y a R --+--= 过圆220x y Dx Ey F ++++=(2240D E F +->)上一点P(x 0,y 0)的切线方程是20000()()22D Exx yy x x y y F R ++++++= (3)如果点P(x 0,y 0)在圆外,那么上述直线方程表示过点P 两切线上两切点的"切点弦"方程.注意: 求过一点的圆的切线方程时要注意点在圆上还是点在圆外7.直线与圆的位置关系: (1)代数方法(判断直线与圆方程联立所得方程组的解的情况)； △>0⇔ 相交; △=0 ⇔ 相切; △<0⇔ 相离.(2)几何方法(比较圆心到直线的距离与半径的大小);设圆心到直线的距离为d, 则d<r ⇔ 相交; d=r ⇔ 相切;d>r ⇔ 相离. (主要掌握几何法)(3)直线被圆所截得的弦长l =8.圆与圆的位置关系: (d 表示圆心距,R,r 表示两圆的半径,R>r)(1)d>R+r ⇔相离; (2)d=R+r ⇔ 相外切 (3) R －r<d<R+r ⇔ 相交; (4)d=R －r ⇔ 内切 (5) 0<d<R －r ⇔ 内含.9.曲线C 1: f(x,y)=0 与C 2: g(x,y)=0的交点坐标⇔ 方程组(,)0(,)0f x y g x y =⎧⎨=⎩的解.10.过两圆C 1: f(x,y)=0、C 2: g(x,y)=0交点的圆(公共弦)系为f(x,y)+λg(x,y)=0, 当且仅当无平方项时,f(x,y)+λg(x,y)=0为两圆公共弦所在直线方程.11.(1)二元一次不等式表示的平面区域: 设点P(x 1,y 1), Q(x 2,y 2), 若Ax 1+By 1+C 与Ax 2+By 2+C 同号,则P,Q 在直线l 的同侧,异号则在直线l 的异侧.(2)求解线性规划问题的步骤: ①根据实际问题的约束条件列出不等式; ②作出可行域,写出目标函数; ③确定目标函数的最优位置,从而获得最优解.圆锥曲线方程1.椭圆方程: 22221x y a b+=(a>b>0), 点P(x,y)在椭圆上, 定点F 1、F 2是椭圆的左、右焦点.(1)离心率: c e a == (2) |PF 1|=a+ex, |PF 2|=a －ex . 2.双曲线方程: 22221x y a b-=(a>0,b>0), 点P(x,y)在双曲线上,定点F 1、F 2是椭圆的左、右焦点.(1)离心率: c e a == (2) |PF 1|=±(a+ex), |PF 2|=±(a －ex) . (左支取负,右支取正) 3.抛物线方程: y 2=2px (p>0) ,点C(x 1,y 1)、D(x 2,y 2)在抛物线上. (1)焦半径 |CF|=x 1+p2(2)以抛物线上的点为圆心,焦半径为半径的圆必与准线相切;以抛物线焦点弦为直径的圆必与准线相切.4.二次函数y=ax 2+bx+c= 224()24b ac b a x a a-++(a ≠0)的图象是抛物线.(1)顶点坐标为 24(,)24b ac b a a -- ; (2)焦点坐标为241(,)24b ac b a a -+-; (3)准线方程是y=2414ac b a--.5.在直线与圆锥曲线的位置关系问题中,有"函数方程思想:和"数形结合思想"两种思路,进行等价转化求解.注意: ①直线与圆锥曲线相交的必要条件是它们构成的方程组有实数解, 当出现一元二次方程时,务必要求"△≥0", 尤其是在应用韦达定理解决问题时, 必须先有"判别式△≥0"②直线与抛物线(相交不定交于两点)、双曲线的位置关系的特殊性,应谨慎处理(注意渐近线) ③设A(x 1,y 1),B(x 2,y 2), 弦长公式12|x x -,12||y y -. ④如果在一条直线上出现"三个或三个以上的点",那么可选择应用 "斜率"为桥梁进行转化. 6.求曲线方程的方法: 待定系数法、定义法、直译法、代点法、参数法等. 7.圆锥曲线的两类对称问题(1)曲线F(x,y)=0关于点P(x 0,y 0)成中心对称的曲线是F(2x 0－x,2y 0－y)=0(2)曲线F(x,y)=0关于直线Ax+By+C=0成轴对称的曲线方程由一方程组得到(代点法求)注意: 曲线F(x,y)=0关于原点O 成中心对称的曲线是F(－x,－y)=0;曲线F(x,y)=0关于x 轴对称的曲线是F(x,－y)=0;曲线F(x,y)=0关于y 轴对称的曲线是F(－x,y)=0;曲线F(x,y)=0关于直线y=x 对称的曲线是F(y,x)=0; 曲线F(x,y)=0关于y=－x 对称的曲线上F(－y,－x)=0.直线、平面、简单几何体1.证明位置关系的主要方法(1)线面平行: a b b a a ααα⎫⎪⊂⎪⎬⊄⎪⎪⎭⇒ a ∥α; a a αβαβ⎫⇒⎬⊂⎭, a a a αββαα⊥⎫⎪⊥⇒⎬⎪⊄⎭(2)线线平行: a a a b b αβαβ⎫⎪⊂⇒⎬⎪⋂=⎭； a a b b αα⊥⎫⇒⎬⊥⎭ ； a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭；a c a b b c ⎫⇒⎬⎭ (3)面面平行 ,,a b a b O a b αααβββ⊂⊂⎫⎪⋂=⇒⎬⎪⎭; a a ααββ⊥⎫⇒⎬⊥⎭；αγαββγ⎫⇒⎬⎭(4)线线垂直: a a b b αα⊥⎫⇒⊥⎬⊂⎭(5)线面垂直: ,,a b a b O l l a l b ααα⊂⊂⎫⎪⋂=⇒⊥⎬⎪⊥⊥⎭;,l a a a l αβαββα⊥⎫⎪⋂=⇒⊥⎬⎪⊂⊥⎭；a a αββα⎫⇒⊥⎬⊥⎭;a b b a αα⎫⇒⊥⎬⊥⎭(6)面面垂直: a a βαβα⊂⎫⇒⊥⎬⊥⎭;a a βαβα⎫⇒⊥⎬⊥⎭注意: 证明立体几何中平行、垂直的基本思想是利用线面关系的转化,即.↔↔⎧⎪⊥↔⊥↔⊥⎨⎪↔⊥↔⎩线线线面面面判定线线线面面面性质线线线面面面2.面积射影定理: 'cos S S θ=(平面多边形及其射影的面积分别是S 、S', 它们所在平面所成锐二面角为θ)3.球: 球的半径是R, 则其体积343V R π=, 其表面积24S R π=. 4.各个棱长都相等的三棱锥的性质: 设棱长为a, 则正四面体中: (1)(2)对棱间的距离为2a , (3)相邻两面所成角的余弦值为13, (3), 外接球的. 5.空间向量的加法与数乘运算的运算律:(1)加法交换律: a +b =b +a (2)加法结合律: (a +b )+c =a +(b +c ) (3)数乘分配律: λ(a +b )=λa +λb6.共线向量定理: 对空间任意两个向量a , b (b ≠0), a ∥b ⇔ 存在实数λ使a =λb ,P 、A 、B 三点共线⇔ AP ∥AB ⇔AP =t AB ⇔OP =(1－t)OA +t OB ; AB ∥CD ⇔AB 、CD 共线且AB 、CD 不共线⇔AB =t CD , 且AB 、CD 不共线;7.共面向量定理: (1)向量p 与两个不共线的向量a 、b 共面⇔存在有序实数对(x,y), 使p =x a +y b . 推论: 空间一点P 位于平面MAB 内⇔存在有序实数对(x,y), 使MP =x MA +y MB ,或对空间任一定点O, 有序实数对(x,y), 使OP =OM + x MA +y MB .(2)对空间任一点O 和不共线的三点A 、B 、C, 满足OP =x OA +y OB +z OC (x+y+z=k), 则当k=1时,对于空间任一点O,总有P 、A 、B 、C 四点共面; 当k ≠1时,若O ∈平面ABC, 则P 、A 、B 、C 四点共面;若O ∉平面ABC, 则则P 、A 、B 、C 四点不共面;(3) A 、B 、C 、D 四点共面⇔AD 与AB 、AC 共面, AD =x AB +y AC ⇔OD =(1－x －y) OA +x OB +y OC (O ∉平面ABC)8.空间向量基本定理: 如果三个向量a 、b 、c 不共面,那么对空间任一向量p ,存在一个唯一的有序实数组(x,y,z), 使p =x a +y b +z c推论: 设O 、A 、B 、C 是不共面的四点,则对空间任一点P, 都存在唯一的有序实数组(x,y,z),使OP =x OA +y OB +z OC9.向量的直角坐标运算: a =（x 1，y 1，z 1），b =（x 2，y 2，z 2），(1)a ±b =（x 1±x 2，y 1±y 2，z 1±z 2）， (2)λa =（λx 1，λy 1，λz 1）(λ∈R); (3) a ·b =x 1x 2+y 1y 2+z 1z 2 (4)A(x 1，y 1，z 1）, B=x 2，y 2，z 2）, 则AB = OB －OA =(x 2－x 1,y 2－y 1,z 2－z 1)10.空间的线线平行或垂直: 设a =（x 1，y 1，z 1），b =（x 2，y 2，z 2）, 则a ∥b ⇔a =λb (b ≠0)⇔121212x xy y z zλλλ=⎧⎪=⎨⎪=⎩, a ⊥b ⇔x 1x 2+y 1y 2+z 1z 2=0.11.夹角公式: 设a =（x 1，y 1，z 1），b =（x 2，y 2，z 2）则cos 〈a ，b 〉=222222212121212121z y x z y x z z y y x x ++++++.推论: (x 1x 2+y 1y 2+z 1z 2)2≤(222111x y z ++)(222222x y z ++)12.异面直线所成角: cos θ=|cos 〈a ，b 〉|=||||||a b ab =(其中θ(0°<θ≤90°)为异面直线a 、b 所成角,a 、b 分别表示异面直线a 、b 的方向向量) 13.直线AB 与平面α所成角β满足: ||sin ||||AB n AB n β=(n 为平面α的法向量)14.二面角α－l －β的平面角θ满足: cos ||||m nm n θ=(m 、n 为平面α、β的法向量)(注意:在处理实际问题时,要根据具体图形确定是锐角还是钝角,以决定角的大小) 15.点B 到平面α的距离: ||||AB n d n =(n 为平面α的法向量,A ∈α,AB 是α的一条斜线段) 排列、组合、二项式定理1.两个基本原理: 分类计数原理(加法原理): N=m 1+m 2+…+m n 分步计数原理(乘法原理) N=m 1×m 2×…×m n2.排列数mn A 、组合数mn C 中(n≥m, n≥1, m≥0,m 、n ∈N*.(1)排列数公式: mn A =n(n －1)(n －2)…(n －m+1)=!()!n n m -(m≤n);n n A = !n =(n(n －1)(n －2)·…·2·1(2)组合数公式: mmn nm mA C A == n ·(n －1)·…·(n －m+1)m ·(m －1)·…·2·1= !)!(!m m n n -(m ≤n);mn A =m!·C m n (3) C m n =C mn n-C m n 1+=C mn +C 1-m n.(m ≤n) 11k k n n kC nC --= r r C +1r r C ++2r r C ++…+r n C =11r n C ++; 0n C +1n C +2n C +…+ n n C =2n1n C +3n C +5n C + … =0n C +2n C +4n C + …=12n -注意: 解排列组合问题的主要方法有: 相邻问题捆绑法; 不相邻(相间)问题插空法;多排问题单排法;定位问题优先法;多元问题分类法;有序问题用除法(组合法);选取问题先选后排法;至多、至少问题间接法,特别地,还要注意隔板法.3.(1)二项式定理: (a+b)n = 0n C n a + 1n C 1n a b -+ … + r n r r n C a b -+… + n n C nb ,其中组合数r n C 叫做第r+1项的二项式系数,展开式共有n+1项,其中第r+1项为1r T +=r n rr n C ab -(2)二项展开式中二项式系数(组合数)的性质: 对称性、增减性与最大值,0n C +1n C +2n C +…+nn C =2n (3)应用"赋值法"同样可得到相关性质或寻求二项展开式中"奇次(数)项""偶次(数)项"的系数和. 如1n C +3n C +5n C + … =0n C +2n C +4n C + …=12n -注意: 二项展开式中区分"二项式系数、项的系数",寻求其中项的系数的最大值是将相邻两项的系数构建不等式进行处理.概率1.事件的关系:(1)事件B 包含事件A: 事件A 发生,则事件B 一定发生,记作: A B ⊆(2)事件A 与事件B 相等: 若A B ⊆, B A ⊆, 则事件A 与B 相等,记作: A=B(3) 和 (并)事件: 某事件发生,当且仅当事件A 发生或事件B 发生, 记作: A+B (或A ∪B) (4)积(交)事件: 某事件发生,当且仅当事件A 发生且事件B 发生, 记作: AB (或A ∩B) (5)事件A 与事件B 互斥: 若A ∩B 为不可能事件(A ∩B=∅), 则事件A 与事件B 互斥. (6)对立事件: A ∩B 为不可能事件, A ∪B 为必然事件,则A 与B 互为对立事件.注意:从集合角度看,互斥事件是交集为空集的事件,对立事件就是互补事件,对立一定互斥,互斥不一定对立,不互斥一定不对立. 2.概率的计算公式.(1)等可能事件的概率计算公式: P(A)=事件A 包含的基本事件数试验的基本事件总数= mn (2)互斥事件的概率计算公式: P(A+B)=P(A)+P(B) (3)对立事件的概率计算公式: P(A )=1－P(A)(4)独立事件同时发生的概率计算公式: P(AB)=P(A)P(B)(5)独立重复试验的概率计算公式: ()(1)k k n kn n P k C p p -=-概率与统计1.离散型随机变量的分布列的两个性质: (1) i p ≥0 (i=1,2,…); (2)p 1+p 2+…+p n =12.数学期望公式: E ξ=x 1p 1+x 2p 2+…+x n p n3.数学期望的性质: (1) E(a ξ+b)=aE ξ+b, (2 ) 若ξ~B(n,p), 则E ξ=np4.方差公式: D ξ=(x 1－E ξ)2·p 1+(x 2－E ξ)2·p 2+ … +(x n －E ξ)2·p n 标准差: σξ=5.方差的性质: (1)D(a ξ+b)=a 2 D ξ (2 ) 若ξ~B(n,p), 则 D ξ=np(1－p). 6.方差与期望的关系:D ξ=2E ξ－2()E ξ7.正态分布密度函数: ()f x22()2x e μσ--, x ∈(－∞,+∞), 式中的实数μ, σ(σ>0)是参数,分别表示总体的平均数与标准差.这个函数的图旬具有怎样的性质? 8.抽样方法:简单随机抽样、分层抽样、系统抽样9.总体分布的估计就是用样本的频率分布估计总体的分布.10.回归方程: y =bx+a 其中 1122211()()()nni i i ii i nni ii i x x y y x y nx yb x x xnxa y nx====⎧---⎪⎪==⎪⎨--⎪⎪=-⎪⎩∑∑∑∑极限1.数列的极限(1)数列极限的四则运算法则: 如果lim∞→n a n =A ，lim∞→n b n =B ，那么lim∞→n (a n ±b n )=A±Blim ∞→n (a n ·b n )=A·Blim ∞→n n n b a =BA(B≠0) 注意: 极限不存在的情况是①±∞=∞→n n a lim ；②极限值不唯一，跳跃，如1，-1，1，-1…. (2)特殊数列的极限:①0, ||1lim 1, 1, ||11n n q q q q q →∞<⎧⎪==⎨⎪>=-⎩不存在或②1101100,lim ,,k k k k i i i n i i kk ia n a n a a k lb n b n b b k l---→∞-⎧<⎪+++⎪==⎨+++⎪⎪>⎩不存在③S= 1(1)lim 1n n a q q →∞--=11a q- (S 为无 穷等比数列{11n a q -}(|q|<1)的和.2.函数的极限: (1)0lim ()x x f x →=a ⇔0lim ()x x f x -→=0lim ()x x f x +→=a (2)函数的夹逼性定理: 如果函数f(x)、g(x)、h(x)在点x 0的附近满足:①g(x)≤f(x)≤h(x)。
陕西陕西省西安交大阳光中学高中物理 6.3.1 万有引力定律导学案(无答案)新人教版必修2
6.地球质量大约是月球质量的81倍，一个飞行器在地球与月球之间，当地球对它们的引力和它的引力大小相等时，这飞行器距地心的距离与距离月球的距离之比为多少
达
标
训
练
1.要使两物体间的万有引力减小到原来的1/4，下列办法不可采用的是（）
A.使两物体的质量各减小一半，距离不变
B.使其中一个物体的质量减小到原来的1/4，距离不变
C.使两物体间的距离增为原来的2倍，质量不变
D.使两物体间的距离和质量都减为原来的1/4
2.火星的半径是地球半径的一半，火星的质量约为地球质量的1/9；那么地球表面50 kg的物体受到地球的吸引力约是火星表面同质量的物体受到火星吸引力的________倍.
§6.3.1万有引力定律
第课时
课题名称
时间
第周Байду номын сангаас期
课型
新授课
主备课人
吴俊峰
目标
1、体会万有引力得出的思路和过程.
2、知道万有引力定律的含义并会推导万有引力定律.
3、知道地面上物体所受的重力与天体间的引力是同一性质的力，即服从平方反比定律的万有引力.记住引力常量G并理解其内涵.
重点
体会万有引力定律的建立过程，记住万有引力定律的内容及表达公式
B.由于苹果质量小，对地球的引力小，而地球质量大，对苹果的引力大造成的
C.苹果与地球间的相互引力是相等的，由于地球质量极大，不可能产生明显加速度D.以上说法都不对
2.两行星的质量分别为 和 ，绕太阳运行的轨道半径分别是 和 ，若它们只要万有引力作用，那么这两个行星的向心加速度之比( )
上海昂立智立方数学高中 高数—10暑—05—集合的概念与表示、集合间的关系—周宝瑞-教师版
高一数学暑假班（教师版）教师日期学生课程编号课型课题集合的概念与表示、集合间的关系教学目标1．理解集合含义，理解元素与集合“属于”关系，深刻理解集合元素的确定性、互异性、无序性；掌握常用数集专用符号；能选择合适的表达方式描述集合；2．深刻理解集合与集合之间的包含以及相等关系；掌握子集、真子集、空集、两个集合相等等概念；会写出任意集合的所有子集、真子集。
教学重点会用列举法、描述法表示集合；掌握集合间的关系教学安排版块时长1例题解析502巩固训练403师生总结104课后练习20一、集合的概念（一）、知识精讲 （1）集合的概念我们把能够确切指定的一些对象组成的整体叫做集合，简称集。
集合中的各个对象叫做这个集合的元素。
对于一个给定的集合，集合中的元素具有确定性、互异性、无序性。
（2）集合的元素特征确定性是指一个对象要么是给定集合的元素，要么不是这个集合的元素，二者必居其一。
比如“著名的数学家”、“较大的数”、“高一一班成绩好的同学”等都不能构成集合，因为组成集合的元素不确定。
互异性是指对于一个给定的集合，集合中的元素是各不相同的，也就是说，一个给定的集合中的任何两个元素都是不同的对象，集合中的元素不重复出现。
例如由元素1,2,1组成的集合中含有两个元素：1,2。
无序性是指组成集合的元素没有次序，只要构成两个集合的元素是一样的，我们就称这两个集集合的概念与表示、集合间的关系例题解析知识梳理集合定义 特征与元素关系表示与集合关系把能够确切指定的对象看作一个整体确定性、无序性、互异性属于、不属于 描述法、列举法、图示法子集、真子集、相等合是相等的。
（3）集合与元素的字母表示、元素与集合的关系集合常用大写字母C B A 、、…来表示，集合中的元素用c b a 、、…表示，如果a 是集合A 的元素，就记作A a ∈，读作“a 属于A ”；如果a 不是集合A 的元素，就记作A a ∉，读作“a 不属于A ”（4）常用的数集及记法数的集合简称数集，我们把常用的数集用特定的字母表示：全体自然数组成的集合，即自然数集，记作N ，不包含零的自然数组成的集合，记作*N 全体整数组成的集合，即整数集，记作Z 全体有理数组成的集合，即有理数集，记作Q 全体实数组成的集合，即实数集，记作R常用的集合的特殊表示法：实数集R （正实数集+R ）、有理数集Q （负有理数集-Q ）、整数集Z （正整数集+Z ）、自然数集N （包含零）、不包含零的自然数集*N ；（5）集合的分类我们把含有有限个元素的集合叫做有限集，含有无限个元素的集合叫做无限集我们引进一个特殊的集合——空集，规定空集不含元素，记作∅，例如，方程012=+x 的实数解所组成的集合是空集，又如，两个外离的圆，它们的公共点所组成的集合也是空集。
上海昂立智立方数学高中 高数—10暑—04—一元二次方程根的分布—周波-教师版
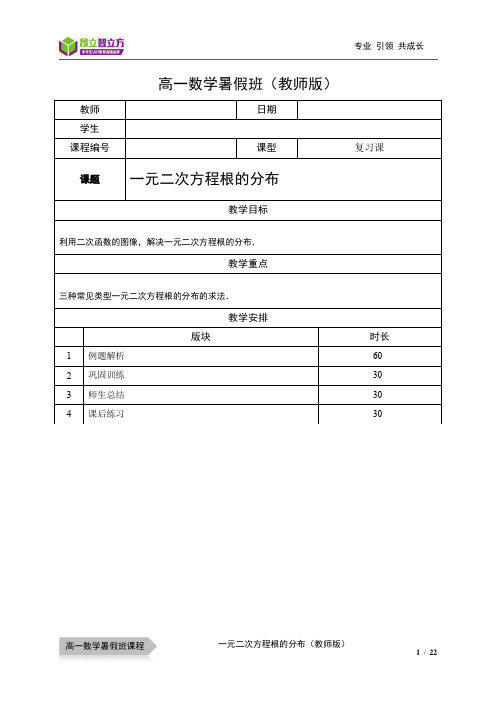
高一数学暑假班（教师版）教师日期学生课程编号课型复习课课题一元二次方程根的分布教学目标利用二次函数的图像，解决一元二次方程根的分布．教学重点三种常见类型一元二次方程根的分布的求法．教学安排版块时长1例题解析60 2巩固训练30 3师生总结30 4课后练习30设方程()200ax bx c a++=≠的不等两根为12,x x且12x x<，相应的二次函数为()20f x ax bx c=++=，方程的根即为二次函数图象与x轴的交点，它们的简单分布情况见下表分布情况两个负根即两根都小于0()120,0x x<<两个正根即两根都大于0()120,0x x>>一正根一负根即一个根小于0，一个大于0()12x x<<大致图象（>a）得出的结论()200baf∆>⎧⎪⎪-<⎨⎪>⎪⎩()200baf∆>⎧⎪⎪->⎨⎪>⎪⎩()00<f大致图象（<a）一元二次方程根的分布知识梳理得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()00>f综合结论（不讨论a）()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()00<⋅f a分布情况两根都小于k即kx k x <<21, 两根都大于k 即 k x k x >>21, 一个根小于k ，一个大于k 即21x k x <<大致图象（>a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f大致图象（<a ）kkk得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()0>k f综合结论（不讨论a）()020b k a a f k ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()020b k a a f k ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()0<⋅k f a分布情况两根都在()n m ,内两根有且仅有一根在()n m ,内（图象有两种情况，只画了一种）一根在()n m ,内，另一根在()q p ,内，q p n m <<<大致图象（>a ）得出的结论()()0002f m f n b m na ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()000f m f n f p f q ⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()0f m f n f p f q <⎧⎪⎨<⎪⎩大致图象（0 < a）得出的结论()()2f mf nbm na∆>⎧⎪<⎪⎪<⎨⎪⎪<-<⎪⎩()()0<⋅nfmf()()()()f mf nf pf q⎧<⎪>⎪⎨>⎪⎪<⎩或()()()()f m f nf p f q<⎧⎪⎨<⎪⎩综合结论（不讨论a）——————()()0<⋅nfmf()()()()⎪⎩⎪⎨⎧<<qfpfnfmf根在区间上的分布还有一种情况：两根分别在区间()nm,外，即在区间两侧12,x m x n<>，（图形分别如下）需满足的条件是（1）0a>时，()()f mf n<⎧⎪⎨<⎪⎩；（2）0a<时，()()f mf n>⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明： （1）两根有且仅有一根在()n m ,内有以下特殊情况：1︒ 若()0f m =或()0f n =，则此时()()0f m f n <g 不成立，但对于这种情况是知道了方程有一根为m 或n ，可以求出另外一根，然后可以根据另一根在区间()n m ,内，从而可以求出参数的值．如方程()2220mx m x -++=在区间()1,3上有一根，因为()10f =，所以()()()22212mx m x x mx -++=--，另一根为2m，由213m <<得223m <<即为所求；2︒ 方程有且只有一根，且这个根在区间()n m ,内，即0∆=，此时由0∆=可以求出参数的值，然后再将参数的值带入方程，求出相应的根，检验根是否在给定的区间内，如若不在，舍去相应的参数．如方程24260x mx m -++=有且一根在区间()3,0-内，求m 的取值范围．分析：①由()()300f f -<g 即()()141530m m ++<得出15314m -<<-；②由0∆=即()2164260m m -+=得出1m =-或32m =，当1m =-时，根()23,0x =-∈-，即1m =-满足题意；当32m =时，根()33,0x =∉-，故32m =不满足题意；综上分析，得出15314m -<<-或1m =-1、与零有关的根的分布【例1】已知方程()2210x m x m -++=有两个不等正实根，求实数m 的取值范围．【难度】★★ 【答案】见解析 【解析】由()()0102200m f ∆>⎧⎪-+⎪->⎨⎪>⎪⎩g ⇒ ()218010m m m m ⎧+->⎪>-⎨⎪>⎩ ⇒ 3223220m m m ⎧<->+⎪⎨>⎪⎩或 ⇒ 例题解析0322m <<-或322m >+即为所求的范围．【例2】若方程05)2(2=-+-+m x m x的根满足下列条件，分别求出实数m 的取值范围．（1） 方程两实根均为正数；（2） 方程有一正根一负根．【难度】★★ 【答案】见解析【解析】分析 讨论二次方程根的分布，应在二次方程存在实根的条件下进行．代数方法与图象法是研究二次方程根的分布问题的主要方法．解1 （1）由题意，得.45244050)2(0)5(4)2(00022121-≤⇒⎪⎩⎪⎨⎧<<≥-≤⇒⎪⎩⎪⎨⎧>->--≥---⇒⎪⎩⎪⎨⎧>>+≥∆m m m m m m m m m x x x x 或所以，当4-≤m时，原方程两实根均为正数；（2）由题意，得.505021>⇒<-⇒⎩⎨⎧<≥∆m m x x 所以，当5>m时，原方程有一正根一负根．解2 二次函数m x m x y -+-+=5)2(2的图象是开口向上的抛物线．（1）如图，由题意，得4052)2(4)2(022050)2(020)0(22-≤⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧≤-+--->-->-⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧≤->->m m m m m m a b f a b f 。
高途课堂初中数学知识手册
数学知识手册书山有路勤为径学海无涯苦作舟目录CONTENTS03 数学·空间与平面几何14 坐数学·标系与函数16数学·统计与概率17数学·数与试23 数学·方程与不等式亲爱的初中生该是你展翅高飞的时刻了阳光在稀疏的树干下挥洒入眼的光刺痛瞳目即便前路坎坷但你要勇敢退缩的懦夫成千上万唯独你要做披着铠甲的战士纵使遍地荆棘也要勇往直前记住成长路上的每份经历都是青春的礼物中考亦是只是有的礼物包装得不那么精美但你要相信世界不会亏欠每一个努力的人只要你能带着信心给自己足够的时间用心地拆开它一定会发现包裹在里面的丰盛和美好成长的意义就在于不断的尝试和探索不断的失败又重来即使开始时会有些慌乱也要坚强勇敢执着奔放只待修炼出坚实的羽翼展翅飞向更宽广美好的世界奋斗吧唯有奋斗的人生才不会留下遗憾这场没有硝烟的战争你能依靠的只有自己以后的路还很长很长每一步都会比现在更好高途课堂真挚地祝福你能够在人生的每场考试中都取得佳绩比心~初中数学知识手册几何图形初步1几何图形: 长方体、圆柱、球、长（正）方形、圆、线段、点等，以及小学学习过的三角形，四边形等，都是从形形色色的物体外形中得出点，它们都是几何图形。
立体图形: 有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各部分不都在同一平面图形内，它们是立体图形。
平面图形: 有些几何图形(如线段、角、三角形、长方形、圆等)的各部分都在同一平面内，它们是平面图形。
几何展开图: 有些立体图形是由一些平面图形围成的，将它们的表面适当剪开，可以展开成平面图形，这样的平面图形称为相应立体图形的展开图。
体: 长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体。
几何体也简称体。
面：包围着体的是面。
线：夜晚流星划过天空时留下一道明亮的光线，节日的焰火画出的曲线组成优美的图案，这些都给我们以线的形象。
点: 天上的星星、世界地图上的城市等都给我们以点的形象。
吉林省长春市第五中学高中物理 第四章 牛顿运动定律 本章优化总结同步创新课件 整理1
例6 如图4－11所示，电 梯与水平面的夹角为30°， 当电梯加速向上运动时， 人对梯面的压力是其重力 的6/5倍，人与电梯面间的 摩擦力是其重力的多少倍？
图4－11
【解析】 对人受力分析：如图4－12甲 所示，重力mg，支持力FN，摩擦力F(摩擦力 方向一定与接触面平行，由加速度的方向推知 F水平向右)．建立直角坐标系：取水平向右(即 F的方向)为x轴正方向，竖直向上为y轴正方向， 此时只需分解加速度，如图乙所示，其中：ax ＝acos30°，ay＝asin30°.
(3)由于细绳只能产生拉力且沿绳的方向， 故 小球受力情况如图 4－10(c)所示，由图可见 F 合 F合 mg g ＝ ，即 a＝ ＝ . sinθ m sinθ
【答案】
见解析
2．正交分解法 所谓正交分解法是指把一个矢量分解在两 个互相垂直的坐标轴上的方法．正交分解法是 一种常用的矢量运算方法．其实质是将复杂的 矢量运算转化为简单的代数运算，从而简捷方 便地解题． 正交分解法是解牛顿运动定律题目的最基 本方法，物体在受三个或三个以上的不在同一 直线上的力作用时一般都用正交分解法．
例1 如图4－1所示，物体质量为m， 靠在粗糙的竖直墙上，物体与墙壁 之间的动摩擦因数为μ，若要使物 体沿着墙壁匀速运动，则外力F的 大小可以是( ) A．mg/sinα B．mg/(cosα－μsinα) 图4－1 C．mg/(sinα－μcosα) D．mg/(sinα＋μcosα)
【解析】 当物体沿墙 壁向下运动时，摩擦力竖直 向上，分析物体的受力如图4 －2所示，把F向竖直和水平 方向正交分解，则 水平方向Fcosα＝FN 竖直方向mg＝Fsinα＋Ff 又Ff＝μFN＝μFcosα
八年级数学上册第一章勾股定理3勾股定理的应用知识点解读素材北师大版
《勾股定理的应用》知识点解读知识点1 确定几何体上的最短路线(重点）重点解读在平面上寻找两点之间的最短路线是根据线段的性质：两点之间，线段最短.在立体图形上，由于受物体与空间的阻隔,两点间的最短路线不一定是两点间的线段长，应将其展成平面图形,利用平面图形中线段的性质确定最短路线。
【例1】有一圆柱形油罐，如图（左)已知油罐的周长是12米，高AB是5米，要以A 点环绕油罐建梯子，正好到A点的正上方B点，问梯子最短需多少米？解析将圆柱的侧面展开,展开图如图(右），是一个矩形，用勾股定理求出AB就是最短路程.答案如图，已知AC=12米（周长)，BC=5米（高)，∠ACB=90°，∴AB2=AC2+BC2=122+52=169=132，∴AB=13(m)，即梯子最短需13米。
变式练习:一只蚂蚁如果沿长方体的表面从A点到B点,那么沿哪条路线爬行最近？你能帮它找出来吗？如图（1)所示,长方体的长为15 cm，宽为10 cm，高为20 cm，点B与点C 的距离为5 cm.答案将两侧面展开，由点A先爬到E点，再爬到B点，路程最短.点拨将两侧面展开，如图（2)所示，连接AB，则AB2=202+152=625.将侧面与上地面展开,如图(3）所示，连接AB，则AB2=102+252=725.警示:有很多学生想不到去比较两个路程的远近而直接转化为求AB的距离。
知识点2 利用三角形三边的关系判断垂直（重点）重点解读本节垂直的识别是指应用三角形的三边关系判别三角形是直角三角形，这是识别垂直的一种方法，在实际生活中长判断两直线是否垂直，解决问题的一般方法是将实际问题转化为数学问题,再利用三角形三边的关系判断垂直.【例2】有一块四边形地ABCD，如图,∠B=90°，AB=4 m，BC=3 m，CD=12 m，DA=13 m，求该四边形地ABCD的面积。
解析连接AC，将四边形地ABCD分为△ABC和△ACD是解题关键。
全优课堂高中物理3.1万有引力定律课件
题后反思：对于此类问题，利用万有引力定律直接求解很困 难，当质点与质量分布均匀的球体间距离较小时，球体虽然不能 m1m2 被看作质点，但仍可用 F＝G r2 计算求解，此时的 r 应等于质 点与球心间的距离．此题目中球体被挖，质量分布不均匀，要先 “填补”变为质量分布均匀的球体再求解．
设地球是半径为 R 的均匀球体，质量为 M，若把质量 为 m 的物体放在地球的中心， 则物体受到地球的万有引力大小为 ( ) Mm A．零 B．G R2 C．无穷大 D．无法确定
三、万有引力定律 1．发现 牛顿 在前人研究的基础上，经严密的推理运算和实践检 ______ 验，提出了万有引力定律． 2．内容 质量 的物体间都存在相互吸引力，其大 宇宙间任意两个有______ 正比 ，与它们间距离的平方成 小与两物体的质量乘积成 ________ 反比 ． ______ m1m2 G r2 ，m 、m 分别是两物体的质 3．数学表达式：F＝________ 1 2 引力常数，英国科学家________ 卡文迪许 量，r 为两物体间的距离．G 为________ 2 2 －11 最先利用扭秤测出：G＝____________ N· m /kg . 6.67×10
公式或图示
行星绕太阳____________ 公转周期 的 开普勒 轨道半长轴 的立 平方和______________ 第三定律 正比 方成_______________
思考：行星绕太阳在椭圆轨道上运行，行星距太阳较近处与 距太阳较远处相比较，运动速率何处较大？
【答案】由开普勒第二定律可知，由于在相等的时间内，行 星与太阳的连线扫过相等的面积，显然相距较近与较远时相比 较，相等时间内经过的弧长必须较长，因此运动速率较大，即行 星距太阳较近处，行星运动速率较大．
【一轮参考】高优指导2022版高三数学一轮课件：8.2 空间几何体的表面积与体积
1.求组合体的表面积时,组合体的衔接部分的面积问题易出错. 2.由三视图计算几何体的表面积与体积时,由于几何体的还原不 准确及几何体的结构特征认识不准易导致错误. 3.易混侧面积与表面积的概念.
-15-
规律总结 考点一 考点二 考点三
考点二空间几何体的体积★★师生互动探究 例题(1)(2014课标全国Ⅱ,文7)正三棱柱ABC-A1B1C1的底面边长 关闭 为2,侧棱长为 ,D为BC中点,则三棱锥A-B1DC1的体积为( )
关闭
-16- 解析 答案
规律总结 考点一 考点二 考点三
(2)某四棱锥的三视图如图所示,该四棱锥的体积为 .
解析 答案
知识梳理 双击自测
知识梳理
123456
规律总结
-11-
自测点评1.求几何体的体积,要注意分割与补形.将不规则的几何 体通过分割或补形将其转化为规则的几何体求解.
2.几何体展开、折叠问题,要抓住前后两个图形结 考点一 考点二 考点三
考点一空间几何体的表面积★自助训练过关
1.对于基本概念和能用公式直接求出棱柱、棱锥、棱台与球的 表面积的问题,要结合它们的结构特点与平面几何知识来解决.
2.求三棱锥的体积时要注意三棱锥的每个面都可以作为底面. 3.与球有关的组合体问题,一种是内切,一种是外接.解题时要认 真分析图形,明确切点和接点的位置,确定有关元素间的数量关系, 并作出合适的截面图.
关闭 关闭
解析 答案
知识梳理
规律总结
-9-
知识梳理 双击自测 1 2 3 4 5 6
5.如图,在直三棱柱ABC-A1B1C1中,△ABC为直角三角 形,∠ ACB=90°,AC=4,BC=CC1=3.P是BC1上一动点,则CP+PA1的最关闭
上海闸北第八中学九年级数学下册第二十九章《投影与视图》知识点(提高培优)
一、选择题1．如图，是由－些小立方块所搭几何体的三种视图，若在所搭几何体的基础上（不改变原几何体中小立方块的位置），继续添加相同的小立方块最后搭成一个大的长方体，至少还需要添加（）个小立方块．A．26 B．38 C．54 D．562．一张矩形纸片在太阳光的照射下，在地面上的投影不可能是（）A．正方形B．平行四边形C．矩形D．等边三角形3．用大小和形状完全相同的小正方体木块搭成一-个几何体，使得它的正视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )A．22个B．19个C．16个D．13个4．由m个相同的正方体组成一个立体图形，下面的图形分别是从正面和上面看它得到的平面图形，则m能取到的最大值是（）A．6 B．5 C．4 D．35．如图所示的几何体，它的左视图是（）A．B．C．D．6．小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况，无意之中，他发现这四个时刻向日葵影子的长度各不相同，那么影子最长的时刻为（）A．上午8时B．上午9时30分C．上午10时D．上午12时7．小明想测量一棵树的高度，他发现树的影子恰好落在地面和一斜坡上；如图，此时测得地面上的影长为8米，坡面上的影长为4米．已知斜坡的坡角为300，同一时刻，一根长为l米、垂直于地面放置的标杆在地面上的影长为2米，则树的高度为（）A．米B．12米C．米D．10米8．如图，身高为1.6m的某学生想测量一棵大树的高度，她沿着树影BA由B向A走去，当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC=3.2m"，CA=0.8m，则树的高度为（）A．4.8m B．6.4m C．8m D．10m9．如图所示几何体的主视图是（）A．B．C．D．10．如图，∠APD=90°，AP=PB=BC=CD，则下列结论成立的是（）A．△PAB∽△PCA B．△ABC∽△DBA C．△PAB∽△PDA D．△ABC∽△DCA 11．下列几何体中，其主视图、俯视图和左视图分别是图中三个图形的是（）A．B．C．D．12．某展厅要用相同的正方体木块搭成一个展台，从正面、左面、上面看到的形状如图所示，请判断搭成此展台共需这样的正方体（）A．3个B．4个C．5个D．6个13．一个几何体由一些大小相同的小正方体组成，如图是它的主视图和左视图，那么组成该几何体所需小正方体的个数最少为()A．4 B．5C．6 D．714．如图所示的几何体的俯视图为( )A．B．C．D．15．如图所示的立体图形的主视图是（）A．B．C．D．二、填空题16．如图所示是一种棱长分别是2cm，3cm，4cm的长方体积木，现要用若干块这样的积木来搭建大长方体，如果用6块积木来搭，那么搭成的大长方体的表面积最小是________2cm．17．已知一个圆锥体的三视图如图所示，则这个圆锥体的侧面积是__________．18．由几个相同的小正方体搭成的一个几何体如图所示，这个几何体的主视图可以看到5个小正方体的面，则俯视图与左视图能看到的小正方体的面的个数和为______．19．某几何体从三个方向看到的图形分别如图，则该几何体的体积为___________.20．若要使图中平面展开图按虚线折叠成正方体后，相对面上的两个数为相反数，则x＋y ＝________．21．如图是某几何体的三视图，则该几何体左视图的面积为_________．22．一个几何体的主视图和俯视图如图所示，若这个几何体最多有m个小正方体组成，最少有n个小正方体组成，m+n＝_____．23．如图是由几个小立方块搭成的几何体的主视图与左视图，这个几何体最多可能有________个小立方块．24．一个几何体的主视图和俯视图如图所示，若这个几何体最多有a个小正方体组成，最少有b个小正方体组成，则a＋b＝_____．25．以下给出的几何体：球、正方体、圆柱、圆锥中，主视图是矩形，俯视图是圆形的是_____．26．将四个棱长为1的正方体如图摆放，则这个几何体的表面积是________.三、解答题27．将6个棱长为2cm的小正方体在地面上堆叠成如图所示的几何体，然后将露出的表面部分染成红色．（1）画出这个的几何体的三视图：（2）该几何体被染成红色部分的面积为________．28．一个几何体由一些大小相同的小正方块儿搭建，如图是从上面看到的这个几何体的形状如图，小正方形的数字表示在该位置的小正方块儿的个数，请在网格中画出从正面和左面看到的几何体的形状图．29．把棱长为1cm的若干个小正方体摆放成如图所示的几何体，然后在露出的表面上涂上颜色(不含底面)()1该几何体中有多少个小正方体？()2画出从正面看到的图形；()3写出涂上颜色部分的总面积.30．如图，是由8块棱长都为1的小正方体组合成的简单几何体.（1）请画出这个几何体的三视图并用阴影表示出来；（2）该几何体的表面积（含下底面）为________.。
知识点大全—第11章《容易几何体》_分享
Word-可编辑沪教版高中数学知识点大全一第 11 章容易几何体第 11 章容易几何体 .111.1 柱体 .111.1.1 棱柱与圆柱 . 111.1.1.1 多面体的概念 .111.1.1.2 棱柱的概念 .111.1.1.3 圆柱的概念 .211.1.2 柱体的体积 . 211.1.2.1 祖暅原理 .211.2.2.2 棱柱与圆柱的体积公式 .211.1.3 柱体的表面积 .311.2 锥体 .311.2.1 棱锥与圆锥 .311.2.1.1 棱锥的概念 .311.2.1.2 圆锥的概念 .411.2.1.3 圆台的概念 .411.2.2 锥体和台体的体积 . 411.2.3 锥体的表面积 .411.3 多面体与旋转体 .611.3.1 多面体 . 6千里之行，始于足下11.3.2 旋转体 .611.3.3* 多面体的欧拉定理 . 611.4 球 .611.4.1 球 .711.4.1.1 球的概念 .711.4.1.2 球的性质 .711.4.2 球的体积 .711.4.3 球的表面积 .811.4.3* 球面距离 811.4.4 几何体与球的“接”与切 811.4.4.1 外接球与内切球的定义 .811.4.4.2 几何体与外接球的常见结论 .811.4.4.3 类型一: 墙角模型 .911.4.4.4 类型二: 对棱相等模型 .911.4.4.5 类型三：汉堡模型（直棱柱的外接球、圆柱的外接球） 10 11.4.4.6 类型四: 类圆锥模型 1011.4.4.7 类型五: 线面垂直模型 1011.4.4.8 类型六: 折叠模型 .1111.4.4.9 类型 7: 锥体的内切球模型 .11朽木易折，金石可镂导图作者: 2025 届徐恺霖、陈思充第 11 章容易几何体11.1 柱体11.1.1 棱柱与圆柱11.1.1.1 多面体的概念由三角形或平面多边形围成的封闭几何体称为多面体 (polyhedron),千里之行，始于足下构成多面体表面的各三角形或平面多边形称为多面体的面 (face)相邻面的公共边称为多面的的棱 (edge), 棱与棱的交点称为多面体的顶点 (vertex).11.1.1.2 棱柱的概念同时满意有一对互相平行的面, 且这两个面是两个全等的三角形或平面多边形, 不在这两个面上的棱都互相平行的多面体叫做棱柱 (prism).其中互相平行的面称为棱柱的底面, 其余的面则称为棱柱的侧面, 不在底面上的棱称为棱柱的侧棱, 而棱柱的两个底面之间的距离称为棱柱的高. 侧棱垂直于底面的棱柱称为直棱柱(right prism), 否则称为斜棱柱 (oblique prism). 底面是正多边形的直棱柱称为正棱柱 (regular prism). 棱柱的侧面都是平行四边形.(2)(3)底面是n边形的棱柱称为n棱柱. 如图 (1) 是斜三棱柱, 图 (2) 是直四棱柱, 图 (3) 是正六棱柱.朽木易折，金石可镂异常的棱柱:(1)名称定义 图形 性质 平行六面体底面是平行四 边形的四棱柱 （1）正对的面是全等的平行四边形 （2）对角面是平行四边形直平行六面体侧棱垂直于底 的平行六面体 （1）侧面、对角面都是矩形 （2）底面是平行四边形 长方体 底面是矩形的 直平行六面体 （1）六个面、对角面都是矩形 （2） n 2=n 2+n 2+n 2 (3) cos 2n +cos 2n +cos 2n =1 . 其中 n ,n ,n 为棱与体对角线的夹角正四 棱柱 底面是正方 形的长方体（1）侧面、对角面都是矩形 （2）底面是正方形 正方体 长、宽、高相等的长方体（1）六个面都是全等的正方形 （2） n =√3n ;n 全=6n 2 11.1.1.3 圆柱的概念将矩形 nnnn 绕其一条边 nn 所在直线旋转一周,所形成的几何体叫做圆柱千里之行，始于足下(cylinder), nn所在直线叫做该圆柱的轴,线段nn和nn分离旋转而成的圆面叫做该圆柱的底面,线段nn旋转而成的曲面叫做该圆柱的侧面, nn叫做该圆柱的母线,圆柱的两个底面间的距离 (即nn的长度) 叫做该圆柱的高.方便起见, 把棱柱和圆柱统称为柱体.11.1.2 柱体的体积11.1.2.1 祖暅原理祖暅原理夹在两个平行平面间的两个几何体, 倘若被平行于这两个平面的随意平面截得的两个截面都有相等的面积, 那么这两个几何体的体积必相等.推广: 夹在两个平行平面间的两个几何体, 倘若被平行于这两个平面的随意平面截得的两个截面面积比为n ,那么这两个几何体的体积比也为n .11.2.2.2 棱柱与圆柱的体积公式n棱柱=n底n=n直n侧,其中n底为棱柱的底面积, n为棱柱朽木易折，金石可镂的高, n直为直截面的面积, n侧为侧棱长.n圆柱=n底n=nn2n ,其中n底为圆柱的底面积, n为圆柱的高, n为圆柱的底面半径.11.1.3 柱体的表面积柱体的表面积等于两个底面的面积再加上所有侧面的面积.其中, 所有侧面的面积之和称为柱体的侧面积.n直棱柱表=nn+2n底,其中n为底面多边形的周长, n底为直棱柱的底面积.n圆柱表=nn+2n底=2nnn+2nn2 . 其中n底为圆柱的底面积, n是圆柱底面的半径.11.2 锥体11.2.1 棱锥与圆锥11.2.1.1 棱锥的概念有一个面是三角形或平面多边形, 且不在这个面千里之行，始于足下上的棱都有一个公共点, 这样的多面体叫做棱锥 (pyramid). 其中, 这个三角形或平面多边形称为棱锥的底面, 其余的面称为棱锥的侧面, 不在底面上的棱称为棱锥的侧棱, 所有侧棱的公共点称为棱锥的顶点, 顶点究竟面的距离叫做棱锥的高, 如果棱锥的底面是正多边形, 且底面中央与顶点的连线垂直于底面, 那么这个棱锥叫做正棱锥 (regular pyramid). 底面是n边形的棱锥称为n棱锥.【注重】区别正棱锥中的角:①侧棱与底边所成的角; ②侧棱与底面所成的角③侧面与底面所成的角; ④相邻侧面所成的角【补充】三棱锥顶点在底面上投影的位置已知在三棱锥n−nnn中,顶点n在底面上的射影为n ( n在△nnn内部)①若nn=nn=nn ,或nn,nn,nn与底面成等角,则n是△nnn的外心:②若三个侧面与底面成等角,或n究竟面三边等距离,则n是△nnn的内心:③若nn,nn,nn两两互相垂直,或有两组对棱互相垂直,则n是垂心11.2.1.2 圆锥的概念直角三角形nnn绕其一条直角边nn所在直线旋转一周,所形成的几何体朽木易折，金石可镂叫做圆锥 (cone). 其中, nn 所在直线叫做圆锥的轴,点 n 叫做圆锥的顶点, 直角边 nn 旋转而成的圆面叫做圆锥的底面,斜边 nn 旋转而成的曲面叫做圆锥 的侧面,斜边 nn 叫做圆锥的母线,圆锥的顶点究竟面间的距离 (即 nn 的长 度) 叫做圆锥的高. 圆锥有无穷多条母线, 且所有的母线都交于圆锥的顶点.圆锥的母线长为 l ,求过圆锥顶点的截面面积的最大值.设截面为 △nnn ,圆锥轴截面的顶角为 n ,显然 ∠nnn ≤n ,n △nnn =12n 2⋅sin∠nnn ①若 n ≤n 2 ,当 ∠nnn =n 时,有 (n △nnn )max =12n 2sin n②若 n >n 2 ,当 ∠nnn =n 2 时,有 (n △nnn )max =n 22 .11.2.1.3 圆台的概念把一个锥体用平行于底面的平面截去含顶点的小锥体后, 剩下的几何体称为台体(frustum).大圆锥截去小圆锥后剩下的几何体称为圆台. 圆台是由直角梯形 绕直角边旋转一周所形 成的几何体.类似地, 倘若棱锥被一个平行于底面的平面所截, 那么截去一个小棱锥后剩下的多面体称 为棱台. 其中, 由正棱锥截得的棱台称为正棱台.与台体有关的问题, 我们一方面可以转化为锥体的问题来解决, 另一方面也可以把锥体和 柱体看作是台体的极端情形.千里之行，始于足下11.2.2 锥体和台体的体积n棱锥=13nn=13n直n ,其中n为棱锥底面的面积, n为棱锥的高.n圆锥=13nn=13nn2n ,其中n为圆锥底面的面积, n为圆锥的高, n为圆锥的底面半径.n台=13(n′+√n′n+n)n ,其中n′和n分离是上、下底面积,上下底面的距离为n .三棱锥n−nnn的体积为n,n、n、n分离为侧棱nn、nn、nn上的点,且满意nn=nnn,nn=nnn,nn=nnn ,则n n−nnn=nnnn .11.2.3 锥体的表面积正棱锥的每个侧面都是全等的等腰三角形, 把这些等腰三角形底边上的高称为棱锥的斜高,记为n′ . 倘若棱锥底面多边形的周长是n ,底面面积是n底,那么n正棱锥侧=12nn′,n正棱锥表=12nn′+n底.n圆锥侧=nnn, n圆锥表=nnn+nn2.在解正棱锥问题时,倘若能够记住正多边形的边长n与外接圆半径n、内切圆半径n和面积n之间的关系,将会给计算带来很大的方便,如下表:图形n n n正三角形√33n√36n√34n2图形n n n 正方形√22n n 2n 2正六边形n√32n 3√32n 2 【补充】正四面体的常见几何参数: 已知正四面体 nnnn 的棱长为 n ,则其（1）底面的高为 √6n3 ; (2) 体积为: √2n 312 ; (3) 表面积为 √3n 2 ;（4）外接球半径:√6n 4 ; (5) 内切球半径: √6n12 (6) 棱切球半径: √2n 4. 11.3 多面体与旋转体11.3.1 多面体由三角形或平面多边形围成的封闭几何体称为多面体 (polyhedron).多面体可以用它的面的数量举行命名,有几个面的多面体就叫做几面体. n 棱锥是 n +1 面 体, n 棱柱或 n 棱台是 n +2 面体. 面数最少的多面体是四面体.倘若一个多面体的所有面都是全等的正三角形或正多边形, 每个顶点聚拢的棱的条数都相 等, 这个多面体就叫做正多面体 (regular polyhedron), 正多面体惟独五种.正六面体正八面体(正方体)正十二面体正二十面体正四面体11.3.2 旋转体由一个平面封闭图形绕其所在平面上的一条定直线旋转一周所形成的空间封闭几何体称为旋转体 (revolving solid), 这条直线叫做该旋转体的轴.一条平面曲线 (包括直线、折线等) 绕其所在平面上的一条直线旋转一周所形成的空间图形称为旋转面.11.3.3* 多面体的欧拉定理容易多面体设想多面体的面都是用具有良好弹性的橡胶做成的, 倘若往这个多面体充沛够多的气体以后能够使这个多面体膨胀成个球体, 那么这个多面体就是一个容易多面体多面体的欧拉定理容易多面体的顶点数n、棱数n与面数n满意: n−n+n=2类型面数棱数顶点数每面边数每顶点棱数正四面体46433正六面体612843正八面体812634正十二面体1232053正二十面体23123511.4 球11.4.1 球11.4.1.1 球的概念将圆心为n的半圆面绕其直径所在的直线旋转一周,所形成的几何体叫做球 (ball),记作球n . 半圆的圆弧绕直径旋转所形成的旋转面叫做球面 (sphere), 点n到球面上随意一点的距离都相等,点n叫做球心,把原半圆的半径和直径分离叫做球的半径和直径.11.4.1.2 球的性质（1）球具有丰盛的对称性, 所有经过球心的直线都可以作为球的旋转轴, 每条旋转轴与球面交点之间的线段都是球的直径.(2) 用平面n去截球,过球心n有且惟独一条过直径nn的直线与平面n垂直,平面n与球面的交线是以n1为圆心,以n1n为半径的圆. 若平面n经过球心,则n1与n重合,此时的截面称为球的大圆 (great circle),球的非大圆截面称为小圆.(3) 用平行于赤道平面的平面截地球得到的小圆 (如圆n1 )的圆周称为纬线,按照南北方向分为南纬和北纬. 过nn的大圆的半圆周 (如半圆nnnn 称为经线.按照约定, 通过英国伦敦格林尼治天文台原址的那条经线称为 0 度经线, 从它开始, 分离按照东西方向分为东经和西经. 地球上某点的纬度是该点和地心连线与赤道平面所成的角, 该点的经度是它所在的经线半圆与 0 度经线半圆所成二面角的度数.（4）经过小圆的直径与小圆面垂直的平面必过球心, 该平面截球所得圆是大圆.(5) 过球心与小圆圆心的直线垂直于小圆所在的平面 (类比: 圆的垂径定理).（6）在同一个球中，过两相交圆的圆心垂直于相应的圆面的直线相交，交点是球心（类比：在同圆中, 两相交弦的中垂线交点是圆心).11.4.2 球的体积构造如图所示的半径为n、高为n的圆柱,并从中切去一个倒置的底面半径为n、高为n的圆锥（圆锥的底面置于圆柱的上底面, 圆锥的顶点置于圆柱下底面的圆心). 用平行于底面的高度为n的平面截这两个几何体,可知截面面积相等,均为n(n2−n2) ,按照祖暅原理则这两个几何体的体积相等.据此可得n球=43nn3 .11.4.3 球的表面积n球=4nn2 .【小结】求体积的常见主意有:①直接法 (公式法); ②割补法; ③转化法 (等体积法、利用祖晒原理) 等割补思想和转化思想是解决体积问题的常用技巧. 此外, 等体积法还常常用来求点到平面的距离或几何体的高, 或进一步求解直线与平面所成的角.11.4.3* 球面距离球面上衔接两点最短路径的长度就是球面上两点的球面距离.11.4.4 几何体与球的“接”与切11.4.4.1 外接球与内切球的定义外接球: 若一个多面体的各个顶点都在一个球的球面上, 则称这个多面体是这个球的内接多面体, 这个球是这个多面体的外接球内切球: 若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体, 这个球是这个多面体的内切球.11.4.4.2 几何体与外接球的常见结论结论 1: 长方体的外接球的球心在体对角线的交点处, 即长方体的体对角线的中点是球心;结论 2: 若某个多面体的所有顶点是某长方体的部分顶点, 该多面体与长方体的外接球重合:结论 3: 长方体的外接球直径就是面向角线, 底面的一条对角线与一条高 (棱) 构成的直角三角形的外接圆是大圆;结论 4: 圆柱的外接球球心在上下两底面圆的圆心连线段中点处;结论 5: 圆柱轴截面矩形的外接圆是大圆, 该矩形的对角线 (外接圆直径) 是球的直径.结论 6: 直棱柱的外接球与该棱柱外接圆柱体有相同的外接球;结论 7: 圆锥体的外接球球心在圆锥的高所在的直线上;结论 8: 圆锥体轴截面等腰三角形的外接圆是大圆, 该三角形的外接圆直径是球的直径.结论 9: 侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.11.4.4.3 类型一: 墙角模型图1-1图1-2图1-3图1-4处理主意: 找到三棱锥中三条两两垂直的线段, (可将三棱锥置于长方体中), 直接使用公式(2n)2=n2+n2+n2 ,即2n=√n2+n2+n2 ,求出n .典例1. 若三棱锥的三个侧面两两垂直，且侧棱长均为√3，则其外接球的表面积是___.【答案】4n2=3+3+3=9,n=4nn2=9n .2. 在正三棱锥n−nnn中, n、n分离是棱nn、nn的中点,且nn⊥nn ,若侧棱nn=2√3 . 则正三棱锥n−nnn外接球的表面积是___.【答案】可证得三棱锥n−nnn的三棱条侧棱两两互相垂直,∴(2n)2=(2√3)2+(2√3)2+(2√3)2=36 ,即4n2=36 ,∴正三棱锥n−nnn外接球的表面积是36n .11.4.4.4 类型二: 对棱相等模型已知某三棱锥 (四面体) 三组对棱分离相等, 求其外接球半径 ( nn=nn,nn=nn,nn=nn ).第一步: 画出一个长方体, 标出三组互为异面直线的对棱; 第二步: 设出长方体的长宽高分离为n,n,n,nn=nn=n , nn=nn=n,nn=nn=n ,列方程组,{n2+n2=n2n2+n2=n2n2+n2=n2⇒(2n)2=n2+n2+n2=n2+n2+n22,第三步: 按照墙角模型得2n=√n2+n2+n2=√n2+n2+n22 ,解得n=√n2+n2+n28.补充: n n−nnn=nnn−16nnn×4=13nnn .11.4.4.5 类型三: 汉堡模型 (直棱柱的外接球、圆柱的外接球)图3-1图3-2图3-3直三棱柱内接于球 (同时直棱柱也内接于圆柱, 棱柱的上下底面可以是随意三角形) 第一步: 决定球心 n 的位置, n 1 是 △nnn 的外心,则 nn 1⊥ 平面 nnn ;第二步: 算出小圆 n 1 的半径 nn 1=n ,nn 1=12nn 1=12n (nn 1=n 也是圆柱的高) ;第三步: 勾股定理: nn 2=n 1n 2+n 1n 2⇒n 2=(n 2)2+n 2⇒n =√n 2+(n2)2,解出 n .11.4.4.6 类型四: 类圆锥模型图4-1图4-2朽木易折，金石可镂图4-3图4-4平面nnn⊥平面nnn ,且nn⊥nn (即nn为小圆的直径), △nnn的外接圆就是大圆,直接用正弦定理nsin n =nsin n=nsin n=2n即可求解出n .11.4.4.7 类型五: 线面垂直模型nn⊥平面nnn ,求外接球半径.解题步骤:第一步: 将△nnn画在小圆面上, n为小圆直径的一个端点,作小圆的直径nn ,衔接nn ,则nn必过球心n ;第二步: n1为△nnn的外心,所以nn1⊥平面nnn ,算出小圆n1的半径n1n=n (利用正弦定理,得nsin n =nsin n=nsin n=2n ), nn1=12nn ;第三步: 利用勾股定理求三棱锥的外接球半径: ①(2n)2=nn2+(2n)2⇔2n=√nn2+(2n)2 :②n2=n2+nn12⇔n=√n2+nn12 .千里之行，始于足下11.4.4.8 类型六: 折叠模型（1）两个全等三角形或等腰三角形拼在一起, 或菱形折叠.第一步: 先画出所示的图形,将△nnn画在小圆上,找出△nnn和nn′nn的外心n1和n2 ;第二步: 过n1和n2分离作平面nnn和平面n′nn的垂线,两垂线的交点即为球心n ,衔接nn,nn ;第三步: 解△nnn1 ,算出nn1 ,在nn△nnn1中,勾股定理: nn12+nn12=nn2(2)两直角三角形拼接在一起 (斜边相同, 也可看作矩形沿对角线折起图7所得三棱锥) 如图 7, ∠nnn=∠nnn=90∘ ,求三棱锥n−nnn外接球半径.nn , ∴n为三棱锥取公共的斜边的中点n ,衔接nn,nn ,则nn=nn=nn=nn=12n−nnn外接球球心, n=1nn .211.4.4.9 类型 7: 锥体的内切球模型1. 如图 8-1,三棱锥n−nnn是正三棱锥,求其内切球的半径.朽木易折，金石可镂图8-2第一步: 先现出内切球的截面图, n,n分离是两个三角形的外心; 第二步: 求nn=13nn,nn=nn−n,nn是侧面△nnn的高; 第三步: 由△nnn相似于△nnn ,建立等式:nn nn =nnnn,可解. 2. 如图 8-2,四棱锥n−nnn是正四棱锥,求其内切球的半径. 第一步: 先现出内切球的截面图, n,n,n三点共线;第二步: 求nn=12nn,nn=nn−n,nn是侧面△nnn的高;第三步: 由△nnn相似于△nnn ,建立等式: nnnn =nnnn,可解.3. 三棱锥n−nnn是随意三棱锥,求其的内切球半径主意: 等体积法, 即内切球球心与四个面构成的四个三棱锥的体积之和相等第一步: 先画出四个表面的面积和囫囵锥体体积;第二步: 设内切球的半径为n ,建立等式: n n−nnn=n n−nnn+n n−nnn+n n−nnn+ n n−nnn⇒n n−nnn=13n△nnn⋅n+13n nnn⋅n+13n nnn⋅n+13n nnn⋅n =13(n△nnn+n△nnn+n nnn+n△nnn)⋅n第三步: 解出n=3n n−nnnn n−nnn+n n−nnn+n n−nnn+n n−nnn.。
第三单元牛顿运动定律-上海市第八中学
第三单元牛顿运动定律本单元知识由牛顿的三个运动定律、国际单位制、牛顿对经典力学的贡献以及经典力学的局限性组成。
其中牛顿第二定律是本单元的重点。
本单元的核心规律是牛顿第二定律，它揭示了运动和力的关系。
在本单元的学习中，应注意与前两个单元知识的联系，在对物体进行运动状态分析和受力分析的基础上，用牛顿第二定律解决涉及运动和力的问题，提高综合运用力学知识的能力。
本单元内容与力学、电学等知识联系紧密，在分析、演绎、理论计算等方面有较高的要求。
本单元的学习要特别注重实验研究的方法，在牛顿第一定律的学习中，感悟理想化实验的重要意义；在牛顿第二定律的学习中，运用控制变量的方法设计实验。
通过学习牛顿第三定律在火箭原理中的重要作用，以及我国火箭发展史，了解有关神舟六号载人飞船和“嫦娥工程”系列成功发射的事迹。
在学习经典力学的适用范围和局限性的同时，领略科学家的科学态度和创新精神。
学习要求内容1．牛顿第一定律。
2．牛顿第二定律。
3．牛顿第三定律。
4．国际单位制。
5．牛顿对科学的贡献。
6．经典力学的局限性。
7．爱因斯坦对科学的贡献。
8．学生实验：用DIS研究加速度与力的关系，加速度与质量的关系。
要求1．理解牛顿第一定律理解惯性，知道惯性是一切物体固有的属性，知道质量是惯性大小的量度；知道伽利略理想实验，通过伽利略斜面理想实验，认识理想实验的科学方法，感悟理想实验的科学方法对人类思想产生了的深远影响；理解牛顿第一定律，能用牛顿第一定律和惯性概念解释一些简单的实际现象。
2．掌握牛顿第二定律在理解力是使物体运动状态变化的原因的基础上，理解牛顿第二定律的内容及其表达式。
能根据实验目的，选择合适的实验器材，运用控制变量等方法，设计用DIS探究加速度与物体质量、物体受力的关系的实验方案，并能根据实际情况修正探究方案，完成实验。
能按照正确的方法和步骤，用牛顿第二定律解决简单的动力学问题。
通过“牛顿定律与交通”等专题的学习，激发社会责任感。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
２0１0年中考数学基础知识大串讲导读:中考大串讲按照代数综合、几何综合、概率统计三大块共分成10个串讲专题.“考点串讲”部分是对所讲专题的重要考点的概括,“新题演练”部分是针对所讲专题重要考点的精例及解析，使您做题后,跳出题海，轻松应对中考,决胜中考!串讲一数与式考点串讲1.实数.考查重点:（1）有理数、无理数、实数、非负数概念；（2)相反数、倒数、数的绝对值概念;（3）在已知中,以非负数a2、|ａ|、a(ａ≥0）之和为零作为条件，解决有关问题. (4）考查实数的运算(有理数的运算种类、各种运算法则、运算律、运算顺序、科学计数法、近似数与有效数字、计算器功能鍵及应用.）2.整式与分式．整式知识点:代数式、代数式的值、整式、同类项、合并同类项、去括号与去括号法则、幂的运算法则、整式的加减乘除乘方运算法则、乘法公式、因式分解.整式考查重点：(1）考查列代数式的能力；(2）考查整数指数幂的运算、零指数. (3）掌握并灵活运用提公因式法和公式法(直接运用公式不超过两次)进行因式分解.分式：分式考查重点:（1）考查整数指数幂的运算，零运算；（２)考查分式的化简求值.3.二次根式．a≥0)叫做二次根式．考查重点:(1）了解二次根式、最简二次根式、同类二次根式的概念，会辨别最简二次根式和同类二次根式.掌握二次根式的性质,会化简简单的二次根式，能根据指定字母的取值范围将二次根式化简；(2）掌握二次根式的运算法则，能进行二次根式的加减乘除四则运算,会进行简单的分母有理化.新题演练:新题1：在实数－23,,－3．14，2π，-0．１0１00１00０1…（每两个1之间依次多1个0），sin ３0°这8个实数中,无理数有（ )Ａ.１个 B.2个 C ．３个 D.4个解析:对实数分类，不能只为表面形式迷惑，而应从最后结果去判断．首先明确无理数的概念，即“无限不循环小数叫做无理数”.一般来说,用根号表示的数不一定就是无理数,如=2是有理数，关键在于这个形式上带根号的数的最终结果是不是无限不循环小数.同样，用三角符号表示的数也不一定就是无理数,如ｓi ｎ30°、ｔａn ４5°等．而－0．1010010001…尽管有规律，•但它是无限不循环小数，是无理数．2π是无理数,而不是分数.在上面所给的实数中,2π,-0．10100１0001…这三个数是无理数，其他五个数都是有理数,故选C.答案：C新题２:已知x 、y 是实数,y 2-６y ＋9）＝0，若a ｘy －3x=ｙ,则实数a 的值是（ )Ａ.14 B.－14 C.74 Ｄ.-74解析：若几个非负数之和等于零，则每个非负数均等于零.这是非负数具有的一个重要性质．（y －3)2均为非负数，它们的和为零,只有３x+４=0,且y-3=0,由此可求得ｘ,y 的值,将其代入axy －３x=y 中，即求得a 的值.答案y －3）２=0 ∴3x ＋4=０，ｙ－3＝０ ∴x ＝－43,y ＝3． ∵axy-3x ＝y ，∴－43×3a-3×（-43）=3 ∴a=14∴选Ａ 新题3：若ａ，ｂ，ｃ是三角形三边的长，则代数式a ２+b 2-ｃ2-2ab 的值（ ）A.大于零 B ．小于零 Ｃ.大于或等于零 D.小于或等于零解析：本题是确定代数式的取值范围与因式分解的综合题,•把所给多项式的部分因式进行因式分解，再结合“a ，b ，c 是三角形的三边”，应满足三角形三边关系是解决这类问题的常用方法．答案：(1）∵ａ２＋ｂ2－c 2-2ab=（a 2-2ab+b ２）－c 2＝（a －b)2－c 2=(a-b+c ）（a －b －c ）,又∵a ，b ，•c 是三角形三边的长．∴ａ+c>ｂ，a<b ＋c,即a-ｂ+c ＞０，a-b-c<0∴(ａ－ｂ+c ）(a －b-c)<0即ａ2+b 2-ｃ2-２ab<0，故选B.新题4:先化简22424422x x x x x x x ⎛⎫--+÷ ⎪-++-⎝⎭,然后请你任取一个合适的数作为ｘ的值代入求值．解析:本题考查整式的因式分解及分式的加减乘除混和运算,要注意运算顺序．先乘除后加减，有括号先算括号里的或按照乘法的分配律去括号．22424422x x x x x x x ⎛⎫--+÷ ⎪-++-⎝⎭()()()22222222x x x x x x x x x +----=⨯-⨯+-()()2222x x x x x -+=-+ ()()()2222822x x x x x +--==++.取值时要考虑分式的意义，即x ≠±２. 答案:原式=22424422x x x x x x x ⎛⎫--+÷ ⎪-++-⎝⎭ ()()()22222222x x x x x x x x x +----=⨯-⨯+-()()2222x x x x x -+=-+取x =6，得原式＝1 串讲二 方程（组)与不等式(组)考点串讲1.一元一次方程.知识点：等式及基本性质、方程、方程的解、解方程、一元一次方程.考查重点：掌握解一元一次方程的一般步骤，能熟练地解一元一次方程.2.二元一次方程（组).了解二元一次方程组及其解法，并灵活运用代入法、加减法解二元一次方程组.重点:掌握消元思想,熟练地解二元一次方程组．会用二元一次方程组解决一些简单的实际问题.难点：图象法解二元一次方程组，数形结合思想.3.一元二次方程.知识点:一元二次方程、解一元二次方程及其应用、一元二次方程根的判别式、判别式与根的个数关系．考查重点:（1)了解一元二次方程的概念，会把一元二次方程化成为一般形式;（2)会用配方法、公式法、因式分解法解一元二次方程；（3）能利用一元二次方程的数学模型解决实际问题.4.分式方程.考查重点：（1）会解分式方程,掌握其基本思想是把分式方程转化为整式方程;（２）分式方程及其实际应用．5.一元一次不等式(组).知识点：不等式概念,不等式基本性质，不等式的解集,解不等式，不等式组,不等式组的解集，解不等式组，一元一次不等式,一元一次不等式组,一元一次不等式组应用.考查重点：考查解一元一次不等式（组)的能力.新题演练:新题1:已知关于x 的方程432x m -=的解是x m =,则m 的值是__＿＿_＿__＿___．解析：本题考查了一元一次方程解的意义.因x m =是该方程的解，所以代入后方程仍然成立,即：432m m -=，解这个关于m 的方程得m=2．答案：ｍ=２新题2:若关于x ,ｙ的二元一次方程组⎩⎨⎧=-=+k y x ,k y x 95的解也是二元一次方程632=+y x 的解,则k 的值为Ａ.43- ﻩB ．43 Ｃ.34 ﻩﻩＤ.34- 解析：由方程组得2x ＝１4ｋ，y ＝－2k ．代入632=+y x ,得１4ｋ－6ｋ=6,解得k =43． 答案：B新题３:解方程:2420x x ++=解析:根据方程的特点， 灵活选用方法解方程.观察本题特点,可用配方法求解．答案:242x x +=- 24424x x ++=-+ 2(2)2x +=2x +=2x =1222x x ∴=-=，新题4:解方程：431222-=-+-x x x . 解析：由分式方程的概念可知,此方程是分式方程,因此根据其特点应选择其方法是──去分母法,并且在解此方程时必须验根．去分母法解分式方程的具体做法是:把方程的分母分解因式后,找出分母的最简公分母;然后将方程两边同乘以最简公分母,将分式方程化成整式方程.注意去分母时，不要漏乘；最后还要注意解分式方程必须验根，并掌握验根的方法．答案:解：去分母得:(x －2)2－(x 2-4)＝3.ﻩ－4x=-５． x=45． 经检验，x ＝45是原方程的解. 新题5：解不等式组:331213(1)8x x x x-⎧+>+⎪⎨⎪---⎩，≤并在数轴上把解集表示出来.解析：一元一次不等式的解法的一般步骤与一元一次方程相同,不等式中含有分母，应先在不等式两边都乘以各分母的最小公倍数去掉分母,在去分母时不要漏乘没有分母的项，再作其他变形．注意:①分数线兼有括号的作用，分母去掉后应将分子添上括号．同时,用分母去乘不等式各项时,不要漏乘不含分母的项;②不等式两边都乘以(或除以）同一个负数时,不等号的方向必须改变；③在数轴上表示不等式的解集,当解集是ｘ＜ａ或x>时,不包括数轴上a 这一点，则这一点用圆圈表示;当解集是ｘ≤a 或x ≥a 时，包括数轴上a 这一点,则这一点用黑圆点表示;④解不等式（组）是中考中易考查的知识点，必须熟练掌握．答案:解:解不等式(1）得1x <,解不等式(2）得2x -≥.所以不等式组的解集为21x -<≤新题6：在我市某一城市美化工程招标时，有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做2４天可完成．（1）乙队单独完成这项工程需要多少天？(2）甲队施工一天,需付工程款3.5万元，乙队施工一天需付工程款2万元.若该工程计划在７0天内完成，在不超过计划天数的前提下，是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱？解析:本题主要考查分式方程的应用，解题时要检验，先检验所求x•的值是否是方程的解,再检验是否符合题意.答案:解:（1)设乙队单独完成需x 天根据题意,得11120()2416060x ⨯++⨯= 解这个方程,得x =９０经检验,x =90是原方程的解 ∴乙队单独完成需９0天(2)设甲、乙合作完成需y 天,则有11()16090y += 解得36y =（天）甲单独完成需付工程款为60×3．5=2１0（万元)乙单独完成超过计划天数不符题意．甲、乙合作完成需付工程款为36（３.5+2）＝198（万元)答：在不超过计划天数的前提下，由甲、乙合作完成最省钱． 串讲三 函数考点串讲1.函数基本概念.知识点:常量与变量、函数与自变量、函数表示方法．考查重点:（1)考查自变量的取值范围，重点考查的是含有二次根式的函数式中自变量的取值范围;(2)函数自变量的取值范围.2.一次函数．知识点：正比例函数及其图象、一次函数及其图象.考查重点：(1）考查正比例函数、一次函数的定义、性质;(２)综合考查正比例、一次函数的图象；（3)考查用待定系数法求正比例、一次函数的解析式．3.二次函数.1 x知识点:二次函数、抛物线的顶点、对称轴和开口方向.考查重点:（1)考查二次函数的定义、性质；（2)综合考查正比例、反比例、一次函数、二次函数的图象;（3)考查用待定系数法求二次函数的解析式；(4）考查用配方法求抛物线的顶点坐标、对称轴、二次函数的极值；（5)考查代数与几何的综合能力，常作为专项压轴题.4.反比例函数.知识点:反比例函数意义；反比例函数 反比例函数图象;反比例函数性质;待定系数法确定函数解析式．考查重点:(1）确定反比例函数表达式;(2)画反比例函数的图象;（３）用反比例函数解决某些实际问题.新题演练：新题1：如图,已知一次函数1y x =+的图象与反比例函数k y x=的图象在第一象限相交于点A ,与x 轴相交于点C AB x ，⊥轴于点B ,AOB △的面积为1,则AC 的长为 （保留根号).解析:本题考查函数图象交点坐标的求法及反比例函数的比例系数k 与其图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S 的关系,即12S k =,由2k =，且图象在第一象限内,所以2k =，由12y x y x =+⎧⎪⎨=⎪⎩得点A 坐标为(１,2)，而1y x =+与x 轴的交点坐标为(-1，0)，所以AB=2，BC=2.由勾股定理得22222AC =+==答案:22新题2:某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于4５%，经试销发现，销售量y (件)与销售单价x （元）符合一次函数y kx b =+,且65x =时,55y =;75x =时，45y =.（1)求一次函数y kx b =+的表达式;(2)若该商场获得利润为W 元,试写出利润W 与销售单价x 之间的关系式；销售单价定yO AC B为多少元时，商场可获得最大利润，最大利润是多少元？（3）若该商场获得利润恰好是500元，试确定销售单价x 是多少元？解析:(1）根据一次函数解析式的特征,直接根据题意列出二元一次方程组,就可以求出一次函数的解析式.（2)在确定函数关系式时，特别注意自变量的取值范围，由本题中“试销期间销售单价不低于成本单价”得x ≥60,由“获利不得高于45%”得x ≤(１＋４５%）×６０，即x ≤87，因此6087x ≤≤．对于求出二次函数的最值问题，同时要考虑在自变量的取值范围;(3)这个问题是把二次函数问题转化为一元二次方程来考虑,要注意的是求出的结果必须要在二次函数的自变量的取值范围内.注意：在二次函数中通过求函数的最大（小）值以解决求实际问题的最大利润、最优方案等,首先考虑利用二次函数y=ａx ２＋ｂx+c 当x=-2b a时，y 取最大（小）值244ac b a -来求，但当x ＝-2b a不在自变量的取值范围时，可利用二次函数的增减性由一个变量的极端值求另一变量的极值．答案：(1）根据题意得65557545.k b k b +=⎧⎨+=⎩， 解得1120k b =-=，． 所求一次函数的表达式为120y x =-+．（2）(60)(120)W x x =--+21807200x x =-+-2(90)900x =--+,抛物线的开口向下，∴当90x <时，W 随x 的增大而增大，而6087x ≤≤，∴当87x =时，2(8790)900891W =--+=.∴当销售单价定为８７元时,商场可获得最大利润,最大利润是891元．(３）由500W =,得25001807200x x =-+-,整理得，218077000x x -+=，解得，1270110x x ==，. 因为6087x ≤≤,所以,销售单价70x =．新题3:如图，在平面直角坐标系中放置一直角三角板，其顶点为(10)A -，，(0B ，(00)O ，，将此三角板绕原点O 顺时针旋转90°，得到A B O ''△．（1）如图,一抛物线经过点A 、B 、B ′,求该抛物线解析式;（２)设点P 是在第一象限内抛物线上一动点,求使四边形PBAB '的面积达到最大时点P 的坐标及面积的最大值．解析:函数是用运动的观点观察事物发展的全过程,利用函数的性质可求最大(小）值.在问题2中,用分割方法把四边形PBAB '分成四个三角形,用点P 的坐标表示其面积,从而建立函数关系式．答案:(１)∵抛物线过(10)A B -，，设抛物线的解析式为(1)(0)y a x x a =+≠．又∵抛物线过(0B ,将坐标代入上解析式得:1(1a a =⨯=-·，．(1)(y x x ∴=-+．即满足条件的抛物线解析式为21)y x x =-+x(２）如图1,∵P 为第一象限内抛物线上一动点,设()P x y ，，则00x y >>，． P点坐标满足21)y x x =-+连接PB PO PB ，，′．BAO PBO POB PBAB S S S S ∴=++△△△′四边形′1)x y x y ==++221)1x x x x ⎛⎤-+- ⎦ ⎝⎭⎣⎦当x ,PBAB S 四边形′最大．此时，y 即当动点P的坐标为⎝⎭时， PBAB S 四边形′最大,串讲四 三角形考点串讲1．三角形的有关概念.知识点:三角形，三角形的角平分线,中线,高线,三角形三边间的不等关系，三角形的内角和,三角形的分类，全等形,全等三角形及其性质，三角形全等判定.考查重点：三角形三边关系,三角形内外角性质.2.等腰三角线与直角三角形．考查重点：(1)等腰（等边）三角形的判定与性质；（2)运用等腰(等边)三角形的判定与性质解决有关计算与证明问题;（3）运用勾股定理及其逆定理计算线段的长，证明线段的数量关系,解决与面积有关的问题以及简单的实际问题；(４)折叠问题;（5)将直角三角形,平面直角坐标系,函数，开放性问题,探索性问题结合在一起综合运用.3．全等三角形．知识点:全等形，全等三角形及其性质，三角形全等判定.考查重点：论证三角形全等，线段的倍分.新题演练:新题1:如果三角形的两边分别为3和5，那么连接这个三角形三边中点，所得的三角形的周长可能是( ）Ａ.4 B ．4．５ C.５ D ．５.５解析:本题考查三角形三边关系、中位线定理,三角形的两边分别为3和５,所以第三边一定大于2小于8,连接这个三角形三边中点，所得的三角形的周长等于原三角形周长的一半，所以一定大于5小于８，故选D.答案：D新题2:如图，将三角尺的直角顶点放在矩形直尺的一边上,则∠３的度数等于( ） A ．50° B.3０ ° C.20 ° Ｄ．１5 °图1321解析：从条件中可得DF ／／EC ，故∠２=∠4．又∵∠4=∠1+∠3,∴∠2∠1＋∠3，∴∠3=∠2-∠1=50°- ３０°=20°．故答案选C答案：C新题3:如图，AD ⊥CD,AB=13，BC=１2，CD=3,AD=4,则si ｎB 等于（ ) Ａ．513 B.1213 C ．35D ．45解析:由AD ⊥DC,知△ADC 为直角三角形．由勾股定理得:AC ２=A Ｄ2+DC 2＝32+42=5，AC ＝５，在△A ＣＢ中,∵AB 2=169,BC 2+AC ２＝５2+１２2=１69,∴ＡB 2=BC 2＋ＡC 2．由勾股定理的逆定理知:△ABC 是直角三角形．∴sinB ＝AC AB =513. 答案：Ａ新题3:如图所示，∠BAC =∠ABD ，AC =B Ｄ，点O 是AD 、B Ｃ的交点，点E 是ＡＢ的中点．试判断OE 和AB 的位置关系,并给出证明.解析：首先进行判断:OE ⊥ＡB ，由已知条件不难证明△ＢA Ｃ≌△A ＢD ,得∠ＯＢA =∠OAB 再利用等腰三角形“三线合一”的性质即可证得结论.解决此类问题,要熟练掌握三角形全等的判定、等腰三角形的性质等知识.答案:OE ⊥ＡＢ.证明：在△B ＡC 和△ABD 中，错误! ∴△ＢA Ｃ≌△ＡBD . ∴∠O ＢA ＝∠OA Ｂ, ∴OA ＝O Ｂ．又∵ＡE =BE , ∴OE ⊥AB ．串讲五 四边形考点串讲１.平行四边形．考查重点:（1）平行四边形的概念和面积的求法；(２)平行四边形的性质和判定；(３)理解平行四边形是中心对称图形,•过对称中心的直线把它分成面积相等的两部分；(４)平行四边形中运用全等三角形和相似三角形的知识解题.２． 矩形、菱形、正方形.考查重点：矩形、菱形、正方形的概念、性质、判定及它们之间的关系，主要考查边长、对角线长、面积等的计算.新题演练：新题1：如果用4个相同的长为3宽为1的长方形,拼成一个大的长方形,那么这个大的长方形的周长可以是_＿＿__________.解析:本题考查了学生的空间想象能力和发散思维能力.解答本题最好能将所有的拼法画出来后再进行求解.本题的不同拼法有：FE D C B A 4321答案:14或16或２6新题2: 如图,在菱形ABCD 中,∠Ａ＝110°，Ｅ,F 分别是边ＡB 和BC的中点,EP ⊥CD 于点P,则∠ＦＰＣ＝( )A.35° B ．45° C.50° D.55°解析:解答本题应首先延长P Ｆ交AB 的延长线于点G ，根据题意,利用角角边可证明BGF ∆≌CPF ∆,于是得到G FPC ∠=∠，ＰＦ=F Ｇ，所以在EGP Rt ∆中,E Ｆ是斜边上的中线,于是得到ＦE=FG ，所以FEG G ∠=∠，又因为E 、F 分别为中点，所以ＥB=FB ，所以，FE ＝F Ｇ=BF ，所以BFE BEF G FPC ∠=∠=∠=∠,又因为∠A=1１０°，所以070=∠EBF ,因此，00180702=+∠FPC ,解得055=∠FPC ．答案:D新题３：如图1，在正方形ABCD 中,E F G H ，，，分别为边AB BC CD DA ，，，上的点，HA EB FC GD ===,连接EG FH ，，交点为O .（1)如图2，连接EF FG GH HE ，，，,试判断四边形EFGH 的形状,并证明你的结论；(2）将正方形ABCD 沿线段,EG HF 剪开，再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形ABCD 的边长为３cm ，1cm HA EB FC GD ====,则图3中阴影部分的面积为___＿__＿__2cm ．解析:（1)结合条件观察图形2容易发现:AEH BFE CGF DHG △≌△≌△≌△,得出:四边形EFG Ｈ是菱形；再由DHG AEH △≌△可知：90DHG AHE ∠+∠=°，从而证得四边形EFGH 是正方形.（2）连接EH 、HG 、GF 、ＦE,由第(1）小题可知：四边形EFGH 是正方形，可得阴影部分面积是1.答案：（1)四边形EFGH 是正方形.证明: 四边形ABCD 是正方形,∴90A B C D AB BC CD DA ∠=∠=∠=∠====°，.HA EB FC GD ===,AE BF CG DH ∴===．AEH BFE CGF DHG ∴△≌△≌△≌△．EF FG GH HE ∴===．∴四边形EFGH 是菱形.由DHG AEH △≌△知DHG AEH ∠=∠．90AEH AHE ∠+∠=°,90DHG AHE ∴∠+∠=°.图1 D C B A OH G F EE B A D C GF H 图2 图390GHE ∴∠=°．∴四边形EFGH 是正方形.(2)1.串讲六 圆考点串讲1.圆的有关概念与性质.考查重点：(1)圆的有关概念，包括圆心、半径、弦、弧等概念;(２)掌握并灵活运用垂径定理及推论，圆心角、弧、弦、弦心距间的关系定理以及圆周角定理及推论；(3)理解并掌握圆内接四边形的相关知识，而圆和三角形、四边形等结合的题型也是中考热点．2.与圆有关的位置关系．知识点：直线和圆的位置关系、切线的判定和性质、三角形的内切圆、切线长定理、弦切角的定理、相交弦、切割线定理．考查重点：(1)考查两圆位置关系中的相交及相切的性质；（２）证明直线是圆的切线；(3)论证线段相等、三角形相似、角相等、弧相等及线段的倍分等，此种结论的证明重点考查了全等三角形和相似三角形判定,垂径定理及其推论、圆周角、圆心角的性质及切线的性质，弦切角等有关圆的基础知识;３.与圆有关的计算．考查重点：(１)灵活求解圆周长、弧长以及圆、扇形、弓形和简单的组合图形的面积;(2)能进行圆柱、圆锥的侧面积、全面积的计算，了解它们的侧面展开图，这也是重点和中考热点．新题演练:新题1:如图，在Ｒｔ△AB Ｃ中,∠C =90°,AB ＝10，若以点Ｃ为圆心，CB 长为半径的圆恰好经过A Ｂ的中点D,则ＡC 的长等于( ）A.53 B ．5 C ．52ﻩD ．６解析:本题考查圆中的有关性质，连接ＣＤ，∵∠C=９0°,D 是AB 中点,AB=１０，∴CD ＝12AB=５,∴ＢC ＝5,根据勾股定理得AC ＝53,故选A. 答案:A新题2:如图所示，ＡＢ是O ⊙直径，OD ⊥弦BC 于点F ,且交O⊙于点E ，若AEC ODB ∠=∠．（1）判断直线BD 和O ⊙的位置关系,并给出证明；(2）当108AB BC ==，时，求BD 的长．解析：圆的切线有三种判定方法:①和圆只有一个公共点的直线是圆的切线；②到圆心的距离等于半径的直线是圆的切线;③过半径外端且和这条半径垂直的直线是圆的切线.在证明时一定要根据题目已知条件合理选择.答案:(１)直线BD 和O ⊙相切.证明：∵AEC ODB ∠=∠,AEC ABC ∠=∠,∴ABC ODB ∠=∠．∵OD ⊥BC ，∴90DBC ODB ∠+∠=°．∴90DBC ABC ∠+∠=°.即90DBO ∠=°.∴直线BD 和O ⊙相切．（２）连接AC ．∵ＡB 是直径，∴90ACB ∠=°.在Rt ABC △中,108AB BC ==，，∴226AC AB BC =-=．B C D A∵直径10AB =，∴5OB =． 由（1),BD 和O ⊙相切,∴90OBD ∠=°.∴90ACB OBD ∠=∠=°.由(１)得ABC ODB ∠=∠，∴ABC ODB △∽△．∴AC BC OB BD=． ∴685BD =，解得203BD =． 新题3:如图,在Rt ABC △中，9042C AC BC ===∠°，，，分别以AC .BC 为直径画半圆,则图中阴影部分的面积为 .（结果保留π） 解析：本题考查直角三角形,扇形面积,由图可知阴影部分的面积﹦半圆ＡＣ的面积＋半圆ＢＣ的面积-Rt ABC △的面积,所以S 阴影﹦221115π2124π42222π+-⨯⨯=-,故填5π42-. 答案:5π42- 串讲七 图形的相似考点串讲１.相似三角形.考查重点：（1）了解线段的比、成比例线段、黄金分割、相似图形有关概念及性质；（2)探索并掌握三角形相似的性质及条件，•并能利用相似三角形的性质解决简单的实际问题；（3）掌握图形位似的概念，能用位似的性质将一个图形放大或缩小.2．锐角三角函数.考查重点：(1)求三角函数值,特别是记忆30°、４5°、6０°的三角函数值；（2）考查互余或同角三角函数间关系;(3）求特殊角三角函数值的混合运算；（4）已知三角函数值会求出相应锐角；(5）掌握三角函数与直角三角形的相关应用,这是考试中的热点.3．解直角三角形及其应用．考查重点:(１)掌握并灵活应用各种关系解直角三角形；（2)了解测量中的概念，并能灵活应用相关知识解决某些实际问题，而在将实际问题转化为直角三角形问题时，怎样合理构造直角三角形以及如何正确选用直角三角形的边角关系是本节难点,也是中考的热点. 新题演练:新题1 ：如图，已知平行四边形ＡＢC Ｄ中,E 是ＡＢ边的中点,DE交A Ｃ于点Ｆ，ＡＣ,DE 把平行四边形ＡBCD 分成的四部分的面积分别为S １,S 2,S 3，S 4．下面结论：①只有一对相似三角形；②ＥＦ:E Ｄ＝1:２;③Ｓ１：Ｓ2:S 3：Ｓ４＝1:2:4:5.其中正确的结论是（ )A ．①③ B.③ C ．① D ．①②解析:∵ＡB ∥ＤＣ,∴△AEF•∽△ＣDF ，•但本题还有一对相似三角形是△ABC•≌△CD Ａ(全等是相似的特例）.∴①是错的. ∵12AE EF CD DF ==，∴②EF:ED=1：2是错的. ∴S △AEF :Ｓ△ＣＤF ＝１：4，S △AE Ｆ：S △ADF =１：2. ∴S １：S 2:S 3：S 4=１:２:4:5，③正确.CA B点拨 ：①利用相似三角形的特征和等高三角形的面积比等于底边之比；(共底三角形的面积之比等于高之比）②和全等三角形一样，中考试题往往把需要证明的两个相似三角形置于其他图形(如等边三角形、等腰直角三角形、平行四边形、矩形、菱形、正方形和梯形)中，在解题时要充分挖掘其中隐含的相等角、成比例的线段和平行线,注意从复杂的图形中分离出基本的相似三角形．答案：Ｂ新题2:已知在Rt ABC △中,390sin 5C A ∠==°，,则tan B 的值为（ ） A.43 ﻩﻩ Ｂ.45 ﻩﻩ C.54 ﻩ D ．34解析：本题考查三角函数的定义和勾股定理，在RT ΔＡBC 中，∠Ｃ=90°,则sin a A c =，tan b B a =和222a b c +=；由3sin 5A =知，如果设3a x =,则5c x =，结合222a b c +=得4b x =;∴44tan 33b xB a x ===,所以选A ． 答案:Ａ新题3:如图，为了测量我国最长的跨海大桥南航道A 型独塔斜拉桥桥墩的高度，小华站在桥面Ｂ处用测角仪测得桥墩顶点E 的仰角为45°，在桥面C 处用测角仪测得顶点E 的仰角为55°,已知测角仪高AB=1米，B Ｃ＝50米 ,桥面到海平面的距离为6米，求该桥墩海平面以上高度是多少?(精确到１米,参考数据:ｓin55°≈０.８２,cos ５5°≈0．57 ，t ａn5５°≈1．4）解析：用锐角三角函数解决实际问题．分别在直角△ＡEF 和直角△ＥＣF 中正切函数求解线段的长度.解决问题的关键在于寻找合适的直角三角形和合适的三角函数,这样会给解题带来方便.答案:在△AEF 中,︒=45tan AGEF . ∴AG ＝E Ｆ. 在△ＥCF 中︒=55tan CG EF ,∴CG=︒55tan EF ， ∴4.1EF EF -≈5０ ∴EF ≈１75， EG=1７６,176+5＝１81答:该桥墩海平面以上高度约是１8１米.串讲八 视图与投影考点串讲知识点:几何体的三视图、侧面展开图、视点、视角、盲区、投影.考查重点:（1）考查几何体的三视图;（２)考查根据光线的方向辨认实物的阴影;(3）掌握中心投影与平行投影的区别与联系.新题1:一个几何体由一些大小相同的小正方体组成，如图是它的主视图和俯视图,那么组成该几何体所需小正方体的个数最少为 （ )A.３ Ｂ．4 C ．5 D ．6解析：本题主要考查三视图的相关知识:主视图主要确定物体的长和55︒45︒E F D A高，左视图确定物体的宽和高，俯视图确定物体的长和宽.由题中所给出的主视图知物体共两列,且左侧一列高一层,右侧一列最高两层;由俯视图可知左侧一行,右侧两行,于是，可确定左侧只有一个小正方体，而右侧可能是一行单层一行两层，出可能两行都是两层.所以图中的小正方体最少4块,最多5块.答案:D新题2:（1）如图1是同一时刻的两棵树及其影子，请你在图中画出形成树影的光线,并判断它是太阳光线还是灯光的光线？若是灯光的光线,请确定光源的位置.(2）请判断如图２所示的两棵树的影子是在太阳光下形成的，还是灯光下形成的?并画出同一时刻旗杆的影子（用线段表示)．分析：本题是由树及其影子寻找光线，具体方法是过树的顶端及其影子的顶端作两条直线作为光线,若两条直线平行，则是太阳光线;若两条直线相交，则是灯光光线,其交点就是光源的位置.答案:(1)如图１所示是灯光的光线．原因是过一棵树的顶端及其影子的顶端作一条直线,再过另一棵树的顶端及其影子的顶端作一条直线,两直线相交,其交点就是光源的位置.（2)如图2所示,是太阳光的光线.原因是过一棵树的顶端及其影子的顶端作一条直线，再过另一棵树的顶端及其影子的顶端作一条直线，两直线平行.然后再过旗杆的顶端作一条与已知光线平行的直线，交地面于一点，连接这点与旗杆底端的线段就是旗杆的影子.串讲九 图形变换考点串讲１.轴对称与中心对称.考查重点:（1)理解轴对称和轴对称图形的联系与区别，•会判断一个图形是否是轴对称图形或中心对称图形;(2)掌握轴对称的基本特征,并能用这些特征解决简单的问题(如折叠）;(3)能用轴对称和中心对称的性质设计图案.２.平移与旋转．考查重点:(1）主要考查平移和旋转的基本性质；（２）会按要求画出平移图形或进行图案设计；（3）灵活运用轴对称、平移和旋转的组合进行图案设计.新题演练：新题1：下列图形中，既是轴对称图形又是中心对称图形的是（ )A 、B 、C 、D 、解析:本题主要考查轴对称、中心对称的概念.由轴对称和中心对称的概念可知，A 、B 仅为中心对称图形,C 仅为轴对称图形，D 既是轴对称图形又是中心对称图形.答案:Ｄ· A 图1 图2。