吉林大学大二上数学实验作业
数学实验(第二版)课后习题答案
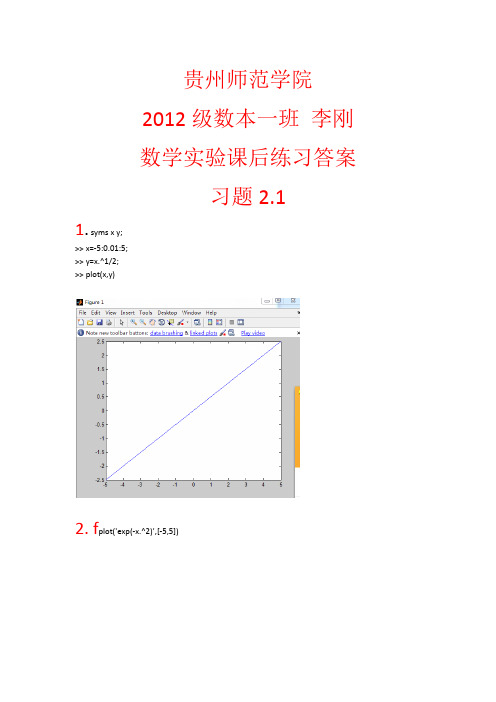
贵州师范学院2012级数本一班李刚数学实验课后练习答案习题2.11. syms x y;>> x=-5:0.01:5;>> y=x.^1/2;>> plot(x,y)2. f plot('exp(-x.^2)',[-5,5])3. ezplot('x.^3+y.^3-3*x*y',[-5,5])4 . ezplot('y.^2-x.^3/(1-x)',[-5,5])5.t=0:0.1:2*pi;x=t-sin(t);y=2*(1-cos(t));plot(x,y)6. t=0:0.1:2*pi; x=cos(t).^3; >> y=sin(t).^3;>> plot(t,y)>>7: t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z)8: x =0:0.1:2*pi; r=x; polar(x,r)9: x =0:0.1:2*pi; r=exp(x); polar(x,r)10: x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)11: x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)12: x =0:0.1:2*pi; r=1+cos(x); polar(x,r)练习2.2 1:(1)(2):syms n; limit('sqrt(n+2)-2*(sqrt(n+1))+sqrt(n)',n,inf)Ans= 0 (3):: (4):(5):(6):2:3:fplot('x.^2*sin(x.^2-x-2)',[-2,2])练习2.3 1:(2):2:练习2.4 1:(1)(2):(3)(4):2:(1):syms x;int(x^(-x),x,0,1)ans =int(x^(-x),x = 0 .. 1)vpa(ans,10)ans =1.291285997(2):syms x;int(exp(2*x)*cos(x)^3,x,0,2*pi)ans =-22/65+22/65*exp(4*pi)(3):syms x; int(exp(x^2/2)/sqrt(2*pi),x,0,1)ans =-1125899906842624/5644425081792261*i*erf(1/2*i*2^(1/2))*pi^(1/2)*2^(1/2) >> vpa(ans,10)ans =.4767191345(4):syms x;int(x*log(x^4)*asin(1/x^2),x,1,3)ans =int(x*log(x^4)*asin(1/x^2),x = 1 .. 3)>> vpa(ans,10)ans =2.459772128(5):syms x ;int(exp(x^2/2)/sqrt(2*pi),x,-inf,inf)ans =Inf(6):syms x ;int(sin(x)/x,x,0,inf)ans =1/2*pi(7):syms x ;int(tan(x)/sqrt(x),x,0,1)Warning: Explicit integral could not be found. > In sym.int at 58ans =int(tan(x)/x^(1/2),x = 0 .. 1)>> vpa(ans,10)ans =.7968288892(8):syms x ;int(exp(-x^2/2)/(1+x^4),x,-inf,inf)ans =1/4*pi^(3/2)*2^(1/2)*(AngerJ(1/2,1/2)-2/pi^(1/2)*sin(1/2)+2/pi^(1/2)*cos(1/2)-WeberE(1/2,1/2 ))>> vpa(ans,10)ans =1.696392536(9):syms x ;int(sin(x)/sqrt(1-x^2),x,0,1)ans =1/2*pi*StruveH(0,1)>> vpa(ans,10)ans =.8932437410练习2.5(1):syms n;symsum(1/n^2^n,n,1,inf)ans =sum(1/((n^2)^n),n = 1 .. Inf)(2):s yms n ;symsum(sin(1/n),n,1,inf)ans =sum(sin(1/n),n = 1 .. Inf)(3):syms n ;symsum(log(n)/n^3,n,1,inf) ans =-zeta(1,3)(4):syms n ;symsum(1/(log(n))^n,n,3,inf) ans =sum(1/(log(n)^n),n = 3 .. Inf)(5):syms n;symsum(1/(n*log(n)),n,2,inf) ans =sum(1/n/log(n),n = 2 .. Inf)(6):yms n;symsum((-1)^n*n/(n^2+1),n,1,inf)ans =-1/4*Psi(1-1/2*i)+1/4*Psi(1/2-1/2*i)-1/4*Psi(1+1/2*i)+1/4*Psi(1/2+1/2*i)第三章练习3.11:(1):a=-30:1:30;b=-30:1:30;[x,y]=meshgrid(a,b);z=10*sin(sqrt(x.^2+y.^2))./(sqrt(1+x.^2+y.^2)); meshc(x,y,z)(2):a=-30:1:30;b=-30:1:30;[x,y]=meshgrid(a,b);z=4*x.^2/9+y.^2;meshc(x,y,z)(3):(4):a=-30:1:30;b=-30:1:30;[x,y]=meshgrid(a,b); z=x.^2/3-y.^2/3; meshc(x,y,z)(5):a=-30:1:30;>> b=-30:1:30;>> [x,y]=meshgrid(a,b); >> z=x*y;>> meshc(x,y,z)(6):(7):a=-30:1:30;>> b=-30:1:30;>> [x,y]=meshgrid(a,b); >> z=sqrt(x.^2+y.^2); >> meshc(x,y,z)(8):(9):a=-30:1:30;>> b=-30:1:30;>> [x,y]=meshgrid(a,b);>> z=atan(x./y);>> meshc(x,y,z)练习3.21;a=-1:0.1:1;>> b=0:0.1:2;>> [x,y]=meshgrid(a,b);>> z=x.*exp(-x.^2-y.^2);>> [px,py]=gradient(z,0.1,0.1);>> contour(a,b,z)>> hold on>> quiver(a,b,px,py)2:a=-2:0.1:1;>> b=-7:0.1:1;>> [x,y]=meshgrid(a,b);>> z=y.^3/9+3*x.^2.*y+9*x.^2+y.^2+x.*y+9; >> plot3(x,y,z)>> grid on3:[x,y]=meshgrid(-2*pi:0.2:2*pi); z=x.^2+2*y.^2;plot3(x,y,z)hold onezplot('x^2+y^2-1',[-2*pi,2*pi]) ; grid on4:t=0:0.03:2*pi;>> s=[0:0.03:2*pi]';>> x=(0*s+1)*cos(t);y=(0*s+1)*sin(t);z=s*(0*t+1); >> mesh(x,y,z)>> hold on>> [x,y]=meshgrid(-1:0.1:1);>> z=1-x+y;>> mesh(x,y,z)5:syms x y z dx dyz=75-x^2-y^2+x*y;zx=diff(z,x),zy=diff(z,y)zx =-2*x+yzy =-2*y+x练习3.31:ezplot('x^2+y^2-2*x',[-2,2]);>> grid onsyms x y ;s=int(int(x+y+1,y,-sqrt(1-(x-1)^2),sqrt(1-(x-1)^2)),x,0,2)s =2*pi2:syms r t ;>> s=int(int(sqrt(1+r^2*sin(t)),r,0,1),t,0,2*pi)s =int(1/2*((1+sin(t))^(1/2)*sin(t)^(1/2)+log(sin(t)^(1/2)+(1+sin(t))^(1/2)))/sin(t)^(1/2),t = 0 .. 2*pi) 3:syms x y z ;>> s=int(int(int(1/(1+x+y+z)^3,z,0,1-x-y),y,0,1-x),x,0,1)s =-5/16+1/2*log(2)4:s=vpa(int(int(x*exp(-x^2-y^2),y,0,2),x,-1,10))s =0.16224980455070416645061789474030练习3.41:(1):y=dsolve('Dy=x+y','y(0)=1','x')得:y =-1-x+2*exp(x)(2):y=dsolve('Dy=2*x+y^2','y(0)=0')y =tan(t*x^(1/2)*2^(1/2))*x^(1/2)*2^(1/2)练习4.11:(1):p=[5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -6 8 0 0 0 -5 0 0]; >> x=roots(p)x =0.97680.9388 + 0.2682i0.9388 - 0.2682i0.8554 + 0.5363i0.8554 - 0.5363i0.6615 + 0.8064i0.6615 - 0.8064i0.3516 + 0.9878i0.3516 - 0.9878i-0.0345 + 1.0150i-0.0345 - 1.0150i-0.4609 + 0.9458i-0.4609 - 0.9458i-0.1150 + 0.8340i-0.1150 - 0.8340i-0.7821 + 0.7376i-0.7821 - 0.7376i-0.9859 + 0.4106i-0.9859 - 0.4106i-1.0416-0.7927(2): p=[8 36 54 23];x=roots(p)x =-1.8969 + 0.6874i-1.8969 - 0.6874i-0.70632:p1=[1 0 -3 -2 -1];p2=[1 -2 5];[q2,r2]=deconv(p1,p2)q2 =1 2 -4r2 =0 0 0 -20 19 3:syms x;f=x^4+3*x^3-x^2-4*x-3;g=3*x^3+10*x^2+2*x-3;p1=factor(f),p2=factor(g)p1 =(x+3)*(x^3-x-1)p2 =(x+3)*(3*x^2+x-1)4:syms x ;f=x^12-1;p=factor(f)p =(-1+x)*(1+x^2+x)*(1+x)*(1-x+x^2)*(1+x^2)*(x^4-x^2+1)5: (1):p=[1 0 1];q=[1 0 0 0 1];[a,b,r]=residue(p,q)a =-0.0000 - 0.3536i-0.0000 + 0.3536i0.0000 - 0.3536i0.0000 + 0.3536ib =0.7071 + 0.7071i0.7071 - 0.7071i-0.7071 + 0.7071i-0.7071 - 0.7071ir =[](2):p=[1];q=[1 0 0 0 1];[a,b,r]=residue(p,q)a =-0.1768 - 0.1768i -0.1768 + 0.1768i0.1768 - 0.1768i0.1768 + 0.1768ib =0.7071 + 0.7071i0.7071 - 0.7071i -0.7071 + 0.7071i -0.7071 - 0.7071ir =[](3):p=[1 0 1];q=[1 1 -1 -1];[a,b,r]=residue(p,q)a =0.5000-1.00000.5000b =-1.0000-1.00001.0000r =[] (4): p=[1 1 0 0 0 -8];[a,b,r]=residue(p,q)a =-4-38b =-11r =1 1 1练习 4.21:(1):D=[2 1 3 1;3 -1 2 1;1 2 3 2;5 0 6 2];det(D)ans =6(2):syms a b c dD=[a 1 0 0 ;-1 b 1 0;0 -1 c 1;0 0 -1 d];det(D)ans =a*b*c*d+a*b+a*d+c*d+12:(1):D=[1 1 1 1; a b c d;a^2 b^2 c^2 d^2;a^3 b^3 c^3 d^3];det(D)ans =b*c^2*d^3-b*d^2*c^3-b^2*c*d^3+b^2*d*c^3+b^3*c*d^2-b^3*d*c^2-a*c^2*d^3+a*d^2*c^3+a *b^2*d^3-a*b^2*c^3-a*b^3*d^2+a*b^3*c^2+a^2*c*d^3-a^2*d*c^3-a^2*b*d^3+a^2*b*c^3+a^ 2*b^3*d-a^2*b^3*c-a^3*c*d^2+a^3*d*c^2+a^3*b*d^2-a^3*b*c^2-a^3*b^2*d+a^3*b^2*c(2): s yms a b x y zD=[a*x+b*y a*y+b*z a*z+b*x; a*y+b*z a*z+b*x a*x+b*y;a*z+b*x a*x+b*y a*y+b*z];det(D)ans =3*a^3*x*z*y+3*b^3*y*x*z-a^3*x^3-a^3*y^3-b^3*z^3-a^3*z^3-b^3*x^3-b^3*y^33: (1): D=[1 1 1 1;1 2 -1 4;2 -3 -1 -5;3 1 2 11];D1=[5 1 1 1;-2 2 -1 4;-2 -3 -1 -5;0 1 2 11];D2=[1 5 1 1;1 -2 -1 4;2 -2 -1 -5;3 0 2 11];D3=[1 1 5 1;1 2 -2 4;2 -3 -2 -5;3 1 0 11];D4=[1 1 1 5;1 2 -1 -2;2 -3 -1 -2;3 1 2 0];x1=det(D1)/det(D);x2=det(D2)/det(D);x3=det(D3)/det(D);x4=det(D4)/det(D);x1,x2,x3,x4x1 =1x2 =2x3 =3x4 =-1(2):D=[5 6 0 0 0;1 5 6 0 0;0 1 5 6 0;0 0 1 5 6;0 0 0 1 5]; D1=[1 6 0 0 0;0 5 6 0 0;0 1 5 6 0;0 0 1 5 6;1 0 0 1 5]; D2=[5 1 0 0 0;1 0 6 0 0;0 0 5 6 0;0 0 1 5 6;0 1 0 1 5]; D3=[5 6 1 0 0;1 5 0 0 0;0 1 0 6 0;0 0 0 5 6;0 0 1 1 5]; D4=[5 6 0 1 0;1 5 6 0 0;0 1 5 0 0;0 0 1 0 6;0 0 0 1 5]; D5=[5 6 0 0 1;1 5 6 0 0;0 1 5 6 0;0 0 1 5 0;0 0 0 1 1]; x1=det(D1)/det(D);x2=det(D2)/det(D);x3=det(D3)/det(D);x4=det(D4)/det(D);x5=det(D5)/det(D);x1,x2,x3,x4,x5x1 =2.2662x2 =-1.7218x3 =1.0571x4 =-0.5940x5 =0.3188练习 4.3 1:A=[1 2 0;3 4 -1; 1 1 -1];B=[1 2 3;-1 0 1;-2 4 -3];A',2+A,2*A-B,A*B,A^2,A^(-1)ans =1 3 12 4 10 -1 -1ans =3 4 25 6 13 3 1ans =1 2 -37 8 -34 -2 1ans =-1 2 51 2 162 -2 7ans =7 10 -214 21 -33 5 0ans =-3.0000 2.0000 -2.00002.0000 -1.0000 1.0000-1.0000 1.0000 -2.0000 2:(1):B=[2 4 3];B'ans =243(2):A=[1 2 3];B=[2 4 3];A.*B,B.*Aans =2 8 9ans =2 8 93:(1):A=[0 1 0;1 0 0;0 0 1];B=[1 0 0;0 0 1;0 1 0];C=[1 -4 3;2 0 -1;1 -2 0];A^(-1),B^(-1),X=A^(-1)*C*B^(-1) ans =0 1 01 0 00 0 1ans =1 0 00 0 10 1 0X =2 -1 01 3 -41 0 -2(2):>> A=[1 2 3;2 2 3;3 5 1];B=[1 0 0;2 0 0;3 0 0];A^(-1),x=A^(-1)*Bans =-1.0000 1.0000 0.00000.5385 -0.6154 0.23080.3077 0.0769 -0.1538x =1 0 00 0 00 0 0练习 4.41:(1):A=[4 2 -1;3 -1 2;11 3 0];b=[2;10;8];B=[A,b];rank(A),rank(B)ans =2ans =3(2):A=[2 1 -1 1;3 -2 1 -3;1 4 -3 5];b=[1;4;-2];B=[A,b];rank(A),rank(B)ans =2ans =2(3):A=[ 1 1 1 1; 1 2 -1 4;2 -3 -1 -5;3 1 2 11];b=[5;-2;-2;0];B=[A,b];rank(A),rank(B)ans =4ans =4(4):A=[ 1 1 2 -1; 2 1 1 -1;2 2 1 2];b=[0;0;0];B=[A,b];rank(A),rank(B)ans =3ans =32:syms a;A=[-2 1 1;1 -2 1;1 1 -2];b=[-2;a;a^2];B=[A,b];rank(A),rank(B)ans =2ans =3练习4.51:(1):A=[0 1;-1 0];[a,b]=eig(A)a =0.7071 0.70710 + 0.7071i 0 - 0.7071ib =0 + 1.0000i 000 - 1.0000i(2):A=[0 0 1;0 1 0;1 0 0];[a,b]=eig(A)a =0.7071 0.7071 00 0 -1.0000-0.7071 0.7071 0b =-1 0 00 1 00 0 1(3):A=[4 1 -1;3 2 -6;1 -5 3];[a,b]=eig(A)a =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170b =-3.0527 0 00 3.6760 00 0 8.3766(4):A=[1 1 1 1;1 1 -1 -1;1 -1 1 -1;1 1 -1 1];[a,b]=eig(A)a =0.5615 0.3366 0.2673 -0.7683-0.5615 -0.3366 0.0000 -0.0000-0.5615 -0.3366 -0.5345 -0.6236-0.2326 0.8125 0.8018 -0.1447b =-1.4142 0 0 00 1.4142 0 00 0 2.0000 00 0 0 2.0000(5):A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10];[a,b]=eig(A)a =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209b =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887(6):A=[5 6 0 0 0;1 5 6 0 0 ;0 1 5 6 0 ;0 0 1 5 6; 0 0 0 1 5 ]; [a,b]=eig(A)a =0.7843 -0.7843 -0.9860 -0.9237 -0.92370.5546 0.5546 0.0000 0.3771 -0.37710.2614 -0.2614 0.1643 -0.0000 0.00000.0924 0.0924 0.0000 -0.0628 0.06280.0218 -0.0218 -0.0274 0.0257 0.02579.2426 0 0 0 00 0.7574 0 0 00 0 5.0000 0 00 0 0 2.5505 00 0 0 0 7.4495 2:(1):A=[0 1;-1 0];[a,b]=eig(A)a =0.7071 0.70710 + 0.7071i 0 - 0.7071ib =0 + 1.0000i 00 0 - 1.0000i>> P=orth(a),B=P'*A*P,P*P'P =-0.7071 -0.70710 - 0.7071i 0 + 0.7071iB =0 + 1.0000i 0 - 0.0000i0 - 0.0000i 0 - 1.0000ians =1.0000 0 + 0.0000i0 - 0.0000i 1.0000>> inv(a)*A*a0 + 1.0000i 000 - 1.0000i3:(1):A=[2 0 0;0 3 2;0 2 3]; [a,b]=eig(A)a =0 1.0000 0-0.7071 0 0.70710.7071 0 0.7071b =1.0000 0 00 2.0000 00 0 5.0000>> P=orth(a),B=P'*A*P,P*P'P =-1.0000 0 -0.00000.0000 0.7071 0.7071-0.0000 -0.7071 0.7071B =2.0000 0.0000 0.00000.0000 1.0000 00.0000 0 5.0000ans =1.0000 -0.0000 0.0000-0.0000 1.0000 -0.00000.0000 -0.0000 1.0000(2):A=[1 1 0 -1;1 1 -1 0;0 -1 1 1;-1 0 1 1];[a,b]=eig(A)a =-0.5000 0.7071 0.0000 0.50000.5000 -0.0000 0.7071 0.50000.5000 0.7071 0.0000 -0.5000-0.5000 0 0.7071 -0.5000 b =-1.0000 0 0 00 1.0000 0 00 0 1.0000 00 0 0 3.0000 >> P=orth(a),B=P'*A*P,P*P'P =-0.5000 -0.4998 -0.4783 -0.52100.5000 -0.4822 0.5212 -0.49580.5000 0.4998 -0.4964 -0.5037-0.5000 0.5175 0.5031 -0.4786 B =-1.0000 0.0000 0.0000 0.00000.0000 2.9988 -0.0362 0.03440.0000 -0.0362 1.0007 -0.00060.0000 0.0344 -0.0006 1.0006 ans =1.0000 0.0000 0.0000 -0.00000.0000 1.0000 -0.0000 00.0000 -0.0000 1.0000 0.0000-0.0000 0 0.0000 1.0000练习5.3 1: [m,v]=unifstat(1,11)m =6v =8.33332:[m,v]=normstat(0,16)m =v =256>> s=sqrt(v)s =163:x=randn(200,6);s=std(x)s =0.9094 0.9757 0.9702 0.9393 0.9272 1.09824: x=normrnd(0,16,300,1);hist(x,10)练习 5.61:x=[352 373 411 441 462 490 529 577 641 692 743];y=[166 153 177 201 216 208 227 238 268 268 274];plot(x,y,'*')4:(1):x=[10 10 10 15 15 15 20 20 20 25 25 25 30 30 30];y=[25.2 27.3 28.7 29.8 31.1 27.8 31.2 32.6 29.7 31.7 30.1 32.3 29.4 30.8 32.8]; plot(x,y,'*')。
数学实验习题

数学实验习题实验1 MATLAB 基本特性与基本运算1. 求解方程02=++c bx ax的根。
其中(1)3,2,1===c b a (2)3,2,1-=-==c b a (提示:运用求根公式。
结果为(1)ix 212,1±-=,(2)3,12,1-=x )2. 已知圆的半径为15,求圆的周长和面积。
3. 输入例1-6中语句,计算三角形的面积并修改边长值重新计算三角形的面积。
4. 查询表1-4中部分常用函数的功能与用法。
5. 设⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--=0220,2112B A ,求矩阵方程X B A AX -=-2的解。
6. 画出231xxy +=和22)1ln(xx z +=在区间[-5,5]上的图形(提示:用 .^ 和 ./ 运算)。
7. 画出x ex e x f xxsin cos )(cos 2sin 2-=在区间[-5,5]上的图形。
8. 设x ex ex f xxsin cos )(cos 2sin 2-=,试在[-5,5]上求出函数的零点及极大、极小值。
9. 求方程0d )cos 32( 03=--+⎰s t t e txt当=s 1、11、21时的根。
10. 已知⎰+=1214dxxπ(试证明),试用不同的积分命令求其近似值(pi=3.14159265358…)。
11.设||sin 12)(/1x ax ex f x-+=-,试求当)(lim 1x f x →存在时a 的大小以及极限值。
12.设)cos sin()(x x x x f ++=,求)(x f 在]4,0[π上的极值、拐点。
13.计算积分(1)⎰dxx x sin ;(2)dxxx ⎰++12)1ln(。
实验2 MATLAB 绘制二维、三维图形1. 在圆域122≤+yx上画出上半球面221yxz --=的图形。
2. 画出椭球面11241222=++zyx的图形。
3. 在矩形域[-2,2]×[-2,2]区域上画出函数)(22y x xez +-=的图形。
数学实验作业1--答案

数学实验-作业1—及部分答案(要求:1. 每次上机课下课之前提交,文件名如:数学091朝鲁第一次作业.doc。
2. 交至邮箱:matlabzuoyetijiao@3.作业实行5分制,依次为A++,A+,A ,A-,A- -)4.作业中,需要编程实现的均要求列出你的代码,以及求解的结果)1.请上网或查阅各种资料并回答:MATLAB是什么?MATLAB能做什么?答:略2.请上网或查阅各种资料并回答:MATLAB语言突出的特点是什么?答:略3.在MATLAB软件中有几种获得帮助的途径?答:help函数,菜单栏help菜单。
4.请上网或查询MATLAB软件中inv函数的功能与特点。
答:用来求可逆矩阵的逆矩阵。
inv(A),即求已知矩阵A的逆矩阵。
5.请上网或查阅各种资料并回答:如何在MATLAB中建立向量和矩阵。
答:如在matlab中创建向量a=(2,-5,6,1);a=[2,-5,6,1];b= [2;-5;6;1];如在matlab中创建矩阵A=;A=[1,2,3;4,5,6;7,8,9];A =1 2 34 5 67 8 96.请上网或查阅各种资料并回答:在MATLAB中,向量和矩阵如何进行基本加减乘除四则运算,以及矩阵的乘法。
答:a=[2,-5,6,1];b= [1,2,3,4];求向量的和与差,直接输入a+b,a-b,即可,当然必须要求两个向量大小一致。
如:>> a=[2,-5,6,1];b= [1,2,3,4];>> a+bans =3 -3 9 5>> a-b1 -7 3 -3>> a.*bans =2 -10 18 4>> a./bans =2.0000 -2.5000 2.0000 0.2500>> a/b向量之间进行除法运算,使用不加点的矩阵除法“A/B”时,问题可以描述为:给定两个向量A、B,求一个常量x,使得A=x * B。
数学实验之学生实验题目

数学实验之学生实验题目 MATLAB 简介实验一:数组操作及运算练习1.设有分块矩阵⎥⎦⎤⎢⎣⎡=⨯⨯⨯⨯22322333S O R E A ,其中E,R,O,S 分别为单位阵、随机阵、零阵和对角阵,试通过数值计算验证⎥⎦⎤⎢⎣⎡+=22S 0RS R EA 。
2.求如下非齐次线性方程组的通解,⎪⎩⎪⎨⎧=--+=+-+=+-+.12,2224,12w z y x w z y x w z y x3.某零售店有9种商品的单件进价(元)、售价(元)及一周的销量下表,问哪种商品的利润最大,哪种商品的利润最小;按收入由小到大,列出所有商品及其收入;求这一周该10种商品的总收入和总利润。
实验二:作图练习1. 用两种方法在同一个坐标下作出y 1= x 2,y 2= x 3,y 3= x 4 y 4= x 5这四条曲线的图形,并要求用两种方法在图上加各种标注。
2.用subplot 分别在不同的坐标系下作出下列四条曲线,为每幅图形加上标题, 1)概率曲线 2exy -=;2)四叶玫瑰线 r =sin2q ;3)叶形线 ⎪⎪⎩⎪⎪⎨⎧+=+=;13,13323t ty t t x 4)曳物线 22111lnyyy x --±= 。
3.作出下列曲面的3维图形,1))sin(22y x z +=π;2)环面:⎪⎩⎪⎨⎧=+=+=,sin ,sin )cos 1(,cos )cos 1(u z v u y v u x )2,0()2,0(ππ∈∈v u 。
实验三:编写M-文件1.建立一个命令M-文件:求所有的“水仙花数”,所谓“水仙花数”是指一个三位数,其各位数字的立方和等于该数本身。
例如,153是一个水仙花数,因为153=13+53+33。
2.编写函数M-文件SQRT.m :用迭代法求a x =的值。
求平方根的迭代公式为迭代的终止条件为前后两次求出的x 的差的绝对值小于10-5。
〈返回〉方程求解实验一:油价与船速的优化问题油价的上涨,将影响大型海船确定合理的航行速度,以优化航行收入。
第一次作业-吉林大学数学学院

高等数学作业CⅡ吉林大学公共数学教学与研究中心2013年3月第一次作业学院 班级 姓名 学号一、单项选择题1.平面1=+z y ( ). (A )平行于yoz 平面; (B )平行于x 轴; (C )平行于xoz 面;(D )平行于xoy 平面.2.平面1=z 与曲面14222=++z y x ( ). (A )不相交;(B )交于一点; (C )交线为一个椭圆;(D )交线为一个圆.3.方程z y x =-4222所表示的曲面为( ). (A )椭球面; (B )柱面; (C )双曲抛物面; (D )旋转抛物面.4.过点(1,2,4)-且与平面234x y z -+=垂直的直线方程是( ). (A )124231x y z -+-==--; (B )238x y z -+=; (C )124124x y z -+-==-;(D )124231x y z ---==-. 5.设有直线182511:1+=--=-z y x L 与⎩⎨⎧=+=-326:2z y y x L ,则L 1与L 2的夹角为( ).(A )6π; (B )4π; (C )3π; (D )2π.6.设有直线⎩⎨⎧=+--=+++031020123:z y x z y x L 及平面0224:=-+-z y x π,则直线L ( ).(A )平行于π; (B )在π上; (C )垂直于π; (D )与π斜交.二、填空题1.设,a b 均为非零向量,且||||+=-a b a b ,则a 与b 的夹角为 . 2.与直线⎩⎨⎧=+-=++0132z y x z y x 平行的单位向量为 .3.点0(1,2,1)M 到平面2210x y z π++=:的距离为 .4.若||3=a ,||2=b ,且a ,b 间夹角为34θπ=,则||+=a b ,||⨯=a b .5.xoz 平面上的曲线1x =绕z 轴旋转一周所形成的旋转曲面方程为 .6.曲线⎩⎨⎧=-+--=032622z y y x z 在xoy 面上的投影曲线方程为 .7.已知向量a ,b ,c 两两相互垂直,且||1=a ,||2=b ,||1=c ,则有||++=a b c .三、计算题 1.求过直线1212:102x y z L --+==-,且平行于直线221:212x y zL +-==--的平面π的方程.2.求点(2,1,3)到直线11321x y z+-==-的距离.3.设空间三点)2,1,1(-A,)4,5,4(B,)2,2,2(C,求三角形ABC的面积.4.设有直线210:210x y z L x y z ++-=⎧⎨-++=⎩,平面:0x y π+=求直线L 与平面π的夹角;如果L 与π相交,求交点.5.求过平面02=+y x 和平面6324=++z y x 的交线,并切于球面4222=++z y x 的平面方程.第二次作业学院 班级 姓名 学号一、单项选择题 1.22003limx y xyx y →→=+( ).(A )32; (B )0; (C )65; (D )不存在.2.二元函数⎪⎩⎪⎨⎧=≠+=)0,0(),(,0)0,0(),(,),(22y x y x y x xyy x f 在)0,0(处( ).(A )连续,偏导数存在;(B )连续,偏导数不存在; (C )不连续,偏导数存在;(D )不连续,偏导数不存在.3.设22(,)(1)(2)f x y y x x y =-+-,在下列求(1,2)x f 的方法中,不正确的一种是( ).(A )因2(,2)2(1),(,2)4(1)x f x x f x x =-=-,故1(1,2)4(1)|0x x f x ==-=; (B )因(1,2)0f =,故(1,2)00x f '==;(C )因2(,)2(1)(2)x f x y y x y =-+-,故12(1,2)(,)0x x x y f f x y ====;(D )211(,2)(1,2)2(1)0(1,2)lim lim 011x x x f x f x f x x →→---===--.4.若(,)f x y 的点00(,)x y 处的两个偏导数都存在,则( ). (A )(,)f x y 在点00(,)x y 的某个邻域内有界; (B )(,)f x y 在点00(,)x y 的某个邻域内连续;(C )0(,)f x y 在点0x 处连续,0(,)f x y 在点0y 处连续; (D )(,)f x y 在点00(,)x y 处连续.5.设22(,),2zz f x y y∂==∂,且(,0)1,(,0)y f x f x x ==,则(,)f x y 为( ).(A )21xy x -+; (B )21xy y ++; (C )221x y y -+; (D )221x y y ++. 二、填空题1.2224ln(1)x y z x y -=--的定义域为 .2.0011limx y xyxy →→--= .3.设22),(y x y x y x f +-+=,则=')4,3(x f ,=')4,3(y f . 4.设ln(32)u x y z =-+,则d u = . 5.设yz x =,则2zx y∂=∂∂ . 三、计算题1.已知(2)z y f x =++,且当1y =时z x =,求()f t 及z 的表达式.2.讨论函数2222222,0,(,)0,0x xyx yf x y x yx y⎧++≠⎪=+⎨⎪+=⎩的连续性.3.设(1)yz xy=+,求d z.4.求2e d yz t xz u t =⎰的偏导数.四、应用题某种数码相机的销售量Q A 除与它自身的价格P A 有关外,还与彩色喷墨打印机的价格P B 有关,具体为210250120B B AA P P P Q --+=,求50=A P ,50=B P 时 (1)Q A 对P A 的弹性;(2)Q A 对P B 的交叉弹性.五、证明题1.设222r x y z =++,验证:当0r ≠时,有2222222r r r x y z r∂∂∂++=∂∂∂.2.证明函数(,)||f x y xy =在点(0, 0)处:(1)连续;(2)偏导数存在;(3)不可微.第三次作业学院 班级 姓名 学号一、单项选择题 1.设22()y z f x y =-,其中()f u 为可导函数,则zx∂∂=( ). (A )2222()xyf x y --;(B )222222()()xyf x y f x y '---;(C )22222()()yf x y f x y '---;(D )2222222()()()f x y yf x y f x y '-----.2.()u f r =,而222r x y z =++,且函数()f r 具有二阶连续导数,则22ux∂+∂2222u uy z ∂∂+=∂∂( ). (A )1()()f r f r r '''+;(B )2()()f r f r r '''+; (C )211()()f r f r r r'''+;(D )212()()f r f r r r '''+.3.设方程(,,)0F x y y z z x ---=确定z 是x ,y 的函数,F 是可微函数,则z x∂∂=( ).(A )13F F '-'; (B )13F F ''; (C )x zy zF F F F --;(D )1323F F F F ''-''-.4.设(,),(,),(,)x x y z y y z x z z x y ===都由方程(,,)0F x y z =所确定的隐函数,则下列等式中,不正确的一个是( ).(A )1x yy x∂∂=∂∂; (B )1x zz x∂∂=∂∂; (C )1x y zy z x∂∂∂=∂∂∂;(D )1x y zy z x∂∂∂=-∂∂∂.5.设(,)u x y 在平面有界闭区域D 上是C (2)类函数,且满足20ux y∂≠∂∂及22220u ux y ∂∂+=∂∂,则(,)u x y 的 ( ). (A )最大值点和最小值点必定都在D 的内部; (B )最大值点和最小值点必定都在D 的边界上; (C )最大值点在D 的内部,最小值点在D 的边界上; (D )最小值点在D 的内部,最得到值点在D 的边界上. 二、填空题 1.设y x u xsin e-=,则y x u ∂∂∂2在⎪⎭⎫ ⎝⎛π1,2处的值为 .2.已知(1,2)4,d (1,2)16d4d ,d (1,4)64d 8d f f x y f x y ==+=+,则(,(,))z f x f x y =在点(1, 2)处对x 的偏导数为 .3.由方程e z xy yz zx -+=所确定的隐函数(,)z z x y =在点(1, 1)处的全微分为 .4.22z x y =+在条件1x y +=下的极小值是 . 三、计算与解答题1.设f 是C (2)类函数,22(e ,)xyz f x y =-,求2zx y∂∂∂.2.设32(32)x y z x y -=-,求d z .3.设22ln arctan y x y x +=,求22d d yx.4.设⎰+-=u v ut t z 222d e ,x u sin =,x v e =,求xz d d .5.求函数22(,)(2)ln f x y x y y y =++的极值.6.求函数22=+≤上的最大值和{(,)|25}D x y x yf x y x y x y(,)1216=+-+在区域22最小值.四、应用题某企业在雇用x名技术工人,y名非技术工人时,产品的产量232+-=,若企业只能雇用230人,那么该雇用多少技术工人,多少非技术12Q-8yxyx工人才能使产量Q最大?第四次作业学院 班级 姓名 学号一、单项选择题1.设(,)f x y 连续,且(,)(,)d d Df x y xy f x y x y =+⎰⎰,其中D 是由0y =,2y x =,1x =所围区域,则(,)f x y 等于( ).(A )xy ;(B )2xy ;(C )18xy +; (D )1xy +.2.设D 是xOy 平面上以(1, 1), (-1, 1)和(-1, -1)为顶点的三角形区域,D 1是D 的第一象限部分,则(cos sin )d d Dxy x y x y +⎰⎰等于( ).(A )12cos sin d d D x y x y ⎰⎰;(B )12d d D xy x y ⎰⎰;(C );14c o s s i n )dd D x y x y xy+⎰⎰((D )0.3.设平面区域22:14,(,)D x y f x y ≤+≤是在区域D 上的连续函数,则()22d d Df x y x y +⎰⎰等于 ( ).(A )212()d rf r r π⎰;(B )21002()d ()d rf r r rf r r π⎡⎤+⎣⎦⎰⎰;(C )2212()d rf r r π⎰; (D )2122002()d ()d rf r r rf r r π⎡⎤+⎣⎦⎰⎰.4.设有空间区域22221:,0x y z R z Ω++≤≥及22222:x y z R Ω++≤,0x ≥,0y ≥,0z ≥,则( ).(A )12d 4d x V x V ΩΩ=⎰⎰⎰⎰⎰⎰; (B )12d 4d y V y V ΩΩ=⎰⎰⎰⎰⎰⎰;(C )12d 4d z V z V ΩΩ=⎰⎰⎰⎰⎰⎰;(D )12d 4d xyz V xyz V ΩΩ=⎰⎰⎰⎰⎰⎰.二、填空题1.积分2220d e d y x x y -=⎰⎰ . 2.交换积分次序:14012d (,)d d (,)d x xxx x f x y y x f x y y --+=⎰⎰⎰⎰ .3.设区域D 为||||1x y +≤,则(||||)d d Dx y x y +=⎰⎰ . 4.设区域D 为222x y R +≤,则2222d d D x y x y ab ⎛⎫+= ⎪⎝⎭⎰⎰ . 5.直角坐标中三次积分222211110d d (,,)d x x y x I x y f x y z z -+---=⎰⎰⎰在柱面坐标中先z 再r 后θ顺序的三次积分是 .三、计算题1.计算|cos()|d d Dx y x y +⎰⎰,其中D 是由直线,0,2y x y x π===所围成的三角形区域.2.计算sin d d Dx yx y y⎰⎰,其中D 是由2y x =和y x =所围成的区域.3.计算22()d d Dx y x y +⎰⎰,其中22{(,)|02,24}D x y x x x y x =≤≤-≤≤-.4.计算23d xy z V Ω⎰⎰⎰,其中Ω是由曲面z xy =与平面,1y x x ==和0z =所围成的闭或区域.5.计算d I xyz V Ω=⎰⎰⎰,其中222{(,,)|1,0,0,0}x y z x y z x y z Ω=++≤≥≥≥.6.设()222()d F t fx y z V Ω=++⎰⎰⎰,其中2222:,()x y z t f t Ω++≤在0t =可导,且(0)0f =,求4()lim t F t t π+→.四、证明题设函数)(x f 在闭区间],[b a 上连续且恒大于零,证明2d ()d ()()bbaaxf x x b a f x ≥-⎰⎰.阶段测试题学院 班级 姓名 学号一、单项选择题(每小题3分,满分21分)1.(3,5,2),(2,1,4),λμ=-=+a b a b 与z 轴垂直,则,λμ满足条件( ). (A )λμ=;(B )λμ=-; (C )2λμ=; (D )2μλ=.2.二元函数(,)z f x y =在00(,)x y 连续,且00(,)x f x y '、00(,)y f x y '存在是(,)z f x y =在00(,)x y 可微的( )条件.(A )充分(B )必要(C )充分必要(D )非充分非必要3.已知(,)x f x y 、(,)y f x y 在(0,0)连续,则(,)z f x y =在(0,0)处,()(,0)x f x φ=在0x =处( ).(A )均连续 (B )均不一定连续(C )均不连续(D )()x φ一定连续,(,)f x y 不一定连续4.设区域D 由曲线x y =与2x y =围成,则⎰⎰Dxy σd 的值为( ).(A )121-; (B )121; (C )241; (D )241-. 5.设D 由21y x =-和0y =围成,则(e sin )d d y Dx y x y +=⎰⎰( ). (A )0(B )1(C )2/3(D )4/36.将极坐标系下的二次积分r r r rf I d )sin ,cos (d sin 20⎰⎰=θπθθθ化为直角坐标系下的二次积分,则I =( ).(A )x y x f y y y d ),(d 22111111⎰⎰-+---; (B )y y x f x x x x x d ),(d 22222⎰⎰---; (C )x y x f y y y y y d ),(d 222211⎰⎰----;(D )y y x f x x x d ),(d 22111111⎰⎰-+---.7.设Ω由22222,2(0)z x y x y z z =+++=≥围成,则三重积分222()d x y z VΩ++⎰⎰⎰化为柱面坐标系下三次积分为( ).(A )2222222d d ()d r rr r r z z πθ-+⎰⎰⎰(B )22222220d d ()d r rr r r z z πθ-+⎰⎰⎰(C )222120d d 2d r rr r z πθ-⎰⎰⎰(D )22212220d d ()d r rr r r z z πθ-+⎰⎰⎰二、填空题(每小题3分,满分18分)1.已知a ,b ,c 都是单位向量,且满足0++=a b c ,则⋅+⋅+⋅=a b b c c a .2.通过点(1,2,1)且与直线⎩⎨⎧=--+=-+-04230532z y x z y x 垂直的平面方程 .3.已知3(,)e ln 2x f x y y =,则1(0,)2x f '= ,(0,1)yyf ''= . 4.11[()()]()d 22x at x atu x at x at f t ta φφ+-=++-+⎰,其中(2),f C φ∈,则 22222u u a t x∂∂-=∂∂ . 5.设Ω为由22z x y =+,2z =围成的空间区域,a 为常数,则d a V Ω=⎰⎰⎰ .6.设2222202I d (,)d d (,)d R x R R x R x f x y y x f x y y -=+⎰⎰⎰⎰,改变积分次序I = ;化为极坐标下二次积分为I = .三、计算题(每小题8分,满分40分)1.(2,sin )(e ln )x z f x y y x xg y =-+,其中f 具有二阶连续偏导数,g 具有二阶导数。
2023学年吉大附中实验高二数学上学期第一次月考卷及答案解析

2023学年吉大附中实验高二数学上学期第一次月考卷考试时间:120分钟,试卷满分:150分第Ⅰ卷(选择题60分)一、单项选择题(本大题包括8个小题,每小题5分,共40分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡上).1.椭圆22145x y +=的焦距为()A .6B .3C .2D .12.直线22x y +=在x 轴上的截距为()A .1B .2C .-2D .-13.若直线210x y +-=是圆()221x a y ++=的一条对称轴,则=a ()A .12B .12-C .1D .1-4.如果0ac <,0bc >,那么直线0ax by c ++=不通过()A .第一象限B .第二象限C .第三象限D .第四象限5.如图,在平行六面体1111ABCD A B C D -中,点M 是棱1CC 的中点,连接1B M 、1BC 交于点P ,则()A .12133DP AB AD AA =-+ B .11233DP AB AD AA =-+C .12233DP AB AD AA =++ D .11122DP AB AD AA =-+6.已知点()1,2-和3,03⎛⎫⎪ ⎪⎝⎭在直线():100l ax y a --=≠的两侧,则直线l 的倾斜角的取值范围是()A .ππ,43⎛⎫- ⎪⎝⎭B .π2π,33⎛⎫ ⎪⎝⎭C .π2π0,,π43⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭D .π3π0,,π34⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭7.在四棱锥P ABCD -中,底面ABCD 为矩形,侧棱PA ⊥底面,3,1,ABCD AB BC PA E ===为PD 的中点,点N 在平面PAC 内,且NE ⊥平面PAC ,则点N 到面PAB 的距离为()A .16B .18C .38D .1788.过点()1,1P -作圆C :()()2221x t y t -+-+=()t R ∈的切线,切点分别为A ,B ,则PA PB ⋅ 的最小值为A .103B .403C .214D .223-二、多项选择题(本大题包括4个小题,每小题5分,共20分,每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分).9.已知直线1l :340ax y ++=,2l :()2250x a y a +-+-=,则()A .若1a =,则1l 的一个方向向量为()3,1-B .若12//l l ,则1a =-或3a =C .若12l l ⊥,则32a =D .1l 恒过定点()0,410.下列结论正确的是()A .两条不重合直线1l ,2l 的方向向量分别是()2,3,1a =- ,()2,3,1b =--,则12//l l B .两个不同的平面α,β的法向量分别是()2,2,1u =- ,()3,4,2v =- ,则αβ⊥C .直线l 的方向向量()1,2,1a =- ,平面α的法向量()3,6,m k =,若l α⊥,则15k =D .若()2,1,4AB =-- ,()4,2,0AC = ,()0,4,8AP =--,则点Р在平面ABC 内11.已知两圆方程为224x y +=与222(3)(4)(0)x y r r -++=>,则下列说法正确的是()A .若两圆外切,则3r =B .若两圆公共弦所在的直线方程为3420x y --=,则=5r C .若两圆的公共弦长为23,则19r =D .若两圆在交点处的切线互相垂直,则4r =12.如图所示,在86⨯的长方形区域(含边界)中有,A B 两点,对于该区域中的点P ,若其到A 的距离不超过到B 距离的一半,则称P 处于A 的控制下.例如原点O 满足11352OA OB =≤=,即有O 点处于A 的控制下.同理若对于该区域中的点P ,其到B 的距离不超过到A 距离的一半,则称P 处于B 的控制下,则下列说法正确的有()A .点()4,2处于A 的控制下B .若点P 不处于A 的控制下,则其必处于B 的控制下C .若P 处于A 的控制下,则13PA ≤D .图中所有处于A 的控制下的点构成的区域面积为85π+第Ⅱ卷(非选择题,共90分)三、填空题(本大题包括4个小题,每小题5分,共20分)13.在空间直角坐标系中,z 轴上与点()1,0,0A 和点()0,2,1B 距离相等的点的坐标为.14.点(3,2)A 关于直线40x y -+=的对称点是.15.如图,已知正方体1111ABCD A B C D -的棱长为1,E 为棱11B C 上的动点,则AE 在AC方向上的投影向量的模的取值范围为.16.已知直线:30l x y m ++=与圆C :()()222216x y -++=相交于A ,B 两点,O 为坐标原点,若,,,A B C O 四点共圆,则m 的值为.四、解答题(本题共6小题,共70分.解答题应写出文字说明、证明过程或演算步骤).17.已知曲线方程22153x y k k+=+-,k ∈R .(1)若方程表示焦点在x 轴上的椭圆,求k 的取值范围;(2)若方程表示焦距为2的椭圆,求k 的值.18.已知点A (2,3),B (4,1),△ABC 是以AB 为底边的等腰三角形,点C 在直线l :x -2y +2=0上.(1)求AB 边上的高CE 所在直线的方程;(2)求△ABC 的面积.19.如图所示的几何体为一个正四棱柱被两个平面AEH 与CFG 所截后剩余部分,且满足////EH FG BD ,22FG BD ==,2EH =.(1)当BF 多长时,AE CG ⊥,证明你的结论;(2)当BF AB =时,求平面AEH 与平面CFG 所成角的余弦值.20.最近国际局势波云诡谲,我国在某地区进行军事演练,如图,O ,A ,B 是三个军事基地,C 为一个军事要塞,在线段AB 上.已知tan 2AOB ∠=-,100km OA =,C 到OA ,OB 的距离分别为50km ,305km ,以点O 为坐标原点,直线OA 为x 轴,建立平面直角坐标系如图所示.(1)求两个军事基地AB 的长;(2)若要塞C 正北方向距离要塞100km 处有一E 处正在进行爆破试验,爆炸波生成h t 时的半径为5r at =(参数a 为大于零的常数),爆炸波开始生成时,一飞行器以3002km /h 的速度自基地A 开往基地B ,问参数a 控制在什么范围内时,爆炸波不会波及到飞行器的飞行.21.如图,三棱柱111ABC A B C -中,面ABC ⊥面111,,2AA C C AB AC AA AB AC ⊥===,160A AC ∠=.过1AA 的平面交线段11B C 于点E (不与端点重合),交线段BC 于点F .(1)求证:四边形1AA EF 为平行四边形;(2)若B 到平面1AFC 的距离为2,求直线11A C 与平面1AFC 所成角的正弦值.22.已知圆心在x 轴上的圆C 与直线:4360l x y +-=切于点36,55M ⎛⎫⎪⎝⎭.(1)求圆C 的标准方程;(2)已知()2,1N ,经过原点且斜率为正数的直线1l 与圆C 交于()11,P x y ,()22,Q x y .求22PN QN +的最大值.1.C【分析】求出c 的值,即可得出所求椭圆的焦距.【详解】在椭圆22145x y +=中,5a =,2b =,则22541c a b =-=-=,因此,椭圆22145x y +=的焦距为22c =.故选:C.2.A【分析】令0y =可得直线22x y +=在x 轴上的截距【详解】由直线22x y +=,令0y =可得1x =.所以直线22x y +=在x 轴上的截距为1.故选:A【点睛】本题考查直线在x 轴上的截距,属于基础题.3.B【分析】将圆心坐标代入直线210x y +-=的方程,可求得实数a 的值.【详解】圆()221x a y ++=的圆心坐标为(),0a -,因为直线210x y +-=是圆()221x a y ++=的一条对称轴,则直线210x y +-=经过圆心(),0a -,则210a --=,解得12a =-.故选:B.4.B【分析】判断直线在x 轴和y 轴上截距的正负,作出直线的图象可得出结论.【详解】如果0ac <,0bc >,则0ab ≠,可知:直线0ax by c ++=在x 轴上的截距为0c a ->,在y 轴上的截距为0cb-<,如下图所示:所以直线0ax by c ++=不通过第二象限.故选:B .5.B【分析】推导出123BP BC = ,利用空间向量的线性运算可得出DP 关于AB、AD 、1AA 的表达式.【详解】在平行四边形11BB C C 中,因为M 为1CC 的中点,连接1B M 、1BC 交于点P ,且11//BB CC ,所以,11112C P C M BP BB ==,则()()111222333BP BC BC BB AD AA ==+=+ ,因此,()11212333DP DA AB BP AD AB AD AA AB AD AA =++=-+++=-+.故选:B.6.D【分析】根据题意求出实数a 的取值范围,利用直线倾斜角与斜率的关系可求得直线l 倾斜角的取值范围.【详解】因为点()1,2-和3,03⎛⎫⎪ ⎪⎝⎭在直线():100l ax y a --=≠的两侧,则()3211030a a a ⎧⎛⎫+--<⎪ ⎪ ⎪⎨⎝⎭⎪≠⎩,即()()1300a a a ⎧+-<⎪⎨≠⎪⎩,解得13a -<<且0a ≠.易知,直线l 的斜率为a ,设直线l 的倾斜角为α,则[)0,πα∈.当10a -<<时,则3ππ4α<<;当03a <<时,则π03α<<.综上所述,直线l 的倾斜角的取值范围是π3π0,,π34⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭.故选:D.7.B【分析】以点A 为原点建立空间直角坐标系,可设AN x AP y AC =+ ,再求出EN,根据NE ⊥平面PAC ,可求出点N 的坐标,即可得解.【详解】如图,以点A 为原点建立空间直角坐标系,则()()()110,0,0,3,1,0,0,0,1,0,,22A C P E ⎛⎫⎪⎝⎭,()()3,1,0,0,0,1AC AP ==,由点N 在平面PAC 内,则可设()3,,AN x AC y AP x x y =+= ,所以()3,,Nx x y ,故113,,22EN x x y ⎛⎫=-- ⎪⎝⎭ ,因为NE ⊥平面PAC ,所以1302102EN AC x x EN AP y ⎧⋅=+-=⎪⎪⎨⎪⋅=-=⎪⎩,解得1812x y ⎧=⎪⎪⎨⎪=⎪⎩,所以311,,888AN ⎛⎫= ⎪ ⎪⎝⎭,又因平面PAB 与面xA z 重合,所以点N 到面PAB 的距离为18.故选:B.8.C【详解】圆C :()()2221x t y t -+-+=的圆心坐标为,2t t -(),半径为1,∴2222132410PC t t t t =++-=-+()(),∴()()2222221131249PA PB PC t t t t ==-=++--=-+,22249cos 2410AB t t APC PC t t -+∠==-+,∴2222222249248242cos 1212410241025t t t t t t cos PAB APC t t t t t t ()-+-+-+∠=∠-=⨯-==-+-+-+,∴22224cos 24925t t PA PB PA PB PAB t t t t -+⋅=⋅∠=-+⋅-+ ()222224252425t t t t t t t t -+⎡⎤=-++-+⋅⎣⎦-+()(),设224t t x -+=,则3x ≥,则()22111x x x PA PB f x x x x x ()+⋅==++⋅=++,∴()22231'01x x f x x ++=>+()恒成立,∴()f x 在[)3,+∞单调递增,∴2134min f x f ==()(),∴PA PB ⋅ 的最小值为214故选C.9.AC【分析】将1a =代入,根据方向向量定义即可判断A ,根据直线平行和垂直与斜率的关系即可判断选项B 、C ;将1l 化简得433a y x =--,结合一次函数的性质可判断D.【详解】对于A ,当1a =,直线1l :340x y ++=,斜率为13-,则其一个方向向量为()3,1-,故A 正确;对于B ,若12//l l ,当2a =时,显然不符合题意,当2a ≠时,即直线1l 的斜率为13ak =-,直线2l 的斜率为212k a -=-,则有12k k =,所以123aa -=--,解得1a =-或3a =;当1a =-时,直线1l :340x y -++=,2l :340x y --=,显然两直线重合,故B 错误;对于C ,若12l l ⊥,当2a =时,显然不符合题意;当2a ≠时可得121123a k k a -⎛⎫⋅=⋅-=- ⎪-⎝⎭,解得32a =,即C 正确;对于D ,将1l 化简得433a y x =--,可知当0x =时,直线过40,3⎛⎫- ⎪⎝⎭,即不论a 为何值时,直线1l 恒过定点40,3⎛⎫- ⎪⎝⎭,即D 错误;故选:AC 10.ABD【分析】对于A ,验证,a b r r 是否平行即可;对于B ,验证,u v 是否垂直即可;对于C ,根据线面关系得//a b ,求解k 得值即可判断;对于D ,验证是否四点共面即可.【详解】解:对于A ,因为()2,3,1a =- ,()2,3,1b =-- ,所以a b =-,又两条不重合直线1l ,2l ,所以12//l l ,故A 正确;对于B ,平面α,β的法向量分别是()2,2,1u =- ,()3,4,2v =- ,且6820u v ⋅=-+-= ,所以u v ⊥,则αβ⊥,故B 正确;对于C ,直线l 的方向向量()1,2,1a =- ,平面α的法向量()3,6,m k = ,若l α⊥,则//a b,则3k =-,故C 错误;对于D ,因为()2,1,4AB =-- ,()4,2,0AC = ,()0,4,8AP =-- ,存在实数,λμ使得AB AC AP μλ=+,则2=41=244=8λ-λ-μ--μ⎧⎪⎨⎪⎩,解得11,22λμ==,则1212AB AC AP =+ ,所以,,,A B C P 四点共面,即点Р在平面ABC 内,故D 正确.故选:ABD.11.AB【分析】根据圆与圆的位置关系对选项进行分析,从而确定正确答案.【详解】设圆224x y +=为圆1C ,圆1C 的圆心为()10,0C ,半径12r =.设圆222(3)(4)(0)x y r r -++=>为圆2C ,圆2C 的圆心为()23,4C -,半径1r r =.125C C =.A 选项,若两圆外切,则1212,52,3C C r r r r =+=+=,A 选项正确.B 选项,由()()22222434x y x y r ⎧+=⎪⎨-++=⎪⎩两式相减并化简得2293402r x y --+=,则22292,25,52r r r -=-==,此时2121123,7,37r r r r C C -=+=<<,满足两圆相交,B 选项正确.C 选项,由()()22222434x y x y r ⎧+=⎪⎨-++=⎪⎩两式相减并化简得2293402r x y --+=,()10,0C 到直线2293402r x y --+=的距离为2229229510r r d --==,所以22221232,43,1r d d d =--==,即22291,291010r r -=-=,则解得19r =或39r =,C 选项错误.D 选项,若两圆在交点处的切线互相垂直,设交点为D ,根据圆的几何性质可知12C D C D ⊥,所以2222212125421,21r C D C C r r ==-=-==,D 选项错误.故选:AB 12.ACD【分析】根据新定义,直接验证判断①,取特殊点判断②,根据定义求出点所在区域,判断③,结合图象求出面积判断④.【详解】由图可知,()()2,3,8,6A B ,设()4,2C ,则1||5||42,||||,2CA CB CA CB ==≤满足1||||2CA CB ≤,故A 正确;点不处于A 的控制下,则,1||||2PA PB >即,||2||PB PA <例如取点()15,3,||3||32|,|2,||,P PA PB PA PB ==>但是,1||||2PB PA >点不处于B 的控制下,即点P 不处于A 的控制下,也不处于B 的控制下,故B 错误;若P 处于A 的控制下,则1||||2PA PB ≤,设(),,(0806),P x y x y ≤≤≤≤,则()()()()2222123862x y x y -+-≤-+-,化简整理得,()22,220x y +-≤作出图象,如图,由图可知,当点在矩形且在圆及圆内部分满足处于的控制下,由图可知,当点处于,,O C D 时,有最大值13,故C 正确;由C 知,处于的控制下点构成的区域面积,可以看作是14圆与矩形的面积之和,如图,故面积为π1520π+42=48⨯+⨯,故D 正确.故答案为:ACD【点睛】关键点睛:本题是一道创新型试题,关键在于理解所给新定义,对于①②可以利用具体点去直接判断结论正确与否,在这一特殊化的过程中进一步理解新定义,对于③需要根据新定义求出点满足的轨迹方程(边界),需要对求平面轨迹方程的方法熟练,关键在于求出点所在区域,利用数形结合思想判断③,对于④关键在于把区域分割为四分之一圆面与矩形,其中需要割补思想的应用.13.()0,0,2【分析】设()0,0,C m ,利用空间两点间距离公式可构造方程求得m ,从而得到所求点坐标.【详解】设所求点()0,0,C m ,由AC BC =得:()2210041m m ++=++-,解得:2m =,()0,0,2C ∴.故答案为:()0,0,2.14.(2,7)-【分析】设出对称点,根据对称的性质列出方程即可求出.【详解】设点(3,2)A 关于直线40x y -+=的对称点是(,)A m n ',则有3240222113m n n m ++⎧-+=⎪⎪⎨-⎪⨯=-⎪-⎩,解得27m n =-⎧⎨=⎩,故点(3,2)A 关于直线40x y -+=的对称点是(2,7)-.故答案为:(2,7)-.15.2,22⎡⎤⎢⎥⎣⎦【分析】以点D 为原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系,设点(),1,1E a ,其中01a ≤≤,利用空间向量数量积的坐标运算可求得AE 在AC方向上的投影向量的模的取值范围.【详解】在正方体1111ABCD A B C D -中,以点D 为原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,则()1,0,0A 、()0,1,0C ,设点(),1,1E a ,其中01a ≤≤,所以,()1,1,0AC =- ,()1,1,1AE a =-,所以,AE 在AC方向上的投影向量的模为222cos ,,2222AE AC a AE AC a AE AE AC AE AE AC AC ⋅⎡⎤-⋅-⋅=⋅===∈⎢⎥⋅⎣⎦.故答案为:2,22⎡⎤⎢⎥⎣⎦.16.4【分析】设出,,,A B C O 所在圆M 的圆心以及圆方程,根据圆心M 坐标满足CO 的垂直平分线,结合直线l 为圆M 与圆C 的相交线直线,比较系数,即可求得结果.【详解】设,,,A B C O 所在圆的圆心为(),M a b ,则圆M 方程为()()2222x a y b a b -+-=+;又,C O 的中点坐标为()1,1-,1CO k =-,故CO 垂直平分线的斜率1k =,则CO 的垂直平分线所在方程为:11y x +=-,即2y x =-,故2a b =+;因为直线l 为圆M 与圆C 的相交弦,故两圆方程作差可得:()()2240a x b y -++-=,即()240bx b y ++-=,又直线l 方程为30x y m ++=,则2431b b m+==-,解得3,4b m =-=.故答案为:4.17.(1)13k -<<(2)12k =-或32k =-【分析】(1)根据椭圆方程的性质建立关于k 的不等式,解出即可;(2)根据椭圆方程的类型,分类讨论确定,a b ,根据222c a b =-求解即可.【详解】(1)若方程表示焦点在x 轴上的椭圆,则530k k +>->,解得13k -<<,即k 的取值范围为13k -<<;(2)若方程表示焦距为2的椭圆,则22c =,所以1c =当方程表示焦点在x 轴上的椭圆,则225,3a k b k =+=-,且13k -<<又()22253221c a b k k k =-=+--=+=,得12k =-;当方程表示焦点在y 轴上的椭圆,则350k k ->+>,解得51k -<<-所以223,5a k b k =-=+,又()22235221c a b k k k =-=--+=--=,得32k =-;综上,12k =-或32k =-.18.(1)10x y --=(2)2【分析】(1)由题意可知,E 为AB 的中点,(3,2)E ,利用斜率计算公式、点斜式即可得出.(2)由22010x y x y -+=⎧⎨--=⎩得(4,3)C ,利用两点之间的距离公式、三角形面积计算公式即可得出.【详解】(1)解:由题意可知,E 为AB 的中点,因为(2,3)A ,(4,1)B ,所以(3,2)E ,31124AB k -==--,所以11CE ABk k =-=,CE ∴所在直线方程为23y x -=-,即10x y --=.(2)解:由22010x y x y -+=⎧⎨--=⎩解得43x y =⎧⎨=⎩,所以(4,3)C ,所以AC 平行于x 轴,CB 平行于y 轴,即AC BC ⊥,22||||(24)(33)2AC BC ∴==-+-=,1||||22ABC S AC BC ∴== .19.(1)2BF =时,AE CG ⊥,证明见解析(2)33【分析】(1)将正四棱柱补全为ABCD KFIG -,取J 为IG 中点,连接,EJ DJ ,由平行四边形性质有//AE JD ,结合已知和△JDG ~△GCD 即证明AE CG ⊥;(2)构建空间直角坐标D xyz -,求平面AEH 与平面CFG 的法向量,应用空间向量求夹角的余弦值.【详解】(1)当2BF =时,AE CG ⊥,证明如下:将正四棱柱补全为ABCD KFIG -,则,ABCD KFIG 均为正方形,又22FG BD ==,所以底面边长为2,又2EH =且////EH FG BD ,所以,E H 分别为,KF KG 中点,取J 为IG 中点,连接,EJ DJ ,则////EJ KG AD 且EJ KG AD ==,即AEJD 为平行四边形,因为2GD BF ==,又112JG IG ==,2DC =,所以22JG GD GD DC ==,所以△JDG ~△GCD ,所以,JDG GCD DJG CGD ∠=∠∠=∠且90JDG DJG GCD CGD ∠+∠=∠+∠=︒,所以90JDG CGD ∠+∠=︒,所以JD CG ⊥,又//AE JD ,故AE CG ⊥.(2)由BF AB =可知,(1)中补全正四棱柱为正方体,构建空间直角坐标D xyz -,如下图,则(2,0,0),(2,1,2),(1,0,2),(0,2,0),(2,2,2),(0,0,2)A E H C F G ,所以(0,1,2),(1,0,2),(2,0,2),(0,2,2)AE AH CF CG ==-==-,设(,,)m x y z = 是平面AEH 的一个法向量,则2020m AE y z m AH x z ⎧⋅=+=⎪⎨⋅=-+=⎪⎩,令1z =,则(2,2,1)m =-;设(,,)n a b c = 是平面CFG 的一个法向量,则220220n CF a c n CG b c ⎧⋅=+=⎪⎨⋅=-+=⎪⎩,令1c =,则(1,1,1)n =-;所以33cos ,333m n m n m n ⋅===⨯,故所求角的余弦值为33.20.(1)2002km(2)当024*******a <<-时,爆炸波不会波及飞行器的飞行【分析】(1)利用直线与圆相切求出C 点坐标,联立直线方程求出B 点坐标,利用两点的距离公式即可求解;(2)由题意得22EF r >对303t ⎡⎤∈⎢⎥⎣⎦,恒成立,即22(30050)(300150)25t t at -+->对303t ⎡⎤∈⎢⎥⎣⎦,恒成立,然后对t进行分类讨论,利用基本不等式即可求解.【详解】(1)则由题设得:()1000A ,,直线OB 的方程为2y x =-,()0050(0)C x x >,,由02225030521x +=+,及00x >解得050x =,所以()5050C ,.所以直线AC 的方程为()100y x =--,即1000x y +-=,由21000y x x y =-⎧⎨+-=⎩,得100x =-,200y =,即()100200B -,,所以()221001002002002AB =--+=,即基地AB 的长为2002km .(2)设爆炸产生的爆炸波圆E ,由题意可得()50150E ,,生成t 小时时,飞行在线段AB 上的点F 处,则3002AF t =,203t ≤≤,所以()100300300F t t -,.爆炸波不会波及卡车的通行,即22EF r >对303t ⎡⎤∈⎢⎥⎣⎦,恒成立.所以2222(30050)(300150)25EF t t r at =-+->=,即22(30050)(300150)25t t at -+->.当0=t 时,上式恒成立,当0t ≠即203t ⎛⎤∈ ⎥⎝⎦,时,100072004800a t t <+-,因为1000100072004800272004800240054800t t t t+-≥⨯-=-,当且仅当10007200t t =,即56t =时等号成立,所以,在024*******a <<-时,r EF <恒最立,亦即爆炸波不会波及飞行的通行.答:当024*******a <<-时,爆炸波不会波及飞行器的飞行.21.(1)证明见解析;(2)24.【分析】(1)在三棱柱111ABC A B C -中,利用线面平行、面面平行的性质推理作答.(2)在平面11AA C C 内过点A 作Az AC ⊥,以点A 为原点建立空间直角坐标系,借助空间向量求解作答.【详解】(1)在三棱柱111ABC A B C -中,11//AA BB ,1BB ⊂平面11BB C C ,1AA ⊄平面11BB C C ,则1//AA 平面11BB C C ,又平面1AA EF 平面11BB C C EF =,1AA ⊂平面1AA EF ,于是得1//AA EF ,而平面//ABC 平面111A B C ,平面1AA EF 平面ABC AF =,平面1AA EF 平面1111A B C A E =,则1//A E AF ,所以四边形1AA EF 为平行四边形.(2)在平面11AA C C 内过点A 作Az AC ⊥,因平面ABC ⊥平面11AA C C ,平面ABC ⋂平面11AA C C AC =,于是得Az ⊥平面ABC ,又AB AC ⊥,以点A 为原点,建立如图所以的空间直角坐标系,因12AA AB AC ===,160A AC ∠=,则11(2,0,0),(0,2,0),(0,1,3),(0,3,3)B C A C ,1(2,0,0),(0,3,3),(2,2,0),(0,2,0)AB AC CB AC ===-=,(0,2,0)(2,2,0)(2,22,0)(01)AF AC CF AC tCB t t t t =+=+=+-=-<<,设平面1AFC 的法向量(,,)n x y z = ,则13302(22)0n AC y z n AF tx t y ⎧⋅=+=⎪⎨⋅=+-=⎪⎩,令y t =,得(1,,3)n t t t =--,点B 到平面1AFC 的距离22222||2(1)2(1)2||(1)4(1)(3)n AB t t d n t t t t t ⋅--====-+-++-,解得13t =,因此,213(,,)333n =-- ,而11(0,2,0)AC = ,设直线11A C 与平面1AFC 所成角为θ,于是得1111112222||23sin |cos ,|4||||213()()()2333n A C n A C n A C θ⋅=〈〉===-++-⨯,所以直线11A C 与平面1AFC 所成角的正弦值为24.22.(1)()2214x y ++=(2)21022+【分析】(1)根据已知条件求得圆心和半径,从而求得圆C 的标准方程.(2)设出直线1l 的方程,并与圆的方程联立,化简写出根与系数关系,求得22PN QN +的表达式,结合换元法以及基本不等式求得22PN QN +的最大值.【详解】(1)由圆心在x 轴上的圆C 与直线:4360l x y +-=切于点36,55M ⎛⎫⎪⎝⎭,设(),0C a ,直线:4360l x y +-=的斜率为43-,则6535CMk a =-,所以6451335a ⎛⎫⋅-=- ⎪⎝⎭-.所以1a =-,所以()1,0C -,22361255CM ⎛⎫=--+-= ⎪⎝ ⎝⎭⎛⎫⎪⎭,即2r =,所以圆C 的标准方程为()2214x y ++=.(2)设直线()1:0l y kx k =>,与圆联立方程组()2214y kxx y =⎧⎪⎨++=⎪⎩,可得()221230k x x ++-=,()241210k ∆=++>,由根与系数的关系得12221x x k +=-+,12231x x k =-+,()()()()22221122222121PN QN x y x y ∴=-++-+-+-()()()()222211222121x kx x kx =-+-+-+-()()()()()22212121221241214210161kk x x k x x k x x k +=++-+-+++=++,令33t k t =+>(),则3k t =-,所以()22124444161616161011013626k t k t t t t t++=+=+≤+++-+-⋅-416210222106=+=+-,当且仅当10t t=,即10=t 时取等号,此时103k =-,所以22||PN QN +的最大值为21022+.【点睛】本题的难点在于第二问,求最值.求解最值有关的题目,首先要将表达式求出,本题是结合根与系数关系求得表达式.然后根据表达式的结构来选择求最值的方法,可考虑二次函数的性质、基本不等式或函数的单调性来求解最值.。
吉林省长春市第二实验中学2024-2025学年高二上学期学科竞赛数学试题

长春二实验中学高二年级学科竞赛数学试卷考生注意:1.满分150分,考试时间120分钟.2.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.3.本卷命题范围:人教A 版选择性必修第一册第三章~第三章3.1.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.直线的倾斜角为( )A.B.C.D.2.若方程表示圆,则实数的取值范围为( )A.B.C.D.3.直线被圆所截得的弦长为( )B.C.5D.104.已知直线经过两条直线的交点,且的一个方向向量为,则直线的方程为( )A. B.C.D.5.若椭圆的两个焦点为,点在椭圆上,且,则( )A.B. C. D.6.已知点,过点的直线与线段有公共点,若点在直线上,则实数的取值范围为( )A. B. C. D.7.已知圆和两点,若圆上存在点,使得0x y +=45 45- 60 1352242x y x y m +-+=m (),5∞--()0,∞+()5,∞-+(),0∞-30x y -+=22240x y x y ++-=l 12:2,:21l x y l x y +=-=l (3,2)v =-l 2350x y +-=2310x y -+=3250x y --=2310x y +-=22:196x y C +=12,F F P C 12PF =12F PF ∠=π6π32π35π6()()2,33,2A B -、()0,2P -l AB (),3Q m l m (]15,2,4∞∞⎡⎫--⋃+⎪⎢⎣⎭15,24⎡⎤--⎢⎥⎣⎦152,4⎡⎤⎢⎥⎣⎦152,4⎡⎤-⎢⎥⎣⎦22:(6)(8)1C x y -+-=()()(),0,,00A m B m m ->C P,则的最大值为( )A.9B.10C.11D.128.若圆上恰有2个点到直线的距离为1,则实数的取值范围为( )A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知直线,下列选项正确的是( )A.过点且垂直于直线的直线方程为B.直线过定点C.当时,D.当时,10.已知椭圆的左、右两焦点分别是,其中.过左焦点的直线与椭圆交于两点.则下列说法中正确的有( )A.的周长为B.若的中点为所在直线斜率为,则C.若的最小值为,则椭圆的离心率D.若,则椭圆的离心率的取值范围是11.已知动点的轨迹方程为,其中不同时为0,则()A.该轨迹关于直线对称B.该轨迹围成的图形面积为C.若点在该轨迹上,则90APB ∠= m ()2221:(1)(2)0C x y rr ++-=>:43100l x y --=r ()3,∞+()5,∞+()3,5[]3,5()()()12:4340,:21250l x y l m x m y m m -+=+-+++=∈R ()1,2-1l 3450x y +-=2l ()3,1-1m =12l l ⊥2m =1l ∥2l ()2222:10x y C a b a b+=>>12F F 、122F F c =,A B 2ABF V 4aAB ,M AB k 22OMc k k a⋅=-AB 3c 13e =2123AF AF c ⋅= 12⎤⎥⎦E 22x y x y +=+,x y y x =π2+()00,x y 0x …D.若圆能覆盖该轨迹,则三、填空题:本题共3小题,每小题5分,共15分.12.已知圆和圆内切,则__________.13.如图,已知,从点射出的光线经直线反射后再射到直线上,最后经直线反射后又回到点,则光线所经过的路程是__________.14.在平面直角坐标系中,已知椭圆,点是椭圆内一点,,若椭圆上存在一点,使得,则的取值范围是__________;当取得最大值时,椭圆的焦距为__________.(第一空2分,第二空3分)四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程及演算步骤.15.(本小题满分13分)(1)已知点,求线段的垂直平分线的方程;(2)求经过点,且在两坐标轴上的截距相等的直线方程.16.(本小题满分15分)已知圆与圆相交于、两点.(1)求公共弦所在直线方程;(2)求过两圆交点,且过原点的圆的方程.17.(本小题满分15分)如图所示的折纸又称“工艺折纸”,是一种把纸张折成各种不同形状物品的艺术活动,在我国源远流长.某些折纸活动蕴含丰富的数学内容,例如,用圆形纸片按如下步骤折纸:步骤1:设圆心是,在圆内(除去圆心)取一点,标记为;步骤2:把纸片折叠,使圆周正好通过;步骤3:把纸片展开,于是就留下一条折痕;步骤4:不停重复步骤2和3,能得到越来越多条的折痕.()2220x y r r +=>r ()222:(3)0C x y r r -+=>22:870D x y y +-+=r =()()4,0,0,4A B ()2,0P AB OB OB P xOy ()22:144y x C m m m +=>-(2,2)A -()0,2B -P 8PA PB +=m m ()()2,1,6,3A B --AB ()3,2P 221:230C x y x +--=222:4230C x y x y +-++=A B AB A B 、O F F这些折痕围成的图形是一个椭圆.若取半径为4的圆形纸片,设定点到圆心的距离为2,按上述方法折纸,如图所示.(1)以所在的直线为轴,的中点为原点建立平面直角坐标系,求折痕围成的椭圆的标准方程;(2)求经过点,且与直线夹角为的直线交椭圆于两点,求的面积.18.(本小题满分17分)如图,已知圆和点,由圆外一点向圆引切线为切点,且有.(1)求点的轨迹方程,并说明点的轨迹是什么样的几何图形;(2)求的最小值;(3)以为圆心作圆,使它与圆有公共点,试在其中求出半径最小的圆的方程.19.(本小题满分17分)已知是椭圆的右焦点,为坐标原点,为椭圆上任意一点,的最大值为,当时,的面积为.(1)求的值;(2)为椭圆的左、右顶点,点满足,当与不重合时,射线交椭圆于点F O FO x FO M F FO π4,C D OCD V 22:4O x y +=()6,8A O P O ,PQ Q PQ PA =P P PQ P O F ()2222:10x y C a b a b+=>>O M MF 2+OM OF =MOF V 12baA B 、P 3AP PB =M ,A B MP C,直线交于点,求的最大值.N ,AM BN T ATB长春二实验中学高二年级学科竞赛数学试卷参考答案、提示及评分细则一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.题号12345678答案DCBABDCC二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.题号91011答案ADADABC1.D 根据直线方程可知其斜率为,设直线倾斜角为,则,可得.故选D.2.C 方程化为标准方程为,有.3.B 圆即,故圆心为,显然圆心在直线上,故直线被圆所截得的弦即为圆的直径,长为B.4.A 联立,解得,即直线的交点为,又直线的一个方向向量,所以直线的斜率为,故直线的方程为,即,故选A.5.B 由题意得,则,在中,由余弦定理可得,所以,故选B.6.D 如图所示,是直线与直线交点的横坐标,当与重合时,取最大值,当与重合时,取最小值,所以的取值范围是.0x y +=1k =-θtan 1θ=-135θ= 22(2)(1)5x y m -++=+5m >-22240x y x y ++-=22(1)(2)5x y ++-=()1,2-30x y -+=221x y x y +=⎧⎨-=⎩11x y =⎧⎨=⎩12:2,:21l x y l x y +=-=()1,1l ()3,2v =-l 23-l ()2113y x -=--2350x y +-=3,a c ==24PF =12F PF V 121cos 2F PF ∠==12π3F PF ∠=m l 3y =l BP m 154l AP m 2-m 152,4⎡⎤-⎢⎥⎣⎦7.C,记中点为,则,故点的轨迹是以原点为圆心,为半径的圆,又在圆上,所以两圆有交点,则,而,得.8.C 如图所示.设与直线平行且与直线之间的距离为1的直线方程为,,解得或,圆心到直线的距离为,圆到直线的距离为,由图可知,圆与直线相交,与直线相离,所以,即.9.AD 对于A ,垂直于直线的直线方程为,将点代入得,故所求直线方程为,A 正确;对于B ,直线化为:,由,求得直线过定点,故B 错误;90APB ∠= AB O OP m =P m P C 11m OC m -+……10OC==911m ……l l 430x y c -+=1=5c =-15c =-()11,2C -4350x y --=13d ()11,2C -43150x y --=25d 1C 4350x y --=43150x y --=12d r d <<35r <<4340x y -+=340x y m ++=()1,2-5m =-3450x y +-=2l ()()2250m x y x y -++-+=20250x y x y -+=⎧⎨-+=⎩2l ()3,1--对于C ,时有:,解得,故C 错误;对于D ,当时,,解得,故D 正确.故选AD.10.AD直线过左焦点的周长为,A 正确;设,则,点.由①-②得,故B 错误;当轴时,最小,令,解得,,整理得,即,解得或(舍去),故C 错误;,,,即,即,可得,则椭圆的离心率的取值范围是,D 正确.故选AD.11.ABC 对于A ,轨迹上任意一点满足,该点关于直线的对称点也满足,即轨迹上任意一点关于直线的对称点仍在该轨迹上,A 正确;12l l ⊥()()42310m m +++=117m =-1l ∥2l ()1225434m m m -+++=≠-2m = AB 12,F ABF ∴V 12124AF AF BF BF a +++=()()1122,,,A x y B x y 1212y y k x x -=-12121212,,22OM x x y y y y M k x x +++⎛⎫∴= ⎪+⎝⎭2211222222221,1,x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩①②()()()()()()2221212121212122222212121,,QM QMx x x x y y y y x x b y y b b k k abx x y y a k a a+-+-+-=-∴=-=-⋅∴⋅=--+AB x ⊥AB 2222,1c y x c a b =-+=2by a=±223b c a∴=222320c ac a +-=22320e e +-=12e =2-()111,AF c x y =--- ()211,,AF x y =--()()22222222212*********c AF AF c x c x y x y c x a c c a ∴⋅=---+=+-=+-= 22222222221120,,22c x a a c x a c a c a⎡⎤∈∴-+--⎣⎦ (2)222223a c c a c -- (2211)54c a ……12c e a ⎤=∈⎥⎦12⎤⎥⎦(),x y 22x y x y +=+y x =(),y x 22y x y x +=+(),x y y x =对于B ,点在该轨迹上,点也都在该轨迹上,则该轨迹关于轴,轴对称,当不同时为0时,该轨迹的方程为,表示以点为圆为半径的圆在直线上方的半圆(含端点),因此,该轨迹是四个顶点为,的正方形各边为直径向正方形外所作半圆围成,如图,所以该轨迹围成的图形面积是,B 正确;对于C ,点在该轨迹上,则,则有,即,解得,C 正确;对于D ,该轨迹上的点到原点距离最大值为,圆能覆盖该轨迹,则不正确.故选ABC.三、填空题:本题共3小题,每小题5分,共15分.12.8圆,圆心,半径为,圆,圆心,半径,因为两圆内切,所以,解得.易得所在直线方程为,由于点关于直线的对称点坐标为,点关于轴的对称点坐标为,则光线所经过的路程即为与两点间的距离,于是14.; 因为点是椭圆内一点,所以,由,可得(),x y ()()(),,,,,x y x y x y ----x y 0,0,,x y x y (22)111222x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭11,22⎛⎫ ⎪⎝⎭1x y +=()()1,0,0,1--()()1,0,0,1211224ππ222⨯⨯+⨯⨯=+()00,x y 2222000000111222x y x y x y ⎛⎫⎛⎫+=+⇔-+-= ⎪ ⎪⎝⎭⎝⎭201122x ⎛⎫- ⎪⎝⎭…0x …0x …=()2220x y r r +=>min D r =()222:(3)0C x y r r -+=>()3,0C r 22:870D x y y +-+=()0,4D 3R =3CD r ==-8r =AB 4x y +=P AB ()14,2P P y ()22,0P -()14,2P ()22,0P -12PP ==(625⎤+⎦4()2,2A -4414m m +<-44144m m m ⎧+<⎪-⎨⎪>⎩.易知为椭圆的下焦点,设椭圆的上焦点为,则.又,当且仅当三点共线时等号成立,所以,所以,所以,故.当取得最大值25时,椭圆的方程为,故其焦距为4.四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程及演算步骤.15.解:(1)线段的中点为,故线段的垂直平分线的方程为,即.(2)①当直线过原点时,所求直线方程为,②当直线不过原点时,斜率为,所求直线方程为:,即,由①②知所求直线方程为或.16.解:(1)①,②①-②得即公共弦所在直线方程为.(2)设圆的方程为,即.因为圆过原点,所以,所以所求圆的方程为17.解:(1)如图,设为椭圆上一点,由题意可知且,所以分别为椭圆的左、右焦点,长轴长,所以,所以椭圆的标准方程为.6m >+()0,2B -F PA PB PA PF +=+-||||||||2PA PF AF -=…,,P A F 22PA PB -++……282-……925m ……625m +<…m 2212521y x +=AB ()1312,1,262AB C k --==--AB ()122y x -=--250x y +-=23y x =1-()23y x -=--5y x =-+23y x =5y x =-+22230x y x +--=224230x y x y +-++=2260x y --=AB 30x y --=()2222234230x y x x y x y λ+--++-++=()()()2211242330x y x y λλλλλ+++-++-+=330,1λλ-+==2230x y x y +-+=P 4PF PO AO +==24FO =<,F O 24,22a c ==2222,1,3a c b a c ===-=22143x y +=(2)经过且与直线夹角为的直线的倾斜角为或,由对称性,不妨取倾斜角为,即,显然,直线.设,联立,消去得.解法1:解得上述值的互换不影响结果,不妨取,将的值分别代入,得,所以,所以.点到直线即的距离,故的面积.(也可以按此解法算得的坐标后,得,F FOπ4π43π4π41k =()1,0F -:1CD y x =+()()1122,,,C x y D x y 221143y x x y =+⎧⎪⎨+=⎪⎩y 27880x x +-=124477x x =-=-124477x x =-=-12,x x 124477x x =-=--12,x x 1y x =+123377y y =+=-4343,7777C D ⎛⎛-+- ⎝⎝247CD ==()1,0O :1CD y x =+10x y -+=d OCD V 12427OCD S =⨯=V 12y y 、12y y -=故.解法2:,且,所以.点到直线即的距离,故的面积.(也可以按此解法算得后,得,,故.18.解:(1)设点的坐标为,,由题意有,整理为:,故点的轨迹方程为,点的轨迹是斜率为,在轴上的截距为的直线.(2)由和(1),的最小值为点到直线的距离,最小值为.(3)由圆的性质可知,当直线与直线垂直时,以此时的点为圆心,且与圆相外切的圆为所求,此时的方程为,1211222OCD S FO y y =-=⨯=V 2Δ84782880=+⨯⨯=>121288,77x x x x +=-=-2247CD x =-===()1,0O :1CD y x =+10x y -+=d OCD V 12427OCD S =⨯=V 121288,77x x x x +=-=-12x x -===()()12121211y y x x x x -=+-+=-=1211222OCD S FO y y =-=⨯=V P (),x y 2222||44PA OP x y ==-=+-2222(6)(8)4x y x y -+-=+-34260x y +-=P 34260x y +-=P 34-y 132PQ PA =PQ A 34260x y +-=245=OP 34260x y +-=P O OP 43y x =联立方程解得点到直线的距离为,可得所求圆的半径为,故所求圆的标准方程为.19.解:(1)因为设椭圆的左焦点为,因为,所以.即,又,所以,所以,所以,所以,因为,所以,所以②,又③,由①②③,解得,所以.(2)由(1)可知椭圆的方程为,因为点满足,所以,设直线的方程为,联立,得,设,易得,则,直线的方程为,直线的方程为,4,334260,y x x y ⎧=⎪⎨⎪+-=⎩78,25104,25x x ⎧=⎪⎪⎨⎪=⎪⎩O 34260x y +-=2652616255-=2278104256252525x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭max ||2MF a c =+=+E 12OM OF EF ==90EMF ∠= 2222||||4ME MF EF c +==2ME MF a +=222||24ME MF ME MF a ++=2222444ME MF a c b =-=22ME MF b =212MEF S ME MF b ==V 12MOF S =V 1MEF S =V 21b =222a b c =+224,3a c ==12b a =C 2214x y +=P 3AP PB = ()1,0P MN 1x my =+22114x my x y =+⎧⎪⎨+=⎪⎩()224230m y my ++-=()()1122,,,M x y N x y Δ0>12122223,44m y y y y m m +=-=-++AM ()1122y y x x =++BN ()2222y y x x =--联立得,因为,所以,解得所以动点的轨迹方程为.由椭圆的对称性不妨设,直线的倾斜角分别为,因为,所以,因为,所以,当且仅当时,等号成立,此时,所以的最大值为.()()()()12121212121122212222123y x y my my y y x x y x y my my y y -+---===+++++()121232my y y y =+()()121121221231321222339233222y y y y y x x y y y y y +-+-===++++4,x =T ()40x y =≠()4,,0T t t >,TA TB ,αβATB ∠βα=-()tan tan tan tan 1tan tan ATB βα∠βαβα-=-=+tan ,tan 62TA TB t t k k αβ====24426tan 1212126t t t ATB t t t t t∠-====++⋅+…t =(π4,,6T ATB ∠=ATB ∠π6。
吉林大学作业及答案-高数A2作业答案

高等数学作业AⅡ答案吉林大学公共数学教学与研究中心2018年3月第一次作业学院 班级 姓名 学号一、单项选择题1.下列反常积分收敛的是( C ). (A )⎰∞+2d ln x xx; (B )⎰∞+2d ln 1x xx ; (C )⎰∞+22d )(ln 1x x x ;(D )⎰∞+2d ln 1x xx .2.下列反常积分收敛的是( D ) A .0cos d x x +∞⎰B .221d (1)x x -⎰C .01d 1x x +∞+⎰D .321d (21)x x +∞-∞+⎰3.设)(x f 、()g x 在],[b a 上连续,则由曲线)(x f y =,()y g x =,直线b x a x ==,所围成平面图形的面积为( C ).(A )[()()]d ba f x g x x -⎰;(B )[|()||()|]d baf xg x x -⎰;(C )|()()|d b af xg x x -⎰; (D )[()()]d b af xg x x -⎰.4.设曲线2y x =与直线4y =所围图形面积为S ,则下列各式中,错误的是 ( C ).(A )2202(4)d S x x =-⎰;(B )402d S y y =⎰; (C )2202(4)d S x y =-⎰;(D )402d S x x =⎰.5.设点(,sin )A x x 是曲线sin (0)y x x π=≤≤上一点,记()S x 是直线OA (O 为原点)与曲线sin y x =所围成图形的面积,则当0x +→时,()S x 与( D ).(A )x 为同阶无穷小; (B )2x 为同阶无穷小; (C )3x 为同阶无穷小; (D )4x 为同阶无穷小.6.设0()()g x f x m <<<(常数),则由(),(),,y f x y g x x a x b ====所围图形绕直线y m =旋转所形成的立体的体积等于( B ).(A )π(2()())(()())d ba m f x g x f x g x x -+-⎰;(B )π(2()())(()())d bam f x g x f x g x x ---⎰;(C )π(()())(()())d bam f x g x f x g x x -+-⎰;(D )π(()())(()())d bam f x g x f x g x x ---⎰.二、填空题 1.已知反常积分⎰∞+0d e 2x x ax 收敛,且值为1,则=a 12-.2.摆线1cos sin x ty t t =-⎧⎨=-⎩一拱(02π)t ≤≤的弧长 8 .3.2d 25x x +∞-∞=+⎰π5. 4.反常积分0d (0,0)1mnx x m n x+∞>>+⎰,当,m n 满足条件1n m ->时收敛. 5.由曲线22,y x x y ==围成图形绕x 轴旋转一周所形成的旋转体体积为 3π10. 三、计算题1.用定义判断无穷积分0e d 1e xxx -∞+⎰的收敛性,如果收敛则计算积分值.解: 000e d(1e )d 1e 1e [ln(1e )]ln 2xxx x x x -∞-∞-∞+=++=+=⎰⎰ 则该无穷积分收敛. 2.判断反常积分的收敛性:13sin d x x x+∞⎰解:33sin 1x xx≤Q而131x +∞⎰收敛. 13sin d xx x+∞∴⎰收敛.3.已知22lim 4e d xx a x x a x x x a +∞-→∞-⎛⎫= ⎪+⎝⎭⎰,求a 的值. 解:()21e lim lim e e1xa ax a a x a x x a a a x a x x a a x ----→∞→∞⋅⎛⎫- ⎪-⎛⎫⎝⎭=== ⎪+⎝⎭⎛⎫+ ⎪⎝⎭. 222222222222222222224e d 2de 2e 4e d 2e 2de 2e 2e 2e d 2e 2e e (221)e .x xaaxx aaa xaa xx aaa a x aa x x x x x xa x a x xa a a a +∞+∞--+∞+∞--+∞--+∞+∞---+∞----=-=-+=-=-+=+-=++⎰⎰⎰⎰⎰由已知222e (221)e a a a a --=++,即(1)0a a +=.所以0a =或1a =-.4.求连续曲线π2cos d x y t t -=⎰的弧长.解:由cos 0x ≥可知ππ22x -≤≤. 因此所求弧长为 π22π21d s y x -'=+⎰()π22021cos d x x =+⎰π2022cos d 42xx ==⎰.5.计算由x 轴,曲线1-=x y 及其经过原点的切线围成的平面图形绕x 轴旋转所生成立体体积.解:设切点为00(,)x y ,则过切点的切线方程为0001()21Y y X x x -=--令0,0X Y ==,得002,1x y ==.2212211π12π(1)d 32πππ.362x V x xx x =⨯⨯--⎛⎫=-=- ⎪⎝⎭⎰6.在第一象限内求曲线21y x =-+上的一点,使该点处的切线与所给曲线及两坐标轴所围成的图形面积为最小,并求此最小面积.解:设所求点为(,)x y ,则过此点的切线方程为2()Y y x X x -=-.由此得切线的x 轴截距为212x a x+=,y 轴截距为21b x =+.于是,所求面积为12031()(1)d 21112.4243S x ab x xx x x =--+=++-⎰令2211()32411130,4S x x x x x x x ⎛⎫'=+- ⎪⎝⎭⎛⎫⎛⎫=-+= ⎪⎪⎝⎭⎝⎭解得驻点13x =.又因为3131126043x S x x =⎛⎫⎛⎫''=+> ⎪ ⎪⎝⎭⎝⎭,所以13x =为极小值点,也是最小值点.故所求点为12,33⎛⎫ ⎪⎝⎭,而所求面积为12(233)93S ⎛⎫=- ⎪⎝⎭.7.在曲线2(0)y x x =≥上某点A 处作一切线,使之与曲线以x 轴所围图形的面积为112,试求: (1)切点A 的坐标;(2)过切点A 的切线方程;(3)由上述所围平面图形绕x 轴旋转一周所围成旋转体体积. 解:设切点00(,)A x y ,则切线方程为:20002()y x x x x -=-,得切线与x 轴交点为0,02x ⎛⎫⎪⎝⎭.由02200011d 2212x x x x x -⋅⋅=⎰,得01x =.∴切点为(1,1)A ,切线方程:21y x =-1222011()d 13230V x x πππ=⋅-⋅⋅⋅=⎰.8.半径为r 的球沉入水中,球的顶部与水面相切,球的密度与水相同,现将球从水中提出,问需作多少功?解:取球浮出水面后球心为原点建立坐标系,则22d ()d ()r y y g r y ωπρ=-⋅⋅+224()()d 43rr g r y r y ygr ωπρπρ-=⋅-+=⎰第二次作业学院 班级 姓名 学号一、单项选择题1. 平面10x y z +--=与22230x y z +-+=的关系( A ). (A )平行,但不重合; (B )重合;(C )垂直;(D )斜交.2.平面1=z 与曲面14222=++z y x ( B ). (A )不相交;(B )交于一点; (C )交线为一个椭圆;(D )交线为一个圆.3.方程z y x =-4222所表示的曲面为( C ). (A )椭球面; (B )柱面; (C )双曲抛物面; (D )旋转抛物面.4.曲面2222x y z a ++=与22(0)x y zax a +=>的交线在xoy 平面上的投影曲线是( D ).(A )抛物线;(B )双曲线;(C )椭圆;(D )圆.5.设有直线182511:1+=--=-z y x L 与⎩⎨⎧=+=-326:2z y y x L ,则L 1与L 2的夹角为( C ).(A )π6; (B )π4; (C )π3; (D )π2. 6.设有直线⎩⎨⎧=+--=+++031020123:z y x z y x L 及平面0224:=-+-z y x π,则直线L ( C ).(A )平行于π; (B )在π上; (C )垂直于π; (D )与π斜交.二、填空题1.设,a b 均为非零向量,且||||+=-a b a b ,则a 与b 的夹角为π2. 2.设向量x 与向量2=-+a i j k 共线,且满足18⋅=-a x ,则=x (6,3,3)-- .3.过点(1,2,1)M -且与直线2,34,1x t y t z t =-+⎧⎪=-⎨⎪=-⎩垂直的平面是 340x y z --+= .4.若||3=a ,||2=b ,且a ,b 间夹角为34θπ=,则||+=a b 5,||⨯=a b 3 .5.xoz 平面上的曲线1x =绕z 轴旋转一周所形成的旋转曲面方程为221x y +=. 6.曲线⎩⎨⎧=-+--=032622z y y x z 在xoy 面上的投影曲线方程为222300x y y z ⎧+--=⎨=⎩.7.若直线L 平行于平面π:3260x y z +-+=,且与已知直线132:241x y zL -+==垂直,则L 的方向余弦(cos ,cos ,cos )αβγ为 65585,,25525⎛⎫- ⎪⎝⎭ .三、计算题 1.求过直线1212:102x y z L --+==-,且平行于直线221:212x y zL +-==--的平面π的方程.解:过L 的平面束为:22(1)0x z y λ+-+-=即(2,,1)λ=n ,由n 与(2,1,2)=--S 垂直,有420,2λλ--== ∴ 所求平面为2240x y z ++-=.2.求点(2,1,3)到直线11321x y z+-==-的距离. 解:(3,2,1)=-s 设0(2,1,3),(1,1,0)M M - 则00(3,0,3)6126i =⨯=--MM S MM j k ∴ 0||621||7d ⨯==S MM S3.求曲面220x y z +-=与平面10x z -+=的交线在Oxy 平面上的投影曲线. 解:因为曲线220,10x y z x z ⎧+-=⎨-+=⎩ 在Oxy 平面上投影就是通过曲线且垂直于Oxy 平面的柱面与Oxy 平面的交线,所以,只要从曲线的两个曲面方程中消去含有z 的项,则可得到垂直于Oxy 平面的柱面方程.由220,10x y z x z ⎧+-=⎨-+=⎩消去z ,得到关于Oxy 平面的投影柱面2210x y x +--=,于是得到在Oxy 平面上的投影曲线为2210,0.x y x z ⎧+--=⎨=⎩4.求过平面02=+y x 和平面6324=++z y x 的交线,并切于球面4222=++z y x 的平面方程.解:过L 平面束为4236(2)0x y z x y λ++-++=. 即(42)(2)360x y z λλ++++-=. 由222|6|2(42)(2)3λλ-=++++得2λ=-则所求平面为2z =.5.设有直线210:210x y z L x y z ++-=⎧⎨-++=⎩,平面π:0x y +=,求直线L 与平面π的夹角;如果L 与π相交,求交点.解:L 的方向向量(1,2,1)(1,2,1)(4,0,4)=⨯-=-S而(1,1,0)=n ∴ ||41sin ||||2422θ⋅===⋅S n S n ,∴ 6πθ=将y x =-代入L 方程.解得111,,222x y z =-==∴ 交点111,,222⎛⎫- ⎪⎝⎭.6.向量a 与x 轴的负向及y 轴、z 轴的正向构成相等的锐角,求向量a 的方向余弦. 解:依题意知ππ,,02αθβθγθθ⎛⎫=-==<< ⎪⎝⎭, 因为222cos cos cos 1αβγ++=,即222cos ()cos cos 1πθθθ-++=, 所以23cos 1θ= 或 3cos 3θ=. 故333cos ,cos ,cos 333αβγ=-==.第三次作业学院 班级 姓名 学号一、单项选择题1.()220lim ln x y xy x y →→+=( B ).(A )1; (B )0; (C )12; (D )不存在.2.二元函数()()()()()22,,0,0,,0,,0,0xyx y x y f x y x y ⎧≠⎪+=⎨⎪=⎩在点)0,0(处( D ).(A )不连续,偏导数不存在; (B )连续,偏导数不存在; (C )不连续,偏导数存在;(D )连续,偏导数存在.3.设22(,)(1)(2)f x y y x x y =-+-,在下列求(1,2)x f 的方法中,不正确的一种是( B ).(A )因2(,2)2(1),(,2)4(1)x f x x f x x =-=-,故1(1,2)4(1)|0x x f x ==-=; (B )因(1,2)0f =,故(1,2)00x f '==;(C )因2(,)2(1)(2)x f x y y x y =-+-,故12(1,2)(,)0x x x y f f x y ====;(D )211(,2)(1,2)2(1)0(1,2)lim lim 011x x x f x f x f x x →→---===--.4.设函数(,)f x y 在点00(,)P x y 的两个偏导数x f '和y f '都存在,则( B ). (A)00(,)(,)lim(,)x y x y f x y →存在; (B) 00lim (,)x x f x y →和00lim (,)y y f x y →都存在;(C) (,)f x y 在P 点必连续; (D) (,)f x y 在P 点必可微.5.设22(,),2zz f x y y∂==∂,且(,0)1,(,0)y f x f x x ==,则(,)f x y 为( B ).(A )21xy x -+; (B )21xy y ++; (C )221x y y -+; (D )221x y y ++. 二、填空题1.0011limx y xyxy →→--= 1/2 .2. 设函数44z x y =+,则(0,0)x z '= 0 .3.设22),(y x y x y x f +-+=,则=')4,3(x f 2/5,=')4,3(y f 1/5 . 4.设xz xy y=+,则d z = 21d d x y x x y y y ⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭. 5.设函数(,)()()()d x yx y u x y f x y f x y g t t +-=++-+⎰,其中f 具有二阶导数,g 具有一阶导数,则2222u ux y∂∂-=∂∂ 0 .三、计算题1.设()0,1y z x x x =>≠,证明12ln x z zz y x x y∂∂+=∂∂. 证明:因为1,ln y y z zyx x x x y-∂∂==∂∂,所以 12ln y y x z zx x z y x x y∂∂+=+=∂∂. 2.讨论函数2222222,0,(,)0,0x xyx y f x y x y x y ⎧++≠⎪=+⎨⎪+=⎩的连续性..解一:当(),p x y 沿y 轴(x=0)趋于0(0,0)时, 2222limlim0x y y x xyx y y →→→+==+ 当(),p x y 沿y x =,趋于0(0,0)时,222220002lim lim 12x x y x x xy x x y x→→=→+==+∴()00lim,x y f x y →→不存在 ∴不连续解二:当(),p x y 沿y kx =趋于0(0,0)时,()()222222200011lim lim11x x y kx k x x xyk x y k k x →→=→+++==+++ 与k 有关,∴不连续 3.设(1)y z xy =+,求d z .()()11211y y z y xy y y xy x--∂=⋅+⋅=+∂ 解一:取对数()ln ln 1z y xy =+()1ln 11z x xy y z y xy ∂⋅=++⋅∂+,∴()()1ln 11y z xy xy xy y xy ⎡⎤∂=+++⎢⎥∂+⎣⎦ 解二:()()()()ln 1ln 1e,e ln 111yy xy y xy z x xy y xy y xy ++⎡⎤∂∂==⋅++⋅=+⎢⎥∂+⎣⎦ ∴()()()12d 1d 1ln 1+xy d 1y y x z y xy x xy y xy -⎡⎤=++++⎢⎥+⎣⎦ 4.求2e d yzt xz u t =⎰的偏导数.t220e d e d xz yzt u t t =-+⎰⎰22x z e uz x∂=-⋅∂ 22y e z uz y∂=⋅∂ 2222x y e e z z ux y z∂=-⋅+⋅∂ 5.设222r x y z =++,验证:当0r ≠时,有2222222r r r x y z r∂∂∂++=∂∂∂.证明:22222r x xx rx y z ∂==∂++ 222223xr x rr x r x r r -⋅∂-==∂,同理:2222222323,r r y r r z y r z r ∂-∂-==∂∂∴()2222222222233322r x y x r r r r x y z r r r-++∂∂∂++===∂∂∂ 6.设222222221()sin ,0(,)0,0x y x y x y f x y x y ⎧++≠⎪+=⎨⎪+=⎩,问在点(0,0)处,(1)偏导数是否存在? (2)偏导数是否连续? (3)是否可微?解:(1)2201()sin(0,0)(0,0)()(0,0)limlim 0x x x x f x f x f xx∆→∆→∆+∆-∆'===∆∆,2201()sin(0,0)(0,0)()(0,0)limlim 0y y y y f y f y f yy∆→∆→∆+∆-∆'===∆∆,故函数在点(0,0)处偏导数存在. (2)当 (,)(0,0)x y ≠时, 222222222112(,)2sin()cos ()x x f x y x x y x y x y x y -'=++⋅+++2222221212sincos x x x y x y x y=-+++, 又 22222200121lim (,)lim(2sincos )x x x y y x f x y x x y x y x y→→→→'=-+++, 当(,)x y 沿x 轴趋于(0,0)时,上式222121lim(2sincos )x y x x x x y →==-+ 不存在, 故偏导数(,)x f x y '在点(0,0)不连续.由函数关于变量,x y 的对称性可知,(,)y f x y '在点(0,0)不连续。
