大学物理(l-1)2-7 力矩转动定律转动惯量共37页

一,刚体的定轴转动(运动)二,力矩,刚体定轴转动的转动定律,转动惯量

二、刚体定轴转动的转动定律
～利用力矩定义＋牛顿第二定律，研究刚体作定轴转动的动力学规律。设：oz为定轴，为 P 刚体中任一质点 i ，其质量为 ∆ m i。质点 iv ur 受外力 F i ，内力 F i ′ 的作用，均在与 O z 轴相垂直的同一平面内。 ①牛顿第二定律： ur r v F i + Fi ′ = ∆ m i a i 建立自然坐标：切向、法向；
三、转动惯量 J 1.转动惯量的物理意义：当以相同的力矩分别作用于两个绕定轴转动的不同刚体时，它们所获得的角加速度一般是不一样的，转动惯量大的刚体所获得的角加速度小，即角速度改变得慢，也就是保持原有转动状态的惯性大；反之，转动惯量小的刚体所获得的角加速度大，即角速度改变得快，也就是保持原有转动状态的惯性小。因此，转动惯量是描述刚体在转动中的惯性大小的物理量。 2.与转动惯量有关的因素：①刚体的质量；②转轴的位置；③刚体的形状。实质与转动惯量有关的只有前两个因素。形状即质量分布，与转轴的位置结合决定转轴到每个质元的矢径。
R 3
例3、求长为L、质量为m的均匀细棒对图中不同轴的转动惯量。 B 解：取如图坐标，dm=λdx A
J
A
=
∫
∫
L
0
x 2 λ dx = mL 2 / 3
A
x λ dx = mL
2 2
JC =
L 2 L − 2
L C L/2 L/2
X B X
/ 12
例4. 求质量 m ,半径 R 的球壳对直径的转动惯量解：取离轴线距离相等的点的集合为积分元
F i t ri + F i t′ ri = ∆ m i ri 2 α
外力矩内力矩
③对所有质元的同样的式子求和：

大学物理学-力矩转动定律转动惯量共28页

6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂，怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
1、不要轻言放弃，否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人，常是愿意去做，并愿意去冒险的人。“稳妥”之船，从未能从岸边走远。-戴尔．卡耐基。
梦境
3、人生就像一杯没有加糖的咖啡，喝起来是苦涩的，回味起来却有久久不会退去的余香。
大学物理学-力矩转动定律转动惯量 4、守业的最好办法就是不断的发展。 5、当爱不能完美，我宁愿选择无悔，不管来生多么美丽，我不愿失去今生对你的记忆，我不求天长地久的美景，我只要生生世世的轮回里有你。
Than

转动惯量和力矩的公式及单位

转动惯量和力矩的公式及单位好嘞，以下是为您生成的文章：咱先来说说转动惯量和力矩这俩概念，这在物理学里可重要啦！转动惯量，简单说就是衡量一个物体转动时惯性大小的量。

就好比一个胖小孩和一个瘦小孩，胖小孩跑起来要更费劲，转动惯量就类似于这个“胖瘦”程度。

它的公式是I = Σ mr² ，这里的 m 是质量，r 是到转轴的距离。

力矩呢，就像是转动的“推动力”。

想象一下你开门，手离门轴越远，就越容易推开，这就是力矩在起作用。

力矩的公式是 M = F × L ，F 是力，L 是力臂。

那这俩家伙的单位又是啥呢？转动惯量的单位是千克·平方米（kg·m²），而力矩的单位是牛顿·米（N·m）。

给您讲个我上学时候的事儿。

有一次物理实验课，老师让我们测一个圆盘的转动惯量。

那圆盘看着普普通通，可真要测准它的转动惯量可不容易。

我们小组几个人，又是测量质量，又是测量距离，忙得晕头转向。

我负责记录数据，结果一不小心记错了一个数，导致整个实验结果都偏差了。

当时那叫一个懊恼啊，小伙伴们也都埋怨我。

后来我们重新做了一遍，这次特别小心，终于得到了准确的数据。

通过那次经历，我深深体会到了物理实验的严谨性，哪怕一个小小的数据错误，都可能让结果相差十万八千里。

在实际生活中，转动惯量和力矩的应用那可多了去了。

比如汽车的发动机，里面的曲轴转动就涉及到转动惯量和力矩。

还有游乐园里的摩天轮，要让它平稳转动，也得考虑这两个因素。

再比如说，家里的电风扇，扇叶转动起来，就有转动惯量。

而电机提供的力产生的力矩让扇叶能持续转动。

要是电机出了问题，力矩变小了，扇叶转得就没劲儿啦。

还有自行车的轮子，轮子的转动惯量决定了它转动起来的稳定性。

力矩呢，就像是我们脚蹬踏板施加的力产生的效果，让轮子能不停地转。

总之，转动惯量和力矩虽然听起来有点复杂，但只要咱们多观察生活中的现象，多做实验，就能更好地理解它们。

大学物理-力矩、转动定律、转动惯量

gh
yLdy
1 2
p0 Lh 2
1 6
gLh2
h
y
o
L
dA
x
dy
y
Q
dy
x
二、转动定律
质点的动力学问题刚体的动力学问题
F ma
M
设刚体有n个质点组成，
先取任一质点i来研究
mi ri
外力：Fi 内力：Fi
由牛顿第二定律得： Fi Fi miai
切线方向：Fit Fit miait
X
dV r2dZ (R2 Z 2 )dZ
其质量：dm dV (R2 Z 2 )dZ
其转动惯量：dJ 1 r 2dm 1 (R2 Z 2 )2 dZ
2
2
dJ 1 r 2dm 2
1 (R2 Z 2 )2 dZ
2
Z r dZ
O
R
Y
J dJ
X
R 1 (R2 Z 2 )2 dZ
比较
牛顿第二定律 F m a
转动定律
M J
三、转动惯量 J miri2 (4 9)
对质量连续分布的刚体 J r 2dm (4 11)
转动惯量的单位：kg m2
影响转动惯量得因素
注意：
（1）、刚体的质量（材料）（2）、刚体质量的分布
质点也有转动惯量
J mr2
（3）、转轴的位置
对质量不连续分布的刚体 J m 2
R 2
8 R5 2 mR2
m 4 R3
3
15
5
例3）求一质量为m的均匀实心球对其一条直径
为轴的转动惯量。
Z x
解：方法二在球上取一体积元
dV
dV dxdydz

大学物理力矩转动定律转动惯量教材

dz
3
r
z
oR
J z2dm R z2 m (R2 z2 )dz
R 4 R3
3

3m 4
R z2 (
R R

z4 R3 )dz

1 mR2 5
4 – 2 力矩转动定律转动惯量
第四章刚体的转动
证明：将均质球体分割成一
z
系列彼此平行且都与对称轴
垂直得圆盘，则有
r
解设圆盘面密度为，
r 在盘上取半径为，宽为 dr
的圆环
圆环质量 dm 2π rdr
O
RR
r
dr
圆环对轴的转动惯量
dJ r2dm 2π r3dr
J R 2π r3dr π R4
0
2
而 m (π R2 )
所以 J 1 mR2 2
4 – 2 力矩转动定律转动惯量
j
j
Mij M ji Mij 0
j
Mej ( mjrj2 )α
j
定义转动惯量 J mjrj2
(Moment of Inertia) j
z
O rj
Fej
m j
Fij
2
J r dm
转动定律
M J
刚体定轴转动的角加速度与它所受的合外力矩成正比，与刚体的转动惯量成反比 .
d 3g sind
2l
代入初始条件积分得
3g (1 cos )
l
4 – 2 力矩转动定律转动惯量
第四章刚体的转动
补充：证明球体对任意直径的转动惯量为：I

2 5

§4.2 刚体的转动惯量

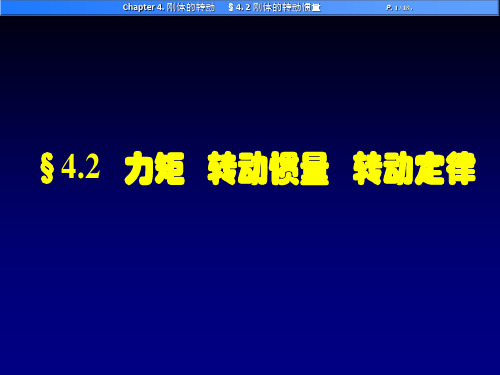
轴转动，求转动惯量 J。
解：质量线密度： m ，建立坐标系(原点在质心上)。
l
取质元：dm dx
l/2
l/2
JC x2dm x2dx
ml
dm
x
l / 2
l / 2
l 2
o x dx
l 2
3
x3
l/2 l / 2
1 12
l3
代入 m l 得：
JC
1 12
ml 2
转轴在何处？ (解毕)
解：质量线密度： m ，建立坐标系如图所示。
l
取质元：dm dx
l
l
J x2dm x2dx
0
0
3
x3
l 0
1 l 3
3
ml
o
x
dm
x
l
dx
代入 m l 得： J 1 ml 2
3
转轴在何处？ (解毕)
Chapte作r 4者. 刚：体杨的茂转田作动者：§杨4.茂2 田刚体的转动惯量
Chapte作r 4者. 刚：体杨的茂转田作动者：§杨4.茂2 田刚体的转动惯量
P. 15 / 18 .
例长为 l、质量为 m 的匀质细杆，绕与杆一端垂直的
轴转动，求转动惯量 J。
解：质量线密度： m ，建立坐标系如图所示。
l
取质元：dm dx
l
l
J x2dm x2dx
0
0
3
l
2
J miri2 i 1
ml
dm
x
m1r12 m2r22
l 2
o x dx
l 2
2mb 2 m( 3b )2
11mb 2 (解毕)

大学物理-第三章刚体力学

向力的作用点P的矢量。 M rF
大小：M rF sin Fd
M

O
z
M
r
d
P*
F
方向：右手螺旋，图中向上
0 , M o，沿转轴向上，使刚体绕转轴逆时针转
2 , M o，沿转轴向下，使刚体绕转轴顺时针转
上一页下一页

2.外力F不在转动平面内 MFOFr FFz r F r Fz
T
N2

mg T2 T2 2m
2mg
解：设整体顺时针运动，即两滑轮转轴正向向内。
右质点2m正向向下，左质点m正向向上，
受力分析如图。
上一页下一页
右质点 2mg T2 2ma
左质点 T1 mg ma
右滑轮 T2 r
Tr
第三章刚体力学
上一页下一页
刚体：不发生形变的物体（理想模型）
刚体模型突出了物体的大小形状，忽略形变和振动。刚体的运动形式：平动、转动、滚动、进动
刚体复杂运动可视为：平动转动（绕某轴线转动）刚体力学研究方法把刚体看成不变质点系(任意两个质元的相对距离保持不变),运用质点系定理和定律研究刚体的运动。

m 2
r
2
左滑轮Tr
T1r

m 2
r 2
关联方程 a r
解出 T 11 mg 8
N1
T

T1
mg
T1 m
mg
T
N2
a
mg T2
T2 2m
2mg
上一页下一页
M,
J

力矩转动定律转动惯量jm汇总课件

力矩的物理意义
总结词
力矩描述了力使物体绕某点转动的趋势或转动效果。
详细描述
力矩决定了物体绕某点转动的趋势或转动效果，其方向与力和力臂的乘积方向相同。力矩越大，物体转动的趋势或转动效果越明显。
力矩的计算方法
总结词
力矩的大小等于力和力臂的乘积，计中力臂是从转动轴（或转动中心）到力的垂直距离。计算公式为 M=FL，其中 M 为力矩，F 为力，L 为力臂。同时，力矩的方向与力和力臂的乘积方向相同。
转动惯量的大小决定了物体旋转运动的加速度、角速度和角动量等参数的变化规律，进而影响物体的运动状态和稳定性。
转动惯量的计算方法
转动惯量的计算方法主要包括平行轴定理和垂直轴定理。
平行轴定理指出，对于一个质量分布均匀的刚体，其相对于某固定轴的转动惯量，等于该刚体的质量乘以质心到该轴的距离的平方，再加上所有相对于此轴的离散质量的转动惯量之和。垂直轴定理则说明，一个质量分布均匀的刚体相对于任一垂直于其对称平面的轴的转动惯量，等于该刚体的质量乘以其对称轴到质心的距离的平方。
车辆工程
在车辆工程中，力矩转动定律用于分析车辆动力学和稳定性问题。例如，通过分析车轮的力矩，可以研究车辆的操控性能和行驶稳定性。
力矩转动定律在科研中的应用
物理学研究
力矩转动定律是物理学中分析转动问题的基本原理，广泛应用于分析天体运动、刚体动力学等问题。
生物学研究
在生物学研究中，力矩转动定律用于分析生物体的运动和平衡机制，如动物的行走、飞行等。
动惯量。
实验步骤
2. 将刚体安装到实验装置上，调整力矩计和角位移传感
器的位置和角度。
1. 准备实验器材：刚体、力矩计、角位移传感器、数据