《位似》相似PPT课件三
合集下载
《位似》相似PPT课件3
y
A
D
A′
B
D′
B′
C
C′
o
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
你还有其他(qítā)办法吗?试试看.
第二十七页,共32页。
x
第二十七页,编辑(biānjí)于星期五:十五点 十四分。
练一练:
1.如图表示△AOB和把它缩小(suōxiǎo)后得到的△COD,求它们的相似比
练一练:
3.如图,已知矩形(jǔxíng)wxyz各点的坐标,如果矩形( jǔxíng)STUV相似于wxyz 点S 的坐标为(2,2),按照下列相似比,分别写出T、U、V各点的坐标.
(1)相似比为 12;
y
z ( 1,4 )
y ( 5,4 )
S ( 2,2 )
W ( 1,1 )
x ( 5,1 )
第十五页,共32页。
第十五页,编辑(biānjí)于星期五:十五点 十四分。
A
O
B C
第十六页,共32页。
第十六页,编辑(biānjí)于星期五:十五点 十四分。
A
以0为中心把△ABC B
缩小为原来(yuánlái)的一半。
C
O C’
B’
A’
第十七页,共32页。
第十七页,编辑(biānjí)于星期五:十五点 十四 分。
为位似中心,相似比为2画它的位似图形.
放大后对应点的坐标(zuòbiāo)分别是多少?
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )
y
A'
6
4
A
3
2
B'
1
A
D
A′
B
D′
B′
C
C′
o
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
你还有其他(qítā)办法吗?试试看.
第二十七页,共32页。
x
第二十七页,编辑(biānjí)于星期五:十五点 十四分。
练一练:
1.如图表示△AOB和把它缩小(suōxiǎo)后得到的△COD,求它们的相似比
练一练:
3.如图,已知矩形(jǔxíng)wxyz各点的坐标,如果矩形( jǔxíng)STUV相似于wxyz 点S 的坐标为(2,2),按照下列相似比,分别写出T、U、V各点的坐标.
(1)相似比为 12;
y
z ( 1,4 )
y ( 5,4 )
S ( 2,2 )
W ( 1,1 )
x ( 5,1 )
第十五页,共32页。
第十五页,编辑(biānjí)于星期五:十五点 十四分。
A
O
B C
第十六页,共32页。
第十六页,编辑(biānjí)于星期五:十五点 十四分。
A
以0为中心把△ABC B
缩小为原来(yuánlái)的一半。
C
O C’
B’
A’
第十七页,共32页。
第十七页,编辑(biānjí)于星期五:十五点 十四 分。
为位似中心,相似比为2画它的位似图形.
放大后对应点的坐标(zuòbiāo)分别是多少?
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )
y
A'
6
4
A
3
2
B'
1
人教版九年级数学下册相似《位似(第3课时)》示范教学课件

确定位似中心
确定位似图形的相似比
位似图形的判定
平面直角坐标系中的图形变换
位似图形性质的应用
位似
利用位似图形解决实际问题
解:△ADE 与△ABC 是位似图形,缩小了.∵DE∥BC,∴△ADE∽△ABC.又∵对应顶点的连线都经过点 A,∴△ADE 与△ABC 是位似图形.∵对应边的比 ,∴△ADE 较△ABC 缩小了.
归纳
两个图形
是
对应点的连线是否交于一点
否不是位似ຫໍສະໝຸດ 形是否是位似图形
不是位似图形
解:如图(示意图),四边形 ABCD(胶片)与四边形A′B′C′D′(屏幕)是位似图形,且相似比为 3.5∶200=7∶400.设四边形 A′B′C′D′ 距光源 O 的距离为 x cm,则有 20∶x=7∶400,得 x= , cm= m.
归纳
利用位似图形解决实际问题时,首先应根据题意画出示意图,然后根据位似图形的性质或相关概念求解.解题时应注意单位的统一.
B
归纳
对于位似图形,将性质“位似图形上任意一对对应点(到位似中心的距离为 0 的点除外)到位似中心的距离之比等于相似比”反过来,即可得到“相似比等于位似图形上任意一对对应点(到位似中心的距离为 0 的点除外)到位似中心的距离之比”.
类型三、位似图形的判定
3.如图,点 D,E 分别是△ABC 的边 AB,AC 上的点,且 DE∥BC,那么△ADE 与△ABC 是位似图形吗?若是,是放大了还是缩小了?
类型四、位似图形性质的应用
4.如图,△ABC 与△A′B′C′ 关于点 O 位似,OB=3,OB′=6.(1)若 AC=5,求 A′C′ 的长;(2)若△ABC 的面积为 7,求△A′B′C′ 的面积.
解:(1)∵△ABC 与△A′B′C′ 是位似图形,相似比为 OB∶OB′=3∶6=1∶2,∴△ABC∽△A′B′C′,且相似比为 1∶2.故 AC∶A′C′=1∶2,即 5∶A′C′=1∶2,∴A′C′=10.(2)根据题意,得 ,即 7∶S△A′B′C′=1∶4,∴S△A′B′C′=7×4=28.
确定位似图形的相似比
位似图形的判定
平面直角坐标系中的图形变换
位似图形性质的应用
位似
利用位似图形解决实际问题
解:△ADE 与△ABC 是位似图形,缩小了.∵DE∥BC,∴△ADE∽△ABC.又∵对应顶点的连线都经过点 A,∴△ADE 与△ABC 是位似图形.∵对应边的比 ,∴△ADE 较△ABC 缩小了.
归纳
两个图形
是
对应点的连线是否交于一点
否不是位似ຫໍສະໝຸດ 形是否是位似图形
不是位似图形
解:如图(示意图),四边形 ABCD(胶片)与四边形A′B′C′D′(屏幕)是位似图形,且相似比为 3.5∶200=7∶400.设四边形 A′B′C′D′ 距光源 O 的距离为 x cm,则有 20∶x=7∶400,得 x= , cm= m.
归纳
利用位似图形解决实际问题时,首先应根据题意画出示意图,然后根据位似图形的性质或相关概念求解.解题时应注意单位的统一.
B
归纳
对于位似图形,将性质“位似图形上任意一对对应点(到位似中心的距离为 0 的点除外)到位似中心的距离之比等于相似比”反过来,即可得到“相似比等于位似图形上任意一对对应点(到位似中心的距离为 0 的点除外)到位似中心的距离之比”.
类型三、位似图形的判定
3.如图,点 D,E 分别是△ABC 的边 AB,AC 上的点,且 DE∥BC,那么△ADE 与△ABC 是位似图形吗?若是,是放大了还是缩小了?
类型四、位似图形性质的应用
4.如图,△ABC 与△A′B′C′ 关于点 O 位似,OB=3,OB′=6.(1)若 AC=5,求 A′C′ 的长;(2)若△ABC 的面积为 7,求△A′B′C′ 的面积.
解:(1)∵△ABC 与△A′B′C′ 是位似图形,相似比为 OB∶OB′=3∶6=1∶2,∴△ABC∽△A′B′C′,且相似比为 1∶2.故 AC∶A′C′=1∶2,即 5∶A′C′=1∶2,∴A′C′=10.(2)根据题意,得 ,即 7∶S△A′B′C′=1∶4,∴S△A′B′C′=7×4=28.
【小学课件】《位似》相似优质PPT课件3
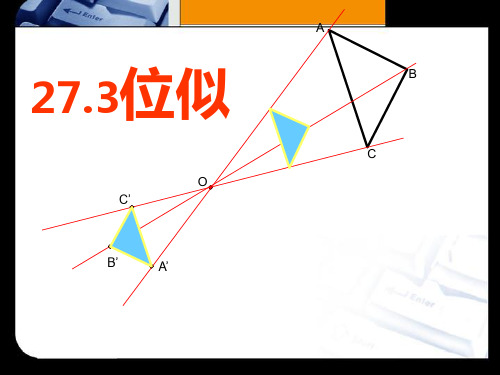
放大后对应点的坐标分别是多少?
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )
y
A'
6
4 A
3
2
B'
C
1
B
o
2
4
6
还有其他办法吗?
C'
x
12
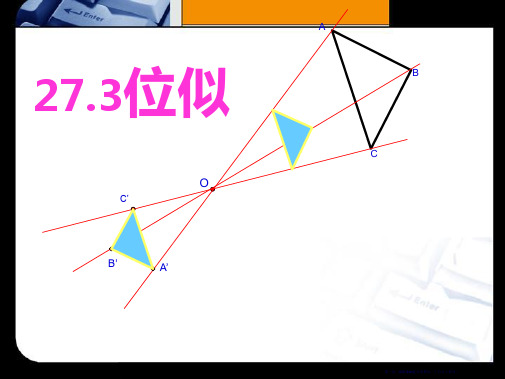
在平面直角坐标系中, △ABC三个顶点的坐标分别 为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相 似比为2,将△ABC放大.
27.3位似
O C’
B’
A’
A B
C
1. 前面我们已经学习了图形的哪些变换?
对称(轴对称与轴对称图形,中心对称与中心对 称图形):对称轴,对称中心. 平移:平移的方向,平移的距离. 旋转:旋转中心,旋转方向,旋转角度. 相似:相似比.
注:图形这些不同的变换是我们学习几何必不可少的重要 工具,它不但装点了我们的生活,而且是学习后续知识的基础.
2.位似图形的性质
位似图形上的任意一对对应点到位似中心的 距离之比等于位似比
3.利用位似可以把一个图形放大或缩小
你能得到的是正立放大的 “像”、正立缩小的“像”、 倒立缩小的“像”吗?
P
得到的是倒立放大的“像”
复习回顾
如何把三角形ABC放大为原来的2倍?
E
B
O
C
F
D
A
D
B
O
C
F
A
E
对应点连线都交于_位___似__中___心___ 对应线段____平__行___或__在___一___条__直___线___上______
87.当一切毫无希望时,我看着切石工人在他的石头上,敲击了上百次,而不见任何裂痕出现。但在第一百零一次时,石头被劈成两半。我体会到,并非那一击,而是前面的敲打使它裂开。――[贾柯·瑞斯] 88.每个意念都是一场祈祷。――[詹姆士·雷德非]
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )
y
A'
6
4 A
3
2
B'
C
1
B
o
2
4
6
还有其他办法吗?
C'
x
12
在平面直角坐标系中, △ABC三个顶点的坐标分别 为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相 似比为2,将△ABC放大.
27.3位似
O C’
B’
A’
A B
C
1. 前面我们已经学习了图形的哪些变换?
对称(轴对称与轴对称图形,中心对称与中心对 称图形):对称轴,对称中心. 平移:平移的方向,平移的距离. 旋转:旋转中心,旋转方向,旋转角度. 相似:相似比.
注:图形这些不同的变换是我们学习几何必不可少的重要 工具,它不但装点了我们的生活,而且是学习后续知识的基础.
2.位似图形的性质
位似图形上的任意一对对应点到位似中心的 距离之比等于位似比
3.利用位似可以把一个图形放大或缩小
你能得到的是正立放大的 “像”、正立缩小的“像”、 倒立缩小的“像”吗?
P
得到的是倒立放大的“像”
复习回顾
如何把三角形ABC放大为原来的2倍?
E
B
O
C
F
D
A
D
B
O
C
F
A
E
对应点连线都交于_位___似__中___心___ 对应线段____平__行___或__在___一___条__直___线___上______
87.当一切毫无希望时,我看着切石工人在他的石头上,敲击了上百次,而不见任何裂痕出现。但在第一百零一次时,石头被劈成两半。我体会到,并非那一击,而是前面的敲打使它裂开。――[贾柯·瑞斯] 88.每个意念都是一场祈祷。――[詹姆士·雷德非]
《位似》相似PPT课件4 (共16张PPT)

①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的 直线都经过同一个点,那么,这两个图形是位似图形; ④位似图形上任意两点与位似中心的距离之比等于位似 比. 【答案】②,③
2.(孝感中考)
( )Biblioteka 【解析】选D.由题意可知∠BOB′=75°,∠BOA=30° ∴∠B′OA=45°∴点B的纵横坐标的绝对值相等,又点B在 第四象限,所以选D.
A
(2,1)
A'
o
(2,0)
B'
B
x
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为 位似中心,相似比为1:3,把线段AB缩小. y A〞(-2,-1),B〞(-2,0) A′(2,1),B′(2,0)
A
A'
B〞
x o
B'
B
A〞
观察对应点之间的坐标的变化,你有什么发现? 在平面直角坐标系中,如果位似变换是以原点为位似中心, 相似比为k,那么位似图形对应点的坐标的比等于k或-k.
成比例 3.两个位似图形中的对应角______, 相等 对应线段________, 对应顶点的连线必经过__________ 位似中心 . 4.位似图形上某一对对应点到位似中心的距离分别为5和 10,则它们的位似比为______ 1:2 . 5.四边形ABCD和四边形A′B′C′D′位似,O为位似中
在平面直角坐标系中, △ABC三个顶点的坐标分别为 A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2, 将△ABC放大. 放大后对应点的坐标分别是多少? y A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 ) A
《位似》相似PPT(第1课时位似图形的概念及画法)

似中心的位似图形,且
′
=
=
′
′
=
′
;五边形ABCDE 与五
边形A′ B′ C′ D′ E′是以点O 为位似中心的位似图形,且′ = ′ =
′
= ′ = ′ .
例1 请指出下列图形那些是位似图形?并指出位似图形图的位似中心?
所示).
课堂小结
两个相似多边形,如果它们对应顶点所在的直线相交于
定义
一点,并且这点与对应顶点所连线段成比例,我们就把这
样的两个图形叫做位似图形,这个交点叫做位似中心.
① 两个图形相似.
位似图形的概念
及画法
性质
②对应点的连线相交于一点,对应边互相
平行或在同一直线上.
③任意一对对应点到位似中心的距离之比
英语课件:/keji an/ying yu/
科学课件:/keji an/kexue/
化学课件:/keji an/huaxue/
地理课件:/keji an/dili/
2
PPT素材:/s ucai/
其与△ABC位似,且位似比为2.
D
解:画射线OA、OB、OC;
在射线OA、OB、OC上分别取点D、E、F,
使OD = 2OA,OE = 2OB,OF = 2OC;
A
E
顺次连结D、E、F,使△DEF与△ABC位似,
B
相似比为2.
想一想:你还有其他的画法吗?
O
C
F
思考:上面点 O取在两个三角形的同侧,如果点 O在两
知识讲解
★
位似图形的概念
问题:下面两个多边形相似,将两个图形的顶点
′
=
=
′
′
=
′
;五边形ABCDE 与五
边形A′ B′ C′ D′ E′是以点O 为位似中心的位似图形,且′ = ′ =
′
= ′ = ′ .
例1 请指出下列图形那些是位似图形?并指出位似图形图的位似中心?
所示).
课堂小结
两个相似多边形,如果它们对应顶点所在的直线相交于
定义
一点,并且这点与对应顶点所连线段成比例,我们就把这
样的两个图形叫做位似图形,这个交点叫做位似中心.
① 两个图形相似.
位似图形的概念
及画法
性质
②对应点的连线相交于一点,对应边互相
平行或在同一直线上.
③任意一对对应点到位似中心的距离之比
英语课件:/keji an/ying yu/
科学课件:/keji an/kexue/
化学课件:/keji an/huaxue/
地理课件:/keji an/dili/
2
PPT素材:/s ucai/
其与△ABC位似,且位似比为2.
D
解:画射线OA、OB、OC;
在射线OA、OB、OC上分别取点D、E、F,
使OD = 2OA,OE = 2OB,OF = 2OC;
A
E
顺次连结D、E、F,使△DEF与△ABC位似,
B
相似比为2.
想一想:你还有其他的画法吗?
O
C
F
思考:上面点 O取在两个三角形的同侧,如果点 O在两
知识讲解
★
位似图形的概念
问题:下面两个多边形相似,将两个图形的顶点
位似--课件

-6
-8
B"
2. 如图,△ABC三个顶 点坐标分别为A(2,-
2),B(4,-5),C C"
(5,-2),以原点O为
8 6
A" 4
2
位似中心,将这个三角 形放大为原来的2倍.
-12 -10-9-8 -6 -4
-2 O 2 4 6
-2 A
C
-4 A'
-6
B
8 9 101112
C'
-8
解:
B'
A'( 4 ,- 4 ),B ' ( 8 , - 10 ),C ' ( 10 ,-4 ),
(1) 从上面练习第 1(1)(4)题图中,我们可以看到,△OAB∽△O A′B′,
则 OA OA′
= OB OB′
= AB A′B′
.从第
2
题的图中同样可以看到AADF
=AACP
=AAEB =BECP =DFPC
一般地,位似图形有以下性质: 位似图形上任意一对对应点到位似中心的距离之
比等于位似比.
是 (2)在平行四边形ABCD中,△ABO与 △CDO
是
不是
练一练:判断下列各对图形哪些是位似图形,哪些不是. (3)正方形ABCD与正方形A′B′C′D′. (4)等边三角形ABC与等边三角形A′B′C′
是
是
练一练:判断下列各对图形哪些是位似图形,哪些不是.
(5)反比例函数 y=6x (x>0)的图像与 y=x6 (x<0)的图像 (6)扇形ABC与扇形A′B′C′,
在日常生活中,我们经常见到这样一类相似的图形, 例如,放映幻灯时,通过光源,把幻灯片上的图形放大到屏 幕上(如图显示了它工作的原理).在照相馆中,摄影师通 过照相机,把人物的形象缩小在底片上.
《位似》相似PPT(上课用)3
O
P
(1)
√
(2)
×
(3)
√
位似中心是点。
位似中心是点。
练
习
.如同,△和△是位似图形,与平行吗? 为什么?
C A D O B
∥
∵△与△是位似图形 ∴△∽△ ∴∠∠
∥
’ ’ ’
'△和点.以为位似中心,求作△的位似图 形,并把△的边长扩大到原来的两倍.
思考:还有没其他作法?
’ ’
.四边形和四边形’’’’位似, 为位似中心,若’,那么 四边形四边形’’’’。
复习回顾
.什么叫位似图形? 如果两个图形不仅相似,而且对应顶点的连线 相交于一点,像这样的两个图形叫做位似图形, 这 个点叫做位似中心, 这时的相似比又称为位似比.
.位似图形的性质
位似图形上的任意一对对应点到位似中心的 距离之比等于位似比 .利用位似可以把一个图形放大或缩小
′( ), ′( ), ′( )
'
探索:
' '
还有其他办法吗?
在平面直角坐标系中, △三个顶点的坐标分别为 ()()(),以原点为位似中心,相似比为,将△放大.
放大后对应点的坐标分别是多少? ′( ), ′( ), ′( )
”
”
例题.在平面直角坐标系中, 四边形的四个顶点的 坐标分别为()()()(),画出它的一个以原点为位似 中心,相似比为的位似图形.
A
D
′
B
′ ′
C
′
′( ), ′( ), ′( ), ′( ) 你还有其他办法吗?试试看.
练一练:
.如图表示△和把它缩小后得到的△,求它们的相似比
练一练:
.如图△的三个顶点坐标分别为()()(),以原点为位似中心,将这 个三角形放大为原来的倍.
人教版九年级下册数学《位似》相似精品PPT教学课件
6
过程与方法
• 经历位似图形性质的探索过程,进一步发 展学生的探究、交流能力、以及动手、动脑、 手脑和谐一致的习惯。
2020/11/22
7
情感态度与价值观
• 利用图形的位似解决一些简单的实际问题,并在此 过程中培养学生的数学应用意识,进一步培养学生动 手操作的良好习惯。 • 发展学生的合情推理能力和初步的逻辑推理能力。
2020/11/22
轴对称
中心对称
30
平移
2020/11/22
旋转
31
相似
2020/11位似中心、位似比:
如果两个图形不仅形状相同,而且每组 对应顶点所在的直线都经过同一个点,那么 这样的两个图形叫做位似图形。
在平面直角坐标系中,有两点A(6,3), B(6,0)。以原点O为位似中心,相似比为1 , 把线段AB缩小。观察对应点之间坐标的变化3, 你有什么发现?
2020/11/22
26
探究
△ABC三个顶点坐标 分别为A(2,3),B(2, 1),C(6,2),以点O 为位似中心,相似比为2, 将△ABC放大,观察对应 顶点坐标的变化,你有什 么发现?
2020/11/22
15
位似图形的性质
✓ 对应点与位似中心共线。 ✓ 不经过位似中心的对应边平行。 ✓ 位似图形上任意一对应点到位似中心的 距离之比等于位似比。
2020/11/22
16
位似的作用 位似可以将一个图形放大或缩小。
2020/11/22
17
小练习
请以坐标原点O为位似中心,作□ ABCD
的位似图形,并把它的边长放大3倍。
分析:根据位似图形上任意一对对应点到位似中 心的距离之比等于位似比,我们只要连结位似中心O
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.位似图形的性质
位似图形上的任意一对对应点到位似中心的 距离之比等于位似比
3.利用位似可以把一个图形放大或缩小
你能得到的是正立放大的 “像”、正立缩小的“像”、 倒立缩小的“像”吗?
P
得到的是倒立放大的“像”
复习回顾
如何把三角形ABC放大为原来的2倍?
E
B
O
C
F
D
A
D
B
O
C
F
A
E
对应点连线都交于_位___似__中___心___ 对应线段____平__行___或__在___一___条__直___线___上______
B
∴∠OAB=∠C
AB∥CD
OA:OA’ =OB:OB’ =OC:OC’= 1:2
A
O.
B
C
B’
A.'
C’
1.如图,已知△ABC和点O.以O为位似中心,求作 △ABC的位似图形,并把△ABC的边长扩大到原来的两倍.
思考:还有没其他作法?
C’
B’
A
. O
B
C
A'
如果位似中心跑到三角形内部呢?
A
O
放大后对应点的坐标分别是多少?
A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )
y
A
C
B
x
o
B”
A”
例题.在平面直角坐标系中, 四边形ABCD的四个顶点的坐
标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以 原点O为位似中心,相似比为1/2的位似图形.
27.3位似
O C’B’A’Fra bibliotekA B
C
1. 前面我们已经学习了图形的哪些变换?
对称(轴对称与轴对称图形,中心对称与中心对 称图形):对称轴,对称中心. 平移:平移的方向,平移的距离. 旋转:旋转中心,旋转方向,旋转角度. 相似:相似比.
注:图形这些不同的变换是我们学习几何必不可少的重要 工具,它不但装点了我们的生活,而且是学习后续知识的基础.
探索1:
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为 位似中心,相似比为1:3,把线段AB缩小.
y A′(2,1), B′(2,0)
A
A'
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以原 点O为位似中心,相似比为1:3,把线段AB缩小.
y
A
D
A′
B
D′
B′
x
C
C′
o
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
你还有其他办法吗?试试看.
练一练:
下面请欣赏如下图形的变换
P
在幻灯机放映 图片的过程中, 这些图片有什 么关系呢?
放映机
在幻灯机上放映幻灯片时,把幻灯片上的图象放大到屏幕上 在照相馆里,摄影师通过照相机把实物的图象缩小在底片上 这样放大或缩小的图形,形状_相__同__,大小__不__同__,所以它们_相__似__.
下列图形中,每个图中的四边形ABCD和四 边形A′B′C′D′都是相似图形.分别观察这五个图,你 发现每个图中的两个四边形各对应点的连线有什么 特征?
3.四边形ABCD和四边形A’B’C’D’位似,
O为位似中心,若OA:OA’=1:4,那么
S四边形ABCD:S四边形A’B’C’D’=_1:_1_6__。
复习回顾
1.什么叫位似图形? 如果两个图形不仅相似,而且对应顶点的连线相
交于一点,像这样的两个图形叫做位似图形, 这个点 叫做位似中心, 这时的相似比又称为位似比.
思考:是否相似图形都是位似图形?
判断下面的正方形是不是位似图形?
A
D
不是
E
F
(1)
B
C
G
显然,位似图形是相似图形的特殊情形.相似图形不 一定是位似图形,可位似图形一定是相似图形
思考:位似图形有何性质?
2. 位似图形的性质
从第 (1),(2)图中,我们可以看到,△OAB∽△O A′B′,则OAO′A =
是位似图形。 位似中心是点A, 位似比是1:2。
哪些图形是位似图形并指出位似图形的位似中 心。
O
(√1)
(2) ×
位似中心是点O。
P
(3) √
位似中心是点P。
练习
1.如同,△OAB和△OCD是位似图形,AB与CD平行吗?
为什么?
C
AB∥CD
A
∵△OAB与△ODC是位似图形
D
∴△OAB∽△OCD
O
A′(2,1),B′(2,0) y
A〞(-2,-1),B(-2,0)
A
A'
B〞
x
o
B'
B
A〞
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,如果位似变换是以原点 为位似中心,相似比为k,那么位似图形对应点 的坐标的比等于k或-k.
探索2:
在平面直角坐标系中, △ABC三个顶点的坐标分别为 A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比 为2画它的位似图形.
1.位似图形的概念
如果两个图形不仅相似,而且每组对应点所 在的直线都经过同一点,对应边互相平行,那 么这样的两个图形叫做位似图形,这个点叫 做位似中心.
相似 对应点的连 对应边平行 线相交一点
1. 判断下列各对图形是不是位似图形. (1)正五边形ABCDE与正五边形A′B′C′D′E′; 是 (2)等边三角形ABC与等边三角形A′B′C′. 是
放大后对应点的坐标分别是多少?
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )
y
A'
6
4 A
3
2
B'
C
1
B
o
2
4
6
还有其他办法吗?
C'
x
12
在平面直角坐标系中, △ABC三个顶点的坐标分别 为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相 似比为2,将△ABC放大.
B C
以0为中心把△ABC 缩小为原来的一半。
O C’
B’
A’
A B
C
面向全体,巩固双基
1.两个位似图形中的对应角_相__等_,对应线 段_成_比__例_,对应顶点的连线必经过_位__似_中__心_。
2.位似图形上某一对对应点到位似中心的
距离分别为5和10,则它们的位似比为___。
1:2
面向全体,巩固双基
OB OB′
=A′ABB′
.从第(3)图中同样可以看到AAFD
=AAPC
=AABE
=EBPC
=DFCP
性质:位似图形上任意一对对应点到位似中心 的距离之比等于相似比.
• 若△ABC与△A’B’C’的相似比为:1:2, 则OA:OA’=(1:2 )。
A’
A
B
B’
O
C
C’
如图P,E,F分别是AC,AB,AD的中点,四 边形AEPF与四边形ABCD是位似图形吗?如果 是位似图形,说出位似中心和位似比.
位似图形上的任意一对对应点到位似中心的 距离之比等于位似比
3.利用位似可以把一个图形放大或缩小
你能得到的是正立放大的 “像”、正立缩小的“像”、 倒立缩小的“像”吗?
P
得到的是倒立放大的“像”
复习回顾
如何把三角形ABC放大为原来的2倍?
E
B
O
C
F
D
A
D
B
O
C
F
A
E
对应点连线都交于_位___似__中___心___ 对应线段____平__行___或__在___一___条__直___线___上______
B
∴∠OAB=∠C
AB∥CD
OA:OA’ =OB:OB’ =OC:OC’= 1:2
A
O.
B
C
B’
A.'
C’
1.如图,已知△ABC和点O.以O为位似中心,求作 △ABC的位似图形,并把△ABC的边长扩大到原来的两倍.
思考:还有没其他作法?
C’
B’
A
. O
B
C
A'
如果位似中心跑到三角形内部呢?
A
O
放大后对应点的坐标分别是多少?
A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )
y
A
C
B
x
o
B”
A”
例题.在平面直角坐标系中, 四边形ABCD的四个顶点的坐
标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以 原点O为位似中心,相似比为1/2的位似图形.
27.3位似
O C’B’A’Fra bibliotekA B
C
1. 前面我们已经学习了图形的哪些变换?
对称(轴对称与轴对称图形,中心对称与中心对 称图形):对称轴,对称中心. 平移:平移的方向,平移的距离. 旋转:旋转中心,旋转方向,旋转角度. 相似:相似比.
注:图形这些不同的变换是我们学习几何必不可少的重要 工具,它不但装点了我们的生活,而且是学习后续知识的基础.
探索1:
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为 位似中心,相似比为1:3,把线段AB缩小.
y A′(2,1), B′(2,0)
A
A'
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以原 点O为位似中心,相似比为1:3,把线段AB缩小.
y
A
D
A′
B
D′
B′
x
C
C′
o
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
你还有其他办法吗?试试看.
练一练:
下面请欣赏如下图形的变换
P
在幻灯机放映 图片的过程中, 这些图片有什 么关系呢?
放映机
在幻灯机上放映幻灯片时,把幻灯片上的图象放大到屏幕上 在照相馆里,摄影师通过照相机把实物的图象缩小在底片上 这样放大或缩小的图形,形状_相__同__,大小__不__同__,所以它们_相__似__.
下列图形中,每个图中的四边形ABCD和四 边形A′B′C′D′都是相似图形.分别观察这五个图,你 发现每个图中的两个四边形各对应点的连线有什么 特征?
3.四边形ABCD和四边形A’B’C’D’位似,
O为位似中心,若OA:OA’=1:4,那么
S四边形ABCD:S四边形A’B’C’D’=_1:_1_6__。
复习回顾
1.什么叫位似图形? 如果两个图形不仅相似,而且对应顶点的连线相
交于一点,像这样的两个图形叫做位似图形, 这个点 叫做位似中心, 这时的相似比又称为位似比.
思考:是否相似图形都是位似图形?
判断下面的正方形是不是位似图形?
A
D
不是
E
F
(1)
B
C
G
显然,位似图形是相似图形的特殊情形.相似图形不 一定是位似图形,可位似图形一定是相似图形
思考:位似图形有何性质?
2. 位似图形的性质
从第 (1),(2)图中,我们可以看到,△OAB∽△O A′B′,则OAO′A =
是位似图形。 位似中心是点A, 位似比是1:2。
哪些图形是位似图形并指出位似图形的位似中 心。
O
(√1)
(2) ×
位似中心是点O。
P
(3) √
位似中心是点P。
练习
1.如同,△OAB和△OCD是位似图形,AB与CD平行吗?
为什么?
C
AB∥CD
A
∵△OAB与△ODC是位似图形
D
∴△OAB∽△OCD
O
A′(2,1),B′(2,0) y
A〞(-2,-1),B(-2,0)
A
A'
B〞
x
o
B'
B
A〞
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,如果位似变换是以原点 为位似中心,相似比为k,那么位似图形对应点 的坐标的比等于k或-k.
探索2:
在平面直角坐标系中, △ABC三个顶点的坐标分别为 A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比 为2画它的位似图形.
1.位似图形的概念
如果两个图形不仅相似,而且每组对应点所 在的直线都经过同一点,对应边互相平行,那 么这样的两个图形叫做位似图形,这个点叫 做位似中心.
相似 对应点的连 对应边平行 线相交一点
1. 判断下列各对图形是不是位似图形. (1)正五边形ABCDE与正五边形A′B′C′D′E′; 是 (2)等边三角形ABC与等边三角形A′B′C′. 是
放大后对应点的坐标分别是多少?
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )
y
A'
6
4 A
3
2
B'
C
1
B
o
2
4
6
还有其他办法吗?
C'
x
12
在平面直角坐标系中, △ABC三个顶点的坐标分别 为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相 似比为2,将△ABC放大.
B C
以0为中心把△ABC 缩小为原来的一半。
O C’
B’
A’
A B
C
面向全体,巩固双基
1.两个位似图形中的对应角_相__等_,对应线 段_成_比__例_,对应顶点的连线必经过_位__似_中__心_。
2.位似图形上某一对对应点到位似中心的
距离分别为5和10,则它们的位似比为___。
1:2
面向全体,巩固双基
OB OB′
=A′ABB′
.从第(3)图中同样可以看到AAFD
=AAPC
=AABE
=EBPC
=DFCP
性质:位似图形上任意一对对应点到位似中心 的距离之比等于相似比.
• 若△ABC与△A’B’C’的相似比为:1:2, 则OA:OA’=(1:2 )。
A’
A
B
B’
O
C
C’
如图P,E,F分别是AC,AB,AD的中点,四 边形AEPF与四边形ABCD是位似图形吗?如果 是位似图形,说出位似中心和位似比.
