概率论实验报告一
中北大学概率论实验报告一
中北大学概率论实验报告一实验一各种分布的密度函数与分布函数一给出下列各题的程序和计算结果1、一大楼装有5个同类型的供水设备，调查表明，在任一时刻t 每个设备被使用的概率为 0.1，问在同一时刻：(1) 恰有两个设备被使用的概率是多少？>> p=binopdf(2,5,0.1)p =0.0729(2) 至少有3个设备被使用的概率是多少？>> p=1-binocdf(3,5,0.1)+binopdf(3,5,0.1)p =0.00862、一电话总机每分钟收到呼唤的次数服从参数为4的泊松分布，求：(1) 每一分钟恰有8次呼唤的概率；>> p=poisspdf(8,4)p =0.0298(2) 某一分钟的呼唤次数大于3的概率。
>> p=1-poisscdf(3,4)p =0.56653、设()X N，求：2,6(1) 2X=时的概率密度值；>> p=normpdf(2,2,sqrt(6))p =0.1629(2) 事件{}218X≤的概率，并比较实际含义；X≤{}X≤-{}2>> p=zeros(1,3);p(1)=normcdf(-2,2,sqrt(6));p(2)=normcdf(2,2,sqrt(6));p(3)=normcdf(18,2,sqrt(6));>> pp =0.0512 0.5000 1.0000(3) 上0.01分位数。
>> p=norminv(0.99,2,sqrt(6))p =7.69844、在一个图中画出任意三个常见分布的密度函数的图形，并进行标注区分。
输入 clear;clc;x=(-4:0.1:6);y1=unifpdf(x,2,6);y2=binopdf(x,10,0.5);y3=normpdf(x,0,1);plot(x,y1,'r-p',x,y2,'g-*',x,y3,'y-d')xlabel('\itx');legend('U(2,6)的密度函数','b(10,0.5)的密度函数','N(0,1)的密度函数') 输出。
概率论教学实践报告总结(3篇)
第1篇一、前言概率论是数学的一个重要分支，它研究随机现象及其规律。
随着我国教育事业的不断发展，概率论在教学中的地位日益重要。
为了提高教学质量，探索有效的教学策略，我们开展了一系列概率论教学实践活动。
现将本次实践活动的总结如下：二、实践目的1. 提高学生对概率论知识的掌握程度，培养学生的逻辑思维能力。
2. 探索适合我国学生特点的概率论教学方法，提高课堂教学效果。
3. 加强师生互动，培养学生的自主学习能力。
4. 丰富教师的教学经验，提高教师的专业素养。
三、实践内容1. 教学方法改革（1）启发式教学：教师在课堂上注重引导学生思考，通过提问、讨论等方式，激发学生的学习兴趣，提高学生的思维能力。
（2）案例教学：结合实际生活中的例子，让学生理解概率论知识在实际中的应用，提高学生的实践能力。
（3）小组合作学习：将学生分成若干小组，共同完成教学任务，培养学生的团队协作能力。
2. 教学手段创新（1）多媒体教学：利用PPT、视频等多媒体手段，使教学内容更加生动形象，提高学生的学习兴趣。
（2）网络教学：通过在线课程、论坛等网络平台，拓宽学生的学习渠道，提高学生的学习效果。
（3）实验教学：开展概率实验，让学生亲身体验概率现象，加深对概率论知识的理解。
3. 教学评价改革（1）过程性评价：关注学生在学习过程中的表现，如课堂发言、作业完成情况等。
（2）结果性评价：关注学生对知识掌握程度，如期中、期末考试等。
（3）多元评价：结合学生自评、互评、教师评价等多种方式，全面评价学生的学习成果。
四、实践效果1. 学生对概率论知识的掌握程度有了明显提高，课堂参与度显著提升。
2. 学生在解决实际问题时，能够运用概率论知识进行分析，提高了解决问题的能力。
3. 学生在团队协作、自主学习等方面取得了较好成绩，综合素质得到提高。
4. 教师的教学经验得到了丰富，教学水平得到提高。
五、存在问题及改进措施1. 存在问题（1）部分学生对概率论知识缺乏兴趣，学习积极性不高。
概率论试验报告
概率论试验报告实验一概率计算实验目的：掌握用MATLAB实现概率中的常见计算1、选择三种常见随机变量的分布，计算它们的期望与方差（参数自己设定）2、已知机床加工得到的某零件尺寸服从期望为20cm,标准差为1.5cm的正态分布。
（1）任意抽取一个零件，求它的尺寸在（19,22）区间的概率；（2）若规定尺寸不小于某一标准值的零件为合格品，要使合格品的概率为0.9，如何确定这个标准值？（3）独立的取25个组成一个样本，求样本均值在（19,22）区间的概率。
3、比较t(10)分布和标准正态分布的图像。
1．均匀分布：设定为服从在（0，1）上的均匀分布。
则代码为：2.参数为1的指数分布：3.标准正态分布：2.（1）。
概率为（2）。
求得的值为：（3）。
由题目可知样本均值服从（20，0.3）的正态分布，所以代码为：3.我们取区间[-3,3]，间隔为0.1，画得的图为：上方的曲线为t分布，下面的为正态分布曲线。
实验二样本的统计与计算实验目的：学习利用MATLAB求来自总体的一个样本的样本均值、中位数、样本方差、样本分位数和其它数字特征，并能作出频率直方图和经验分布函数来自某总体的样本观察值如下，计算样本的样本均值、中位数、样本方差、画出频率直方图经验分布函数图。
A=[16 25 19 20 25 33 24 23 20 24 25 17 15 21 22 26 15 23 22 20 14 16 11 14 28 18 13 27 31 25 24 16 19 23 26 17 14 30 21 18 16 18 19 20 22 19 22 18 26 26 13 21 13 11 19 23 18 24 28 13 11 25 15 17 18 22 16 13 12 13 11 09 15 18 21 15 12 17 13 14 12 16 10 08 23 18 11 16 28 13 21 22 12 08 15 21 18 16 16 19 28 19 12 14 19 28 28 28 13 21 28 19 11 15 18 24 18 16 28 19 15 13 22 14 16 24 20 28 18 18 28 14 13 28 29 24 28 14 18 18 18 08 21 16 24 32 16 28 19 15 18 18 10 12 16 26 18 19 33 08 11 18 27 23 11 22 22 13 28 14 22 18 26 18 16 32 27 25 24 17 17 28 33 16 20 28 32 19 23 18 28 15 24 28 29 16 17 19 18]代码为：代码为：[a,b]=hist(A); bar(b,a/sum(a))画得的图为：实验三数理统计中的常用方法实验目的：能熟练用matlab做参数点估计、区间估计和假设检验。
中北大学概率论实验报告一分析
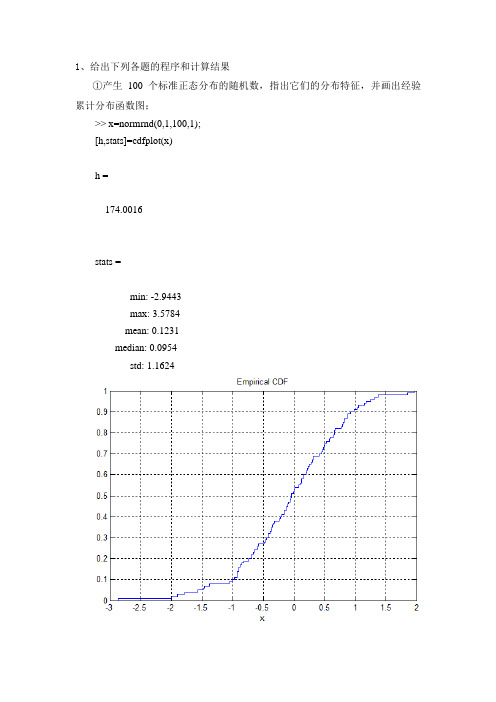
1、给出下列各题的程序和计算结果①产生100 个标准正态分布的随机数，指出它们的分布特征，并画出经验累计分布函数图；>> x=normrnd(0,1,100,1);[h,stats]=cdfplot(x)h =174.0016stats =min: -2.9443max: 3.5784mean: 0.1231median: 0.0954std: 1.1624②产生100 个均值为1，标准差为1的正态分布的随机数，画出它们的直方图并附加正态密度曲线，观察它们之间的拟合程度；x=normrnd(1,1,100,1);h=histfit(x);set(h(1),'FaceColor','c','EdgeColor','b')set(h(2),'color','g')③产生100 个均匀分布的随机数，对这100 个数据的列向量，用加号“*”标注其数据位置，作最小二乘拟合直线；x=1:1:100;y=unifrnd(0,1,1,100);n=1;a=polyfit(x,y,n);y1=polyval(a,x);plot(x,y,'g*',x,y1,'r-')④产生100个参数为5的指数分布的随机数，再产生100个参数为1的指数分布的随机数，用箱形图比较它们均值不确定性的稳健性。
x1=exprnd(5,100,1);x2=exprnd(1,100,1);x=[x1 x2];boxplot(x,1,'m+',0,0)课后题：P261、1题：以下是某工厂通过抽样调查得到的10名工人一周内生产的产品数：149 156 160 138 149 153 153 169 156 156试由这批数据构造经验分布函数并作图。
>> x=[149;156;160;138;149;153;153;169;156;156];[h,stats]=cdfplot(x)h =174.0023stats =min: 138max: 169mean: 153.9000median: 154.5000std: 8.0340P261、3题：假若某地区30名2000年某专业毕业生实习期满后的月薪数据如下：909 1086 1120 999 1320 10911071 1081 1130 1336 967 1572825 914 992 1232 950 7751203 1025 1096 808 1224 1044871 1164 971 950 866 738（1）构造该批数居的频率分布表；（2）画出直方图。
概率论实验报告1
课程：概率论实验实验名称：各种分布的密度函数和分布函数第页系别：实验日期 2012 年 6 月 2日专业班级：组别___ 实验报告日期 2012年 6 月 2 日姓名：学号_ 报告退发 ( 订正、重做 )同组人_________________________________ 教师审批签字一.实验名称：各种分布的密度函数和分布函数二.实验目的通过用matlab软件对常见随机变量进行期望与方差计算，熟悉变量，深化理解。
三.实验内容（1）在常见随机变量中选择3种计算它们的期望和方差（参数自己设定）。
解：a.均匀分布的期望和方差a = 1:8;b = 3.*a;[M,V] = unifstat(a,b)结果：M =2 4 6 8 10 12 14 16V =0.3333 1.3333 3.0000 5.3333 8.333312.0000 16.3333 21.3333b.正态分布的期望和方差a = 1:8;b = 3.*a;[M,V]=normstat(a,b)结果：M =1 2 3 4 5 6 7 8V =9 36 81 144 225 324 441 576c.二项分布的期望和方差[m,v]=binostat(10,0.3)m =3v =2.1000（2）某人向空中抛硬币100次，落下为正面的概率为0.5。
记正面向上的次数为X，（1）计算和的概率。
（2）给出随机数X的概率分布函数图像和概率密度函数图像。
解：a.计算P（X=45）>> binopdf(45,100,0.5)ans =0.0485b.计算P（X<=45）>> binocdf(45,100,0.5)ans =0.1841c.画X的概率分布函数图像和概率密度函数图像x=0:100;y1=binopdf(x,100,0.5);y2=binocdf(x,100,0.5);plot(x,y1,'r')hold onplot(x,y2,'g')gtext(‘红概率密度图像’)gtext(‘绿概率分布图像’)（3）比较自由度是10的t分布和标准正态分布的概率密度图像（要求写出程序并作图）。
统计学实验---概率论
实验报告须知
1、学生填写实验报告，请参照实验大刚规定的实验项目填写。
2、学生应该填写的内容包括：封面相关栏目、实验项目、时间、地点、实验性质、
实验目的、内容、结果和分析总结。
3、学生完成的主要内容有：文档、表格、演示文稿、程序、数据库设计、操作过程、
必要的截图等。
4、指导教师应该填写的内容包括：每次实验报告的成绩、评价并签名，最后实验最
终成绩汇总签字。
5、教师根据每学期该课程的实验教学要求，评定学生的实验成绩。
在课程结束后两
周内将教学班的实验报告汇总教学办存档。
《实验一：统计学基础——概率论》实验报告
图1 图2 图3。
概率论实验报告一
实验报告一、问题描述1.研究一些概率密度函数的估计的特性：（a ）编写程序，根据均匀分布产生位于单位立方体内的样本点，即-1/2≤xi ≤1/2，其中i=1,2,3.共产生10^4个点。
（b ）编写程序，基于这10^4个样本点，估计原点附近的概率密度，作为边长为h 的立方体体积的函数，并且对于0<h ≤1，画出估计的函数图像。
（c ）估计原点附近的概率密度，使用n 个样本点，并且选择窗使得恰好包含进n 个样本点。
对于n=1,2，……10^4，画出估计的函数图像。
（d ）编写程序，产生服从球形高斯分布的概率密度并且以原点为中心的样本点。
重复（b ），（c ）。
（e ）定性的讨论在一致和高斯密度两种情况下，估计结果对函数形式的依赖性的异同。
2.考虑对于表格中的数据进行Parzen 窗估计和设计分类器。
窗函数为一个球形的高斯函数，如下： ()()()()()[]22/exp /h x x x x h x x i t i i ---∝-ϕ（a ）编写程序，使用Parzen 窗估计方法对一个任意的测试样本点x 进行分类。
对分类器的训练则使用表格中的三维数据。
同时令h=1，分类样本点为（0.5，1.0，0.0）^t,(0.31,1.51,-0.50)^t ，（-0.3，0.44，-0.1）^t 。
（b ）令h=0.1，重复（a ）。
二、复现代码及结果题目1：(a)clc;clear;Upb=0.5*ones(3,10000);Lob=-0.5*ones(3,10000);%先设置分布的上、下界、样本点的维度以及样本数量X=unifrnd(Lob,Upb);%用unifrnd函数生成规定数目的样本点scatter3(X(1,:),X(2,:),X(3,:),'filled');%以散点图形式绘制在三维坐标系下(b)count=zeros(100,1);for h=1:100%选择不同的边长hl=h/200;for i=1:10000if(abs(X(1,i))<l&&abs(X(2,i))<l&&abs(X(3,i))<l)count(h,1)=count(h,1)+1;endendcount(h,1)=count(h,1)/(10000*8*l^3);endplot(count);xlabel('100*h');ylabel('p(h)=k(h)/(n*h^3)');%通过公式 p k=k估计原点附近的概率密度，并画出 h-k h的分布图nV k(c)k=sort(max(abs(X),[],1));%取各样本点绝对值最大分量，这个分量表示能刚好将它包围在内的立方体边长的一半%并从小到大排序，排序后数组中第k个元素就是包围k个样本点所需的最小立方体边长的一半for i=1:10000k(i)=i/(10000*8*k(i)^3);endplot(k);xlabel('k');ylabel('p(k)=k/(n*V(k))');估计原点附近的概率密度，并画出 k-p k的分布图%通过公式 p k=knV k(d)X=normrnd(0,1,3,10000);scatter3(X(1,:),X(2,:),X(3,:),'filled');%调用内置函数normrnd生成样本点并绘制散点分布图l=zeros(10000,1);l(:,1)=sqrt(X(1,:).^2+X(2,:).^2+X(3,:).^2);l=sort(l);%统计每个样本点到原点的距离并排序count=zeros(10000,1);%统计半径r不同的球形包围的样本点个数k rfor i=1:10000r=max(l)*i/10000;%选择不同的距离rk=1;while(r>l(k))count(i)=count(i)+1;k=k+1;endcount(i)=count(i)/(10000*0.75*pi*r^3);endplot(count);xlabel('10000*r/max(r),max(r)=4.7407');ylabel('p(r)=k(r)/(nV)');%，并画出 r-p r的分布图count=zeros(10000,1);for k=1:10000count(k)=k/(10000*0.75*pi*l(k)^3);%通过公式p r=k r(V=0.75πr3) 估计原点附近的概率密度nVendplot(count);xlabel('k');ylabel('p(k)=k/(nV(k))');%画出 k-p k的分布图（e）对于同一概率密度分布，使用窗函数法和k-近邻法估计概率密度的结果基本相同。
概率论实验报告
概率论实验报告班级：电气211姓名：***学号：**********第一次实验实验一1、实验目的熟练掌握MATLAB软件关于概率分布作图的基本操作会进行常用的概率密度函数和分布函数的作图绘画出分布律图形2、实验要求掌握MATLAB的画图命令plot掌握常见分布的概率密度图像和分布函数图像的画法3、实验内容1、设X~b(20,0,25)(1)生成X的概率密度；(2)产生18个随机数（3行6列）(3)又已知分布函数F(x)=0.45，求x(4)画出X的分布律和分布函数图形4、实验方案了解到MATLAB在二项分布中有计算概率密度函数binopdf，产生随机数的函数binornd，计算确定分布函数值对应的自变量x的函数binoinv，可以直接生成X的概率密度和产生18个随机数（3行6列），求已知分布函数F(x)=0.45对应的x的值。
最后用binopdf函数、binocdf函数和plot函数画出X的分布律和分布函数图形5、实验过程(1)生成X的概率密度binopdf(0:20,20,0.25)ans =Columns 1 through 120.0032 0.0211 0.0669 0.1339 0.1897 0.2023 0.16860.1124 0.0609 0.0271 0.0099 0.0030Columns 13 through 210.0008 0.0002 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000(2)产生18个随机数（3行6列）binornd(20,0.25,3,6)ans =6 4 1 2 6 44 3 6 2 6 24 5 6 6 5 6(3)已知分布函数F(x)的值，求xbinoinv(0.45,20,0.25)ans =5(4) 画出X的分布律和分布函数图形x=0:20;y=binopdf(x,20,0.25);subplot(1,2,1);plot(x,y,'*');x=0:0.01:20;y=binocdf(x,20,0.25);subplot(1,2,2);plot(x,y)6、 小结1.上机时对于matlab 的命令应该灵活使用，明白命令中每个参数的意义及输出内容的意义，对于matlab 命令的理解也应该联系概率论的理论基础2.学习matlab 的命令注意学会总结各个命令的用处与差异，不至于对相似的命令混淆。
概率论与数理统计实验报告
概率论与数理统计实验报告概率论与数理统计实验报告引言：概率论与数理统计是数学的两个重要分支，它们在现代科学研究和实际应用中起着重要的作用。
本次实验旨在通过实际操作，加深对概率论与数理统计的理解，并探索其在实际问题中的应用。
实验一：掷硬币实验实验目的：通过掷硬币实验，验证硬币正反面出现的概率是否为1/2。
实验步骤：1. 准备一枚硬币，标记正反面。
2. 进行100次连续掷硬币实验。
3. 记录每次实验中正面朝上的次数。
实验结果与分析：经过100次掷硬币实验，记录到正面朝上的次数为47次。
根据概率论的知识，理论上硬币正反面出现的概率应为1/2。
然而，实验结果显示正面朝上的次数并未达到理论值。
这表明在实际操作中，概率与理论可能存在一定的差异。
实验二：骰子实验实验目的：通过骰子实验，验证骰子的点数分布是否符合均匀分布。
实验步骤：1. 准备一个六面骰子。
2. 进行100次连续投掷骰子实验。
3. 记录每次实验中骰子的点数。
实验结果与分析：经过100次投掷骰子实验，记录到骰子点数的分布如下：1出现了17次；2出现了14次；3出现了20次；4出现了19次；5出现了16次；6出现了14次。
根据概率论的知识，理论上骰子的点数分布应符合均匀分布，即每个点数出现的概率相等。
然而，实验结果显示骰子点数的分布并未完全符合均匀分布。
这可能是由于实际操作的不确定性导致的结果差异。
实验三：正态分布实验实验目的：通过测量人体身高数据，验证人体身高是否符合正态分布。
实验步骤：1. 随机选择一定数量的被试者。
2. 测量每个被试者的身高。
3. 统计并绘制身高数据的频率分布直方图。
实验结果与分析：通过测量100名被试者的身高数据，统计得到的频率分布直方图呈现出典型的钟形曲线，符合正态分布的特征。
这与概率论中对正态分布的描述相吻合。
结论：通过以上实验，我们对概率论与数理统计的一些基本概念和方法有了更深入的了解。
实验结果也向我们展示了概率与理论之间的差异以及实际操作的不确定性。
[工学]概率实验报告全三次
![[工学]概率实验报告全三次](https://img.taocdn.com/s3/m/eaaf1b2f5f0e7cd1842536f3.png)
• 从自动车床加工的同类零件中抽取10件,测量其长 度为A=[12.15 12.12 12.01 12.28 12.09 12.03 12.01 12.11 12.06 12.14] ; • sprintf('样本的均值%f',mean(A)) • %计算方差 • sprintf('样本的方差%f',std(A)) • %零件长度的均值mu和方差的置信水平为% % 0.95的置信区间 • [junzhi,fangcha,junzhi_zhixinqujian,facha_zhixinquji an]=normfit(A);
图象为：
２．绘制指数分布的概率密度图象
x 0 : 0.1: 30; y exppdf ( x, 4); plot ( x, y, 'o ')回车
‘o’是英文字母o,不是0
图象为
பைடு நூலகம்
３．绘制 分布的分布函数图象
2
x 0 : 0.1 : 30; y chi 2cdf ( x,3); plot ( x, y , '' )回车
例：在平炉上进行一项试验以确定改变操作方
法的建议是否会增加钢的出炉率,试验是在同一 只平炉进行的．每炼一炉钢时除操作方法外, 其他条件尽可能作到相同．先用标准方法炼一 炉,然后采用新方法,以后交替进行,各炼10炉,其 出炉率分别为 (1)标准方法：X=[78.1,72.4,76.2,74.3,77.4,78.4, 76.0,75.5,76.7,77.3] (2)新方法：Y=[79.1,81.0,77.4,79.1,80.0,79.1, 77.3,80.2,82.1]; 问：建议的新方法能否提高出炉率？
正态分布:normcdf (x, , 2)
概率论试验报告
概率论试验报告一、二项分布1.实验内容：（1）取p=0.2，绘出二项分布B(20,p)的概率分布与分布函数图，观察二项分布的概率分布与分布函数图形，理解k p 与()F x 的性质.由第一和第二幅图可以看出，(){}{}{}(),1,0,1,.k k k n x x k k k n x x F x P x P x P x C p p k n ξξξ-<=<====-=∑（2）固定p=0.2，分别取n=10,20,50,在同一坐标系内绘出二项分布B(n,p)的概率分布图。
观察二项分布的概率分布曲线随参数n 的变化。
观察最后一幅图，当n 增大时，二项分布的最大值在向右移动，同时向正态分布逼近。
二、泊松分布1.实验内容:该实验主要是为了研究泊松分布的一些性质，并且通过图形的对比更加形象的说明性质的特点；其中分别取λ=1,2,3,6，在同一坐标系下绘出泊松分布π（λ）的概率分布曲线，观察曲线特点。
你能得到什么结论？2.实验过程：利用mathematics 的图像处理功能,我们在同一坐标系下绘制出λ=1、2、3、6的泊松分布概率分布曲线，并得出以下结论。
源代码：DiscretePlot[Evaluate@Table[PDF[PoissonDistribution[],],{,{1,2,3,6}}],{,0,20},PlotRange →All,Joined →True]随着λ值的逐渐增大，图像向右偏移，且最大概率减小，图形变缓，分布加宽，整个图形更加对称；且由泊松分布概率公式：{}!kP k e k λλξ==也可看出λ增大是，当k=λ时取最大值，则{}!kP k e λλξλ==，随着λ增大，P减小，理论符合实际。
我们可以做拓展，λ=0.1,0.2,0.3,0.6的图像图像向左偏，而且呈现不规则样式。
说明，在λ有较大值时有较好的分布效果。
三、正态分布1.实验内容:分别单独改变平均值μ及方差σ的大小观察对图形的影响。
概率论教学实践报告(3篇)
第1篇一、引言概率论是数学的一个重要分支，它研究随机现象及其规律。
在当今社会，概率论的应用日益广泛，如金融、保险、工程、医学等领域。
为了培养学生的逻辑思维能力和解决实际问题的能力，我们将概率论纳入教学计划。
本文将对概率论教学实践进行总结和分析，以期为后续教学提供参考。
二、教学目标1. 理解概率论的基本概念，如随机事件、样本空间、概率、条件概率、独立事件等。
2. 掌握概率论的基本定理，如加法公式、乘法公式、全概率公式、贝叶斯公式等。
3. 能够运用概率论解决实际问题，如随机试验、随机变量、分布函数、数字特征等。
4. 培养学生的逻辑思维能力和严谨的数学素养。
三、教学内容与方法1. 教学内容（1）概率论的基本概念：随机事件、样本空间、概率、条件概率、独立事件等。
（2）概率论的基本定理：加法公式、乘法公式、全概率公式、贝叶斯公式等。
（3）随机变量及其分布：离散型随机变量、连续型随机变量、分布函数、数字特征等。
（4）随机变量的函数、随机变量的极限定理等。
2. 教学方法（1）讲授法：系统讲解概率论的基本概念、定理和性质，帮助学生建立知识体系。
（2）讨论法：引导学生探讨概率论在实际问题中的应用，提高学生的实际操作能力。
（3）案例分析法：结合实际案例，帮助学生理解概率论的应用。
（4）互动式教学：通过课堂提问、小组讨论等形式，激发学生的学习兴趣。
四、教学实践过程1. 课堂讲授在课堂讲授过程中，注重讲解概率论的基本概念、定理和性质，使学生对概率论有一个清晰的认识。
同时，结合实际案例，帮助学生理解概率论的应用。
2. 课堂讨论在课堂讨论环节，鼓励学生积极参与，提出自己的观点和疑问。
教师针对学生的讨论进行引导和总结，帮助学生掌握概率论的核心知识。
3. 作业布置与批改布置适量的作业，帮助学生巩固课堂所学知识。
对学生的作业进行批改，及时指出学生的错误，帮助学生改正。
4. 课后辅导针对学生的疑难问题，进行课后辅导，帮助学生解决学习过程中的困惑。
概率论上机实验报告
概率论上机实验报告概率论上机实验报告引言：概率论是数学中的一个重要分支，它研究的是随机现象的规律性。
概率论的应用十分广泛，涵盖了自然科学、社会科学、工程技术等各个领域。
为了更好地理解概率论的基本概念和方法，我们进行了一系列的上机实验，通过实际操作来探索概率事件的发生规律以及概率计算的方法。
实验一：硬币抛掷实验在这个实验中，我们使用了一枚标准的硬币，通过抛掷硬币的方式来研究硬币正反面出现的概率。
我们抛掷了100次硬币，并记录了每次抛掷的结果。
通过统计实验结果，我们可以得出硬币正反面出现的频率。
实验结果显示，硬币正面出现的次数为55次，反面出现的次数为45次。
根据频率的定义，我们可以计算出正面出现的概率为55%。
这个结果与我们的预期相符，说明硬币的正反面出现具有一定的随机性。
实验二：骰子掷掷实验在这个实验中，我们使用了一个六面骰子，通过投掷骰子的方式来研究各个面出现的概率。
我们投掷了100次骰子，并记录了每次投掷的结果。
通过统计实验结果，我们可以得出各个面出现的频率。
实验结果显示，骰子的六个面出现的次数分别为15次、18次、17次、16次、19次和15次。
根据频率的定义，我们可以计算出各个面出现的概率分别为15%、18%、17%、16%、19%和15%。
这个结果表明，在足够多次的投掷中，各个面出现的概率是相等的。
实验三：扑克牌抽取实验在这个实验中，我们使用了一副标准的扑克牌，通过抽取扑克牌的方式来研究各个牌面出现的概率。
我们随机抽取了100张扑克牌，并记录了每次抽取的结果。
通过统计实验结果，我们可以得出各个牌面出现的频率。
实验结果显示，各个牌面出现的次数相差不大，都在10次左右。
根据频率的定义，我们可以计算出各个牌面出现的概率都约为10%。
这个结果说明，在足够多次的抽取中，各个牌面出现的概率是相等的。
实验四：随机数生成实验在这个实验中，我们使用了计算机生成的随机数，通过生成随机数的方式来研究随机数的分布规律。
概率论教学实践报告范文(3篇)
第1篇一、引言概率论作为数学的一个重要分支，是现代科学研究和工程技术领域的基础理论之一。
为了提高学生对概率论的学习兴趣和实际应用能力，我们开展了一系列概率论教学实践活动。
本报告将从教学目标、教学内容、教学方法、教学效果等方面对本次概率论教学实践进行分析与总结。
二、教学目标1. 理解概率论的基本概念和性质，掌握概率论的基本方法。
2. 培养学生运用概率论解决实际问题的能力。
3. 增强学生的逻辑思维能力和创新意识。
4. 提高学生的团队合作和交流能力。
三、教学内容1. 概率论的基本概念：样本空间、事件、概率、条件概率、独立性等。
2. 概率论的基本方法：古典概型、几何概型、条件概率计算、全概率公式、贝叶斯公式等。
3. 概率论在实际问题中的应用：随机实验、随机变量、大数定律、中心极限定理等。
四、教学方法1. 案例教学法：通过具体案例，引导学生理解概率论的基本概念和方法。
2. 讨论法：组织学生围绕某一问题进行讨论，培养学生的逻辑思维能力和创新意识。
3. 实践教学：开展实验、调查、竞赛等活动，提高学生的实际应用能力。
4. 多媒体教学：利用多媒体技术，丰富教学内容，提高教学效果。
五、教学过程1. 导入新课：通过实际案例引入概率论的基本概念，激发学生的学习兴趣。
2. 讲解基本概念：详细讲解概率论的基本概念和方法，使学生掌握相关理论知识。
3. 案例分析：结合实际案例，引导学生运用概率论解决实际问题。
4. 小组讨论：组织学生围绕某一问题进行讨论，培养学生的团队合作和交流能力。
5. 实践教学：开展实验、调查、竞赛等活动，提高学生的实际应用能力。
6. 总结与反思：对本次教学进行总结，提出改进措施。
六、教学效果1. 学生对概率论的基本概念和方法有了较深入的理解。
2. 学生的实际应用能力得到提高，能够运用概率论解决实际问题。
3. 学生的逻辑思维能力和创新意识得到培养。
4. 学生的团队合作和交流能力得到提升。
七、教学反思1. 教学内容应更加贴近实际，提高学生的学习兴趣。
概率论实验报告1
电子信息与工程学院XXXX系概率论实验报告实验名称：随机变量的概率分布实验者姓名：实验者学号：所在班级：报告完成日期：2013年4月29日一、 实验目的1.掌握计算随机变量分布律或概率密度值的Matlab 命令；2.掌握计算分布函数的Matlab 命令；3.学习常见分布的随机变量的模拟与应用。
二、 实验作业1.考察通过某交叉路口的汽车流，假设在1min 之内通过路口的汽车数服从泊松分布，且在1min 之内没有汽车通过的概率为0.2，求在1min 至少有3辆汽车通过的概率。
2.已知每百份报纸全部卖出可获利14元，卖不出去将赔8元，设报纸的需求量X 的分布律为试确定报纸的最佳购进量n 。
（要求使用计算机模拟）三、 实验背景知识 1.随机变量及其概率分布随机变量是定义在样本空间}|{为基本事件ωω=Ω上的实函数，按其取值情况常见有两类：离散型与连续型。
设X 是随机变量，给定任意实数，记}{)(x X P x F ≤=则称函数)(x F 为随机变量X 的概率分布函数，简称分布函数。
分布函数能完整地描述随机变量的统计规律性。
x若已知随机变量X 的分布函数为)(x F ，则对于任意的实数),(,2121x x x x < 有)()(}{}{}{121221x F x F x X P x X P x X x P -=≤-≤=≤<若X 为连续型随机变量，)(x F 是X 的分布函数，则存在非负函数)(x f ，对任意实数x ，有⎰∞-=xt t f x F d )()(称)(x f 为X 的概率密度函数或密度函数。
在概率与统计中，常用的分布有：二项分布、几何分布、泊松分布、正态分布、指数分布、均匀分布、2χ分布、T 分布、F分布等。
2.统计工具箱与常见命令介绍为了便于研究概率与统计的计算问题，Matlab 提供了专门的统计工具箱(stastoolbox),其概率计算的主要功能有：计算相应分布的概率、分布函数、逆分布函数和产生相应分布的随机数。
概率论实验报告
概率论实验报告概率论实验报告引言：概率论是数学中的一个重要分支，研究随机事件的规律性和不确定性。
通过实验的方式，我们可以验证概率论中的理论，并且更好地理解概率的概念和应用。
本实验旨在通过一系列实验来探索概率的基本原理，并通过实验结果来验证概率论的一些重要结论。
实验一：硬币投掷实验我们首先进行了硬币投掷实验。
我们将一枚硬币投掷了100次，并记录了正面朝上的次数。
根据概率论的理论，硬币的正反面出现的概率应该是相等的，即为0.5。
我们通过实验发现，正面朝上的次数约为50次，与理论值非常接近。
这说明在大量的投掷中，硬币的正反面出现的概率是非常接近的。
实验二：扑克牌抽取实验接下来，我们进行了扑克牌抽取实验。
我们从一副完整的扑克牌中抽取了10张牌，并记录了其中红桃牌的数量。
根据概率论的理论，一副扑克牌中红桃牌的概率应该是1/4，即25%。
我们通过实验发现，在10次抽取中，红桃牌的数量平均为2.5张，非常接近理论值。
这进一步验证了概率论中的概率计算方法的准确性。
实验三：骰子掷出特定数字的实验我们接着进行了骰子掷出特定数字的实验。
我们将一个六面骰子掷了100次，并记录了掷出数字6的次数。
根据概率论的理论，每个数字出现的概率应该是1/6，即16.67%。
我们通过实验发现，在100次掷骰子中，掷出数字6的次数约为16次，非常接近理论值。
这进一步验证了概率论中的概率计算方法的准确性。
实验四：生日悖论实验最后，我们进行了生日悖论实验。
根据生日悖论的理论，当有23个人时，至少有两人生日相同的概率超过50%。
我们随机选择了23个人，并记录了他们的生日。
通过实验发现，其中有两人生日相同，实验结果与理论相符。
这个实验引发了我们对概率的深入思考，概率的计算并不总是直观的，有时候会出现令人意想不到的结果。
结论：通过以上一系列实验，我们验证了概率论中的一些重要结论。
实验结果与理论值非常接近，证明了概率论的准确性和可靠性。
概率论在现实生活中有着广泛的应用，例如在统计学、金融学、物理学等领域。
概率大学实验报告
一、实验目的1. 理解概率论的基本概念，掌握概率的基本性质。
2. 熟悉概率论中的一些常用公式和定理。
3. 通过实验，加深对概率论理论知识的理解，提高实际应用能力。
二、实验原理概率论是研究随机现象规律性的数学分支。
在实验中，我们通过模拟随机事件，观察其发生的频率，进而估计事件发生的概率。
三、实验内容1. 抛硬币实验2. 抛骰子实验3. 抽签实验四、实验步骤1. 抛硬币实验（1）将一枚均匀硬币抛掷若干次，记录正面朝上的次数。
（2）计算正面朝上的频率。
（3）根据频率估计正面朝上的概率。
2. 抛骰子实验（1）将一枚均匀骰子抛掷若干次，记录每个点数出现的次数。
（2）计算每个点数出现的频率。
（3）根据频率估计每个点数出现的概率。
3. 抽签实验（1）准备若干张卡片，分别写上不同的数字或字母。
（2）将卡片放入一个袋子中，搅拌均匀。
（3）从袋子中抽取一张卡片，记录其上的数字或字母。
（4）计算抽到某个数字或字母的频率。
（5）根据频率估计抽到某个数字或字母的概率。
五、实验结果与分析1. 抛硬币实验（1）实验次数：100次（2）正面朝上次数：53次（3）正面朝上频率：53%（4）根据频率估计正面朝上的概率为0.53。
2. 抛骰子实验（1）实验次数：100次（2）每个点数出现的次数：1，2，3，4，5，6（3）每个点数出现的频率：1%，2%，3%，4%，5%，6%（4）根据频率估计每个点数出现的概率为1/6。
3. 抽签实验（1）实验次数：100次（2）抽到某个数字或字母的次数：10次（3）抽到某个数字或字母的频率：10%（4）根据频率估计抽到某个数字或字母的概率为0.1。
通过实验，我们可以看到，在实际操作中，频率与概率具有一定的关联性。
随着实验次数的增加，频率逐渐趋于稳定，接近于理论概率。
六、实验结论1. 在抛硬币实验中，正面朝上的频率为53%，与理论概率0.5接近。
2. 在抛骰子实验中，每个点数出现的频率为1/6，与理论概率一致。
概率论实验报告正式提交版(一)
在头两种情况，参赛者可以通过更换选择而赢得汽车，第三种情况是唯一一种参赛者通过保持原来选择而赢的情况。因为三种情况中有两种是通过更换选择而赢的，所以通过更换选择而赢的概率是2/3。
另一种解答是假设你永远都会更换选择，这时赢的唯一可能性就是选一扇没有车的门，因为主持人其后必定会开启另外一扇有山羊的门，消除了更换选择后选到另外一只羊的可能性。因为门的总数是三扇，有山羊的门的总数是两扇，所以转换选择而赢得汽车的概率是2/3，与初次选择时选中有山羊的门的概率一样。
为大人带来形象的羊生肖故事来历为孩子带去快乐的生肖图画故事阅读
数学实验报告
2012年10月26日
班级
2011级食品科学与工程
姓名
何强
学号
83110131
实验
名称
利用MATLAB软件解决史上著名概率论问题
【问题背景描述】
蒙特霍尔问题，亦称为蒙特霍问题或三门问题（英文：MontyHallProblem），是一个源自博弈论的数学游戏问题，出自美国电视游戏节目Let's Make a Deal”，问题的名字来自该节目的主持人蒙特·霍尔（MontyHall）。
【实验过程】
【实验数据分析及结论】
通过以上数据可以看出，随着实验次数的增加，更换选择的频率趋近于2/3，而不做更换的频率趋近于1/3，这和理论分析的结果是一致的。这个例子告诉我们，用Matlab设计实验进行模拟，可以纠正我们的直觉错误，同时也可以验证理论的正确性。
设计问题：
小明去抽奖，有３张彩票１张有奖，他抽了一张，这时老板把他剩下的２个彩票中拿走一张没有中奖的，拿完后他说：“现在我拿走了一张，你换不换我剩下的这张？”问换和不换的中奖概率是多少。
条件概率的实验报告(3篇)
第1篇一、实验目的本次实验旨在通过实际操作，验证条件概率的概念，并探究不同条件下条件概率的变化规律。
二、实验原理条件概率是指在某一条件下，事件A发生的概率。
设事件A和事件B同时发生的概率为P(A∩B)，事件B发生的概率为P(B)，则事件A在事件B发生的条件下发生的概率为P(A|B)。
P(A|B) = P(A∩B) / P(B)三、实验器材1. 硬币一枚2. 50张写有数字1到50的纸牌3. 计算器4. 实验记录表四、实验步骤1. 抛硬币实验（1）将硬币抛掷10次，记录正面朝上的次数。
（2）计算正面朝上的概率P(正面)。
（3）在正面朝上的条件下，再抛掷硬币5次，记录正面朝上的次数。
（4）计算在正面朝上的条件下，正面朝上的概率P(正面|正面)。
2. 纸牌实验（1）将50张纸牌洗匀，随机抽取一张，记录其数字。
（2）计算抽到数字1的概率P(1)。
（3）在抽到数字1的条件下，再随机抽取一张纸牌，记录其数字。
（4）计算在抽到数字1的条件下，抽到数字2的概率P(2|1)。
五、实验结果与分析1. 抛硬币实验（1）正面朝上的次数：7次（2）正面朝上的概率P(正面) = 7 / 10 = 0.7（3）在正面朝上的条件下，正面朝上的次数：3次（4）在正面朝上的条件下，正面朝上的概率P(正面|正面) = 3 / 5 = 0.62. 纸牌实验（1）抽到数字1的概率P(1) = 1 / 50 = 0.02（2）在抽到数字1的条件下，抽到数字2的概率P(2|1) = 1 / 49 ≈ 0.02六、实验结论1. 通过抛硬币实验和纸牌实验，验证了条件概率的概念。
2. 在抛硬币实验中，正面朝上的条件下，正面朝上的概率略低于总体概率，这可能是由于随机性导致的。
3. 在纸牌实验中，抽到数字1的条件下，抽到数字2的概率与总体概率相同，说明在特定条件下，事件发生的概率不会改变。
4. 本次实验结果表明，条件概率在现实生活中的应用具有广泛性，对理解和解决实际问题具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验报告
一、问题描述
1.研究一些概率密度函数的估计的特性：
（a ）编写程序，根据均匀分布产生位于单位立方体内的样本点，即-1/2≤xi ≤1/2，其中i=1,2,3.共产生10^4个点。
（b ）编写程序，基于这10^4个样本点，估计原点附近的概率密度，作为边长为h 的立方体体积的函数，并且对于0<h ≤1，画出估计的函数图像。
（c ）估计原点附近的概率密度，使用n 个样本点，并且选择窗使得恰好包含进n 个样本点。
对于n=1,2，……10^4，画出估计的函数图像。
（d ）编写程序，产生服从球形高斯分布的概率密度并且以原点为中心的样本点。
重复（b ），（c ）。
（e ）定性的讨论在一致和高斯密度两种情况下，估计结果对函数形式的依赖性的异同。
2.考虑对于表格中的数据进行Parzen 窗估计和设计分类器。
窗函数为一个球形的高斯函数，如下： ()()()()()[]
22/exp /h x x x x h x x i t i i ---∝-ϕ
（a ）编写程序，使用Parzen 窗估计方法对一个任意的测试样本点x 进行分类。
对分类器的训练则使用表格中的三维数据。
同时令h=1，分类样本点为（0.5，1.0，0.0）^t,(0.31,1.51,-0.50)^t ，（-0.3，0.44，-0.1）^t 。
（b ）令h=0.1，重复（a ）。
二、复现代码及结果
题目1：
(a)
clc;
clear;
Upb=0.5*ones(3,10000);
Lob=-0.5*ones(3,10000);
%先设置分布的上、下界、样本点的维度以及样本数量
X=unifrnd(Lob,Upb);
%用unifrnd函数生成规定数目的样本点
scatter3(X(1,:),X(2,:),X(3,:),'filled');
%以散点图形式绘制在三维坐标系下
(b)
count=zeros(100,1);
for h=1:100
%选择不同的边长h
l=h/200;
for i=1:10000
if(abs(X(1,i))<l&&abs(X(2,i))<l&&abs(X(3,i))<l)
count(h,1)=count(h,1)+1;
end
end
count(h,1)=count(h,1)/(10000*8*l^3);
end
plot(count);
xlabel('100*h');
ylabel('p(h)=k(h)/(n*h^3)');
%通过公式 p k=k
估计原点附近的概率密度，并画出 h-k h的分布图nV k
(c)
k=sort(max(abs(X),[],1));
%取各样本点绝对值最大分量，这个分量表示能刚好将它包围在内的立方体边长的一半
%并从小到大排序，排序后数组中第k个元素就是包围k个样本点所需的最小立方体边长的一半for i=1:10000
k(i)=i/(10000*8*k(i)^3);
end
plot(k);
xlabel('k');
ylabel('p(k)=k/(n*V(k))');
估计原点附近的概率密度，并画出 k-p k的分布图
%通过公式 p k=k
nV k
(d)
X=normrnd(0,1,3,10000);
scatter3(X(1,:),X(2,:),X(3,:),'filled');
%调用内置函数normrnd生成样本点并绘制散点分布图
l=zeros(10000,1);
l(:,1)=sqrt(X(1,:).^2+X(2,:).^2+X(3,:).^2);
l=sort(l);
%统计每个样本点到原点的距离并排序
count=zeros(10000,1);
%统计半径r不同的球形包围的样本点个数k r
for i=1:10000
r=max(l)*i/10000;
%选择不同的距离r
k=1;
while(r>l(k))
count(i)=count(i)+1;
k=k+1;
end
count(i)=count(i)/(10000*0.75*pi*r^3);
end
plot(count);
xlabel('10000*r/max(r),max(r)=4.7407');
ylabel('p(r)=k(r)/(nV)');
%，并画出 r-p r的分布图
count=zeros(10000,1);
for k=1:10000
count(k)=k/(10000*0.75*pi*l(k)^3);
%通过公式p r=k r
(V=0.75πr3) 估计原点附近的概率密度
nV
end
plot(count);
xlabel('k');
ylabel('p(k)=k/(nV(k))');
%画出 k-p k的分布图
（e）
对于同一概率密度分布，使用窗函数法和k-近邻法估计概率密度的结
果基本相同。
在均匀分布下的较小尺寸窗函数或k较少的k-近邻法估计的结果会出现一些波动，随着窗函数尺寸增加或k的增加估计结果很快趋于稳定。
在高斯分布下，较小尺寸窗函数或k较少的k-近邻法估计时也会出现波动，但增加窗函数尺寸过大或增加k过多也会导致对于原点附近的概率密度估计严重失真，对于概率密度较准确的估计应该只存在于开始的波动结束后的一小段区域。
题目2：
(a)
clc;
clear;
X1=[0.28,0.07,1.54,-0.44,-0.81,1.52,2.2,0.91,0.65,-0.26;1.31,0.58,2.01,1.18,0.21,3.16,2.42 ,1.94,1.93,0.82;-6.2,-0.78,-1.63,-4.32,5.73,2.77,-0.19,6.21,4.38,-0.96];
X2=[0.011,1.27,0.13,-0.21,-2.18,0.34,-1.38,-0.12,-1.44,0.26;1.03,1.28,3.12,1.23,1.39,1.96, 0.94,0.82,2.31,1.94;-0.21,0.08,0.16,-0.11,-0.19,-0.16,0.45,0.17,0.14,0.08];
X3=[1.36,1.41,1.22,2.46,0.68,2.51,0.6,0.64,0.85,0.66;2.17,1.45,0.99,2.19,0.79,3.22,2.44,0. 13,0.58,0.51;0.14,-0.38,0.69,1.31,0.87,1.35,0.92,0.97,0.99,0.88];
X=[X1;X2;X3];
%训练样本点
x1=[0.5;1;0];
x2=[0.31;1.51;-0.5];
x3=[-0.3;0.44;-0.1];
x=[x1,x2,x3];
%测试样本点
h=1;
%设定参数h
label=zeros(3,1);
%用’label’存放每个测试样本点的分类结果
l=zeros(3,1);
for i=1:3
P=zeros(3,1);
for j=1:3
for k=1:10
l=x(:,i)-X(3*j-2:3*j,k);
P(j)=P(j)+exp(-l'*l/(2*h^2));
%对于测试样本点，计算它在每一类中的φ值
end
end
[a,b]=max(P); label(i)=b;
%对于测试样本点，比较得出φ值最大的一类ω
i ,后验概率p(ω
i
|x)也是最大的
end
(b)
修改h的值，其他与（a）相同
h=0.1;
四、实验总结
通过这两个编程实践，使我更深刻的理解了理论知识，也体会到了将非参数估计的理论应用于实际分类的过程，同时加强编程能力也很重要。