中考数学 热点专题六图形与证明
中考数学几何模型专题专题六—勾股定理
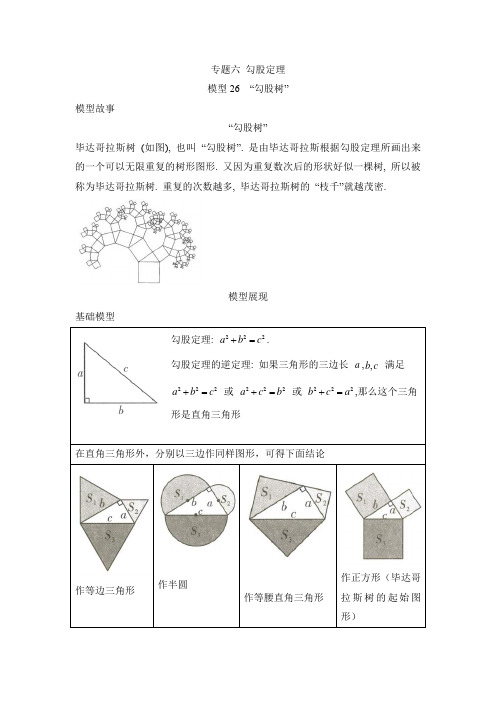
专题六勾股定理模型26 “勾股树”模型故事“勾股树”毕达哥拉斯树(如图), 也叫“勾股树”. 是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形. 又因为重复数次后的形状好似一棵树, 所以被称为毕达哥拉斯树. 重复的次数越多, 毕达哥拉斯树的“枝千”就越茂密.模型展现基础模型勾股定理: 222a b c+=.勾股定理的逆定理: 如果三角形的三边长a,,b c满足222a b c+=或222a c b+=或222b c a+=,那么这个三角形是直角三角形在直角三角形外,分别以三边作同样图形,可得下面结论作等边三角形作半圆作等腰直角三角形作正方形(毕达哥拉斯树的起始图形)怎么用?1. 找模型分别以直角三角形三边为边作相同图形2. 用模型根据勾股定理的关系及等式性质求解, 常用来解决面积问题结论分析:结论: 123S S S +=以作等边三角形为例.证明: 如解图, 过点 D 作 DM AC ⊥ 于点 M ,ACD 是等边三角形, 12AM MC b ∴==, 在 Rt ADM 中, 3tan tan602DM AM DAC AM b ∠=⋅=⋅=, 2111332224S DM AC b b b ∴=⋅⋅=⋅⋅=, 同理可得, 222333,44S a S c ==, ()222212333444S S a b a b ∴+=+=+, Rt ABC 满足 222a b c +=,()222123344S S a b c ∴+=+=.123.S S S ∴+=拓展延伸其余图形的证明, 均是用面积的计算, 然后求和即可, 同学们可以参考给出的证明过程, 自行完成.满分技法以三边分别为边作相同的图形, 解题的基本思想是勾股定理, 但所作图形的性质也是解题的关键.勾股数中常见图形面积公式:1 ;2S =⨯⨯三角形底高2 S =等边三角形边长; 21;2360n r S π=⨯半圆 2 S =正方形边长典例小试例 1 如图,和 AC 为直径的半圆的面积(与模型的作图方法一致), 则123,S S S 和满足的关系式(求面积,可使用结论)为( )A . 123S S S +=B . 123S S S =+C . 123S S S >+D . 123S S S =⋅考什么?圆的面积计算,勾股定理思路点拨满足模型,选填项目中,可直接使用结论,高效解题。
中考数学复习·图形的相似+相似三角形专题(位似、相似、相似三角形证明及应用)名校名师全解全练精品课件

A.12.36 cm C.32.36 cm
5-1 【解析】∵黄金比为 ≈0.618 , ∴ 它 的 宽 约 为 2 0.618×20≈12.36 cm.
【答案】A
上一页
下一页
宇轩图书
考
点
训
a
练
首页
2 . (2010 中考变式题 )已知 = = ,且 a + b+ c≠0 ,则 2 5 7 2a+3b-2c 的值为( a+b+c 5 A. 14 )
的周长与五边形 A′B′C′D′E′的周长的比值为
上一页
下一页
宇轩图书
中考典例精析
(2011·河北)如图所示,在6×8网格图中,每 个小正方形边长均为1.点O和△ABC的顶点均为小正方形
首页
的顶点.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和 △ABC位似,且位似比为1∶2. (2)连接(1)中的AA′,求四边形AA′C′C的周长.(结果保留根号) 【点拨】位似图形一定是相似图形,可以利用相似图形的性质计算或 证明. 【 解 答 】 (1) 如 图 所 示. (2)AA′ =CC′ = 2. 在
目录
第六章 图形的相似与解直角三角形 第23讲 图形的相似与位似
考点知识精讲
中考典例精析
举一反三
考点训练
宇轩图书
考点知识精讲
考点一 成比例线段与比例的定义及性质
首页
1.对于四条线段 a、b、c、d,如果 做成比例线段,简称比例线段.
那么这四条线段叫
2.表示两个比相等的式子叫做比例式,简称比例. 3.连比:连在一起的三个数的比,叫做连比. a c 4.比例的基本性质:如果 = ,那么 ad=bc ,反之也成立.其中 b d a b a 与 d 叫做比例外项,b 与 c 叫做比例内项.特殊地 = ⇔b2=ac. b c
初三数学图形的认识、图形与证明知识精讲 北师大版

初三数学图形的认识、图形与证明知识精讲一. 本周教学内容:图形的认识、图形与证明(三)相似三角形二. 教学目标:通过对相似三角形基础知识的复习,解决中考中常见的问题三. 教学重点、难点:熟练地解决与相似三角形相关的问题四. 课堂教学:中考导航⎪⎩⎪⎨⎧黄金分割比例的性质成比例线段比例线段⎩⎨⎧相似三角形判定相似三角形性质相似三角形中考课程标准要求考点考纲要求 了解 理解 掌握 灵活应用 概念√ 性质 √ 比例线段黄金分割 √ 了解概念√ 相似三角形的判定 √ 射影定理 √ 相似三角形相似三角形的性质√ 位似图形位似√例1. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC 相似的是( )答案:B例2. 如图,在矩形ABCD 中,AB=3,AD=4,P 是AD 上的动点,PE ⊥AC 于E ,PF ⊥BD 于F ,则PE +PF 的值为( )A.512 B. 2 C.25D.513答案:A例 3. 某装饰公司要在如图所示的五角星形中,沿边每隔20厘米装一盏闪光灯。
若)15(BC -=米,则需安装闪光灯( )A. 100盏B. 101盏C. 102盏D. 103盏答案:A例4. △ABC 中,AD 是BC 边上的中线,F 是AD 上的一点,且AF :FD=1:5,连接CF ,并延长交AB 于点E ,则AE :EB 等于( )A. 1:8B. 1:6C. 1:9D. 1:10答案:D例5. (1)如图1所示,已知△ABC 中,AB>AC ,试用直尺(不带刻度)和圆规在图1中过点A 作一条直线l ,使点C 关于直线l 的对称点在边AB 上(不要求写作法,也不必说明理由,但要保留作图痕迹。
)图1(2)如图2所示,已知格点△ABC,请在图2中分别画出与△ABC相似的格点△A1B1C1和格点△A2B2C2,并使△A1B1C1与△ABC的相似比等于2,而△A2B2C2与△ABC的相似比等于5。
(最新)2020年中考数学复习 专题6 四边形与三角形的综合(精讲)试题

专题六四边形与三角形的综合毕节中考备考攻略纵观近4年毕节中考数学试卷,四边形与三角形的综合是每年的必考考点,其中2015年第24题综合考查平行四边形和直角三角形;2016年第25题综合考查菱形和三角形全等;2017年第24题综合考查平行四边形与三角形相似、解直角三角形;2018年第24题综合考查平行四边形、三角形和菱形.预计2019年将继续综合考查四边形与三角形.熟练掌握特殊四边形的性质与判定、特殊三角形的性质、全等三角形的判定与性质、相似三角形的判定与性质,掌握三角形中位线和梯形中位线性质的推导和应用,会画出四边形全等变换后的图形.解决问题时必须充分利用几何图形的性质及在题设的基础上挖掘几何图形中隐含的数量关系和位置关系,在复杂的“背景”下辨认、分解基本图形,通过添加辅助线补全或构造基本图形,并善于联想所学知识,突破思维障碍,合理运用各种数学方法.中考重难点突破四边形与特殊三角形例1 如图,在四边形ABCD 中,AB ∥DC,AB =AD,对角线AC,BD 交于点O,AC 平分∠BAD ,过点C 作CE⊥AB 交AB 的延长线于点E,连接OE.(1)求证:四边形ABCD 是菱形; (2)若AB =5,BD =2,求OE 的长.【解析】(1)先判断出∠OAB=∠DCA,进而判断出∠DAC=∠DCA ,得出CD =AD =AB,即可得出结论; (2)先判断出OE =OA =OC,再求出OB =1,利用勾股定理求出OA,即可得出结果. 【答案】(1)证明:∵AB∥CD ,∴∠CAB =∠ACD. ∵AC 平分∠BAD ,∴∠CAB =∠CAD , ∴∠CAD =∠ACD ,∴AD =CD. 又∵AD=AB,∴AB =CD.又∵AB∥CD ,∴四边形ABCD 是平行四边形. 又∵AB=AD,∴四边形ABCD 是菱形; (2)解:∵四边形ABCD 是菱形,∴AC ⊥BD,OA =OC =12AC,OB =OD =12BD =1.在Rt △AOB 中,∠AOB =90°,∴OA =AB 2-OB 2=2. ∵CE ⊥AB,∴∠AEC =90°. 在Rt △AEC 中,O 为AC 中点, ∴OE =12AC =OA =2.四边形与三角形全等例2 (2018·张家界中考)在矩形ABCD 中,点E 在BC 上,AE =AD,DF ⊥AE,垂足为点F. (1)求证:DF =AB ;(2)若∠FDC=30°,且AB =4,求AD.【解析】(1)利用“AAS ”证△ADF≌△EAB 即可得证;(2)由∠ADF+∠FDC=90°,∠DAF +∠ADF=90°得∠FDC=∠DAF=30°,据此知AD =2DF,根据DF =AB 可得答案.【答案】(1)证明:在矩形ABCD 中,AD ∥BC, ∴∠AEB =∠DAF.又∵DF⊥AE ,∴∠DFA =90°,∴∠DFA =∠B. 又∵AD=EA,∴△ADF ≌△EAB,∴DF =AB ;(2)解:∵∠ADF+∠FDC =90°,∠DAF +∠ADF=90°,∴∠FDC =∠DAF=30°,∴AD =2DF.∵DF =AB =4,∴AD =2AB =8.四边形与三角形相似例3 (2018·资阳中考)已知:如图,在Rt △ABC 中,∠ACB =90°,点M 是斜边AB 的中点,MD ∥BC,且MD =CM,DE ⊥AB 于点E,连接AD,CD.(1)求证:△MED∽△BCA; (2)求证:△AMD≌△CMD;(3)设△MDE 的面积为S 1,四边形BCMD 的面积为S 2,当S 2=175S 1时,求cos ∠ABC 的值.【解析】(1)易证∠DME=∠CBA ,∠ACB =∠DE M =90°,从而可证明△MED∽△BCA;(2)由∠ACB=90°,点M 是斜边AB 的中点,可知BM =CM =AM,又由MD∥BC 可证明∠AMD=∠CMD ,从而可利用全等三角形的判定方法证明△AMD≌△CMD;(3)易证DM =12AB,由(1)可知△MED∽△BCA ,所以S 1S △ACB =⎝ ⎛⎭⎪⎫DM AB 2=14,所以S △MCB =12S △ACB =2S 1,从而可求出S △EBD =S 2-S △MCB -S 1=25S 1,由于S 1S △EBD =ME EB ,从而可知ME BE =52,设ME =5x,EB =2x,从而用x 表示出AB,BC,最后根据锐角三角函数的定义即可求出答案.【答案】(1)证明:∵MD∥BC ,∴∠DME =∠CBA. ∵∠ACB =∠DEM=90°,∴△MED ∽△BCA ; (2)证明:∵∠ACB=90°,点M 是斜边AB 的中点, ∴BM=CM =AM,∴∠MCB =∠MBC. ∵∠DMB =∠MBC , ∴∠MCB =∠DMB=∠MBC. ∵MD ∥BC,∴∠CMD =180°-∠MCB. 又∵∠AMD=180°-∠DMB , ∴∠AMD =∠CMD. 在△AMD 与△CMD 中, ⎩⎪⎨⎪⎧MD =MD ,∠AMD =∠CMD,AM =CM ,∴△AMD ≌△CMD(SAS );(3)解:∵DM=CM,∴AM =CM =DM =BM, ∴DM =12AB.由(1)可知△MED∽△BCA ,∴S 1S △ACB =⎝ ⎛⎭⎪⎫DM AB 2=14,∴S △ACB =4S 1. ∵CM 是△ACB 的中线,∴S △MCB =12S △ACB =2S 1,∴S △EBD =S 2-S △MCB -S 1=25S 1,∴S 1S △EBD =ME EB ,∴S 125S 1=ME EB ,∴ME EB =52. 设ME =5x,EB =2x,则BM =7x, ∴AB =2BM =14x. ∵MD AB =ME BC =12,∴BC =10x, ∴cos ∠ABC=BC AB =10x 14x =57.1.(2018·贺州中考)如图,在△ABC 中,∠ACB =90°,O,D 分别是边AC,AB 的中点,过点C 作CE ∥AB 交DO 的延长线于点E,连接AE.(1)求证:四边形AECD 是菱形;(2)若四边形AECD 的面积为24,tan ∠BAC =34,求BC 的长.(1)证明:∵点O 是AC 的中点,∴OA =OC.∵CE ∥AB,∴∠DAO =∠ECO. 又∵∠AOD=∠COE ,∴△AOD ≌△COE(ASA ),∴AD =CE, ∴四边形AECD 是平行四边形. 又∵CD 是Rt △ABC 斜边AB 上的中线, ∴CD =AD =12AB,∴四边形AECD 是菱形;(2)由(1)知,四边形AECD 是菱形,∴AC ⊥ED.在Rt △AOD 中,tan ∠DAO =OD OA =tan ∠BAC =34,可设OD =3x,OA =4x, 则ED =2OD =6x,AC =2OA =8x.由题意可得12·6x·8x=24,∴x =1,∴OD =3.∵O,D 分别是AC,AB 的中点, ∴OD 是△ABC 的中位线, ∴BC =2OD =6.2.(2018·盐城中考)在正方形ABCD 中,对角线BD 所在的直线上有两点E,F 满足BE =DF,连接AE,AF,CE,CF,如图.(1)求证:△AB E≌△ADF;(2)试判断四边形AECF 的形状,并说明理由. (1)证明:∵四边形ABCD 是正方形,∴AB =AD, ∴∠ABD =∠ADB ,∴∠ABE =∠ADF. 在△ABE 与△ADF 中,⎩⎪⎨⎪⎧AB =AD ,∠ABE =∠ADF,BE =DF ,∴△ABE ≌△ADF(SAS ); (2)解:四边形AECF 是菱形. 理由:连接AC,交BD 于点O. ∵四边形ABCD 是正方形, ∴OA =OC,OB =OD,AC ⊥EF, ∴OB +BE =OD +DF,即OE =OF. ∵OA =OC,OE =OF,∴四边形AECF 是平行四边形, 又∵AC⊥EF ,∴四边形AECF 是菱形.3.(2018·湖州中考) 已知在Rt △ABC 中,∠BAC =90°,AB ≥AC,D,E 分别为AC,BC 边上的点(不包括端点),且DC BE =ACBC=m,连接AE,过点D 作DM ⊥AE,垂足为点M,延长DM 交AB 于点F. (1)如图1,过点E 作EH⊥AB 于点H,连接DH.①求证:四边形DHEC 是平行四边形; ②若m =22,求证:AE =DF ; (2)如图2,若m =35,求DFAE的值.(1)证明:①∵EH⊥AB ,∠BAC =90°, ∴EH ∥CA,∴△BHE ∽△BAC,∴BE BC =HEAC .∵DC BE =AC BC ,∴BE BC =DC AC ,∴HE AC =DC AC, ∴HE =DC.∵EH ∥DC,∴四边形DHEC 是平行四边形; ②∵AC BC =22,∠BAC =90°,∴AC =AB.∵DC BE =22,HE =DC,∴HE BE =22. 又∵∠BHE=90°,∴BH =HE. ∵HE =DC,∴BH =CD,∴AH =AD. ∵DM ⊥AE,EH ⊥AB, ∴∠EHA =∠AMF=90°,∴∠HAE +∠HEA=∠HAE+∠AFM=90°, ∴∠HEA =∠AFD.∵∠EHA =∠FAD=90°,∴△HEA ≌△AFD,∴AE =DF ; (2)解:过点E 作EG⊥AB 于点G.∵CA ⊥AB,∴EG ∥CA,∴△EGB ∽△CAB, ∴EG CA =BE BC ,∴EG BE =CA BC =35. ∵CD BE =35,∴EG =CD. 设EG =CD =3x,AC =3y,则BE =5x,BC =5y, ∴BG =4x,AB =4y. ∵∠EGA =∠AMF=90°, ∴∠GEA +∠EAG=∠EAG+∠AFM ,∴∠AFM=∠AEG.∵∠FAD=∠EGA=90°,∴△FAD∽△EGA,∴DFAE=ADAG=3y-3x4y-4x=34.毕节中考专题过关 1.(2018·乌鲁木齐中考)如图,在四边形ABCD 中,∠BAC =90°,E 是BC 的中点,AD ∥BC,AE ∥DC,EF ⊥CD 于点F.(1)求证:四边形AECD 是菱形;(2)若AB =6,BC =10,求EF 的长.(1)证明:∵AD∥BC ,AE ∥DC,∴四边形AECD 是平行四边形.∵∠BAC =90°,E 是BC 的中点,∴AE =CE =12BC,∴四边形AECD 是菱形;(2)解:过A 作AH⊥BC 于点H.∵∠BAC =90°,AB =6,BC =10,∴AC =102-62=8.∵S △ABC =12BC·AH=12AB·AC ,∴AH =6×810=245.∵点E 是BC 的中点,BC =10,四边形AECD 是菱形,∴CD =CE =5.∵S ▱AECD =CE·A H =CD·EF ,∴EF =AH =245.2.(2018·青岛中考)已知:如图,▱ABCD 的对角线AC 与BD 相交于点E,点G 为AD 的中点,连接CG,CG 的延长线交BA 的延长线于点F,连接FD.(1)求证:AB =AF ;(2)若AG =AB,∠BCD =120°,判断四边形ACDF 的形状,并证明你的结论.(1)证明:∵四边形ABCD 是平行四边形,∴AB ∥CD,AB =CD,∴∠AFG =∠DCG.又∵GA=GD,∠AGF =∠CGD ,∴△AGF ≌△DGC,∴AF =CD.∴AB =AF ;(2)解:四边形ACDF 是矩形.证明:∵AF=CD,AF ∥CD,∴四边形ACDF 是平行四边形.∵四边形ABCD 是平行四边形,∴∠BAD =∠BCD=120°.∴∠FAG =60°.∵AB =AG =AF,∴△AFG 是等边三角形,∴AG =GF.∵四边形ACDF 是平行四边形,∴FG =CG,AG =DG.∴AD=CF.∴四边形ACDF 是矩形.3.已知:如图,四边形ABCD 中,AD ∥BC,AD =CD,E 是对角线BD 上一点,且EA =EC.(1)求证:四边形ABCD 是菱形;(2)如果BE =BC,且∠CBE∶∠BCE=2∶3,求证:四边形ABCD 是正方形.证明:(1)在△ADE 与△CDE 中,⎩⎪⎨⎪⎧AD =CD ,DE =DE ,EA =EC ,∴△ADE ≌△CDE,∴∠ADE =∠CDE.∵AD ∥BC,∴∠ADE =∠CBD ,∴∠CDE =∠CBD ,∴BC =CD.∵AD =CD,∴BC =AD,∴四边形ABCD 为平行四边形.∵AD =CD,∴四边形ABCD 是菱形;(2)∵BE=BC,∴∠BCE =∠BEC.∵∠CBE ∶∠BCE =2∶3,∴∠CBE =180×22+3+3=45°. ∵四边形ABCD 是菱形,∴∠ABE =∠CBE=45°,∴∠ABC =90°,∴四边形ABCD 是正方形.4.(2018·眉山中考)如图①,在四边形ABCD 中,AC ⊥BD 于点E,AB =AC =BD,点M 为BC 的中点,N 为线段AM 上的点,且MB =MN.(1)求证:BN 平分∠ABE;(2)若BD =1,连接DN,当四边形DNBC 为平行四边形时,求线段BC 的长;(3)如图②,若点F 为AB 的中点,连接FN,FM,求证:△MFN∽△BDC.(1)证明:∵AB=AC,∴∠ABC =∠ACB.∵M 为BC 的中点,∴AM ⊥BC.在Rt △ABM 中,∠MAB +∠ABC=90°.在Rt △CBE 中,∠EBC +∠ACB=90°,∴∠MAB =∠EBC.又∵MB =MN,∴△MBN 为等腰直角三角形,∴∠MNB =∠MBN=45°,∴∠EBC +∠NBE=45°,∠MAB +∠ABN=∠MNB=45°,∴∠NBE =∠ABN ,即BN 平分∠ABE;(2)解:设BM =CM =MN =a.当四边形DNBC 是平行四边形时,DN =BC =2a.在△ABN 和△DBN 中,⎩⎪⎨⎪⎧AB =DB ,∠NBD =∠NBA,BN =BN ,∴△ABN ≌△DBN(SAS ),∴AN =DN =2a.在Rt △ABM 中,由AM 2+BM 2=AB 2,得(2a +a)2+a 2=1,解得a =±1010(负值舍去),∴BC =2a =105;(3)证明:在Rt △MAB 中,F 是AB 的中点,∴MF =AF =BF,∴∠MAB =∠FMN.又∵∠MAB=∠CBD ,∴∠FMN =∠DBC. ∵MFAB =MNBC =12,∴MF BD =MN BC =12,∴△MFN ∽△BDC.5.(2018·枣庄中考)如图,将矩形ABCD 沿AF 折叠,使点D 落在BC 边的点E 处,过点E 作EG∥CD 交AF 于点G,连接DG.(1)求证:四边形EFDG 是菱形;(2)探究线段EG,GF,AF 之间的数量关系,并说明理由;(3)若AG =6,EG =25,求BE 的长.(1)证明:∵GE∥DF ,∴∠EGF =∠DFG.由翻折的性质可知DG =EG,DF =EF,∠DGF =∠EGF ,∴∠DGF =∠DFG ,∴DG =DF,∴DG =EG =DF =EF,∴四边形EFDG 是菱形;(2)解:EG 2=12GF·AF.理由:连接DE,交AF 于点O.∵四边形EFDG 是菱形,∴GF ⊥DE,OG =OF =12GF.∵∠DOF =∠ADF=90°,∠OFD =∠DFA , ∴△DOF ∽△ADF,∴DF AF =OF DF ,即DF 2=OF·AF.∵OF =12GF,DF =EG,∴EG 2=12GF·AF;(3)解:过点G 作GH⊥DC ,垂足为点H. ∵EG 2=12GF·AF ,AG =6,EG =25,即GF 2+6GF -40=0,解得GF =4,GF =-10(舍去).∵DF =EG =25,AF =AG +GF =10, ∴AD =AF 2-DF 2=4 5.∵GH ⊥DC,AD ⊥DC,∴GH ∥AD, ∴△FGH ∽△FAD,∴GH AD =GF AF ,即GH 45=410,∴GH =855.∴BE =AD -GH =45-855=1255.。
南昌市中考数学专题题型复习06:四边形有关的计算与证明

南昌市中考数学专题题型复习06:四边形有关的计算与证明姓名:________ 班级:________ 成绩:________一、解答题 (共12题;共71分)1. (10分)如图,已知AB=AC,AD=AE,BE与CD相交于O,求证:△ABE≌△ACD.2. (5分)(2017·绿园模拟) 如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC 的延长线于点E.若点F是AE的中点,求证:BF⊥AF.3. (5分)如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.(1)求∠ABC的度数;(2)如果AC=4,求DE的长.4. (6分) (2018八下·瑶海期中) 如图,将矩形ABCD(纸片)折叠,使点B与AD边上的点K重合,EG为折痕;点C与AD边上的点K重合,FH为折痕.已知∠1=67.5°,∠2=75°,EF= +1,求BC的长.5. (5分)如图,已知△ABC和直线m ,画出与△ABC关于直线m对称的图形(不要求写出画法,但应保留作图痕迹)6. (5分) (2020九上·岐山期末) 如图,在菱形ABCD中,点E是边AD上一点,延长AB至点F,使BF=AE,连接BE、CF求证:BE=CF。
7. (5分)在▱ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,求证:CH=EH.8. (5分)(2017·吴忠模拟) 如图,在正方形ABCD中,点E、F在对角线BD上,且BE=EF=FD,连接AF,AE,CE,CF,请你判断四边形AECF的形状,并证明你的结论.9. (10分) (2015八下·嵊州期中) 如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD 的两个顶点所形成的四边形是平行四边形?10. (5分)如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠C=45°,BC=4,AD=2.求四边形ABCD的面积.11. (5分)(2016·鄞州模拟) 如图,在平行四边形ABCD中,对角线AC,BD并于点O,经过点O的直线交AB于E,交CD于F.(1)求证:OE=OF.(2)连接DE,BF,则EF与BD满足什么条件时,四边形DEBF是矩形?请说明理由.12. (5分) (2016九上·长春期中) 如图,四边形OABC是平行四边形,点A,B,C在⊙O上,P为上一点,连接AP,CP,求∠P的度数.二、综合题 (共27题;共278分)13. (10分)(2018·沧州模拟) 如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:(1)求证:△BEF∽△DCB;(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;(4)当t为何值时,△PQF为等腰三角形?试说明理由.14. (10分)(2015·宁波模拟) 【试题背景】已知:l ∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1、d2、d3 ,且d1 =d3 = 1,d2 = 2 .我们把四个顶点分别在l、m、n、k这四条平行线上的四边形称为“格线四边形”.(1)【探究1】如图1,正方形ABCD为“格线四边形”,BE L于点E,BE的反向延长线交直线k于点F.求正方形ABCD的边长.(2)【探究2】矩形ABCD为“格线四边形”,其长:宽 = 2 :1 ,求矩形ABCD的宽(3)【探究3】如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形,于点E,∠AFD=90°,直线DF分别交直线l、k于点G、M.求证:EC=DF.(4)【拓展】如图3,l ∥k,等边三角形ABC的顶点A、B分别落在直线l、k上,于点B,且AB=4 ,∠ACD=90°,直线CD分别交直线l、k于点G、M,点D、E分别是线段GM、BM上的动点,且始终保持AD=AE,于点H.猜想:DH在什么范围内,BC∥DE?直接写出结论。
九年级数学中考复习专题六 图形与证明

中考复习专题六图形与证明【考点聚焦】图形与证明是空间与图形的核心内容之一,它贯穿在整个几何知识的学习及运用之中. 内容主要有:了解定义、命题、定理、互逆命题、反证法的含义;掌握平行线的性质定理和判定定理、全等三角形的性质定理和判定定理、直角三角形全等的判定定理;掌握三角形的内角和定理和推论、角平分线和垂直平分线性质定理及逆定理、三角形中位线定理;掌握等腰三角形、等边三角形、直角三角形性质与判定定理;掌握平行四边形、矩形、菱形、正方形、等腰梯形的性质和判定定理.【热点透视】热点1:把握三角形全等的性质,考查线段相等的证明.例1 (2008某某)如图1,菱形ABCD 中,E F ,分别为BC 、CD 上的点,且CE CF =.求证:AE AF =.分析:本题中灵活运用菱形的性质:四边相等,两组对角分别相等.找到全等三角形的对应元素是解本题的关键.证明:∵四边形ABCD 是菱形,∴AB BC CD AD ===,B D ∠=∠.∵CE CF =,∴BE DF =.在ABE △与ADF △中,AB AD =,B D ∠=∠,BE DF =.∴ABE ADF △≌△,∴AE AF =.点评:掌握全等三角形的概念和性质,还要能准确辨认全等三角形中的对应元素,通过证明全等来证明线段相等或者角相等.热点2:紧扣三角形全等的判定,考查三角形全等的开放型问题.例2(2008某某)如图2,在正五边形ABCDE 中,连结对角线AC 、AD 和CE ,AD 交CE 于F .(1)请列出图中两对全等三角形_________________(不另外添加辅助线);(2)请选择所列举的一对全等三角形加以证明.分析:由正多边形的性质可知:正多边形的各边相等,各角相等.这是一类结论不惟一的试题.解决此类问题的关键是依据图形,通过准确辨认全等三角形的对应元素,证明三角形全等.解:(1)△ABC ≌△AED ,△ABC ≌△EDC ;(2)证明:在正五边形ABCDE 中,AB BC CD DE EA ====,∠EAB =∠B =∠BCD =∠CDE =∠DEA ,故在△ABC 与△AED 中,AB =AE ,∠B =∠DEA ,BC =DE ,∴△ABC ≌△AED , 在△ABC 与△EDC 中,AB =ED ,∠B =∠CDE ,BC =DC ,∴△ABC ≌△EDC .点评:本考题题干简单清晰,但考点的内容与正多边形的知识相结合,需要具有分解基本图形的能力和基本的探究能力,才能顺利解题.热点3:合理添加辅助线,构造全等三角形解决相关问题.例3 (2008某某)如图3,已知AB AC =,(1)若CE BD =,求证:GE GD =;(2)若CE m BD =(m 为正数),试猜想GE 与GD 有何关系(只写结论,不证明).分析:证明在不同三角形中的两条线段和两个角相等的常用方法就是证明两个三角形全等,要证明线段GE 和GD 相等,在辨认三角形全等对应元素时,发现图中没有三角形全等,需要通过合理添加辅助线构造三角形全等.(1)证明:过D 作DF ∥CE ,交BC 于F ,∠E =∠GDF ,∵AB =AC ,DF ∥CE ,∴∠DFB =∠ACB =∠ABC ,∴DF =DB =EC .又∠DGF =∠EGC ,∴△GDF ≌△GEC .∴GE =GD .(2)GE m GD =.点评:在证明三角形全等时,可以通过翻折法、旋转法、平移法找到对应元素,或者合理添加辅助线构造全等三角形的对应元素.热点4:定义、命题、定理、互逆命题的考查.例4 (2008永州)下列命题是假命题的是( )(A)四个角相等的四边形是矩形(B)对角线互相平分的四边形是平行四边形(C)四条边相等的四边形是菱形(D)对角线互相垂直且相等的四边形是正方形分析:掌握平行四边形、矩形、菱形、正方形的判定方法是解决本题的关键. 解:选(D ).点评:本题考查同学们对平行四边形及特殊的平行四边形的判定方法的把握,遇到这种题,同学们可利用数形结合的思想将其中的文字语言转化为图形语言,便能迅速作出准确判断.热点5:平行四边形、矩形、菱形、正方形、等腰梯形的性质与判定的考查.例5(2008某某)如图5,已知点D 在ABC △的BC △边上,DE AC ∥交AB 于E ,DF AB ∥交AC 于F .(1)求证:AE DF =;(2)若AD 平分BAC ∠,试判断四边形AEDF 的形状,并说明理由.分析:本题主要考查同学们对平行四边形及特殊的平行四边形的判定方法的把握. 证明:(1)∵DE AC ∥,∴ADE DAF ∠=∠,同理DAE FDA ∠=∠.∵AD DA =,∴ADE DAF △≌△,∴AE DF =.(2)若AD 平分BAC ∠,四边形AEDF 是菱形.证明:∵DE AC ∥,DF AB ∥,∴四边形AEDF 是平行四边形,∵FAD EAD ∠=∠,∴AF DF =,∴平行四边形AEDF 为菱形.点评:三角形全等及平行四边形的性质都可以证明两线段相等,此类题起点低,注重基础知识及基本技能的考查,考查了同学们最基本的几何推理证明能力.热点6:圆的有关概念及性质的考查例6(2008某某)如图6,AB 是O 的直径,C 是O 上一点,过圆心O 作OD AC ⊥,D 为垂足,E 是BC 上一点,G 是DE 的中点,OG 的延长线交BC 于F .(1)图中线段OD 、BC 所在直线有怎样的位置关系?写出你的结论,并给出证明过程;(2)猜想线段BE EF FC ,,三者之间有怎样的数量关系?写出你的结论,并给出证明过程.分析:平面内两直线的位置关系只有平行和相交两种,先通过观察图形可猜想OD ∥BC ,再利用圆的有关概念及性质得证.解:(1)结论:OD BC ∥.证明:∵AB 是O 的直径,C 是O 上一点,∴90ACB ∠=,即BC ⊥AC .又OD ⊥AC ,∴OD ∥BC .(2)结论:EF BE FC =+.证明:∵OD ⊥AC ,∴AD =DC .又O 为AB 的中点,∴OD 是△ABC 的中位线.∴BC =2OD .在△ODG 与△EFG 中,∵DG =EG ,∠GOD =∠GFE ,∠ODG =∠FEG ,∴ODG FEG △≌△.∴OD =EF .∴22BE EF FC BC OD EF ++===.∴EF BE FC =+.点评:为了使同学们对推理论证的必要性有更深刻的理解,新课程中的逻辑推理常在探究、猜想的前提下进行.本题就采用了这种方式.该题主要考查了直径与圆周角、垂直于弦的直径等概念之间的联系.【考题预测】1.下列命题中真命题的个数是( )①两个相似多边形面积之比等于相似比的平方;②两个相似三角形的对应高之比等于它们的相似比;③在ABC △与A B C '''△中,AB AC A B A C ='''',A A '∠=∠,那么ABC A B C '''△∽△;④已知ABC △及位似中心O ,能够作一个且只能作一个三角形,使位似比为. (A)1个 (B)2个 (C)3个 (D)4个2.已知如图7,在四边形ABCD 中,对角线AC ,BD 交于点E ,且AC 平分∠DAB ,AB =AE ,AC =AD .下四个结论:①AC ⊥BD ;②CB =DE ;③12DBC DAB ∠=∠;④△ABE 是等边三角形.请写出正确的结论序号____________(把你认为正确的结论序号填上,并证明其中一个).3.如图8,菱形ABCD 中,E 、F 分别为CB 、CD 延长线上的点,且CE CF =.求证:AE AF =.4.如图9,在Rt △ABC 中,90ACB ∠=,2AB AC =,DE 垂直平分BC ,垂足为D ,交AB 于点E .又点F 在DE 的延长线上,且2EF DE =.求证:四边形ACEF 是菱形.5.如图10,D 是ABC △边AB 上一点,DE 交AC 于点E ,DE EF =,FC AB ∥. 求证:AE CE =.6.如图11,已知AC 切O 于A ,CB 顺次交O 于D B ,两点,6AC =,5BD =,连结AD ,AB .(1)求证:CAD CBA △∽△;(2)求线段DC 的长.7.如图12,ABC △是O 的内接三角形,AC BC =,D 为O 中上一点,延长DA 至点E ,使CE CD =.(1)求证:AE BD =;(2)若AC BC ⊥,求证:AD BD CD +=.8.如图13,已知:C 是以AB 为直径的半圆O 上一点,CH ⊥AB 于点H ,直线AC 与过B 点的切线相交于点D ,E 为CH 中点,连结AE 并延长交BD 于点F ,直线CF 交AB 的延长线于点G .(1)求证:点F 是BD 中点;(2)求证:CG 是O 的切线;(3)若2FB FE ==,求O 的半径.。
2012中考分类-图形与证明

(广州)在平面中,下列命题为真命题的是( )。
(A )、四边相等的四边形是正方形(B )、对角线相等的四边形是菱形(C )、四个角相等的四边形是矩形(D )、对角线互相垂直的四边形是平行四边形解析:此题主要考查命题的真假判断,比较简单,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理A 、四边相等的四边形不一定是正方形,例如菱形,故此选项错误;B 、对角线相等的四边形不是菱形,例如矩形,等腰梯形,故此选项错误;C 、四个角相等的四边形是矩形,故此选项正确;D 、对角线互相垂直的四边形不一定是平行四边形,如右图所示,故此选项错误.故选C .黄冈 下列说法中 ①若式子有意义,则x >1.②已知∠α=27°,则∠α的补角是153°.③已知x=2 是方程x 2-6x+c=0 的一个实数根,则c 的值为8. ④在反比例函数中,若x >0 时,y 随x 的增大而增大,则k 的取值范围是k >2. 其中正确命题有A. 1 个B. 2 个C. 3 个D. 4 个深圳 下列命题:①方程x 2=x 的解是x =1②4的平方根是2③有两边和一角相等的两个三角形全等④连接任意四边形各边中点的四边形是平行四边形其中真命题有( )A .4个B .3个C .2个D .1个解:①方程x2=x 的解是x1=0,x2=1,故错误;②4的平方根是±2,故错误;③有两边和夹角相等的两个三角形全等,故错误;④连接任意四边形各边中点的四边形是平行四边形,正确.故正确的个数有1个.故选D .凉山 下列命题:①圆周角等于圆心角的一半;②2x =是方程11x -=的解;③平行四边形既是中心对称图形又是周对称图形;④4。
其中真命题的个数有( )A .1B .2C .3D .4乐山 下列命题是假命题的是C(A )平行四边形的对边相等 (B )四条边都相等的四边形是菱形(C )矩形的两条对角线互相垂直 (D )等腰梯形的两条对角线相等如图4,在△ABC 中,∠C =90º,AC =BC =4,D 是AB 的中点,点E 、F 分别在AC 、BC 边上运动(点E 不与点A 、C 重合),且保持AE =CF ,连接DE 、DF 、EF . 在此运动变化的过程中,有下列结论:① △DFE 是等腰直角三角形;② 四边形CEDF 不可能为正方形;③ 四边形CEDF 的面积随点E 位置的改变而发生变化; ④ 点C 到线段EF其中正确结论的个数是B(A )1个 (B )2个 (C )3个 (D )4个呼和浩特D资阳 如图,△ABC 是等腰三角形,点D 是底边BC 上异于BC 中点的一个点,∠ADE =∠DAC ,DE =AC .运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题?A .一组对边平行,另一组对边相等的四边形是平行四边形B .有一组对边平行的四边形是梯形C .一组对边相等,一组对角相等的四边形是平行四边形D .对角线相等的四边形是矩形梅州 如图,AC 是⊙O 的直径,弦BD 交AC 于点E 。
中考数学图形与证明热点专题

热点专题六 图形与证明【考点聚焦】图形与证明是空间与图形的核心内容之一,它贯穿在整个几何知识的学习及运用之中. 内容主要有:了解定义、命题、定理、互逆命题、反证法的含义;掌握平行线的性质定理和判定定理、全等三角形的性质定理和判定定理、直角三角形全等的判定定理;掌握三角形的内角和定理和推论、角平分线和垂直平分线性质定理及逆定理、三角形中位线定理;掌握等腰三角形、等边三角形、直角三角形性质与判定定理;掌握平行四边形、矩形、菱形、正方形、等腰梯形的性质和判定定理.【热点透视】热点1:把握三角形全等的性质,考查线段相等的证明.例1 (2008郴州)如图1,菱形ABCD 中,E F ,分别为BC 、CD 上的点,且CE CF =.求证:AE AF =.分析:本题中灵活运用菱形的性质:四边相等,两组对角分别相等.找到全等三角形的对应元素是解本题的关键.证明:∵四边形ABCD 是菱形,∴AB BC CD AD ===,B D ∠=∠.∵CE CF =,∴BE DF =.在ABE △与ADF △中,AB AD =,B D ∠=∠,BE DF =.∴ABE ADF △≌△,∴AE AF =.点评:掌握全等三角形的概念和性质,还要能准确辨认全等三角形中的对应元素,通过证明全等来证明线段相等或者角相等.热点2:紧扣三角形全等的判定,考查三角形全等的开放型问题.例2 (2008湘潭)如图2,在正五边形ABCDE 中,连结对角线AC 、AD 和CE ,AD 交CE 于F .(1)请列出图中两对全等三角形_________________(不另外添加辅助线);(2)请选择所列举的一对全等三角形加以证明.分析:由正多边形的性质可知:正多边形的各边相等,各角相等.这是一类结论不惟一的试题.解决此类问题的关键是依据图形,通过准确辨认全等三角形的对应元素,证明三角形全等.解:(1)△ABC ≌△AED ,△ABC ≌△EDC ;(2)证明:在正五边形ABCDE 中,AB BC CD DE EA ====,∠EAB =∠B =∠BCD =∠CDE =∠DEA ,故在△ABC 与△AED 中,AB =AE ,∠B =∠DEA ,BC =DE ,∴△ABC ≌△AED , 在△ABC 与△EDC 中,AB =ED ,∠B =∠CDE ,BC =DC ,∴△ABC ≌△EDC .点评:本考题题干简单清晰,但考点的内容与正多边形的知识相结合,需要具有分解基本图形的能力和基本的探究能力,才能顺利解题.热点3:合理添加辅助线,构造全等三角形解决相关问题.例3 (2008常德)如图3,已知AB AC =,(1)若CE BD =,求证:GE GD =;(2)若C E m B D =(m 为正数),试猜想GE 与GD 有何关系(只写结论,不证明).分析:证明在不同三角形中的两条线段和两个角相等的常用方法就是证明两个三角形全等,要证明线段GE 和GD 相等,在辨认三角形全等对应元素时,发现图中没有三角形全等,需要通过合理添加辅助线构造三角形全等.(1)证明:过D 作DF ∥CE ,交BC 于F ,∠E =∠GDF ,∵AB =AC ,DF ∥CE ,∴∠DFB =∠ACB =∠ABC ,∴DF =DB =EC .又∠DGF =∠EGC ,∴△GDF ≌△GEC .∴GE =GD .(2)GE m GD =.点评:在证明三角形全等时,可以通过翻折法、旋转法、平移法找到对应元素,或者合理添加辅助线构造全等三角形的对应元素.热点4:定义、命题、定理、互逆命题的考查.例4 (2008永州)下列命题是假命题的是( )(A)四个角相等的四边形是矩形(B)对角线互相平分的四边形是平行四边形(C)四条边相等的四边形是菱形(D)对角线互相垂直且相等的四边形是正方形分析:掌握平行四边形、矩形、菱形、正方形的判定方法是解决本题的关键. 解:选(D ).点评:本题考查同学们对平行四边形及特殊的平行四边形的判定方法的把握,遇到这种题,同学们可利用数形结合的思想将其中的文字语言转化为图形语言,便能迅速作出准确判断.热点5:平行四边形、矩形、菱形、正方形、等腰梯形的性质与判定的考查.例5 (2008娄底)如图5,已知点D 在ABC △的BC △边上,DE AC ∥交AB 于E ,DF AB ∥交AC 于F .(1)求证:AE DF =;(2)若AD 平分BAC ∠,试判断四边形AEDF 的形状,并说明理由.分析:本题主要考查同学们对平行四边形及特殊的平行四边形的判定方法的把握.证明:(1)∵DE AC ∥,∴ADE DAF ∠=∠,同理DAE FDA ∠=∠.∵AD DA =,∴ADE DAF △≌△,∴AE DF =.(2)若AD 平分BAC ∠,四边形AEDF 是菱形.证明:∵DE AC ∥,DF AB ∥,∴四边形AEDF 是平行四边形,∵FAD EAD ∠=∠,∴AF DF =,∴平行四边形AEDF 为菱形.点评:三角形全等及平行四边形的性质都可以证明两线段相等,此类题起点低,注重基础知识及基本技能的考查,考查了同学们最基本的几何推理证明能力.热点6:圆的有关概念及性质的考查例6 (2008益阳)如图6,AB 是O 的直径,C 是O 上一点,过圆心O 作OD AC ⊥,D 为垂足,E 是BC 上一点,G 是DE 的中点,OG 的延长线交BC 于F .(1)图中线段OD 、BC 所在直线有怎样的位置关系?写出你的结论,并给出证明过程;(2)猜想线段BE EF FC ,,三者之间有怎样的数量关系?写出你的结论,并给出证明过程.分析:平面内两直线的位置关系只有平行和相交两种,先通过观察图形可猜想OD ∥BC ,再利用圆的有关概念及性质得证.解:(1)结论:OD BC ∥.证明:∵AB 是O 的直径,C 是O 上一点,∴90ACB ∠=,即BC ⊥AC .又OD ⊥AC ,∴OD ∥BC .(2)结论:EF BE FC =+.证明:∵OD ⊥AC ,∴AD =DC .又O 为AB 的中点,∴OD 是△ABC 的中位线.∴BC =2OD .在△ODG 与△EFG 中,∵DG =EG ,∠GOD =∠GFE ,∠ODG =∠FEG ,∴ODG FEG △≌△.∴OD =EF .∴22BE EF FC BC OD EF ++===.∴EF BE FC =+.点评:为了使同学们对推理论证的必要性有更深刻的理解,新课程中的逻辑推理常在探究、猜想的前提下进行.本题就采用了这种方式.该题主要考查了直径与圆周角、垂直于弦的直径等概念之间的联系.【考题预测】1.下列命题中真命题的个数是( )①两个相似多边形面积之比等于相似比的平方;②两个相似三角形的对应高之比等于它们的相似比;③在ABC △与A B C '''△中,AB AC A B A C ='''',A A '∠=∠,那么ABC A B C '''△∽△; ④已知ABC △及位似中心O ,能够作一个且只能作一个三角形,使位似比为0.5. (A)1个 (B)2个 (C)3个 (D)4个2.已知如图7,在四边形ABCD 中,对角线AC ,BD 交于点E ,且AC 平分∠DAB ,AB =AE ,AC =AD .下四个结论:①AC ⊥BD ;②CB =DE ;③12D B C D A B ∠=∠;④△ABE 是等边三角形.请写出正确的结论序号____________(把你认为正确的结论序号填上,并证明其中一个).3.如图8,菱形ABCD 中,E 、F 分别为CB 、CD 延长线上的点,且CE CF =.求证:AE AF =.4.如图9,在Rt △ABC 中,90ACB ∠=,2AB AC =,DE 垂直平分BC ,垂足为D ,交AB 于点E .又点F 在DE 的延长线上,且2EF DE =.求证:四边形ACEF 是菱形.5.如图10,D 是ABC △边AB 上一点,DE 交AC 于点E ,DE EF =,FC AB ∥.求证:AE CE =.6.如图11,已知AC 切O 于A ,CB 顺次交O 于D B ,两点,6AC =,5BD =,连结AD ,AB .(1)求证:CAD CBA △∽△;(2)求线段DC 的长.7.如图12,ABC △是O 的内接三角形,AC BC =,D 为O 中上一点,延长DA至点E ,使CE CD =.(1)求证:AE BD =;(2)若AC BC ⊥,求证:AD BD CD +=.8.如图13,已知:C 是以AB 为直径的半圆O 上一点,CH ⊥AB 于点H ,直线AC 与过B 点的切线相交于点D ,E 为CH 中点,连结AE 并延长交BD 于点F ,直线CF 交AB 的延长线于点G .(1)求证:点F 是BD 中点;(2)求证:CG 是O 的切线;(3)若2FB FE ==,求O 的半径.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
热点专题六 图形与证明
【考点聚焦】
图形与证明是空间与图形的核心内容之一,它贯穿在整个几何知识的学习及运用之中. 内容主要有:了解定义、命题、定理、互逆命题、反证法的含义;掌握平行线的性质定理和判定定理、全等三角形的性质定理和判定定理、直角三角形全等的判定定理;掌握三角形的内角和定理和推论、角平分线和垂直平分线性质定理及逆定理、三角形中位线定理;掌握等腰三角形、等边三角形、直角三角形性质与判定定理;掌握平行四边形、矩形、菱形、正方形、等腰梯形的性质和判定定理.
【热点透视】
热点1:把握三角形全等的性质,考查线段相等的证明.
例1 (2008郴州)如图1,菱形ABCD 中,E F ,分别为BC 、
CD 上的点,且CE CF =.求证:AE AF =.
分析:本题中灵活运用菱形的性质:四边相等,两组对角分别相
等.找到全等三角形的对应元素是解本题的关键.
证明:∵四边形ABCD 是菱形,
∴AB BC CD AD ===,B D ∠=∠.
∵CE CF =,∴BE DF =.
在ABE △与ADF △中,AB AD =,B D ∠=∠,BE DF =.
∴ABE ADF △≌△,∴AE AF =.
点评:掌握全等三角形的概念和性质,还要能准确辨认全等三角形中的对应元素,通过证明全等来证明线段相等或者角相等.
热点2:紧扣三角形全等的判定,考查三角形全等的开放型问题.
例2 (2008湘潭)如图2,在正五边形ABCDE 中,连结对角线AC 、
AD 和CE ,AD 交CE 于F .
(1)请列出图中两对全等三角形_________________(不另外添加辅
助线);
(2)请选择所列举的一对全等三角形加以证明.
分析:由正多边形的性质可知:正多边形的各边相等,各角相等.这
是一类结论不惟一的试题.解决此类问题的关键是依据图形,通过准确辨认全等三角形的对应元素,证明三角形全等.
解:(1)△ABC ≌△AED ,△ABC ≌△EDC ;
(2)证明:在正五边形ABCDE 中,AB BC CD DE EA ====,
∠EAB =∠B =∠BCD =∠CDE =∠DEA ,
故在△ABC 与△AED 中,AB =AE ,∠B =∠DEA ,BC =DE ,∴△ABC ≌△AED , 在△ABC 与△EDC 中,AB =ED ,∠B =∠CDE ,BC =DC ,∴△ABC ≌△EDC .
点评:本考题题干简单清晰,但考点的内容与正多边形的知识相结合,需要具有分解基本图形的能力和基本的探究能力,才能顺利解题.
热点3:合理添加辅助线,构造全等三角形解决相关问题.
例3 (2008常德)如图3,已知AB AC =,
(1)若CE BD =,求证:GE GD =;
(2)若CE m B D = (m 为正数),试猜想GE 与GD 有何关系(只写结论,不证明).
分析:证明在不同三角形中的两条线段和两个角相等的常用方法就是证明两个三角形全等,要证明线段GE 和GD 相等,在辨认三角形全等对应元素时,发现图中没有三角形全等,需要通过合理添加辅助线构造三角形全等.
(1)证明:过D 作DF ∥CE ,交BC 于F ,
∠E =∠GDF ,
∵AB =AC ,DF ∥CE ,
∴∠DFB =∠ACB =∠ABC ,
∴DF =DB =EC .
又∠DGF =∠EGC ,∴△GDF ≌△GEC .
∴GE =GD .
(2)GE m GD =
. 点评:在证明三角形全等时,可以通过翻折法、旋转法、平移法找到对应元素,或者合理添加辅助线构造全等三角形的对应元素.
热点4:定义、命题、定理、互逆命题的考查.
例4 (2008永州)下列命题是假命题的是( )
(A)四个角相等的四边形是矩形
(B)对角线互相平分的四边形是平行四边形
(C)四条边相等的四边形是菱形
(D)对角线互相垂直且相等的四边形是正方形
分析:掌握平行四边形、矩形、菱形、正方形的判定方法是解决本题的关键. 解:选(D ).
点评:本题考查同学们对平行四边形及特殊的平行四边形的判定方法的把握,遇到这种题,同学们可利用数形结合的思想将其中的文字语言转化为图形语言,便能迅速作出准确判断.
热点5:平行四边形、矩形、菱形、正方形、等腰梯形的性质与判定的考查.
例5 (2008娄底)如图5,已知点D 在ABC △的BC △边上,
DE AC ∥交AB 于E ,DF AB ∥交AC 于F .
(1)求证:AE DF =;
(2)若AD 平分BAC ∠,试判断四边形AEDF 的形状,
并说明理由.
分析:本题主要考查同学们对平行四边形及特殊的平行四边
形的判定方法的把握.
证明:(1)∵DE AC ∥,
∴ADE DAF ∠=∠,同理DAE FDA ∠=∠.
∵AD DA =,
∴ADE DAF △≌△,∴AE DF =.
(2)若AD 平分BAC ∠,四边形AEDF 是菱形.
证明:∵DE AC ∥,DF AB ∥,
∴四边形AEDF 是平行四边形,
∵FAD EAD ∠=∠,∴AF DF =,
∴平行四边形AEDF 为菱形.
点评:三角形全等及平行四边形的性质都可以证明两线段相等,此类题起点低,注重基础知识及基本技能的考查,考查了同学们最基本的几何推理证明能力.
热点6:圆的有关概念及性质的考查
例6 (2008益阳)如图6,AB 是O 的直径,C 是O 上一点,
过圆心O 作OD AC ⊥,D 为垂足,E 是BC 上一点,G 是DE 的中点,
OG 的延长线交BC 于F .
(1)图中线段OD 、BC 所在直线有怎样的位置关系?写出你的结论,
并给出证明过程;
(2)猜想线段BE EF FC ,,三者之间有怎样的数量关系?
写出你的结论,并给出证明过程.
分析:平面内两直线的位置关系只有平行和相交两种,先通过观察图形可猜想OD ∥BC ,再利用圆的有关概念及性质得证.
解:(1)结论:OD BC ∥.
证明:∵AB 是O 的直径,C 是O 上一点,
∴90ACB ∠= ,即BC ⊥AC .
又OD ⊥AC ,∴OD ∥BC .
(2)结论:EF BE FC =+.
证明:∵OD ⊥AC ,∴AD =DC .
又O 为AB 的中点,∴OD 是△ABC 的中位线.
∴BC =2OD .
在△ODG 与△EFG 中,
∵DG =EG ,∠GOD =∠GFE ,∠ODG =∠FEG ,
∴ODG FEG △≌△.∴OD =EF .
∴22BE EF FC BC OD EF ++===.
∴EF BE FC =+.
点评:为了使同学们对推理论证的必要性有更深刻的理解,新课程中的逻辑推理常在探究、猜想的前提下进行.本题就采用了这种方式.该题主要考查了直径与圆周角、垂直于弦的直径等概念之间的联系.
【考题预测】
1.下列命题中真命题的个数是( )
①两个相似多边形面积之比等于相似比的平方;
②两个相似三角形的对应高之比等于它们的相似比;
③在ABC △与A B C '''△中,AB AC A B A C
='''',A A '∠=∠,那么ABC A B C '''△∽△; ④已知ABC △及位似中心O ,能够作一个且只能作一个三角形,使位似比为0.5. (A)1个 (B)2个 (C)3个 (D)4个
2.已知如图7,在四边形ABCD 中,对角线AC ,BD 交于点
E ,且AC 平分∠DAB ,AB =AE ,AC =AD .下四个结论:①AC ⊥BD ;
②CB =DE ;③1
2
D B C D A B ∠=∠;④△AB
E 是等边三角形.请写
出正确的结论序号____________(把你认为正确的结论序号填上,并证明其中一个).
3.如图8,菱形ABCD 中,E 、F 分别为CB 、CD 延长线上的点,且CE CF =.求证:AE AF =.
4.如图9,在Rt △ABC 中,90ACB ∠=
,2AB AC =,DE 垂直平分BC ,垂足为D ,交AB 于点E .又点F 在DE 的延长线上,且2EF DE =.求证:四边形ACEF 是菱形.
5.如图10,D 是ABC △边AB 上一点,DE 交AC 于点E ,DE EF =,FC AB ∥.求证:AE CE =.
6.如图11,已知AC 切O 于A ,CB 顺次交O 于D B ,两点,6AC =,5BD =,连结AD ,AB .
(1)求证:CAD CBA △∽△;
(2)求线段DC 的长.
7.如图12,ABC △是O 的内接三角形,AC BC =,D 为O 中上一点,延长DA 至点E ,使CE CD =.
(1)求证:AE BD =;
(2)若AC BC ⊥,求证:AD BD CD +=.
8.如图13,已知:C 是以AB 为直径的半圆O 上一点,CH ⊥AB 于点H ,直线AC 与过B 点的切线相交于点D ,E 为CH 中点,连结AE 并延长交BD 于点F ,直线CF 交AB 的
延长线于点G .
(1)求证:点F 是BD 中点;
(2)求证:CG 是O 的切线;
(3)若2FB FE ==,求O 的半径.。
