高中数学对数函数练习题突破训练
对数函数经典练习题
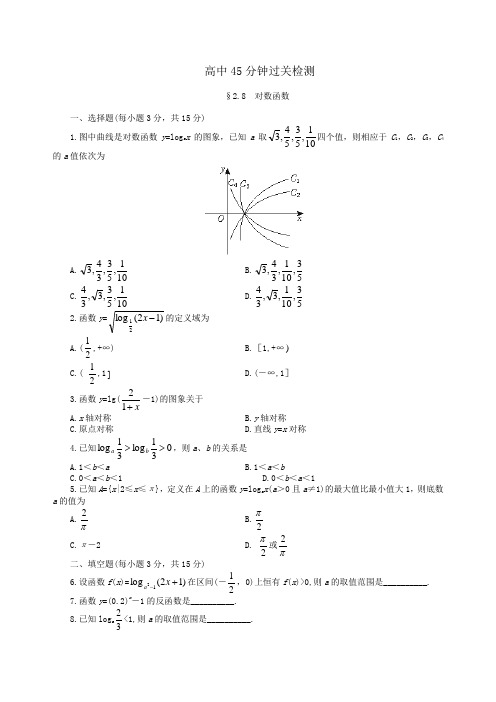
高中45分钟过关检测§2.8 对数函数一、选择题(每小题3分,共15分)1.图中曲线是对数函数y =log a x 的图象,已知a 取101,53,54,3四个值,则相应于C 1,C 2,C 3,C 4的a 值依次为A.101,53,34,3 B.53,101,34,3 C.101,53,3,34 D.53,101,3,34 2.函数y =)12(log 21-x 的定义域为 A.(21,+∞) B.[1,+∞) C.( 21,1] D.(-∞,1] 3.函数y =lg(x+12-1)的图象关于 A.x 轴对称B.y 轴对称C.原点对称D.直线y =x 对称 4.已知031log 31log >>b a ,则a 、b 的关系是 A.1<b <a B.1<a <bC.0<a <b <1D.0<b <a <15.已知A ={x |2≤x ≤π},定义在A 上的函数y =log a x (a >0且a ≠1)的最大值比最小值大1,则底数a 的值为 A.π2B.2π C.π-2 D. 2π或π2 二、填空题(每小题3分,共15分)6.设函数f (x )=)12(log 12+-x a 在区间(-21,0)上恒有f (x )>0,则a 的取值范围是__________. 7.函数y =(0.2)x -1的反函数是__________.8.已知log a 32<1,则a 的取值范围是__________.9.函数f (x )=|lg x |,则f (41),f (31),f (2)的大小关系是__________. 10.函数f (x )=x 2-2ax +a +2,若f (x )在[1,+∞)上为增函数,则a 的取值范围是__________,若f (x )在[0,a ]上取得最大值3,最小值2,则a =__________.三、解答题(共20分)11.(6分)已知m >1,试比较(lg m )0.9与(lg m )0.8的大小.12.(7分)已知f (x )=(3-2x -x 2)21,求y =f (lg x )的定义域、值域、单调区间.13.(7分)已知函数f (x )=log a (a -a x )且a >1,(1)求函数的定义域和值域;(2)讨论f (x )在其定义域上的单调性;(3)证明函数图象关于y =x 对称.参考答案一、1.A 2.C 3.C 4.D 5.D二、6.-2<a <-1或1<a <27.y =log 0.2(x +1)(x >-1)8.a >1或0<a <32 9.f (41)>f (31)>f (2) 10.(-∞,1] 1三、11.解:当lg m >1即m >10时,(lg m )0.9>(lg m )0.8;当lg m =1即m =10时,(lg m )0.9=(lg m )0.8;当0<lg m <1即1<m <10时,(lg m )0.9<(lg m )0.8.12.定义域[3101,10],值域[0,2],增区间[3101,101],减区间[101,10] 13.(1)定义域为(-∞,1),值域为(-∞,1)(2)解:设1>x 2>x 1∵a >1,∴12x x a a,于是a -2x a <a -1x a则log a (a -a 2x a )<log a (a -1x a ) 即f (x 2)<f (x 1)∴f (x )在定义域(-∞,1)上是减函数(3)证明:令y =log a (a -a x )(x <1)则a -a x =a y ,x =log a (a -a y )∴f -1(x )=log a (a -a x )(x <1)故f (x )的反函数是其自身,得函数f (x )=log a (a -a x )(x <1)图象关于y =x 对称.。
高中数学人教A版必修第一册 课时训练 分层突破 对数函数的图象和性质的应用(习题课)

第2课时对数函数的图象和性质的应用(习题课)选题明细表基础巩固1.函数y=ln x,x∈(1,e3]的值域是( B )A.(0,+∞)B.(0,3]C.(-∞,3]D.[3,+∞)解析:由于对数函数y=ln x在其定义域上是增函数,当x∈(1,e3]时,ln 1<ln x≤ln e3,即0<ln x≤3,因此,函数y=ln x(x∈(1,e3])的值域是(0,3].故选B.2.设函数f(x)=log2x,若f(a+1)<2,则a的取值范围为( A )A.(-1,3)B. (-∞,3)C. (-∞,1)D. (-1,1)解析:由题意知,log2(a+1)<2,即log2(a+1)<log24,所以0<a+1<4,解得-1<a<3.即a的取值范围是(-1,3).故选A.3.a=lo g 13π,b=log 3π,c=log 4π,则( A )A.a<c<bB.c<b<aC.a<b<cD.b<c<a解析:由已知a=lo g 13π<lo g 131=0,又b=log 3π=1log π3>0,c=log 4π=1log π4>0,因为log π3<log π4,所以1log π3>1log π4,即b>c.综合得a<c<b. 故选A.4.(2021·四川成都期中)已知函数f(x)=log a x+2(a>0,且a ≠1)在区间[12,4]上的最大值为4,则a 的值为( D )A.12B.2C.√22D.2或√22解析:当a>1时,f(x)在[12,4]上单调递增,f(x)max =f(4)=log a 4+2=4,所以a=2.当0<a<1时,f(x)在[12,4]上单调递减,f(x)max =f(12)=log a 12+2=4,所以a=√22. 综上,a 的值为2或√22.故选D.5.已知函数f(x)=log (2a-1)(x 2-1)在区间(2,+∞)上是减函数,则a 的取值范围是( B ) A.0<a<12B.12<a<1C.0<a<1D.a>1解析:y=x 2-1在区间(2,+∞)上是增函数,所以2a-1∈(0,1)时,函数f(x)=log (2a-1)(x 2-1)在区间(2,+∞)上是减函数, 所以12<a<1.故选B.6.(2021·云南玉溪高一期中改编)已知函数f(x)=log2(2x-1),函数f(x)的单调递增区间是;若x∈[1,92],则函数f(x)的值域是.解析:因为函数f(x)=log2(2x-1)的定义域为(12,+∞).令t=2x-1,易知t=2x-1在(12,+∞)上单调递增,而y=log2t在(0,+∞)上单调递增,故函数f(x)的单调递增区间是(12,+∞).因为函数f(x)=log2(2x-1)在[1,92]上是增函数,所以f(1)≤f(x)≤f(92),所以0≤f(x)≤3,故所求函数的值域为[0,3].答案:(12,+∞) [0,3]能力提升7.已知函数f(x)=log2(1+4x)-x,则下列说法正确的是( D )A.函数f(x)在(-∞,0]上为增函数B.函数f(x)的值域为RC.函数f(x)是奇函数D.函数f(x)是偶函数解析:根据题意,函数f(x)=log2(1+4x)-x,其定义域为R,有f(-x)=log2(1+14x)+x=log2(1+4x)-x=f(x),所以函数f(x)是偶函数,则D正确,C错误;对于A,f(-1)=log252>1=f(0),f(x)不是增函数,A错误;对于B,f(x)=log2(1+4x)-x=log2(12x +2x),设t=12x+2x≥2,当且仅当x=0时,等号成立,则t的最小值为2,故f(x)≥log22=1,即函数的值域为[1,+∞),B错误.故选D.8.(多选题)已知a=log32,b=ln 2,c=lo g132,d=12,则( AD )A.a<bB.b<cC.a<dD.b>d解析:对于A,因为log3e<log33=1,所以a=log32<log32log3e=ln 2=b,故A正确;对于B,因为b=ln 2>ln 1=0,c=lo g132<lo g131=0,所以b>c,故B错误;对于C,因为2>√3,所以a=log32>log3√3=12=d,故C错误;对于D,因为2>√e,所以b=ln 2>ln √e=12=d,故D正确.故选AD.9.已知f(x)在(0,+∞)上是减函数,且f(x)+f(y)=f(xy)+1对任意的x∈(0,+∞)都成立,写出一个满足以上特征的函数f(x)= . 解析:不妨设f(x)=-log3x+b,因为f(x)+f(y)=f(xy)+1,所以-log3x+b-log3y+b=-log3(xy)+b+1,所以b=1,所以f(x)= -log3x+1.答案:-log3x+1(答案不唯一)10.已知函数f(x)=lo g12(x2-2ax+3).(1)若f(-1)=-3,求f(x)单调区间;(2)是否存在实数a,使f(x)在(-∞,2)上为增函数?若存在,求出a 的范围;若不存在,说明理由.解:(1)因为f(-1)=-3,所以a=2.因为f(x)=lo g12(x2-4x+3),x2-4x+3>0,x<1或x>3.设m(x)=x2-4x+3,对称轴为直线x=2,所以m(x)在(-∞,1)上为减函数,在(3,+∞)上为增函数,所以f(x)在(-∞,1)上为增函数,在(3,+∞)上为减函数.(2)设t(x)=x2-2ax+3,则y=lo g12t在(0,+∞)上是减函数,t(x)在(-∞,a)上为减函数,在(a,+∞)上为增函数,因为f(x)在(-∞,2)上为增函数,则需t(x)在(-∞,a)上为减函数,且t(2)≥0,所以{a≥2,4-4a+3≥0,所以a≥2,且a≤74,不可能同时成立.所以不存在实数a,使f(x)在(-∞,2)上为增函数.11.设函数f(x)=log3(9x)·log3(3x),且19≤x≤9;(1)求f(3)的值.(2)令t=log3x,将f(x)表示成以t为自变量的函数;并由此,求函数f(x)的最大值与最小值及与之对应的x的值.解:(1)因为函数f(x)=log3(9x)·log3(3x),且19≤x≤9,故f(3)= log327·log39=3×2=6.(2)令t=log3x,19≤x≤9,则-2≤t≤2,且f(x)=(log3x+2)(1+log3x)=t2+3t+2,令g(t)=t 2+3t+2=(t+32) 2-14,t ∈[-2,2],故当t=-32时,函数g(t)取得最小值为-14,即函数f(x)的最小值为-14,此时求得x=3-32=√39;当t=2时,函数g(t)取得最大值为12,即函数f(x)的最大值为12,此时求得x=9.应用创新12.已知f(x)=ln(e x +a)是定义域为R 的奇函数,g(x)=λf(x). (1)求实数a 的值;(2)若g(x)≤xlog 2x 在x ∈[2,3]上恒成立,求λ的取值范围. 解:(1)函数f(x)=ln(e x +a)是定义域为R 的奇函数, 则f(0)=0,即ln(1+a)=0,解得a=0, 故函数f(x)=ln e x =x.显然有f(-x)=-f(x),函数f(x)=x 是奇函数,满足条件,所以a=0. (2)由(1)知f(x)=x ,g(x)=λx ,则λx ≤xlog 2x 在x ∈[2,3]上恒成立,即λ≤log 2x 在x ∈[2,3]上恒成立,因为函数y=log 2x 在x ∈[2,3]上单调递增,最小值为log 22=1, 所以λ≤1,即λ的取值范围为(-∞,1].。
指数函数与对数函数专项训练(解析版)

指数函数与对数函数专项训练一、单选题1.(23-24高一下·云南玉溪·期末)函数()()2lg 35f x x x =-的定义域为()A .()0,∞+B .50,3⎛⎫⎪C .()5,0,3∞∞⎛⎫-⋃+ ⎪D .5,3⎛⎫+∞ ⎪【答案】C【详解】由题意知,2350x x ->,即(35)0x x ->,所以0x <或53x >.故选:C.2.(23-24高一上·云南昭通·期末)函数()327x f x x =+-的零点所在的区间是()A .()0,1B .31,2⎛⎫ ⎪⎝⎭C .3,22⎛⎫⎪D .()2,3【答案】B【详解】∵3x y =和27y x =-均在R 上单调递增,∴()327x f x x =+-在R 上单调递增;又()12f =-,327402f ⎛⎫=-> ⎪⎝⎭,∴()f x 在31,2⎛⎫ ⎪⎝⎭上有唯一的零点,故选:B.3.(23-24高一上·云南昆明·期末)滇池是云南省面积最大的高原淡水湖,一段时间曾由于人类活动的加剧,滇池水质恶化,藻类水华事件频发.在适当的条件下,藻类的生长会进入指数增长阶段.滇池外海北部某年从1月到7月的水华面积占比符合指数增长,其模型为23 1.65x y -=⨯.经研究“以鱼控藻”模式能有效控制藻类水华.如果3月开始向滇池投放一定量的鱼群后,鱼群消耗水华面积占比呈现一次函数 5.213.5y x =-,将两函数模型放在同期进行比较,如图所示.下列说法正确的是(参考数据:671.6520.2,1.6533.3≈≈)()A .水华面积占比每月增长率为1.65B .如果不采取有效措施,到8月水华的面积占比就会达到60%左右C .“以鱼控藻”模式并没有对水华面积占比减少起到作用D .7月后滇池藻类水华会因“以鱼控藻”模式得到彻底治理【答案】B【详解】对于A ,由于模型23 1.65x y -=⨯呈指数增长,故A 错误;对于B ,当8x =时,8220.63 1.605326.y -⨯==⨯≈,故B 正确;对于C ,因为鱼群消耗水华面积占比呈现一次函数 5.213.5y x =-,所以“以鱼控藻”模式对水华面积占比减少起到作用,故C 错误;对于D ,由两函数模型放在同期进行比较的图象可知,7月后滇池藻类水华并不会因“以鱼控藻”模式得到彻底治理,故D 错误.故选:B.4.(23-24高一上·云南昭通·期末)()()1log 14a f x x =-+(0a >且1a ≠)的图象恒过定点M ,幂函数()g x 过点M ,则12g ⎛⎫⎪⎝⎭为()A .1B .2C .3D .4【答案】D【详解】()()1log 14a f x x =-+,令11x -=,得2x =,()124f =,则()()1log 14a f x x =-+(0a >且1a ≠)恒过定点12,4M ⎛⎫⎪⎝⎭,设()g x x α=,则124α=,即2α=-,即()2g x x -=,∴142g ⎛⎫= ⎪⎝⎭,故选:D.5.(23-24高一下·云南楚雄·期末)已知0.320.3lo g 3,2,lo g 2a b c -===,则()A .c b a <<B .<<b c aC .<<c a bD .a b c<<【答案】A【详解】因为2log y x =在(0,)+∞上单调递增,且234<<,所以222log 2log 3log 4<<,所以21log 32<<,即12a <<,因为2x y =在R 上递增,且0.30-<,所以0.300221-<<=,即01b <<,因为0.3log y x =在(0,)+∞上单调递减,且12<,所以0.30.3log 1log 2>,所以0.3log 20<,即0c <,所以c b a <<.故选:A6.(23-24高一上·云南·期末)若()21()ln 1||f x x x =+-,设()0.3(3),(ln2),2a f b f c f =-==,则a ,b ,c 的大小关系为()A .c a b >>B .b c a >>C .a b c >>D .a c b>>【答案】D【详解】由题意知()(),00,x ∈-∞⋃+∞,由()()()21ln 1f x x f x x⎡⎤-=-+-=⎣⎦-,所以()f x 为偶函数,图象关于y 轴对称,当0x >时,由复合函数的单调性法则知()f x 随x 的增大而增大,即()0,x ∈+∞,()21()ln 1||f x x x =+-单调递增,因为()()33a f f =-=,()0.3(ln2),2b f c f ==,且00.3112222=<<=,0ln2lne 1<<=,所以0.3ln 223<<,所以()()()0.3ln223f f f <<-,即b c a <<,也就是a c b >>.故选:D7.(23-24高一下·云南·期末)设222,0()log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩,若关于x 的方程2[()](2)()20f x a f x a -++=恰有5个不同实数解,则实数a 的取值范围是()A .[]1,2B .(2,3]C .()2,+∞D .()3,+∞【答案】B【详解】方程2[()](2)()20f x a f x a -++=化为[()2][()]0f x f x a --=,解得()2f x =或()f x a =,函数()f x 在(,0]-∞上单调递增,函数值的集合为(2,3],在(0,1]上单调递减,函数值的集合为[0,)+∞,在[1,)+∞上单调递增,函数值的集合为[0,)+∞,在同一坐标系内作出直线2,y y a ==与函数()y f x =的图象,显然直线2y =与函数()y f x =的图象有两个交点,由关于x 的方程2[()](2)()20f x a f x a -++=恰有5个不同实数解,则直线y a =与函数()y f x =的图象有3个交点,此时23a <≤,所以实数a 的取值范围是(2,3].故选:B8.(23-24高一下·云南昆明·期末)若()12:lo g 11,:39a p a q --<<,则p 是q 的()条件A .充分不必要B .必要不充分C .充要D .既不充分也不必要【答案】A【详解】对于()22:log 11log 2p a -<=,则012a <-<,解得13a <<;对于1:39a q -<,则12a -<,解得3a <;因为{}|13a a <<是{}|3a a <的真子集,所以p 是q 的充分不必要条件.故选:A.二、多选题9.(23-24高一上·云南迪庆·期末)已知函数()()2ln 2f x x x =-,则下列结论正确的是()A .函数()f x 的单调递增区间是[)1,+∞B .函数()f x 的值域是RC .函数()f x 的图象关于1x =对称D .不等式()ln 3f x <的解集是()1,3-【答案】BC【详解】对于A ,当1x =时,2210x x -=-<,此时()()2ln 2f x x x =-无意义,故A 错误;对于B ,由于()22y g x x x ==-的值域为[)1,-+∞,满足()[)0,1,+∞⊆-+∞,所以函数()f x 的值域是R ,故B 正确;对于C ,由题意()()()22ln 2ln 11f x x x x ⎡⎤=-=--⎣⎦,且定义域为()(),02,-∞+∞ ,它满足()()()21ln 11f x x f x+=-=-,即函数()f x 的图象关于1x =对称,故C 正确;对于D ,由于()f x 的定义域为()(),02,-∞+∞ ,故D 错误.故选:BC.10.(23-24高一上·云南昆明·期末)已知函数2212,0()2|log ,0x x x f x x x ⎧--≤⎪=⎨⎪⎩,若1234x x x x <<<,且()()()()1234fx fx fx fx ===,则下列结论中正确的是()A .122x x +=-B .1204x x <<C .()41,4x ∈D .342x x +的取值范围是332,4⎡⎫⎪⎢⎣⎭【答案】BC【详解】作出函数2212,0()2|log ,0x x x f x x x ⎧--≤⎪=⎨⎪⎩的图像如图.对于选项A,根据二次函数的对称性知,12()224x x +=⨯=--,故A 项错误;对于选项B ,因120x x <<,由上述分析知124x x +=-,则21212120()()()42x x x x x x --<=-⋅-≤=,因12x x ≠,故有1204x x <<,即B 项正确;对于选项C ,如图,因0x ≤时,2211()2(2)2222f x x x x =--=-++≤,0x >时,2()|log |f x x =,依题意须使20|log |2x <<,由2|log |0x >得1x ≠,由2|log |2x <解得:144x <<,故有3411,144x x <<<<,即C项正确;对于选项D ,由图知2324log log x x -=,可得341x x =,故431x x =,则343322x x x x ++=,3114x <<,不妨设21,(,1)4y x x x =+∈,显然函数2y x x =+在(1,14)上单调递减,故23334x x <+<,即342x x +的取值范围是(333,4),故D 项错误.故选:BC.11.(23-24高一上·云南昆明·期末)关于函数()ln f x x x =+,以下结论正确的是()A .方程()0f x =有唯一的实数解c ,且(0,1)c ∈B .对,0,()()()x y f xy f x f y ∀>=+恒成立C .对()1212,0x x x x ∀>≠,都有()()1212f x f x x x ->-D .对12,0x x ∀>,均有()()121222f x f x x x f ++⎛⎫≤⎪【答案】AC【详解】A 选项,由于1y x =在R 上单调递增,2ln y x =在()0,∞+上单调递增,故()ln f x x x =+在定义域()0,∞+上单调递增,又()11ln 30,11033f f ⎛⎫=-<=> ⎪⎝⎭,故由零点存在性定理可得,方程()0f x =有唯一的实数解c ,且(0,1)c ∈,A 正确;B 选项,()ln f xy xy xy =+,()()ln ln ln f x f y x x y y x y xy +=+++=++,显然,0x y ∀>,由于xy 与x y +不一定相等,故()()f x f y +与()f xy 不一定相等,B 错误;C 选项,由A 选项可知,()ln f x x x =+在定义域()0,∞+上单调递增,对()1212,0x x x x ∀>≠,都有()()12120f x f x x x ->-,C 正确;D 选项,12,0x x ∀>,均有121212ln 222x xx x x x f +++⎛⎫=+ ⎪⎝⎭,()()12112212121212ln ln ln ln 22222f x f x x x x x x x x x x x x x ++++++==+=+,由于12122x x x x +≥,当且仅当12x x =时,等号成立,故1212ln ln 2x x x x +≥,即()()121222f x f x x x f ++⎛⎫≥ ⎪⎝⎭,D 错误.故选:AC 三、填空题12.(23-24高一上·云南昆明·期末)()()2,(1)29,1x a x f x x ax a x ⎧>⎪=⎨-++-≤⎪⎩是R 上的单调递增函数,则实数a 的取值范围为.【答案】[]2,5【详解】因为在R 递增,则112129a a a a a⎧⎪⎪≥⎨⎪-++-≤⎪⎩>,解得:25a ≤≤,故答案为:[]2,513.(23-24高一下·云南昆明·期末)设函数()ln(1)f x x =+,2()g x x a =-+,若曲线()y f x =与曲线()y g x =有两个交点,则实数a 的取值范围是.【答案】(0,)+∞【详解】当0x ≥时,()ln(1),f x x =+当0x <时()ln(1),f x x =-+函数图象示意图为则2()g x x a =-+与()ln (1)f x x =+有两个零点知a 的取值范围是(0,)+∞.故答案为:(0,).+∞14.(23-24高一下·云南玉溪·期末)苏格兰数学家纳皮尔(J.Napier ,1550-1617)在研究天文学的过程中,经过对运算体系的多年研究后发明的对数,为当时的天文学家处理“大数”的计算大大缩短了时间.即就是任何一个正实数N 可以表示成10(110,)n N a a n =⨯≤<∈Z ,则lg lg (0lg 1)N n a a =+≤<,这样我们可以知道N 的位数为1n +.已知正整数M ,若10M 是10位数,则M 的值为.(参考数据:0.9 1.1107.94,1012.56≈≈)【答案】8或9【详解】依题意可得910101010M ≤<,两边取常用对数可得91010lg10lg lg10M ≤<,即910lg 10M ≤<,所以0.9lg 1M ≤<,即0.91010M ≤<,又M 为正整数,所以8M =或9M =.故答案为:8或9四、解答题15.(23-24高一上·云南昆明·期末)设函数()log (3)(,10a f x x a =-+>且1)a ≠.(1)若(12)3f =,解不等式()0f x >;(2)若()f x 在[4,5]上的最大值与最小值之差为1,求a 的值.【答案】(1)10(,)3+∞(2)2a =或12a =【详解】(1)由(12)3f =可得log (123)13a -+=,解得3a =,即3()log (3)1,(3)f x x x =-+>,则()0f x >,即3log (3)10x -+>,即310,1333x x x >⎧⎪∴>⎨->⎪⎩,故不等式()0f x >的解集为10(,)3+∞;(2)由于()f x 在[4,5]上的最大值与最小值之差为1,故log 11(log 21)1a a +-+=,即log 21,2a a =∴=或12a =,即a 的值为2a =或12a =.16.(23-24高一上·云南昭通·期末)化简求值:(1)()13103420.027π4160.49--++;(2)ln22311lg125lg40.1e log 9log 1632-+++⨯.【答案】(1)8(2)9【详解】(1)()13103420.027π4160.49--++()()()1313423420.3120.7⎡⎤⎡⎤⎡⎤=-++⎣⎦⎣⎦⎣⎦0.3180.78=-++=;(2)ln22311lg125lg4lg 0.1e log 9log 1632-++++⨯3211112lg34lg2lg5lg23222lg2lg3=+-++⨯lg 5lg28=++9=.17.(23-24高一上·云南·期末)已知定义域为R 的函数()11333xx m f x +-⋅=+是奇函数.(1)求m 的值并利用定义证明函数()f x 的单调性;(2)若对于任意t ∈R ,不等式()()22620f t t f t k -+-<恒成立,求实数k 的取值范围.【答案】(1)1m =,证明见解析(2)3k <-【详解】(1)因为()f x 是奇函数,函数的定义域为R ,所以(0)0f =,所以1033m-=+,所以1m =,经检验满足()()f x f x -=-易知()11312133331x x x f x +-⎛⎫==-+ ⎪++⎝⎭设12x x <,则2112122(33)()()3(31)(31)x x x x f x f x --=++因为3x y =在实数集上是增函数,故12()()0f x f x ->.所以()f x 在R 上是单调减函数(2)由(1)知()f x 在(,)-∞+∞上为减函数.又因为()f x 是奇函数,所以()()22620f t t f t k -+-<等价于()()2262f t t f k t-<-,因为()f x 为减函数,由上式可得:2262t t k t ->-.即对一切t R ∈有:2360t t k -->,从而判别式361203k k ∆=+<⇒<-.所以k 的取值范围是3k <-.18.(23-24高一下·云南昆明·期末)已知函数1()xx f x a a ⎛⎫=- ⎪⎝⎭ (0a >且1a ≠).(1)讨论()f x 的单调性(不需证明);(2)若2a =,(ⅰ)解不等式3()2≤f x x;(ⅱ)若21()(22))2(x g f x t x x f +=-+在区间[]1,1-上的最小值为74-,求t 的值.【答案】(1)答案见解析(2)(ⅰ)(](],10,1-∞-⋃;(ⅱ)2t =-或2t =【详解】(1)若1a >,则1()()x xf x a a=-在R 上单调递增;若01a <<,则1()()x xf x a a=-在R 上单调递减.(2)(ⅰ)3()2≤f x x ,即132()022xx x --≤,设13()2()22xx g x x=--,则(1)0g =,()()g x g x -=-,所以()g x 为奇函数,当0x >时,()g x 单调递增,由()(1)g x g ≤,解得01x <≤,根据奇函数的性质,当0x <时,()(1)g x g ≤的解为1x ≤-,综上所述,3()2≤f x x的解集为(](],10,1-∞-⋃.(ⅱ)2122()2(2)2()222(22)x x x x x g x f x tf x t +--=-+=++-,令22x x m --=,因为[]1,1x ∈-,则33,22m ⎡⎤∈-⎢⎥⎣⎦,所以2()()22g x h m m tm ==++,其图象为开口向上,对称轴为m t=-的抛物线,①当32t -≤-,即32t ≥时,min 39177()()3232444h m h t t =-=-+=-=-,解得2t =.②当3322t -<-<,即3322t -<<时,222min 7()()2224h m h t t t t =-=-+=-+=-,解得1152t =,2152t =-矛盾.③当32t -≥,即32t ≤-时,min 39177()()3232444h m h t t ==++=+=-,解得2t =-.综上所述,2t =-或2t =.19.(23-24高一上·云南昆明·期末)函数()e (0)x f x mx m =-<.(1)求(1)f -和(0)f 的值,判断()f x 的单调性并用定义加以证明;(2)设0x 是函数()f x 的一个零点,当1em <-时,()02f x k >,求整数k 的最大值.【答案】(1)1(1)e f m --=+,(0)1f =,()f x 在定义域R 上单调递增,证明见解析,(2)整数k 的最大值为1-【详解】(1)1(1)e f m --=+,(0)1f =,判断()f x 在定义域R 上单调递增,证明如下:在R 上任取1x ,2x ,且12x x <,则1212121212()()e (e )(e e )()x x x x f x f x mx mx m x x -=---=---,因为12x x <,0m <,所以12e e x x <,120x x -<,0m ->,所以12e e 0x x -<,12()0m x x --<,所以1212(e e )()0x x m x x ---<,即12())0(f x f x -<,所以12()()f x f x <,所以()f x 在定义域R 上单调递增.(2)由题意得0()0f x =,即00e 0x mx -=,1em <-,则10e m +<,即0(1)0()f f x -<=,由()f x 是R 上的增函数,所以01x -<,又0(0)10()f f x =>=,所以010x -<<,0200(2)e 2x f x mx =-002e 2e x x =-,令01e (ext =∈,1),则22()2(1)1g t t t t =-=--,所以()g t 在1(e ,1)上单调递减,所以()()11g t g >=-,即0(2)1f x >-,当1em <-时,0(2)f x k >,所以1k ≤-,所以整数k 的最大值为1-.。
高一数学同步练习——对数函数练习题及解答解析

对数资料(1) 对数与对数函数测试题一、 选择题: 1.已知3a=5b= A ,且a 1+b1= 2,则A 的值是( ). (A).15 (B).15 (C).±15 (D).225 2.已知a >0,且10x= lg(10a)+lga1,则x 的值是( ). (A).-1 (B).0 (C).1 (D).2 3.若x 1,x 2是方程lg 2x +(lg3+lg2) lg x +lg3·lg2 = 0的两根,则x 1x 2的值是( ). (A).lg3·lg2 (B).lg6 (C).6 (D).61 4.若log a (a 2+1)<log a 2a <0,那么a 的取值范围是( ). (A).(0,1) (B).(0,21) (C).(21,1) (D).(1,+∞) 5. 已知x =31log 121+31log 151,则x 的值属于区间( ).(A).(-2,-1) (B).(1,2) (C).(-3,-2) (D).(2,3) 6.已知lga ,lgb 是方程2x 2-4x +1 = 0的两个根,则(lgba )2的值是( ). (A).4 (B).3 (C).2 (D).1 7.设a ,b ,c ∈R ,且3a= 4b= 6c,则( ). (A).c 1=a 1+b 1 (B).c 2=a 2+b 1 (C).c 1=a 2+b 2 (D).c 2=a 1+b2 8.已知函数y = log 5.0(ax 2+2x +1)的值域为R ,则实数a 的取值范围是( ). (A).0≤a ≤1 (B).0<a ≤1 (C).a ≥1 (D).a >1 9.已知lg2≈0.3010,且a = 27×811×510的位数是M ,则M 为( ).(A).20 (B).19 (C).21 (D).22 10.若log 7[ log 3( log 2x)] = 0,则x 21为( ).(A).321 (B).331 (C).21 (D).42 11.若0<a <1,函数y = log a [1-(21)x]在定义域上是( ). (A).增函数且y >0 (B).增函数且y <0 (C).减函数且y >0 (D).减函数且y <012.已知不等式log a (1-21+x )>0的解集是(-∞,-2),则a 的取值范围是( ). (A).0<a <21 (B).21<a <1 (C).0<a <1 (D).a >1 二、 填空题13.若lg2 = a ,lg3 = b ,则lg 54=_____________. 14.已知a = log 7.00.8,b = log 1.10.9,c = 1.19.0,则a ,b ,c 的大小关系是_______________.15.log12-(3+22) = ____________.16.设函数)(x f = 2x(x ≤0)的反函数为y =)(1x f -,则函数y =)12(1--x f 的定义域为________.三、 解答题17.已知lgx = a ,lgy = b ,lgz = c ,且有a +b +c = 0,求xcb 11+·yac 11+·xba 11+的值.18.要使方程x 2+px +q = 0的两根a 、b 满足lg(a +b) = lga +lgb ,试确定p 和q 应满足的关系. 19.设a ,b 为正数,且a 2-2ab -9b 2= 0,求lg(a 2+ab -6b 2)-lg(a 2+4ab +15b 2)的值. 20.已知log 2[ log 21( log 2x)] = log 3[ log 31( log 3y)] = log 5[ log 51( log 5z)] = 0,试比较x 、y 、z 的大小.21.已知a >1,)(x f = log a (a -a x).⑴ 求)(x f 的定义域、值域; ⑵判断函数)(x f 的单调性 ,并证明; ⑶解不等式:)2(21--x f>)(x f .22.已知)(x f = log 21[ax2+2(ab)x -bx2+1],其中a >0,b >0,求使)(x f <0的x 的取值范围.参考答案:一、选择题:1.(B).2.(B). 3.(D).4.(C).5.(D).6.(C).7.(B).8.(A). 9.(A).10.(D).11.(C).12.(D). 提示:1.∵3a+5b= A ,∴a = log 3A ,b = log 5A ,∴a 1+b1= log A 3+log A 5 = log A 15 = 2,∴A =15,故选(B).2.10x= lg(10 a)+lga 1= lg(10a ·a1) = lg10 = 1,所以 x = 0,故选(B). 3.由lg x 1+lg x 2=-(lg3+lg2),即lg x 1x 2= lg 61,所以x 1x 2=61,故选(D).4.∵当a ≠1时,a 2+1>2a ,所以0<a <1,又log a 2a <0,∴2a >1,即a >21,综合得21<a <1,所以选(C). 5.x = log 3121+log 3151= log 31(21×51) = log 31101= log 310,∵9<10<27,∴ 2<log 310<3,故选(D).6.由已知lga +lgb = 2,lga ·lgb =21,又(lg ba )2= (lga -lgb)2= (lga +lgb)2-4lga ·lgb = 2,故选(C).7.设3a= 4b= 6c= k ,则a = log 3k ,b= log 4k ,c = log 6k ,从而c 1= log k 6 = log k 3+21log k 4 =a 1+b 21,故c 2=a 2+b1,所以选(B). 8.由函数y = log 5.0(ax 2+2x +1)的值域为R ,则函数u(x) = ax 2+2x +1应取遍所有正实数,当a = 0时,u(x) = 2x +1在x >-21时能取遍所有正实数; 当a ≠0时,必有⎩⎨⎧≥-=∆.44,0a >a ⇒0<a ≤1.所以0≤a ≤1,故选(A).9.∵lga = lg(27×811×510) = 7lg2+11lg8+10lg5 = 7 lg2+11×3lg2+10(lg10-lg2) = 30lg2+10≈19.03,∴a = 1003.19,即a 有20位,也就是M = 20,故选(A).10.由于log 3( log 2x) = 1,则log 2x = 3,所以x = 8,因此 x 21-= 821-=81=221=42,故选(D). 11.根据u(x) = (21)x 为减函数,而(21)x >0,即1-(21)x <1,所以y = log a [1-(21)x]在定义域上是减函数且y >0,故选(C). 12.由-∞<x <-2知,1-21+x >1,所以a >1,故选(D). 二、填空题13.21a +23b 14.b <a <c . 15.-2. 16.21<x ≤1 提示: 13.lg 54=21lg(2×33) =21( lg2+3lg3) =21a +23b . 14.0<a = log 7.00.8<log 7.00.7 = 1,b = log 1.10.9<0,c = 1.19.0>1.10= 1,故b <a <c .15.∵3+22= (2+1)2,而(2-1)(2+1) = 1,即2+1= (2-1)1-,∴log 12-(3+22) =log 12-(2-1)2-=-2.16.)(1x f-= log 2x (0<x ≤1=,y =)12(1--x f 的定义域为0<2x -1≤1,即21<x ≤1为所求函数的定义域. 三。
4.3对数(AB分层训练)解析版 2023-2024学年高一数学重难点突破
4.3 对数考点一 对数的概念如果a x =N (a >0,且a ≠1),那么x 叫做以a 为底N 的对数,记作x =log a N ,其中a 叫做对数的底数,N 叫做真数.考点二 对数的性质、换底公式与运算性质(1)对数的性质:①a log a N =N ;②log a a b =b (a >0,且a ≠1).(2)对数的运算法则如果a >0且a ≠1,M >0,N >0,那么①log a (MN )=log a M +log a N ;②log a M N=log a M -log a N ;③log a M n =n log a M (n ∈R);④log a m M n =n mlog a M (m ,n ∈R ,且m ≠0).(3)换底公式:log b N =log a N log a b(a ,b 均大于零且不等于1).(一) 求对数型函数的定义域问题例1.(1)、下列对数式中,与指数式79x =等价的是( )A .7log 9x =B .9log 7x =-C .7log 9x =D .log 97x =【答案】C【分析】根据指数式与对数式的关系直接判断即可.【详解】对于A ,7log 9x =等价于97x =,A 错误;对于B ,9log 7x =-等价于79x -=,B 错误;对于C ,7log 9x =等价于79x =,C 正确;对于D ,log 97x =等价于()790,1x x x =>≠,D 错误.故选:C.(2).(2021·全国·高一专题练习)(多选)下列选项中错误的是( )A .零和负数没有对数B .任何一个指数式都可以化成对数式C .以10为底的对数叫做自然对数D .以e 为底的对数叫做常用对数【答案】BCD【分析】对于A :由对数的定义即可判断;对于B :用对数的定义即可判断;对于C :由常用对数的定义即可判断;对于D :由自然对数的定义即可判断.【详解】对于A :由对数的定义可知:零和负数没有对数.故A 正确;对于B :只有符合0a >,且10a N ≠>,,才有log x a a N x N =⇔=,故B 错误;对于C :以10为底的对数叫做常用对数,故C 错误;对于D :以e 为底的对数叫做自然对数,故D 错误.故选:BCD.【变式训练1-1】、(2021·江西省吉水中学高一阶段练习)使式子()211log 2x x --有意义的x 的取值范围是( )A .()2,+∞B .1,22⎛⎫ ⎪C .(),2-∞D .()1,11,22⎛⎫ ⎪(二) 对数与指数互化例2.(1)、(2021·全国·高一单元测试)(多选题)下列指数式与对数式互化正确的是( )A .45625=与4log 6255=B .2100.01-=与lg 0.012=-C .41162-⎛⎫= ⎪⎝⎭与41log 162-=D .1293=与91log 32=(2)、(多选题)(2021·全国高一专题练习)下列指数式与对数式互化正确的一组是( )A .0101=与lg 1=0B .1327-=13与log 2713=-13C .log 39=2与129=3D .log 55=1与51=5【答案】ABD【分析】根据指数式与对数式互化的结论逐个分析可得答案.【详解】对于A ,0101=lg10⇔=,A 正确;对于B ,132711127log 333-=⇔=-,B 正确;对于C ,23log 9239=⇔=,C 不正确;对于D ,15log 5155=⇔=,D 正确.故选:ABD.(三) 解对数方程例3.(1)、(2021·江苏·淮安市淮安区教师发展中心学科研训处高一期中)若2log 3x =-,则x =_______.【答案】18##0.125【变式训练3-2】、(2022·安徽·合肥一六八中学模拟预测(文))方程()3ln log 0x =的解是( )A .1B .2C .eD .3【答案】D【分析】利用指数与对数的转化即可得到结果.【详解】∵()3ln log 0x =,∴03log e 1x ==,∴3x =.故选:D.例4.(2023·全国·高一假期作业)求下列各式中x 的值.(1)()()345log log 1log x =(2)()()345l 0log lo og g x =【答案】(1)645x =;(2)625.【分析】(1)利用对数式与指数式的关系化简即可;(2)利用对数式与指数式的关系化简即可.【详解】(1)由()()345log log 1log x =可得,()453log log x =,则354l 6g 4o x ==,所以645x =.(2)由()()345l 0log lo og g x =可得,()45log log 1x =,(四) 用对数型公式及换底公式化简求值例5.(1)、(2020·全国高一课时练习)log513+log53等于()A.0B.1C.-1D.log510 3【答案】A【解析】因为555511log log 3log 3log 1033⎛⎫+=⨯== ⎪⎝⎭.故选:A.【变式训练5-2】、(2021·上海市行知中学高三开学考试)已知实数,x y 满足:32272x y ⎛⎫== ⎪⎝⎭,则11x y +=________.(五) 与对数有关的条件求值问题例7、(2020·浙江高一课时练习)已知二次函数2()(lg )24lg f x a x x a =++的最小值为3,求()2log 5a +log 2log 50a a ⋅的值.【答案】1.【解析】∵2()(lg )24lg f x a x x a =++的最小值为3,∴lg 0a >,min 21111()lg 24lg 4lg 3lg (lg )lg lg f x f a a a a a a a ⎛⎫⎛⎫=-=⨯+⨯-+=-= ⎪ ⎪⎝⎭⎝⎭,即24(lg )3lg 10a a --=,∴(4lg 1)(lg 1)0a a +-=,则lg 1a =,∴10a =.∴()222log 5log 2log 50(lg5)lg 2lg50(lg5)lg 2(lg51)lg5(lg5lg 2)lg 21a a a +⋅=+⋅=++=++=.例8、(2021·安顺市第三高级中学(文))(1)已知2lg(2)lg lg x y x y -=+,求x y 的值.(2)设1x 满足2ln 3x x +=,2x 满足ln(1)21x x --=求12x x +的值.【答案】(1)4x y =;(2)1.【分析】(1)利用对数运算化简已知条件,因式分解然后求得x y的值.(2)利用换元法化简已知条件,结合函数()2ln f x x x =+的单调性求得121x x =+.【详解】(1)由2lg(2)lg lg x y x y -=+得2lg(2)lg()x y xy -=,∴2(2)x y xy-=∴22540x xy y -+=,∴()(4)0x y x y --=,即1x y=或4.又0,0,20x y x y >>->, ∴1x y =舍去,故4x y=.(2)由题意得()11222ln 3,ln 121x x x x +=--=,()()22ln 1213x x -+-=,令21x t -=,则2ln 3t t +=.∵()2ln f x x x =+在(0,)+∞单调递增,∴1t x =,∴121x x =+.【点睛】本小题主要考查对数运算,考查对数型函数的单调性,属于中档题.(六) 对数的综合应用例11.(1)、(2023秋·河北保定·高三校联考开学考试)在百端待举、日理万机中,毛泽东主席仍不忘我国的教育事业.1951年9月底,毛主席在接见安徽参加国庆的代表团时,送给代表团成员——渡江小英雄马毛姐一本精美的笔记本,并在扉页上题词:好好学习,天天向上.这8个字的题词迅速在全国传播开来,影响并指导着一代代青少年青春向上,不负韶华.他告诉我们:每天进步一点点,持之以恒,收获不止一点点.把学生现在的学习情况看作1.每天的“进步率”为3%,那么经过一个学期(看作120天)后的学习情况为()12013%34.711+≈,如果每天的“迟步率”为3%,同样经过一个学期后的学习情况为()12013%0.026-≈,经过一个学期,进步者的学习情况是迟步者学习情况的1335倍还多,按上述情况,若“进步"的值是“迟步”的值的10倍,要经过的天数大约为(保留整数)(参考数据:lg103 2.013≈,lg 97 1.987≈)( )A .28B .38C .60D .100【答案】B(2)、(2022·广东汕头·高三阶段练习)核酸检测分析是用荧光定量PCR 法,通过化学物质的荧光信号,对在PCR 扩增进程中成指数级增加的靶标DNA 实时监测,在PCR 扩增的指数时期,荧光信号强度达到阀值时,DNA 的数量X 与扩增次数n 满足0lg lg(1)lg n X n p X =++,其中0X 为DNA 的初始数量,p 为扩增效率.已知某被测标本DNA 扩增12次后,数量变为原来的1000倍,则扩增效率p 约为( )(参考数据:0.250.2510 1.778,100.562-≈≈)A .22.2%B .43.8%C .56.2%D .77.8%()2429a a ∴==;故答案为:9.【变式训练11-2】.(2022·江西·高二开学考试)《中华人民共和国国家标准污水综合排放标准》中一级标准规定的氨氮含量允许排放的最高浓度为15mg/L .某企业生产废水中的氨氮含量为450mg/L ,现通过循环过滤设备对生产废水的氨氮进行过滤,每循环一次可使氨氮含量减少13,要使废水中的氨氮含量达到国家排放标准,最少要进行循环的次数为( )(参考数据:lg 20.3010≈,lg30.4771≈)A .8B .9C .10D .11。
高中数学对数函数经典练习题及答案(优秀4篇)

高中数学对数函数经典练习题及答案(优秀4篇)对数函数练习题篇一一、选择题1、下列函数(1)y= x (2)y=2x-1 (3)y=1x (4)y=2-1-3x (5)y=x2-1中,是一次函数的有( )A.4个B.3个C.2个D.1个2、A 、B(x2,y2)是一次函数y=kx+2(k>0)图像上的不同的两点,若则( )A.t0 C.t>1 D. t≤13、直线y=x-1与坐标轴交于A、B两点,点C在坐标轴上,△ABC为等腰三角形,则满足条件的三角形最多有( )A. 5个B.6个C.7个D.8个4、把直线y=﹣x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是( )A.11 D.m0的解集是( )A.x>3B.-2-29.一次函数y=ax+1与y=bx-2的图象交于x轴上一点,那么a:b等于( )A. B.C. D.以上答案都不对10、函数y=kx+b,那么当y>1时,x的取值范围是:( )A、x>0B、x>2C、x212、在平面直角坐标系中,线段AB的端点A(-2,4),B(4,2),直线y=kx-2与线段AB有交点,则k的值不可能是( )A.5B.-5C.-2D.3二、填空题13、如果直线y = -2x+k与两坐标轴所围成的三角形面积是9,则k的值为_____.14、平面直角坐标系中,点A的坐标是(4,0),点P在直线y=-x+m上,且AP=OP=4.则m的值是。
15、直线y=kx+2经过点(1,4),则这条直线关于x轴对称的直线解析式为:。
16、已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x 轴、y轴分别交与点C、点D.若DB=DC,则直线CD的函数解析式为 .17、点A的坐标为(-2,0),点B在直线y=x-4上运动,当线段AB最短时,点B的坐标是___________。
18、已知三个一次函数y1=x,y2= x+1,y3=- x+5。
高一对数函数题型练习(全)
对数函数知识梳理一、对数函数的定义一般地,函数(,且)叫做对数函数,其中是自变量,函数的定义域是.二、对数函数的图象与性质图象定义域值域性质过定点,即时,减函数增函数特别提醒:当且时,函数的与的图象关于轴对称.三、底数对对数函数图象的影响底数对对数函数图象的影响:当时,“底大图低”,当时,“底大图高”.设,,,的图象,则必有.题型训练题型一对数函数的定义1.函数是对数函数,则实数2.已知函数(,且)满足,则3.下列函数是对数函数的是()A.B.(,且)C.D.(,且)4.已知对数函数过点,则的解析式为?5.函数为对数函数,则等于()A.B.C.D.题型二图像问题1.图中曲线是对数函数的图象,已知值取,,,,则相应于,,,的值依次为()A.,,,B.,,,C.,,,D.,,,2.如图所示的曲线是对数函数,,,的图象,则,,,与的大小关系为?3.已知,且,函数,,在同一坐标系中的图象可能是()A.B.C.D.4.函数,则使的集合是()A.B.C.D.5.已知,且,则函数与的图象只能是()A.B.C.D.6.函数的单调递增区间是()A.B.C.D.题型三过定点1.函数(,且)的图象必经过点()A.B.C.D.2.函数(,且)的图象恒过点?3.函数的图象必经过定点的坐标为()A.B.C.D.4.已知函数恒过定点,则5.函数的图象恒过定点?6.函数的图象恒过定点,点在指数函数的图象上,则.题型四对数函数定义域和值域1.求下列函数的定义域.(1);(2);(3);(4).2.函数的值域为()A.B.C.D.3.函数,的值域是?4.函数的定义域为?5.求下列函数的定义域.(1).(2);(3);(4)(,且).6.若函数在区间上的最大值是最小值的倍,则的值为()A.B.C.D.7.函数的定义域为()A.B.C.D.8.若函数(且)在区间上的最大值与最小值之差为,则?9.设函数(,)在上的最大值是,最小值是,且,则实数()A.B.C.或D.或10.求下列函数的定义域、值域:(1);(2).题型五比大小1.比较大小:和,和.2.设,,,则()A.B.C.D.3.比较下列各组中两个值的大小.(1),;(2),(,且);(3),;(4),.4.已知,,,则,,的大小关系是()A.B.C.D.5.设,,则()A.B.C.D.6.设,,,则,,的大小关系是()A.B.C.D.7.已知,,,则,,的大小关系为()A.B.C.D.题型六解不等式1.不等式的解集为()A.B.C.D.2.若,则的取值范围是()A.B.C.D.或3.满足不等式的所有实数的取值范围是()A.B.C.D.4.不等式的解集为()A.B.C.D.题型七含参问题1.若(,且),则实数的取值范围是()A.B.C.D.2.若,则取值范围是()A.B.C.D.或3.设,则实数的取值范围是()A.B.C.或D.4.在中,实数的取值范围是()A.或B.或C.D.5.(1)已知,则的取值范围为;(2)已知,则的取值范围为;(3)当时,,则的取值范围是.题型八复合函数1.函数的单调递增区间是()A.B.C.D.2.求函数的定义域、值域和单调区间.3.若函数,则函数的单调递减区间为()A.B.C.D.。
【高中数学专项突破】专题26对数函数(含答案)
【⾼中数学专项突破】专题26对数函数(含答案)【⾼中数学专项突破】专题26 对数函数题组1 对数函数的概念1.给出下列函数:①y =23log x 2;②y =log 3(x -1);③y =log (x +1)x ;④y =log πx .其中是对数函数的有( ) A.1个B.2个C.3个D.4个2.下列函数,是对数函数的是( ) A.y=lg10x B.y=log 3x 2 C.y=lnxD.y=log 13(x –1)3.下列各函数中,表⽰同⼀函数的是() A.与y=x+1B.y=x 与(a >0且a≠1)C.与y=x ﹣1D.y=lgx 与题组2 对数函数的定义域4.函数y =1g (1-x )+22x x -++的定义域是() A.[]2,1B.[)1,1- C.[]1,2-D.(]1,2 5.已知函数y =f (x +1)的定义域为[-2,6],则函数y =f (3-4x )的定义域是() A.[]1,1-B.[]3,5-C.35 ,44??-D.13 ,226.函数y=的定义域是()A.(1,2]B.(1,2)C.(2,+∞)D.(﹣∞,2) 7.函数y =+lg (2-x )的定义域是()A.(1,2)B.[1,4]C.(1,2]D.[1,2)8.定义在R 上的函数f(x)的导函数为f′(x),已知f(x +1)是偶函数,(x -1)f′(x)<0.若x 12,则f(x 1)与f(x 2)的⼤⼩关系是()A.f(x 1)B.f(x 1)=f(x 2)C.f(x 1)>f(x 2)D.不确定9.已知全集U =R ,集合?U A ={x |0≤x ≤4},B ={x |x >2},则A ∪B =( ) A.{x |x >2} B.{x |22} 10.函数f(x)264x -log 2(2sin x -1)的定义域是________.11.设函数f (x )=-x +2,则满⾜f (x -1)+f (2x )>0的x 的取值范围是______.12.已知全集U =R ,集合A ={x |x <a },B ═{x |-1<x <2},且A ∪?U B =R ,则实数a 的取值范围是______.题组3 对数函数的实际应⽤13.某种动物繁殖数量 y (只)与时间x (年)的关系为 y =a log 2(x +1),设这种动物第1年有100只,则到第7年它们发展到( )A.300只B.400只C.500只D.600只14.⼀个容器装有细沙3acm ,细沙从容器底下⼀个细微的⼩孔慢慢地均速漏出, min t 后剩余的细沙量为()3bt y ae cm -=,经过8min 后发现容器内还有⼀半的沙⼦,则再经过()min ,容器中的沙⼦只有开始时的⼋分之⼀. A.8B.16C.24D.3215.我们处在⼀个有声世界⾥,不同场合,⼈们对声⾳的⾳量会有不同要求.⾳量⼤⼩的单位是分贝(dB ),对于⼀个强度为I 的声波,其⾳量的⼤⼩η可由如下公式计算:010lgII η=(其中0I 是⼈⽿能听到的声⾳的最低声波强度),则60dB 的声⾳强度1I 是50dB 的声⾳强度2I 的() A.7610倍C.10倍D.7ln 6倍16.对于任意实数x ,符号[]x 表⽰x 的整数部分,即[]x 是不超过x 的最⼤整数,例如[]22=;[]2.12=;则[][][][]3333log 1log 2log 3log 27++++的值为() A.42B.43C.44D.4517.已知某种药物在⾎液中以每⼩时20%的⽐例衰减,现给某病⼈静脉注射了该药物2500mg ,设经过x 个⼩时后,药物在病⼈⾎液中的量为ymg .()1y 与x 的关系式为______;()2当该药物在病⼈⾎液中的量保持在1500mg 以上,才有疗效;⽽低于500mg ,病⼈就有危险,要使病⼈没有危险,再次注射该药物的时间不能超过______⼩时(精确到0.1).(参考数据:0.30.20.6≈, 2.30.80.6≈,7.20.80.2≈,9.90.80.1)≈18.2012年9⽉19⽇凌晨3时10分,中国在西昌卫星发射中⼼⽤“长征三号⼄”运载⽕箭,以“⼀箭双星”⽅式,成功将第14和第15颗北⽃导航卫星发射升空并送⼊预定转移轨道.标志着中国北⽃卫星导航系统快速组⽹技术已⽇臻成熟.若已知⽕箭的起飞重量M 是箭体(包括搭载的飞⾏器)的重量m 和燃料重量x 之和,在不考虑空⽓阻⼒的条件下,假设⽕箭的最⼤速度y 关于x 的函数关系式为:[ln()2)]5ln 2y k m x m =+-+ (其中k≠0).当燃料重量为(1)e m 吨(e 为⾃然对数的底数,2.72e ≈)时,该⽕箭的最⼤速度为5km /s.(1)求⽕箭的最⼤速度y(千⽶/秒)与燃料重量x(吨)之间的关系式()y f x = .(2)已知该⽕箭的起飞重量是816吨,则应装载多少吨燃料,才能使该⽕箭的最⼤飞⾏速度达到10千⽶/秒,顺利地把卫星发送到预定的轨道?专题四不同函数增长的差异19.图中曲线是对数函数log ay x =的图象,已知a 取3,43,35,110四个值,则相应于1C ,2C ,3C ,4C 的a 值依次为( )B.3,43,110,35C.43,3,35,110D.43,3,110,3520.在天⽂学中,天体的明暗程度可以⽤星等或亮度来描述.两颗星的星等与亮度满⾜212152–lg E m m E =,其中星等为m k 的星的亮度为E k (k =1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的⽐值为( ) A.1010.1B.10.1C.lg10.1D.10.110-21.函数()1ln f x x x ??=-的图象⼤致是() A. B.C. D.22.函数2ln 2()||x f x x x =的图象⼤致为()A. B.C. D.23.⾼为H 、满缸⽔量为V 的鱼缸的轴截⾯如图所⽰,现底部有⼀个⼩洞,满缸⽔从洞中流出,若鱼缸⽔深为h 时⽔的体积为v ,则函数()v f h =的⼤致图像是()A. B.C. D.25.已知()()1log 011axf x a a x+=>≠-,(1)求()f x 的定义域;(2)判断()f x 的奇偶性并予以证明; (3)求使()0f x >的x 的取值范围.26.(1)求满⾜不等式()20.50.52log 9log 90x x ++≤的x 的范围. (2)当x 在(1)中求得的范围内变化时,求函数22()log log 24x xf x =?的最⼤值和最⼩值. 专题26 对数函数题组1 对数函数的概念1.给出下列函数:①y =23log x 2;②y =log 3(x -1);③y =log (x +1)x ;④y =log πx .其中是对数函数的有( ) A.1个 B.2个C.3个D.4个【答案】A【解析】①②不是对数函数,因为对数的真数不是只含有⾃变量x ;③不是对数函数,因为对数的底数不是常数;④是对数函数. 故选A2.下列函数,是对数函数的是( ) A.y=lg10xB.y=log 3x 2C.y=lnxD.y=log 13(x –1)【答案】C【解析】由对数函数的定义,形如y=log a x (a>0,a≠1)的函数是对数函数,由此得到:y=lg10x =x ,y=23log x =23log x 、y=()13log 1x -都不是对数函数,只有y=lnx 是对数函数.故选C.3.下列各函数中,表⽰同⼀函数的是() A.与y=x+1【解析】对于选项A :函数的定义域不包含1,⽽⼀次函数y=x+1的定义域是R ,显然不是同⼀个函数.对于选项B :因为=xlog a a=x ,且定义域都为R ,所以为同⼀个函数.对于选项C :函数=|x|﹣1与⼀次函数y=x ﹣1的对应法则不同,故不是同⼀个函数.对于选项D :函数y=lgx 的定义域为x >0,⽽函数y=lgx 2的定义域是x≠0,显然不是同⼀个函数. 故选B.题组2 对数函数的定义域4.函数y =1g (1-x )22x x -++的定义域是() A.[]2,1 B.[)1,1- C.[]1,2-D.(]1,2 【答案】B【解析】要使原函数有意义,则:210,20x x x ->??-++≥? 解得-1≤x <1;∴原函数的定义域是[-1,1). 故选B.5.已知函数y =f (x +1)的定义域为[-2,6],则函数y =f (3-4x )的定义域是() A.[]1,1- B.[]3,5-C.35 ,44??-D.13 ,22-【答案】A【解析】∵函数y=f(x+1)的定义域为[-2,6],即-2≤x≤6,得-1≤x+1≤7,∴f(x)的定义域为[-1,7],由-1≤3-4x≤7,可得-1≤x≤1.∴函数y=f(3-4x)的定义域是[-1,1].故选:A.D.(﹣∞,2)【答案】B【解析】∵log2(x﹣1),∴x﹣1>0,x>1根据,得出x≤2,⼜在分母上不等于0,即x≠2∴函数y=的定义域是(1,2)故选B.7.函数y=+lg(2-x)的定义域是()A.(1,2)B.[1,4]C.(1,2]D.[1,2)【答案】D【解析】由得,由得,两部分取交集为.8.定义在R上的函数f(x)的导函数为f′(x),已知f(x+1)是偶函数,(x-1)f′(x)<0.若x12,则f(x1)与f(x2)的⼤⼩关系是()A.f(x1)B.f(x1)=f(x2)C.f(x1)>f(x2)D.不确定【答案】C【解析】由(x-1)f′(x)<0可知,当x>1时,f′(x)<0,函数递减.当x<1时,f′(x)>0,函数递增;因为函数f(x +1)是偶函数,所以f(x +1)=f(1-x),f(x)=f(2-x),即函数的对称轴为x=1.所以若1f(x2).若x1<1,则x2>2-x1>1,此时由f(x2)f(x2)9.已知全集U=R,集合?U A={x|0≤x≤4},B={x|x>2},则A∪B=( )A.{x|x>2}B.{x|2C.RD.{x|x<0或x>2}【答案】D【解析】∵?U A ={x |0≤x ≤4},∴A ={x |x <0,或x >4}.∴A ∪B ={x |x <0,或x >4}∪{x >2} ={x |x <0,或x >2}.选D10.函数f(x)--?? ? ? ???????【解析】由题意,得2640210x sinx ?-≥?->?,①,②由①得-8≤x ≤8,由②得sin x >12,由正弦曲线得6π+2k ππ+2k π(k ∈Z). 所以不等式组的解集为117513,,,866666πππππ--?? ? ?11.设函数f (x )=-x +2,则满⾜f (x -1)+f (2x )>0的x 的取值范围是______. 【答案】5,3?-∞【解析】根据题意,函数()2f x x =-+,则(1)(2)[(1)2][(2)2]35f x f x x x x -+=--++-+=-+,若(1)(2)0f x f x -+>,即350x -+>,解可得:53x <,即x 的取值范围为5(,)3-∞;故答案为:5(,)3-∞.12.已知全集U =R ,集合A ={x |x <a },B ═{x |-1<x <2},且A ∪?U B =R ,则实数a 的取值范围是______. 【答案】a ≥2【解析】∵全集U=R ,B={x|-1<x <2},∴?U B={x|x≤-1或x≥2},∵A={x|x <a},A ∪(?U B )=R ,∴a≥2,则a 的取值范围为a≥2. 故答案为:a≥2题组3 对数函数的实际应⽤13.某种动物繁殖数量 y (只)与时间x (年)的关系为 y =a log 2(x +1),设这种动物第1年有100只,则到第7年它们发展到( )A.300只B.400只C.500只D.600只【答案】A【解析】由题意,繁殖数量y (只)与时间x (年)的关系为y=alog 2(x+1),这种动物第1年有100只∴100=alog2(1+1),∴a=100,∴y=100log 2(x+1),∴当x=7时,y=100 log 2(7+1)=100×3=300. 故选A.14.⼀个容器装有细沙3acm ,细沙从容器底下⼀个细微的⼩孔慢慢地均速漏出, min t 后剩余的细沙量为3bt y ae cm -=,经过8min 后发现容器内还有⼀半的沙⼦,则再经过()min ,容器中的沙⼦只有开始时的⼋分之⼀. A.8 B.16C.24D.32【答案】B 【解析】依题意有8bae-= 12a ,即8b e -= 12,两边取对数得ln281ln28ln ln228t b b y ae--==-∴=∴= 当容器中只有开始时的⼋分之⼀,则有ln2ln2881188t t aea e --=∴= 两边取对数得ln21ln 3ln22488t t -==-∴=,所以再经过的时间为24-8=16min .故选B. 15.我们处在⼀个有声世界⾥,不同场合,⼈们对声⾳的⾳量会有不同要求.⾳量⼤⼩的单位是分贝(dB ),对于⼀个强度为I 的声波,其⾳量的⼤⼩η可由如下公式计算:010lgII η=(其中0I 是⼈⽿能听到的声⾳的最低声波强度),则60dB 的声⾳强度1I 是50dB 的声⾳强度2I 的()A.76倍 B.7610倍C.10倍D.7ln 6倍【答案】C【解析】解:由题意,令106010I lgI =,解得,61010I I =?,令2210I I = 故选:C.16.对于任意实数x ,符号[]x 表⽰x 的整数部分,即[]x 是不超过x 的最⼤整数,例如[]22=;[]2.12=;则[][][][]3333log 1log 2log 3log 27++++的值为() A.42 B.43 C.44 D.45【答案】D【解析】由题意可知:3[log 1]0=,3[log 3]1=,3[log 27]3=[]33333[log 1][log 2][log 3][log 26log 27]+++?++00111111222223=++++++++++++?+++,(6个1,18个2) 62183=+?+45=.故选:D .17.已知某种药物在⾎液中以每⼩时20%的⽐例衰减,现给某病⼈静脉注射了该药物2500mg ,设经过x 个⼩时后,药物在病⼈⾎液中的量为ymg .()1y 与x 的关系式为______;()2当该药物在病⼈⾎液中的量保持在1500mg 以上,才有疗效;⽽低于500mg ,病⼈就有危险,要使病⼈没有危险,再次注射该药物的时间不能超过______⼩时(精确到0.1).(参考数据:0.30.20.6≈, 2.30.80.6≈,7.20.80.2≈,9.90.80.1)≈【答案】25000.8xy =? 7.2【解析】()1由题意知,该种药物在⾎液中以每⼩时20%的⽐例衰减,给某病⼈注射了该药物2500mg ,经过x 个⼩时后,药物在病⼈⾎液中的量为()2500(120%)25000.8x xy mg =?-=?,即y 与x 的关系式为25000.8xy =?;()2当该药物在病⼈⾎液中的量保持在1500mg 以上,才有疗效;⽽低于500mg ,病⼈就有危险,令25000.8500x ?≥,0.80.2x ∴≥,7.20.80.2≈,0.8xy =是单调减函数,7.2x ∴≤,所以要使病⼈没有危险,再次注射该药物的时间不能超过7.2⼩时. 故答案为()125000.8xy =?,()27.2.18.2012年9⽉19⽇凌晨3时10分,中国在西昌卫星发射中⼼⽤“长征三号⼄”运载⽕箭,以“⼀箭双星”⽅式,成功将第14和第15颗北⽃导航卫星发射升空并送⼊预定转移轨道.标志着中国北⽃卫星导航系统快速组⽹技术已⽇臻成熟.若已知⽕箭的起飞重量M 是箭体(包括搭载的飞⾏器)的重量m 和燃料重量x 之和,在不考虑空⽓阻⼒的条件下,假设⽕箭的最⼤速度y 关于x 的函数关系当燃料重量为1)m 吨(e 为⾃然对数的底数,2.72e ≈)时,该⽕箭的最⼤速度为5km /s.(1)求⽕箭的最⼤速度y(千⽶/秒)与燃料重量x(吨)之间的关系式()y f x = .(2)已知该⽕箭的起飞重量是816吨,则应装载多少吨燃料,才能使该⽕箭的最⼤飞⾏速度达到10千⽶/秒,顺利地把卫星发送到预定的轨道? 【答案】(1) 10ln()m x y m+= (2) 应装载516吨【解析】(1)依题意,把)1,5x m y ==代⼊函数关系())ln ln5ln2y k m x ??=+-+?,解得k=10,所以所求的函数关系式为())10ln ln5ln2y m x ??=+-+=?10ln m x m +?? ???(2)设应装载x 吨燃料⽅能满⾜题意,此时816,10m x y =-=,代⼊函数关系式10ln m x y m +??= ?,得816ln1816x =-,解得516x =吨,故应装载516吨燃料⽅能顺利地把飞船发送到预定的轨道.专题四不同函数增长的差异19.图中曲线是对数函数log a y x=的图象,已知a取3,43,35,110四个值,则相应于1C,2C,3C,4C的a值依次为()343,35,110343,35C.433,35,110D.433110,35【答案】A【解析】由已知中曲线是对数函数log a y x=的图象,由对数函数的图象和性质,可得1C,2C,3C,4C的a值从⼩到⼤依次为:C,2C,1C,由a343,35,110四个值,故1C,2C,3C,4C的a3,43,35,110,故选:A.20.在天⽂学中,天体的明暗程度可以⽤星等或亮度来描述.两颗星的星等与亮度满⾜212152–lgEm mE=,其中星等为m k的星的亮度为E k(k=1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的⽐值为( )A.1010.1B.10.1C.lg10.1D.10.110-【答案】A【解析】两颗星的星等与亮度满⾜12125lg2Em mE-=,令211.45,26.7m m=-=-,()10.111212222lg( 1.4526.7)10.1,1055E Em mE E=?-=-+==.故选A.21.函数()1ln f x x x ??=-的图象⼤致是() A. B.C. D.【答案】B【解析】当2x =时,110x x-=>,函数有意义,可排除A ;当2x =-时,1302x x -=-<,函数⽆意义,可排除D ;⼜∵当1x >时,函数1 y x x=-单调递增,结合对数函数的单调性可得函数()1ln f x x x ?=-单调递增,可排除C ;故选B.22.函数2ln 2()||x f x x x =的图象⼤致为()A. B.C. D.【答案】B【解析】函数()f x 的定义域为{}|0x x ≠,⼜()()()2222ln ()||ln x x x f x f x x x x---===---,所以函数()f x 是奇函数,故排除A ,C ;⼜因为11()2ln 024f =<,故排除D. 故选:B23.⾼为H 、满缸⽔量为V 的鱼缸的轴截⾯如图所⽰,现底部有⼀个⼩洞,满缸⽔从洞中流出,若鱼缸⽔深为h 时⽔的体积为v ,则函数()v f h =的⼤致图像是()A. B.C. D.【答案】B【解析】根据题意知,函数的⾃变量为⽔深h ,函数值为鱼缸中⽔的体积,所以当0h =时,体积0v =,所以函数图像过原点,故排除A 、C ;再根据鱼缸的形状,下边较细,中间较粗,上边较细,所以随着⽔深的增加,体积的变化速度是先慢后快再慢的,故选B.24.下列散点图中,估计有可能⽤函数lg (0)y a b x b =+>来模拟的是()A. B.C. D.【答案】C【解析】由于函数lg y x =在定义域内单调递增,且是上凸的,⼜0b >,所以当0x >时,lg (0)y a b x b =+>的图象是单调递增且上凸的. 故选:C.25.已知()()1log 011axf x a a x+=>≠-, (1)求()f x 的定义域;(2)判断()f x 的奇偶性并予以证明; (3)求使()0f x >的x 的取值范围.【答案】(1)()1,1-;(2)见解析;(3)见解析. 【解析】(1)由>0 ,解得x ∈(-1,1).(2)f(-x)=log a=-f(x),且x ∈(-1,1),∴函数y =f(x)是奇函数.(3)若a>1,f(x)>0,则>1,解得00,则0<<1,解得-126.(1)求满⾜不等式()20.50.52log 9log 90x x ++≤的x 的范围. (2)当x 在(1)中求得的范围内变化时,求函数22()log log 24x xf x =?的最⼤值和最⼩值. 【答案】(1)228x ≤≤;(2)max ()2f x =.min1()4f x =-.【解析】(1)令0.5log t x =,则原不等式可化为22990t t ++≤,由⼆次函数图象解得332 t -≤≤-,即0.533log 2x -≤≤-.⼜30.53log 0.5--=,320.53log 0.52--=,∴3320.50.5x --≤≤,即8x ≤≤.(2)将()f x 变形为关于2log x 的形式:()()22222()log 1log 2log 3log 2f x x x x x =-?-=-+2231log 24x ?=--.由(1)知23log 32x ≤≤.∴当23log 2x =,即x =min 1()4f x =-;当2log 3x =,即8x =时,max ()2f x =.。
高一数学对数函数练习题
高一数学对数函数练习题高一数学对数函数练习题在高中数学中,对数函数是一个非常重要的概念。
它在各个领域都有广泛的应用,尤其是在科学和工程领域。
对数函数的特点是可以将复杂的指数运算转化为简单的加减运算,从而简化计算过程。
为了帮助同学们更好地理解和掌握对数函数,下面将给出一些高一数学对数函数练习题。
练习题一:已知log2(x) = 3,求x的值。
解析:根据对数函数的定义,log2(x) = 3 可以转化为2^3 = x,即x = 8。
练习题二:已知log3(a) = 2,求a的值。
解析:根据对数函数的定义,log3(a) = 2 可以转化为3^2 = a,即a = 9。
练习题三:已知log5(b) = -2,求b的值。
解析:根据对数函数的定义,log5(b) = -2 可以转化为5^(-2) = b,即b = 1/25。
练习题四:已知log4(c) = 1/2,求c的值。
解析:根据对数函数的定义,log4(c) = 1/2 可以转化为4^(1/2) = c,即c = 2。
练习题五:已知loga(1/8) = -3/2,求a的值。
解析:根据对数函数的定义,loga(1/8) = -3/2 可以转化为a^(-3/2) = 1/8,即a = (1/8)^(-2/3) = 2。
练习题六:已知logb(27) = 1/3,求b的值。
解析:根据对数函数的定义,logb(27) = 1/3 可以转化为b^(1/3) = 27,即b = 27^3 = 19683。
练习题七:已知log2(x) + log2(x + 8) = 4,求x的值。
解析:根据对数函数的性质,log2(x) + log2(x + 8) = log2(x(x + 8))。
所以,log2(x(x + 8)) = 4 可以转化为2^4 = x(x + 8),即16 = x^2 + 8x。
整理得到x^2 + 8x - 16 = 0,解这个二次方程可以得到x的值。
专题09 对数与对数函数(重难点突破)原卷版附答案.pdf
ab 2b
2
.
11
(2). 求下列函数的定义域: 1
(1)f(x)=lg(x-2)+x-3;(2)f(x)=log(x+1)(16-4x). 【解析】 (1)要使函数有意义,需满足Error!解得 x>2 且 x≠3, 所以函数定义域为(2,3)∪(3,+∞). (2)要使函数有意义,需满足Error!解得-1<x<0 或 0<x<4, 所以函数定义域为(-1,0)∪(0,4).
底数,N 叫做真数.
重难点二 对数的性质、换底公式与运算性质
(1)对数的性质:①alogaN=N;②logaab=b(a>0,且 a≠1). (2)对数的运算法则
如果 a>0 且 a≠1,M>0,N>0,那么 ①loga(MN)=logaM+logaN;
M ②loga N =logaM-logaN;
B. y ln(2 x) C. y ln(1 x)
D.
3
y ln(2 x)
(3).函数 f(x)=ax-b 的图象如图所示,其中 a,b 为常数,则下列结论正确的是( )
A.a>1,b<0
B.a>1,b>0
C.0<a<1,b>0
D.0<a<1,b<0
(4).当 a>1 时,在同一坐标系中,函数 y=a-x 与 y=logax 的图象为( )
例 2 求下列函数的定义域:
1
1
(1)f(x)=
;(2)f(x)= +ln(x+1);
1
2-x
log x+1
2
1
1
【解析】(1)要使函数 f(x)有意义,则 log x+1>0,即 log x>-1,解得 0<x<2,即函数 f(x)的定义
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A 组 基础对点练1.函数y =1log 2(x -2)的定义域是( )A .(-∞,2)B .(2,+∞)C .(2,3)∪(3,+∞)D .(2,4)∪(4,+∞)解析:要使函数有意义,应满足⎩⎪⎨⎪⎧x -2>0,log 2(x -2)≠0,即⎩⎪⎨⎪⎧x >2,x -2≠1,解得x >2且x ≠3.故选C. 答案:C2.设a =⎝⎛⎭⎫12,b =log 2,c =log 123,则( ) A .a >b >c B .a >c >b C .b >c >aD .c >a >b解析:∵b =-log 32∈(-1,0),c =-log 23<-1,a =⎝⎛⎭⎫1213>0,∴a >b >c ,选A. 答案:A3.(2016·高考全国卷Ⅱ)下列函数中,其定义域和值域分别与函数y =10lg x 的定义域和值域相同的是( )A .y =xB .y =lg xC .y =2xD .y =1x解析:函数y =10lg x 的定义域为(0,+∞),又当x >0时,y =10lg x =x ,故函数的值域为(0,+∞).只有D 选项符合.答案:D4.函数y =⎩⎪⎨⎪⎧3x ,x ∈(-∞,1),log 2x ,x ∈[1,+∞)的值域为( )A .(0,3)B .[0,3]C .(-∞,3]D .[0,+∞)解析:当x <1时,0<3x <3;当x ≥1时,log 2x ≥log 21=0,所以函数的值域为[0,+∞).答案:D5.(2018·焦作模拟)若函数y =a |x |(a >0,且a ≠1)的值域为{y |y ≥1},则函数y =log a |x |的图象大致是( )解析: 若函数y =a |x |(a >0,且a ≠1)的值域为{y |y ≥1},则a >1,故函数y =log a |x |的大致图象如图所示.故选B. 答案:B6. 已知函数y =log a (x +c )(a ,c 为常数,其中a >0,a ≠1)的图象如图,则下列结论成立的是( )A .a >1,c >1B .a >1,0<c <1C .0<a <1,c >1D .0<a <1,0<c <1解析:由对数函数的性质得0<a <1,因为函数y =log a (x +c )的图象在c >0时是由函数y =log a x 的图象向左平移c 个单位得到的,所以根据题中图象可知0<c <1.答案:D7.(2018·吉安模拟)如果log 12x <log 12y <0,那么( )A .y <x <1B .x <y <1C .1<x <yD .1<y <x解析:因为y =log 12x 在(0,+∞)上为减函数,所以x >y >1.答案:D8.函数y =x 2ln|x ||x |的图象大致是( )解析:易知函数y =x 2ln |x ||x |是偶函数,可排除B ,当x >0时,y =x ln x ,y ′=ln x +1,令y ′>0,得x >e -1,所以当x >0时,函数在(e -1,+∞)上单调递增,结合图象可知D 正确,故选D.答案:D9.已知f (x )是定义在R 上的偶函数,且在区间(-∞,0]上单调递增,若实数a 满足()()3log 22a f f >-,则a 的取值范围是( )A .(-∞,3)B .(0,3)C .(3,+∞)D .(1,3)解析:本题主要考查函数的奇偶性及单调性.∵f (x )是定义在R 上的偶函数,且在区间(-∞,0]上单调递增,∴f (x )在区间[0,+∞)上单调递减.根据函数的对称性,可得f (-2)=f (2),∴f (2log 3a )>f (2).∵2log 3a >0,f (x )在区间[0,+∞)上单调递减,∴0<2log 3a <2⇒log 3a <12⇒0<a <3,故选B.答案:B10.已知函数y =f (x )是定义在R 上的偶函数,当x ∈(-∞,0]时,f (x )为减函数,若a =f (20.3),b =f (log 124),c =f (log 25),则a ,b ,c 的大小关系是( )A .a >b >cB .c >b >aC .c >a >bD .a >c >b解析:函数y =f (x )是定义在R 上的偶函数, 当x ∈(-∞,0]时,f (x )为减函数, ∴f (x )在[0,+∞)上为增函数, ∵b =f (log 4)=f (-2)=f (2), 又1<20.3<2<log 25,∴c >b >a .故选B. 答案:B11.已知b >0,log 5b =a ,lg b =c,5d =10,则下列等式一定成立的是( ) A .d =ac B .a =cd C .c =adD .d =a +c解析:由已知得5a =b,10c =b ,∴5a =10c ,∵5d =10,∴5dc =10c ,则5dc =5a ,∴dc =a ,故选B.答案:B12.已知函数f (x )=ln(1+4x 2-2x )+3,则f (lg 2)+f ⎝⎛⎭⎫lg 12=( ) A .0 B .-3 C .3D .6解析:由函数解析式,得f (x )-3=ln(1+4x 2-2x ),所以f (-x )-3=ln(1+4x 2+2x )=ln11+4x 2-2x=-ln(1+4x 2-2x )=-[f (x )-3],所以函数f (x )-3为奇函数,则f (x )+f (-x )=6,于是f (lg 2)+f ⎝⎛⎭⎫lg 12=f (lg 2)+f (-lg 2)=6.故选D. 答案:D13.已知4a =2,lg x =a ,则x =________.解析:∵4a =2,∴a =12,又lg x =a ,x =10a =10.答案:1014.已知f (x )是定义在R 上的奇函数,当x >0时,f (x )=log 2x -1,则f ⎝⎛⎭⎫-22=________. 解析:因为f (x )是定义在R 上的奇函数,所以f ⎝⎛⎭⎫-22=-f ⎝⎛⎭⎫22=-⎝⎛⎭⎫log 222-1=32. 答案:3215.函数f (x )=log 2(-x 2+22)的值域为________.解析:由题意知0<-x 2+22≤22=232,结合对数函数图象(图略),知f (x )∈⎝⎛⎦⎤-∞,32,故答案为⎝⎛⎦⎤-∞,32. 答案:⎝⎛⎦⎤-∞,32 16.若log 2a 1+a 21+a <0,则a 的取值范围是________.解析:当2a >1时,∵log 2a 1+a 21+a <0=log 2a 1,∴1+a 21+a <1.∵1+a >0,∴1+a 2<1+a , ∴a 2-a <0,∴0<a <1,∴12<a <1.当0<2a <1时,∵log 2a 1+a 21+a <0=log 2a 1,∴1+a 21+a>1. ∵1+a >0,∴1+a 2>1+a .∴a 2-a >0,∴a <0或a >1,此时不合题意. 综上所述,a ∈⎝⎛⎭⎫12,1. 答案:⎝⎛⎭⎫12,1B 组 能力提升练1.已知函数f (x )=⎩⎪⎨⎪⎧⎝⎛⎭⎫12x ,x ≥4f (x +1),x <4,则f (1+log 25)的值为( )A.14B.⎝⎛⎭⎫121+log 25C.12D.120解析:∵2<log 25<3,∴3<1+log 25<4,则4<2+log 25<5,f (1+log 25)=f (1+1+log 25)=f (2+log 25)=⎝⎛⎭⎫12=14×⎝⎛⎭⎫12=14×15=120,故选D. 答案:D2.(2018·四川双流中学模拟)已知a =log 29-log 23,b =1+log 27,c =12+log 213,则( )A .a >b >cB .b >a >cC .c >a >bD .c >b >a解析:a =log 29-log 23=log 233,b =1+log 27=log 227,c =12+log 213=log 226,因为函数y =log 2x 是增函数,且27>33>26,所以b >a >c ,故选B.答案:B3.设f (x )=lg ⎝⎛⎭⎫21-x +a 是奇函数,则使f (x )<0的x 的取值范围是( )A .(-1,0)B .(0,1)C .(-∞,0)D .(-∞,0)∪(1,+∞)解析:∵f (x )=lg ⎝⎛⎭⎫21-x +a 是奇函数,∴对定义域内的x 值,有f (0)=0, 由此可得a =-1,∴f (x )=lg 1+x1-x, 根据对数函数单调性,由f (x )<0,得0<1+x1-x <1,∴x ∈(-1,0).答案:A4.已知a ,b >0,且a ≠1,b ≠1.若log a b >1,则( ) A .(a -1)(b -1)<0 B .(a -1)(a -b )>0 C .(b -1)(b -a )<0D .(b -1)(b -a )>0解析:根据题意,log a b >1⇔log a b -log a a >0⇔log a ba>0⇔⎩⎪⎨⎪⎧ 0<a <10<ba <1或⎩⎪⎨⎪⎧a >1b a>1,即⎩⎪⎨⎪⎧ 0<a <10<b <a 或⎝ ⎛ a >1b >a .当⎩⎪⎨⎪⎧ 0<a <10<b <a 时,0<b <a <1,∴b -1<0,b -a <0;当⎩⎪⎨⎪⎧a >1b >a 时,b >a >1,∴b -1>0,b -a >0.∴(b -1)(b -a )>0.故选D. 答案:D5.已知函数f (x )是定义在(-∞,+∞)上的奇函数,若对于任意的实数x ≥0,都有f (x +2)=f (x ),且当x ∈[0,2)时,f (x )=log 2(x +1),则f (2 014)+f (-2 015)+f (2 016)的值为( )A .-1B .-2C .2D .1解析:∵当x ≥0时,f (x +2)=f (x ),∴f (2 014)=f (2 016)=f (0)=log 21=0,∵f (x )为R 上的奇函数,∴f (-2 015)=-f (2 015)=-f (1)=-1.∴f (2 014)+f (-2 015)+f (2 016)=0-1+0=-1.故选A.答案:A6.设函数f (x )=ln(1+x )-ln(1-x ),则f (x )是( ) A .奇函数,且在(0,1)上是增函数 B .奇函数,且在(0,1)上是减函数 C .偶函数,且在(0,1)上是增函数 D .偶函数,且在(0,1)上是减函数解析:由题意可得,函数f (x )的定义域为(-1,1),且f (x )=ln1+x1-x=ln ⎝⎛⎭⎫21-x -1,易知y =21-x -1在(0,1)上为增函数,故f (x )在(0,1)上为增函数,又f (-x )=ln(1-x )-ln(1+x )=-f (x ),故f (x )为奇函数,选A.答案:A7.已知f (x )是偶函数,且在[0,+∞)上是减函数,若f (lg x )>f (2),则x 的取值范围是( ) A.⎝⎛⎭⎫1100,1 B.⎝⎛⎭⎫0,1100∪(1,+∞) C.⎝⎛⎭⎫1100,100D .(0,1)∪(100,+∞)解析:不等式可化为⎩⎪⎨⎪⎧ lg x ≥0lg x <2或⎩⎪⎨⎪⎧lg x <0-lg x <2,解得1≤x <100或1100<x <1.∴1100<x <100.故选C. 答案:C8.已知函数f (x )=|log 12x |,若m <n ,有f (m )=f (n ),则m +3n 的取值范围是( )A .[23,+∞)B .(23,+∞)C .[4,+∞)D .(4,+∞)解析:由f (x )=|log 12x |,m <n ,f (m )=f (n )可知,log 12m =-log 12n >0,从而0<m =1n <1,m+3n =m +3m (0<m <1),若直接利用基本不等式,则m +3m ≥23(当且仅当m =3m =3时取得最小值,但这与0<m <1矛盾),利用函数g (x )=x +3x 的单调性(定义或导数)判断当0<x <1时g (x )单调递减,故g (x )>g (1)=4,可知选D.答案:D9.已知函数y =f (x )(x ∈D ),若存在常数c ,对于∀x 1∈D ,存在唯一x 2∈D ,使得f (x 1)+f (x 2)2=c ,则称函数f (x )在D 上的均值为c .若f (x )=lg x ,x ∈[10,100],则函数f (x )在[10,100]上的均值为( )A .10 B.34 C.710D.32解析:因为f (x )=lg x (10≤x ≤100),则f (x 1)+f (x 2)2=lg x 1x 22等于常数c ,即x 1x 2为定值,又f (x )=lg x (10≤x ≤100)是增函数,所以取x 1=10时,必有x 2=100,从而c 为定值32.选D.答案:D10.已知函数f (x )=(e x -e -x )x ,f (log 5x )+f (log 15x )≤2f (1),则x 的取值范围是( )A.⎣⎡⎦⎤15,1 B .[1,5] C.⎣⎡⎦⎤15,5D.⎝⎛⎦⎤-∞,15∪[5,+∞) 解析:∵f (x )=(e x -e -x )x ,∴f (-x )=-x (e -x -e x )=(e x -e -x )x =f (x )(x ∈R ),∴函数f (x )是偶函数. ∵f ′(x )=(e x -e -x )+x (e x +e -x )>0在(0,+∞)上恒成立. ∴函数f (x )在(0,+∞)上单调递增. ∵f (log 5x )+f (log 15x )≤2f (1),∴2f (log 5x )≤2f (1),即f (log 5x )≤f (1), ∴|log 5x |≤1,∴15≤x ≤5.故选C.答案:C11.设方程log 2x -⎝⎛⎭⎫12x =0与log 14x -⎝⎛⎭⎫14x=0的根分别为x 1,x 2,则( ) A .0<x 1x 2<1 B .x 1x 2=1 C .1<x 1x 2<2D .x 1x 2≥2解析:方程log 2x -⎝⎛⎭⎫12x =0与log 14x -⎝⎛⎭⎫14x =0的根分别为x 1,x 2,所以log 2x 1=⎝⎛⎭⎫12x 1,log 14x 2=⎝⎛⎭⎫14x 2,可得x 2=12,令f (x )=log 2x -⎝⎛⎭⎫12x ,则f (2)f (1)<0,所以1<x 1<2,所以12<x 1x 2<1,即0<x 1x 2<1.故选A.答案:A12.(2017·江西红色七校模拟)已知函数f (x )=lne x e -x,若 f ⎝⎛⎭⎫e 2 013+f ⎝⎛⎭⎫2e 2 013+…+f ⎝⎛⎭⎫2 012e 2 013=503(a +b ),则a 2+b 2的最小值为( ) A .6 B .8 C .9D .12解析:∵f (x )+f (e -x )=ln e x e -x +ln e (e -x )x =ln e 2=2,∴503(a +b )=f ⎝⎛⎭⎫e 2 013+f ⎝⎛⎭⎫2e 2 013+…+f ⎝⎛⎭⎫2 012e 2 013=12⎣⎡ f ⎝⎛⎭⎫e 2 013+f ⎝⎛⎭⎫2 012e 2 013+f ⎝⎛⎭⎫2e 2 013+f ⎝⎛⎭⎫2 011e 2 013+…+f ⎝⎛⎭⎫2 012e 2 013+f⎦⎤⎝⎛⎭⎫e 2 013=12×(2×2 012)=2 012, ∴a +b =4,∴a 2+b 2≥(a +b )22=422=8,当且仅当a =b =2时取等号. ∴a 2+b 2的最小值为8. 答案:B13.若函数f (x )=⎩⎪⎨⎪⎧log a x , x >2,-x 2+2x -2, x ≤2(a >0,且a ≠1)的值域是(-∞,-1],则实数a 的取值范围是________.解析:x ≤2时,f (x )=-x 2+2x -2=-(x -1)2-1, f (x )在(-∞,1)上递增,在(1,2]上递减,∴f (x )在(-∞,2]上的最大值是-1,又f (x )的值域是(-∞,-1],∴当x >2时, log a x ≤-1,故0<a <1,且log a 2≤-1, ∴12≤a <1. 答案:⎣⎡⎭⎫12,114.(2018·湘潭模拟)已知函数f (x )=ln x 1-x ,若f (a )+f (b )=0,且0<a <b <1,则ab 的取值范围是________.解析:由题意可知ln a 1-a +ln b1-b=0,即ln ⎝⎛⎭⎫a 1-a ×b 1-b =0,从而a 1-a ×b1-b =1,化简得a +b =1,故ab =a (1-a )=-a 2+a =-⎝⎛⎭⎫a -122+14,又0<a <b <1,∴0<a <12,故0<-⎝⎛⎭⎫a -122+14<14. 答案:⎝⎛⎭⎫0,14。
