第六章定积分的应用例题

合集下载

CH6(1)定积分——典型例题

典型例题7
例7 求 4 lnsin 2 xdx.
解
0
令 2x t,
4
lnsin 2 xdx
1
2 lnsin tdt.
0
20
I 4 lnsin 2xdx 4 ln(2sin xcos x)dx
0
0
4 (ln 2 lnsin x lncos x)dx
0
ln 2 4 ln 2
故f f x < 0，从而F ( x) < 0, a < < x.
F x < F a 0 x a,b
F b < 0即得证.
THANK YOU
2 0
sin
sin x
x cos
x
dx,
J
2 0
sin
cos x
x cos
x
dx,
I J
2
dx
,
0
2
I J
2 0
sin sin
x x
cos cos
x x
dx
2
d(cos
x
sin
x
)
0 sin x cos x
0.
故得 2I , 2
即
I
.
4
典型例题
典型例题6
例6 求 ln2 1 e2 x dx. 0
x 0 ln 2
解令 ex sin t,
t
x lnsin t , dx cos t dt .
2
6
sin t
原式
6 2
cos
t(
cos t sin t
)dt
2 6
cos2 t sin t
dt

ch6定积分及其应用——定积分应用典型例题

第六章定积分及其应用定积分应用习题课典型例题典型例题1例1 由 1. 求其所围成的图形的面积.⎪⎭⎫ ⎝⎛≤≤===40cos ,sin ,0πx x y x y x 所围的平面图形如图所示0xy 14πxy sin =xy cos =2. 它绕x 轴旋转而成的旋转体体积解()4cos sin d A x x x π=-⎰[]12cos sin 40-=+=πx x 1. 2. ()4220cos sin d V x x xππ=-⎰4cos2d x xππ=⎰22sin 240πππ=⎥⎦⎤⎢⎣⎡=x 0xy 14πxy sin =xy cos =典型例题典型例题2例2 求抛物线21x y -=在(0,1) 内的一条切线, 使它与两坐标轴和抛物线所围图形的面积最小.解设抛物线上切点为)1,(2x x M -则该点处的切线方程为)(2)1(2x X x x Y --=--它与 x , y 轴的交点分别为,)0,(212xx A +)1,0(2+x B 所指面积=)(x S 22(1)122x x+12(1)d x x--⎰22(1)243x x+=-oxyM1B 1A=')(x S )13()1(22412-⋅+x x x ,33<x 0)(<'x S ,33>x 0)(>'x S 且为最小点 .故所求切线为3433Y X =-+,0)(='x S 令得[ 0 , 1] 上的唯一驻点33=x ,]1,0[)(33上的唯一极小点在是因此x S x =oxyM1B 1A典型例题典型例题3例3 设非负函数()[0,1]f x 在上满足()()x f x f x '=曲线)(x f y =与直线1=x 及坐标轴所围图形(1) 求函数;)(x f (2) a 为何值时，所围图形绕 x 轴一周所得旋转体体积最小？解 (1)时，当0≠x 由方程得a xx f x f x 23)()(2=-'[]a x x f 23)(=',223x a +面积为 2 ,即xC x a x f +=223)(故得又⎰=10d )(2x x f ()x x C x a d 23210+=⎰22Ca +=a C -=4xa x a x f )4(23)(2-+=(2) 旋转体体积V x x f d )(102⎰=π()1610132++=a a π(),01513=+='a V π令5-=a 得又V ''5-=a ,015>=π5-=∴a 为唯一极小点,因此5-=a 时 V 取最小值 .x o y 1典型例题典型例题4轴所围图及表示x t x x f y t V )0(,)()(>==例4 设)(x f y =在 x ≥0 时为连续的非负函数, 且,0)0(=f 形绕直线 x ＝t 旋转一周所成旋转体体积 ,证明:.)(2)(t f t V π=''x)(x f xoyt证利用柱壳法xx f x t V d )()(2d -=π则xx f x t t V td )()(2)(0-=⎰πx x f t t d )(20⎰=πx x f x td )(20⎰-πx x f t V t d )(2)(0⎰='π)(2t f t π+)(2t f t π-()2().V t f t π''=故典型例题典型例题5例5 求曲线132--=x y 与 x 轴围成的封闭图形绕直线 y ＝3 旋转所得旋转体的体积.故旋转体体积为=V 432⋅⋅πx x d )]2(3[2122⎰+--π1222221362(1)d 2(1)d x x x xπππ=----⎰⎰222=362(1)d x xππ--⎰448.15π=解利用对称性 ,⎩⎨⎧=y 10≤≤x ,22+x 21≤<x ,42x -在第一象限 xx d )]4(3[22122⎰---πo xy A 123BC典型例题典型例题6)d 5(d x u =故所求旋转体体积为x x xd 5)2(2251⋅-⋅=π165.75π=xx x V d 5)2(222051-=⎰πu V d d 2ρπ=旋转所得旋转体体积.解曲线与直线的交点坐标为),4,2(A 曲线上任一点)4,(2x x x P -到直线x y 2=的距离为xx 2251-=ρ),(2如图为数轴以u x y =则2oxyA)d 5(d x u =故所求旋转体体积为xx xd 5)2(2251⋅-⋅=π165.75π=xx x V d 5)2(222051-=⎰πu V d d 2ρπ=旋转所得旋转体体积.解曲线与直线的交点坐标为),4,2(A 曲线上任一点)4,(2x x x P -到直线x y 2=的距离为xx 2251-=ρ),(2如图为数轴以u x y =则2oxyA典型例题典型例题7解方法一)()()()1(x C x R x L '-'='边际利润xx x L 02.018202.020)(-=--='故得9000)(=='x x L 得驻点令()0.020L x ''=-<又.900件时，总利润最大当产量为∴9500(2)(90050)(180.02)d 8075()L x x +=-=⎰元.807550900元件，总利润为件又多生产即从8000(3)(800)(180.02)d 8000()L x x =-=⎰元.8000800元件时的总利润为即生产方法二(0)0C =Q 固定成本为x x C 2)(=∴2(0)200.01R x x=+-(0)0R =Q 201.020)(x x x R -=∴总利润函数为∴xx x x C x R x L 201.020)()()(2--=-=201.018)(x x x L -=即2()(0)2d (0)2C x C x C x =+=+⎰先求总成本函数0()(0)(200.02)d x R x R x x =+-⎰总收入为9000)(=='x x L 解得令()0.020L x ''=-<Q 件时，总利润最大．当产量为900∴)(807595001.095018)50900()2(2元=⨯-⨯=+L 元．总利润为件时，件多生产即从产量为807550900)(800080001.080018)800()3(2元=⨯-⨯=L 元．件时的总利润为即生产8000800201.018)()1(xx x L -='典型例题典型例题8例8某企业购置一台设备需购置成本1000元，在10年中每年收益为200元，若连续利率为5%，假设购置的设备在10年后完全失去价值，求价值的资本价值．100.050200d 1000t v e t -=-⎰0.0510200(1)10000.05e -⨯=--)(88.573元≈元．即收益的资本价值为88.573是有限的，为而资本价值仍若收益流量是无限期的,0.05200lim[(1)1000]0.0520010003000().0.5t t v e -→+∞=--=-=元解THANK YOU。

第六章定积分的应用

d
0
2
2a
2
cos
2
2
0
2 a2(1 cos )2 a2 sin2 d 8a 0
24
四、变力沿直线段作功
恒力作功：W F s
设有一变力F(x)随位移x而变，求它把物体由 a 移动到 b 所作
的功。 F(x)
•
••
Oa
bX
取 x为积分变量，它的变化区间为[a, b]，
于是变力F x所做的功为：
20
解建立直角坐标系如图。
－R
则底圆的方程为：x2 y2 R2
过任意点 x R, R作垂直于 x 轴的
O
Y
截面，截面为一直角三角形，
x x2 y2 R2
它的两条直角边的长分别为 R2 x2 及
RX
R2 x2 tan , 因而截面积为 A( x) 1 (R2 x2 )tan
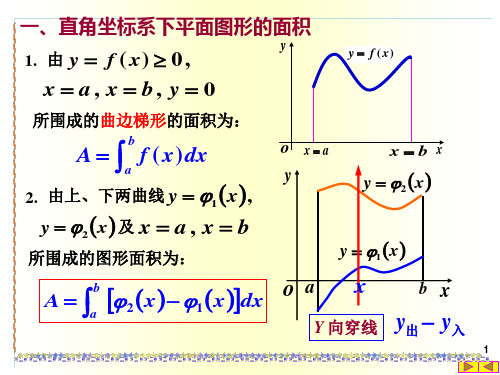
一、直角坐标系下平面图形的面积
y
1. 由 y f ( x) 0 ,
y f (x)
x a, x b, y 0
所围成的曲边梯形的面积为：
b
A a f ( x) dx
2. 由上、下两曲线 y 1x,
y 2x及 x a , x b
所围成的图形面积为：
o xa
y
xb x
y 2x
y 1x
x
1 x
dx
x2 2
ln
2 x
1
3 2
ln
2
2. y e x , y e x 与直线x 1.
解如图所示, 所求面积为
A 1 e x e x dx 0
ex ex
1 0
e e1 2
y x
1,1

定积分及其应用

①.若a=b, 则
b
f (x)dx 0.
a
②.若a>b, 则
b
a
f(x)dx f(x)dx.
a
b
从而可消除对定积分上下限的大小限制.
四.定积分的几何意义
由定义1知, 当连续函数
f (x) 0 且a<b时, 定积分
b f ( x ) d x 表示一个在 x 轴上方的曲边梯形的面积; a
当 f (x) 0, 且 a < b时,
[a, b]的一个局部(小区间)来看, 它也是一个变量;
但因ƒ(x)连续, 从而当Δ x →0时, Δy→0,
故可将此区间的高近似看为一个常量,
从而此区间对应的小窄曲边梯形CEFH
y
y=ƒ(x)
A
C
B
Δy {
DH
的面积近似等于小窄矩形DEFH的面积.
oa
EF
x x+Δx b x
因而, 如果把区间[a, b]任意地划分为n个小区间, 并在每一
就有定积分的定义:
定义1.设ƒ(x)在[a, b]上有定义, 点 a x 0 x 1 x 2 x n 1 x n b
将区间[a, b]任意地划分为n个小区间; 每个小区间
[ xi1 , xi ]
的长度为 xi xi xi1(i1,2, ,n),在每个小区间 [ xi1 , xi ]
n
个区间上任取一点, 再以该点的高来近似代替该小区间上窄曲边梯形的高, 从而每个窄曲边梯形就可近似地
视为一个小窄矩形, 而且全部窄矩形的面积之和也可作为曲边梯形面积的近似值.
要想得精确值, 只需区间[a, b]的分法无限细密(即每个小区间的长度Δ x →0)时, 全部窄矩形的面积之和的极限一定是曲边

第六章定积分的应用经典例题

第六章定积分的应用例8 求出12222≤+by ax 和12222≤+ay bx 的图形的公共部分的面积（其中0>>b a ）.解如图(见系统演示)，由对称性可知，所求面积为阴影部分面积的8倍，且线段OA 在直线x y =上. 令,sin ,cos θθr y r x ==代入方程12222=+ay bx得其极坐标方程为θθ2222222sin cos b a ba r +=于是所求面积可表示为 θθθθθππd b a ba d r S ⎰⎰+=⨯=422222242sin cos 4)(218.tan4tan arctan 14422ab abacr a b ab b a =⎪⎭⎫⎝⎛⋅=πθ例2 (E03) 两根电线杆之间的电线,由于其本身的重量，下垂成曲线形. 这样的曲线叫悬链线. 适当选取坐标系后，悬链线的方程为kxk y cosh =, 其中k 为常数. 计算悬链线上介于b x -=与b x =之间一段弧的长度.解如图，由于对称性，要计算弧长为相应于x 从0到b 的一段曲线弧长的两倍.,c x y sh='弧长微元: dx cx ds 2sh 1+=.dx cx ch=故所求弧长为⎰=bc xc s 0ch 2boc x c ⎥⎦⎤⎢⎣⎡=sh 2.c b c sh 2=例6 证明正弦线)20(sin π≤≤=x x a y 的弧长等于椭圆 )20(sin 1cos 2π≤≤⎩⎨⎧+==t ta y t x 的周长. 证设正弦线的弧长为,1s 则dx y s ⎰'+=π20211dx x a ⎰+=π2022cos1,dx x a ⎰+=π22cos12设椭圆的周长为,2s 则dt y x s t t ⎰'+'=π20222)()(dt t a t ⎰++=π222))(cos 1()(sin 2（利用椭圆的对称性）dt t a ⎰+=π22cos 12dx x a ⎰+=π22cos12,1s =故原结论成立.例7 求极坐标系下曲线)30,0(3sin 3πθθ≤≤>⎪⎭⎫ ⎝⎛=a a r 的长.解313c o s 3s i n 32⋅⋅⎪⎭⎫ ⎝⎛='θθa r ,3c o s 3s i n 2θθ⋅⎪⎭⎫ ⎝⎛=aθθθβαd r r s ⎰'+=∴)()(22θθθθπd a a ⎰⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=30242623cos 3sin 3sin θθπd a⎰⎪⎭⎫ ⎝⎛=3023sin.a π23=。

定积分及其应用习题章节-资料

积分中值公式
嘉兴学院
12/3/2019
第六章定积分
第11页
5、牛顿—莱布尼茨公式
定理1 如果f(x)在[a,b]上连续，则积分上限的函数
(x)ax f(t)dt在[a,b]上具有导数，且它的导数是 (x)ddxax f(t)dt f(x) (axb)
定理2（原函数存在定理）如果f(x) 在 [a,b] 上
x
12/3/2019
第六章定积分
平行截面面积为已知的立体的体积
A( x)
oa
x xdx b
x
VabA(x)dx
第20页
嘉兴学院
12/3/2019
第六章定积分
第21页
(3) 平面曲线的弧长
y
A．曲线弧为 yf(x)
弧长
b
sa
1y2dx
dy
B．曲线弧为

x y

b
c
b
af(x)d x af(x)d x cf(x)dx
嘉兴学院
12/3/2019
第六章定积分
第9页
性质4
b
b
a1d x ad x ba
性质5 如果在区间 [ a ,b ] 上 f ( x ) 0 ，
则 a bf(x )d x 0 (ab )
推论：（1）如果在区间 [ a , b ] 上 f ( x ) g ( x ) ，
嘉兴学院
12/3/2019
第六章定积分
第8页
4、定积分的性质
性质1 a b [f(x ) g (x )d ] x a b f(x ) d x a b g (x ) dx 性质2 a b k(x f ) d x k a b f(x ) dx k (为常数 )

第6章定积分的应用习题集及答案

第六章习题定积分的应用一．选择题1．曲线x y ln =、a y ln =、b y ln =（b a <<0）和y 轴所围图形的面积为（ C ）（A ）⎰ba xdx ln ln ln ；（B ）⎰be a e xdx e ；（C ）⎰ba ydy e ln ln ；（D ）⎰ae b e xdx ln ．2．曲线x e y =下方与该曲线过原点的切线左方和y 轴右方所围图形的面积为（a ）（A ）⎰-10)(dx ex e x ；（B ）⎰-edy y y y 1)ln (ln ；（C ）⎰-e x x dx x e e 1)(；（D ）⎰-10)ln (ln dy y y y ．3．摆线)sin (t t a x -=、)cos 1(t a y -=（0>a ）的一拱（π20≤≤t ）与x 轴所围图形绕x 轴旋转一周所成旋转体的体积为（ D ）（A ）⎰-ππ2022)cos 1(dt t a ；（B ）⎰--at t a d t a ππ2022)]sin ([)cos 1(；（C ）⎰-a dt t a ππ2022)cos 1(；（D ）⎰--ππ2022)]sin ([)cos 1(t t a d t a ． 4．曲线θρcos 2a =(0>a )所围图形的面积为（ D ）（A ）⎰22)cos 2(21πθθd a ；（B ）⎰-ππθθd a 2)cos 2(21；（C ）⎰πθθ202)cos 2(21d a ；（D ）⎰202)cos 2(212πθθd a ．5．连续曲线)(x f y =与直线a x =、b x =（b a <≤0）及x 轴围成的图形绕y 轴旋转一周生成的旋转体体积为（ B ）（A ）⎰ba dx x xf )(2π；（B ）⎰ba dx x f x )(2π；（C ）⎰ba dx x xf )(22π；（D ）⎰ba dx x f x )(22π． 6．半径为R 的半球形水池已装满水．要将水全部吸出水池，需做功的为（ C ）（A ）⎰-Rdy y R 022)(π；（B ）⎰Rdy y 02π；（C ）⎰-Rdy y R y 022)(π；（D ）⎰Rdy y 03π．二．计算题1．求曲线221x y =与822=+y x 所围图形（上半平面部分）的面积．解：易知：曲线221x y =与822=+y x 的交点为(2,2)±。

高数例题第六章定积分的应用

s

t t dt
例17. 计算摆线

x a sin y a 1 cos
的
一拱
(0 2 ) 的长度。
2、直角坐标情形设曲线弧由直角坐标方程
y f x a x b 给出 f x 在a, b
球体体积的一半,试求该圆孔的直径.
(二)平行截面面积为已知的立体的体积
已知立体在过点 x a, x b且垂直于x 轴的两个平面之间，且垂直于轴的截面面积为 A x , A x 为连续函数，则
V A x dx
a
b
例14.一平面经过半径为R的圆柱体的底圆中心,并与底面交成角

,计
算这平面截圆柱体所得立体的体积.
例15．求以半径为R的圆为底，平行且等于底圆直径的线段为顶，高为h
的正劈锥体的体积。
例16. 证明由平面图形
0 a x b 0 y f ( x)
绕
y
轴旋转所成的旋转体的体积
b
为
V 2 xf x dx
a
三、平面曲线的弧长 (一)平面曲线弧长的概念 1、定义：设A,B是曲线弧上的两个端点，在弧 AB 上依次任取分点
把区间 a, b 分成许多部分区间,则所求量相应地分成许多部分量 ui ,而所求量等于所有部分量之和，这一性质称为所求量对于区间 a, b 具有可加性。
三.用定积分来表达的量 u 应具备的条件 1. 是与一个变量 x 的变化区间 a, b 有关的量。 2.量对于区间 a, b 具有数量的可加性。 3.部分量 ui 的近似值可表示为
在 , 上 , 围成，

高等数学习题详解-第6章定积分

习题6-11．利用定积分的几何意义求定积分：利用定积分的几何意义求定积分：(1) 12xdx ò； (2) 220aa x dx -ò(0)a >．解 (1) 根据定然积分的几何意义知, 102xdx ò表示由直线2,1y x x ==及x 轴所围的三角形的面积,而此三角形面积为1,所以1021xdx =ò．(2) 根据定积分的几何意义知,22aa x dx -ò表示由曲线22,0,y a x x x a =-==及x 轴所围成的14圆的面积,而此14圆面积为214πa ,所以222014aa x dx a -=òπ. 2．根据定积分的性质，比较积分值的大小：根据定积分的性质，比较积分值的大小：(1) 12x dx ò与13x dx ò； (2) 10xe dx ò与1(1)x dx +ò．解 (1) ∵当[0,1]x Î时,232(1)0x x x x -=-³,即23x x ³, 又2x3x ,所以11230x dx x dx >òò．(2) 令()1,()1x xf x e x f x e ¢=--=-,因01x ££,所以()0f x ¢>, 从而()(0)0f x f ³=,说明1xe x ³+，所以11(1)xe dx x dx >+òò.3．估计下列各积分值的范围：估计下列各积分值的范围：(1) 421(1)x dx +ò； (2) 313arctan x xdx ò；(3) 2axae dx --ò（0a >)； (4) 22xxedx -ò．解 (1) 在区间[]1,4上，函数2()1f x x =+是增函数，故在[1,4]上的最大值(4)17M f ==,最小值(1)2m f ==,所以4212(41)(1)17(41)d x x -£+£-ò, 即 4216(1)51x dx £+£ò．(2) 令()arctan f x x x =,则2()arctan 1x f x x x ¢=++,当1[,3]3x Î时,()0f x ¢>,从而()f x 在1[,3]3上是增函数,从而f (x )在1[,3]3上的最大值(3)3πM f ==,最小值1()363πm f ==,所以所以 313112(3)arctan (3)9363333x xdx =-££-=òππππ即3132arctan 93x xdx ££òππ． (3) 令2()x f x e-=,则2()2xf x xe -¢=-,令()0f x ¢=得驻点0x =，又(0)1f =， 2()()a f a f a e-=-=,a >0时, 21ae -<,故()f x 在[],a a -上的最大值1M =，最小值，最小值2ea m -=,所以所以2222aa x aa dx a---££òee . (4) 令2()x x f x e -=,则2()(21)x xf x x e -¢=-,令()0f x ¢=得驻点12x =,又(0)1,f = 1241(),(2)2f e f e -==,从而()f x 在[]0,2上的最大值2M e =,最小值14m e -=,所以所以 2122402x xeedx e --££ò．习题6-21．求下列导数：求下列导数：(1) 201x d t dt dx +ò; (2) 5ln 2x td te dt dx -ò； (3) cos 20cos()xd t dt dx p ò; (4) sin x d t dt dx tp ò (0x >)．解 (1) 22011xd t dt x dx +=+ò. (2)55ln 2x tx d t e dt x e dx --=ò. (3) cos 2220cos()cos(cos )(cos )sin cos(cos )x d t dt x x x x dxp p p ¢=×=-ò(4)sin sin sin x xdt d t x dt dt dx t dx t xp p =-=-òò. 2．求下列极限：求下列极限：(1) 02arctan limxx tdt x ®ò； (2) ()2220020e lime x t xx t dt t dt®òò．解 (1) ()0022000021arctan arctan arctan 11(1)lim lim lim lim 222x x x x x x tdt tdt x x x x x ®®®®¢éù--ëû+====-¢òò．(2) ()()22222222222000020000220022lim lim lim lim x x x x t t t x t x x x x x x x t x t e dt e dt e dt e dt xe xe te dt te dt ®®®®¢éù×êúëû===¢éùëûòòòòòòe []2222202000222lim lim lim 2122x t x x x x x x x e dt e x e xe xxe ®®®¢éùëû====+¢+×ò． 3．求由方程e cos 0yx tdt tdt +=òò所确定的隐函数()y y x =的导数．的导数．解方程两边对x 求导数得: cos 0e yy x ¢×+=, cosey x y ¢\=-，又由已知方程有000sin e yxtt +=,即1sin sin 00e yx -+-=，即1sin e yx =-,于是有cos cos sin 1eyxx y x ¢=-=-．4．计算下列定积分：计算下列定积分： (1) 41xdx ò； (2) 221d x x x --ò；(3) 设,0,2()sin ,2x x f x x x p p p ì££ïï=íï££;ïî，求0()f x dx p ò (4)320(2)x dx -ò．解 (1)44321121433xdx x ==ò.(2)2122222111()()()dx x x dx x x dx x x dx x x --=-+-+--òòòò012322332101111111116322332x x x x x x -æöæöæö=++=---ç÷ç÷ç÷èøèøèø．(3) ()22220022()sin 1cos 82x f x dx xdx xdxx p pp pp ppp =+=+=+-òòò(4) 33232002(2)2(2)(2)x dx xdx x dx x dx -=-=-+-òòòò232202115(2)(2)222x x x x =-+-=．5．设函数()f x 在区间[],a b 上连续上连续,,在(),a b 内可导内可导,,()0f x ¢£,1()()xaF x f t dt x a =-ò；证明：在(),a b 内有()0F x ¢£．证明证明 22111()()()()()()()()xx aa F x f t dt f x x a f x f t dt x a x a x a éù¢=-+=--êúëû---òò[][][]21()()()(),(,,)()x a f x x a f a x a b x a x x =---ÎÎ-(),((,)(,))x f x a b x ax h h x -¢=ÎÎ-．由已知条件可知结论成立．由已知条件可知结论成立．习题习题 6-3 6-31．计算下列积分：计算下列积分： (1) 3sin()x dx pp p +3ò； (2) 32(115)dx x 1-+ò； (3) 11154dx x--ò； (4) 320sin cos d j j j pò；(5) 22cos udu p p 6ò； (6) 2e 11ln dx x x+ò；(7) 32211dx xx +ò； (8) 2202x dx -ò； (9) ln 3ln 2e e x x dx--ò； (10)3222dxx x +-ò．解 (1) 333sin()sin()()[cos()]x dx x d x x pp p pp p p p p p +=++=-+3333òò42cos cos 033p p =-+=.(2) 123322211(511)151(511)(115)5(511)10512dxd x x x x 11---+==-=+++òò(3)1111111111(54)154425454dx d x x x x---=--=-=---òò.(4)233422011sin cos cos cos cos 44d d p ppj j j j j j=-==-òò.(5)222221cos 211cos cos 2(2)224u udu du du ud u pp p p ppp p 6666+==+òòòò26131sin 2268264up p p p p æö=+=--ç÷èø. (6) 222111(ln 1)22(31)1ln 1ln 1ln e e e dx d x x x x x+===-+++òò. (7) 令tan x t =，则2sec dx tdt =，当1x =时，4t p =；当3x =时，3t p =；于是于是 333222144cos 2123sin 3sin 1dx t dt t t x x p p p p==-=-+òò． (8) 令2sin x t =,则2cos dx tdt =,当0x =时，0t =；当2x =时,2t p=；于是2222220122cos (1cos 2)(sin 2)22x dx tdt t dt tt pppp-==+==+òòò．(9) 令xe t =，则1ln ,d x t x dt t ==，当ln 2x =时，2t =;；当ln 3x =时,3t =；于是于是3ln3332ln 22221113111(ln ln)12222111x xdxdt t dt e e t t t t --æö====-ç÷---++èøòòò．(10)333222211111()ln 231232dx x dx x x x x x -=-=+--++òò 1211(ln ln )ln 2ln 53543=-=- 2．计算下列定积分：计算下列定积分： (1) 10e x x dx -ò； (2)e1ln x xdx ò；(3) 41ln x dx x ò； (4) 324sin xdx xpp ò； (5) 220e cos x xdx p ò； (6) 221log x xdx ò；(7)π20(sin )x x dx ò； (8) e1sin(ln )x dx ò．解 (1) (1)111100xxxxxedx xdexee dx ----=-=-+òòò1110121x e ee e e e----=--=--+=-．(2) 2222211111111111ln ln ln (1)222244e e e ee x xdx xdx x x xdx e x e ==-=-=+òòò． (3) 4444411111ln 12ln 2ln 28ln 24x dx xd x x x x dx x x x ==-×=-òòò 8ln 24=-．(4) 333324444cot cot cot sin x dx xd x x x xdx x p p p pp p p p =-=-+òòò34π131ln ln sin 492249x ppp p 3æö3=-+=+-ç÷èø． (5) 222222220cos sin sin 2sin xx x x exdx e d x e x e xdx p p p p ==-òòò222222002cos 2cos 4cos xxxe e d x e e xe xdx pp ppp=+=+-òò220e 24cos x e xdx pp =--ò于是于是221cos (2)5x e xdx e pp =-ò． (6) ()2222222111122221111log ln ln 2ln 22ln 211ln 2ln 22x xdx xdx x x xdx x x x ==-æö=-ç÷ç÷èøòòò 133(4ln 2)22ln 224ln 2=-=-． (7) 223200001111(sin )(1cos 2)(sin2)2232x x dx x x dx x x d x pp p p =-=-òòò 33200011(sin 22sin2)cos26464x x x xdx xd x p p p p p =--=-òò 3001(cos 2cos2)64x x xdx p p p =--ò 3301sin 264864x p p p p p=-+=-．(8)111sin(ln )sin(ln )cos(ln )eee x dx x x x dx =-òò11sin1cos(ln )sin(ln )ee e x x x dx =--ò1sin1cos11sin(ln )e e e x dx =-+-ò所以所以11sin(ln )(sin1cos11)2ex dx e e =-+ò．3．利用被积函数的奇偶性计算下列积分：利用被积函数的奇偶性计算下列积分：(1) 121ln(1)x x dx -++ò ；（2）1212sin 1xdx x -++ò (3) 2222(4)x x dx -+-ò; (4) 4224cos d q q pp -ò．解 (1) 2ln(1)x x ++ 是奇函数，是奇函数， 121ln(1)0x x dx -\++=ò．(2) 2sin 1x x+ 是奇函数，121sin 01x dx x -\=+ò，因此因此 111221112sin 22arctan 11x dx dx x x x p ---+===++òò． (3) 222222222(4)(424)416x x dx x x dx dx ---+-=+-==òòò． (4) ()244222022201cos 24cos 8cos 82212cos 2cos231384222d d d d q q q q q qq q qp p pp p p -p+æö==ç÷èø=++=×××=òòòò．4．证明下列等式：证明下列等式：(1) 证明：1100(1)(1)mnn m x x dx x x dx -=-òò；(2) 证明：1122111xx dx dx x x=++òò (0x >)； (3) 设()f x 是定义在区间(,)-¥+¥上的周期为T 的连续函数，则对任意(,)a Î-¥+¥，有()()a TTaf x dx f x dx +=òò．证 (1)令1x t -=，则dx dt =-，当0x =时，1t =；当1x =时，0t =；于是于是1111(1)(1)()(1)(1)m n m n n m n mx x dx t t dt t t dt x x dx -=--=-=-òòòò，即11(1)(1)m n n m x x dx x x dx -=-òò．(2) 令1x t =则21dx dt t-=，于是11111112222211211111111111t x x t tdx dt t dt dx x t t x t tæö=×=-×==-ç÷++++èø+òòòòòd ，即1122111xxdxdxx x =++òò．(3) 因为因为()()()a TT a Taa f x dx f x dx f x dx ++=+òòò，而，而()()()a Taaaf x dx x t Tf t T dt f t dt +=++=òòò令 0()()()aTTaf x dx f x dx f x dx ==-òòò故()()a TTaf x dx f x dx +=òò．4．若()f t 是连续函数且为奇函数，是连续函数且为奇函数，证明证明0()xf t dt ò是偶函数；若()f t 是连续函数且为偶函数，证明()xf t dt ò是奇函数．是奇函数．证令0()()xF x f t dt =ò．若()f t 为奇函数，则()()f t f t -=-，令t u =-，可得，可得()()()()()xxxF x f t dt f u du f u du F x --==--==òòò, 所以0()()xF x f t dt =ò是偶函数．是偶函数．若()f t 为偶函数，则()()f t f t -=，令t u =-，可得，可得()()()()()xxxF x f t dt f u du f u du F x --==--=-=-òòò, 所以0()()xF x f t dt =ò是奇函数．是奇函数．5．利用分部积分公式证明：利用分部积分公式证明：()()()()d xxu f u x u du f x x du -=òòò．证令0()()uF u f x dx =ò则()()F u f u ¢=, 则(())()()()xu xxxf x dx du F u du uF u uF u du ¢==-òòòò()()()()xxxxF x uf u du xf x dx uf u du =-=-òòò()()()()xxxxx f u du uf u du xf u du uf u du =-=-òòòò()()xx u f u du =-ò．习题6-41．求由下列曲线所围成的平面图形的面积：求由下列曲线所围成的平面图形的面积：(1) 2y x =与22y x =-； (2) x y e =与0x =及y e =； (3) 24y x =-与0y =； (4) 2y x =与y x =及2y x =；(5) 1y x =与y x =及2x =； (6) 2y x =与2y x =-； (7) ,xx y e y e -==与1x =；(8) sin (0)2y x x p =££与0,1x y ==．解 (1)两曲线的交点为(1,1),(1,1)-，取x 为积分变量，[]1,1x Î-，面积元素22(2)dA x x dx =--，于是所求的面积为，于是所求的面积为112311182(1)2()33A x dx x x --=-=-=ò．(2) 曲线x y e =与y e =的交点坐标(1,)e ， x y e =与0x =的交点为(0,1)，取y 为积分变量，[]1,y e Î，面积元素ln dA ydy =；于是所求面积为；于是所求面积为111ln (ln )1eeeA ydy ydy y y y ===-=òò． (3)曲线24y x =-与0y =的交点为(2,0),(2,0)-，取x 为积分变量，[]2,2x Î-，面积元素2(4)dA x dx =-，于是所求的面积为，于是所求的面积为222322132(4)(4)33A x dx x x --=-=-=ò． (4) 曲线2y x =与y x =的交点为(0,0),(1,1)；2y x =与2y x =的交点为(0,0),(2,4)；它们所围图形面积为：它们所围图形面积为：1212220101(2)(2)(2)A x x dx x x dx xdx x x dx =-+-=+-òòòò2231201117()236x x x =+-=．(5) 曲线1y x =与y x =的交点为(1,1)，1y x=与2x =的交点为1(2,)2；取x 积分变量，[]1,2x Î，面积元素1()dA x dx x =-，于是所求的面积为，于是所求的面积为22211113()(ln )ln 222A x dx x x x =-=-=-ò．(6) 曲线2y x =与2y x =-的交点为()()114,2-，和，取y 作积分变量，[]1,2y Î-，面积元素2(2)dA y y dy =+-，于是所求的面积为，于是所求的面积为2222311117(2)(2)232A y y dy y y y --=+-=+-=ò．(7) 曲线x y e =与xy e -=的交点(0,1)，取x 作积分变量,[]0,1x Î，面积元素()xxdA e e dx -=-，于是所求图形的面积为，于是所求图形的面积为10)()2xxxxA e e dx e e e e--=-=+=+-ò11(．(8)取x 作积分变量，0,2x p éùÎêúëû，面积元素(1sin )dA x dx =-，于是所求的面积为，于是所求的面积为220(1sin )(cos )12A x dx x x ppp =-=+=-ò．2．求由下列曲线围成的平面图形绕指定坐标轴旋转而成的旋转体的体积：求由下列曲线围成的平面图形绕指定坐标轴旋转而成的旋转体的体积：(1) ,1,4,0y x x x y ====，绕x 轴；轴； (2) 3,2,y x x x ==轴，分别绕x 轴与y 轴；轴；(3) 22,y x x y ==，绕y 轴；轴；(4) 22(5)1x y -+=，绕y 轴．轴．解 (1)取x 作积分变量，[]1,4x Î，体积元素2()dV x dx xdx p p ==，于是所求旋转体的体积为的体积为442111522V xdx x p p p ===ò．(2)绕x 轴旋转时，取x 作积分变量，[]0,2x Î，体积元素32()x dV x dx p =，于是，于是22267012877x V x dx xp p p ===ò；同理可求平面图形绕y 旋转所成的旋转体的体积旋转所成的旋转体的体积8582233003642()(4)55yV y dy y y pp péù=-=-=ëûò． (3)曲线2y x =与2x y =的交点为(0,0),(1,1)，取y 作积分变量[]0,1y Î，体积元素222()()dV y y dyp éù=-ëû，于是所求的旋转体的体积为，于是所求的旋转体的体积为114250113()()2510V y y dx y y p p p =-=-=ò． (4) 取y 作积分变量[]1,1y Î-，体积元素22222(51)(51)201dV y y dy y dy p p éù=+----=-ëû，于是所求的旋转体的体积为于是所求的旋转体的体积为 122120120102V y dy ppp p -=-=×=ò．3．设某企业边际成本是产量Q （单位）的函数0.2()2QC Q e ¢=（万元／单位），其固定成本为090C =（万元），求总成本函数．，求总成本函数．解总成本函数为总成本函数为0.200()()290QQQ C Q C Q dQ C e dQ ¢=+=+òò0.20.2010901080Q QQ e e =+=+．4．设某产品的边际收益是产量Q （单位）的函数()152R Q Q ¢=-（元／单位），试求总收益函数与需求函数．益函数与需求函数．解总收益函数为总收益函数为20()(152)15QR Q Q dQ Q Q =-=-ò需求函数为需求函数为()15R Q P Q Q==-．5．已知某产品产量的变化率是时间t (单位：单位：月月)的函数()25,0f t t t =+³，问：问：第一个第一个5月和第二个5月的总产量各是多少? 解设产品总产量为()Q t ,则()()Q t f t ¢=,第一个5月的总产量月的总产量5525100()(25)(5)50Q f t dt t dt t t ==+=+=òò．第二个5月的总产量为月的总产量为10102102555()(25)(5)100Q f t dt t dt t t ==+=+=òò．6．某厂生产某产品Q (百台)的总成本()C Q (万元)的变化率为()2C Q ¢=(设固定成本为零)，总收益()R Q (万元)的变化率为产量Q (百台)的函数()72R Q Q ¢=-．问：．问： (1) 生产量为多少时，总利润最大?最大利润为多少? (2) 在利润最大的基础上又多生产了50台，总利润减少了多少? 解 (1)总利润()()()L Q R Q C Q =-当()0L Q ¢=即()()0R Q C Q ¢¢-=即7220Q --=, 2.5Q =(百台)时,总利润最大，此时的总成本和总收益分别为总利润最大，此时的总成本和总收益分别为2.52.52.5()225C C Q dQ dQ Q¢====òò2.52.52.520()(72)(7)11.25R R Q dQ Q dQ Q Q ¢==-=-=òò总利润11.255 6.25L R C =-=-=(万元). 即当产量为2.5(百台)时,总利润最大，最大利润是6.25万元．万元．(2)在利润最大的基础上又生产了50台,此时产量为3百台, 总成本3300()26C C Q dQ dQ ¢===òò，总收入3323000()(72)(7)12R R Q dQ Q dQ Q Q ¢==-=-=òò，总利润为1266L R C =-=-=(万元)．减少了6.2560.25-=万元．万元．即在利润最大的基础上又生产了50台时,总利润减少了0.25万元．万元．习题习题 6-51．判断下列反常积分的敛散性，若收敛，则求其值：判断下列反常积分的敛散性，若收敛，则求其值：(1) 41dxx+¥ò； (2)1dx x+¥ò；(3) 0xe dx +¥-ò (a ＞0); (4) 0sin xdx +¥ò; (5)1211dxx--ò； (6) 222dxx x +¥-¥++ò； (7) 211xdx x -ò； (8)10ln x xdx ò； (9) e211ln dxx x-ò； (10)23(1)dxx -ò．解 (1) 14311133dx x x +¥+¥=-=ò．此反常积分收敛．．此反常积分收敛． (2) 112dx x x+¥+¥==+¥ò．此反常积分发散．．此反常积分发散．(3) 101x xe dx e +¥--+¥=-=ò．此反常积分收敛．．此反常积分收敛．(4) 00sin cos lim cos 1x xdx x x +¥+¥®+¥=-=-+ò不存在，此反常积分发散．不存在，此反常积分发散．(5) 11121arcsin 1dx x x p --==-ò．此反常积分收敛．．此反常积分收敛．(6)22(1)arctan(1)22(1)1dx d x x x x x p +¥+¥+¥-¥-¥-¥+==+=++++òò．此反常积分收敛．．此反常积分收敛．(7)2322211001112lim lim (1)21113xdx x dx x x x x e e e e +++®®+-+éù==-+-êú--ëûòò320222lim 222333e e e +®æö==--ç÷èø．此反常积分收敛．．此反常积分收敛． (8)1112222100111111ln limln limln limln 222424x xdxxdxx xxdx eee e e e ee e ®®®æöæö==-=--ç÷ç÷èøèøòòò，所以11220001111ln lim ln lim (ln )4244x xdx x xdx e e e e e e ++®®==--=-òò．此反常积分收敛．．此反常积分收敛． (9) 12211ln πarcsin(ln )21(ln )1(ln )e e e dx d x x x x x ===--òò．此反常积分收敛．．此反常积分收敛． (10) 212333001(1)(1)(1)dx dx dxx x x =+---òòò，因为反常积分1132001(1)(1)dx x x ==¥--ò发散，所以反常积分230(1)dxx -ò发散．发散． 2．当k 为何值时，反常积分+2(ln )kdxx x ¥ò收敛?当k 为何值时，这反常积分发散? 解当1k =时，时，++222ln ln(ln )ln ln dxd x x x x x¥¥+¥===+¥òò,发散发散.. 当1k ¹时,1++122211(ln )(1)(ln 2)(ln )ln (ln )11kk k k k dx x k x d xx x kk -¥¥--+¥ì>ï-===í-ï+¥<îòò所以，当1k >时，此广义积分收敛；当1k £时，此广义积分发散．时，此广义积分发散． 3．利用递推公式计算反常积分+0e n xn I x dx ¥-=ò．解 ++1100n x n xn xn n I x de x e n x e dx nI ¥¥----+¥-=-=-+=òò, 因为因为 +101xx xI xde xe e ¥---+¥+¥=-=--=ò,所以所以 121(1)(1)2!n n n I nI n n I n n I n --==-=-= .复习题6（A ）1、求下列积分：求下列积分：（1）121tan sin 1xdx x -+ò；（2）1202x x dx -ò；（3）22204x x dx -ò；（4）ln 21x e dx -ò；（5）21220(1)x dx x +ò；（6）2211x dx x -ò；（7）120xx e dx -ò； (8) 21(ln )ex dx ò；(9) 401cos 2x dx xp+ò； (10) 20cos xe xdx p -ò； (11) 20sin 1cos x x dx x p++ò； (12) 40ln(1tan )x dx p+ò．解 (1) 因为被积函数2tan sin 1x x +是奇函数是奇函数,,所以121tan 0sin 1xdx x -=+ò． (2) 1122021(1)x x dx x dx -=--òò，令1sin x t -=，则cos dx tdt =；当0x =时，2t p=-；当1x =时，0t =；所以；所以010*******1cos 2sin 22cos 2244t t t x x dx tdt dt p p p p ---+éù-===+=êúëûòòò． (3) 令2sin x t =，则2cos dx tdt =，当0x =时，0t =；当2x =时，2t p =；所以222222222044sin 4cos 4sin 22(1cos 4)xx dx t tdt tdt t dt p pp-=×==-òòòò2012(sin 4)4t t pp =-=．(4) 令1x e t -=，则221t dx dt t =+，当0x =时，0t =；当ln 2x =时，1t =；所以2ln 2112000212(arctan )2(1)14x t e dx dt t t t p -==-=-+òò． (5) 令tan x t =，则2sec dx tdt =，当0x =时，0t =；当1x =时，4t p=；所以22412442240000tan 1cos 2sin 21sec ()(1)sec 22484x t t t t dx tdt dt x t pp pp -===-=-+òòò．(6) 令sec x t =，则sec tan dx t tdt =，当1x =时，0t =；当2x =时，3t p=；所以22233301001tan sec tan tan (tan )3sec 3x t dx t tdt tdt t t x t p p pp -===-=-òòò． (7) 111112221000022xxxxx x e dx x dex exe dx e xde ------=-=-+=--òòòò111111000223225xxxe xee dx e e e ------=--+=--=-ò． (8) 22111111(ln )ln 2ln 2ln 22e e e e e x dx x x x x dx e x x dx e x=-×=-+=-òòò．(9) 444400tan tan tan 1cos 2x dx xd x x x xdx xpppp==-+òòò401ln cos ln 2442x pp p =+=-．(10) 2222000cos cos cos sin xxxxe xdx xdee x e xdx pppp----=-=--òòò22201sin 1sin cos xxxxdee x e xdx ppp ---=+=+-òò2201cos x ee xdx pp--=+-ò，所以所以 2201cos (1)2x e xdx e p p--=+ò．(11) 22222000002sin sin cos tan 1cos 1cos 21cos 2cos2x x x x x d x dx dx dx xd x x x x p p p p p +=+=-+++òòòòò2222200tantan ln(1cos )222ln cos ln(1cos )22x x x dx x x x p pp ppp=--+=--+ò20ln 22ln cos 222xp pp=++=． (12) 44440cos sin ln(1tan )lnln(cos sin )ln cos cos x x x dx dx x x dx xdx xpppp++==+-òòòò令4x u p-=，可得044041ln(cos sin )ln 2cos()(ln 2ln cos )42x x dx x dx u du p p p p éù+=-=-+êúëûòòò40ln 2ln cos 8xdx p p =+ò所以所以4ln 2ln(1tan )8x dx pp +=ò．2、设()f x 在[],a b 上连续，且()1b af x dx =ò，求()b af a b x dx +-ò．解令a b x t +-=，则dx dt =-，当x a =时，t b =；当x b =时，t a =；所以；所以 ()()()1b ababaf a b x dx f t dt f t dt +-=-==òòò．3、设()f x 为连续函数，试证明：()()(())xxtf t x t dt f u du dt -=òòò．证用分部积分法，000(())()(())xx t tx tf u du dt tf u du td f u du =-òòòòò()()()()x x x x x f u du tf t dt xf t dt tf t dt =-=-òòòò()()xf t x t dx =-ò．4、设()u j 为连续函数，试证明：22()2()aaa x dx x dx j j -=òò．证2220()()()aa aaa x dx x dx x dx j j j --=+òòò，令x t =-，则00222200()(())()()aaa a x dx t dt t dt x dx j j j j -=--==òòòò 所以22220()()()2()aa aaaaa x dxx dx x dx x dx j j j j --=+=òòòò． 5、计算下列反常积分：、计算下列反常积分：（1）2048dx x x +¥++ò；（2）21arctan x dx x+¥ò；（3）101(1)dx x x -ò；（4）1ln e dx x x ò．解 (1) 222000(2)12arctan 48(2)2228dx d x x x x x p +¥+¥+¥++===++++òò． (2) 221111arctan 1arctan 1arctan (1)x x dx xddx x xxx x +¥+¥+¥+¥=-=-++òòò22111ln ln 242142xx p p +¥=+=++. (3) 1110001122arcsin (1)1dx d x x x x x p éù===ëû--òò．(4) 111ln 2ln 2ln ln e eedxd xx x x x ===òò．6、求抛物线22y px =及其在点(,)2p p 处的法线所围成的平面图形的面积．处的法线所围成的平面图形的面积．解抛物线22y px =在点(,)2p p 处的法线方程为32x y p +=，两曲线的交点为9(,3),(,)22p p p p -；取y 作积分变量3p y p -££，所求的平面图形面积为，所求的平面图形面积为 2232333131116()()222263p pp pA p y y dy py y y p p p --=--=--=ò． 7、求由曲线32y x =与直线4,x x =轴所围图形绕y 轴旋转而成的旋转体的体积．轴旋转而成的旋转体的体积．解曲线32y x =与直线4x =的交点为(4,8)，取y 作积分变量，08y ££，体积元素2232434()(16)dy y dy y dy p p éù=-=-ëû于是，所求的旋转体的体积为于是，所求的旋转体的体积为88437303512(16)(16)77V y dy y y p p p =-=-=ò． 8、设某产品的边际成本为()2C Q Q ¢=-（万元/台），其中Q 代表产量，固定成本022C ==（万元），边际收益()204R Q Q ¢=-（万元/台）．试求：．试求： (1) 总成本函数和总收益函数；总成本函数和总收益函数； (2) 获得最大利润时的产量；获得最大利润时的产量；(3) 从最大利润时的产量又生产了4台，总利润的变化．台，总利润的变化．解 (1)总成本函数201()(2)2222QC Q Q dQ C Q Q =-+=-+ò，总收益函数20()(204)202QR Q Q dQ Q Q =-=-ò． (2)利润函数23()()()18222L Q R Q C Q Q Q =-=--，令()0L Q ¢=,得6Q =(台)，而(6)30L ¢¢=-<，所以当产量6Q =(台)时，利润最大．时，利润最大．(3)(10)(6)83224L L -=-=-，所以从最大利润时的产量又生产了4台，总利润减少了24（万元）．(B)1、填空题：填空题：(1) 22cos xd x t dt dx =ò . (2) (2) 设设()f x 连续，220()()x F x xf t dt =ò，则()F x ¢= .(3)2sin()xd x t dt dx-=ò.(4) (4) 设设()f x 连续，则220()xd tf x t dt dx -=ò . (5) (5) 设设20cos ()1sin x t f x dt t =+ò,则220()1()f x dx f x p¢=+ò . (6) (6) 设设()f x 连续，且10()2()f x x f x dx =+ò，,则()f x = .(7) (7) 设设()f x 连续，且()1cos xtf x t dtx -=-ò,则20()f x dx p=ò .(8)2ln e dxx x +¥=ò .解 (1) 2220002224cos (cos )cos (cos )2x xx d dx t dt x t dt t dt x x x dx dx ==+-×òòò2224cos 2cos x t dt x x =-ò.(2) 2222200()(())()()2xx d F x xf t dt f t dt x f x x dx ¢==+××òò 22220()2()x f t dt x f x =+ò.(3) (3) 令令x t u -=,则22200sin()sin ()sin xxx x t dt u du u du -=-=òòò 所以所以22200sin()sin sin xxddx t dt u du x dx dx -==òò.(4) (4)令令22x t u -= 则222222001()()()2x x tf x t dt f x t d x t -=---òò220011()()22x x f u du f u du =-=òò．所以．所以 2222001()()()2xx d d tf x t dt f u du xf x dx dx -=×=òò．(5)22200()arctan ()arctan ()arctan (0)1()2f x dx f x f f f x ppp ¢==-+ò，而02222000cos cos (0)0,()arctan(sin )1sin 21sin 4t t f dt f dt t t t pp p p =====++òò，所以220()arctan 1()4f x dx f x pp ¢=+ò (6) (6) 等式等式1()2()f x x f x dx =+ò两边在区间[]0,1积分得积分得111101()2()2()2f x dx xdx f x dx f x dx =+=+òòòò11()2f x dx =-ò，所以所以()1f x x =-．(7) (7)令令x t u -=，则du dt =-，于是，于是00()()()xxtf x t dt x u f u du -=-òò原等式化为原等式化为()()1cos xxxf u du uf u du x -=-òò两边对x 求导求导()sin xf u du x =ò在上式中，令2x p=，得，得()1xf x dx =ò．。

(完整版)§定积分的应用习题与答案

第六章定积分的应用（A ）1、求由下列各曲线所围成的图形的面积 1）221x y =与822=+y x （两部分都要计算）2）xy 1=与直线x y =及2=x3）xe y =，xe y -=与直线1=x4）θρcos 2a =5）t a x 3cos =，t a y 3sin =１、求由摆线()t t a x sin -=，()t a y cos 1-=的一拱()π20≤≤t 与横轴所围成的图形的面积２、求对数螺线θρae=()πθπ≤≤-及射线πθ=所围成的图形的面积３、求由曲线x y sin =和它在2π=x 处的切线以及直线π=x 所围成的图形的面积和它绕x 轴旋转而成的旋转体的体积４、由3x y =，2=x ，0=y 所围成的图形，分别绕x 轴及y 轴旋转，计算所得两旋转体的体积５、计算底面是半径为R 的圆，而垂直于底面上一条固定直径的所有截面都是等边三角形的立体体积６、计算曲线()x y -=333上对应于31≤≤x 的一段弧的长度７、计算星形线t a x 3cos =，t a y 3sin =的全长８、由实验知道，弹簧在拉伸过程中，需要的力→F （单位：N ）与伸长量S （单位：cm ）成正比，即：kS =→F （k 是比例常数），如果把弹簧内原长拉伸6cm ，计算所作的功９、一物体按规律3ct x =作直线运动，介质的阻力与速度的平方成正比，计算物体由0=x 移到a x =时，克服介质阻力所作的功１０、设一锥形储水池，深15m ，口径20m ，盛满水，将水吸尽，问要作多少功？１１、有一等腰梯形闸门，它的两条底边各长10cm 和6cm ，高为20cm ，较长的底边与水面相齐，计算闸门的一侧所受的水压力１２、设有一长度为λ，线密度为u 的均匀的直棒，在与棒的一端垂直距离为a 单位处有一质量为m 的质点M ，试求这细棒对质点M 的引力(B)1、设由抛物线()022>=p px y 与直线p y x 23=+ 所围成的平面图形为D 1）求D 的面积S ;2）将D 绕y 轴旋转一周所得旋转体的体积2、求由抛物线2x y =及x y =2所围成图形的面积，并求该图形绕x 轴旋转所成旋转体的体积3、求由x y sin =，x y cos =，0=x ，2π=x 所围成的图形的面积，并求该图形绕x 轴旋转所成旋转体的体积4、求抛物线px y 22=及其在点⎪⎭⎫⎝⎛p p ,2处的法线所围成的图形的面积5、求曲线422+-=x x y 在点()4,0M 处的切线MT 与曲线()122-=x y 所围成图形的面积6、求由抛物线ax y 42=与过焦点的弦所围成的图形面积的最小值7、求由下列曲线所围成图形的公共部分的面积 1）θρcos 3=，θρcos 1+=2）θρsin a =，()θθρsin cos +=a ，0>a8、由曲线()16522=-+y x 所围成图形绕x 轴旋转所成旋转体的体积9、求圆心在()b ,0半径为a ，()0>>a b 的圆，绕x 轴旋转而成的环状体的体积10、计算半立方抛物线()32132-=x y 被抛物线32x y =截得的一段弧的长度(C)1、用积分方法证明半径为R 的球的高为H 的球缺的的体积为⎪⎭⎫ ⎝⎛-=32H R H V π2、分别讨论函数x y sin =⎪⎭⎫⎝⎛≤≤20πx 在取何值时，阴影部分的面积1S ，2S 的和21S S S +=取最大值和最小值3、求曲线x y =()40≤≤x 上的一条切线，使此切线与直线0=x ， 4=x 以及曲线x y =所围成的平面图形的面积最小4、半径为r 的球沉入水中，球的上部与水面相切，球的密度与水相同，现将球从水中取出，需作多少功？第六章定积分应用习题答案（A ）1、1）342+π，346-π 2）2ln 23- 3）21-+ee 4）2a π 5）283a π2、23a π 3、()ππ2224--e e a 4、12-π，42π 5、7128π，564π 6、3334R 7、3432- 8、a 6 9、kJ 18.0 10、3732727a kc （其中k 为比例常数）11、()kJ 5.57697 12、()kN 14373 13、取y 轴经过细直棒⎪⎪⎭⎫⎝⎛+-=2211t a aGmu F y 22t a a Gmu F x +-=λ(B)1、1）⎰-=⎪⎪⎭⎫ ⎝⎛--=pp p dy p y y p S 322316223 或()⎰⎰=⎪⎭⎫⎝⎛+-++=20229231622322pp p p dx px x p dx px px S2）⎰⎰--=⎪⎪⎭⎫⎝⎛-⎪⎭⎫⎝⎛-=pp p p p dy p y dy y p V 33322215272223πππ 2、()⎰=-=10231dx x x A ()()ππ⎰=⎪⎭⎫⎝⎛-=10222103dx x x V3、()()⎰⎰-=-+-=244222cos sin sin cos πππdx x x dx x x A()()()()()()⎰⎰=-+-=24224022cos sin sin cos πππππdx x x dx x x V4、抛物线在点⎪⎭⎫⎝⎛p p ,2处的法线方程为： p y x 23=+，以下解法同第一题2316p A = 5、MT ：x y 24-=，切线MT 与曲线()122-=x y 的交点坐标为⎪⎭⎫⎝⎛1,23，()2,3- ⎰-=⎪⎪⎭⎫ ⎝⎛---=122491224dy y y A 6、提示：设过焦点()0,a 的弦的倾角为α则弦所在直线的方程为()a x y -=αtan由()a x y -=αtan ，ax y 42=得两交点纵坐标为()()21csc 2csc 2y ctg a ctg a y =+<-=αααα所以()()dy a y yctg a A y y ⎰⎥⎦⎤⎢⎣⎡-+=2142αα ()()32222csc 34csc 4csc 4ααααa ctg a a -+=()()3232csc 34csc 4ααa a -=()32csc 38αa =因为πα<<0 当2πα=时 ()3csc α取得最小值为1所以当2πα=时过焦点的弦与抛物线ax y 42=所围成的图形面积()32csc 382απa A =⎪⎭⎫ ⎝⎛最小7、1）()()πθθθθπππ45cos 321cos 1212232302=⎥⎦⎤⎢⎣⎡++=⎰⎰d d A2）()()[]⎰⎰-=++=ππππθθθθθ22220241cos sin 21sin 21a d a d a A 8、()()⎰⎰------+=44442222165165dx xdx xV ππ()()⎰-=⎭⎬⎫⎩⎨⎧----+=4422222160165165ππdx xx9、解法同题810、提示：()32132-=x y ，32x y = 联立得交点⎪⎪⎭⎫ ⎝⎛36,2，⎪⎪⎭⎫ ⎝⎛-36,2 所求弧长()⎰+=212'12dx y s由()32132-=x y 得()yx y 2'1-=于是()()()()()1231321134222'-=--=⎪⎪⎭⎫ ⎝⎛-=x x x y x y于是得()⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛=⎥⎦⎤⎢⎣⎡-+=⎰12598123122321221dx x S(C)1、证明：此处球缺可看作由如图阴影（图222R y x =+的一部分）绕y 轴旋转而成所以()⎰⎰---==RHR RHR dy y R dy x V 222ππR HR R HR y yR ---=332ππ()[]()[]3323H R R H R R R -----=ππ⎪⎭⎫ ⎝⎛-=32H R H π2、解：()⎰-=tdx x t S 11sin sin ()⎰-=22sin sin πtdx t x S()()⎰-=tdx x t t S 1sin sin +()⎰-2sin sin πtdx t x=⎪⎭⎫ ⎝⎛≤≤-⎪⎭⎫⎝⎛-+201sin 22cos 2ππt t t t ()0cos 22'=⎪⎭⎫⎝⎛-=t t t S π，得驻点2421ππ==t t易知()()002''1''<>t S t S122max -=⎪⎭⎫ ⎝⎛=∴ππS S ，124min -=⎪⎭⎫⎝⎛=πS S3、解：设()00,y x 为曲线x y =()40≤≤x 上任一点，易得曲线于该点处的切线方程为：()00021x x x y y -=- 即0022x x y y +=得其与0=x ， 4=x 的交点分别为⎪⎭⎫ ⎝⎛2,00y ，⎪⎪⎭⎫⎝⎛+0022,4y y 于是由此切线与直线0=x ， 4=x 以及曲线x y =所围的平面图形面积为：3164222004000-+=⎪⎪⎭⎫ ⎝⎛-+=⎰x y dx x x x y S3164200-+=x x 问题即求31642-+=xx S ()40≤≤x 的最小值令022321=+=--xxS 得唯一驻点2=x 且为唯一极小值所以当2=x 时，S 最小即所求切线即为：2222+=x y 4、如图：以水中的球心为原点，上提方向作为坐标轴建立坐标系易知任意[]dx x x +,段薄片在提升过程中在水中行程为r －x ，而在水上的行程为2r －（r －x ）＝r ＋x因为求的密度与水相同，所以在水中提升过程中浮力与重力的合力为零，不做功，而在水面上提升时，做功微元为()()dx x r x r g dW +-=22π()()g r dx x r x r g dW W r r r r 42234ππ⎰⎰--=+-==。

(完整版)高等数学定积分应用习题答案

第六章定积分的应用习题 6-2 (A)1．求下列函数与 x 轴所围部分的面积：]3,0[,86)1(2+-=x x y ]3,0[,2)2(2x x y -=2．求下列各图中阴影部分的面积： 1.图 6-13．求由下列各曲线围成的图形的面积：;1,)1(===-x e y e y x x 与;)0(ln ,ln ,0ln )2(>>====a b b y a y x x y 与;0,2)3(2==-=y x y x x y 与;)1(,2)4(22--==x y x y;0,2)1(4)5(2=-=-=y x y x y 与;2,)6(2x y x y x y ===与;)0(2sin ,sin 2)7(π≤≤==x x y x y;8,2)8(222（两部分都要计算）=+=y x x y4．的图形的面积。

所围成与直线求由曲线e x e x y x y ====-,,0ln 15．的面积。

处的切线所围成的图形和及其在点求抛物线)0,3()3,0(342--+-=x x y6．的面积。

处的法线所围成的图形及其在点求抛物线),2(22p ppx y = 7．形的面积。

与两坐标轴所围成的图求曲线a y x =+8．所围图形的面积。

求椭圆12222=+by a x9．。

与横轴所围图形的面积（的一拱求由摆线)20)cos 1(),sin (π≤≤-=-=t t a y t t a x10．轴之间的图形的面积。

的切线的左方及下方与由该曲线过原点求位于曲线x e y x =11．求由下列各方程表示的曲线围成的图形的面积： ;)0(sin 2)1(>=a a θρ;)0()cos 2(2)2(>+=a a θρ ;2cos 2)3(2（双纽线）θρ=抛物体的体积。

轴旋转，计算所得旋转所围成的图形绕及直线把抛物线x x x x ax y )0(4.12002>==体的体积。

旋转轴旋转，计算所得两个轴及所围成的图形，分别绕由y x y x x y 0,2,.133===14．求下列已知曲线所围成的图形，按指定的轴旋转所产生的旋转体的体积： ;,0,,0)1(轴绕与x y a x x axcha y ====;,2sin )2(轴绕与x xy x y π== ;,)20(cos sin )3(轴绕与x x x y x y π≤≤==;0,2,ln )4(轴绕与y y x x y === ;0,2)5(2轴绕与y y x y x x y ==-=;,16)5()6(22轴绕y y x =+-。

微积分第六章第四节定积分的应用

4ab
1
ab .
0
22
2 0
sinn
xdx
n
n
n
n
1 1
n n n n
3 2 3 2
3 4 4 5
1 2 2 3
, n为正偶数
2
, n为大于1的奇数
19
例4 计算由曲线 y2 2x 和直线 y x 4所围成
的图形的面积. 解两曲线的交点
y
y2 2x
(8, 4)
2
Vy 2
1 x 2x2dx .
0
o 1x
35
例12 求由曲线 y ( x 1)( x 2) 和 x 轴所围平面图
形绕 y 轴旋转一周而成的旋转体体积.
解
Vy 2
2
x( x 1)( x 2)dx
.
1
2
y
y
a
b
12
o
xo
x
y f (x)
“套筒法”推广：
由平面图形 0 a x b, f ( x) y 0 绕 y 轴
t (t 2 x2 )dx
1
(
x2
t
2
)
dx
0
t
y
1
y = x2
[t 2 x
x3 3
]
t 0
x3 [
3
t
2
x]
1 t
4t 3 t 2 1 ， 0 t 1
3
3
t2
S2
S1
o
t1 x
S 4t 2 2t
令
2t(2t 1)
0 ，得驻点:
t
0, t
1，
2
经比较，当t 1 时两面积和最小.

定积分及其应用习题章节-PPT课件

b
n
嘉兴学院
2/25/2019
第六章定积分
第7页
3、存在定理
可积的两个充分条件：
称在区间上可积 . f ( x ) [ a , b ]
函数在区间上连续时， f ( x ) [ a , b ] 定理1 当
定理2 设函数 f ( x ) 在区间 [ a , b ] 上有界，
a b
第六章定积分
第3页
1、问题的提出
实例1 （求曲边梯形的面积A）
y f ( x ) ( f ( x ) 0 ) 、曲边梯形由连续曲线
x b 所围成 . x x a 轴与两条直线、
A lim f( x i) i
0 i 1
2/25/2019
第六章定积分
第11页
5、牛顿—莱布尼茨公式
f(x )在 [ a ,b ]上果连续，则积分上限的函数定理1 如 (x ) f(t) dt [ a ,b ]上在具有导数，且它的导数 a d x (x (axb ) ) f(t) dt f(x ) 是 a dx
a a
b
b
（ 2）
嘉兴学院
f ( x ) dx f ( x ) dx (ab ) a a2/25/2019b Nhomakorabeab
第六章定积分
第10页
在区间 f ( x ) [ a , b ] 性质6 设 M 及分别是函数 m
上的最大值及最小值，
m ( b a ) f ( x ) dx M ( b a ) 则 .

定积分应用1(6-1--6-5)精品文档18页

第六章定积分的应用内容概要课后习题全解习题6-2★ 1．求由曲线xy =与直线x y =所围图形的面积。

知识点：平面图形的面积思路：由于所围图形无论表达为X-型还是Y-型，解法都较简单，所以选其一做即可解：见图6-2-1∵所围区域D 表达为X-型：⎩⎨⎧<<<<x y x x 10，（或D 表达为Y-型：⎩⎨⎧<<<<yx y y 210）★ 2．求在区间[0，π/2]上，曲线x y sin =与直线0=x 、1=y 所围图形的面积知识点：平面图形面积思路：由于所围图形无论表达为X-型还是Y-型，解法都较简单，所以选其一做即可解：见图6-2-2∵所围区域D 表达为X-型：⎪⎩⎪⎨⎧<<<<1sin 20y x x π，（或D 表达为Y-型：⎩⎨⎧<<<<y x y arcsin 010） ★★3．求由曲线x y =2与42+-=x y 所围图形的面积知识点：平面图形面积思路：由于所围图形表达为Y-型时解法较简单，所以用Y-型做解：见图6-2-3∵两条曲线的交点：⎩⎨⎧±==⇒⎩⎨⎧+-==22422y x x y x y ， ∴所围区域D 表达为Y-型：⎩⎨⎧-<<<<-22422yx y y ，（由于图形关于X 轴对称，所以也可以解为：★★4．求由曲线2x y =、24x y =、及直线1=y 所围图形的面积知识点：平面图形面积思路：所围图形关于Y 轴对称，而且在第一象限内的图形表达为Y-型时，解法较简单解：见图6-2-4一象限所围区域1D 表达为Y-型：∵第⎩⎨⎧<<<<y x y y 210，（若用X-型做，则第一象限内所围区域=1D ba D D ，其中aD ：⎪⎩⎪⎨⎧<<<<22410x y x x ， 5．求由曲线xy 1=与直线xy =★★及2=x 所围图形的面积知识点：平面图形面积思路：由于所围图形表达为X-型,解法较简单，所以用X-型做解：见图6-2-5∵两条曲线xy 1=和x y =的交点为（1，1）、（-1，-1），又这两条线和2=x 分别交于 ∴所围区域D 表达为X-型：⎪⎩⎪⎨⎧<<<<x y xx 121，★★★6．抛物线x y 22=分圆822=+y x 的面积为两部分，求这两部分的面积知识点：平面图形面积思路：所围图形关于X 轴对称，而且在第一象限内的图形表达为Y-型时，解法较简单解：见图6-2-6，设阴影部分的面积为1D S ，剩余面积为2D S∵两条曲线x y 22=、822=+y x 的交于(2,2)±（舍去4-=x 的解），∴所围区域1D 表达为Y-型：⎪⎩⎪⎨⎧-<<<<-228222y x y y ；又图形关于x 轴对称，（其中222cos 18cos 22cos 228404sin 2222+=+=⨯=-⎰⎰⎰=πππdt ttdt t dyy ty ） ★★★7．求由曲线x e y =、x e y -=与直线1=x 所围图形的面积知识点：平面图形面积思路：由于所围图形表达为X-型时，解法较简单，所以用X-型做解：见图6-2-7条曲线x e y =和x e y -=的交点为（0，∵两又这两条线和1=x 分别交于1），) ,1(e 和) ,1(1-e围区域D表达为X-型：∴所⎩⎨⎧<<<<-x x ey e x 10，8．求由曲线x y ln =与直线ay ln =★★★及b y ln =所围图形的面积)0(>>a b知识点：平面图形面积思路：由于所围图形表达为Y-型时，解法较简单，所以用Y-型做解：见图6-2-8∵在x ln的定义域范围内所围区域D ：⎩⎨⎧<<<<yex by a 0ln ln ， ★★★★9．求通过（0，0），（1，2）的抛物线，要求它具有以下性质：（1）它的对称轴平行于y 轴，且向下弯；（2）它与x 轴所围图形面积最小知识点：平面图形面积和求最值解：由于抛物线的对称轴平行于y 轴，又过（0，0），所以可设抛物线方程为bx ax y +=2，（由于下弯，所以0<a），将（1，2）代入bx ax y +=2，得到2=+b a ，因此x a ax y )2(2-+=该抛物线和X 轴的交点为0=x 和aa x 2-=， ∴所围区域D ：2200(2)a x ay ax a x-⎧<<⎪⎨⎪<<+-⎩ 得到唯一极值点：4-=a ，∴所求抛物线为：x x y 642+-=★★★★10．求位于曲线x e y =下方，该曲线过原点的切线的左方以及x 轴上方之间的图形的面积知识点：切线方程和平面图形面积思路：先求切线方程，再作出所求区域图形，然后根据图形特点，选择积分区域表达类型解：x e y =⇒xe y ='，∴在任一点0x x =处的切线方程为)(000x x e e y x x -=-而过（0，0）的切线方程就为：)1(-=-x e e y ，即ex y =所求图形区域为21D D D =,见图6-2-10X-型下的1D ：⎩⎨⎧<<<<∞-x e y x 00，2D ：⎩⎨⎧<<<<xe y ex x 1★★★11．求由曲线θcos 2a r=所围图形的面积知识点：平面图形面积思路：作图可知该曲线是半径为a 、圆心（0 ,a ）的圆在极坐标系下的表达式，可直接求得面积为2a π，也可选择极坐标求面积的方法做。