山东省2020年春节高二数学寒假作业天天练 练习(第8天)新人教版
新课标高二数学寒假作业8(必修5选修23)

新课标高二数学寒假作业8(必修5选修23)14.(本小题满分12分)(1)若的展开式中,的系数是的系数的倍,求;(2)已知的展开式中, 的系数是的系数与的系数的等差中项,求;(3)已知的展开式中,二项式系数最大的项的值等于,求. 15.(本小题满分1分)已知函数f(x)=lnx-ax2-2x(a0).(I)若函数f(x)在定义域内单调递增,求a的取值范围; (Ⅱ)若a=-且关于x的方程f(x)=-x+b在上恰有两个不相等的实数根,求实数b的取值范围.16.(本题满分1分)如图,分别是椭圆的左、右焦点,且焦距为,动弦平行于轴,且(Ⅰ)求椭圆的方程;(Ⅱ)若点是椭圆上异于点的任意一点,且直线分别与轴交于点,若的斜率分别为,求的取值范围.选修2-3参考答案1.A2.D3.B4.C5.D6.C7.B8.B9.210.11.7212.13.(1)由,得或.所以,当或时,为实数;3分(2)由,得且.所以,当且时,为虚数;6分(3)由得所以,当时,为纯虚数;9分(4)由得所以,当时,复数对应的点在第四象限.12分14.(1)的二项式系数是,的二项式系数是.依题意有1分4分(2)依题意,得5分即8分(3)依题意得9分10分即解得,或所以.12分15.16.(Ⅰ)因为焦距为,所以 2分由椭圆的对称性及已知得又因为所以因此 4分于是因此椭圆的方程为 6分(Ⅱ)设,则直线的方程为,令,得故同理可得 9分所以,因此因为在椭圆上,所以故 12分所以 14分又因为当时重合,即重合,这与条件不符,所以因此的取值范围是 15分高中是人生中的关键阶段,大家一定要好好把握高中,编辑老师为大家整理了2019年高二数学寒假作业,希望大家喜欢。
高二数学上学期寒假作业8
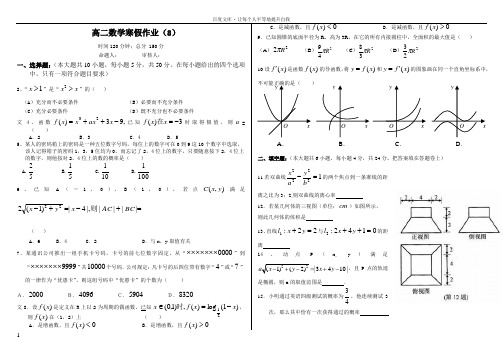
高二数学寒假作业(8)时间120分钟;总分 150分 命题人: 审核人:一、选择题:(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项符合题目要求)2、“1x >”是“2xx >”的( )(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件 文4、函数,93)(23-++=x ax x x f 已知3)(-=x x f 在时取得极值,则a=( )A .2B .3C .4D .55、某人的密码箱上的密码是一种五位数字号码,每位上的数字可在0到9这10个数字中选取,该人记得箱子的密码1,3,5位均为0,而忘记了2,4位上的数字,只要随意按下2,4位上的数字,则他按对2,4位上的数的概率是( ) A.52 B.51 C.101 D.10016、已知A (-1,0),B (1,0),若点),(y x C 满足=+-=+-|||||,4|)1(222BC AC x y x 则( )A .6B .4C .2D .与x ,y 取值有关7、某通讯公司推出一组手机卡号码,卡号的前七位数字固定,从“0000⨯⨯⨯⨯⨯⨯⨯”到“9999⨯⨯⨯⨯⨯⨯⨯”共10000个号码.公司规定:凡卡号的后四位带有数字“4”或“7”的一律作为“优惠卡”,则这组号码中“优惠卡”的个数为( ) A.2000B.4096C.5904D.8320文8.设)(x f 是定义在R 上以2为周期的偶函数,已知,则)(x f 在(1,2)上 ( )A .是增函数,且0)(<x fB .是增函数,且0)(>x fC .是减函数,且0)(<x fD .是减函数,且0)(>x f9.已知圆锥的底面半径为R ,高为3R ,在它的所有内接圆柱中,全面积的最大值是( ) (A )22R π (B )249Rπ (C )238R π (D )223R π10.设()f x '是函数()f x 的导函数,将()y f x =和()y f x '=的图象画在同一个直角坐标系中,不可能正确的是( )二、填空题:(本大题共6小题,每小题4分,共24分。
山东省春节高中高二数学寒假作业天天练学习练习第8天新人教版本
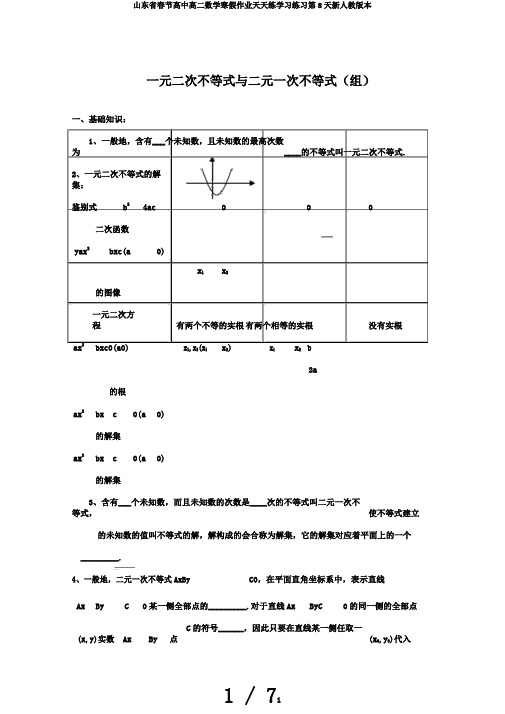
一元二次不等式与二元一次不等式(组)一、基础知识:1、一般地,含有___个未知数,且未知数的最高次数为____的不等式叫一元二次不等式.2、一元二次不等式的解集:鉴别式b24ac000二次函数yax2bxc(a0)x1x2的图像一元二次方程有两个不等的实根有两个相等的实根没有实根ax2bxc0(a0)x1,x2(x1x2)x1x2b2a的根ax2bx c0(a0)的解集ax2bx c0(a0)的解集3、含有___个未知数,而且未知数的次数是____次的不等式叫二元一次不等式,使不等式建立的未知数的值叫不等式的解,解构成的会合称为解集,它的解集对应着平面上的一个_________.4、一般地,二元一次不等式AxBy C0,在平面直角坐标系中,表示直线Ax By C0某一侧全部点的_________.对于直线Ax ByC0的同一侧的全部点(x,y)实数Ax ByC的符号______,因此只要在直线某一侧任取一点(x0,y0)代入Ax By C,由Ax0By0C的符号即可判断出Ax ByC0表示的是直线的哪一侧的点集.5、一般地,在线性拘束条件下求线性目标函数的最大值或最小值问题,称为___________问题,知足线性拘束条件的解叫做________,由全部可行解构成的会合叫做________,使目标函数获得最大值或最小值的可行解叫做该问题的_________.二、选择题:1、不等式2x0的解集是() x1A.(,1)(1,2] B.[-1,2] C.(,1)(2,) D.(-1,2]2、已知对于x的方程x2(m3)x m20有一个根大于1,而另一个根小于1,那么实数m的取值范围是()A.(-2,1)B.(,2)(1,) C.(-1,2) D.(,1)(2,)3、不等式x2ax b0的解集为{x|2x3},则不等式bx2ax10的解集为()A.{x|3x2}B.{x|1x1}C.{x|1x1}D.空集32234、下边给出的四个点中,到直线x y10的距离为2,且位于x y10x y1表示的平20面地区内的点是()A.(1,1) B.(-1,1) C.(-1,-1)D.(1,-1)x y205、在平面直角坐标系中,不等式组x y20表示的平面地区的面积是()y0A.42 C.22x y16、假如实数x,y知足拘束条件x y1,则目标函数z4x y的最大值为()3x y3y0y17x,yx y0,则u()知足不等式组取值范围是、若实数x2xy201A.[1,1]B.[1,1]C.[1,)D.[1,1)323228、设a1,b1,c1,a2,b2,c2均为非零实数,不等式a1x2b1x c10和a2x2b2xc20的解集分别为会合M和N,则“a1b1c1”是“M=N”的()a2b2c2A.充足不用要条件 B.必需不充足条件C.充要条件D.既不充足也不用要条件y2xy129、变量x,y知足条件2x9y36,则使z3x2y取B C 2x3y24x0,y0得最小值的最优解为______A x10、如下图A(1,0),B(0,1),C(2,4),目标O函数tax y的可行域为四边形35 OABC,若当且仅当x 24,y时目标函数t获得最小值,则35实数a的取值范围是_______11、对于x的不等式(a2)x22(a2)x40对随意实数恒建立,则实数a的取值范围为_______12、某产品的总成本y(万元)与产品x(台)之间的函数关系是y300020x2,此中x (0,240)若每台产品的售价是25万元,则生产者不赔本(即销售收入不小于总成本)时的最低产量为______2x y513、(1)已知实数x,y知足3x y5,求u(x1)2(y1)2的最大值和最小值;x2y50(2)若二次函数y f(x)的图像过原点,且1f(1)2,3f(1)4,求f(2)的取值范围.14、解对于x的不等式ax2(a1)x10,(a0)15、某人上午7:00时,乘摩托艇以匀速v海里/时(4v20)从A港出发到相距50海里的B港去,而后乘汽车以匀速w千米/时(30w100)自B港向距300千米的C市驶去,要求在当日16:00时到21:00时这段时间抵达C市.设汽车、摩托艇所需要的时间分别是x,y小时.(1)作图表示知足上述条件的x,y的范围;(2)假如已知所要的经费:p1003(5x)2(8y)(元),那么v,w分别是多少时,所要的经费最少?此时需花销多少元?答案:1.D2.A3.C4.C5.B6.B7.D8.D9.(3,6)12a311.2a212.15010.10 513.(1)x3,y4时获得最大值且umax41,x2,y1时获得最小值且umin136f(2)1014.当a0时解集为{x|x1};当0a1时解集为{x|1x1};当a 1时解集为空1时解集为{x|1a集;当a x1}a3x1015.(1)x,y知足的拘束条件是5y25,图略229xy14(2)当x 10,y 4时,p最小,此时v 12.5,w 30,p min93元。
高二数学寒假作业:(八)(Word版含答案)

高二数学寒假作业(八)一、选择题,每小题只有一项是正确的。
1.已知{}n a 为等比数列,472a a +=,568a a =-,则110a a += ( )A 、7B 、 5C 、-5D 、-7 2.下列结论正确的是( )A .当0>x 且1≠x 时,x x lg 1lg +≥2B .当0>x 时,xx 1+≥2 C .当x ≥2时,x x 1+的最小值为2 D .当x <0≤2时,xx 1-无最大值 3.设变量y x ,满足约束条件⎪⎩⎪⎨⎧-≥-≤+≥+144222y x y x y x ,则目标函数y x z-=3的取值范 围是( )A .⎥⎦⎤⎢⎣⎡-6,23 B. ⎥⎦⎤⎢⎣⎡--1,23 C .[]6,1- D. ⎦⎤⎢⎣⎡-23,6 4.已知双曲线)0,0(1:2222>>=-b a bx a y C 的离心率为25,则C 的渐近线方程为( ) A .x y 2±= B .x y 21±= C .x y 4±= D .x y 41±= 5.已知()0,12,1--=t t ,()t t ,,2=的最小值为( )A. 2B. 6C. 5D. 36.在正方体1111D C B A ABCD -中,M 、N 分别为棱1AA 和1BB 的中点,则><N D CM 1,sin 的值为( )A. 91B. 594C. 592D. 32 7.设等差数列{a n }的前n 项和为S n ,若S 2=4,S 4=20,则该数列的公差d=A .2B .3C .6D .78.数列{}n a 的通项公式2=n a n n +,则数列1n a ⎧⎫⎨⎬⎩⎭的前10项和为 A .910 B .1011 C .1110 D .12119.已知椭圆的一个焦点为F ,若椭圆上存在点P ,满足以椭圆短轴为直径的圆与线段PF 相 切于线段PF 的中点,则该椭圆的离心率为 ( )2359 二、填空题10.在====∆A AC BC AB ABC 则中,,4,13,3 .11.设等差数列{}n a 的前n 项和为n S ,若1133,,122k k a a S +=-==-,则正整数K=____.12.数列{a n }的前n 项和是S n ,若数列{a n }的各项按如下规则排列:,…,若存在整数k ,使S k <10,S k+1≥10,则a k = _________ .13.已知ABC ∆的三边,,a b c 成等差数列,且22263a b c ++=,则b 的最大值是▲ .三、计算题14.(10分)在ΔABC 中 ,已知,3,30,30=︒==︒c B A 解三角形ABC 。
高二数学寒假作业8

高二数学假期作业8(理科)一、选择题1.如果实数y x ,满足不等式组30,230,1.x y x y x +-≤⎧⎪--≤⎨⎪≥⎩目标函数z kx y =-的最大值为6,最小值为0,则实数k 的值为A .1 B .2 C .3 D .4( )2.高三某班有学生36人,现将所有同学随机编号,用系统抽样的方法,抽取一个容量为4的样本,已知5号、23号、32号学生在样本中,则样本中还有一个学生的编号为A . 13 B . 14 C . 18 D . 26( )3.一个样本a ,3,5,7的平均数是b ,且a , b 分别是数列{}()2*2n n N -∈的第2项和第4项,则这个样本的方差是A . 3 B . 4 C . 5 D . 6( ) 4.已知x 、y 取值如下表:从所得的散点图分析可知: y 与x 线性相关,且线性回归方程为0.95y x a =+,则a = A . 1.30 B . 1.45 C . 1.65 D . 1.80( )5.数列{}n a 中, ()*12211,n n n a a a a a n N ++===+∈,设计一种计算{}n a 的前n 项和的算法框图如右,其中赋值框中应填入的是( ) A . ,a b b a b ==+ B . ,b a b a b =+=C . ,,x b a x b a b ===+D . ,,x b b a b a x ==+=6.如图,是由一个圆、一个三角形和一个长方形构成的组合体,现用红、蓝两种颜色为其涂色,每个图形只能涂一种颜色,则三个形状颜色不全相同的概率为( )A .43B .83C .41 D .817.某人睡午觉醒来,发现表停了,他打开收音机,想听电台报时,则他等待时间不多于15分钟的概率为A .12B .14C .23D .348.某班班会准备从含甲、乙、丙的7名学生中选取4人发言,要求甲、乙两人至少有一个发言,且甲、乙都发言时丙不能发言,则甲、乙两人都发言且发言顺序不相邻的概率为A . 217B . 316C . 326D . 328( )9.如图所示:在杨辉三角中,斜线上方箭头所连的数组成一个齿形的数列: 记这个数列前项和为,则等于( )A . 128B . 144C . 155D . 16410.在5()ax x-的展开式中3x 的系数等于5-,则该展开式各项的系数中最大值为( )A .5B .10C .15D .20 二、填空题11.给出下列四个命题中:①命题“2,13x R x x ∃∈+>”的否定是“2,13x R x x ∀∈+≤”;②“2m =-”是“直线(2)10m x my +++=与直线(2)(2)30m x m y -++-=相互垂直”的必要不充分条件;③设圆22220(40)x y Dx Ey F D E F ++++=+->与坐标轴有4个交点,分别为1212(,0),(,0),(0,),(0,)A x B x C y D y ,则12120x x y y -=;④对x ∀∈+R,不等式1x ≥恒成立, 则2≤a其中所有真命题的序号是 ▲ .12.如图所示,此程序框图运行后输出的值是________.13.若变量,x y 满足约束条件0{102 10x y y x x -≤≤--≥,则2z x y =-的最小值为__________.14. 5个人排成一排,其中甲与乙必须相邻,而丙与丁不能相邻,则不同的排法种数有 种.三、解答题15.在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率; (2)由表中统计数据填写下边列联表,试采用独立性检验进行分析,能否在犯错误的概率不”. 参考数据与公式:,其中.16.乒乓球比赛规则规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换.每次发球,胜方得1分,负方得0分.设在甲、乙的比赛中,每次发球,发球方得1分的概率为0.6,各次发球的胜负结果相互独立.甲、乙的一局比赛中,甲先发球.随机变量ξ表示开始第4次发球时甲的得分....,求ξ的分布列和期望。
山东省2020年春节高二数学寒假作业天天练 练习(第6天) 新人教版

数列求和一、基础知识:1、 公式法求和(1) 等差数列的前n 项和n S =__________=_____________(2) 等比数列的前n 项和n S =_______________2、非等差、等比数列的求和常用方法(1)分组求和:通项虽不是等差、等比数列,但通过分组可化为由等差、等比的和的形式,如数列9,99,999,9999,…的前n 项和的计算(2)裂项相消法:将通项表示为差的形式,求和时,中间若干项可正负相消,然后将保留的部分求和即可.举例分拆如111)1(1+-=+=n n n n a n ,11++=n n b n n n -+=1(3)错位相减法:等比数列求和公式推导过程的推广,此法适用于等差数列与等比数列乘积形式的数列求和.二、巩固练习:1、已知数列}{n a 的前n 项和n n S n 92-=,第k 项满足85<<k a ,则k 等于( )A. 6B. 7C.8D. 92、计算102411024818414212++++Λ所得结果为( ) A.102410232046 B.102410232047 C.102412047 D.102412046 3、设n S n n 1)1(4321+-++-+-=Λ,则2217S S +的值为( )A. -2B. -1C. 0D. 14、设}{n a 为等比数列,}{n b 为等差数列,且n n n b a c b +==,01,若数列}{n c 是1, 1,2,…,则}{n c 的前10项之和为( )A. 978B. 557C.476D. 5865、已知数列}{n a 的通项公式11++=n n a n ,前n 项和为9,则n 等于( )A. 10B.100C. 9D.99 6、化简 1+211++3211+++…+n++++Λ3211的结果是( ) A. 1+n n B. 12+n n C. 122+n n D. 12+n n 7、数列Λ,1614,813,412,211⨯⨯⨯⨯的前n 项和为( )A. n n n 21221--+ B. 12122---n n n C. n n n 21)2(212-++ D. 1211)1(21+-++n n n 8、计算n n )1(201262-+++++Λ等于( ) A. 3)1(2-n n B. 6)2)(1(--n n n C. 3)12)(1(-+n n n D. 6)12)(1(+-n n n 9、已知数列}{n a 的前n 项和n S 满足2,121==S S ,)2(2311≥-=-+n S S S n n n ,则 =n a __________10、数列7,77,777,7777,…的前n 项和=n S __________11、数列}{n a 中,1,311-+==+n a a a n n ,则=n a ____________12、数列}{n a 中,)(23,21111+++∈=+=N n a a a n n n ,则数列}{n a 的前99项的和 =99S _____,前100项的和=100S _____13、已知数列-1,4,-7,10,…,)23()1(--n n,…,求其前n 项和14、已知数列}{n a 的前n 项和n n S n 22+= (1)求数列的通项公式n a ;(2)设14332211111+++++=n n n a a a a a a a a T Λ,求n T15、设有数列}{n a ,651=a ,若以Λ,,,321a a a 为系数的二次方程: )2,(0121≥∈=+-+-n N n x a x a n n 都有根βα,,且满足133=+-βαβα(1)求证:}21{-n a 为等比数列;(2)求数列}{n a 的前n 项和n S参考答案:1. C2. A3. A4. C5. D6. B7.B8. A9.⎩⎨⎧≥=-)2(2)1(12n n n 10.8170631071--⨯+n n 11.2832+-n n 12.99211-,100211- 13.⎪⎩⎪⎨⎧+-=)(,23)(,213为偶数为奇数n n n n S n 14.(1)12+=n a n (2)96+=n n T n 15.解:(1)依题意1-=+n n a a βα,11-=n a αβ11311=-∴--n n n a a a 整理得31311+=-n n a a ,即)21(31211-=--n n a a 又31211=-a ,}21{-∴n a 是等比数列,首项和公比都等于31 (2) 由(1)得21)31(+=n n a 2)313131(2n S n n ++++=∴Λn n 32121⨯-+=。
人教A版数学必修四高二数学寒假作业.docx
高中数学学习材料马鸣风萧萧*整理制作安陆一中10-11学年度高二数学寒假作业姓名: 班级编号: 分数:一、选择题:本大题共10题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 下列语句中,是命题的个数是( )①|x +2| ②-5∈Z ③π∉R ④{0}∈N A.1 B.2 C.3 D.42. 抛物线y = 1a x 2 (a ≠0)焦点坐标是( )A .(0, a 4 )或(0, –a 4 )B .(0, a 4 )C .(0 , 14a )或(0,–14a )D .(0, 14a)3. 某食品的广告词为:“幸福的人们都拥有”,初听起来,这似乎只是普通的赞美说词,然而他的实际效果大哩,原来这句话的等价命题是( ) A .不拥有的人们不一定幸福 B .不拥有的人们可能幸福 C .拥有的人们不一定幸福 D .不拥有的人们不幸福 4. 不等式04)2(2)2(2<--+-x a x a 对于R x ∈恒成立,那么a 的取值范围是( )A .)2,2(-B .]2,2(-C .]2,(-∞D .)2,(--∞5. 方程231x y =-所表示的曲线是( )A .双曲线B .椭圆C .双曲线的一部分D .椭圆的一部分6. 如果双曲线136y 64x 22=-上一点P 到它的右焦点的距离是8,那么P 到它的左准线距离是( )A .965B .865C .856D .8367. 直线y x b =+与抛物线22x y =交于A 、B 两点,O 为坐标原点,且OA OB ⊥,则b =( ).2A .2B - .1C .1D -8. 函数f (x )=x |x +a |+b 是奇函数的充要条件是( )A .ab =0B .a +b =0C .a =bD .a 2+b 2=09. 椭圆192522=+y x 上一点M 到焦点1F 的距离为2,N 是1MF 的中点,则ON 等于( ) A .2 B .4 C .6 D .2310. 过抛物线y 2= 2px (p >0)的焦点F 作一条直线l 交抛物线于A 、B 两点,以AB 为直径的圆和该抛物线的准线l 的位置关系是( )A .相交B .相离C .相切D .不能确定答题卡 题号 1 2 3 4 5 6 7 8 9 10 答案二、填空题:请把答案填在题中横线上(每小题5分,共25分).11.若关于x 的方程22(1)260x a x a +-++=有一正一负两实数根,则实数a 的取值范围_____________。
2020-2021学年高二上学期数学寒假作业全套(共16套)
第一章 数列(寒假第1天)一、选择题1.已知等差数列{a n }中,a 2+a 4=6,则a 1+a 2+a 3+a 4+a 5=( )A .30B .15C .5 6D .10 62.等比数列{a n }中,a 2=4,a 7=116,则a 3a 6+a 4a 5的值是( ) A .1B .2C .12D .143.设{a n }是递增等差数列,前三项的和为12,前三项的积为48,则它的首项是( )A .1B .2C .4D .64.记S n 为等差数列{a n }的前n 项和.若a 4+a 5=24,S 6=48,则{a n }的公差为( )A .1B .2C .4D .85.已知数列{a n }满足a 1=1,a n +1=23a n ,n ∈N +,其前n 项和为S n ,则( ) A .S n =2a n -1B .S n =3a n -2C .S n =4-3a nD .S n =3-2a n二、填空题6.在等差数列{a n }中,a 9=8,a 12≥23,则公差d 的取值范围为 .7.等比数列{a n }的前n 项和为S n ,若S 3+3S 2=0,则公比q = .8.若数列{a n }满足2a n =a n +1+a n -1,且a 15=8,a 60=20,则a 75= .9.已知数列{a n }中,a 1=1,a n =a n -1+12(n ≥2),则数列{a n }的前9项和等于 . 10.已知数列{}n a 中22n n a =+,求前n 项和n S = .三、解答题11.(1)已知{a n}是等差数列,且a1-a4+a8-a12+a15=2,求a3+a13的值;(2)已知在等差数列{a n}中,若a49=80,a59=100,求a79.12.已知{a n}为等比数列.(1)若a n>0,a2a4+2a3a5+a4a6=25,求a3+a5;(2)若a n>0,a5a6=9,求log3a1+log3a2+…+log3a10的值第二章 解三角形(寒假第2天)一、选择题1.在△ABC 中,若3a =2b sin A ,则B =( )A .π3B .π6C .π3或2π3D .π6或5π62.已知△ABC 的三个内角之比为A ∶B ∶C =3∶2∶1,那么,对应的三边之比a ∶b ∶c 等于( )A .3∶2∶1B .3∶2∶1C .3∶2∶1D .2∶3∶13.在△ABC 中,已知a =4,b =6,C =120° ,则边c 的值是( )A .8B .217C .6 2D .219 4.在△ABC 中,sin(A +B )sin(A -B )=sin 2C ,则此三角形的形状是( )A .等腰三角形B .直角三角形C .等边三角形D .等腰直角三角形5.在△ABC 中,a =5,b =15,A =30°,则c 等于( )A .2 5 B. 5 C .25或 5 D .以上都不对二、填空题6.在锐角△ABC 中,角A 、B 、C 的对边分别为a ,b ,c ,且a =4b sin A ,则cos B = .7.在△ABC 中,若a =2,b =3,C =60°,则sin A = .8.在△ABC 中,若m =(sin A ,cos A ),n =(cos B ,sin B ),m ·n =sin 2C ,则角C = .9.在C ∆AB 中,3a =,b =23π∠A =,则∠B = . 10.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知A =6π,a =1,b =3,则B = .三、解答题11.在△ABC 中,3sin 2B =2sin 2B ,(1)求角B 的值;(2)若a =4,b =27,求c 的值.12.设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若a =3,sin B =12,C =π6,求b .第三章 不等式(寒假第3天)一、选择题1.(x -2)(3x +5)<0的解集为( )A .⎝ ⎛⎭⎪⎫-53,+∞ B .⎝ ⎛⎭⎪⎫-∞,-53∪(2,+∞) C .(2,+∞)D .⎝ ⎛⎭⎪⎫-53,2 2.若不等式ax 2+5x +c >0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ 13<x <12,则a ,c 的值为( ) A .a =6,c =1B .a =-6,c =-1C .a =1,c =6D .a =-1,c =-6 3.已知集合M =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x +3x -1<0,N ={x |x ≤-3},则集合{x |x ≥1}等于( ) A .M ∩N B .M ∪N C .∁R (M ∩N ) D .∁R (M ∪N ) 4.设x >0,则y =3-3x -1x 的最大值是( )A .3B .3-2 2C .3-2 3D .-1 5.若x ,y 满足⎩⎪⎨⎪⎧ 2x -y ≤0x +y ≤3x ≥0,则2x +y 的最大值为( )A .0B .3C .4D .5二、填空题6.不等式x 2+x -2<0的解集为 .7.不等式2x +13-x≥1的解集为 . 8.函数f (x )=x (4-2x )的最大值为 . 9.已知x ,y 满足约束条件04,03,28,x y x y ≤≤⎧⎪≤≤⎨⎪+≤⎩则25z x y =+的最大值为 .10.已知06x <<,则(6)x x -的最大值是 .三、解答题11.解下列不等式(1)2x 2+7x +3>0; (2)-x 2+8x -3>0;12.若1->x ,则x 为何值时11++x x 有最小值,最小值为几?第四章 圆锥曲线与方程(寒假第4天)一、选择题1.椭圆2213y x +=的焦点坐标是( )A .()2,0,()2,0-B .),()C .(,(0,D .()0,2,()0,2-2.椭圆22143x y +=的焦距为( ) A .1 B .2 C .3 D .43.下列双曲线中离心率为2的是( ) A .22124x y -= B .22142x y -= C .22146x y -= D .221410x y -= 4.已知双曲线2222:14x y C t t-=,则双曲线C 的离心率是( )A .2BCD 5.过抛物线24y x =的焦点作直线交抛物线于()11,A x y ,()22,B x y 两点,如果126x x +=,那么||AB =( )A .10B .9C .8D .6二、填空题6.已知椭圆方程221516x y +=表示椭圆,焦点1F ,2F ,椭圆上有一动点P ,则12PF PF += . 7.过椭圆221169x y +=的焦点F 的弦中最短弦长是 . 8.若抛物线24y x =上一点M 到焦点F 的距离为4,则M 点的横坐标为 .9.已知抛物线方程为2x y =,则其焦点坐标为 . 10.已知双曲线的方程为2213x y -=,则焦点到渐近线的距离为 .三、解答题11.求椭圆22925225x y +=长轴长、短轴长、离心率、焦点坐标、和顶点坐标.12.在平面直角坐标系xOy 中,直线l 与抛物线24y x =相交于不同的,A B 两点.(1)如果直线l 的方程为1y x =-,求弦AB 的长;(2)如果直线l 过抛物线的焦点,求OA OB ⋅的值.第五章 变化率与导数(寒假第5天)一、选择题1.若曲线2y ax =在x a =处的切线与直线210x y --=平行,则a =( )A .1-B .1C .1-或1D .12-或12.曲线()ln f x x =在点()1,0处的切线方程为( )A .10x y --=B .10x y -+=C .10x y +-=D .10x y ++=3.函数f (x )=1﹣x +x 4的导数记为()f x ',则()1f '-等于( )A .﹣2B .﹣3C .﹣4D .﹣54.已知函数()y f x =在0x x =处的导数为1,则()()000lim 2x f x x fx x ∆→+∆-=∆()A .0B .12 C .1 D .25.已知ln ()xf x x =,则()f x '=( )A .21xB .11x - C .1ln x - D .21ln xx -二、填空题6.曲线ln 1y x x =++的一条切线的斜率为2,则切点坐标为 .7.函数()ln f x x x =,在点(),P e e 处的切线方程为 .8.函数y =f (x )的图象在A (2,f (2))处的切线方程是y =3x ﹣1,则f (2)+f ′(2)= . 9.已知函数()sin f x x =的导函数为f x ,则π()2f '= .10.已知()()32'0f x x xf =+,则()'1f = .三、解答题11.已知()ln f x x x =,求函数()y f x =的图象在e x =处的切线方程.12.()32f x ax bx cx d =+++,且()03f =,()00f '=,()13f '=-,()20f '=;求a b c d ,,,的值第六章 导数应用(寒假第6天)一、选择题1.函数22y x x=+的单调递增区间为( ) A .(),1-∞B .2,)+∞C .()1,+∞D .(),0-∞2.函数()22ln f x x x =-的递增区间是( ) A .10,2⎛⎫ ⎪⎝⎭B .1,02⎛⎫-⎪⎝⎭和1,2⎛⎫+∞ ⎪⎝⎭C .1,2⎛⎫+∞⎪⎝⎭D .1,2⎛⎫-∞-⎪⎝⎭和10,2⎛⎫⎪⎝⎭3.函数4()3ln f x x x x=+-的单调递减区间是( ) A .(1,4)-B .(0,1)C .(4,)+∞D .(0,4)4.如图是函数y =f (x )的导数y =f '(x )的图象,则下面判断正确的是( ) A.在(﹣3,1)内f (x )是增函数 B .在x =1时,f (x )取得极大值C.在(4,5)内f (x )是增函数 D .在x =2时,f (x )取得极小值5.函数()sin xf x ae x =-在0x =处有极值,则a 的值为( )A .1-B .0C .1D .e二、填空题6.函数()43ln f x x x x=++的单调递减区间是 . 7.函数()52ln f x x x =-的单调递减区间是 . 8.函数()21xf x x =+的单调递增区间为 . 9.函数322611y x x =-+的单调减区间是 . 10.函数32()34f x x x =-+在x = 处取得极小值.三、解答题11.函数()ln 1f x x x ax =-+在点(1,(1))A f 处的切线斜率为2-. (1)求实数a 的值;(2)求()f x 的单调区间和极值.12.已知函数3()31f x x x =-+. (1)求()f x 的单调区间; (2)求函数的极值;(要列表).第七章 综合作业一(寒假第7天)一、选择题1.已知等差数列{}n a 中,7916+=a a ,41a =,则12a 的值是( ) A .15B .30C .3D .642.已知等差数列{}n a 的前n 项和为n S ,且310179a a a ++=,则19S =( ) A .51B .57C .54D .723.在ABC 中,已知30A =,60B =,10a =,则b 等于( )A .B .C D .4.不等式2230x x +->的解集是( )A .{13}xx -<<∣ B .{31}xx -<<∣ C .{1xx <-∣ 或3}x > D .{3}xx <∣ 5.已知直线:30l x y +-=,椭圆2214x y +=,则直线与椭圆的位置关系是( )A .相交B .相切C .相离D .相切或相交二、填空题6.已知等比数列{}n a 的前n 项和为n S ,42S S =2,则数列{}n a 的公比q = . 7.若实数列1,a ,b ,c ,4是等比数列,则b 的值为 .8.已知a ,b ,c 为ABC 的三边,120B =︒,则222a c ac b ++-= . 9.已知1x >,函数41y x x =+-的最小值是 .. 10.在等差数列{a n }中,a 2=1,a 4=3,则a 3= .三、解答题11.已知曲线 y = x 3 + x -2 在点 P 0 处的切线 1l 平行于直线4x -y -1=0,且点 P 0 在第三象限, ⑴求P 0的坐标;⑵若直线 1l l ⊥ , 且 l 也过切点P 0 ,求直线l 的方程.12.求适合下列条件的抛物线的标准方程: (1)过点()6,6M -;(2)焦点F 在直线:3260l x y --=上 .第八章 综合作业二(寒假第8天)一、选择题1.已知{}n a 中,11a =,112n n a a +=,则数列{}n a 的通项公式是( ) A .2n a n = B .12n a n =C .112n n a -=D .21n a n=2.若数列{}n a 是等比数列,且17138a a a =,则311a a =( ) A .1B .2C .4D .83.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,右a =1,c =2,∠B =600,则b =( ) A .1BC.D .24.已知ABC 的内角,,A B C 的对边分别为,,a b c ,若2a =,b =c =,则C =( )A .3π B .23π C .34π D .56π 5.已知不等式210ax bx +->的解集为{|34}x x <<,则a b +=( ) A .12B .12-C .34D .34-二、填空题6.若关于x 的二次不等式210x mx ++≥的解集为实数集R ,则实数m 的取值范围是 . 7.若0a >,0b >且240a b +-=,则12a b+的最小值为 . 8.数列{}n a 的前n 项和28n S n n =-,则该数列的通项公式为 .9.已知等差数列{a n }满足a 1=1,a 2=2,则{ a n }的前5项和S 5= . 10.求111112233420192020++++=⨯⨯⨯⨯ .三、解答题11.若实数x ,y 满足约束条件02030x y x y x -≥⎧⎪++≥⎨⎪-≤⎩(1)在平面直角坐标系中画出此约束条件所表示的平面区域; (2)若2z x y =-,求z 的最大值.12.如图,已知△ABC 中,AB =362,∠ABC =45°,∠ACB =60°.(1)求AC 的长;(2)若CD =5,求AD 的长.第九章 综合作业三(寒假第9天)一、选择题1.“3x >”是“5x >”成立的是( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件2.若p :1x >,q :12x <<,则p 是q 成立的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件3.椭圆2213y x +=的焦点坐标是( )A .()2,0,()2,0-B .),()C .(,(0,D .()0,2,()0,2-4.已知双曲线2222:14x y C t t-=,则双曲线C 的离心率是( )A .2B C D 5.函数()25xf x e x =-+的图像在点()()0,0f 处的切线方程是( ) A .60x y +-= B .60x y --=C .60x y ++=D .60x y -+=二、填空题6.抛物线2x y =-的准线方程是 .7.抛物线的焦点为椭圆22154x y +=的右焦点,顶点在椭圆的中心,则抛物线方程为 .8.已知函数()ln f x x x =,则()y f x =的极小值为 .9.已知0a >,函数3()2f x x ax =-在[1,)+∞上是单调增函数,则a 的最大值是 .10.已知方程22153x y m m +=-+表示椭圆,则m 的取值范围为 .三、解答题11.求与椭圆221259x y +=有相同焦点,且过点的椭圆的标准方程.12.求导:(1)()33cos f x x x x =+;(2)()212x x f x ee e -+=++第十章 综合作业四(寒假第10天)一、选择题1.已知角α的终边上有一点()1,2P -,则tan α的值为( ) A .-2B .12-CD. 2.已知向量(1,2)a =,(2,1)b =-,则a b +等于( ) A .(3,1)--B .(1,3)-C .(1,3)D .(3,1)3.sin160cos10cos20sin10︒︒+︒︒=( ) A. B .12-C .12D.24.已知直线过()31A m +,,()4,21B m +两点且倾斜角为56π,则m 的值为( )A.BC.3-D.35.已知直线210x ay +-=与直线(2)20a x ay --+=平行,则a 的值是( )A .23-B .23-或0 C .0或32D .32二、填空题6.函数f (x )=a x +1+1(a >0且a ≠1)的图象恒过定点 . 7.函数2()log (3)f x x =-的定义域为 .8.设函数()122,11log ,1x x f x x x -⎧≤=⎨->⎩,则()4f f =⎡⎤⎣⎦. 9.函数()1lg 2y x =-的定义域为 .10.已知实数x ,y 满足2525x y x y x ≥⎧⎪≤-⎨⎪≥-⎩,则2z x y =-的最大值为 .三、解答题11.已知对数函数()log (0,1)a f x x a a =>≠的图象经过点(9,2). (1)求函数()f x 的解析式;(2)如果不等式(1)1f x +<成立,求实数x 的取值范围.12.在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知8b =,3c =,3A π=.(1)求a ;(2)求ABC 的面积.第十一章 综合作业五(寒假第11天)一、选择题1.已知集合{}2,3,4A =,{}2,5B =,则A B =( )A .{}5B .{}1,2,5C .{}2D .∅2.函数()()2lg 4x f x x -=-的定义域是( ) A .()2,4 B .()3,4C .()(]2,33,4 D .[)()2,33,43.已知函数21,0(),0x x f x x x +≥⎧=⎨<⎩,则()()1f f -=( )A .2B .1C .0D .124.与函数y x =表示同一个函数的是( ) A .2y x =B .2y xC .2log 2xy =D .2log 2xy =5.如果直线l 的倾斜角为6π,则该直线的斜率为( ) A .12B .33C .32D 3二、填空题6.点()2,3P 到直线320x -=的距离为 .7.如图,1111ABCD A B C D -为正方体,异面直线AD 与1CB 所成的角为_ . 8.已知向量4,a m m ⎛⎫= ⎪⎝⎭,(),4b m m =--,若//a b ,则m = . 9.已知1tan 2α=,则2cos πcos 22αα=⎛⎫- ⎪⎝⎭ . 10.函数224y x π⎛⎫=- ⎪⎝⎭的最小正周期为 .三、解答题11.已知数列{}n a 满足11(1)(1)3()n n n n a a a a ++--=-,12a =,令11n n b a =-. (1)证明:数列{}n b 是等差数列; (2)求数列{}n a 的通项公式.12.在ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若2222sin sin sin sin sin 3A CB AC +-=,2c =. (1)求sin B 的值;(2)设D 在BC 边上,且2BD AD DC ==,求ABC 的面积.第十二章 综合作业六(寒假第12天)一、选择题1.平面上动点M 到点F (3,0)的距离等于M 到直线l :x=-3的距离,则动点M 满足的方程是( ) A .y 2=6xB .y 2=12xC .x 2=6yD .x 2=12y2.命题“x R ∀∈,2210x x ++>”的否定是( ) A .0x R ∃∈,使得200210x x ++> B .0x R ∃∈,使得200210x x ++≤ C .x R ∀∈,2210x x ++≤ D .x R ∀∈,2210x x ++<3.已知点P 为双曲线2214y x -=右支上一点,12,F F 分别为双曲线左右焦点,若2||4PF =,则1||PF =( )A .2B .3C .5D .64.若点P 在抛物线2y x =上,点Q 在圆M :()2231x y -+=上,则|PQ|的最小值是( )A 1B 1-C .2D .12- 5.已知函数()f x 的导函数为()'f x ,且满足()3(1)ln f x xf x '=+,则(1)f '=A .12-B .12C .1-D .e二、填空题6.设函数e ()xf x x a =+.若(1)4e f '=,则a = .7.已知函数f (x )=2f π⎛⎫'⎪⎝⎭sin x +cos x ,则4f π⎛⎫' ⎪⎝⎭= . 8.已知点F 1(4-,0)和F 2(4,0),一曲线上的动点P 到F 1,F 2的距离的差的绝对值是6,该曲线方程是 .9.已知双曲线的方程为2213x y -=,则焦点到渐近线的距离为 .10.函数32()34f x x x =-+在x = 处取得极小值.三、解答题11.已知函数()()ln ,f x x a x a R =+∈. (1)讨论函数()f x 的单调性; (2)当1a =时,如果函数()()212g x f x x tx =++在定义域内单调递增,求实数t 的取值范围.12.已知椭圆的两个焦点坐标分别是()2,0-,()2,0,并且经过点53,22⎛⎫- ⎪⎝⎭. (1)求椭圆的标准方程;(2)若直线1y x =+与椭圆交于A 、B 两点,求AB 中点的坐标和AB 长度.第十三章 综合作业七(寒假第13天)一、选择题1.若,,a b c ∈R 且a b >,则下列不等式一定成立的是( ) A .ac bc >B .2()0a b c ->C .11a b< D .22c a c b -<-2.不等式2230x x +->的解集是( )A .{13}xx -<<∣ B .{31}xx -<<∣ C .{1xx <-∣ 或3}x > D .{3}xx <∣ 3.已知等比数列{}n a 中,21274a a a =,数列{}n b 是等差数列,且77b a =,则311b b +=( ) A .3B .6C .7D .84.在等比数列{}n a 中,11a =,12q =,132n a =,则项数n 为( ) A .5B .6C .15D .165.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,右a =1,c =2,∠B =600,则b =( ) A .1BC.D .2二、填空题6.在ABC中,若3,4b c C π===,则角B 的大小为 .7.设等差数列{}n a 的前n 项为n S ,若533a a =,则64S S = . 8.已知等差数列{}n a 中,5a ,13a 是方程2610x x --=的两根,则7891011a a a a a ++++= .9.已知实数x ,y 满足不等式组2034802x y x y x +-≥⎧⎪-+≥⎨⎪≤⎩,则区域面积是 .10.数列{-n 2+12n -7}的最大项为第 项.三、解答题11.已知数列{}n a 是等差数列,其前n 项和为n S ,数列{}n b 是等比数列,且112a b ==,4427a b +=,4410S b -=.(1)求数列{}n a 与{}n b 的通项公式;(2)设n n n c a b =⋅,求数列{}n c 的前n 项的和n T .12.若二次函数()f x 满足()1()2f x f x x +-=,且()02f =. (1)求()f x 的解析式;(2)若不等式2()0f x mx mx -+>对于x ∈R 恒成立,求实数m 的取值范围.第十四章 综合作业八(寒假第14天)一、选择题1.下列函数既是幂函数又是偶函数的是( ) A .2()3f x x = B .()f x x =C .41()f x x =D .3()-=f x x2.已知函数()2141f x x -=- ()x R ∈,若()15f a =,则a 的值为( ) A .5B .6C .7D .83.已知直线420ax y +-=与直线250x y b -+=互相垂直,垂足为()1,c ,则a b c ++的值为( ) A .0B .-4C .24D .-224.函数()()2,0,2f x x x πωϕωϕ⎛⎫=+∈>< ⎪⎝⎭R 的部分图象如图所示,则ω的值是( ) A .4B .2C .65D .1255.已知数列{}n a 中,11a =,134n n a a -=+(n *∈N 且2n ≥),则数列{}n a 通项公式n a 为( ) A .13n -B .132n +-C .32n -D .3n二、填空题6.若2παπ<<且1cos 3α=-,则tan α= . 7.已知向量(,12,1)OA k =,(4,5,1)OB =,(,10,1)OC k =-,且A 、B 、C 三点共线,则k = .8.若关于x 的不等式()()0x m x n --≤的解集为{}24x x ≤≤,则m n += .9.在ABC 中,三个内角,,A B C 的对边分别为,,a b c .若5,4b B π==,tan 2C =,则c = .10.经过点((),P Q -的双曲线的标准方程为 .三、解答题11.已知命题p :22310x x -+≤和命题q :2(21)(1)0x a x a a -+++≤(1)若12a =,且p 和q 都是真命题,求实数x 的取值范围. (2)若p 是q 的充分不必要条件,求实数a 的取值范围.12.已知函数323()2f x x x a =-+的极大值为2. (1)求a 的值和()f x 的极小值; (2)求()f x 在2x =处的切线方程.第十五章 综合作业九(寒假第15天)一、选择题1.已知点P (-3,1),点Q 在y 轴上,且直线PQ 的倾斜角为120° ,则Q 点的坐标为( ) A .(0,2) B .(0,-2) C .(2,0)D .(-2,0)2.数列{a n }的通项公式a n =2n +5,则此数列( ) A .是公差为2的递增等差数列B .是公差为5的递增等差数列C .是首项为7的递减等差数列D .是公差为2的递减等差数列3.若a =(2,3),b =(―4,7),则a 在b 方向上的投影为( )A .5C .5D 4.在)2,0(π内,使x x cos sin >成立的x 取值范围为( ) A.)45,()2,4(ππππ B.),4(ππC.)45,4(ππ D.)23,45(),4(ππππ 5.设圆x 2+y 2-8x -9=0的弦AB 的中点为P (5,2),则直线AB 的方程为( ) A .2x -5y =0 B .2x -y -8=0 C .x +2y -9=0D .5x -2y -21=0二、填空题6.当a 为任意实数时,直线ax -y +1-3a =0恒过定点 .7.等比数列中S n =48,S 2n =60,则S 3n 等于 . 8.函数)32cos(π--=x y 的单调递增区间是 .9.若关于x 的不等式2260ax x a -+<的解集为(1,)m ,则实数m 等于 . 10.函数f (x )=x 3-15x 2-33x +6的递减区间为 .三、解答题11.已知tan()34πθ+=,求2sin 22cos θθ-的值.12.已知函数()2cos()(0)3f x x πωω=+>的最小正周期为π.(1)求ω的值; (2)求()f x 在,44ππ⎡⎤-⎢⎥⎣⎦上的取值范围.。
新人教版高二数学寒假作业
高二数学寒假作业6一、单选题1.如图,长方体ABCD -A 1B 1C 1D 1中,AA 1=AB =2,AD =1,E 、F 、G 分别是DC 、AB 、CC 1的中点,则异面直线A 1E 与GF 所成角的余弦值是A .0B .3 C .5D .15 2.已知空间四边形ABCD 中,AC=BD,顺次连接各边中点P,Q,R,S,如图,所得图形是( )A .长方形B .正方形C .梯形D .菱形3.在四面体O-ABC 中,G 1是△ABC 的重心,G 是OG 1上的一点,且OG=3GG 1,若OG =x OA +y OB +z OC ,则(x ,y ,z )为( )A .111,,444⎛⎫⎪⎝⎭B .333,,444⎛⎫ ⎪⎝⎭C .111,,333⎛⎫ ⎪⎝⎭D .222,,333⎛⎫⎪⎝⎭4.设平面上有四个互异的点A 、B 、C 、D ,已知(2)()0DB DC DA AB AC +-⋅-=,则ABC ∆ 的形状是 A .直角三角形B .等腰三角形C .等腰直角三角形D .等边三角形5.已知在平行六面体1111ABCD A B C D -中,过顶点A 的三条棱所在直线两两夹角均为60︒,且三条棱长均为1,则此平行六面体的对角线1AC 的长为 A 3B .2C 5D 66.设A ,B ,C ,D 是空间不共面的四点,且满足0AB AC ⋅=,0AC AD ⋅=,0AB AD ⋅=,则BCD ∆是 A .锐角三角形B .钝角三角形C .直角三角形D .不确定7.已知在正方体1111ABCD A B C D -中,P ,M 为空间任意两点,如果1111764PM PB BA AA A D =++-,那么点M 必( )A .在平面1BAD 内B .在平面1BA D 内C .在平面11BAD 内 D .在平面11AB C 内 8.已知向量a =(2,3),b =(k ,1),若a +2b 与a -b 平行,则k 的值是( ) A .-6B .-23C .23D .149.在四面体O -ABC 中,G 是底面△ABC 的重心,且OG =x OA +y OB +z OC ,则log 3|xyz |等于( )A .-3B .-1C .1D .310.点P 是矩形ABCD 所在平面外一点,且PA ⊥平面ABCD ,M ,N 分别是PC ,PD 上的点,且23PM PC =,=PN ND 则满足MN x AB y AD z AP =++的实数,,x y z 的值分别为( ) A .211,,366- B .211,,366- C .211,,366--D .211,,366--11.下列能使向量MA ,MB ,MC 成为空间的一个基底的关系式是( ) A .111333OM OA OB OC =++ B .MA MB MC =+ C .OM OA OB OC =++D .2MA MB MC =-12.若向量m 垂直于向量a 和b ,向量n a b λμ=+(λ,μ∈R 且λ,μ≠0),则( ) A .m n ∥ B .m n ⊥ C .m 不平行于n ,m 也不垂直于n D .以上三种情况都有可能 13.在如图所示的正方体中,下列各对向量的夹角为45°的是( )A .AB 与AC '' B .AB 与C A '' C .AB 与AD '' D .AB 与B A ''14.已知A 、B 、C 三点不共线,对平面ABC 外的任一点O ,下列条件中能确定点M 与点A 、B 、C 一定共面的是( ) A .OM OA OB OC =++ B .111333OM OA OB OC =++ C .1123OM OA OB OC =++D .2OM OA OB OC =--15.平行六面体1111ABCD A B C D -中,12,AM MC =1AM xAB yAD zAA =++,则实数x ,y ,z 的值分别为A .1,32,323B .2,31,323C .2,32,313D .2,31,22316.对于空间任意一点O 和不共线的三点A ,B ,C ,有如下关系:623OP OA OB OC =++,则( )A .四点O ,A ,B ,C 必共面 B .四点P ,A ,B ,C 必共面 C .四点O ,P ,B ,C 必共面D .五点O ,P ,A ,B ,C 必共面17.如图所示,在空间四边形OABC 中,,,OA a OB b OC c ===,点M 在OA 上,且2OM MA =,N 为BC 中点,则MN ( )A .121232a b c -+B .211322a b c -++ C .111222a b c +- D .221332a b c -+-18.已知()()1,2,1,1,2,1a a b =--=--,则b 等于( ) A .(2,-4,2) B .(-2,4,-2) C .(-2,0,-2)D .(2,1,-3)19.在空间直角坐标系中,P (2,3,4)、Q (−2,−3,−4)两点的位置关系是 A .关于x 轴对称 B .关于yOz 平面对称 C .关于坐标原点对称 D .以上都不对20.点(023)A -,,在空间直角坐标系中的位置是( ).A .在x 轴上B .在xOy 平面内C .在yOz 平面内D .在xOz 平面内 21.已知{},,a b c 是空间的一个基底,若p a b,q a b =+=-,则( ) A .a,p,q 是空间的一组基底 B .b,p,q 是空间的一组基底C .c,p,q 是空间的一组基底D .,p q 与,,a b c 中的任何一个都不能构成空间的一组基底 22.在正方体1111ABCD A B C D -中,有下列命题:①221()3||AA AD AB AB ++=;②1111()0AC A B A A ⋅-=;③1AD 与1A B 的夹角为60︒.其中正确的命题有 A .1个 B .2个C .3个D .0个二、填空题23.在等边三角形ABC 中,点P 在线段AB 上,满足AP AB λ=,若CP AB PA PB ⋅=⋅, 则实数λ的值是___________.24.如图,点M 为OA 的中点,{},,OA OC OD 为空间的一个基底,DM xOA yOC zOD =++,则有序实数组(x ,y ,z )=________.25.在空间直角坐标系中,点(2,4,3)M --在xOz 平面上的射影为点1M , 则1M 关于原点的对称点坐标是________.三、解答题如图所示,在正方体ABCD -A 1B 1C 1D 1中,点E ,F ,G 分别是AB ,BC ,A 1C 1的中点。
山东省春节高二数学寒假作业天天练 练习(第7天) 新人教版
均值不等式一、基础知识:1、均值不等式(均值定理):如果0,0>>b a ,那么2____b a ab +,当且仅当_____ 时等号成立.2、若b a ,是正数,则2b a +叫做_______________,ab 叫做_______________,均值不等式也可表述为_________________________________.3、已知0,0>>y x ,则(1)若s y x =+(和为定值),则当______时,积xy 取最大值______;(2)若p xy =(积为定值),则当______时,和y x +取最小值______。
二、巩固练习:1、已知0<ab ,则b aa b +有( )A.最小值2B.最小值-2C.最大值-2D.最大值22、下列函数中,最小值为2的是( ) A.)0(,1≠+=x x x y B.)101(,lg 1lg <<+=x x x y C. )20(,sin 1sin π<<+=x x x y D.xx y -+=223、设0>x ,则x x y 133--=的最大值是( )A.3B.233-C.323-D. -14、设10,10<<<<b a ,且b a ≠,下列各式的值最大的是( )A.22b a +B.b a +C.ab 2D.ab 25、设实数b a ,满足3=+b a ,则b a 22+的最小值是( ) A. 24 B. 6 C. 62 D. 86、设正数y x ,满足404=+y x ,则y x lg lg +的最大值是( )A.40B.10C.4D.27、若0,0>>y x 且2=++xy y x ,则y x +的最小值为( ) A.23B.13+C.232-D.32-8、设+∈>>N n c b a , ,且c a nc b b a -≥-+-11恒成立,则n 的最大值是()A.5B.4C.3D.29、若+∈N y x ,,且14=+y x ,则xy 的最大值为_______10、函数xx y 3+=的值域为____________________ 11、若0,0>>b a 且ab b a =++8,则b a +的最小值为_______12、若直角三角形的周长为1,则它的面积的最大值为_________13、已知0,0>>b a ,且1=+b a ,求证:9)11)(11(≥++b a14、(1)已知21>x ,求函数128-+=x x y 的最小值及取得最小值时的x 的值; (2)已知0,0>>y x ,且191=+yx ,求y x +的最小值15、某水产养殖场拟造一个平面图为矩形且面积为160平方米的水产养殖网箱,为了避免混养,箱中要安装一些筛网,平面图如图示.如果网箱四周网衣(图中实线部分)建造单价为每米长112元,筛网(图中虚线部分)的建造单价为每米长96元,网箱底面建造单价为每平方米.长米(1)把建造网箱的总造价y (元)表示为网箱的长x (如图示,单位为米)的函数,并求出最低造价;(2)若要求网箱的长与宽都不能超过15米,则当网箱的长与宽各为多少米时,可使总造价最低(精确到0.01米)?参考答案:1. C2. D3. C4. B5. A6. D7. C8. B9. 161 10. ),32[]32,(+∞--∞ 11.8 12.4223- 13.证明:1,0,0=+>>b a b a 41)2(2=+≤∴b a ab ab ab b a ab b a b a 111111)11)(11(+++=+++=++∴98121=+≥+=ab当且仅当21==b a 时,式中等号成立 14. 解:(1)设0,21,12>∴>-=t x x t , 29218222182821=+⋅≥++=++=∴t t t t t t y 当且仅当t t 82=即4=t 也即25=x 时取“=”,29m i n =∴y (2) 0,0>>y x ,且191=+yx 16106109)91)((=+≥++=++=+∴yx x y y x y x y x 当且仅当y x x y 9=,又191=+yx ,即12,4==y x 时上式取“=” 故当12,4==y x 时16)(min =+y x15. 解(1)160100)3160(96)21602(112⨯+⨯++⨯+=xx x x y 2624016000)256(320≥++=xx 当且仅当x x 26=即16=x 时上式取“=” 所以网箱长16米时总造价最低,最低造价26240元 (2)⎪⎪⎩⎪⎪⎨⎧≤≤>15160150xx x 15332≤≤∴x 设)15332(,256)(≤≤+=x x x x g ,任取]15,332[,21∈x x 且21x x < 则)2561)(()()(212121x x x x x g x g --=- 1533221≤<≤x x ,02561,02121<-<-∴x x x x )()(21x g x g >∴)(x g ∴在]15,332[上是减函数 所以当15=x 时)(x g 有最小值.故当网箱长15米,宽约为10.67米时,可使总造价最低。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元二次不等式与二元一次不等式(组)
一、基础知识:
1、 一般地,含有___个未知数,且未知数的最高次数为____的不等式叫一元二次不等式.
3、含有___个未知数,并且未知数的次数是____次的不等式叫二元一次不等式,使不等式成立的未知数的值叫不等式的解,解构成的集合称为解集,它的解集对应着平面上的一个_________.
4、一般地,二元一次不等式0>++C By Ax ,在平面直角坐标系中,表示直线
0=++C By Ax 某一侧所有点的_________.对于直线0=++C By Ax 的同一侧的所有点),(y x 实数C By Ax ++的符号______,所以只需在直线某一侧任取一点),(00y x 代入C By Ax ++,由C By Ax ++00的符号即可判断出0>++C By Ax 表示的是直线的哪一
侧的点集. 5、一般地,在线性约束条件下求线性目标函数的最大值或最小值问题,称为___________问题,满足线性约束条件的解叫做________,由所有可行解组成的集合叫做________,使目标函数取得最大值或最小值的可行解叫做该问题的_________. 二、选择题: 1、不等式
01
2≥+-x x
的解集是( ) A.]2,1()1,(---∞Y B.[-1,2] C.),2()1,(+∞--∞Y D.(-1,2]
2、已知关于x 的方程0)3(2
2
=+-+m x m x 有一个根大于1,而另一个根小于1,那么实数m 的取值范围是( )
A. (-2,1)
B. ),1()2,(+∞--∞Y
C. (-1,2)
D. ),2()1,(+∞--∞Y
3、不等式02
<--b ax x 的解集为}32|{<<x x ,则不等式012
>--ax bx 的解集为( ) A.}23|{-<<-x x B.}2131|
{<<x x C.}3
1
21|{-<<-x x D. 空集 4、下面给出的四个点中,到直线01=+-y x 的距离为22
,且位于⎩
⎨⎧>+-<-+0101y x y x 表示的平
面区域内的点是( )
A.(1,1)
B.(-1,1)
C.(-1,-1)
D.(1,-1)
5、在平面直角坐标系中,不等式组⎪⎩
⎪
⎨⎧≥≥+-≤-+00202y y x y x 表示的平面区域的面积是( )
A.24
B.4
C.22
D.2
6、如果实数y x ,满足约束条件⎪⎩
⎪
⎨⎧≤-≥+-≥-3311y x y x y x ,则目标函数y x z +=4的最大值为( )
A.4
B.11
C.12
D.14
7、若实数y x ,满足不等式组⎪⎩
⎪
⎨⎧
≥--≥-≥0
2200y x y x y ,则11+-=x y u 取值范围是( )
A.]31,1[-
B.]31,21[-
C.),21[+∞-
D.)1,2
1[- 8、设111,,c b a ,222,,c b a 均为非零实数,不等式0112
1>++c x b x a 和 0
222
2>++c x b x a 的解集分别为集合M 和N ,则“
2
1
2121c c b b a a ==”是 “M=N ”的( ) A.充分不必要条件 B. 必要不充分条件 C.充要条件 D.既不充分也不必要条件
9、变量y x ,满足条件⎪⎪⎩⎪
⎪⎨⎧≥≥≥+≥+≥+0
,024*********y x y x y x y x ,则使y x z 23+= 取
得最小值的最优解为______
10、如图所示A(1,0),B(0,1),)5
4
,32(C ,目标
函数y ax t -=的可行域为四边形OABC ,若当
且仅当5
4
,32==
y x 时目标函数t 取得最小值,则 实数a 的取值范围是_______
11、关于x 的不等式04)2(2)2(2
<----x a x a 对任意实数恒成立,则实数a 的取值范围为_______
12、某产品的总成本y (万元)与产品x (台)之间的函数关系是2
1.0203000x x y -+=,其中)240,0(∈x 若每台产品的售价是25万元,则生产者不亏本(即销售收入不小于总成本)时的最低产量为______
13、(1) 已知实数y x ,满足⎪⎩
⎪⎨⎧≥+-≤-≥+052535
2y x y x y x ,求2
2)1()1(+++=y x u 的最大值和最小值;
(2)若二次函数)(x f y =的图像过原点,且2)1(1≤-≤f ,4)1(3≤≤f ,求)2(-f 的取值范围.
14、解关于x 的不等式)0(,01)1(2
≥<++-a x a ax
15、某人上午7:00时,乘摩托艇以匀速v 海里/时)204(≤≤v 从A 港出发到相距50海里的B 港去,然后乘汽车以匀速w 千米/时)10030(≤≤w 自B 港向距300千米的C 市驶去,要求在当天16:00时到21:00时这段时间到达C 市.设汽车、摩托艇所需要的时间分别是y x ,小时.
(1)作图表示满足上述条件的y x ,的范围;
(2)如果已知所要的经费:)8(2)5(3100y x p -+-+=(元),那么w v ,分别是多少时,所要的经费最少?此时需花费多少元? 答案:
1. D
2. A
3. C
4. C
5. B
6. B
7. D
8. D
9. (3,6) 10. 10
3
512-<<-
a 11. 22≤<-a 12. 150 13.(1) 4,3==y x 时取得最大值且41max =u ,1,2==y x 时取得最小值且13min =u (2) 10)2(6≤-≤f
14. 当0=a 时解集为}1|{>x x ;当10<<a 时解集为}1
1|{a
x x <<;当1=a 时解集为空集;当1>a 时解集为}11
|
{<<x a
x
15.(1)y x ,满足的约束条件是⎪⎩⎪⎨⎧≤+≤≤
≤≤≤14
9225
2
5103y x y x ,图略 (2)当4,10==y x 时,p 最小,此时30,5.12==w v ,93min =p 元。
